Vortex Lattice Formation in Spin–Orbit-Coupled Spin-2 Bose–Einstein Condensate Under Rotation

Abstract

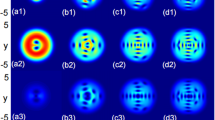
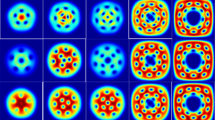
We investigate the vortex lattice configuration in a rotating spin orbit-coupled spin-2 Bose–Einstein condensate confined in a quasi-two-dimensional harmonic trap. By considering the interplay between rotation frequency, spin–orbit couplings, and interatomic interactions, we explore a variety of vortex lattice structures emerging as a ground state solution. Our study focuses on the combined effects of spin–orbit coupling and rotation, analyzed by using the variational method for the single-particle Hamiltonian. We observe that the interplay between rotation and Rashba spin–orbit coupling gives rise to different effective potentials for the bosons. Specifically, at higher rotation frequencies, isotropic spin–orbit coupling leads to an effective toroidal potential, while fully anisotropic spin–orbit coupling results in a symmetric double-well potential. To obtain these findings, we solve the five coupled Gross–Pitaevskii equations for the spin-2 BEC with spin–orbit coupling under rotation. Notably, we find that the antiferromagnetic, cyclic, and ferromagnetic phases exhibit similar behavior at higher rotation.

Appendix

The single-particle Hamiltonian for case I is

$$\begin{aligned} H_{\textrm{rot}}= \left( \frac{\hat{p}_x^2+ \hat{p}_y^2}{2} + \frac{x^2+y^2}{2}-\Omega L_z\right) \times {\mathbbm {1}}+\gamma _x S_x p_x, \end{aligned}$$

(17)

Under a unitary transformation the $H_{\textrm{rot}}$ can be diagonalised, which has the eigenvalues

$$\begin{aligned} E_{\pm 2}(k_x,k_y)&=\frac{1}{2} \left[ k_x^2+k_y^2 \pm 4\gamma _xk_x\right] -\Omega (xk_y-yk_x), \end{aligned}$$

(18a)

$$\begin{aligned} E_{\pm 1}(k_x,k_y)&=\frac{1}{2} \left[ k_x^2+k_y^2 \pm 2\gamma _xk_x\right] -\Omega (xk_y-yk_x), \end{aligned}$$

(18b)

$$\begin{aligned} E_0(k_x,k_y)&= \frac{1}{2}(k_x^2+k_y^2)-\Omega (xk_y-yk_x), \end{aligned}$$

(18c)

The spectrum in Eqs. (18a)–(18b) around a minima can be described by a parabola of form $(k_x-k_{x\min })^2+(k_y-k_{y\mathrm min})^2+E_{\min }$, which describes the particle moving in an effective gauge field $(\textbf{A},\bar{\Phi })=(\{k_{x\min },k_{y\min },0\},E_{\min })$, where $\textbf{A}$ and $\bar{\Phi }$ are vector and scalar potentials, respectively [10, 11]. In the presence of rotation term $k_{x\min }, k_{y\min }$ and $E_{\min }$ become spatially dependent [10, 11]. Rewriting Eqs. (18a)–(18b) as

$$\begin{aligned} E_{\pm 2}(k_x,k_y)&=\frac{1}{2} \left[ (k_x\pm (2\gamma _x \pm y\Omega ))^2 +(k_y-x\Omega )^2\right] \nonumber \\&\quad +E_{\pm 2}^\textrm{min}(x,y), \end{aligned}$$

(19a)

$$\begin{aligned} E_{\pm 1}(k_x,k_y)&=\frac{1}{2} \left[ (k_x\pm (\gamma _x \pm y\Omega ))^2 +(k_y-x\Omega )^2\right] \nonumber \\&\quad +E_{\pm 1}^\textrm{min}(x,y), \end{aligned}$$

(19b)

$$\begin{aligned} E_0(k_x,k_y)&= \frac{1}{2}((k_x+y\Omega )^2+(k_y-x\Omega )^2)\nonumber \\&\quad +E_0^\textrm{min}(x,y), \end{aligned}$$

(19c)

where $\textbf{A}_{\pm 2} = \mp (2\gamma _x\pm y\Omega ,x\Omega ),\quad \textbf{A}_{\pm 1} = \mp (\gamma _x\pm y\Omega ,x\Omega ),\quad \textbf{A}_0 = (-y\Omega ,x\Omega )$, and $\bar{\Phi }_j = E_j^{\min }$ with ($j = 0,\pm 1,\pm 2$). The effective potentials, which are the sums of trapping and scalar potentials [10, 11], can now be written as

$$\begin{aligned} V_\textrm{eff}^{\pm 2}(x,y)&= \frac{1}{2}\left[ (1-\Omega ^2)(x^2+y^2)-4\gamma _x^2 \mp 4y \gamma _x\Omega \right] , \end{aligned}$$

(20a)

$$\begin{aligned} V_\textrm{eff}^{\pm 1}(x,y)&= \frac{1}{2}\left[ (1-\Omega ^2)(x^2+y^2)-\gamma _x^2\mp 2y \gamma _x\Omega \right] , \end{aligned}$$

(20b)

$$\begin{aligned} V_\textrm{eff}^0(x,y)&= \frac{1}{2}\left[ (1-\Omega ^2)(x^2+y^2)\right] . \end{aligned}$$

(20c)

From Eqs. (20a)–(20c), the effective potential curves correspond to $V_{\textrm{eff}}^{\pm 2}$ are the lowest lying depending on the region.