1 Introduction

Among the remaining interpretations of quantum mechanics, one particular element would appear to divide these interpretations into two classes—the retrocausal interpretations [1,2,3,4,5] and the non-retrocausal interpretations such as superdeterminism [6,7,8,9]. Experiments to date relying upon statistical analysis of data have not managed to settle this vital question of whether information can propagate backward through time. If retrocausality is indeed a reality of nature, surely this would allow for information paradoxes akin to the famous Grandfather paradox. However, the literature does not show any experimental tests to date that provide a clear solution to this paradox. We propose an experiment that attempts to set-up an instance of this paradox by introducing a feedback loop into the traditional DCQE photonic experiment.

Many of the most interesting and intriguing quantum optics experiments often rely on measuring an interference pattern across a plane. Typically, one must choose to perform either photon counting measurements, where detectors such as single-photon avalanche diodes (SPADs) [10] are used in a raster scan format, or simultaneous coverage of the plane with a traditional charge-coupled device (CCD) but at the cost of significant noise and the loss of photon counting ability. The introduction of superconducting detector arrays into such experiments allows both of the above to be achieved, providing coverage of a significant detection area with good spatial resolution, and allowing energy-resolving, photon counting with excellent time resolution. In this paper we provide one specific example of a classic quantum experiment that could significantly benefit from these superconducting detector technologies, and we postulate the insights that may be gained as a result.

2 The Delayed Choice Quantum Eraser

First proposed by John Wheeler as a thought experiment 43 years ago [11], the delayed-choice version of the famous Young’s slits experiment has intrigued physicists ever since. While Wheeler mainly focused on gravitational lensing effects by large-mass galaxies to produce two independent (time-delayed) beams of light from the same source, modern laboratory techniques quickly caught-up and began to realise his thought-experiment within just a few years. In 1982 a proposed design for a bench-top implementation of Wheeler’s idea was laid out and published [12]. It took some time for a physical implementation of this experiment to be carried-out, but at the turn of the century we began to see attempts to demonstrate this phenomenon in the lab [13]. Since then, the so-called delayed choice quantum eraser (DCQE) has been measured in ever-more sophisticated and precise ways. Anton Zeilinger’s group in Vienna have progressed this experiment by pushing the limits of the optical path-length difference (OPD) between the ‘signal’ and the (entangled) paired ‘idler’ photons [14]. As recent as 2017, others have tried to ‘tame’ the strangeness of the DCQE with theoretical descriptions showing that no experiments to date demonstrate any ambiguity in either the standard or de Broglie-Bohm pictures of quantum mechanics [15]. Yet, debate continues on the interpretations of the DCQE and the physics invloved. Two of the many competing ideas are the the retrocausal interpretations [1,2,3,4,5] and the non-retrocausal interpretations such as superdeterminism [6,7,8,9]. We believe that the extension to the DCQE proposed here will help settle this debate, and provide additional evidence for one or other interpretation.

A DCQE set-up allows one to investigate the strange consequences of the classic double-slit experiment by exploiting the effects of quantum entanglement. As claimed by the authors of previous studies (e.g. Kim et al. [16]), the DCQE allows the ’which-path’ or ’both-path’ information of a signal photon to be erased or marked by measuring its entangled twin in one of two ways, even after the detection of the signal photon. Previous experiments reported in the literature used a movable detector to raster-scan across the plane of the interference pattern. That approach relied on building-up sufficient photon statistics over time to show the wave-like or particle-like pattern on the detector plane. By substituting the sensor on the far-field image plane with a large-format array of superconducting photon counting detectors, deeper insights into the physics involved in the DCQE may be gained.

3 Proposed Extension to the DCQE

A particularly proven class of large-format superconducting detector arrays is the microwave kinetic induction detector (MKID) [17] which has been demonstrated for astronomy applications [18, 19] as well as applications not related to astronomy [20]. We propose to use an array of MKIDs, as they meet our requirements, and the author has significant experience working with these devices for astronomy applications. The MKIDs’ ability to simultaneously monitor the full image plane with < 1 microsecond time-resolution for each pixel and spatial resolution better than 100 \(\upmu \)m will open up new experimental tests not possible with room temperature photon counting detector technologies. While microwave kinetic inductor detectors (MKIDs) are suggested here, other technologies such as superconducting nanowire single-photon detectors (SNSPDs) may be well suited for similar experiments [21,22,23]. Indeed, SNSPDs may be better suited for the proposed experiment outlined here, if it is determined that higher time resolution is required, and energy resolution is deemed unnecessary. Although, the MKIDs’ energy-resolving ability to easily distinguish the higher-energy pump photons form the down-converted photons may well prove useful in the proposed experiment.

An array of MKIDs can sample the spatial domain to a resolution of better than 100 microns, while providing time resolution of around 100 ns on each pixel with effectively zero read noise. This ability to time-stamp photons with zero read noise allows each pixel to operate in a pulse-triggered format which gives rise to a mechanism to open or close the optical gate to the eraser section of the experiment. As such, if there was truly information going backward in time (as is claimed by some studies [16]), this new detection approach would potentially allow the observer to measure this process. How that would look exactly is unclear, and serves to point out the absurdity of this common interpretation of the DCQE experiment. Using a pulse-triggered approach to actively open/close the gate to the eraser allows one to set-up an analogue of the famous Grandfather paradox. It will be shown that an MKIDs-based DCQE can be used to test this measurement paradox realised by the author. This curiosity is realised by introducing a feedback loop into the DCQE apparatus. It seems that the common retrocausal interpretation of this experiment cannot predict what will happen when the measurements will be performed, and thus demands investigation through experimental test.

The DCQE typically relies on the employment of quantum entanglement. Thus, in sticking with similar experiments to date, the approach taken in this paper will use entangled photon states. Now, the most practical method to create entangled photon states is to use nonlinear down-conversion [24]. This technique typically utilises nonlinear crystals such as barium borate (BBO), whereby a monochromatic light source illuminates the crystal with wavelength \(\lambda _0\) thereby placing the crystal in an excited energy state. When the atoms within the crystal de-excite, a pair of down-converted photons (\(\lambda _{\mathrm{DC}}\)) are emitted, each with exactly half the energy of the incident photon (\(\lambda _{\mathrm{DC}} = 2\lambda _0\)). Now, given the difficulty in producing short-wavelength lasers, and the limits on the operational frequency range of nonlinear crystals, experiments to date have typically used blue or ultraviolet ’pump’ frequencies to excite the crystals, typically \(\lambda _0 \approx 350\) nm [13, 14]. The resulting down-converted photons will then each exhibit a wavelength of \(\lambda _{\mathrm{DC}} = 700\) nm, or red photons. The problem that commonly arises when trying to measure individual photons at these low-energies, is that conventional detector arrays such as CCDs simply can not reliably count individual photons due to read noise; the semiconductor energy band bap is the same order of magnitude as the energy of the photons themselves (\(\approx \) a few eV). As such, any noise contributions can be incorrectly interpreted as photon events, and only a large number of photon events can generate a reliable signal. This is obviously not ideal for photon-counting experiments (such as we would like to do with the quantum eraser). Some experiments have successfully gotten around this issue by using a photon-counting optical detector in a time-division multiplexed format to spatially sample the primary detection plane using a raster scan stage [13, 14]. However, this approach comes at the cost of an inability to simultaneously count photons at each spatial position on the primary detection plane. Time-division multiplexed here simply means that each point along the primary detection plane is measured at a separate moment in time. In contrast, the frequency-division multiplexing scheme that will be employed with the MKID array in the experiment proposed in this paper, allows each pixel to be monitored and readout simultaneously.

4 Experimental Design

4.1 Optical Train

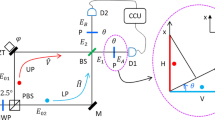
The basic optical lay-out of the proposed experiment is shown in Figs. 1 and 2. A pair of optical gates serve to either feed detectors D\(_1\) and D\(_2\) through reflection, or feed the ‘eraser’ apparatus (D\(_3\) and D\(_4\) ) through transmission. Experiments to date which aim to implement the‘delayed choice’ part of this system have focused on ensuring the optics which control the entangled idler photons are causally disconnected from the primary detection plane. Here, the concern is simply to ensure enough optical path length (OPL) in the idler path to allow enough time for the triggering electronic signals and shuttering mechanism to perofrm their operations. The minimum OPL can be determined with a standard light cone calculation. Effectively, for every 100 m of OPL, a causal time of 0.33 \(\upmu \)s results. By using a variable length of fibre optic cable for the propagation of the idler photons, we can adjust the ‘hang-time’ of the idler photons. Figure 3 shows a schematic of the proposed cryogenic set-up. The pump laser will be fed into the 4K stage of a 3-stage cryogenic system via a fiberoptic cable. Within the 4K stage, the pump photons will propagate through the 2 slits, and then illuminate the BBO crystal. The signal photons will illuminate the MKIDs, causing a change in readout signal amplitude and phase. The four feedlines will carry the signals to and from a radio-frequency system-on-chip (RF-SoC) integrated fpga and data converter board. One of the four feedlines, which will couple only to the pixels covering the nulls of the interference pattern, will have its signal split via a power divider, and half the power will be sent directly to the optical gate apparatus to trigger the optical gates to open. In this format, there will be an ability to calibrate and tune the readout signals using standard frequency division multiplexing techniques [25,26,27], while also allowing a direct signal path to the optical gates of the eraser apparatus for a much faster triggering process.

The Pockels effect [28] can be used for opening/closing the optical gate, triggered by an increase in power through the feedline to either provide a bias current (or not). Of course, the Pockels effect is dependent on polarisation, which may prove undesirable, or even problematic. Although, one could possibly exploit this polarisation effect imposed by the gate-state to play a role in the measurement under investigation (and control of same). This has precedent in other DCQE set-ups [14], and can indeed be useful for selecting/encoding states on photons. For now, we will assume we have a fast-acting mechanism to open/close the optical gate upon triggering by particular MKID pixels on the array. Mechanically rotating mirrors can potentially be used, by increasing or reducing the rotation speed in such a manner that it will transmit or reflect an incident photon. These active optical gate mechanisms will be investigated in future work.

Fig. 1
figure 1

(Color figure online) Schematic of the optical layout for the instance when the optical gate is closed, reflecting the ‘idler’ photons to the ‘which-way’ detectors D\(_1\) or D\(_2\). Since the ‘which-way’ information is known, no interference can be observed on the primary measurement plane. Throughout this paper, the ‘signal’ photons are those propagating in the upward-right direction toward the primary detection plane. The ‘idler’ photons are those propagating in the downward-right direction toward the eraser apparatus

Full size image
Fig. 2
figure 2

(Color figure online) Schematic of the optical layout for the instance when the optical gate is open, transmitting the ‘idler’ photons to the eraser detectors D\(_3\) or D\(_4\). Since the ‘which-way’ information is now scrambled, interference can now be observed on the primary measurement plane

Full size image
Fig. 3
figure 3

(Color figure online) Schematic of the planned cryogenic set-up, where everything within the green box is cryogenically cooled and under vacuum. The components in the red box represent the up and down-mixing electronics at room temperature, and the blue box represents a radio-frequency system-on-chip (RF-SoC) integrated fpga and data converter board for signal generation and processing (also at room temperature). The thick blue line going from the room temperature amplifier directly to the eraser gate apparatus represents the one feedline that cover the first four nulls in the interference pattern of the two slits (see the red feedline in Fig. 7). The HEMT within the 4K stage is a low-noise high electron mobility amplifier. The thick red lines represent the fiber optic lines that feed-in the pump photons (left side), and the two fiber optic lines that allow the idler photons to propagate out of the cryostat to the room temperature optical delay line and eraser apparatus

Full size image

4.2 Detector Array Format and Readout

We propose to place an array of MKID detectors along the primary detector plane. The array will consist of 256 pixels in the direction of interference, x, and 32 pixels in the direction of uniform bands, y. The pixels will have a centre-to-centre separation of \(100\times 100\) \(\upmu \)m, which includes the space required for the CPW (co-planar waveguide) feedlines - the remaining detector requirements can be seen in Table 1.This array of 8192 pixels can be readout with four feedlines (2048 per line) over the RF frequency range 4–8 GHz [25,26,27]. Figure 4 illustrates how pixels along the column 3 (\(D_S1,3\)), etc. could be used to trigger the eraser gate to open. Since these pixels should be dark when the eraser is open/on (in an idealised interference pattern), they should not have been able to trigger the gate to open in the first place. Again, this results in somewhat of a paradox.

Table 1 Detector Requirements - the energy resolution value of '>2' (Optional) corresponds to a potential use of energy resolving ability, where a resolution of 2 will be sufficient
Full size table
Fig. 4
figure 4

(Color figure online) Illustration showing the dimension of the proposed MKID array, with an example interference pattern overlaid. The interference pattern and its dimensions are not accurate here, and it is for illustrative purposes only

Full size image

The response time for MKIDs can be tailored to a below 1 microsecond, where here the response time is defined as the time required for the pulse maximum to be reached. It should be noted that the term response time often describes the rise-time and fall-time together (or Cooper pair breaking/recombination, respectively). While the fall-time (typically between 10s to 100s of microseconds for MKIDs) can limit the time resolution of a device in a high-flux environment, this is not a concern for the experiment described in this paper as the source can be attenuated to extremely low intensities. Indeed, single-photon propagation through the system is desirable here, so only the pulse rise-time is important. While writing the current paper, the MKIDs under study were quarter-wavelength microstrip design, and demonstrated a relatively slow rise-time (roughly 7 \(\upmu \)s). The lumped element MKIDs currently under development at the Dublin Institute for Advanced Studies (DIAS) can yield response times of a less than 1 microsecond, dependent on materials chosen and operational temperature. However, the full rise time is not required for triggering the gate. Once a set threshold value in amplitude or phase is surpassed, the triggering process can initiate. If the rise above threshold is ultimately tracked back to a noise fluctuation or a cosmic ray, the data point can be excluded in post-processing. If, however, the response time of the MKIDs cannot be increased to that required for this experiment, then other, faster superconducting detector technologies such as SNSPDs [21,22,23] will be considered as a replacement detector technology (Fig. 5).

Fig. 5
figure 5

(Color figure online) A colour-coding for the different sections of the expected interference pattern. Each rectangular colour block corresponds to 256 pixels, 16 in the horizontal direction (across the interference pattern), and 32 in height (in/out of the screen in reality)

Full size image

The detectors for the idler photons on both the ‘which-way‘ sensors and the ‘eraser’ sensors will be standard room-temperature single-photon avalanche diodes (SPADs) [10]. No novel detector technology is required for this part of the set-up.

5 Measurement Paradox

It should be pointed out here that the default ‘setting’ of the signal photons (i.e. if we did absolutely nothing to the idler photon, and let it propagate off through empty space) is to not show interference on the detector plane [14]. It would seem that the mere possibility that we may choose to measure the entangled partner at some point in the future is enough to destroy interference on the primary plane. So, we will focus on triggering the eraser to switch ‘on’ from its default position of ‘off’ for the remainder of this paper (Figs. 6, 7).

Fig. 6
figure 6

(Color figure online) Illustration showing one manner in which the rows of detectors could be fed, with 2048 pixels per feedline

Full size image
Fig. 7
figure 7

(Color figure online) Pulse profiles for a red photon (\(\approx 680\) nm) and a blue (\(\approx 410\) nm) photon. The authors acknowledge the Netherlands Institute for Space Research (SRON), Utrecht, for loaning the MKID array to DIAS for purposes of calibrating the cryogenic and readout systems in the new MKID lab. The pulse data shown here was captured with the SRON MKID array

Full size image

As mentioned above, it is proposed to change the typically used 50/50 beam splitters (which randomly reflect/transmit the idler photons), with a controllable electro-optical gate (using the Pockell’s effect [28], for example), or a mechanically fast-rotating mirror. Either way, with an active gate, we can then employ the pulse-triggered method on the primary/interference plane to either open or close the gate to the eraser apparatus. Then, each time we detect a photon on a pixel corresponding to a low chance of interference (i.e. the photon would be striking on a null if there was interference), we can use that readout pulse as a trigger to ‘open the gate’ to the quantum eraser. Doing this should then erase the ‘which-path’ information, and thus interference should have taken place. As such, the detection should not have occurred in the first place to do the triggering, or at least there should have been a very low probability of the detection occurring, as shown in Fig. 9. Of course some level of statistical analysis will still be required, as there will be a non-zero chance of the initial detection either way. However, these statistics are well understood and predictable, and the measured photon-count statistics will inform on the physics at play, and potentially help to distinguish between the straightforward explanation in [15], the various retrocausal interpretations [1,2,3,4,5] and the non-retrocausal interpretations such as superdeterminism [6,7,8,9].

Figure 8 shows a 1-D cut through the expected results on the primary detection plane. If we endeavour to know the ‘which-way’ information, we of course lose coherence and observe the green line which is a linear sum of the diffraction patterns from each of the two slits (red and blue). If we choose not to measure the which-way information, we expect to observe the interference pattern denoted in black. Figure 9 shows how the difference in probability of a photon being detected (over the area of a typical MKID pixel) is orders of magnitude in difference, depending on whether you choose to measure the which-way information, or not. So much so, that a close-up of the tiny area that would be expected to be illuminated under interference is shown in Fig. 10, which corresponds to the small red box highlighted in Fig. 9. The footprint of a typical optical MKID is overlaid for illustrative purposes.

Knowing that the default ‘setting’ of the photons is to not be involved in interference [14], we can simply focus on the pixels that should be dark in the scenario where interference would occur. Focusing only on these columns of pixels, and having a dedicated feedline that drives only these pixels, we can use a change in signal throughput on this feedline to trigger the optical gate to the eraser to open. Once the gate is triggered to open, and the eraser apparatus is thus used to erase the ’which-way’ information, it thereby leads back to the paradox. Since the entangled partner-photon has gone through the eraser, and should therefore have allowed the interference pattern to show, these pixels along the null columns shouldn’t have been illuminated and thus should not have opened the gate in the first place (or should have had a very low probablity of doing so, at least).

Fig. 8
figure 8

(Color figure online) Realistic, simulated interference pattern for down-converted photons of wavelength 700 nm, propagated over 1 m optical path length from illumination of two 50 \(\upmu \)m wide slits separated by 100 \(\upmu \)m. In the figure, ‘Int.’ indicates interference, and ‘Diff.’ indicates diffraction

Full size image
Fig. 9
figure 9

(Color figure online) Realistic, simulated interference pattern for down-converted photons of wavelength 700 nm, propagated over 1 m optical path length from illumination of two 50 \(\upmu \)m wide slits separated by 100 \(\upmu \)m

Full size image
Fig. 10
figure 10

(Color figure online) An expanded view of the red-boxed area in Fig. 9. Only the width of the overlaid detector (and detector footprints) is relevant here, but a single pixel is shown as an example, where detector’s height would extend in/out of the screen. The single MKID in the bottom left was fabricated at the Dublin Institute for Advanced Studies (DIAS) and Trinity College Dublin

Full size image

6 Summary of Conclusions

Superconducting detector arrays, such as MKIDs, can offer a new window into DCQE experiments by enabling precise spatio-temporal measurements of photons. Our proposed technique should help distinguish between the straightforward explanation by Fankhauser [15], the various retrocausal interpretations, and the non-retrocausal interpretations such as superdeterminism. While researching for this paper, it was concluded that alternative detector technologies may well be better suited for such experiments; specifically superconducting nanowire single-photon detectors (SNSPDs). These SNSPD devices (and others) will be considered as the experiment is implemented in the coming months.