1 Introduction to COSMO Experiment

COSmic Monopole Observer (COSMO) [1] is a ground based cryogenic Martin–Puplett Interferometer to be operated in Dome-C, Antarctica, aiming at measuring the isotropic y-distortions of the cosmic microwave background (CMB) [2]. Such distortions are produced by physical processes commonly referred to as the thermal Sunyaev–Zeldovich (SZ) effect, arising from energy exchange between CMB photons and hot electrons along the thermal history of the Universe. However, to date, no isotropic spectral distortions have been detected at mm wavelengths, and the upper limit is \(\sim 10^{-5}\), as placed by COBE-FIRAS (1990) [3] and then confirmed by other experiments, i.e., the TRIS experiment [4].

COSMO exploits a cryogenic differential Fourier Transform Spectrometer (FTS) to measure the spectral brightness of the sky in two frequency bands, the low frequency channel at 120–180 GHz and the high frequency channel at 210–300 GHz. The instrument will measure the difference in brightness between the radiation coming from the sky and the radiation coming from the internal cryogenic reference blackbody. An ambient temperature spinning wedge mirror allows for fast sky modulation (2400 rpm expected) to remove the atmospheric emission and its fluctuations. There will be two focal planes equipped by 9 pixels for each array of multi-mode Kinetic Inductance Detectors (KIDs) [5, 6], which are designed to have a time constant of about \(\tau = 60\,\upmu \hbox {s}\). This time constant value requires a fast readout electronics: indeed the frequency noise of the detectors goes up to their maximum frequency, in the order of 3\(/\tau \). For this reason, together with the fast scanning mirror we need a fast readout electronics of about 60 kHz.

2 Readout Electronics

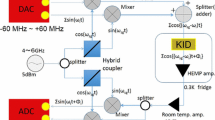
The system is based on a commercial bus architecture (PXI) developed by National Instruments. It is composed of two FPGAs Xilinx Virtex-5 NI7966R,Footnote 1 on PXI express bus operating two transceivers NI5791.Footnote 2 Two transceivers are used along with power combiners to double the RF bandwidth (see Fig. 1). The signal is digitally generated in the I-Q domain by the two FPGAs and converted to analog by the four Digital to Analog Converters (DACs) inside the transceivers. The two RF signals are added together by a Wilkinson power divider, attenuated by a programmable attenuator (PXI-5695), and fed into the cryostat. Stainless Steel and Niobium coaxial cables are used inside the cryostat to reduce thermal loading. The signal emerging from the KIDs is divided by another Wilkinson power divider, fed into the two transceivers’ inputs and I-Q detected. A schematic drawing of our readout is in Fig. 2.

Fig. 1
figure 1

Architecture of NI 5791 (picture taken from the NI data sheet)

Full size image
Fig. 2
figure 2

Block-diagram of our readout based on two NI transceivers (model 5791). The two outputs are added by a Wilkinson power divider (Narda 4426LB-2). After that, the sum signal is attenuated by a programmable variable attenuator (PXI-5695) to adjust the power level. The comb signal enters the cryostat by means of a vacuum feedthrough and a sequence of a Stainless Steel coaxial cable and a Nb coaxial cable to minimize the heat load. The same kind of cables are used to reach a second feedthrough. With this set-up there is no need for a LNA. The signals coming out of the cryostat are split with a second Wilkinson power divider before being fed into the two transceivers

Full size image

Our readout electronics operate as a finite state machine that works in three states. In the first state our algorithm performs a sweep to find the resonant tones of the KIDs. The sweep is made using an up-chirp signal varying the frequency over time. In the second state each resonant tones are generated by a COordinate Rotation DIgital Computer algorithm (CORDIC) [7], then added together to form a comb, which is acquired only once and thus it is saved in a look-up table. In the end, during the third state the signal is transmitted. We acquire I and Q signals so that we can easily evaluate the amplitude and phase in order to measure the variation of the working point of the KIDs. Each KID resonance frequency is evaluated by means of a Direct Down Converter (DDC) algorithm. This is the same approach used for the first time in the NIKA experiment [8]. This method was preferred to the poly-phase filter banks approach [9] because it is more computationally efficient and requires fewer resources with our small number of detectors.

We implemented a Graphical User Interface (GUI) using a LabView environment. Two examples of its functionalities are shown in Figs. 3 and 4. The presence of a GUI allows the user to monitor status and set FPGA parameters easily without modifying the software at lower levels. In addition, a real time plot of the amplitude helps to have a visual feedback during the first and the third state of the machine. It is also possible to manually set the comb frequencies, or to select peaks found during a sweep corresponding to resonator frequencies. The GUI also greatly simplifies the tuning of the input signal parameters such as the trigger, the output power or the number of samples to be used.

Fig. 3
figure 3

An example of the functionalities of our GUI, which is made to interactively control the readout electronics. The FPGA parameters can be set in the left box, while in the right one we can visualize the real time plot of the first (here), and third (see Fig. 4) state of the machine. We can also set the parameters of the state

Full size image
Fig. 4
figure 4

An example of the functionalities of our GUI, showing the comb signal (third state). The signal is depicted by using two colors, representing the two transceivers. We reported two different time instants in order to appreciate the amplitude variation with respect to the temperature oscillations (lowest level on the left, highest level on the right)

Full size image

In both Figs. 3 and 4, it is possible to see the 23 tones that we detect. We added a test tone for each FPGA, the frequency for the first one is 1.9030 GHz, and for the second one is 1.9760 GHz. Thus, we can receive and transmit 25 tones in total. We chose these values because at these frequencies the signal is not attenuated by any other close resonance. The presence of the test tones allows us to check the behavior of the resonant tones and to have an estimation of the noise.

3 Test Results

We use Niobium KIDs (designed at AstroParticule et Cosmologie in Paris and manufactured at Paris Observatory) to test our electronics with real devices. The transition temperature of these KIDs is around 9 K and their measured quality factors are higher than 5000 at 4.9 K. This is the working temperature of our cryostat maintained by an RDK-408 SHI GM cryocooler under the set-up heat load. The Q factor could be higher but, for the purpose of this study, it was enough to have well defined resonances with a frequency spacing around 5–10 MHz so we adopted this device that was optimized for other studies. However, the COSMO detectors will be made by Aluminum to be compliant with the frequency coverage of the experiment [10] and they will work in the 0.3 K COSMO cryostat.

To date, we can reach a sampling rate of around 8 kHz on the 25 frequencies (23 effective resonances plus two test tones) saving in HDF5 format. We are still a factor of 8 far from the COSMO requirements (18 detectors sampled at 60 kHz). To increase the sampling frequency we plan to improve the data saving with binary compressed format and to move the calculation of the amplitude and phase shift of each tone to the FPGA.

Due to the intrinsic mechanical oscillations of the cooler, the temperature has a fluctuations of \(\sim 20\) mK with a frequency \(\sim 1\) Hz, typical of the cooler. The temperature oscillations make the initial search for resonators difficult and for this reason we repeat the sweep multiple times. Indeed, in this way we can map the oscillations of the resonances and find the minimum transmission. This state corresponds to the minimum temperature achieved by the cryocooler with the installed set-up and consequentially gives the information about the tone of each resonance. Moreover, we can test some key parameters of the readout system with these oscillations. In fact, we use the temperature oscillations to verify that the system can track the tones during testing phase. Their presence is also a prominent feature that should be clearly visible in the phase time stream plot (Fig. 5) and can be used to evaluate the quality of our analysis.

Fig. 5
figure 5

Chunk of the phase timestream. The test tone (frequency 1.976 GHz) is depicted in orange, the resonant tone (2.00930 GHz) is in red and the temperature oscillations are in blue

Full size image

In Fig. 5, we present a chunk of the phase time stream. We decided to show only the tone at resonant frequency 2.00930 GHz because it is one of the deepest (− 11.264 dB), but we have obtained similar wave-forms for the other frequency tones. In the same plot we report the temperature fluctuations and we can notice a sync between this signal and the phase timestream. This evidence confirms that the KID responds correctly with respect to the variation of the quasi-particles density. On the contrary, we can also see the behavior of the test tone (frequency 1.976 GHz), which is not affected by the change of temperature, as expected.

By repeating the comparison between the test tone (1.976 GHz) and one resonant tone (2.00930 GHz), we analyzed different kinds of noise: the phase and IQ noise [\(\sqrt{I_{\mathrm{noise}}^2 +Q_{\mathrm{noise}}^2 }\)] of KIDs signal (Fig. 6), the noise arising from the cold loop back signal (Fig. 7) and the noise arising from the warm loop back signal (Fig. 8). With cold loop back we mean the signal passing through everything inside the cryostat, except the array of KIDS, while the warm loop back is the signal without passing through the cryostat.

Fig. 6
figure 6

Data noise. Upper plot: the phase noise of the best tone is plotted in blue, the one of the test tone is in red. Lower part: the noise of the IQ signal of the best tone is depicted in green, the one of the test tone is in orange

Full size image
Fig. 7
figure 7

Cold noise (loop back). Upper plot: the phase cold loop back of the best tone is plotted in blue, the one of the test tone is in red. Lower part: the cold loop back of the IQ signal of the best tone is depicted in green, the one of the test tone is in orange

Full size image
Fig. 8
figure 8

Warm noise (loop back). Upper plot: the phase warm loop back of the best tone is plotted in blue, the one of the test tone is in red. Lower part: the warm loop back of the IQ signal of the best tone is depicted in green, the one of the test tone is in orange

Full size image

In Fig. 6, the phase noise is shown in the upper part: as expected the resonant tone (2.00930 GHz) is higher than the test tone. Thus also the white noise level is higher compared to the test tone one. In addition, we can notice the presence of the 1 Hz peak also in the test tone. Indeed, as we can see in the cold loop back signal (in Fig. 7—upper part), the resonant tone and the test tone are very comparable and the 1 Hz peak is due to the presence of the Nb cables which transmission is slightly modulated by the temperature. Concerning the cold noise (without the presence of the KIDs) in Fig. 7, the white noise is lower compared to Fig. 6 since the signal is not attenuated by any resonant frequencies. The same consideration applies also looking at the warm loop back noise in Fig. 8. Looking at IQ signals, the noise is in Fig. 6—lower part, while the cold loop back and the warm loop back are in Fig. 7—lower part and Fig. 8—lower part. The same considerations about the white noise applies here, with the exception of the cold loop back noise.

All the data were collected for about 30 min so that it is possible appreciate also the 1/f noise (on the right part of the plots). All the plots end at frequency of about 4 kHz, and thus our sampling rate is around 8 kHz.

4 Conclusion and Next Step

This contribution demonstrates that we can develop a working readout electronics for KIDs with a modular architecture using commercial devices which are capable of a bandwidth of 100 MHz per module and a sampling rate (still not optimized) of about more than 8 kHz for 23 effective resonators plus two test tones. The main advantage of our readout electronics is the access to hardware and software solutions which greatly reduce the time needed to achieve a working readout chain and to develop a Graphical User Interface.

In future, we are planning to use a single FPGA with a transceiver with a RF bandwidth wider than the sum of the two employed in this experiment. We also think that using a single FPGA could speed-up the sample rate because we will avoid the sharing of the data bus.

Finally, a complete NEP investigation will be performed on each single component (especially on the COSMO KIDs) in order to achieve better NEP performance. Indeed in the current version of our readout we are not using a LNA and thus the estimation of the noise can be overestimated.