1 Introduction

The SPICA telescope was a joint collaboration between the European and Japanese space organizations ESA and JAXA. The mission was designed as the newest space mission observing in the mid- and far-infrared, as a successor to the highly successful Herschel mission [1].

The satellite design supported a 2.5 m mirror, actively cooled to below 8 Kelvin in order to reduce the thermal radiation of the mirror itself. The three instruments on board operated in the mid- and far-infrared: SAFARI, SMI, and POL [1]. SPICA’s powerful detectors provide two orders of magnitude greater sensitivity compared to the previous-generation Herschel and SOFIA instruments, in part because the SPICA instruments are not limited by radiation coming from the telescope itself. This increased sensitivity would have enabled the SAFARI, POL, and SMI instruments to investigate the spectroscopic details of both close-by and far away galaxies in unprecedented detail [2,3,4,5,6].

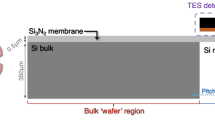
For the SAFARI instrument, there are four focal plane arrays (FPAs). To reach the mission requirements of extremely low noise, field of view, and Nyquist sampling of the spectra, each of these FPAs should hold around 4000 low noise TESs [7]. These TESs are made from Ti/Au patterned on an island of SiN, next to an absorber made of tantalum (Ta). This island is suspended to a Si wafer structure using four long SiN legs [8]. Above these islands are pyramidically shaped horns which focus the light on the TES and absorber. All important dimensions are also listed in [8].

Cosmic rays (CRs) originate either from the sun or at high energetic events outside of our solar system. The CRs at L2 orbit consist of \(89\%\) protons, as found by the Planck satellite [9]. The impact rate for all CRs at L2 as reported by [10] for the Herschel telescope is between 2.8 and 3.5 counts/s cm2, comparable to the rate found by Planck [9]. The energy distribution of these CRs extends over a large domain as can be seen in [11]. The SPICA design includes a cosmic radiation shield for protons less energetic than 35 MeV. Hence, we have a clear cut-off below the 35 MeV energy level.

This paper focuses on the introduced noise from the thermal heating of the wafer due to CR impact. When a CR hits either the supporting wafer or the suspending legs of the structure, it induces a thermal spike. The photon-induced power depends on the bath temperature \(T_\mathrm{bath}\). This bath temperature is the temperature of the suspending legs. Therefore, when these legs suffer from thermal spikes, there will be additional noise on the readout of the TESs.

2 Methods

The heat transfer simulation is conducted using COMSOL. The simulations shown in this work are conceptually close to earlier work by Marcel Bruin for SAFARI and a similar simulation for the X-IFU detector on Athena by [12].

The geometry was defined using the latest design provided by the SAFARI engineering team. The wafer is a perforated piece of pure silicon with outer dimensions of \(31\times 24\times 0.35\) mm\(^3\). The holes are in the z-direction, in the centre of which the TESs are suspended. Because of the symmetry and relative small size in the z-direction and computational restrictions, we use a 2D (x, y) model of the wafer.

At the beginning of the simulations, the whole wafer is initialized at a temperature of \(50\,\)mK. During the simulations, 26.7 CRs hit the wafer on average every second. This impact rate is calculated using the dimensions of the wafer and the rate of impact as given by [11].

The energy of the impacting CRs is randomly chosen from the energy distribution in [11]. To check whether the samples are a good representation of the distribution, we split the group of samples in half and calculated the total variation distance between both halves. When this total variation distance shrank below 0.05, both halves were similar enough to assume they were not dominated by outliers. The same assumption could subsequently be made for the group of samples as a whole, and we could treat the group of samples as a valid representation of the distribution as a whole. In this paper, we have a group of 128 samples that satisfy this condition. Each of these CRs has a random impact location and time assigned. The energy that each of these CRs would transfer to wafer after impact is calculated using the Bethe equation and considered as a heat event in the simulation.

Each CR is approximated as a circular heat source of \(r= 10^{-4}\,\)m with an exponential time behaviour [13]. With the two time constants controlling the exponential rise and fall time: \(t_f = 10^{-10}\) s and \(t_r = 10^{-10.5}\) s, respectively.

In the simulation, the time sampling is nonlinear around each pulse. The time stepping is chosen in order to minimize the total amount of steps, while still being able to resolve at least \(99.99\%\) of the energy pulse using trigonometric integration. This time stepping only controls the points for which the temperature data is extracted. For the internal calculation of these temperature profiles, the simulation model is free to determine smaller step sizes in order to converge with numerical errors within the imposed tolerances.

A connection to a heat sink can influence the calculation by extracting heat from the wafer and actively cooling the structure. The simulation is run both without any heat sink connection and with four heat sink connections of varying efficiency. The connection to the heatsink is simulated as an extra thin strip of silicon added at the boundary of the wafer. The arbitrary size of this strip influences the total heat capacity of the wafer but is small enough not to affect the cooling capacities for the same total thermal conductance. The difference in heat conductivity of the cooling connection is the main influence on the efficiency of the cooling capacities. Four final heat sink connections are simulated with the properties as shown in Table 1.

Table 1 Properties of the connection to the heat sink in separate simulations
Full size table

The TESs are influenced by thermal changes in the wafer because their base power is a function of the thermal bath. The TESs are biased at a fixed voltage and have a rest current flowing through them, combining into a base power. This base power is a function of both the temperature of the TES and the temperature of the bath around it. This \(T_\mathrm{bath}\) is the temperature of the wafer at the point of connection. The change in temperature on the wafer happens irregularly, so it presents itself as another noise source for the TESs. The base power follows the following equation [14]:

$$\begin{aligned} P_b = k(T_\mathrm{TES}^n - T_\mathrm{bath}^n) \end{aligned}$$
(1)

where n is the thermal conductance exponent and k a constant depending on the thermal conductance, n and the TES temperature. Typical numbers are given in Table 2. If the change in base power is equally discretized in time, it can be transformed using the discrete Fourier transform to the Noise Equivalent Power (NEP) with the equation below. The data from the simulations is nonlinear, with more temporal sampling around the start of each impact. Therefore, the equal sampling in the time domain is done using a numerical interpolation.

$$\begin{aligned} \mathrm{NEP} = \frac{P(f)}{\sqrt{\Delta f}} \end{aligned}$$
(2)

The measurements are done with a frequency of around \(100\,\)Hz as in [8]; so we highlight the NEP at this frequency in order to compare it with the other noise sources.

Table 2 Typical values for a dark TES [8]
Full size table

3 Results

To see the thermal increase due to the impact of CRs across the wafer, four different points on the wafer are probed. P1 is the central point, which is furthest from the cooling band. P2 and P3 lay at the extends of the legs on which the left outermost TES are suspended. The last point, P4, is chosen to lay exactly at the point of impact of an CR. These points are visualized in Fig. 1.

Fig. 1
figure 1

Points at which the thermal behaviour is measured in the simulations (P1–P4) are overlaid on the geometry in red. The small black circles are the locations where the CR impact the wafer. The numbers on the axes are the distance in meters from the centre of the wafer (Color figure online)

Full size image

When the connection to the heat sink is not simulated, the whole structure steadily heats up in time. The increase in temperature was analytically calculated, and verified by the simulation, to be \(0.001\,\)K per \(0.1\,\)MeV added energy from the CRs.

In Fig. 2, the thermal response of the different simulations is shown at the different points on the wafer. The spikes due to the near impacts show the same profile as the one without a heat sink. This outcome is expected because the initial cooling of these spikes is due to the spreading over the total wafer. It is interesting to note that, with the thermal external connection, the wafer is able to lose the extra energy resulting from each CR impact. For each of the simulated heat sink connections, the cooling rate is faster than the impact rate of the CRs and the wafer returns to 50 mK after each impact.

The thermal profiles are more dependent on the distance from the different CR impacts than to the efficiency of the thermal connection. The amplitude of the spikes, however, differs between the different heat sink connections. The effects on the amplitudes are most visible for P2 and P3. The closer a CR is to the heat sink, the sooner the cooling process starts. The CRs that induce the clearest heat surges at a measurement point are the CRs closest to the measurement point. Since point P2 and P3 lie close to the cooling boundary, the most significant CR impacts are also closer to the cooling boundary and more damped by the cooling connection. P1 is least affected by the fast dampening because it is at the centre of the wafer and thus relatively far from the boundary. On the other hand, P4 does not show this effect since it is completely dominated by the CR hit at its location, and the peak amplitude of that CR hit is only a function of its energy.

In Fig. 3, the cooling of a single CR impact is shown as dominated by the cooling efficiency. The difference in cooling rate becomes apparent both in peak amplitude and the cooling timescale. We define the cooling timescale as the time the wafer takes to reach the peak temperature and cool again to \(\frac{1}{e}\) times of the peak amplitude. Below we give the linear estimations of this quantity for all configurations.

The most efficient thermal connection displays the fastest cooling timescale (\(0.13\,\)ms) and lowest peak amplitude (\(50.051\,\)mK). The cooling timescale (\(0.26\,\)ms) and peak amplitude (\(50.48\,\)mK) of the medium heat sink follows. This succession is inline with our expectations.

Also, note that the thick and thin heat sink connections (resp. set-up 4 and 3) compare very well in both peak amplitude (respectively \(51.23\,\)mK, \(51.4\,\)mK) and time scale (respectively \(1.21\,\)ms, \(1.1\,\)ms). So we can conclude that the used set-up does not heavily depend on the arbitrarily chosen geometry of the heat sink connection, but rather on the thermal conductance of the heat sink.

Fig. 2
figure 2

The temperature variation in time for the different measurement points (P1–P4) on the rows and with the different thermal connections on the columns. The distribution of the peaks is mostly a function of the location of the measurement, while the total height of these peaks is determined mostly by the thermal connection (Color figure online)

Full size image
Fig. 3
figure 3

Close-up of the cooling time profile of the CR impact at \(3.742\,\)s as viewed from P2. This CR impact is the most central isolated impact. The cooling decay as viewed at P2 can be assumed to be dominated by the heat sink connection instead of thermal dissipation. The different thermal connections are displayed with different colours and markers. The time is shown logarithmically, starting from \(10^{-5}\,\)s when the temperature increase has spread to P2, until \(3\times 10^{-3}\,\)s when the peak is subsided in the two most efficient cases (Color figure online)

Full size image

Without a heat sink, the outcome is different. The structure cannot stabilize back to \(50\,\)mK after each CR impact. Therefore, the induced NEP at \(100\,\)Hz is on the order of \(10^{-17}\,\mathrm {W/\sqrt{Hz}}\), which is two orders of magnitude higher than the noise requirement for SAFARI.

In Fig. 4, the NEP of each point is plotted. The NEP requirement of \(2\times 10^{-19}\) is marked as well as the \(100\,\)Hz line. When the NEP is below this NEP level, the noise requirements of SAFARI can be met. We make use of multiple temporal interpolation resolutions to make sure that we are not limited by undersampling of the results of our simulations. The difference between different temporal interpolation resolutions is most evident in the second set-up. This difference is most likely due to the fact that the temperature increases are smallest for this set-up, so small numerical differences between interpolations with different resolutions will have a bigger impact on the calculation of the NEP.

Table 3 shows the weighted average of the NEP at \(100\,\)Hz at each point for each heat sink connection. Including a connection to the heat sink has an important effect on the total noise levels on the detector, which drops by at least an order of magnitude. The thermal connection with a \(G=2\times 10^{-6}\) is the set-up with the lowest noise levels, as could be expected. For this set-up, the noise is well below the requirement noise level for all points on the wafer. Finally, the thermal connection with \(G=2\times 10^{-8}\) does not cool efficiently enough and lies significantly above the noise requirement level for all measurement points.

Fig. 4
figure 4

The noise equivalent power (NEP) as a function of frequency. Each row displays a different heat sink connection and each column a different measuring location (P1–P4). The different colours depict different interpolation step sizes. This calculation is conducted as if there is a unique TES connected to each of these points (Color figure online)

Full size image
Table 3 The weighted average NEP level at \(100\,\)Hz for the different points and simulations
Full size table

4 Discussion

In this work, a cooling connection is implemented with an additional band of silicon around the wafer. Although the dimensions of this band do not show a significant effect on our results, this band is still a basic approximation of the actual thermal connection. Instead, wire bonds could be approximated with a golden band of comparable dimensions.

The design of the cooling connection is constrained by multiple factors such as cost and limited space, so there is a limited number of wire bonds available as well as a limited area to which they can be connected. Furthermore, more effects become important with a transfer of temperature between two metals, such as Kapitza coupling [12]. Follow-up research should take all these constraints and extra physics into account to give a more accurate estimation of the requirements of the thermal heat sink.

Another important issue is the connection between the wafer and other structures. The wafer is mounted on a larger structure with the read-out electronics, the LC-circuits, and an aluminium support structure. The mounting of the wafer to these structures is done using four golden clamps on the sides. It means that the induced heat from the CRs will be distributed over a larger structure, with a higher heat capacity. On the flip side, CR hits on these other parts will also reach the wafer. The complexity of these simulations desires more work. The work of [12] shows some of the additional upgrades to CR impact simulations in good detail, especially cooling through the golden wire bonding and the layer structure.

The final main caveat is the singular focus on the primary CRs and the neglecting of other particles. When a high-energy proton goes through the shielding, it will knock out some electrons as well. Using the simulation program GEANT4 designed for particle cascade simulations, [11] found that the secondary particles contribute about \(1.3\,\)counts/s/cm\(^2\) extra on the detector. However, the used impact rate by [11] is already around 1 counts/s/cm\(^2\) higher than found by Herschel and Planck. Therefore, the deviations caused by secondary particles are not expected to be high.

There are multiple other ways in which CRs might influence the detection and noise limits. Including direct hits on the TESs, hits on the suspending legs of the TES or hits on the LC-circuits connected to each TES. Each of these scenarios is beyond the scope of this study, but are important in creating an overview of all the complications with which CRs might influence the instrument in L2 orbit.

5 Conclusion

The goal for SAFARI is to have a sensitivity characterized by an NEP of \(2\times 10^{-19} \mathrm {W/\sqrt{Hz}}\). This high sensitivity is due to the TES detectors and the cooled mirror of SPICA itself. The noise levels for these TES detectors can be seriously dominated by cosmic rays as was seen previously at Planck and Herschel.

Using the simulation program COMSOL 5.4, we have created a 2D model of the structure on which the TESs are suspended. This structure was bombarded with 128 randomly generated cosmic rays following observed property distributions at L2. When no connection to the heat sink is implemented, the NEP effect due to this bombardment is shown to be \(10^{-17} \mathrm {W/\sqrt{Hz}}\).

Additionally, 4 different connections to the heat sink are simulated. The cooling in each simulation is mainly influenced by the thermal conductance, which determined its efficiency and cooling time scale. When the thermal conductance is \(2\times 10^{-7}\,\)W/K, the cooling was sufficient to keep the noise lower than the operating requirement for SAFARI on the whole wafer. With a 10 times less efficient cooling, the whole wafer experiences noise levels exceeding this requirement.

With this study, we show that the thermal noise due to CRs has a serious impact on the noise budget of SAFARI instrument. However, more research is desired as a follow-up study in three main areas:

  1. 1.

    A detailed study of the thermal connection to the heat sink and other thermally connected elements.

  2. 2.

    The precise energy distribution and impact rate of the CR after interaction with the shielding of the telescope.

  3. 3.

    A verification of the thermal simulations using proton and \(\alpha\)-particle sources.

These studies will show the feasibility of the desired sensitivity for SAFARI and comparable instruments in the future.