1 Introduction

Electrons and ions at the surface of liquid helium are examples of particularly well-defined two-dimensional (2D) Coulomb systems [1], which have been widely used as a model for studying fundamental phenomena like Wigner crystallization [2], magneto-transport [3] or transport in confined geometry [4]. Furthermore, they have served as probes for investigating the properties of helium, e.g., the superfluidity of liquid 3He [5,6,7] and the crystal growth of solid 4He [8]. Bare electrons can be trapped above the liquid helium surface, in a potential well provided by the (attractive) image potential due to the finite polarizability of helium, and the potential barrier of about 1 eV that the electrons encounter when penetrating into the liquid [9, 10]. Single-electron bubbles, on the other hand, which consist of an electron confined in liquid helium in a bubble of ~ 3 nm diameter [11], can be trapped below the liquid surface, in a potential well formed by the (in this case repulsive) image potential and an externally applied electric field of appropriate sign. The same is true for He+ ions, which form “snowballs” inside liquid helium [12, 13]. For other ions, in particular metals, which have been thoroughly studied in bulk liquid helium, mainly by spectroscopic means [14] this trapping at the liquid helium surface should also be possible; however, such investigations of ions other than He+ do not yet exist to the best of our knowledge.

In a homogeneous electric field, the charge density of an electron or ion pool at the liquid surface is limited to enc = (gργ/4π2)1/4 [15, 16], where e is the elementary charge, nc is the critical number density of the charges, γ is the surface tension, g the acceleration due to gravity, and ρ the density of the liquid (the vapor density can be neglected for the temperature range T < 2 K, which we consider in this investigation). For 4He at temperatures below the lambda point, this gives a maximum electron or ion density nc ~ 2.4 × 1013 m−2. Above this critical value, an electro-hydrodynamic (EHD) instability develops, connected with a soft mode in the dispersion relation of surface waves [17, 18]. The homogeneous distribution of charges then breaks up into a lattice of separated multi-electron dimples or multi-ion hillocks, with a lattice constant equal to the wavelength of the soft mode, λc = 2πa ~ 2 mm, where a = (γ/gρ)1/2 is the capillary length of helium. Upon further increasing the electric field, the charges undergo a collective breakthrough and form multi-electron bubbles in the liquid, or multi-ion droplets in the gas [19,20,21,22], each holding up to 106 elementary charges.

In this work, we describe our investigations of the critical charge behavior at liquid helium surfaces in inhomogeneous electric fields. For this purpose, we consider a metallic pin, placed slightly below or above the surface (for electrons or ions, respectively), to which a high voltage is applied, such that the charges accumulate near the pin and due to the electrostatic pressure deform the surface. The motivation for these studies was twofold:

  • Searching for Majorana quasi-particles at the surface of superfluid 3He [23], we planned to accumulate Ba+ ions below the liquid surface as a sensitive spectroscopic probe. Preliminary measurements with 4He, however, did not reveal any optical spectroscopic signal related to Ba+ trapped at the surface, although in bulk He spectra of these ions could be detected. We therefore intended to aggregate the ions in the inhomogeneous E field below the pin, thus increasing their density, and in addition learn about the total amount and the density of positive charges by an analysis of the surface deformation near the pin. It could indeed be shown—on the basis of the simulations described here in comparison with the observed charge-induced surface deformation—that pools containing up to 108 positive elementary charges could be accumulated under the liquid surface below the pin (see Fig. 1). As it turned out, however, the deformation was mostly due to charged Ba nanoparticles rather than Ba+ ions. These investigations are described in more detail in Ref [24].

  • A second motivation is that up to now experiments with surface state electrons (SSE) on bulk helium have been restricted by the EHD instability to the “low-density” non-degenerate regime where the electrons behave purely classically, because the Fermi energy h2n/4πm is much lower than the Boltzmann energy kBT. (Here h is the Planck constant, m the electron mass, kB the Boltzmann constant and T the temperature.) On the other hand, complementary 2D electron systems in solids, e.g., at semiconductor heterostructure interfaces, so far have always been in the “high-density” degenerate Fermi regime even at the lowest achieved densities [25, 26]. It appears tempting to close the gap between these two regimes and study the phase diagram of 2D electrons [27] over a wider parameter range, in particular into a region where quantum effects due to the Fermi nature of the electrons start coming into play. One promising route in this direction is to make use of the above-mentioned multi-electron bubbles (MEBs), which are stabilized by the counteracting forces resulting from surface tension and Coulomb repulsion. It is expected that electron densities well in excess of what can be achieved on a plane helium surface can be reached in MEBs. Although experiments on the properties of the surface state electrons in MEBs are missing so far, because the trapping and manipulation of such bubbles is not trivial, remarkable progress has been made recently [21, 28]. Another approach toward electron densities beyond the limit imposed by the EHD instability is based on the additional stabilizing van der Waals forces in thin He films on suitable substrates. Electron densities up to 1016 m−2 have been reported [29, 30]. So far, however, these experiments are hampered by the fact that the ideal character of the helium surface is partly lost due to imperfections of the solid substrates.

Fig. 1
figure 1

The center of this image shows the static deformation of the free surface of superfluid 4He (Taylor cone) resulting from the trapped charge below the surface in the static electric field of a charged pin. The pin diameter is 1.6 mm, the temperature T = 2.1 K

Full size image

Hence, there is persistent interest in alternative routes toward high electron densities, and a goal of our simulations was to determine the maximum achievable densities on bulk liquid helium in locally confined electric fields. In the following, we give a brief account of the simulation conditions and then present results for various combinations of physical parameters of the system.

2 Simulations

As mentioned above, the accumulation of charges under the He surface below the pin gives rise to a surface deformation u(r) due to the electrostatic pressure, given by the electron density n and the z-component of the electric field E, which is counteracted by surface tension and gravity:

$$ - \gamma \nabla^{2} \left( u \right) \, + g\rho u = {{enE}}_{z} $$
(1)

Equation (1) is based on the approximation that the radius of curvature of the surface deformation is much larger than u, i.e., the treatment given here does not cover the region very close to the EHD instability, where the surface profile develops a sharp tip and a liquid jet starts to form [24].

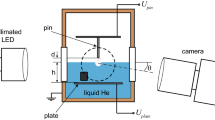
In our calculations, the surface displacement u(r) and the corresponding charge density n(r) were determined self-consistently, using finite element simulations and the commercial software package COMSOL Multiphysics. Figure 2 gives a schematic of the simulated domain, with dimensions similar to the experimental cell used for the measurements in Ref. [24]. Sketched is here the case when the pin to which the high voltage is applied is above the surface, and the charges are below. The calculations also apply, however, to the inverted situation, with electrons above the surface and the pin below, just the deformation will have the opposite sign. The cell is cylindrical with a diameter of 54 mm and a height of 70 mm; its walls are on ground potential. The (bottom) plate electrode and the (top) pin electrode are at potentials Ubottom and Upin, respectively; the distance between pin and plate is 19 mm. The pin is a cylinder with a diameter of d, terminated with a spherical cap, and the pin apex is assumed to be at a height h above the (unperturbed) He level. The electrostatic potential in the charge pool which forms below the pin is not fixed, but is assumed to be constant throughout the charge distribution. This condition is fulfilled because the charges are free to move along the surface. Therefore, the component of the electric field parallel to the surface has to vanish in the pool in the static case. The distribution of the electrostatic potential U in the sample cell was calculated using E =  − grad (U) and div D = e n(r), where D is the electric displacement. The material parameters of liquid helium used in the calculations are γ = 3 × 10–4 N/m, ρ = 145 kg/m3 and εr = 1.059 for the relative dielectric constant of the liquid.

Fig. 2
figure 2

Schematic of the sample cell with top (pin) and bottom (plate) electrodes and the helium surface, red marking the charged and blue the uncharged region (Color figure online)

Full size image

3 Results

In the following, we present results from these calculations for the electrostatic potential in the sample cell, the charge-induced surface deformation of the liquid and the inhomogeneous charge density underneath the tip. Two geometries are studied: One is similar to the experiments reported in Ref. [24], where the height of the pin above the liquid surface and the pin diameter were of the order of 1 mm (geometry A); in the second part (geometry B), these typical values are reduced by one order of magnitude in order to see the influence of the length scales.

3.1 Geometry A

The diameter of the pin d and its height above the helium level h are chosen as d = 1.0 mm and h = 1.3 mm. For the sake of simplicity and in order to keep the number of variables small, we fix the potential of the bottom plate to zero in what follows.

We start with the potential distribution. Figure 3 shows an example where the potential at the pin is 700 V. In addition to the color-coded potential values, some field lines (white) are plotted, which indicate the local direction of the electric field. Also shown is the profile of the liquid surface. The total number of elementary charges in this simulation was N = 2.28 × 108.

Fig. 3
figure 3

Electrostatic potential distribution in the sample cell in the vicinity of the tip, for d = 1.0 mm, h = 1.3 mm, Ubottom = 0, Upin = 700 V, and total number of elementary charges N = 2.28 × 108. The thick red and light blue lines mark the charged and uncharged part of the helium surface, respectively (Color figure online)

Full size image

An important quantity which can directly be derived from Fig. 3 is the size of the ion pool. It follows from the shape of the electric field lines at the He surface: In the region of surface charge, the field lines have to be perpendicular to the surface, because any field component parallel to the surface would lead to a redistribution of the charges, until the field parallel to the surface vanishes. Outside of the charge pool, however, this condition does no longer hold, and the field lines in general are inclined to the surface. In addition, they exhibit a slight kink at the surface, arising from the discontinuity in the dielectric constant.

The surface deformation of the liquid below the pin, generated by the electrostatic pressure of the ion pool, is hardly discernible on the scale of Fig. 3. We therefore show representative examples for the surface profile on a vertically expanded scale in Fig. 4 for two cases: Fig. 4a is for a relatively small total number of elementary charges N = 1.23 × 107, Fig. 4b for N = 2.28 × 108. First of all, the hillock is much higher for the larger charge, as expected. As the graphs further indicate, the full width at half maximum (FWHM) of the hillock profile in Fig. 4b is larger than in 4a, implying that the hillocks also grow in width as more charges are added to the pool.

Fig. 4
figure 4

Calculated surface profile of an inhomogeneously charged He surface. The applied voltage is ΔU = 700 V; a N = 1.23 × 107 and b N = 2.28 × 108 elementary charges. Note the different vertical scales (Color figure online)

Full size image

It is revealing to compare the surface deformation in Fig. 4 with the charge distribution in the ion pool, as it is plotted in Fig. 5 for the same parameters. A first glance already shows that the FWHM of the charge profiles is similar to the FWHM of the surface profiles, but a closer inspection discloses a distinct difference between the two profile types: While the surface deformation varies smoothly as a function of radial position, the charge distribution displays a kink at the edge of the charge pool, rather prominent in Fig. 5a, with a nearly vertical tangent. For the larger pool in Fig. 5b, the difference between charge and surface profile is less pronounced, but the finite slope of the charge profile at the edge of the charge pool persists. This implies a well-defined, sharp boundary of the charge pool.

Fig. 5
figure 5

Profile of the charge density in a Taylor cone for two different hillock charges; the parameters are the same as in Fig. 4a and b. The blue dashed lines represent the surface profiles from Fig. 4. Note again the different vertical scales in a) and b) (Color figure online)

Full size image

For a given geometry, the height of the Taylor cone depends on the applied potential difference ΔU = Ubottom − Upin between tip and plate, and on the number of elementary charges in the ion pool. As ΔU is raised, the deformation increases nonlinearly, shown in Fig. 6a for several constant pool charges between 107 and 5 × 108 e. It is to be noted that there are no hillock heights above about 300 µm; the curves end because the self-consistent calculations do no longer converge. This is an indication that the Taylor cone becomes unstable, in principle similar to the already mentioned EHD instability of a plane liquid surface. The numerical value of this critical hillock height should not be taken too literally, because, as pointed out earlier, the approximations entering the simulations do not hold for large deformations with a relatively sharp apex. Qualitatively, however, such an instability is expected and is also observed experimentally, as described in Ref. [24]: Above some critical deformation, the surface becomes unstable, a liquid jet develops, and charges are lost from the surface. This EHD phenomenon is called a Taylor jet in the literature [24].

Fig. 6
figure 6

Hillock height (a), width (b), and apex curvature (c) as a function of the applied voltage ΔU for different fixed hillock charges between 107 and 5 × 108 e. Slight kinks and fluctuations in the length of the various curves are numerical artifacts due to the finite resolution of the grid on which the calculations are done (Color figure online)

Full size image

In Fig. 6b and c, we have plotted the hillock width and the inverse radius of curvature of the hillock apex for the same set of parameters as in Fig. 6a. As the voltage is increased at constant hillock charge, the FWHM decreases, and the cone profile is getting sharper. Again, the terminations of the curves at high voltage mark the points where the calculations do not converge any more. There is no big change in the values of the width, just a reduction by about a factor of 2. The inverse radii of curvature in Fig. 6c, however, exhibit pronounced divergences close to the end points of the curves, a clear signal for approaching the instability.

It has already been pointed out that one of the aims of this study is to determine the maximum charge density that can be achieved in the apex, as compared to the maximum charge density on a flat surface. Results for this quantity are plotted in Fig. 7, as a function of total hillock charge and for a set of voltages ΔU. A similar behavior as for the hillock height in the previous graphs is observed: As the voltage ΔU or the charge Q is increased, also the charge density n rises, until at some critical values the curves terminate, because the simulations do no longer converge. The bending upward in the curves for U > 500 V indicates that the system starts to develop into a positive feedback runaway situation: The charged surface is attracted by the tip, which brings the electrons closer to the tip, which attracts more electrons, thereby increasing the charge density in the center, which moves the surface closer to the tip, and so on. As long as the fields are small, this feedback is significantly less than unity and gravity alone is enough to stabilize the system. The bend upwards is the regime where gravity is no longer sufficient to prevent the jet instability; instead, the surface tension contributes the main part for stabilizing the small area under the tip. If the field or charge is increased further, even the surface tension is not enough, and the instability develops.

Fig. 7
figure 7

Maximum charge density n at the hillock apex as a function of the pool charge and for a set of voltages applied between pin and bottom plate. The pin-surface distance is 1.3 mm, the pin diameter 1.6 mm (Color figure online)

Full size image

The maximum charge densities found in the calculations are on the order of 2.5 × 1013 e m−2. This is close to the critical value obtained for a plane, homogeneously charged He surface [31], which means that using the combined action of surface tension and gravity in an inhomogeneous electric field on bulk helium does not allow a noticeable increase in n beyond what is accessible in a homogeneous field, at least not for the geometry investigated so far.

3.2 Geometry B

For charge pool dimensions smaller than the capillary length a, the forces due to surface tension will dominate over gravity. One might expect that under such a condition higher electron densities will be stable at the liquid surface. We have therefore repeated the simulations for a reduced distance h = 130 µm between pin and (unperturbed) helium surface, i.e., a factor of ten smaller than in the previous chapter, and also the pin diameter was reduced by about an order of magnitude (to 160 µm). This should allow one to confine the charge pool to a radius well below a.

Results for the calculations of the height and charge profiles on this restricted length scale are shown in Figs. 8 and 9. In contrast to Fig. 5, the charge profile is now indeed distinctly narrower than the surface profile, its radius being a factor of 5 below the capillary length. Data for the hillock height, width and curvature as a function of the applied voltage are plotted in Fig. 10, again for a set of pool charges. Qualitatively, the behavior is similar to the results in the previous chapter, in particular the nonlinear growth of the height and the inverse radius of curvature with increasing voltage, terminating at end points given by the non-convergence of the simulation. Due to the smaller length scales, the absolute values of the applied voltage and the profile height are clearly reduced compared to Fig. 6.

Fig. 8
figure 8

Calculated surface profile of an inhomogeneously charged He surface for a pin-surface distance h = 130 µm. The applied voltage is ΔU = 70 V; a N = 2.23 × 106 and b N = 9.54 × 106 elementary charges. Note the different vertical scales (Color figure online)

Full size image
Fig. 9
figure 9

Profile of the charge density in a Taylor cone for two different hillock charges, the parameters are the same as in Fig. 8a and b. The blue dashed lines represent the surface profiles from Fig. 8. Note again the different vertical scales in a) and b) (Color figure online)

Full size image
Fig. 10
figure 10

Hillock height (a), width (b), and inverse radius of apex curvature (c) as a function of the applied voltage ΔU for different fixed hillock charges between 105 and 8 × 106 e (Color figure online)

Full size image

The influence of the smaller geometry on the maximum charge density in the apex, however, is quite small, as is illustrated by a comparison of Fig. 11 with Fig. 7. A slight increase from about 2.5 × 1013 m−2 to 3 × 1013 m−2 is discernible, but this is not a big step toward a more complete investigation of the phase diagram of surface state electrons. In order to achieve bigger effects, one obviously would have to go to still smaller distances between tip and helium surface, which, however, would imply serious experimental challenges for the configuration “pin—bulk He surface” which is considered here. Even slight vibrations will lead to liquid surface waves with amplitudes larger than a tip-surface distance in the few micrometer range, and if both come into contact the charges will be lost. A way out could be fixing the helium surface as a thick “suspended film” by means of capillary forces in a narrow mesoscopic channel [4, 16]. In fact, first experiments in such a channel geometry have demonstrated that electron densities up to 1014 m−2 can be reached [32]. This should allow one to study signatures of quantum corrections in the SSE system. Efforts to increase the density to even higher values, which would be desirable for investigating the full phase diagram of SSE, have so far led to sudden irreversible losses of charge, probably at some irregularities of the conductive channel walls. Therefore, better nanoscale control of the He films will be required in order to achieve higher electron densities up to the degenerate Fermi regime.

Fig. 11
figure 11

Maximum charge density n at the hillock apex as a function of the pool charge and for a set of voltages applied between pin and bottom plate. The pin-surface distance is here 130 µm, the pin diameter 160 µm (Color figure online)

Full size image

4 Conclusions

The results presented here provide a method for determining the total number of electrons or ions trapped at the surface in an inhomogeneous electric field, by analyzing the observed surface profile of the Taylor hillock or dimple, respectively. This has been used successfully in Ref. [24] to obtain information about the charge density of barium ions/nanoparticles trapped at the liquid helium surface. Our simulations also show that in equilibrium the maximum density of surface state electrons in a dimple is limited to values comparable to the flat He surface, at least for experimentally feasible pin-surface distances h > 100 µm. This means that also for SSE trapped in dimples, like for SSE on a flat He surface, one is restricted to the regime where the electrons behave as a classical particle system. However, this only holds for the static case. Distinctly higher densities might be achievable in such a dimple for times shorter than the response time of the liquid and the formation of the EHD instability (i.e., << ms) [24]. For this purpose, one could use an additional pulsed electric field applied to the pin, superimposed on the static one considered in this work: The electrons because of their high mobility will follow the transient field on a time scale much faster than the surface deformation, and the degenerate regime of SSE might be accessible, albeit only for a limited time interval. Future experiments will have to show whether this strategy enables one to study so far inaccessible regions of the phase diagram of 2D electron systems.