1 Introduction

Confinement in porous Vycor glass has long been used to study effects of finite size and disorder on phase transitions in helium. For example, the melting curve and the lambda line of \(^{4}\)He are both shifted by confinement in Vycor’s nanoscale pores [1, 2]. The superfluid critical behavior of thin helium films adsorbed on Vycor has been studied using an ultrasonic technique [3] and the torsional oscillator (TO) technique [4]. More recently, TO experiments with solid \(^{4}\)He in Vycor [5] showed an unexpected frequency increase at temperatures below 200 mK; similar behavior was subsequently seen for bulk \(^{4}\)He [6]. This was interpreted as evidence of mass decoupling, the “non-classical rotational inertia” (NCRI) that would characterize a supersolid phase. However, the shear modulus of solid \(^{4}\)He also changes [7] below 200 mK, raising the possibility that the observed TO frequency changes were due to elastic stiffening rather than to mass decoupling. Recent analyses [8, 9] have shown that in most torsional oscillators the observed frequency changes can be explained by stiffening effects from changes in the shear modulus of the solid helium. An experiment in which a compound TO was used to study \(^{4}\)He in Vycor [10] at two frequencies showed that the behavior was consistent with elastic effects but not with mass decoupling. When the original Vycor experiments [5] were recently repeated [11] with the Vycor coated by epoxy to eliminate any gaps, the TO anomaly disappeared. This strongly suggests that the anomaly originated in the bulk helium in gaps between the Vycor and walls. However, since the dimensions of these gaps are not known for the original oscillator, it has not been possible to confirm that elastic effects are of the correct magnitude to explain the observed frequency changes. Elastic changes in the solid \(^{4}\)He within the Vycor pores may also contribute to the TO response.

The elastic properties of solid helium confined in Vycor have been studied in several ultrasonic experiments. The first of these [1] used 20 MHz shear waves to study the freezing and melting curves of \(^{4}\)He confined in Vycor. These measurements were made at temperatures above 300 mK but subsequent experiments [12] extended to lower temperatures (100 mK) and covered a range of frequencies (5 to 140 MHz). Freezing was accompanied by an increase in the shear modulus of the Vycor/helium system of about 0.7 %, roughly the change expected from the contribution of solid \(^{4}\)He to the system’s total shear modulus [1]. However, the modulus changes were gradual, beginning at the onset of freezing around 2 K and extending to temperatures below 0.5 K. The stiffening was also frequency-dependent, shifting to higher temperatures as the frequency increased. This behavior was interpreted in terms of stress relaxation in the confined solid helium via thermally activated vacancy diffusion. Extrapolating the frequency dependence seen at MHz frequencies to a typical TO frequency (1 kHz) would predict stiffening near 0.5 K.

The apparent discovery of supersolidity in the Vycor/helium system created new interest in acoustic measurements. Since the transverse sound speed \(v_{t}=\sqrt{\mu /\rho }\) depends on the system’s total density \(\rho \), as well as on its shear modulus \(\mu \), \(v_{t}\) would increase if superfluid decoupled from the Vycor and reduced the system’s effective density [1]. Previous measurements extended to 100 mK [12] but did not show such an anomaly in the transverse sound speed. However, the TO anomaly began to disappear above an apparent “critical velocity” (about 10 \(\upmu \)m/s) and the ultrasonic measurements were made at higher oscillation speeds. More recently, an experiment was reported [13] that was designed to search for supersolidity in Vycor using longitudinal ultrasound at 8 MHz. It extended the temperature range to 50 mK but, more importantly, used a continuous standing wave technique to make measurements at velocities as low as 0.1 \(\upmu \)m/s. Decoupling of 1 % of the solid helium’s mass would have been detectable but no such velocity increase was observed.

If the elastic behavior of solid helium in the Vycor pores is similar to that of bulk \(^{4}\)He, much larger sound speed changes would be expected in the temperature range between 50 and 200 mK. Shear modulus changes as large as 80 % have been seen in low frequency measurements on bulk \(^{4}\)He [14]. A comparable change for helium in Vycor would change the system’s transverse sound speed by about 0.2 %. However, the shear modulus changes in bulk \(^{4}\)He are due to the motion of dislocations which can glide very easily in the basal plane of hcp \(^{4}\)He [14–17]. At high frequencies these dislocations are strongly damped by thermal phonons, which greatly reduces their effects on elastic constants. At ultrasonic (MHz) frequencies, velocity changes due to dislocations in solid \(^{4}\)He are orders of magnitude smaller, around 0.2 % [18] and the corresponding changes in the Vycor/helium system’s sound speed would be extremely small (less than 10 ppm). At an even more basic level, we would not expect dislocation motion in solid helium confined in the pores of Vycor. Even if bulk-like dislocations could exist in such small pores (diameter around 3 nm), they would be very strongly pinned by the pore walls. The effects of pore walls on dislocations have been tested [19] by freezing \(^{4}\)He inside silica aerogel, a much more open porous material whose silica strands should be effective dislocation pinning centers. As expected, the low frequency shear modulus did not show large changes below 200 mK. Instead, it increased gradually over the entire temperature range between freezing (around 2 K) and the lowest temperatures (40 mK).

In this paper we report low frequency measurements of the shear modulus of Vycor whose pores contain solid \(^{4}\)He. We do not observe any sudden changes in the temperature range below 200 mK where previous TO and elastic measurements showed anomalies. Instead, we found a small, gradual increase in the system’s shear modulus as it was cooled from 1 K to the lowest temperature (20 mK). This supports the conclusion from recent Vycor TO experiments that the low temperature anomalies seen in previous experiments must have originated in elastic effects in bulk helium in gaps around the Vycor. Confinement in the small pores of Vycor eliminates the dislocation movement responsible for the low temperature modulus changes in bulk solid \(^{4}\)He. The gradual modulus changes we observe in the present experiments appear at lower temperatures than the corresponding stiffening seen in previous ultrasonic measurements at MHz frequencies, as expected for a thermally activated relaxation process in the solid helium in the pores. The modulus changes due to the helium, combined with those due to two-level systems (TLS) in the Vycor [13, 20, 21], would produce a background temperature dependence in the frequency of a TO containing solid helium-filled Vycor.

2 Experiment

The shear modulus of the Vycor/helium system is dominated by that of the Vycor since the shear modulus of Vycor (\(\approx \) \(10^{10}\) Pa) is approximately 1,000 times greater than that of solid helium. This means that a 1 % change in the helium’s shear modulus only changes the modulus of the system by about a factor of \(10^{-5}\). Ultrasonic velocity measurements can detect relative changes as small as \(10^{-6}\), but it is challenging to achieve comparable resolution at low frequencies. We would like to have a resolution of order \(10^{-5}\) for our measurements but this is not practical with the direct shear modulus method we have used for low frequency measurements on bulk \(^{4}\)He. High \(Q\) TOs have been highly developed for the study of superfluidity because of their extremely high mass sensitivity and have been used to study solid helium for the same reason. However, TOs unexpectedly turned out to be quite sensitive to elastic effects, for example to changes in the shear modulus of solid helium in the hole typically found in their torsion rod [8]. This led us to design a TO in which the Vycor sample was essentially the torsion rod, rather than the inertial element of the oscillator.

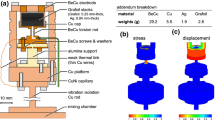
Figure 1 shows a model of the TO assembly. The torsion rod consists of a 3.45 mm diameter Vycor porous glass cylinder coated by a 0.5 mm thickness of Stycast 1266 epoxy. The Vycor is about 30 % porous with a typical pore diameter of 4 nm. The bottom of the Vycor cylinder was first glued into a socket formed by a narrow lip on top of the copper pedestal labeled in Fig. 1 using Stycast 2850. A jig was used to keep the Vycor cylinder aligned with the axis of the copper pedestal as the Stycast 2850 cured. The Vycor was then potted in Stycast 1266 out to the diameter of the pedestal. The Stycast 1266 was then machined to a 4.5 mm diameter, leaving the end and the side of the Vycor cylinder sealed by epoxy. The copper pedestal had an axial hole that was connected to a CuNi capillary on the bottom so that the Vycor could be pressurized with helium. At room temperature, we observed diffusion of helium through the epoxy layer, but the diffusion signal vanished at low temperatures, indicating that the fill line was open and the Vycor was sealed. The magnesium inertial element was glued onto the torsion rod with Stycast 1266. Since the screws that fastened the fixed electrode went into slots, there was some freedom in the orientation of the fixed electrode, and it was only necessary to approximately orient the inertial element on the torsion rod before the epoxy cured. One end of a 0.2 mm diameter copper wire was screwed to the top of the inertial element and the other end was screwed to the copper bottom plate (Fig. 1). This wire was used to ground the inertial element thermally and electrically. The geometry of the inertial element and the density of magnesium (1.74 g/cc) imply that the moment of inertia of the TO was \(I=3.03\) g cm\(^{2}\) (the moment of inertia of the torsion rod is only 0.01 g cm\(^{2}\)). The low temperature shear moduli of Vycor and Stycast 1266 are respectively 7.0 [22] and 2.0 GPa [23], so that their contributions to the torsion constant \(\kappa _{0}=18\) N m of the composite torsion rod were respectively 12 and 6.2 N m. Thus the resonant frequency is expected to be 1,200 Hz.

Fig. 1
figure 1

Opposite views of the torsional oscillator assembly. The torsional oscillator consists of a Vycor torsion rod (A) and a magnesium inertial element (B), and its motion is driven and detected by a fixed electrode (C). The screw (D) is used to press a grounding wire against the inertial element (not shown). The torsion rod was glued to a pedestal (E), which was screwed to a bottom plate (F), which was in turn screwed to a massive vibration isolation plate (G). A slot (H) was cut in the bottom plate to make room for the fill line (not shown). The back of the fixed electrode is shown in the opposite view, with a hole for the MCX electrical connector (J) (Color figure online)

Full size image

The bottom plate of the TO assembly was screwed to a 1 kg copper vibration isolation plate (Fig. 1). This vibration isolation plate was suspended from the refrigerator by a long, thin copper rod, forming a second TO with a torsional resonance at about 10 Hz. Thus vibrations of the TO were in principle attenuated by the square of the ratio of the frequencies of the TOs, i.e., a factor of 10,000. In addition, the entire refrigerator was floating on air legs, thus further decreasing vibrations of the TO.

Figure 2 shows the circuit used to drive and detect the motion of the TO. The resonant frequency of the TO was inferred from free decay measurements, and the same fixed electrode was used to drive the TO and measure the decay of its amplitude of motion. In both drive and detect modes, a bias voltage \(V_{0}=60\) V was applied across the capacitor formed by the inertial element of the TO and the fixed electrode. In drive mode, a signal near the resonant frequency of the TO with a magnitude of order 1 V was added to the voltage across this capacitor by switching to the function generator (Fig. 2). Thus the TO was driven by a force proportional to the product of the dc and ac components of the drive voltage. After the TO reached its equilibrium response amplitude, the switch was set to the voltage preamplifier. Due to the high input impedance of the preamplifier, the charge on the capacitor labeled “TO” remained approximately constant on the time scale of the TO oscillation period. Thus the oscillation amplitude of the TO is given by \(d=VC_{\text {coax}}d_{0}/V_{0}C_{\text {TO}}\), where \(V\) is the voltage at the input of the preamplifier, \(d_{0}=0.3\) mm is the equilibrium spacing between the inertial element and the fixed electrode, and \(C_{\text {coax}}\approx 300\) pF and \(C_{\text {TO}}\approx 8\) pF are respectively the capacitances labeled “coax” and “TO” in Fig. 2. In detect mode, the reference frequency of the lockin amplifier was set close to the resonant frequency of the TO.

Fig. 2
figure 2

Circuit for excitation of the torsional oscillator and measurement of its motion during its free decay. The Keithley 7001 switch is used to select drive or detect modes, and the dashed box indicates the cryogenic portion of the circuit. The capacitor labeled “TO” represents the 8.0 pF capacitance between the inertial element and the fixed electrode, which varies as the TO oscillates. The capacitor labeled “coax” is the \(\approx \)300 pF capacitance of the coaxial cable that connects the TO to the measurement system. C1 and C2 are 3 nF capacitors and R1 and R2 are 10 M\(\Omega \) resistors. An Agilent 33521A function generator was used to drive the motion, and a Stanford Research 560 voltage amplifier and a Stanford Research 830 lockin amplifier were used to detect the motion

Full size image

The maximum shear strain in the Vycor is given by \(d\left( D_{\text {vy}}/D_{\text {wing}}L\right) \), where \(D_{\text {vy}}=3.45\) mm is the diameter of the Vycor, \(D_{\text {wing}}=23\) mm is the distance between the midpoints of the two fixed electrodes, and \(L=8.5\) mm is the length of the torsion rod. The top panel of Fig. 3 shows three examples of the magnitude of the maximum shear strain in the Vycor and its phase relative to the lockin reference frequency during the free decay. Those three measurements were made at 20 mK and with solid helium-filled Vycor pores (crystal X1, see below). The time derivative of the strain yields a TO quality factor \(Q\approx 1,500\). The three different colors correspond to different lockin reference frequencies within the width of the TO resonance \(f/Q\approx 1~Hz\). The difference between the oscillation frequency of the TO and the lockin reference is given by the time derivative of the phase of the shear strain. Thus we can determine the resonant frequency of the TO as a function of time, and thus as a function of strain, since the TO oscillates at the resonant frequency during free decay. The bottom panel of Fig. 3 shows the resonant frequency of the TO as a function of strain. These data points were determined from the average of many repetitions of the measurement shown in the top panel. The fact that the measured resonant frequency is nearly independent of the lock-in reference frequency demonstrates the reliability of this measurement technique, and the absence of strain dependence of the resonant frequency demonstrates that nonlinear effects are negligible in this strain range.

Fig. 3
figure 3

Free decay of torsional oscillations with solid-helium filled Vycor pores at 20 mK. The measurements were made with the lockin reference frequency at the resonant frequency \(f=1,230.7\) Hz (green) and near the half-power points of the resonance (blue and red). Upper panel Magnitude of the maximum shear strain in the Vycor rod and its phase relative to the lockin reference signals at the three different frequencies. Lower panel Resonant frequency \(f\) of the torsional mode as a function of strain, obtained by averaging the time derivative of the phase over many free decays. This panel shows that the value of \(f\) that we obtain is independent of strain as well as the reference frequency (Color figure online)

Full size image

For this experiment, we used natural purity helium, which has a nominal \(^{3}\)He concentration of \(3 \times 10^{-7}\). The solid samples were formed using the blocked capillary technique, so that their growth occurred at nearly constant volume. The volume of the fill line connected to the TO was relatively large, and it was significant compared with the volume of the pores in the Vycor. Thus the growth technique was chosen to minimize the amount of liquid removed from the Vycor due to freezing of the bulk helium in the fill line, which occurred first. After ceasing to pump on the 1 K pot in order to grow a new solid sample, the TO was allowed to warm to a target temperature. During this process, the “1 K” pot reached temperatures as high as 3 K. The helium pressure was set low enough so that the helium was liquid in the pores and the fill line. We assumed that at this point the temperature along the fill line increased from the TO to the 1 K pot. Thus when the pressure in the fill line was subsequently increased with the TO at the target temperature, the solid plug should have formed in the fill line close to the TO, where the temperature and consequently the melting pressure were lowest. Having the plug form close to the TO minimized the pressure decrease in the Vycor pores as the rest of the helium in the fill line solidified after restarting the 1 K pot.

3 Results and Discussion

Figure 4 shows the dependence of the resonant frequency of the TO on the pressure inside the Vycor. In between the two sets of measurements presented in this paper (denoted as “first run” and “second run”), the TO was warmed to room temperature. In the second run, the dependence of the resonance on pressure was larger (\(\approx \)5 bar/Hz) (Fig. 4). The pressure dependence was measured at temperatures near 3 K with liquid helium filling the Vycor pores. This effect cannot be due to an increase in the moment of inertia of the torsion rod due to an increase of its diameter under pressure because that would cause the resonant frequency to decrease with pressure, which is the opposite of the behavior in Fig. 4. It is likely that the epoxy bulged out and partially detached from the Vycor in response to the pressure, while still maintaining the seal, thus increasing the diameter of this epoxy shell and consequently increasing the torsion constant. The decrease of the resonant frequency of the TO in the second run relative to the first run may have been caused by differential thermal expansion of the Vycor and epoxy, which could have produced cracks in the epoxy that softened it. This softening of the epoxy would also have caused the epoxy to bulge out more in response to pressure, producing the higher pressure sensitivity of the resonant frequency that was observed in the second run (Fig. 4).

Fig. 4
figure 4

The resonant frequency of the torsional oscillator as a function of the pressure of liquid helium in the Vycor pores measured at temperatures near 3 K (Color figure online)

Full size image

The pressure decrease due to solidification of the helium in the Vycor and the fill line causes a decrease in the resonant frequency of the TO as large as 8 Hz between the bulk melting temperature and 1 K. However, if we assume that solidification of the helium in the Vycor pores is complete by the time the TO temperature reaches 1 K, then the change in the resonant frequency of the TO due to pressure changes should be negligible below this temperature. The pressure of bulk helium at constant volume decreases by less than 50 mbar as it is cooled from 1 to 0 K [24]. If we assume that the pressure change of helium in Vycor is similar to that of bulk helium, then a 50 mbar pressure decrease should cause a TO frequency decrease of only 10 mHz, which is much less than the measured frequency increase between 0 and 1 K (see below).

Figure 5 shows the resonant frequency of the TO as a function of temperature for empty, liquid helium-filled and solid helium-filled pores. Due to the pressure dependence of the resonant frequency discussed above, there were significant offsets in the resonant frequencies measured at different pressures. In Fig. 5, the curves are shifted so that they overlap at 15 mK, and the offset frequency \(f_{0}\) for each curve is noted in the legend, along with the pressure in the fill line measured at room temperature just before it was blocked by solid helium. The measurements with empty and liquid-filled pores show the background contribution of the amorphous materials (Vycor and epoxy) used to construct the torsion rod. The temperature dependence is probably due to a broad distribution of tunneling two level systems (TLS). The TLS cause a maximum in the stiffness of amorphous materials at a temperature that scales as the cube root of the drive frequency [25]. The resonant frequency of the TO is sufficiently small so that this maximum is at or below the base temperature of our cryostat, so that the background contribution to the resonant frequency decreases with temperature. The small difference between the measurements with an empty cell and with liquid-filled pores could be due to the effect of the liquid helium on the relaxation of the TLS [21]. The measurements shown in Fig. 5 with solid helium-filled pores show the combined effects of the TLS in the amorphous materials and the solid helium in the pores.

Fig. 5
figure 5

The resonant frequency \(f\) versus the temperature \(T\) with solid-filled, liquid-filled or empty Vycor pores at a strain of 10\(^{-7}\). The measurements were made on warming. For the solid samples, the pressure before the helium in the fill line froze is indicated in the legend. The \(T\) dependence of \(f\) with liquid-filled or empty pores is due to the amorphous solids composing the torsion rod. With solid-filled Vycor, vacancy diffusion in the helium also contributes to the \(T\) dependence. The variation of the offset frequencies \(f_{0}\) is mainly due to the pressure dependence of the resonance (Fig. 4) (Color figure online)

Full size image

The TO has a \(Q\approx 1,500\) below 1 K, with a slight increase at the lowest temperatures. This is consistent with the nearly universal and temperature independent \(Q\) of amorphous solids that is observed above the temperature of the stiffness maximum and below a few kelvin [23]. If a process with a single relaxation time were responsible for the TO frequency shift caused by the solid helium in the pores (Fig. 5), then a dissipation peak should appear near the temperature of the midpoint of the frequency shift in the case of solid-filled pores. The magnitude of this dissipation peak should be of order the frequency shift [26], i.e., of order \(10^{-3}\) in this experiment (Fig. 5). The absence of such a dissipation peak suggests that the relaxation process in the solid helium has a distribution of relaxation times, so that the process causes a smaller dissipation peak for a given frequency shift.

An increase in the shear modulus of the helium filling the Vycor pores will cause the shear modulus of the helium+Vycor system to increase. However, we emphasize that the change in the shear modulus of the helium+Vycor is not equivalent to the change in the shear modulus of the helium. Instead, the change in the shear modulus of the helium+Vycor should be of the order of the porosity of the Vycor times the change in the shear modulus of the helium [9]. The change in the contribution of the helium to the shear modulus of the torsion rod can be determined from the measurements of the resonant frequency with solid-filled pores (Fig. 5) by subtracting the background contribution. The resonant frequency of the TO is

$$\begin{aligned} f=\frac{1}{2\pi }\sqrt{\frac{\kappa }{I}} \end{aligned}$$
(1)

where \(\kappa \) is the torsion constant. Since the moment of inertia is dominated by the magnesium inertial element, and thus is independent of temperature, the relative change in the resonant frequency is

$$\begin{aligned} \frac{\delta f}{f_{0}}=\frac{1}{2}\frac{\kappa -\kappa _{0}}{\kappa _{0}} \end{aligned}$$
(2)

where \(\delta f\left( T,p\right) =\) \(f-f_{0}=f-f\left( T=15\text { mK},p\right) \) is the quantity plotted in Fig. 5, \(p\) is the pressure, and \(\kappa _{0}=\kappa \left( T=15\text { mK},p\right) \). We have

$$\begin{aligned} \kappa \left( T,p\right) =\kappa _{0}+\Delta \kappa _{\text {TLS}}+\frac{\pi D_{\text {vy}}^{4}}{32L}\Delta \mu _{\text {He}} \end{aligned}$$
(3)

where \(\Delta \kappa _{\text {TLS}}\left( T\right) \) is the change in the torsion constant due to two level systems relative to \(\kappa _{0}\), and \(\Delta \mu _{\text {He}}\left( T,p\right) \) is the change in the contribution of the helium to the shear modulus relative to its contribution at 15 mK and pressure \(p\). As explained above, the contribution of the helium to the shear modulus of the torsion rod is distinct from the shear modulus of the helium itself. With liquid filled pores at 10 bar, \(\Delta \mu _{\text {He}}=0\), so that Eqs. 2 and 3 yield

$$\begin{aligned} \Delta \kappa _{TLS}=\frac{2\kappa _{0}}{f_{0}}\delta f\left( T,10\text { bar}\right) \end{aligned}$$
(4)

and with solid-filled pores at pressure \(p_{s}\) Eq. (2) yields

$$\begin{aligned} \kappa -\kappa _{0}=\frac{2\kappa _{0}}{f_{0}}\delta f\left( T,p_{s}\right) \end{aligned}$$
(5)

where \(\kappa _{0}/f_{0}=0.015\) N m/Hz was calculated from the values of \(I\) and \(\kappa _{0}\) given above. Rearranging Eq. (3) and substituting Eqs. 4 and 5, we obtain

$$\begin{aligned} \Delta \mu _{He}=\frac{64L\kappa _{0}}{\pi D_{\text {vy}}^{4}f_{0}}\left[ \delta f\left( T,p_{s}\right) -\delta f\left( T,10\text { bar}\right) \right] \end{aligned}$$
(6)

The temperature dependence of \(\Delta \mu _{He}\) for the three solid samples in Fig. 5 is shown in Fig. 6. Below \(\approx \)150 mK, \(\Delta \mu _{He}\) is temperature independent within 0.5 MPa. As the temperature is increased above 150 mK, \(\Delta \mu _{He}\) gradually decreases and levels off at \(\approx \)900 mK. The magnitude of the softening over the entire temperature range increases with the initial pressure in the fill line, as expected since the shear modulus of solid helium increases with pressure [27]. The temperature dependence in Fig. 6 is qualitatively different from that of the shear modulus of bulk \(^{4}\)He with 300 ppb \(^{3}\)He at \(\approx \)1 kHz. Indeed, in the bulk case, there is a relatively sudden decrease in the shear modulus near 100 mK due to thermal unbinding of \(^{3}\)He atoms from dislocations, above which the shear modulus is nearly temperature independent up to 1 K [16]. Thus the softening in Fig. 6 is not due to dislocations, as expected since the pores of Vycor are too small to accommodate dislocations.

Fig. 6
figure 6

The contribution of the solid helium to the shear modulus of the torsion rod versus temperature for the three solid samples of Fig. 5, determined using Eq. (6) (Color figure online)

Full size image

The softening observed in ultrasonic measurements of the shear modulus of helium-filled Vycor [12] was explained in terms of vacancy diffusion, and we think the same physics is responsible for the softening in Fig. 6. Vacancy flow relaxes stress gradients by transporting mass. The relaxation time for a crystal of size \(L\) is [12]

$$\begin{aligned} \tau =\frac{k_{B}TL^{2}}{2\alpha \mu VD} \end{aligned}$$
(7)

where \(\alpha \) is a shape dependent numerical factor, \(\mu \) is the shear modulus, and \(V\) is the vacancy volume. The self-diffusion coefficient of solid helium is given by

$$\begin{aligned} D=D_{0}e^{-E_{V}/k_{B}T} \end{aligned}$$

where \(E_{V}\) is the activation energy for vacancy diffusion. For \(\omega \tau <<1\), there is sufficient time for vacancies to relax the stress on each strain cycle, whereas for \(\omega \tau >>1\), there is not. Here, \(\omega =2\pi f\). Thus we expect the midpoint of the stiffening transition to occur near a temperature \(T_{\text {max}}\) such that \(\omega \tau =1\):

$$\begin{aligned} \omega T_{\text {max}}=\left[ \frac{\alpha \mu VD_{0}}{k_{B}L^{2}}\right] e^{-E_{V}/k_{B}T_{\text {max}}} \end{aligned}$$
(8)

In [12], \(E_{V}\) for helium in Vycor was determined from the \(\omega \) dependence of the attenuation peak that occurs at \(T_{\text {max}}\). In [28], the same technique was used to show that \(E_{V}\) is 21.9 K, 17.7 K and 13.6 K for pressures of 81.6 bar, 55.8 bar and 43.6 bar, respectively. Thus \(E_{V}\) increases with pressure, and the temperature of the midpoint of the stiffening transition increases with initial pressure in Fig. 6, as expected from Eq. (8). Since \(\Delta \mu _{He}\) could only be measured at a single frequency in the present work, and the pressure in the Vycor is not precisely known, \(E_{V}\) could not be determined. However, the pressure of the solid in the Vycor for the present measurements is between the maximum pressure in the fill line before it was plugged (i.e. 62 bar) and the minimum freezing pressure in Vycor (\(\approx \)40 bar [1]). If we make a linear fit to the pressure dependence of \(E_{V}\) observed in [28], then \(E_{V}\) in the present work would be between 13.3 and 18.1 K. Following Ref. [12], we take \(\alpha =16\), \(V=3.2\times 10^{-29}\) m\(^{3}\), \(\mu =1.9\times 10^{7}\) Pa, \(L=3.1\times 10^{-9}\) m and \(D_{0}=1.4\times 10^{-8}\) m\(^{2}\)/s. For \(f=1,200\) Hz, Eq. (8) then implies that \(T_{\text {max}}\) is between 0.67 K and 0.93 K. (The calculated value of \(T_{\text {max}}\) depends weakly on the value of \(\mu \).) This range in \(T_{\text {max}}\) is at the upper end of the range of temperatures over which \(\Delta \mu _{\text {He}}\) varies in Fig. 6. However, for a Debye relaxation process, \(T_{\text {max}}\) should be at the midpoint of the stiffening transition [26]. This discrepancy could have the same explanation as the absence of a resolvable dissipation peak at the midpoint of the stiffening transition with solid-filled pores, i.e., a distribution of relaxation times. The behavior observed in Ref. [12] also could not be explained by a Debye relaxation process with a single activation energy.

The torsion constant of our TO was not significantly affected by the bulk helium region between the Vycor and its epoxy layer that would have existed if the epoxy partially detached from the Vycor in response to pressure (see above). Experimentally, this is clear from the observed temperature dependence: we did not observe a sharp increase in the torsion constant near 100 mK due to \(^{3}\)He pinning of dislocations in the buk region. This is not surprising because such a bulk region would be small enough so that a change in its shear modulus would not greatly affect our results. A 120 \(\upmu \)m radial expansion of the epoxy shell is required to account for the \(\approx \) \(5~\%\) change in the torsion constant between 0 and 60 bar in the second run (Fig. 4). To simplify our calculation of the expansion, we have neglected the probable increase in the shear modulus of the epoxy layer and the decrease in its thickness after expansion. Below 1 K, the pressure of the 120 \(\upmu \)m thick bulk \(^{4}\)He region would be less than 60 bar, so that its intrinsic shear modulus would be less than 20 MPa. If we assume that dislocation motion causes the shear modulus of the bulk region to vanish at 1 K, then the maximum corresponding decrease in the torsion constant would be 0.05 %. In fact, a smaller decrease is expected, since the decrease in the shear modulus for polycrystals is typically smaller than in single crystals and is sometimes as small as 10 % [7]. In comparison, the maximum observed change in the torsion constant between 0 and 1 K was 0.4 % (Fig. 5).

Figure 7 shows the behavior of the resonant frequency of the TO upon thermal cycling between 0 and 1 K. The curve labeled “1st cooling” was obtained just after freezing the helium and is different from the results of the subsequent measurements. After the first cooling, the results were reproducible. This suggests that a slow relaxation process occurred during the first cooling. It seems unlikely that this is relaxation of pressure gradients on the length scale of the torsion rod by vacancy diffusion because the corresponding stress relaxation time increases exponentially as temperature is decreased, and yet significant relaxation continues down to the base temperature, as demonstrated by the difference between the blue curve and the others at low temperatures in Fig. 7. Using Eq. (7) with \(E_{V}=13.3\) K, \(L=1\) mm and with the other parameters taking the values from [12] given above, we obtain \(\tau =8\) days at \(T=0.8\) K. The measurements shown in Figs. 5 and 6 were made on warming, so that the results were reproducible.

Fig. 7
figure 7

The resonant frequency \(f\) versus temperature for two thermal cycles of sample \(\times \)4. As in the other samples, a slow relaxation process occurred during the first cooling of each sample, after which the measurement was reproducible upon thermal cycling. The measurement was made at a strain of 10\(^{-7}\) (Color figure online)

Full size image

In Kim and Chan [11], the TO frequency shifts that occurred as the helium in the Vycor froze and with solid helium in the Vycor were attributed to the stiffening of the Vycor/helium composite. However, it is not clear how such large frequency shifts could be produced by this stiffening. We can calculate the expected frequency shift of the TO in [11] using the technique from [29]: We take the thick part of the torsion rod, the Invar plate and the wings to be a perfectly rigid bob. The wings might not be perfectly rigid, but that should be a small, temperature independent perturbation to the resonant frequency. Then one calculates the torque \(\tau _{v}\) on the bob due to the helium-filled Vycor, accounting for the finite shear modulus of the Vycor. Inserting \(\tau _{v}\) into the equation of motion for the bob, one can obtain a first order solution for the resonant frequency as a function of the shear modulus of the Vycor+helium. The period shift \(dp\) of the TO is then related to a change in the shear modulus of the Vycor+helium \(d\mu \) as

$$\begin{aligned} dp=-\frac{2\pi ^{2}}{3}\frac{I_{v}}{I_{b}}\frac{h^{2}\rho }{p\mu _{\text {V}}^{2} }d\mu \end{aligned}$$
(9)

where \(h=10\) mm is the height of the Vycor cylinder, \(\rho =\) 1.6 g/cc is the density of Vycor porous glass, \(p=1.15\) msec is the oscillation period of the TO, \(\mu _{\text {V}}=7\) GPa [22] is the shear modulus of Vycor porous glass and \(I_{b}=170\) g cm\(^{2}\) (D.Y. Kim, Personal communication) and \(I_{v}=60\) g cm\(^{2}\) are respective estimates of the moments of inertia of the bob and Vycor assuming they are perfectly rigid. Equation (9) implies that the \(20\) MPa change in the shear modulus of the Vycor+helium observed below 1 K in the present work (Fig. 6) corresponds to a period shift of \(dp=130\) psec, but a period shift of 900 ps relative to the empty cell was observed between 30 and 900 mK in [11]. The discrepancy between the apparent and expected changes in the shear modulus in [11] is even larger at higher temperatures. Equation (9) implies that the period shift exceeding 5 nsec observed during freezing and melting of the helium in the Vycor in [11] corresponds to an apparent shear modulus change of 770 MPa. The contribution of the helium to the shear modulus of the Vycor+helium system should be of order the stiffness of the helium [1], but 770 MPa is almost ten times greater than \(c_{33}\), the largest component of helium’s stiffness tensor [27], at the 65 bar maximum pressure of the measurement in [11]. It is more likely that the period increases in [11] mainly result from bulging of the Vycor portion of the TO and consequent increases in the moment of inertia due to increases in helium pressure. A 10 nsec shift in the period of the TO corresponds to a relative shift in the total moment of inertia of the torsional oscillator of 18 ppm, or a relative increase in the moment of inertia of the Vycor portion by 69 ppm. This in turn corresponds to an increase in the radius of the Vycor by 17 ppm or 120 nm. It is difficult to compare this with an estimate of the deformation of the Vycor in response to changes in pressure because of the porous geometry.

In conclusion, we have shown that resonant frequency shifts observed in previous TO measurements on solid \(^{4}\)He in Vycor [5, 11] were not mainly due to changes in the shear modulus of the Vycor+helium system \(\Delta \mu _{\text {He}}\). In the case of [5], the sudden frequency shift that was observed near 100 mK is inconsistent with the temperature dependence of \(\Delta \mu _{\text {He}}\). We found that \(\Delta \mu _{\text {He}}\) is nearly temperature independent below 150 mK and slowly decreases as the temperature is increased from 200 mK to 1 K. Thus the sudden frequency shift near 100 mK in [5] must have been due to an elastic effect involving a layer of bulk solid helium between the Vycor and the cell wall, as argued in [11]. In the case of the TO used in [11], the frequency shifts measured during freezing of the helium in the Vycor and at lower temperatures are too large to have been caused by changes in the shear modulus of the helium-filled Vycor torsion bob. Finally, we believe that the explanation for the temperature dependence of \(\Delta \mu _{\text {He}}\) is the freezing of a thermally activated relaxation process, probably helium vacancy diffusion.