A surrogate-assisted a priori multiobjective evolutionary algorithm for constrained multiobjective optimization problems

Abstract

We consider multiobjective optimization problems with at least one computationally expensive constraint function and propose a novel surrogate-assisted evolutionary algorithm that can incorporate preference information given a priori. We employ Kriging models to approximate expensive objective and constraint functions, enabling us to introduce a new selection strategy that emphasizes the generation of feasible solutions throughout the optimization process. In our innovative model management, we perform expensive function evaluations to identify feasible solutions that best reflect the decision maker’s preferences provided before the process. To assess the performance of our proposed algorithm, we utilize two distinct parameterless performance indicators and compare them against existing algorithms from the literature using various real-world engineering and benchmark problems. Furthermore, we assemble new algorithms to analyze the effects of the selection strategy and the model management on the performance of the proposed algorithm. The results show that in most cases, our algorithm has a better performance than the assembled algorithms, especially when there is a restricted budget for expensive function evaluations.

1 Introduction

Many real-world problems involve multiple conflicting objective functions to be optimized simultaneously, subject to constraints, see, e.g., [1,2,3]. Such problems are known as constrained multiobjective optimization problems (CMOPs). Because of the conflict between the objective functions, many so-called Pareto optimal solutions usually exist, representing different trade-offs. In the absence of additional information, all Pareto optimal solutions are mathematically incomparable. Typically, a domain expert called a decision maker (DM) provides preference information to find the most preferred Pareto optimal solution for practical implementation.

There are three significant challenges in solving real-world CMOPs. First, the evaluation of one (or more) objective or constraint functions can be time-consuming. For instance, many engineering problems rely on simulations, where function evaluation can take minutes or hours [4,5,6,7,8,9,10]. Such problems are referred to as computationally expensive ones. We can find computationally expensive problems in various fields such as ergonomic well-being [1], manufacturing design [2], shape and design optimization [4,5,6,7] and the configuration of energy sources [11].

In this paper, we focus on CMOPs that have at least one computationally expensive constraint function. For simplicity, we refer to them as computationally expensive CMOPs.

The second challenge is to handle the constraints so that we can generate feasible Pareto optimal solutions. In computationally expensive CMOPs, we typically have a limited function evaluation budget that should not be exceeded. Moreover, sometimes, function evaluations for infeasible solutions may take longer than feasible ones [9]. Therefore, evaluating too many infeasible solutions should be avoided. Moreover, generating solutions that the DM is not interested in is a waste of resources.

In addition, comparing many solutions to find the most preferred one can increase the cognitive load set on the DM. Therefore, it is important to generate solutions that reflect the DM’s preferences. This is the third challenge. In this way, she/he only needs to compare a handful of solutions that are of interest.

There have been separate studies in the literature that address each of the three challenges mentioned in the previous paragraphs [12, 13]. However, there is currently no algorithm that addresses all three challenges simultaneously. This paper aims to fill this gap by introducing a novel algorithm for CMOPs that can handle all three challenges effectively.

Multiobjective evolutionary algorithms (MOEAs) are well-known algorithms to solve CMOPs [14]. They are population-based algorithms that find an approximation of the set of Pareto optimal solutions (also known as a Pareto front) and have certain advantages that have made them popular over the years. For example, they can handle different kinds of decision variables and deal with objective or constraint functions that are discontinuous or nondifferentiable [14, 15]. In the literature, many different MOEAs have been proposed, see, e.g. [16] and references therein. Among them, decomposition-based MOEAs have become prevalent [17] in recent years.

Decomposition-based MOEAs can scale better than other MOEAs as the number of objective functions increases [17, 18]. Moreover, decomposition-based algorithms can be modified to easily take the DM’s preferences into account by focusing on a specific subspace of the objective space that represents the preferences [18]. On the other hand, all MOEAs need many function evaluations to converge toward Pareto optimality [19], and this makes them impractical for computationally expensive CMOPs. For example, according to [20], MOEAs require quite many function evaluations for some test problems.

To speed up computations, one can train computationally inexpensive surrogate models to mimic the behavior of the computationally expensive functions as closely as possible [19]. One then evaluates the expensive functions at new samples iteratively to update the accuracy of the surrogate models and we refer to this as model management (also known as active learning [21]). Kriging models (also known as Gaussian process regression) [22] are widely used surrogate models [12, 19], because they provide uncertainty information of a predicted solution along with the predicted value. This information can be helpful to MOEAs and can be utilized in different ways for model management (see, e.g., [11, 23, 24]). In this paper, we focus on using Kriging in a decomposition-based MOEA.

There have been many studies on solving CMOPs when the constraints are computationally inexpensive, see, e.g., the survey [25] and recent studies [26,27,28]. Furthermore, as mentioned, e.g., in [29], most constraint handling techniques developed for single-objective optimization can be utilized in multiobjective optimization. However, in a recent survey [30], it is mentioned that this is not always straightforward. Moreover, some studies assume that the objective functions are computationally expensive, but the constraints are still considered to be computationally inexpensive [24, 31].

Although many engineering CMOPs can have computationally expensive objective and constraint functions (see e.g. [1, 2, 32]), there are only a handful of surrogate-assisted MOEAs that can handle them [32,33,34,35,36,37,38]. Many take a Bayesian approach for model management (we refer to it as Bayesian model management) based on an acquisition function that is used to select a solution for updating the surrogate models [36]. For example, in [39], an acquisition function is created based on expected hypervolume improvement [40] and the probability of feasibility (POF) of the solutions.

So far, we have discussed the first two challenges in solving CMOPs. The third challenge is to incorporate a DM’s preferences. Few studies have incorporated a DM’s preferences in the acquisition function [41,42,43,44,45]. In most surrogate-assisted MOEAs for computationally expensive CMOPs, the DM is assumed to select the most preferred solution after a representative set of Pareto optimal solutions has been generated (these are called a posteriori algorithms [46]). However, as mentioned earlier, we typically can only afford a limited number of function evaluations when solving computationally expensive CMOPs, and a posteriori algorithms tend to waste resources and also find solutions that the DM is not interested in. One can address this by asking for the DM’s preferences before the optimization process ( they are called a priori algorithms [46]). Here, by considering the DM’s preferences, we need to find feasible and Pareto optimal solutions that satisfy the DM.

In this paper, we develop a novel Kriging-assisted a priori MOEA for computationally expensive CMOPs, called KAEA-C. To the best of our knowledge, KAEA-C is the first algorithm to incorporate the DM’s preferences in problems with at least one computationally expensive constraint. We assume that the preference information is provided as a reference point consisting of desirable values for each objective function. We call the components of the reference point as aspiration levels.

The contributions of this paper are as follows: First, we propose a novel selection strategy for choosing a new population in each generation of the proposed algorithm, employing two distinct criteria for feasible and infeasible solutions. This strategy utilizes either surrogate models or original functions (if they are computationally inexpensive), enabling the generation of more feasible solutions that align with the DM’s preferences while converging toward the Pareto optimal solutions.

Second, we devise a unique model management strategy that seeks two types of solutions: those that significantly improve the accuracy of surrogate models, and feasible solutions that closely adhere to the DM’s preferences. Our selection strategy increases the likelihood of obtaining feasible solutions, making it more likely to find desired solutions during the model management phase, where we must evaluate expensive functions within a limited budget.

The remainder of the paper is organized as follows. Section 2 presents background material, concepts, and notations. In Sect. 3, we introduce the proposed algorithm KAEA-C. Section 4 is dedicated to numerical experiments, evaluating KAEA-C’s performance against state-of-the-art algorithms and analyzing the effects of KAEA-C’s selection strategy and model management on its performance. Finally, Sect. 5 offers concluding remarks and discusses future research directions.

2 Background: basic concepts and notation

In this section, we cover some basic concepts, notation, and relevant terminology in multiobjective optimization that we need. Then, we provide background information about different ways to incorporate DM’s preferences and Kriging-assisted MOEAs for CMOPs.

2.1 Multiobjective optimization

We consider problems of this form:

$$\begin{aligned} \begin{aligned} \text {minimize }\;&f(x) = (f_1(x),\; \dots ,\;f_{\textrm{k}}(x))\\ \text {subject to }&g_i(x) \ge 0,&i = 1,\dots , m\\&x_i^l \le x_i \le x_i^u&i = 1,\dots , n, \end{aligned} \end{aligned}$$

(1)

where f(x) denotes an objective vector which consists of the values of $\textrm{k}$ conflicting objective functions at $x= (x_1,\dots ,x_n)^T$, an n-dimensional decision variable vector (for short, decision vector). In this paper, we refer to objective vectors as solutions. We call a decision vector x, and the corresponding solution f(x) feasible, if x satisfies all the constraints. The set of all feasible decision vectors is called a feasible region ${\mathbb {F}}$. On the other hand, a decision vector and the corresponding solution are infeasible if x violates at least one of the constraints.

For the m inequality constraint functions, the individual constraint violation value $cv_i(x)$, with $i=1,\dots ,m$ of the decision vector x can be defined as follows:

$$\begin{aligned} cv_i(x)= {\left\{ \begin{array}{ll} 0, &{}\text {if } g_i(x) \ge 0\\ |g_i(x) |&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(2)

We perform a min-max normalization [47] within the box constraints of problem (1), because the constraint functions can have different scales, and the normalization scales the magnitude of violations. In real-world problems, where we do not know the upper and lower bounds for the constraint violations, we can use the current population violations and update it iteratively. Then, we can calculate the sum of all individual constraint violations so that all constraints have an equal effect on the overall constraint violation value. The sum of all individual constraint violations provides the overall constraint violation for a given decision vector:

$$\begin{aligned} \begin{aligned}&CV(x) = \sum _{i=1}^m{cv_i(x).}\\ \end{aligned} \end{aligned}$$

(3)

We will use both Eqs. (2) and (3) in Sect. 3.

A feasible decision vector $x^\star \in {\mathbb {F}}$ and the corresponding $f(x^\star )$ are called Pareto optimal, if there does not exist another decision vector $x \in {\mathbb {F}}$ such that $f_i(x)\le f_i(x^\star )$ for all $i=1, \dots , k$, and $f_j(x)<f_j(x^\star )$ for at least one index j. A feasible decision vector $x^\star \in {\mathbb {F}}$ and the corresponding $f(x^\star )$ are called weakly Pareto optimal if there does not exist another feasible decision vector $x \in {\mathbb {F}}$ such that $f_i(x)<f_i(x^\star )$ for all $i=1, \dots , k$.

Assume that the set $X=\{x^1,\dots , x^p\}$ is an arbitrary subset of feasible decision vectors, and $F(X)= \{f(x^1), \dots , f(x^p) \}$ is the set of corresponding solutions in the objective space. A solution $f(x^i)$, with $i = 1, \dots , p$, that satisfies the definition of Pareto optimality within the set F(X), is called a nondominated solution [14]. Sometimes, nondominated solutions and Pareto optimal solutions are regarded as synonyms in the literature, but we distinguish the terms since MOEAs can only guarantee nondominance within a set considered but not Pareto optimality. A Pareto optimal solution is always nondominated, but the reverse situation is not necessarily true.

In this paper, we utilize several concepts and notations. We summarize them in Tables 1 and 2, respectively.

Table 1 The concepts (and their descriptions) used in this paper

Moreover, we use an achievement scalarizing function (ASF) [49] to sort nondominated solutions based on a given reference point ${\hat{z}} \in {\mathbb {R}}^k$. There are different ways to formulate an ASF. Here, we use the following formulation to be minimized:

$$\begin{aligned} \max _{i = 1,\dots ,k}[w_i(f_i(x)-{\hat{z}}_i)]+ \rho \sum _{i = 1}^k w_i(f_i(x)-{\hat{z}}_i), \end{aligned}$$

(4)

where $w_i=\frac{1}{z^u_i - z^{nad}_i}$, and $\rho \sum _{i = 1}^k w_i(f_i(x) - {\hat{z}}_i)$ with $\rho > 0$ is an augmentation term to avoid finding weakly Pareto optimal solutions [46, 49]. We use an $\textrm{ASF}$ to order solutions in a set. The lower the $\textrm{ASF}$ value for a given x, the ”closer“ it is to the DM’s reference point [46, 49]. We refer to this as how well the solution reflects the DM’s preferences.

Table 2 Notation (and their descriptions) used in this paper

2.2 Preference incorporation

Multiobjective optimization algorithms can be classified based on the timing a DM provides preferences [46, 50]: after optimization (a posteriori algorithms), iteratively during the optimization (interactive algorithms), or before optimization (a priori algorithms). In a posteriori algorithms, the DM selects the most preferred solution after seeing a set of solutions representing the Pareto front. The DM actively interacts with the algorithm in the second class of algorithms and provides preferences during an iterative solution process. In a priori algorithms, the DM expresses one’s preferences before the solution process. Then, at the end of the optimization process, the DM gets a set of solutions that best reflect the preferences.

A posteriori algorithms need a lot of computing resources since they try to represent the whole range of different Pareto optimal solutions. Therefore, the computation resources can go to waste by generating solutions that do not interest the DM. These algorithms are suitable when the DM wants to see a wide range of trade-offs. On the other hand, the DM is actively involved in the optimization process in interactive algorithms, which needs time and involvement. The advantages of interactive algorithms are that the DM can learn about the reachable solutions and adjust her/his preferences iteratively. In a priori algorithms, the DM gets to express her/his preferences before the optimization begins and, thereby, limits the region of interest and chooses the most preferred solution at the end. The drawback of a priori algorithms is that the DM may provide unrealistic preferences and be disappointed in the solutions obtained. A priori algorithms are suitable when the DM cannot interactively provide preferences but has knowledge of what kind of solutions are desirable.

In a priori algorithms, computation resources are saved compared to a posteriori algorithms. Besides, the cognitive load set on the DM is not as extensive since she/he needs to consider only a set of Pareto optimal solutions in her/his region of interest. To the best of our knowledge, there are no a priori or interactive surrogate-assisted MOEAs designed for CMOPs with computationally expensive constraints. In this paper, we focus on a priori algorithms. In this way, we avoid shortcomings of a posteriori algorithms and avoid making assumptions on the DM having much time to participate in an interactive solution process.

2.2.1 A priori decomposition-based MOEAs

The current decomposition-based MOEAs can easily be adapted to handle a priori preferences. With minor adjustments, most of them can utilize a DM’s preferences to decompose the objective space into several subspaces [13]. For example, the weights in MOEA/D [51], the reference vectors in RVEA [52], the reference points in NSGA-III [53], and many more MOEAs (see [54] for more details) can be adjusted to incorporate the DM’s preferences.

We can modify any of the above-mentioned algorithms to incorporate a DM’s reference point. In this paper, we use the reference vectors (used by RVEA) as an example. Besides, in two recent studies [13, 18], it has been explicitly mentioned that among decomposition-based MOEAs, RVEA has a straightforward way for incorporating a DM’s preferences. DMs can express preferences in different ways [55]. We use reference points as preference information because they have been proven to be something that is understandable to the DM [56, 57] (they are in the objective space like objective vectors that a priori MOEAs generate and show to the DM).

2.2.2 Reference vectors

Next, we describe how reference vectors are used in RVEA since we use them in the proposed algorithm KAEA-C. RVEA uses uniformly distributed reference vectors (using the simplex-lattice design algorithm [58]) to divide the objective space into subspaces. Then, solutions are assigned to the closest reference vectors in each generation. Each set of solutions assigned to a reference vector is called a subpopulation. Next, a scalarization function is used to form a single-objective optimization problem. Here, we refer to the scalarization function as a fitness function. Finally, the best solution is selected for the next generation by solving the single-objective optimization problems in each subpopulation.

Moreover, RVEA has an a priori extension (we refer to it as AP-RVEA) that incorporates a reference point ${\hat{z}}$ [52]. AP-RVEA positions the reference vectors $v^i$ ($i = 1,\dots , p$) based on a normalized reference vector $v^c =\{v^c_1, \dots , v^c_j\}$ (for $j=\{1,\dots ,k\}$) according to the following equation:

$$\begin{aligned} v^i = \frac{r\cdot v^i+(1-r)\cdot v^c}{||r\cdot v^i+(1-r)\cdot v^c||}, \end{aligned}$$

(5)

where $v^c_j = \frac{{\hat{z}}_j}{||{\hat{z}}||}$, and $||{\hat{z}}|| \ge 0$ is the Euclidean norm of the reference point. If $||{\hat{z}}||=0$, then we set $v^c$ to be the unit vector. The parameter $r\in (0,1)$ controls how the reference vectors are adjusted towards the reference point. If r is close to 1, then the reference point has less effect on the reference vectors, and if it is close to 0, they will get closer to the reference point. Moreover, the cosine value of the angle $\gamma$ of a solution y and a reference vector v can be used to measure the angle-based distance between them. We calculate this by the following equation:

$$\begin{aligned} \cos {\gamma } = \frac{y\cdot v}{||y||\cdot ||v||}. \end{aligned}$$

(6)

Fig. 1

Example of how reference vectors are distributed a uniformly and b when we incorporate a reference point ${\hat{z}}$ (red cross)

Assume $V = \{v_1,\dots , v_5\}$ is a set of reference vectors. Figure 1a demonstrates how V is uniformly distributed in the objective space. Here, we can observe that y should be assigned to either $v_2$ or $v_3$. First, we calculate the angles ($\gamma _2$ and $\gamma _3$) between y and these two vectors. Then, we assign y to the reference vector with the smallest angle, which is $v_3$.

In Fig. 1b, we observe how the reference vectors are distributed if a reference point ${\hat{z}}$ is provided. Here $\theta$ is the angle between y and ${\hat{z}}$. We will use $\theta$ later in Sect. 3 for the selection strategy in KAEA-C. It is worth mentioning that the reference point only provides a search direction and does not matter if it is attainable or unattainable

2.3 Kriging-assisted MOEAs

As mentioned in Sect. 1, we can use surrogate models which are computationally inexpensive to evaluate to replace expensive functions. Naturally, we only fit surrogate models to computationally expensive functions.

Moreover, we use Kriging models as surrogates because of the uncertainty information that they provide [12, 33]. One of the essential functionalities of uncertainty information is that it helps in managing the Kriging models. There are different types of model management in the literature [13]. For example, in [23], the surrogate solutions that have the highest uncertainty are selected to update the Kriging models because the global accuracy of the Kriging models is important in that work. On the other hand, in [11], the surrogate solutions with the lowest uncertainty are chosen because the DM’s preferences are involved, and it is important to make sure some expensive solutions follow the preferences.

Another type of model management in Kriging-assisted MOEAs is the Bayesian model management. In Sect. 4, we compare our proposed model management to a Bayesian approach. Because of this reason, we outline the basics of Bayesian evolutionary optimization [59] in this subsection. In Bayesian evolutionary optimization, surrogate models are trained for objective and constraint functions and optimized using an evolutionary algorithm. Then, an acquisition function is created [13]. Next, the acquisition function value for each decision vector in the offspring population is calculated. Finally, the decision vectors with the maximum acquisition function values are chosen to update the surrogate models.

Fig. 2

A diagram of Bayesian evolutionary optimization

An acquisition function can incorporate different criteria. For example, the expected hypervolume improvement for unconstrained problems or the combination of the POF and expected hypervolume improvement for constrained problems can be utilized in an acquisition function. Figure 2 provides a diagram of the main steps of Bayesian evolutionary optimization.

Table 3 summarizes surrogate-assisted MOEAs in the literature that handle constraints or incorporate DM’s preferences. None of them is able to handle both computationally expensive constraints and incorporate preferences.

Table 3 A list of surrogate-assisted MOEAs and weather they can handle expensive constraints, DM’s preferences and if they have been applied to real-world problems

3 KAEA-C

In this section, we introduce a novel Kriging-assisted a priori multiobjective evolutionary algorithm with the ability to handle computationally expensive objective and constraint functions, called KAEA-C. Moreover, we assume the following: the DM provides the maximum number of expensive solutions, $N_S$, that she/he wants to see at the end of the optimization process, we have at least one computationally expensive constraint and a limited budget for expensive function evaluations.

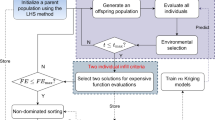
The main idea of KAEA-C is to find feasible expensive solutions reflecting the DM’s reference point. Here, we have three main phases: initialization, selection strategy, and model management. The novelty of KAEA-C lies in the latter two phases. In the selection strategy phase, we use Kriging models and focus on generating feasible surrogate solutions. On the other hand, in the model management phase, our goal is to generate feasible expensive solutions that improve the Kriging model’s accuracy or nondominated feasible expensive solutions that follow the DM’s reference point. Figure 3 provides a flowchart of the main steps of KAEA-C.

Fig. 3

Flowchart of KAEA-C

In the initialization phase, we train surrogate models for the expensive functions. Additionally, it is important to start the optimization process with some feasible surrogate solutions in the initial population [31]. To find some feasible surrogate solutions, we simultaneously minimize the individual constraint violation for each constraint (equation (2)).

We introduce a novel selection strategy by using two fitness functions and prioritizing the feasible surrogate solutions. In the selection strategy, we calculate the angle between surrogate solutions and the reference point ($\theta$ in Fig. 1b) as the first fitness function in each subpopulation and the distance between surrogate solutions to the unconstrained ideal point as the second fitness function. Then, we select two types of surrogate solutions to update the Kriging models in model management. Firstly, we select surrogate solutions that can improve the accuracy of the Kriging models the most (they have a high uncertainty). Secondly, we select some feasible surrogate solutions that follow the DM’s reference point the best (by using (4)) and have a low uncertainty to update the Kriging models. We repeat these three phases iteratively until the budget of expensive evaluations runs out.

3.1 Description of the KAEA-C algorithm

Algorithm 1 shows the main steps of KAEA-C. The input of Algorithm 1 are as follows: $t_{max}$ is the maximum number of generations in each iteration, $FE_{max}$ is the budget of expensive evaluations, $N_u$ is the maximum number of surrogate solutions that we choose to update the Kriging models, and $|P_r|$ is the size of a randomly generated population. In addition, we ask the DM to provide the reference point ${\hat{z}}$ and $N_S$, which is the maximum number of expensive solutions that she/he wants to see. Note that we ask the DM for the upper bound $N_S$ based on her/his cognitive capacity.

As mentioned earlier, in the initialization phase, we minimize individual constraint violations of each constraint that was defined in (2) to find feasible surrogate solutions and add their corresponding decision vectors to a randomly generated population $P_r$. Moreover, we have an archive A to store all expensive solutions and their corresponding decision vectors. Next, we train Kriging models for each expensive function. We continue optimization with the Kriging models and original functions that are computationally inexpensive. Then, in each generation t, we generate an offspring population $Q_t$ using evolutionary operations crossover and mutation. To select the population $P_{t+1}$ for the next generation, we propose a novel selection strategy which is described in Algorithm 2, where we demonstrate how to push the algorithm to generate more feasible surrogate solutions.

In the model management, we select two types of surrogate solutions to evaluate the expensive functions at them: The surrogate solutions that can improve the accuracy of the Kriging models the most, and feasible expensive solutions that reflect the DM’s reference point the best. Then, we store these expensive solutions in the archive A and update the Kriging models.

Lastly, after we have used the whole budget of expensive evaluations (when $FE = FE_{max}$), we must select at most $N_S$ expensive solutions from the archive A to show to the DM. The selected expensive solutions must be feasible, nondominated, and they should follow the DM’s reference point. As we mentioned in Sect. 2, we use the $\textrm{ASF}$ (equation (4)) to determine how well a solution reflects the DM’s reference point. Therefore, we calculate the $\textrm{ASF}$ values for feasible nondominated expensive solutions in the archive A. Then, we select up to $N_S$ expensive solutions with the lowest $\textrm{ASF}$ values to show to the DM.

3.2 Initialization

In KAEA-C, the optimization process is performed on the Kriging models and the computationally inexpensive functions. It is important to start the optimization process with an initial population with some feasible surrogate solutions [31].

First, we generate the random population $P_r$ (e.g., by using Latin hypercube sampling [61]). The size of $P_r$ is denoted as $|P_r|$. Then, we evaluate the expensive functions at the decision vectors in $P_r$ and store their original function values in the archive A (along with the corresponding decision vectors). Next, we use the archive A to train Kriging models for expensive functions.

To increase the likelihood that we have some feasible decision vectors in the initial population $P_0$, we first formulate the following multiobjective optimization problem:

$$\begin{aligned} \begin{aligned} \text {minimize }\;&\{cv_1(x),\dots , cv_m(x)\}\\ \text {subject to }&x^l_i \le x_i \le x^u_i,&i = 1,\dots ,n,\; \end{aligned} \end{aligned}$$

(7)

where we simultaneously minimize the individual constraint violations in problem (1), and x is a decision vector with the same box constraints as in problem (1). Note that the individual constraint violations in problem (7) are calculated with regard to the Kriging models or original functions that are computationally inexpensive. In step 5 of Algorithm 1, we solve problem (7) by an MOEA, which is appropriate for this problem. After solving problem (7), we have the final population $P_c$ and we select feasible decision vectors $P_f$ satisfying Kriging models of the constraints from $P_c$ and combine the decision vectors in $P_f$ and $P_r$ to create $P_0$. Finally, we remove the duplicate decision vectors from $P_0$.

Moreover, to save computation resources, we do not evaluate expensive functions at $P_f$. Therefore, we have two types of decision vectors in $P_0$, those used for expensive evaluations (they could be feasible or infeasible) and those that satisfy the surrogate constraints. In addition, we assume that we can solve problem (7) and generate some feasible surrogate solutions. Discussing the case where we cannot find any feasible surrogate solutions is beyond the scope of this paper.

Algorithm 1

KAEA-C

3.3 Selection strategy

In the selection strategy of KAEA-C, we generate the next population while using the Kriging models instead of the expensive functions. Typically, in decomposition-based MOEAs, we select one decision vector per subproblem based on a fitness function [17, 18]. This selection strategy can bring up some issues when incorporating DM’s reference point in computationally expensive problems. For instance, if very few subproblems generate the majority of feasible surrogate solutions, we do not have enough feasible surrogate solutions to select in the model management for updating the Kriging models. In addition, this can lead to not having enough feasible expensive solutions to show to the DM. In the proposed KAEA-C, we increase the number of feasible surrogate solutions generated by appointing two fitness functions and selecting a set of nondominated solutions based on the two fitness functions in each subproblem.

We take two steps to maximize our selection strategy’s likelihood of generating enough feasible surrogate solutions to show to the DM. First, we separate infeasible and feasible surrogate solutions. Second, we provide a unique selection algorithm for generating $P_{t+1}$.

In each subproblem, our priority is to select feasible surrogate solutions. Here, we create a bi-objective subproblem with two fitness functions for feasible surrogate solutions, and we select a set of nondominated surrogate solutions based on the two fitness functions. However, if all the surrogate solutions are infeasible, we use a ranking system that considers the overall constraint violation and the number of violated constraints. Algorithm 2 shows the main steps of our selection strategy.

3.3.1 Dealing with feasible surrogate solutions

If feasible surrogate solutions exist for any subpopulation, we only consider them in the selection strategy. We are interested in generating feasible surrogate solutions, and one way to focus on that is to increase the number of feasible surrogate solutions when the next population $P_{t+1}$ is being generated. Then, crossover and mutation have a higher chance of generating feasible surrogate solutions. Therefore, we aim to select only feasible surrogate solutions if possible.

We use two fitness functions. The first is the distance d of the surrogate solutions to the unconstrained ideal point $z^\star$, and the second fitness function is the angle $\theta$ between feasible surrogate solutions and the reference point ${\hat{z}}$ (see Fig. 1b). We can calculate $\theta$ by replacing v with ${\hat{z}}$ in (6). Therefore, d and $\theta$ are the two fitness functions we use in our novel selection strategy, where we select nondominated surrogate solutions based on them.

Fig. 4

An example of the selection strategy for feasible surrogate solutions described in Algorithm 2

Figure 4 illustrates how our selection strategy works for feasible surrogate solutions in a bi-objective case. In Fig. 4a, $\{y_1, \dots , y_5\}$ are feasible surrogate solutions of a subpopulation (black dots), ${\hat{z}}$ is the reference point (red cross), and $z^\star$ is the unconstrained ideal point (blue square). After calculating the fitness function values d and $\theta$ for all feasible surrogate solutions, we can identify the nondominated solutions based on these two fitness functions (see Fig. 4b). In this example, based on Fig. 4b, it is clear that $y_2,y_3$, and $y_4$ are the nondominated surrogate solutions for the next generation.

Since we select a set of solutions for each subproblem, the computation time for optimizing the surrogate models would increase compared to typical decomposition-based MOEAs. However, thanks to the low computation time of surrogate evaluations, we can afford to generate more surrogate solutions during the selection strategy. In return, we will have more candidate solutions to choose from in the model management, and therefore, more likely find feasible expensive solutions that reflect the DM’s preferences.

3.3.2 Dealing with infeasible surrogate solutions

In case all the surrogate solutions in a subpopulation are infeasible, we focus on moving toward the feasible region to generate feasible surrogate solutions in the next generation. Here, we create a ranking system by considering two factors, the overall constraint violation, which is calculated by equation (3), and the number of constraints that are violated. In each subpopulation, we pick the infeasible surrogate solution with the lowest rank for the next generation. If two infeasible surrogate solutions have the same rank, we select one of them randomly.

Assume the surrogate solutions in $\{y_1,\dots , y_q\}$ are infeasible. To select the best surrogate solution for the next generation, we define:

$$\begin{aligned} N_T(y_j) = N_V(y_j)+ N_{CV}(y_j), \end{aligned}$$

(8)

where $j = 1, \dots , q$, $N_V(y_j)$ is the number of surrogate solutions that violate fewer constraints than $y_j$, $N_{CV}(y_j)$ is the number of surrogate solutions that have a lower overall constraint violation value than $y_j$, and their sum is denoted by $N_T$. We rank all infeasible surrogate solutions based on $N_T(y_j)$ and refer to their rank as $R(y_j)$. Note that the rank 0 represents the best infeasible solution.

Table 4 shows an example of how the ranking system works for four infeasible solutions $\{y_1, \dots , y_4 \}$. Here, $y_2$ is the best surrogate solution because there is only one surrogate solution that violates fewer constraints ($N_V(y_2) = 1$), and none of the infeasible surrogate solutions have a lower overall constraint violation ($N_{CV}(y_2) = 0$). Therefore, $y_2$ has the lowest rank ($R(y_2) = 0$), and it is selected for the next generation.

Table 4 An example of how an infeasible surrogate solution is selected

Algorithm 2

Selection strategy

In Algorithm 2 we use the current population ($P_t$), the number of reference vectors (h), the unconstrained ideal point, and ${\hat{z}}$ as the input. If an unconstrained ideal point is not available, it can be estimated at every generation from the current population. Next, we generate the reference vectors by using (5). In step 3 of Algorithm 2, we generate the set of subpopulations Y by assigning each surrogate solution to the closest reference vector. Then, we look for feasible surrogate solutions in each subpopulation. For a subpopulation $Y_i$, if there is no feasible surrogate solution, we use (8) to select the best infeasible surrogate solution for this subpopulation.

On the other hand, when feasible surrogate solutions exist in $Y_i$, then two cases can happen. If there is only one feasible surrogate solution, it is selected as the best one for the current subpopulation. The second case is when more than one feasible surrogate solutions exist in a subpopulation. Here, we calculate the distance $A_d$ of feasible surrogate solutions to the unconstrained ideal point and the angle $A_\theta$ between feasible surrogate solutions and ${\hat{z}}$. Then, based on $A_\theta$ and ${\hat{z}}$ we select nondominated feasible surrogate solutions and store them in $P_{t+1}$.

3.4 Model management

After each iteration, we update the Kriging models. Typically, in Kriging-assisted optimization algorithms, the surrogate solutions with the highest uncertainty (standard deviation of the predicted value) are chosen to update the Kriging models since they can potentially improve the most with these surrogate solutions [23]. It is essential to evaluate expensive functions at some decision vectors with a high uncertainty (regardless of whether they are feasible or infeasible). As mentioned in [13], assume a decision vector $x'$ is infeasible regarding the Kriging models of the constraints. If $x'$ has a high uncertainty, then its corresponding expensive solution may be feasible. Therefore, if we do not evaluate the expensive functions at such decision vectors, the algorithm may not identify the feasible region correctly, and the search direction may be misleading.

In addition, we are interested in finding feasible expensive solutions reflecting the DM’s preferences. As mentioned earlier, the most common approach is to use a Bayesian evolutionary optimization algorithm that uses an acquisition function that considers some criteria to select some surrogate solutions to update the surrogate models. However, in our case, creating an acquisition function that can consider selecting surrogate solutions with a high uncertainty and feasible surrogate solutions with a low uncertainty that follow the DM’s preferences could be complicated. Therefore, we select surrogate solutions that have a high uncertainty and ignore whether they violate constraints or not. We select some of the feasible surrogate solutions reflecting the DM’s reference point and having a low uncertainty to increase the likelihood of finding such expensive solutions separately. The main steps of the model management are shown in Algorithm 3.

In case some of the functions are inexpensive, we do not train any Kriging models for them. Therefore, the uncertainty for these objectives is zero. Here, for a surrogate solution y, we define the uncertainty information $U_y$ as:

$$\begin{aligned} U_y = \prod _{j}^{\bar{m}}{\frac{u_{j} - u_{j_{min}}}{u_{j_{max}} - u_{j_{min}} }} \le 1, \end{aligned}$$

(9)

where, $\bar{m}$ is the number of expensive functions, $u_{j}$ is the uncertainty information from the j-th Kriging model for y, and $u_{j_{min}}$ and $u_{j_{max}}$ are the minimum and maximum uncertainties of the $j^{th}$ corresponding Kriging function, respectively. Note that, the values of $u_{j_{min}}$ and $u_{j_{max}}$ are updated after each iteration.

Algorithm 3

Model management

As input, Algorithm 3 needs FE and $FE_{max}$ from Algorithm 1, the current population, $N_u$, and the archive A from Algorithm 1. In steps 1–3, we check how many expensive evaluations are left. In this paper, improving the Kriging models’ accuracy is as important as finding feasible expensive solutions that follow the DM’s preferences. Therefore, we spend half of $N_u$ on expensive evaluations that can improve the Kriging models, and the other half on expensive evaluations that can lead to finding feasible expensive solutions reflecting the DM’s reference point.

To update the Kriging models, we select $N_u/2$ surrogate solutions with the highest uncertainty to improve the Kriging models in areas with the most potential of improving their accuracy and store them in $A_u$. Then, we select $N_u$ feasible surrogate solutions with the lowest $\textrm{ASF}$ values and store them in $A_{asf}$. Next, we select $N_u/2$ surrogate solutions with the lowest uncertainty values from $A_{asf}$ and store them in $A_u$. After that, we evaluate the expensive functions at the corresponding decision vectors of $A_u$ that are not in the archive A. Finally, we add all new expensive solutions to the archive A, update FE, and train the Kriging models again with the archive A. Note that, in case $N_U$ is an odd number, use $N_U- 1$ as the maximum number of expensive evaluations per update.

As we mentioned earlier, in the selection strategy, we select a set of nondominated surrogate solutions based on their distance to the unconstrained ideal point and their angles with the reference point. Moreover, the proposed selection strategy complements the proposed model management by enabling us to spend the available limited budget for expensive evaluations wisely in two main ways. First, sometimes one subproblem can lead to a set of feasible surrogate solutions that follow the DM’s reference point better than other subproblems. In a typical decomposition-based MOEA’s selection strategy, only one of these solutions makes it to the next generation, and this can lead to a lack of surrogate solutions for expensive evaluations in the model management phase. On the other hand, in our proposed selection strategy, we keep all the surrogate solutions that follow the DM’s preferences better than other surrogate solutions, and this helps the model management select the best surrogate solution available for expensive evaluations. The second way that the selection strategy complements the model management is when most of the surrogate solutions are assigned to one reference vector. Here, if we choose only one solution to pass on to the next generation, it is possible not to have enough surrogate solutions for the model management phase to use for expensive evaluations. However, by selecting a set of nondominated solutions, we increase the number of solutions we can choose from in the model management phase.

4 Numerical experiments

In this section, we demonstrate the performance of the proposed KAEA-C algorithm. We first compare it with some existing algorithms. Moreover, we analyze the effect of Algorithms 2 and 3 on the performance of KAEA-C. In the evaluation, we use 12 problems and two performance indicators.

4.1 Algorithms compared with

As mentioned in Sect. 1, KAEA-C is the first algorithm for the purpose considered. However, we can adjust some existing algorithms in the literature for comparison. First, we use a random search approach as our baseline algorithm. Next, we chose two algorithms from the RVEA family, which had competitive results with many MOEAs on different benchmark problems [52] as examples. Here, we selected AP-RVEA and interactive K-RVEA (IK-RVEA) [11] for comparison. They both use (5) to decompose the objective space and employ a fitness function called angle penalized distance [52] to select the best solution for each sub-space. In the following, we adapt these algorithms to handle computationally expensive constrained problems.

To modify AP-RVEA (which was not originally proposed for expensive problems), we train Kriging models for expensive functions and, in the end, randomly select some of the surrogate solutions generated by AP-RVEA for expensive evaluations. For IK-RVEA, we use the same reference point for every iteration to treat it as an a priori algorithm. Additionally, we need to implement a constraint handling technique for IK-RVEA. In this case, we apply AP-RVEA’s constraint handling technique. Thus, the key difference between IK-RVEA and AP-RVEA lies in IK-RVEA’s model management. To highlight the importance of proper model management, we do not modify these two algorithms in this aspect. AP-RVEA does not have model management, and we do not create one for it. Conversely, IK-RVEA possesses model management that considers the DM’s preferences, but it has not been designed for computationally expensive constraints. We follow the suggestions in the original papers to set their parameters for the problems.

4.2 Using different components

The majority of KAEA-C’s novelty lies within the selection strategy (Algorithm 2) and the model management (Algorithm 3). These two components have a modular structure, which means that we can combine different model management and selection strategies to assemble new algorithms. 

For the selection strategies, we choose the RVEA’s selection strategy (referred to as $\text {RVEA}^{SS}$) since it has a competitive performance compared to other algorithms according to [52], and it is straightforward to reflect the DM’s preferences [13]. Additionally, we also choose the R-NSGA-III [62] selection strategy ($\text {R-NSGA-III}^{SS}$) to be able to assemble more algorithms. 

For model management, we need an algorithm that is suitable for problems with expensive objectives and constraints. Model managements used in Bayesian optimization usually have this property [13]. In this paper, we use the model management used in an algorithm called BMOO [63], which uses the POF and expected hypervolume improvement to create an acquisition function. Then, in each iteration, the solution with the highest acquisition function value is selected to update the surrogate models. We refer to this model management as $\text {BMOO}^{MM}$. We choose $\text {BMOO}^{MM}$ because it efficiently performed on multiple benchmark problems in [33, 63]. Finally, we combine the model management used in [41] with POF to create a new model management that can handle DM’s preferences along with computationally expensive constraints.

Surrogate-assisted evolutionary algorithms typically feature a modular design, dividing functionalities between model management and selection strategy. This modularity facilitates the theoretical assembly of novel algorithms through the integration of diverse selection strategies and model management modules from various evolutionary algorithms. In this work, we leverage this flexibility to assemble eight distinct algorithms, succinctly denoted as assembled algorithms (AAs), AA1 through AA8. They are formed by combining the selection strategy from KAEA-C (Algorithm 2) and the model management from Algorithm 3 with external modules such as the AP-RVEA selection strategy and BMOO model management. The specific configurations of these assembled algorithms are detailed in Table 5, providing a clear depiction of the module combinations in use. It is imperative to emphasize that the primary objective of this endeavor is not the creation of new algorithmic entities, but rather a comprehensive assessment of the performance characteristics of Algorithms 2 and 3, ensuring a robust evaluation of their capabilities in diverse situations.

Table 5 Assembled algorithms by using different selection and model management strategies

Note that there are many different selection strategies and model managements in the literature that we can use to assemble new algorithms (e.g., see [13]). However, in this research, our goal is to show a gap in the literature for algorithms like KAEA-C. Analyzing all the algorithms that can be assembled is outside of the scope of this research.

4.3 Problems considered

There are not many constrained benchmark problems with more than two objective functions in the literature [64]. Constrained versions of well-known benchmark problems DTLZ [65] (referred to as CDTLZ) are introduced in [66]. We begin with a relatively simple problem, C2DTLZ2, to examine whether all the algorithms can successfully solve it. Furthermore, we choose C3DTLZ4, which according to [67], is one of the few problems in the CDTLZ family that genuinely requires a constraint-handling technique. For this reason, we select C3DTLZ4 from the CDTLZ family. In addition to the CDTLZ family, we also utilize some test problems introduced in [68]. Here, the problems named “MW4”, “MW8”, and “MW14” are CMOPs (single constraint) with a scalable number of objectives [68].

We use a total of 14 problems to evaluate the performance of KAEA-C. In Table 6, we display their dimensions and references. The superscript in the problem name refers to the number of objectives. In the C3DTLZ4 problem, the objective functions are the same as in DTLZ4, but the constraints make DTLZ4’s Pareto front infeasible. We use C3DTLZ4 with three objectives ($C_3^3DTLZ4$) and seven objectives ($C_3^7DTLZ4$) and assume that all functions are computationally expensive. In addition to the benchmark problems, we also employ four real-world problems, which include conceptual marine design (CMD) [69], the car-side impact (CSI) problem [66], the water resource (WR) problem [70], and the multiple-disk clutch brake design (MDCBD) problem [71]. In the first two problems, we assume that all functions are computationally expensive. However, for the MDCBD problem, we consider the last three objectives inexpensive since they are individual decision variables. The formulations of all these problems can be found in the supplementary materials.

Table 6 The number of objectives (k), constraints (m), and decision variables (n) in the problems considered with references

4.4 Parameter settings

For the experiments, we need to set the values of five parameters. Based on [73, 74], we set the size of the randomly generated population $P_r$ as

$$\begin{aligned} |P_r| = 11n - 1, \end{aligned}$$

(10)

where n is the number of decision variables. The DM must provide the maximum number of expensive solutions that she/he wants to see ($N_{S}$), and it can be different for each problem. However, we use here the same number for all problems for simplicity, and we set $N_S = 5$. The next parameter is the maximum number of expensive evaluations at each iteration ($N_u$). In Algorithm 3 we use $N_u / 2$ expensive evaluations for finding feasible expensive solutions that follow the DM’s reference point. Therefore, in a worst-case scenario, we should have $N_u = 2N_S$ so that if we have only one iteration, we attempt to find $N_S$ new expensive solutions to show to the DM at least once. Hence, we set $N_u = 10$.

Moreover, the maximum number of expensive evaluations ($FE_{max}$) determines the number of iterations that we can have. There is no exact way of allocating the correct value for $FE_{max}$ [75]. In practice, we can set $FE_{max}$ according to the amount of time that the DM has. However, in this paper, we assume that we have the function evaluation budget of 100 after we have generated $P_0$, and therefore, $FE_{max} = P_r + 100$. The last parameter is the maximum number of generations ($t_{max}$) at each iteration, where we use the surrogate evaluations. Since this part of the optimization process is computationally inexpensive, we use 40000 surrogate evaluations. We set $N_u = 10$, and $N_S = 5$. In the $\textrm{ASF}$ function (equation (4)), we set $\rho =0.0001$.

4.5 Performance indicators

Typically, in a posteriori MOEAs, we aim at the convergence of solutions toward the Pareto front and the diversity of solutions to evaluate the performance of an algorithm [76]. However, when dealing with a priori algorithms, where the DM’s preferences are incorporated in the solution process, the performance should be evaluated regarding the region in which the DM is most interested in. This region is also known as a region of interest. Different performance indicators in the literature can incorporate DM’s preferences (expressed as a reference point) (see, e.g., [11, 77,78,79,80,81]). In most of the performance indicators that we mentioned, the DM must provide additional information such as the size of the region of interest to evaluate the performance of an algorithm. To reduce the cognitive load and simplicity, we choose two parameterless indicators. For the first performance indicator, we use the ASF, which does not need any new information from the DM, and has been used to evaluate the performance of different algorithms [11, 82]. The second parameterless indicator we use is the expanding hypercube-metric (EH-metric) in [81]. In [81], the EH-metric is compared to the well-known performance indicator R-metric [77], and there are some examples where the EH-metric and the R-metric disagree on which algorithm is better, and after visualizing the solutions, it is evident that the EH-metric was able to identify the best performance. Based on [81], the EH-metric is more consistent to find the better algorithm than the R-metric.

4.6 Experimental results

As previously mentioned, we compared 12 algorithms, focusing on their performance for feasible, computationally expensive solutions. We generated 15 random reference points for each problem as preference information. Each algorithm was independently run 31 times for every reference point and problem, after which we calculated the median $\textrm{ASF}$ and EH-metric values of the final five ($N_S=5$) expensive solutions. All 12 algorithms were able to find at least five feasible expensive solutions.

We employed a pairwise Wilcoxon significance test [83] to compare the 12 algorithms, using a significance level of $\alpha = 0.05$. Subsequently, we implemented a scoring system to rank the algorithms. For each test, a score of 0 was assigned to a pair if the performance difference between the algorithms was insignificant, +1 to an algorithm if it significantly outperformed the other algorithm and -1 to the algorithm that performed significantly worse. We then ranked all 12 algorithms in an descending order based on the sum of these scores, with rank 1 indicating the best performance and rank 12 representing the worst performance.

Figure 5 presents the heatmaps for the rankings of $\textrm{ASF}$ and EH-metric scores across the 12 problems and their 15 reference points. A paired colormap (employing Viridis color code) was utilized to generate the heatmaps, with darker colors indicating better ranks (dark blue for rank 1 and yellow for rank 12). As illustrated in Fig. 5, KAEA-C outperformed the other five algorithms for the majority of the problems based on both performance indicators.

Upon analyzing the results with a budget of 100 function evaluations, IK-RVEA, AP-RVEA, and RS demonstrated inferior performance. Furthermore, AA1, AA6, AA7, and AA8 consistently exhibited darker colors compared to AA3, AA4, and AA5. KAEA-C’s performance displayed darker colors than all other algorithms for both $\textrm{ASF}$ and EH results, signifying its superior performance for most problems.

These observations indicate that other algorithms struggle to effectively reflect the DM’s reference point in computationally expensive constrained problems. The poor performance stems from their reliance on constraints solely within their selection strategies and the fact that their model management is not specifically designed to handle constraints. It is also noteworthy that IK-RVEA, which incorporates model management, generally outperformed AP-RVEA, which lacks model management, further underscoring the significance of model management.

Fig. 5

Heatmaps of the rankings of a $\textrm{ASF}$ and b EH-metric scores for 12 problems and their 15 reference points for KAEA-C, AA1-AA8, IK-RVEA, AP-RVEA and RS, respectively

Building on our previous analysis, we further examine the results of the two performance indicators by presenting the frequency of appearance for each rank across all problems as boxplots in Fig. 6. As demonstrated, both indicators exhibit similar outcomes in identifying KAEA-C as the superior performing algorithm compared to the other algorithms. Additionally, the other assembled algorithms display somewhat comparable performances. However, it is worth noting that AA1 and AA6 appear to have better median values than the other algorithms, indicating that they may be more consistent in their performance across the problems.

Fig. 6

Boxplot of frequency for each rank for KAEA-C, AA1-AA8, IK-RVEA, AP-RVEA and RS, respectively

We report additional experiments with increased numbers of function evaluations (200 and 300) in the supplementary materials. As the number of function evaluations increases, the performance of all algorithms improves, reaching a point where, with 300 function evaluations, most performances become competitive. However, the results obtained with 100 expensive evaluations indicate that KAEA-C’s performance outshines that of AP-RVEA, IK-RVEA, and the assembled algorithm. This observation has practical relevance since real-world problems often involve working with a limited number of function evaluations.

The EH-metric results reveal that solutions generated by KAEA-C exhibit better diversity and convergence around the reference point for the majority of the tests conducted. Furthermore, the $\textrm{ASF}$ results suggest that our proposed algorithm can more effectively generate solutions that align with the DM’s preferences compared to the other algorithms examined in this paper.

In real-world problems, we cannot assume to have access to such information. We can the utilize the current population at the end of each iteration to update the estimates, ensuring that our algorithm remains applicable in practice.

5 Conclusions

In this paper, we introduced KAEA-C, a novel Kriging-assisted a priori multiobjective evolutionary algorithm designed for computationally expensive problems with at least one expensive constraint. To the best of our knowledge, no other algorithm in the literature simultaneously incorporates DM’s preferences and handles computationally expensive constraints. As the name suggests, KAEA-C employs Kriging models as surrogates to replace computationally expensive functions.

KAEA-C decomposes the objective space into subspaces and employs a novel selection strategy, wherein each subspace solves a bi-objective subproblem, and the nondominated solutions form the offspring population. In this selection strategy, surrogate evaluations generate the offspring population, allowing for numerous function evaluations. KAEA-C leverages this opportunity by selecting a set of nondominated solutions based on two fitness functions rather than selecting one solution per subproblem. Subsequently, we designed a model management strategy that capitalizes on our selection approach. Here, we evaluate the expensive functions for some decision vectors generated during the optimization process. Our selection strategy provides numerous options to choose from, increasing our probability of finding feasible expensive solutions aligned with the DM’s preferences.

We compared KAEA-C with 11 other algorithms and observed that its performance consistently outperformed the others, even under a limited function evaluation budget of 100 function evaluations. When we increased the budget, the performance of other methods improved, but KAEA-C still remained competitive. This result highlights the ability of KAEA-C to perform well under restricted function evaluation budgets, which is often the case in real-world applications.

We examined various combinations of selection and model management strategies, with results indicating that the proposed ones perform best when used together. Furthermore, we observed that altering any of KAEA-C’s two components led to a worse performance appearing more frequently, signifying that the assembled algorithms’ performance was not as strong as KAEA-C’s.

For future research, we plan to develop an interactive algorithm based on KAEA-C that can adapt to potentially significant changes in the DM’s preference information. Additionally, we have assumed that the latencies of the expensive functions are relatively uniform. In future work, we aim to address problems with nonuniform latencies and explore strategies for effectively utilizing computing time.