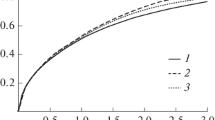
Systematizing the partial solutions of the nonstationarity heat conduction problem of a flat wall in comparison with the general asymptotic solution of this problem, we have found the transverse temperature distributions with any monotone change in the ambient conditions and elucidated the heat conduction properties of the wall under these conditions. The asymptotic solution is given by semiconvergent series and definite integrals and has been investigated for power time dependences with an exponent of 0–2, which has enabled us to justify the concept of quasi-stationarity of the thermal parameters of the wall and obtain asymptotic errors and corrections defining the deviations of these parameters from their stationary values. The features of the average heat flows most resistant to thermal disturbances as to both time and amplitude have been considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
O. V. Korshunov and V. I. Zuev, Measurement of the thermal resistance of exterior walls, Énergobezop. Énergosberezh., No. 2, 40–45 (2011).
O. V. Korshunov and V. I. Zuev, Applicability of the quasi-stationary method of determining the thermal resistance of walls, Énergobezop. Énergosberezh., No.3, 27–34 (2011).
O. V. Korshunov, Quasi-stationarity of thermal processes, Inzh.-Fiz. Zh., 85, No. 2, 392–399 (2012).
J. V. Bek, B. Blackwell, and Ch. R. St. Clair Jr., Ill-Posed Inverse Heat Conduction Problems [Russian translation], Mir, Moscow (1989).
O. N. Budadin, A. I. Potapov, V. I. Kolganov, T. E. Troitskii-Markov, and E. V. Abramova, Thermal Nondestructive Testing of Products [in Russian], Nauka, Moscow (2002).
O. V. Lebedev, O. N. Budadin, S. V. Baranov, and V. G. Avramenko, Thermal fl aw detection of multilayer products on the basis of solving inverse nonstationary heat conduction problems, Kontr. Diagnost., No. 6, 16–23 (2007).
A. V. Lukov, Heat Conduction Theory [in Russian], Vysshaya Shkola, Moscow (1967).
A. S. Telegin, V. S. Shvydkii, and Yu. G. Yaroshenko, Heat and Mass Transfer, Ch. 2. Heat Conduction [in Russian], 2nd edn., Akademkniga, Moscow (2002).
É. M. Kartashov, Analytical Methods in the Theory of Heat Conduction of Solids [in Russian], Vysshaya Shkola, Moscow (2001).
A. P. Prudnikov, Yu. A. Brychkov, and O. I. Marichev, Integrals and Series [in Russian], Nauka, Moscow (1981).
G. Korn and T. Korn, Handbook of Mathematics [Russian translation], 4th edn., Nauka, Moscow (1977).
E. von Kamke, Differentialtechungen Lösungsmethoden und Lösungen [Russian translation], Nauka, Moscow (1976).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 87, No. 4, pp. 802–813, July–August, 2014.
Rights and permissions
About this article
Cite this article
Korshunov, O.V. Heat Conduction of Walls with a Monotone Temperature Change. Asymptotics and Quasi-Stationarity. J Eng Phys Thermophy 87, 827–838 (2014). https://doi.org/10.1007/s10891-014-1078-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-014-1078-1