Autonomous and Non-autonomous Unbounded Attractors in Evolutionary Problems

Abstract

If the semigroup is slowly non-dissipative, i.e., its solutions can diverge to infinity as time tends to infinity, one still can study its dynamics via the approach by the unbounded attractors—the counterpart of the classical notion of global attractors. We continue the development of this theory started by Chepyzhov and Goritskii (Unbounded attractors of evolution equations. Advances in Soviet mathematics, American Mathematical Society, Providence, 1992). We provide the abstract results on the unbounded attractor existence, and we study the properties of these attractors, as well as of unbounded $\omega$-limit sets in slowly non-dissipative setting. We also develop the pullback non-autonomous counterpart of the unbounded attractor theory. The abstract theory that we develop is illustrated by the analysis of the autonomous problem governed by the equation $u_t = Au + f(u)$. In particular, using the inertial manifold approach, we provide the criteria under which the unbounded attractor coincides with the graph of the Lipschitz function, or becomes close to the graph of the Lipschitz function for large argument.

1 Introduction and Summary of Concepts

Typically, to build the theory of the global attractors (and their non-autonomous counterparts) one needs the dynamical system to be dissipative, i.e. there should exist a bounded absorbing set [2, 7, 12, 19, 30]. However, starting from the work of Chepyzhov and Goritskii [9], the concept of the global attractor has been generalized to the case of slowly non-dissipative systems, i.e. such that the orbits are not absorbed by one given bounded set, and they possibly diverge to infinity when time tends to infinity, but there is no blow-up in finite time. We remark, that in recent years, stemming from [9], there appeared significant work in the framework of unbounded attractors, cf., [3, 6, 13, 18, 21, 27]. An abstract approach to autonomous and non-autonomous unbounded attractors has been very recently proposed in [4].

To illustrate the underlying concept we start from two simple motivating examples.

Example 1

Consider the ODE

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = x,\\ y' = -y. \end{array}\right. } \end{aligned}$$

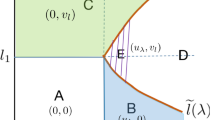
The point (0, 0) is the equilibrium. Solutions starting from (x, 0) tends to (plus of minus) infinity in x as time tends to infinity, and tend to (0, 0) as time tends to $-\infty$. Any solution starting from (0, y) goes to (0, 0) as time tends to infinity. All other solutions are unbounded both in past and in future. The set $\{ (x,0)\,:\ x\in {{\mathbb {R}}}\}$ is invariant, attracting, and unbounded. Moreover every solution in this set is bounded in the past.

Example 2

Consider another ODE

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = y,\\ y' = -x,\\ z'=-z. \end{array}\right. } \end{aligned}$$

Again, the point (0, 0, 0) is the equilibrium. All other solutions with $z=0$ are periodic—they are circles in (x, y) centered at zero. In fact every (x, y) circle centered at zero is a periodic solution. The set $\{ (x,y,0)\, :\ (x,y)\in {{\mathbb {R}}}^2 \}$ is invariant, unbounded and attracting. Every solution in this set is bounded both in the past and in the future. All other solutions are unbounded in the past and bounded in the future.

Above two examples show that it is natural to consider the points in the phase space through which there exists a solution defined for all $t\in {\mathbb {R}}$ which is bounded in the past, and one can expect that the set of such points should be invariant, and, in appropriate sense, attracting. This observation allowed Chepyzhov and Goritskii [9] to define the concept of unbounded attractor for the problem governed by the PDE $u'=Au + f(u)$ as a the set of initial conditions of solutions which bounded in the past. In this paper we follow the same concept.

The key contribution of the present article is the refinement and extension in several directions of the results from [9]. We pass to the detailed description of the contribution and novelty of our work in comparison with the previous research on unbounded attractors. First of all we provide the new criteria for the semigroup of operators $\{S(t)\}_{t\ge 0}$ on a Banach space X to have the unbounded attractor. This semigroup does not have necessarily to be governed by the differential equation, be it PDE or ODE. Hence, the result on the existence of the unbounded attractor, Theorem 3, the first important theorem of the present article, is formulated and proved for an abstract semigroup. We stress, that while the argument to prove this theorem mostly follows the lines of the corresponding proofs in [9], the present contribution lies in finding the abstract criteria, cf., (H1)–(H3) in the sequel, which guarantee its existence.

The important property needed in the proof is to be able to split the phase space of the problem X as the sum of two spaces $X=E^+\oplus E^-$ such that the projection P on $E^+$ of the solution can possibly diverge to infinity, and its projection on $E^-$ denoted by $I-P$ enjoys the dissipative properties. For the general setup of semigroups, following [9], under our criteria, the unbounded attractor ${\mathcal {J}}$ attracts bounded sets B only in bounded sets in $E^+$, that is

$$\begin{aligned} \lim _{t\rightarrow \infty }\text {dist}\, (S(t)B \cap \{ \Vert Px\Vert \le R\}, {\mathcal {J}}) = 0, \end{aligned}$$

(1)

as long as the sets $S(t)B \cap \{ \Vert Px\Vert \le R\}$ stay nonempty. A natural question that appears is, when one can remove the set $\{ \Vert Px\Vert \le R\}$ from the above attracting property. While in [9] the authors prove such convergence if the linear manifold $E^+$ is attracting for the solutions that diverge to infinity, we provide more general criterion [see condition (A1) in Sect. 2.3], and show such attraction in Theorem 4. The criterion says that the attraction in the whole space occurs if there exists the attracting set with the thickness in space $E^-$ tending to zero as $\Vert Pu\Vert$ tends to infinity. This result later becomes useful in the part on inertial manifolds for the problem governed by PDEs, see Sect. 4.4.3.

We compare the results of our article with the results of the very recent paper of Bortolan and Fernandes [4], where another abstract framework also stemming from the work of [9] has been proposed. The authors there provide abstract conditions which guarantee the existence of unbounded attractor, which they define as the smallest closed set ${\mathcal {U}}$ which is at the same time invariant and attracting in the sense that

$$\begin{aligned} \lim _{t\rightarrow \infty }\textrm{dist}(S(t)B,{\mathcal {U}}) = 0. \end{aligned}$$

(2)

Similar to us, and following the approach of Chepyzhov and Goritskii [9], the authors of [4] consider the maximal invariant set ${\mathcal {I}}$ of a semigroup and find the conditions which guarantee that it is an unbounded attractor. The crucial difference between [4] and our approach is the way to obtain the key property of this attractor: that it attracts. Namely, in [4] it is assumed that the maximal invariant set attracts the absorbing set, which allows the authors to get the attraction (2). This assumption on one hand appears strong, but, on the other hand, allows the authors to build an abstract framework without the need of the spaces $E^+$ and $E^-$. Our approach is based on these spaces which, in principle, makes it less general, but, at the same time, we do not need to assume any attraction, we recover it from the existence of appropriate absorbing set and generalized asymptotic compactness. Moreover, in our approach the attraction is considered in bounded sets in the sense (1). After we obtain it, we provide additional criterion on the thickness of absorbing set, under which the attraction occurs in the standard sense (2). Same comparison extends to the non-autonomous theory built in [4] and in the present paper.

The next series of our results is inspired by the works of [6, 18] later extended and refined in [3, 21, 27]. Namely, for the case of the semigroup governed by the following PDE in one space dimension

$$\begin{aligned} u_t = u_{xx} + bu +f(u,u_x,x), \end{aligned}$$

on the space interval, with appropriate (typically Neumann) boundary data, and sufficiently large constant $b>0$ the authors there study the detailed structure of the unbounded attractor which consists of equilibria, their heteroclinic connections, appropriately understood ‘equilibria at infinity’ and their connections, as well as heteroclinic connections from the equilibria to ‘equilibria at infinity’. We present the new abstract results on the global attractor structure for the general, not necessarily gradient case. Clearly, for such general case it is not possible to fully describe the structure of the attractor. However, we prove in Sect. 2.4, that the unbounded attractor must consist of an invariant set ${\mathcal {J}}_b$, built from points through which passes a bounded, both in the past and in the future, solution and the remainder, ${\mathcal {J}}\setminus {\mathcal {J}}_b$ which consists of the heteroclinics to infinity, namely of the points for which the alpha limits belong to ${\mathcal {J}}_b$ and for which the dynamics diverges to infinity as time tends to infinity. We study the properties of these sets, and in particular we show that ${\mathcal {J}}_b$ enjoys properties of the global attractor: it is compact under additional natural assumption (H4), which, however excludes the cases like Example 2 above, cf. Theorem 8, and by taking the set of points in the phase space which upon evolution converge to it, one obtains a complete metric space on which it is a classical global attractor, cf. Lemma 8.

We conclude the abstract results on slowly non-dissipative autonomous problems with several observations, which are, to our knowledge, new. The first one is, that the unbounded attractor coincides with a multivalued graph over $E^+$, which we call a multivalued inertial manifold in spirit of [15, 29], cf., our Sect. 2.5. The second observation concerns the unbounded $\omega$-limit sets, whose properties we study in Sect. 2.6, and which, to our knowledge, have not been studied before. Interestingly, while we prove the unbounded counterparts of the classical properties of $\omega$-limit sets, i.e. invariance, compactness, and attraction, we were not able to prove their connectedness, and we leave, for now, the question of their connectedness open. Finally, in Sect. 2.7, we discus, on an abstract level, the dynamics at infinity, which corresponds to the equilibria at infinity and their connections in [3, 6, 18, 21, 27], and we prove, using the Hopf lemma, and homotopy invariance of the degree, that the attractor at infinity always coincides with the whole unit sphere in $E^+$.

The study on unbounded non-autonomous attractors has been initiated by Carvalho and Pimentel in [13]. The authors study there the non-autonomous problem governed by the equation

$$\begin{aligned} u_t = u_{xx} + b(t)u + f(u). \end{aligned}$$

For this problem they formulate the definition of the unbounded pullback attractor, being the natural extension of the autonomous definition, and provide the result on its existence. We continue the study on pullback unbounded attractors: we give the general definition of such object and prove the result on its existence in the abstract framework, cf., Theorem 11, for slowly non-dissipative processes. The unbounded pullback attractor is the family of sets $\{{\mathcal {J}}(t) \}_{t\in {\mathbb {R}}}$, each of them being unbounded, we obtain the result on its structure similar as in the autonomous situation. ${\mathcal {J}}(t) = {\mathcal {J}}_b(t) \cup ({\mathcal {J}}(t)\setminus {\mathcal {J}}_b(t))$, where ${\mathcal {J}}_b(t)$ shares the properties of classical pullback attractors, and the solutions through points in ${\mathcal {J}}(t)\setminus {\mathcal {J}}_b(t)$ (at time t) that diverge to infinity forward in time. Note that the construction of sets ${\mathcal {J}}_b(t)$ is not the simple transition to non-autonomous case of the autonomous one. In the autonomous case the corresponding set ${\mathcal {J}}(t)$ is constructed using the concept of $\alpha$-limit sets, while in the non-autonomous situation we need to study the forward behavior of the points from the unbounded pullback attractor. Finally, we provide the construction of pullback $\omega$-limit sets in the unbounded non-autonomous framework. As we prove, there naturally appear two universes of sets for which one can define such $\omega$-limits: the backward bounded ones, and the ones whose forward solutions stay bounded. We prove that for the first universe non-autonomous $\omega$-limit sets are attracting and invariant in ${\mathcal {J}}(t)$, while for the second one they are attracting and invariant in ${\mathcal {J}}_b(t)$.

The second part of this paper is devoted to the study of the unbounded attractors for the dynamical system governed by the following differential equation in the Banach space X

$$\begin{aligned} u_t = Au + f(u), \end{aligned}$$

where A is the linear, closed and densely defined operator, which is sectorial, has compact resolvent and no eigenvalues on the imaginary axis. Denoting by P its spectral projector on the space associated with $\{ \text {Re}\, \lambda > 0 \}$, which is our space $E^+$, we have

$$\begin{aligned} \begin{aligned}&\Vert e^{A(t-s)}\Vert \le M e^{\gamma _0(t-s)}\quad \text {for}\ \ \ t\ge s,\\&\Vert e^{A(t-s)}(I-P)\Vert \le M e^{-\gamma _2(t-s)}\quad \text {for}\ \ \ \ t\ge s,\\&\Vert e^{A(t-s)}P\Vert \le M e^{\gamma _1(t-s)}\quad \text {for}\ \ \ \ t\le s, \end{aligned} \end{aligned}$$

(3)

where $\gamma _0, \gamma _1, \gamma _2, M$ are positive constants. Thus, our analysis is based on the general concept of the mild solutions and the Duhamel formula, rather then on weak solutions, and energy estimates as in [9]. Our first interest lies in showing, in Theorem 15, that if f(u) tends to zero, with appropriate rate, as $\Vert Pu\Vert$ tends to infinity, then the thickness of the unbounded attractor also tends to zero. In such case one can remove the restriction in the definition of the unbounded attractor that the attraction takes place in balls. Similar result has already been obtained in [9], where, however, the polynomial decay of f is assumed, namely, $\Vert f(u)\Vert \le \frac{C}{\Vert Pu\Vert ^\alpha }$. We recover and improve this result in the framework of mild solutions, by allowing for very slow decay, such as $\Vert f(u)\Vert \le \frac{C}{\ln (\Vert Pu\Vert )}$ for large $\Vert Pu\Vert$.

We continue the analysis by trying to answer the question whether the thickness of the unbounded attractor can tend to zero (and thus the attraction by the unbounded attractor can occur in the whole space) without the decay of f. We give the positive answer to this question with the help of the theory of inertial manifolds. Inertial manifolds in the framework of the unbounded attractors have already been studied by Ben-Gal [6]. In this classical approach the spectral gap can be taken between any two (sufficiently large) eigenvalues of $-A$, and leads to the inertial manifold which contains the unbounded attractor. We follow the different path: namely we choose the spectral gap exactly between the spaces $E^+$ and $E^-$. While this gives strong restriction on the Lipschitz constant of the nonlinearity, interestingly, as we show, such approach leads to the inertial manifold which exactly coincides with the unbounded attractor. We construct this manifold by the two methods: the Hadamard graph transform method, where we base our approach on the classical article [24] (note that the non-autonomous version of the construction of inertial manifolds by the graph transform method valid in context of the unbounded attractors but based on the energy estimates rather than the Duhamel formula has been realized in [17]), and the Lyapunov–Perron method, based on its modern and non-autonomous rendition in framework of inertial manifolds [11]. We find out, that while the graph transform method works only for the case $M=1$, from the numerical comparison of the restrictions on $L_f$, the Lipschitz constants of f, which we found in both methods, that the graph transform approach gives the better (i.e. larger, although still expected to be non-sharp, cf. [31, 32]) bound on $L_f$ than the Lyapunov–Perron method. Both above restrictions likely occur due to unoptimality of our approach (see, for example [28], where the author, for the case of dissipative and self adjoint principal operator reduces a version of the Lyapunov–Perron method to the verification of the cone condition, and thus shows that the restriction on the Lipschitz constant in both approaches is the same), but we cannot entirely exclude the possibility that for the problem under consideration there exist some inherent limitations of both approaches. The question to optimize the constant in Lyapunov–Perron method and realize the graph transform for $M>1$, in our opinion, deserves further study.

In our further analysis we demonstrate that it is in fact sufficient to assume that the nonlinearity has the small Lipschitz constant only for large $\Vert Pu\Vert$, while for small $\Vert Pu\Vert$ it does not have to be Lipschitz at all. While in such a case the unbounded attractor does not have to be a Lipschitz manifold, we demonstrate by the appropriate modification of the nonlinearity f, that for large $\Vert Pu\Vert$ it has to stay close to a Lipschitz manifold, whence its thickness, although it may be nonzero contrary to the case of small global Lipschitz constant, tends to zero with increasing $\Vert Pu\Vert$.

In the last result of this article we discuss the asymptotic behavior at infinity, which is the more general version of the results from [13, 18]. Namely, we show that the rescaled problem at infinity is asymptotically autonomous, and hence its $\omega$-limits coincide with the $\omega$-limits of the finite dimensional autonomous problem at infinity whose dynamics can be explicitly constructed.

We stress that while we endeavor on building the comprehensive theory of unbounded attractors, our approach still has limitations. While we consider only the possibility of grow-up solutions, there are other possibilities of asymptotic behaviors which we could encompass in our theory (see [8] for a recent and comprehensive overview). Moreover, in most of the results we consider only directions that are dissipative (those in $E^-$) and expanding (those in $E^+$). It would be interesting to extend the analysis of the case of neutral dimensions, in which the solutions are not absorbed in finite time by a given bounded set, but still stay bounded, such as in Example 2, especially that such problems has recently arisen a significant interest in fluid mechanics, cf. [5].

The plan of this article is the following: Sect. 2 is devoted to the autonomous abstract theory of unbounded attractors. In the next Sect. 3 we study, on abstract level, the non-autonomous unbounded attractors in the abstract framework. Finally, in Sect. 4 we present the results on unbounded attractors for the problem governed by the equation $u_t = Au + f(u)$.

2 Unbounded Attractors and $\omega$-Limit Sets: Autonomous Case

2.1 Non-dissipative Semigroups and Their Invariant Sets

If X is a metric space (${\mathcal {P}}(X)$ represents the subsets of X and ${\mathcal {P}}_0(X)$ represents the non-empty subsets of X) then ${\mathcal {P}}(X)$ are its nonempty subsets and ${\mathcal {B}}(X)$ are its nonempty and bounded subsets.

Definition 1

Let X be a metric space. A family of mappings $\{ S(t):D(S(t)) \subset X \rightarrow X \}_{t\ge 0}$ is a solution operator family if

• $D(S(0))=X$ and $S(0) = I$ (identity on X),

• For each $x\in X$ there exists a $\tau _x\in (0,\infty ]$ such that $x\in D(S(t))$ for all $t\in [0,\tau _x)$.

• For every $x\in X$ and $t,s\in {{\mathbb {R}}}^+$ such that $t+s\in [0,\tau _x)$ we have $S(t+s)x = S(t)S(s)x$,

• If $E=\{(t,x)\in {{\mathbb {R}}}^+\times X: t\in [0,\tau _x)\}$, the mapping $E \ni (t,x)\mapsto S(t)x\in X$ is continuous.

If $\tau _x=+\infty$ for all $x\in X$, $D(S(t))=X$ for all $t\ge 0$ and $E={{\mathbb {R}}}^+\times X$. In this case we say that the family $\{ S(t)\}_{t\ge 0}$ is a continuous semigroup.

When we will apply the above definition to differential equations, the mapping S(t) will assign to the initial data the value of the solution at the time t.

Definition 2

The function $[0,\tau _x)\ni t \mapsto S(t)x\in X$ is called a solution.

Definition 3

The function $\gamma :{\mathbb {R}}\rightarrow X$ is a global solution if $S(t)\gamma (s) = \gamma (s+t)$ for every $s\in {\mathbb {R}}$ and $t\ge 0$.

Definition 4

The global solution $\gamma$ is bounded in the past if the set $\gamma ({\mathbb {R}}^-)=\{\gamma (t)\in X:t\le 0\}$ is bounded.

Definition 5

The global solution $\gamma$ is bounded if the set $\gamma ({\mathbb {R}})=\{\gamma (t)\in X:t\in {\mathbb {R}}\}$ is bounded. If $x=\gamma (0)$ we say that $\gamma :{{\mathbb {R}}}\rightarrow X$ is a global solution through x.

The non-dissipativity of the problem can be manifested threefold:

• (A) solutions may cease to exist (e.g. blow up to infinity) in finite time, that is, for some $x\!\in \! X$, $\tau _x\!<\!\infty$.

• (B) solutions may grow-up, that is, it could happen that $\tau _x=\infty$ for some $x\in X$, with the set $\{ S(t)x: t\ge 0\}$ being unbounded (this is the case in Example 1),

• (C) all solutions may stay bounded but, even so, there may not exist a bounded set which absorbs all of them (this is the case in Example 2).

We will assume that $\tau _x=\infty$ for all $x\in X$, that is, that $\{S(t)\}_{t\ge 0}$ is a semigroup. Hence we exclude the situation of item (A) above.

Systems which exhibit the behaviors (B) or (C) for some solutions are called slowly non-dissipative, cf. [6]. In case of grow-up, i.e. in the case (B), it is still possible to distinguish between two situations: either for some $x\in X$ we have that $\lim _{t\rightarrow \infty }d(S(t)x,x) = \infty$ (solution diverges) or $\limsup _{t\rightarrow \infty }d(S(t)x,x)=+\infty$ but the solution does not diverge (oscillate). To see that the latter situation is possible, a simple non-autonomous example is

$$\begin{aligned} x'(t) = \sin (t) - t\cos (t), \end{aligned}$$

then if $x(0) = 0$ the solution is $x(t) = t\sin (t)$, so we have the oscillations with the amplitude growing to infinity as $t\rightarrow \infty$. Later we will introduce the assumption on the semigroup which exclude such situation.

We define two notions of invariant sets for non-dissipative semigropups. The first definition follows [9] where it is called the maximal invariant set.

Definition 6

Let $\{ S(t) \}_{t\ge 0}$ be a continuous semigroup. The set ${\mathcal {I}}$ is the maximal invariant set if

$$\begin{aligned} {\mathcal {I}} = \{ x\in X\,:\text { there is a global solution } \gamma :{{\mathbb {R}}}\rightarrow X \ \text {through } x \text { which is bounded in the past}\} \end{aligned}$$

It is also possible to define another notion, which coincides with the classical concept in the theory of global attractors.

Definition 7

Let $\{ S(t) \}_{t\ge 0}$ be a continuous semigroup. The set ${\mathcal {I}}_b$ maximal invariant set of bounded solutions if

$$\begin{aligned} {\mathcal {I}}_b = \{ x\in X\,:\text { there is a global bounded solution } \gamma :{{\mathbb {R}}}\rightarrow X \text {through } x \} \end{aligned}$$

We make a simple observation.

Observation 1

We have ${\mathcal {I}}_b \subset {\mathcal {I}}$ with the possibility of strict inclusion. ${\mathcal {I}}$ is unbounded and ${\mathcal {I}}_b$ may be unbounded. Both sets are invariant, i.e. $S(t) {\mathcal {I}} = {\mathcal {I}}$ and $S(t) {\mathcal {I}}_b = {\mathcal {I}}_b$ for all $t\ge 0$. Furthermore,

$$\begin{aligned} x \in {\mathcal {I}}\setminus {\mathcal {I}}_b \Longleftrightarrow x \in {\mathcal {I}}\ \ \text {and} \ \ \{ S(t)x\}_{t\ge 0}\ \ \text {is unbounded}. \end{aligned}$$

In Example 2 above ${\mathcal {I}} = {\mathcal {I}}_b = {\mathbb {R}}^2$. In Example 1 above ${\mathcal {I}} = \{0\}\times {\textbf{R}}$ and ${\mathcal {I}}_b =\{ (0,0) \}$. Note that in Example 1${\mathcal {I}}\setminus {\mathcal {I}}_b$ consists of heteroclinics to infinity as defined by [6], see also [18] and the articles [3, 13, 21, 27].

2.2 Existence of Unbounded Attractors

The content of this chapter relies in putting to the abstract setting the results of Chepyzhov and Goritskii [9] obtained there for the particular initial and boundary value problem governed by the PDE $u' = \Delta u + \beta u + f(u)$ on a bounded domain with the homogeneous Dirichlet boundary data. We will frequently use in the proofs the following result which appears in [9, Lemma 2.1].

Lemma 1

Let $\{L_n\}$ be a sequence of nested sets in a Banach space X, i.e.

$$\begin{aligned} L_1 \supset L_2 \supset L_3 \supset \ldots , \end{aligned}$$

such that every set $L_n$ lies in the $\epsilon _n$-neighborhood of some compact subset $K_n$, namely $L_n\subset {\mathcal {O}}_{\epsilon _n}(K_n)$, with $\lim _{n\rightarrow \infty }\epsilon _n= 0$. Then from any sequence of points $\{y_n\}$, where $y_n\in L_n$, we can choose a convergent subsequence. Moreover the set $L = \bigcap _{n=1}^\infty {\overline{L}}_n$ is compact.

Definition 8

The semigroup $\{S(t)\}_{t\ge 0}$ is generalized asymptotically compact if for every $B\in {\mathcal {B}}(X)$ and every $t>0$ there exists a compact set $K(t,B)\subset X$ and $\varepsilon (t,B)\rightarrow 0$ as $t\rightarrow \infty$ such that

$$\begin{aligned} S(t)B\subset {\mathcal {O}}_\varepsilon (K(t,B)). \end{aligned}$$

Now let X be a Banach space and let $E^+$ and $E^-$ its subspaces. We assume that $E^+$ is finite dimensional and that $E^-$ is closed. Moreover, $X= E^+ \oplus E^-$, i.e. we can uniquely represent any $x\in X$ as $x=p+q$ with $p\in E^+$ and $q\in E^-$. Then we will denote $p = Px$ and $q=(I-P)x$. The closed graph theorem implies that the projections P and $I-P$ are continuous. We will use the shorthand notation $\{ \Vert Px\Vert \le R\} = \{ x\in X\;:\ \Vert Px\Vert \le R \}$ and $\{ \Vert (I-P)x\Vert \le D\} = \{ x\in X\;:\ \Vert (I-P)x\Vert \le D \}$. We will impose the following assumptions to the semigroup $\{S(t)\}_{t\ge 0}$, in order to prove the existence of an unbounded attractor

• (H1) There exist $D_1, D_2 > 0$ and a closed set Q with $\{ \Vert (I-P)x\Vert \le D_1\} \subset Q \subset \{ \Vert (I-P)x\Vert \le D_2\}$ such that Q absorbs bounded sets, and is positively invariant, i.e. for every $B\in {\mathcal {B}}(X)$ there exists $t_0(B) > 0$ such that $\bigcup _{t\ge t_0}S(t)B \subset Q$ and $S(t)Q \subset Q$ for every $t\ge 0$.

• (H2) There exist the constants $R_0$ and $R_1$ with $0<R_0\le R_1$ and an ascending family of closed and bounded sets $\{H_R\}_{R\ge R_0}$ with $H_R \subset Q$, such that

  • (1) for every $R\ge R_1$ we can find $S(R)\ge R_0$ such that $\{ \Vert Px\Vert \le S(R)\} \cap Q \subset H_R$ and moreover $\lim _{R\rightarrow \infty } S(R) = \infty$,

  • (2) for every $R\ge R_1$ we have $H_{R} \subset \{ \Vert Px\Vert \le R\}$,

  • (3) and $S(t)(Q \setminus H_R) \subset Q \setminus H_R$ for every $t\ge 0$.

• (H3) The semigroup $\{S(t)\}_{t\ge 0}$ is generalized asymptotically compact.

Define the unbounded attractor as

$$\begin{aligned} {\mathcal {J}} = \bigcap _{t\ge 0}\overline{S(t)Q} \end{aligned}$$

(4)

It is clear that the unbounded attractor is a closed set. We begin with establishing the relation between the maximal invariant set ${\mathcal {I}}$ and the unbounded attractor ${\mathcal {J}}$. The argument follows the lines of the proof of [9, Proposition 2.7 and Proposition 2.10 c)].

Theorem 1

If (H1)–(H3) hold, then ${\mathcal {I}} = {\mathcal {J}}$.

Proof

We first prove that ${\mathcal {I}}\subset {\mathcal {J}}$. To this end assume that $u \in {\mathcal {I}}$ and denote by $\gamma$ the bounded in the past solution such that $u = \gamma (0)$. Moreover let T be such that $S(T)\{ \gamma (s)\,:\ s\le 0 \} \subset Q$. If $t\ge 0$ then $S(T+t)\{ \gamma (s)\,:\ s\le 0 \} \subset S(t)Q$. But, since $u = S(T+t)\gamma (-T-t)$, then $u\in S(t)Q$ and, consequently $u\in {\mathcal {J}}$.

We establish the converse inclusion. To this end take $u\in {\mathcal {J}}$. Then there exists a sequence $\{y_n\} \subset Q$ such that $S(n)y_n \rightarrow u$ as $n\rightarrow \infty$. Since $\{ S(n)y_n \}$ is a convergent sequence, it is bounded, it follows that $\{ S(n)y_n \} \subset H_R$ for some $R\ge R_0$ and $u\in H_R$. By item 3 of (H2) this means that for every n and for every $t\in [0,n]$ we have $S(t)y_n \in H_R$. As $S(n)y_n = S(1)S(n-1)y_n$ we deduce that $S(n-1)y_n \in H_R\cap S(n-1)H_R = H_R \cap S(n-1)Q$. By (H3) and by Lemma 1, it follows that, for a subsequence, $S(n-1)y_n \rightarrow z$, whence $S(1)z = u$ and $z\in H_R$. Picking $t\ge 0$, for n large enough $S(t)Q \ni S(t)S(- t+n-1)y_n = S(t - t+n-1)y_n \rightarrow z$ and hence $z\in {\mathcal {J}}$. Proceeding recursively, we can construct the solution $\{ \gamma (t)\,:\ t\le 0\} \subset Q$ such that $\gamma (0) = u$. As $u\in H_R$, by item 3 of (H2) it must be that $\gamma (t) \in H_R$ for every $t\le 0$ and the proof is complete. $\square$

We formulate a simple lemma on the possible behavior of bounded sets upon evolution.

Lemma 2

Assume (H1)–(H2) and let $R\ge R_0$. If $B\in {\mathcal {B}}(X)$ then exactly one of three cases holds:

• (1) there exists $t_1 > 0$ such that for every $t\ge t_1$

  $$\begin{aligned} S(t)B \subset Q \setminus H_R. \end{aligned}$$

• (2) there exists $t_1 > 0$ such that for every $t\ge t_1$

  $$\begin{aligned} S(t)B \cap H_R \ne \emptyset \ \ \text {and}\ \ S(t)B \cap (Q \setminus H_R) \ne \emptyset . \end{aligned}$$

• (3) there exists $t_1 > 0$ such that for every $t\ge t_1$

  $$\begin{aligned} S(t)B \subset H_R . \end{aligned}$$

Proof

Suppose that (3) does not hold. This means that there exists $t_1 > t_0(B)$ such that $S(t_1)B \cap (Q\setminus H_R) \ne \emptyset$. By (H2) we deduce that $S(t)B \cap (Q\setminus H_R) \ne \emptyset$ for every $t\ge t_1$. If for some $t_2\ge t_1$ there holds $S(t_2) B \cap H_R = \emptyset$ then $S(t_2)B\subset Q\setminus H_R$ and (H2) implies that $S(t)B\subset Q\setminus H_R$ for every $t\ge t_2$, which completes the proof. $\square$

The proof of the following result is established in [9, Lemma 2.8], here we present the proof that makes the explicit use of the Brouwer degree. This result, in particular, implies that the set ${\mathcal {I}} = {\mathcal {J}}$ is nonempty.

Lemma 3

Assume (H1)–(H3). For every $p \in E^+$ there exists $q\in E^-$ such that $p+q \in {\mathcal {J}}$.

Proof

Let $p\in E^+$. By item 1 of (H2) there exists $R\ge R_0$ such that $\{x\in E^+ \,:\ \Vert x\Vert \le \Vert p\Vert +1 \} \subset H_R$. Define $B = \{ x\in E^+\, :\ \Vert x\Vert < R + 1\}$. Since, by item 2 of (H2), $p \in B$ it is clear that the Brouwer degree $\text {deg}(I,B,p)$ is equal to one, cf. [25, Theorem 1.2.6 (1)]. Pick $t>0$ and define the mapping $[0,1]\times {\overline{B}} \ni (\theta ,p) \mapsto P S(\theta t) p \in E^+$. This mapping is continuous. Moreover, as, by item 3 of (H2), $\partial B = \{ x\in E^+\, :\ \Vert x\Vert = R + 1 \} \subset Q\setminus H_R$ we deduce that $p \not \in PS(\theta t)\partial B$ for every $\theta \in [0,1]$. Hence, by the homotopy invariance of the Brouwer degree, cf. [25, Theorem 1.2.6 (3)] we deduce that $\text {deg}(P S(t),B,p) = 1$, whence, cf. [25, Theorem 1.2.6 (2)], there exists $p_t\in B$ such that $PS(t) p_t = p$. Let $t_n\rightarrow \infty$. There exists a sequence $p_n \in B$ such that $PS(t_n)p_n = p$. Hence we can find $q_n \in E^-$ such that $y_n = p+q_n = S(t_n)p_n \in S(t_n) Q$. From the fact that $p\in B$ we deduce by item 1 of (H2) that there exists $R' \ge R_1$ such that $y_n \in H_{R'}$ for every n. This means that $y_n \in S(t_n)H_{R'} \cap H_{R'}$. As $H_{R'}$ is bounded and the sequence of sets $S(t_n)H_{R'} \cap H_{R'}$ is nested, we can use (H3) and Lemma 1 to deduce that, for a subsequence, $y_n \rightarrow y$. Since for every $t\ge 0$ we have $y_n \in S(t)Q$ for every n such that $t\le t_n$ it follows that $y\in {\mathcal {J}}$. The continuity of P implies that $Py = p$ and the proof is complete. $\square$

The proof of the following result uses the argument of [9, Proposition 3.4]

Theorem 2

Let (H1)–(H3) hold. Let $R\ge R_1$ and let $B\in {\mathcal {B}}(X)$. Then either there exist $t_1>0$ such that for every $t\ge t_1$ we have $S(t)B\subset Q\setminus H_{R}$ or

$$\begin{aligned} \lim _{t\rightarrow \infty }\textrm{dist}(S(t)B\cap \{\Vert Px\Vert \le R\},{\mathcal {J}}) = 0. \end{aligned}$$

Proof

We can assume that there exists $t_1>0$ such that $S(t)B \cap H_{R}\ne \emptyset$ for every $t\ge t_1(B)$ (i.e. 2. or 3. Lemma 2 hold). Then for $t\ge t_1$ the sets $S(t)B \cap H_{R} \subset S(t)B \cap \{ \Vert Px\Vert \le R\}$ are nonempty. For the proof by contradiction let us take the sequences $\{x_n\}\subset B$ and $t_n \rightarrow \infty$ such that $S(t_n)x_n \in S(t_n)B \cap \{ \Vert Px\Vert \le R \}$ for every n, and

$$\begin{aligned} \textrm{dist} (S(t_n)x_n,{\mathcal {J}})>\varepsilon \end{aligned}$$

for some $\varepsilon >0$. By (H1) we can assume without loss of generality that $B\subset Q$. Denote $y_n=S(t_n)x_n$. Then by item 1 of (H2) we can find ${\overline{R}}\ge R_0$ such that $\{y_n\}\subset H_{{\overline{R}}}$ and it is a bounded sequence. By item 3 of assumption (H2) we know that $\{x_n\}\subset H_{{\overline{R}}}$. We define the nested sequence of sets $L_n=S(t_n)Q\cap H_{{\overline{R}}}=S(t_n)H_{{\overline{R}}}\cap H_{{\overline{R}}}$, and by assumption (H3) we know that for every n there exist a compact set $K_n$ such that $L_n\subset {\mathcal {O}}_{\epsilon _n}(K_n)$, and $\varepsilon _n\rightarrow 0$ when $n\rightarrow \infty$. By Lemma 1 there exists y such that $y_n\rightarrow y$, so by definition, $y\in {\mathcal {J}}$, and then, we arrive to a contradiction. $\square$

The above result guarantees only the attraction in the bounded sets. The next example of an ODE in 2D shows that under our assumptions the ’classical’ notion of attraction, in the sense $\lim _{t\rightarrow \infty }\textrm{dist}(S(t)B,{\mathcal {J}}) = 0$, cannot hold.

Example 3

The vector field for the next system of two ODEs is defined only in the quadrant $\{ x\ge 0, y\ge 0\}$. In the remaining three quadrants it can be extended by the symmetry.

$$\begin{aligned}&x'(t) = x(t),\\&y'(t) = {\left\{ \begin{array}{ll} -y(t) + \frac{x(t)y(t)}{1+x(t)}\ \ \text {if}\ \ y(t)\in [0,1],\\ -y(t) + (2-y(t))\frac{x(t)y(t)}{1+x(t)}\ \ \text {if}\ \ y(t)\in [1,2],\\ -y(t)\ \ \text {if}\ \ y(t)\ge 2. \end{array}\right. } \end{aligned}$$

Then

• the maximal invariant set is given by ${\mathcal {J}} = \{(x,0)\,:\ x\in {\mathbb {R}}\}$,

• the set $Q = \{ (x,y)\in {\mathbb {R}}^2\,:\ |y|\le 2 \}$ is absorbing and positively invariant,

• the sets $\{ (x,y)\in {\mathbb {R}}^2\,:\ |y|\le 2,|x|>a \}$ are positively invariant for every $a>0$,

• the image of a bounded set by S(t) is relatively compact, and we have the continuous dependence on initial data,

• the set ${\mathcal {J}}$ is not attracting as one can construct solutions satisfying $x(t)\rightarrow \infty$ and $y(t) \rightarrow c$ for every $c\in (0,1)$.

Finally, the following result on $\sigma$-compactness is a counterpart of [9, Proposition 2.6]

Lemma 4

For every bounded and closed set B the set ${\mathcal {J}}\cap B$ is compact. Hence, ${\mathcal {J}}$ is a countable sum of compact sets.

Proof

Since ${\mathcal {J}}\cap B$ is closed it is enough to show that it is relatively compact. To this end, it is sufficient to prove that for every $R\ge R_0$ the set ${\mathcal {J}}\cap H_R$ is relatively compact. Assume that $\{ u_n\} \subset {\mathcal {J}}\cap H_R$ is a sequence. By invariance of ${\mathcal {J}}$ there exists $x_n\in {\mathcal {J}}$ such that $u_n = S(n) x_n$. It must be that $x_n\in H_R$ and hence $u_n\in S(n)H_R \cap H_R = S(n)Q \cap H_R$. Using (H3) and Lemma 1 we obtain the assertion. $\square$

The last result is on the unbounded attractor minimality

Lemma 5

Assume (H1)–(H3). If C is a closed set such that for every $B\in {\mathcal {B}}(X)$ for which there exists $t_1>0$ and $R\ge R_1$ such that $S(t)B\cap \{\Vert Px\Vert \ge R\}$ is nonempty for $t\ge t_1$ we have $\lim _{t\rightarrow \infty }\textrm{dist}(S(t)B\cap \{\Vert Px\Vert \le R\},C) = 0,$ then ${\mathcal {J}}\subset C$.

Proof

Suppose, for contradiction, that $v \in {\mathcal {J}} \setminus C$. There exists the global solution $\gamma$ with $\gamma (0) = 0$ such that $\gamma ((-\infty ,0])$ is a bounded set. Moreover there exists $R\ge R_1$ such that $v = S(t)\gamma (-t) \in S(t) \gamma ((-\infty ,0]) \cap \{\Vert Px\Vert \le R \}$. Hence

$$\begin{aligned} \text {dist}(v,C)\le & {} \lim _{t\rightarrow \infty } \text {dist}(S(t) \gamma ((-\infty ,0]) \cap \{\Vert Px\Vert \le R \},C) \\= & {} 0, \end{aligned}$$

whence it must be that $v\in C$ which concludes the proof. $\square$

We summarize the results of this section in the following result.

Theorem 3

Assume (H1)–(H3). Then the set ${\mathcal {J}}$ given by (4) is the unbounded attractor for the semiflow $\{ S(t) \}_{t\ge 0}$, that is:

• ${\mathcal {J}}$ is nonempty, closed, and invariant,

• intersection of ${\mathcal {J}}$ with any bounded set is relatively compact,

• if for some $R\ge R_1$, $B\in {\mathcal {B}}(X)$, and $t_1>0$ the sets $S(t)B \cap \{ \Vert Px\Vert \le R \}$ are nonempty for every $t\ge t_1$ then

  $$\begin{aligned} \lim _{t\rightarrow \infty } \textrm{dist}(S(t)B\cap \{\Vert Px\Vert \le R\},{\mathcal {J}}) = 0, \end{aligned}$$

  and ${\mathcal {J}}$ is the minimal closed set with the above property.

Moreover $P{\mathcal {J}}=E^+$ and ${\mathcal {J}}$ is the maximal invariant set for $\{ S(t) \}_{t\ge 0}$, that is it consists of those points through which there exists a global solution bounded in the past.

2.3 Attraction of All Bounded Sets

We will impose additional assumption.

• (A1) There exists a closed set $Q_1\subset Q$ such that:

  • (a) For every $\varepsilon >0$ there exist $r>0$ such that for every $p\in E^+$ for which $\left\| {p}\right\| \ge r$ there holds $\textrm{diam }( Q_1\cap \{x\in X: Px=p\} )\le \varepsilon$.

  • (b) The set $Q_1$ is attracting, that is for every $B\in {\mathcal {B}}(x)$ we have $\lim _{t\rightarrow \infty }\textrm{dist}(S(t) B, Q_1) = 0.$

We will prove following theorem.

Remark 1

If the conditions (H1)–(H3) and (A1) hold, then ${\mathcal {J}}\subset Q_1.$ In fact, if $u\in {\mathcal {J}}={\mathcal {I}}$, there is a global solution $\gamma :{\mathbb {R}}\rightarrow X$ through u ($\gamma (0)=u$) which is bounded in the past. As $\gamma ((-\infty ,0]) \subset S(t)\gamma ((-\infty ,0])$ then $\text {dist}(\gamma ((-\infty ,0]),Q_1) \le \text {dist}(S(t)\gamma ((-\infty ,0]),Q_1)\rightarrow 0$ as $t\rightarrow \infty$. Hence, as $Q_1$ is closed $u\in Q_1$.

Theorem 4

Assume that (H1)–(H3) and (A1) hold. Then for every bounded set B we have

$$\begin{aligned} \lim _{t\rightarrow \infty } \textrm{dist}(S(t)B,{\mathcal {J}})= 0. \end{aligned}$$

Proof

Assume that there are sequences $t_n\rightarrow \infty$ and $u_n\in B$ such that $\inf _{j\in {\mathcal {J}}}\left\| { S(t_n)u_n- j}\right\| >\varepsilon ,$ for some $\varepsilon <1.$ By Theorem 3 it follows that $\left\| {P S(t_n)u_n}\right\| \rightarrow \infty .$ By item (a) of (A1) we can pick $r>0$ such that for every $x_0\in X$ for which $\left\| {Px_0}\right\| >r$ we have $\textrm{diam }(Q \cap \{x\in X: Px= Px_0\}) \le \frac{\varepsilon }{4}.$ Then we pick $n_0$ such that $S(t_{n_0})u_{n_0} \in S(t_{n_0}) B \subset {\mathcal {O}}_{\frac{\varepsilon }{8}}(Q_1)$ and $\left\| { PS(t_{n_0})u_{n_0}}\right\| \ge r+1.$ So we find $v\in Q_1$ such that $\left\| { S(t_{n_0})u_{n_0}-v}\right\| \le \frac{\varepsilon }{4}.$ Observe that $\left\| {Pv}\right\| \ge r+\frac{1}{2}.$ Indeed if $\left\| {Pv}\right\|$ would be less than $r+\frac{1}{2}$ then we would have that $\left\| { S(t_{n_0})u_{n_0}-v}\right\| \ge \left\| {P(S(t_{n_0})u_{n_0}-v)}\right\| \ge \frac{1}{2}.$ By Lemma 3 we can find $w\in {\mathcal {J}}$ such that $Pv = Pw.$ Observe that $w,v\in Q_1 \cap \{x\in X: Pw = Px\}$ and $\left\| {Pv}\right\| >r.$ We deduce that $\left\| {w-v}\right\| \le \frac{\varepsilon }{4}.$ We observe that

$$\begin{aligned} \left\| {S(t_{n_0})u_{n_0}-w}\right\| \le \left\| {S(t_{n_0})u_{n_0}-v}\right\| +\left\| {v-w}\right\| \le \frac{\varepsilon }{2}. \end{aligned}$$

which is contradiction. $\square$

2.4 Structure of the Unbounded Attractor

Since the unbounded attractor is an invariant set, there exists a global (eternal) solution bounded in the past in the attractor through each point in it. Some of these solutions may be bounded and others may be unbounded in the future, and, due to the forward uniqueness, for a given point in ${\mathcal {J}}$ only one of these two possibilities may occur. We remember, that a bounded invariant set ${\mathcal {I}}_b$ consisted of those points through which there exist the complete bounded solutions. This gives us the decomposition of the unbounded attractor into two disjoint sets ${\mathcal {J}} = {\mathcal {I}}_b \cup ({\mathcal {J}} \setminus {\mathcal {I}}_b)$. We will provide the properties of this decomposition. Observe that ${\mathcal {J}}$, as a nonempty and closed subset of a Banach space, is a complete metric space. We denote by ${\mathcal {B}}({\mathcal {J}})$ the family of nonempty and bounded subsets of ${\mathcal {J}}$. We shall start from the definition of the $\alpha$-limit set.

Definition 9

Let $B\in {\mathcal {B}}({\mathcal {J}})$. We define the $\alpha$-limit set of B as

$$\begin{aligned} \alpha (B) = \{ u\in {\mathcal {J}}\,:\ \text {there exists}\ t_n\rightarrow \infty \ \text {and} \ \ u_n \in {\mathcal {J}}\ \ \text {such that} \ \ S(t_n)u_n\in B\ \ \text {and}\ \ u_n\rightarrow u\}. \end{aligned}$$

In the next result we establish the properties of the $\alpha$-limit set.

Theorem 5

Let $B\in {\mathcal {B}}({\mathcal {J}})$ and assume (H1)–(H3). Then $\alpha (B)$ is nonempty, compact, invariant, and attracts B in the past, i.e.

$$\begin{aligned} \lim _{t\rightarrow \infty } \textrm{dist}(S(t)^{-1}B,\alpha (B)) = 0. \end{aligned}$$

Proof

Pick $B\in {\mathcal {B}}({\mathcal {J}})$. Let $u_n \in {\mathcal {J}}$ and $t_n\rightarrow \infty$ be such that $S(t_n)u_n \in B$. As B is bounded, then $B\in H_R$ for some R and it must be that $u_n \in H_R$. As $H_R\cap {\mathcal {J}}$ is a compact set it must be that, for a subsequence, $u_n \rightarrow u$ for some $u\in {\mathcal {J}}\cap H_R$ and hence $\alpha (B)$ is nonempty. Moreover $\alpha (B) \subset {\mathcal {J}} \cap H_R$ so it must be relatively compact. To prove that it is closed pick a sequence $\{v_n\} \subset \alpha (B)$ with $v_n\rightarrow v$. There exist sequences $t_n^k\rightarrow \infty$ as $k\rightarrow \infty$ and $\{ v^n_k\}_{k=1}^\infty \subset {\mathcal {J}}$ with $S(t^n_k)v^n_k\in B$ and $v^n_k \rightarrow v_n$ as $k\rightarrow \infty$. It is enough to use a diagonal argument to get that $v\in \alpha (B)$. Hence $\alpha (B)$ is a compact set. To establish the invariance let us first prove that $S(t)\alpha (B) \subset \alpha (B)$. To this end let $u\in \alpha (B)$ and $t>0$. By continuity, $S(t)u_n \rightarrow S(t)u$, and $S(t_n-t)S(t)u_n = S(t_n)u_n \in B$, whence $S(t)u \in \alpha (B)$. To establish negative invariance also take $u\in \alpha (B)$ and $t>0$. There exist $v_n \subset {\mathcal {J}}\cap H_R$ such that $S(t)v_n = u_n$. By compactness, for a subsequence, $v_n\rightarrow v$ and by continuity $S(t)v_n \rightarrow S(t)v$, whence $S(t)v = u$. Moreover $S(t_n+t)v_n = S(t_n)u_n \in B$, whence $v\in \alpha (B)$, which ends the proof of invariance. The proof of attraction is also standard. For contradiction assume that there exists $t_n\rightarrow \infty$ and $u_n\in {\mathcal {J}}$ with $S(t_n)u_n\in B$ such that $\textrm{dist}(u_n,\alpha (B)) \ge \varepsilon$ for every n and some $\varepsilon > 0$. As $u_n \in {\mathcal {J}}\cap H_R$, by compactness we obtain that $u_n\rightarrow u$, for a subsequence and it must be $u\in \alpha (B)$ which is a contradiction. $\square$

An alternative approach to prove the above result would be to inverse time, which is possible on the unbounded attractor, and consider the $\omega$-limit set of inversed in time dynamical system, which can be possibly multivalued, as we do not assume the backward uniqueness.

As a consequence of the above result we obtain the following corollary

Corollary 1

For every $B \in {\mathcal {B}}({\mathcal {J}})$ there holds $\alpha (B)\subset {\mathcal {I}}_b$. In consequence, ${\mathcal {I}}_b$ is nonempty.

Define the set

$$\begin{aligned} {\mathcal {J}}_b = \bigcup _{R\ge R_0}\alpha ({\mathcal {J}}\cap H_R). \end{aligned}$$

For elements of ${\mathcal {J}}$ we define $S(t)^{-1}$ as the inverse in ${\mathcal {J}}$ which, as we do not assume backward uniqueness, can be possibly multivalued.

Theorem 6

There holds ${\mathcal {J}}_b = {\mathcal {I}}_b$. Moreover for every $B\in {\mathcal {B}}({\mathcal {J}})$ there holds

$$\begin{aligned} \lim _{t\rightarrow \infty } \textrm{dist}(S(t)^{-1}B, {\mathcal {J}}_b) = 0. \end{aligned}$$

Proof

If $u \in {\mathcal {J}}_b$ then $u\in \alpha ({\mathcal {J}}\cap H_R)$ for some R, an invariant and compact set. Hence there exists a bounded global solution through u in ${\mathcal {J}}$ and thus $u\in {\mathcal {I}}_b$. To get the opposite inclusion assume that $u\in {\mathcal {I}}_b$ whence $\{S(t)u\}_{t\ge 0}$ is bounded and there exists $R>0$ such that $S(t)u \in {\mathcal {J}}\cap H_R$ for every $t\ge 0$. It means that $u\in \alpha ({\mathcal {J}}\cap H_R)$.

To get the backward attraction observe that $B\subset {\mathcal {J}}\cap H_R$ for some R and hence $\alpha (B) \subset \alpha (J\cap H_R)$ which yields the assertion. $\square$

It is easy to see that if ${\mathcal {J}}_b$ is bounded then it has to be closed. In general, however, ${\mathcal {J}}_b$ can be unbounded and then it does not have to be a closed set as seen in the following example.

Example 4

The vector field is defined only in the quadrant $\{ x\ge 0, y\ge 0 \}$. It can be extended to other quadrants by the symmetry. Namely, we consider the following system of two ODEs,

$$\begin{aligned}&y' = {\left\{ \begin{array}{ll} &{}-y + 1 \ \ \text {for}\ \ y\ge 1,\\ &{} 0 \ \ \text {for}\ \ y\in [0,1]. \end{array}\right. }\\&\text {if}\ \ y>0\ \ \text {then}\ \ x' = {\left\{ \begin{array}{ll} &{} \max \{3y,1\}x\ \ \text {for}\ \ x\in \left[ 0,\min \left\{ \frac{1}{3y},1\right\} \right] ,\\ &{} 1\ \ \text {for}\ \ x\in \left[ \min \left\{ \frac{1}{3y},1\right\} ,\frac{2}{3y}\right] ,\\ &{} -3yx+3\ \ \text {for}\ \ x\in \left[ \frac{2}{3y},\frac{1}{y}\right] ,\\ &{} x-\frac{1}{y}\ \ \text {for}\ \ x\ge \frac{1}{y}. \end{array}\right. } \ \ \text {and} \ \ x'=\max \{x,1\}\ \text {for}\ \ y=0. \end{aligned}$$

The unbounded attractor is given by ${\mathcal {J}} = {{\mathbb {R}}}\times [-1,1]$, and the bounded invariant set is given by

$$\begin{aligned} {\mathcal {J}}_b = \{ (0,0)\} \cup \bigcup _{|y|\in (0,1]} \left[ -\frac{1}{|y|},\frac{1}{|y|}\right] \times \{ y\}. \end{aligned}$$

We have proved that ${\mathcal {J}}_b$ attracts in the past the bounded sets in ${\mathcal {J}}$. We will next show that it attracts in the future such bounded sets from X, which upon evolution stay in a bounded set, namely we prove the following result.

Theorem 7

If $B\in {\mathcal {B}}(X)$ is such that there exist $t_1>0$ and $R\ge R_0$ with $S(t)B\subset H_R$ for $t\ge t_1$, i.e. the case (3) from Lemma 2 holds, then

$$\begin{aligned} \lim _{t\rightarrow \infty }\textrm{dist}(S(t)B,{\mathcal {J}}_b) = 0. \end{aligned}$$

Proof

Define the $\omega$-limit set $\omega (B)=\bigcap _{s\ge t_1}\overline{\bigcup _{t\ge s}S(t)B}$. We will show that this set is compact, nonempty, invariant, and it attracts B, whence it must be that $\omega (B) \subset {\mathcal {J}}_b$ and the assertion will follow. Observe that the family of sets

$$\begin{aligned} \left\{ \overline{\bigcup _{t\ge s}S(t)B} \right\} _{s\ge t_1} \end{aligned}$$

is decreasing. Moreover

$$\begin{aligned} S(t)B = S(t_1 + t-t_1) B \subset S(t-t_1)H_R \cap H_R = S(t-t_1)Q \cap H_R. \end{aligned}$$

Hence

$$\begin{aligned} \overline{\bigcup _{t\ge s}S(t)B} \subset \overline{\bigcup _{t\ge s}S(t-t_1)Q} \cap H_R = \overline{S(s-t_1)Q} \cap H_R. \end{aligned}$$

If $x\in \overline{S(s-t_1)Q} \cap H_R$ then $x\in H_R$ and $x = \lim _{n\rightarrow \infty } x_n$, where $x_n \in S(s-t_1)Q$. We deduce that, for sufficiently large n, there holds $x_n \in H_{{\overline{R}}}$, where ${\overline{R}}$ depends only on R. This means that $x_n\in S(s-t_1)H_{{\overline{R}}} \cap H_{{\overline{R}}}$, whence $x\in \overline{S(s-t_1)H_{{\overline{R}}}} \cap H_{{\overline{R}}}$. We are in position to use (H3) and Lemma 1 to deduce that $\omega (B)$ is nonempty and compact. The proof that $\omega (B)$ attracts B is standard and follows the lines of the argument in Theorem 2. Also the proof of invariance of $\omega (B)$ is classical, once we have the compactness, and follows the lines of the proof in Theorem 5. $\square$

In a straightforward way, by taking as B the sets $\alpha ({\mathcal {J}}\cap H_R)$, we obtain the following characterization of ${\mathcal {J}}_b$

$$\begin{aligned} {\mathcal {J}}_b = \bigcup _{{\mathop { B \ \text {is type 3.}}\limits ^{B\in {\mathcal {B}}(X)}}} \omega (B), \end{aligned}$$

where the summation is made over all bounded sets which for some $R\ge R_0$ and some $t_1 > 0$ satisfy the assertion 3. of Lemma 2.

Remembering the decomposition ${\mathcal {J}} = {\mathcal {J}}_b \cup ({\mathcal {J}}\setminus {\mathcal {J}}_b)$ we know from Corollary 1 that the set ${\mathcal {J}}_b$ is nonempty. The set ${\mathcal {J}}\setminus {\mathcal {J}}_b$ can, however, be empty as the following example shows.

Example 5

Consider the following system of two ODEs

$$\begin{aligned}&y' = {\left\{ \begin{array}{ll} &{}-y+1\ \ \text {as}\ y>1,\\ &{} 0\ \ \text {as}\ \ |y|\le 1,\\ &{} y + 1 \ \ \text {as}\ y<-1. \end{array}\right. },\\&x'=0. \end{aligned}$$

Clearly ${\mathcal {J}} = {\mathcal {J}}_b = {\mathbb {R}}\times [-1,1]$.

We can make, however, the following easy observation which says that if $u\in {\mathcal {J}}\setminus {\mathcal {J}}_b$ then it must be $\lim _{t\rightarrow \infty }\Vert S(t)u\Vert = \infty$, i.e. it excludes the situation when $\lim _{t\rightarrow \infty }\Vert S(t)u\Vert$ does not exist, but $\Vert S(t)u\Vert$ is unbounded. This means that the unbounded attractor consists of the set ${\mathcal {J}}_b$, a global-attractor-like object, and the solutions which are backward in time attracted to ${\mathcal {J}}_b$ and whose norm, forward in time, has to go to infinity.

Lemma 6

If $u \in {\mathcal {J}}\setminus {\mathcal {J}}_b$ then $\lim _{t\rightarrow \infty } \Vert S(t)u\Vert = \infty$.

Proof

We know that S(t)u is unbounded. If for some sequence $t_n\rightarrow \infty$ there holds $S(t_n)u\in H_R$ for some $R\ge R_0$ then it has to be $S(t)u\in H_R$ for every t and we have the contradiction. $\square$

A similar simple argument allows us to split all points of X into two sets, those points whose $\omega$-limits are well defined compact and invariant subsets of ${\mathcal {J}}_b$ and those points, whose solutions are unbounded in the future.

Lemma 7

If $u \in X$ then either there exists $t_1>0$ and $R\ge R_1$such that $S(t)u \in H_R$ for $t\ge t_1$ and then $\omega (u) \subset {\mathcal {J}}_b$ is a compact and invariant set which attracts u, or $\Vert S(t)u\Vert \rightarrow \infty$ as $t\rightarrow \infty$.

Proof

If there exists $R\ge R_0$ and $t\ge t_1$ such that $S(t)u \in H_R$ for every $t\ge t_1$ then the result holds by Theorem 7. Otherwise, by Lemma 2 for every $R\ge R_0$ there exists $t_1$ such that $S(t)u\in Q\setminus H_R$ for $t\ge t_1$ and the proof is complete. $\square$

If we reinforce the item 3. of the assumption (H2) to its stronger version which states that the sets $Q\setminus H_R$ are not only positively invariant, but the evolution in them is expanding to infinity, then we can guarantee compactness (and hence closedness) and the simpler characterization of ${\mathcal {J}}_b$. We make the following assumption.

• (H4) For every $R \ge R_0$ there exists $t=t(R)>0$ such that $S(t)(Q\setminus H_{R_0}) \subset Q\setminus H_{R}$.

Theorem 8

Assuming (H1)–(H4), the set ${\mathcal {J}}_b = \alpha ({\mathcal {J}}\cap H_{R_0})$ is compact. Moreover the set ${\mathcal {J}}\setminus {\mathcal {J}}_b$ in the decomposition of the unbounded attractor ${\mathcal {J}}_b \cup ({\mathcal {J}}\setminus {\mathcal {J}}_b)$ is nonempty.

Proof

It is sufficient to prove that if $R\ge R_0$ then $\alpha ({\mathcal {J}}\cap H_R) = \alpha ({\mathcal {J}}\cap H_{R_0})$. To see that this is true, take $u\in \alpha ({\mathcal {J}}\cap H_R)$. This means that there exists $u_n\rightarrow u$ in ${\mathcal {J}}$ and $t_n\rightarrow \infty$ such that $S(t_n)u_n \in {\mathcal {J}}\cap H_R$. Now (H4) implies that $S(t_n-t(R)-1)u_n \in {\mathcal {J}}\cap H_{R_0}$ and the assertion follows. $\square$

Assumption (H4) also implies that the set of those points in X whose $\omega$-limit sets are well defined and compact is a closed subset of the space X. Hence the set of those points constitutes a complete metric space, and then ${\mathcal {J}}_b$ is the global attractor of $\{ S(t) \}_{t\ge 0}$ on that space.

Lemma 8

The set of points $u\in X$ which have the compact and invariant $\omega$-limit set $\omega (u)\subset {\mathcal {J}}_b$ is a closed set in X.

Proof

Assume for contradiction that $u_n\rightarrow u$ with $\lim _{t\rightarrow \infty }\textrm{dist}(S(t)u_n,{\mathcal {J}}_b) = 0$ and $\lim _{t\rightarrow \infty }\Vert S(t)u\Vert = \infty$. For every large R there exists $t_0>0$ such that for every $t\ge t_0$ we can find $n_0$ such that for every $n\ge n_0$ we have $\Vert S(t)u_n\Vert \ge R$. But we can find sufficiently large R and $t_0$ such that this means that for some t and for sufficiently large n there holds $S(t)u_n\in Q\setminus H_{R_0}$ which means that $\Vert S(t)u_n\Vert \rightarrow \infty$, a contradiction. $\square$

2.5 Multivalued Inertial Manifold

The concept of multivalued inertial manifolds has been introduced in [15] and further developed in [29]. While, classically, inertial manifolds require the so called spectral gap condition to exist, their multivalued counterpart, as shown in [15, 29], does not require such condition, at the price of ’multivaluedness’. Motivated by Lemma 3, we show that the concept of multivalued inertial manifold is compatible with unbounded attractors. Namely, Lemma 3 states that for every $p\in E^+$ there exists at least one $q\in E^-$ such that $p+q\in {\mathcal {J}}$. This makes it possible to define the multivalued mapping $\Phi :E^+ \rightarrow {\mathcal {P}}(E^-)$ by

$$\begin{aligned} \Phi (p) = \{q\in E^-\,:\ p+q\in {\mathcal {J}} \}. \end{aligned}$$

Then Lemma 3 states that for every $p\in E^+$ the set $\Phi (p)$ is nonempty. We continue by the analysis of $\Phi$.

Lemma 9

Under assumptions (H1)–(H3) the multifuction $\Phi$ has nonempty, compact values, closed graph, and is upper-semicontinuous.

Proof

The graph of $\Phi$ is ${\mathcal {J}}$, a closed set. Moreover $\Phi (p)$ is closed for every $p\in E^+$, an since by Lemma 4 it must be relatively compact, it is also compact. Since, by the same Lemma, for every bounded set $B \in {\mathcal {B}}(E^+)$ the set $\overline{\Phi (B)}$ is compact, using Proposition 4.1.16 from [14] we deduce that $\Phi$ is upper-semicontinuous, and hence also Hausdorff upper-semicontinuous, i.e. if $p_n\rightarrow p$ in $E^+$, then $\lim _{n\rightarrow \infty }\text {dist}(\Phi (p_n),\Phi (p)) \rightarrow 0$. $\square$

If, in addition to (H1)–(H3), we assume (A1), we arrive at the next result which follows directly from Remark 1.

Remark 2

Assume (H1)–(H3) and (A1). Then

$$\begin{aligned} \lim _{\Vert p\Vert \rightarrow \infty } \textrm{diam}\,\Phi (p) = 0. \end{aligned}$$

2.6 Unbounded $\omega$-Limit Sets and Their Properties

Following the classical definition we can define the $\omega$-limit sets for slowly non-dissipative dynamical systems

Definition 10

An $\omega$-limit set of the set $B\subset {\mathcal {B}}(X)$ is the set

$$\begin{aligned} \omega (B) = \{ x\in X\;:\ \text {there exists}\ \ t_n\rightarrow \infty \ \ \text {and}\ \ u_n\in B\ \ \text {such that}\ \ S(t_n)u_n\rightarrow x \} \end{aligned}$$

Using Lemma 2 and Theorem 7 we can formulate the following result on $\omega$-limit sets.

Corollary 2

Assume (H1)–(H3). Let $B\in {\mathcal {B}}(X)$. If there exists $R\ge R_0$ and $t_1>0$ such that for every $t\ge t_1$ we have $S(t)B \subset H_{R}$ then $\omega (B) \subset {\mathcal {J}}_B$ is a nonempty, compact and invariant set which attracts B. If for every $R\ge R_0$ there exists $t_1>0$ such that for every $t\ge t_1$ we have $S(t)B \in Q\setminus H_{R}$ holds then $\omega (B)$ is empty.

We continue by the analysis of the situation when both $S(t)B \cap H_R$ and $S(t)B \cap (Q\setminus H_R)$ are nonempty. The next result is a complement to Theorem 7.

Lemma 10

Assume (H1)–(H3) and let $B\in {\mathcal {B}}(X)$. If there exists $R\ge R_0$ and $t_1 > 0$ such that for every $t\ge t_1$ both sets $S(t)B \cap H_R$ and $S(t)B \cap (Q\setminus H_R)$ are nonempty (i.e. case (2) of Lemma 2 holds), then $\omega (B) \subset {\mathcal {J}}$ is a nonempty, closed, and invariant set which attracts B in the bounded sets in $E^+$, i.e.

$$\begin{aligned} \lim _{t\rightarrow \infty }\textrm{dist}(S(t)B\cap \{ \Vert Px\Vert \le S\},\omega (B)) = 0\ \ \text {for every}\ \ S\ge 0. \end{aligned}$$

Proof

Take $t_n\rightarrow \infty$. There exists $u_n \in B$ such that $S(t_n)u_n \in H_R$, whence, arguing as in the proof of Theorem 2, $S(t_n)u_n$ is relatively compact and hence $\omega (B)$ is nonempty. Its closedness follows by a diagonal argument, while the fact that $\omega (B) \subset {\mathcal {J}}$ follows from the definition of ${\mathcal {J}}$ and the fact that Q is absorbing and positively invariant. The proof of invariance of $\omega (B)$ is straightforward and follows from the fact that we can enclose the convergent sequence $S(t_n)u_n$ in some $H_{{\overline{R}}}$. Finally the attraction in bounded sets is obtained in the same way as in Theorem 2. $\square$

2.7 The Dynamics at Infinity

In [6, 13, 27] the authors define the dynamics at infinity by means of the Poincaré projection. Observe, however, that for the solutions u(t) that diverge to infinity, the projection $(I-P)u(t)$ remains bounded, and $\Vert Pu(t)\Vert$ tends to infinity. Hence, when we rescale those solutions by $\Vert P u(t)\Vert$, i.e. we consider

$$\begin{aligned} \frac{u(t)}{\Vert Pu(t)\Vert } = \frac{Pu(t)}{\Vert Pu(t)\Vert } + \frac{(I-P)u(t)}{\Vert Pu(t)\Vert }, \end{aligned}$$

the infinite dimensional component, which belongs to $E^-$ tends to zero, while the term $\frac{Pu(t)}{\Vert Pu(t)\Vert }$ evolves on the unit sphere. We recover the dynamics at infinity by the analysis of the asymptotic behavior of this, rescaled, Pu(t). Denoting the unit sphere in $E^+$ by ${\mathbb {S}}_{E^+} = \{ x\in E^+\; :\ \Vert x\Vert = 1\}$, we have the next result. Note that this result actually describes the dynamics at infinity if we assume (H4) in addition to (H1)–(H3) but it is valid in the more general case.

Lemma 11

Assume (H1)–(H3). Then for every $R\ge R_0$

$$\begin{aligned} \bigcap _{t\ge 0} \overline{ \bigcup _{x\in S(t)(Q\setminus H_R)} \left\{ \frac{Px}{\Vert Px\Vert } \right\} } = {\mathbb {S}}_{E^+}. \end{aligned}$$

Moreover ${\mathbb {S}}_{E^+}$ is the smallest closed set such that for every $B\in {\mathcal {B}}(X)$ satisfying 1. of Lemma 2 for sufficiently large R, there holds

$$\begin{aligned} \lim _{t\rightarrow \infty }\textrm{dist}\left( \left\{ \frac{Px}{\Vert Px\Vert }\,:\ x\in S(t)B\right\} ,{\mathbb {S}}_{E^+}\right) = 0. \end{aligned}$$

Proof

We will prove that

$$\begin{aligned} \bigcup _{x\in S(t)(Q\setminus H_R)} \left\{ \frac{Px}{\Vert Px\Vert } \right\} = {\mathbb {S}}_{E^+}. \end{aligned}$$

By Lemma 3, the fact that ${\mathcal {J}}\subset Q$ and the invariance of ${\mathcal {J}}$ it follows that $\{ Px: x\in S(t)Q\} = E^+.$ Now

$$\begin{aligned} E^+ = P S(t)Q = PS(t) H_R \cup PS(t)(Q\setminus H_R). \end{aligned}$$

Since by (H3) the set $PS(t) H_R$ is bounded, there exists $R>0$ such that $\{ x\in E^+\,:\ \Vert x\Vert =R \} \subset PS(t)(Q\setminus H_R)$ and the assertion follows.

To get the second assertion pick $R\ge R_0$ and choose $B = \{ x\in E^+ \, :\ \Vert x\Vert = {\overline{R}} \}$, where ${\overline{R}}$ is sufficiently large to get $S(t) B \subset Q\setminus H_R$ for every $t\ge 0$ (and hence B satisfies 1. of Lemma 2). Such choice of ${\overline{R}}$ is possible by (H2). We will show that

$$\begin{aligned} \left\{ \frac{Px}{\Vert Px\Vert }\,:\ x\in S(t)B \right\} = {\mathbb {S}}_{E^+}. \end{aligned}$$

To this end choose $t > 0$ and consider the mapping $H:[0,1]\times {\mathbb {S}}_{E^+}\rightarrow {\mathbb {S}}_{E^+}$ defined as

$$\begin{aligned} H(\theta ,x) = \frac{P S(\theta t) ({\overline{R}}x) }{\Vert P S(\theta t) ({\overline{R}}x)\Vert }. \end{aligned}$$

Clearly $H(0,\cdot )$ is an identity, and H is continuous. Hence, by the Hopf lemma, the degree of the mapping H(1, x) is equal to the degree if the identity of the sphere, that is, one. On the other hand assume for contradiction that the image of $H(1,\cdot )$ is not equal to the whole ${\mathbb {S}}_{E^+}$. Then, as the image of $H(1,\cdot )$ is compact, it is included in ${\mathbb {S}}_{E^+} \setminus U$ for some nonempty open set U. This set is contractible to one point, which in turn means that $H(1,\cdot )$ must be homotopic to a constant map, which has the degree zero, a contradiction. $\square$

We can also define $\omega$-limits in ${\mathbb {S}}_{E^+}$ of nonempty bounded sets $B \subset Q\setminus H_{R_0}$.

$$\begin{aligned} \omega _\infty (B) = \left\{ x\in E^+\,:\ \text {there exists}\ \ u_n\in B \ \ \text {and}\ \ t_n\rightarrow \infty \ \ \text {such that}\ \ \frac{PS(t_n)u_n}{\Vert PS(t_n)u_n\Vert }\rightarrow x\right\} \end{aligned}$$

Lemma 12

Let $B \subset Q\setminus H_{R_0}$ be bounded. Then $\omega _\infty (B)$ is nonempty, compact, and attracts B in the sense

$$\begin{aligned} \lim _{t\rightarrow \infty }\textrm{dist}\left( \left\{ \frac{Px}{\Vert Px\Vert }\,:\ x\in S(t)B\right\} ,\omega _\infty (B) \right) = 0. \end{aligned}$$

Proof

Non-emptiness follows from the compactness of ${\mathbb {S}}_{E^+}$ and we can obtain closedness (and hence compactness) of $\omega _\infty (B)$ from a diagonal argument, the argument closely follows the classical proof of closedness of $\omega$-limit sets. Also the proof of the attraction is standard: for contradiction assume that for some B there exists the sequence $\{x_n \} \subset B$ and $t_n\rightarrow \infty$ such that

$$\begin{aligned} \textrm{dist}\left( \frac{PS(t_n)x_n}{\Vert PS(t_n)x_n\Vert },\omega _\infty (B) \right) \ge \varepsilon . \end{aligned}$$

But for a subsequence, still denoted by n

$$\begin{aligned} \frac{PS(t_n)x_n}{\Vert PS(t_n)x_n\Vert } \rightarrow y, \end{aligned}$$

where, by definition $y\in \omega _\infty (B),$ a contradiction. $\square$

For particular slowly non-dissipative semigroups it is possible to construct the dynamical system on $E^+$ such that $\omega _\infty (B)$ are invariant and whole ${\mathbb {S}}_{E^+}$ is the global attractor. This dynamical system reflects the dynamics at infinity of the original problem. We will present such construction in the part of the paper devoted to the example of a slowly non-dissipative problem governed by a PDE.

3 Non-autonomous Unbounded Attractors and Their Properties

The non-autonomous version of the definition of the pullback attractor was proposed in [13, Definition 3.1] together with a result on its existence for the problem governed by the following PDE

$$\begin{aligned} u_t = u_{xx} + b(t)u + g(u), \end{aligned}$$

where the space domain is the one-dimensional (an interval) with homogeneous Dirichlet boundary conditions. The function b(t) is allowed to oscillate between two gaps of the spectrum of the leading elliptic operator. In this section we propose a systematic abstract approach to non-autonomous unbounded pullback attractors.

3.1 Definition of Pullback Unbounded Attractor

We first note that, if X is a normed space, than any family of nonempty sets $\{ {\mathcal {A}}(t) \}_{t\in {\mathbb {R}}}$ in X will be called a non-autonomous set. We will also use the notation ${\mathcal {A}}(\cdot )$ for such sets. Exactly as in the autonomous case we will assume that the phase space X is Banach, and can be represented as $X=E^+\oplus E^-$, with $E^+$ being finite dimensional. Using the same notation as in Sect. 2 we can represent any $x\in X$ as $x=p+q$. We remind some definitions concerning the dissipative non-autonomous dynamical systems, beginning with the definition of a process and its pullback attractor, see [12] for the systematic treatise on the theory. In the same way as in the autonomous case, in our requirement for the attraction we impose that it takes place only in the bounded sets in $E^+$.

Definition 11

Let X be a metric space. A family of mappings $\{ S(t,s)\}_{t\ge s}$, where $S(t,s):X\rightarrow X$ is a continuous process if

• $S(t,t) = I$ (identity on X) for every $t\in {\mathbb {R}}$,

• for every $t\ge \tau \ge s$, and for every $x\in X$ we have $S(t,s)x = S(t,\tau )S(\tau ,s)x$,

• the mapping $(t,s,x)\mapsto S(t,s)x$ is continuous for every $t\ge s$, $x\in X$.

Definition 12

A family of sets $\{{\mathcal {A}}(t)\}_{t\in {\mathbb {R}}}$ is the unbounded pullback attractor for a process $S(\cdot ,\cdot )$ if

• (1) ${\mathcal {A}}(\cdot )$ are nonempty and closed,

• (2) ${\mathcal {A}}(\cdot )$ is invariant with respect to $S(\cdot ,\cdot )$, that is

  $$\begin{aligned} S(t,\tau ){\mathcal {A}}(\tau )={\mathcal {A}}(t) \ \text { for every } \ t,\tau \in {\mathbb {R}} \ \text { with } \ t\ge \tau . \end{aligned}$$

• (3) for every $t\in {\mathbb {R}}$ the set ${\mathcal {A}}(t)$ is pullback attracting in the bounded sets in $E^+$ at time t, that is

  $$\begin{aligned} \lim _{s\rightarrow -\infty } \textrm{dist} (S(t,s)B\cap \{ \Vert Px\Vert \le R \},{\mathcal {A}}(t))=0 \end{aligned}$$

  for every $B\in {\mathcal {B}}(X)$ and every $R>0$ for which there exists $t_1\le t$ such that $S(t,s)B\cap \{ \Vert Px\Vert \le R \}$ is nonempty for every $s\le t_1$.

• (4) ${\mathcal {A}}(\cdot )$ is the minimal family of closed sets with property (3).

We will also need the notions of pullback absorption and pullback positive invariance.

Definition 13

A set $B\subset X$ pullback absorbs bounded sets at time $t\in {\mathbb {R}}$ if, for each bounded subset D of X, there exists $T=T(t,D)\le t$ such that

$$\begin{aligned} S(t,s)D\subset B \text { for all } s\le T. \end{aligned}$$

Definition 14

A non-autonomous set $\{Q(t)\}_{t\in {\mathbb {R}}}$ is positively invariant if

$$\begin{aligned} S(t,s)Q(s)\subset Q(t) \ \ \ \text { for every } s\le t. \end{aligned}$$

Finally, we propose the concept of generalized pullback asymptotic compactness, as a non-autonomous variant of the notion given in Definition 8,

Definition 15

A process $S(\cdot ,\cdot )$ is generalized pullback asymptotically compact if for every $B\in {\mathcal {B}}(X)$ and for every $t,s\in {\mathbb {R}}$, $s\le t,$ there exists a $K(t,s,B)\subset X$ and $\varepsilon (t,s,B)\rightarrow 0$ when $s\rightarrow -\infty$ such that

$$\begin{aligned} S(t,s)B\subset {\mathcal {O}}_{\varepsilon }(K). \end{aligned}$$

3.2 Existence of Unbounded Pullback Attractors

The following assumptions which are the non-autonomous versions of (H1)–(H3) from Sect. 2 will guarantee the existence of the unbounded pullback attractor.

• (H1)$_{\textrm{NA}}$ There exist $D_1,D_2>0$ and the closed sets $\{Q(\cdot )\}_{t\in {\mathbb {R}}}$ such that for every $t\in {\mathbb {R}}$,

  $$\begin{aligned} \{ \Vert (I-P)x\Vert \le D_1 \} \subset Q(t) \subset \{ \Vert (I-P)x\Vert \le D_2 \} \end{aligned}$$

  such that Q(t) pullback absorbs bounded sets at time t and family $Q(\cdot )$ is positively invariant.

• (H2)$_{\textrm{NA}}$ There exists the constants $R_0$ and $R_1$ with $0< R_0\le R_1$ and an ascending family of closed and bounded sets $\{\{H_R(\cdot )\}_{t\in {\mathbb {R}}}\}_{R\ge R_0}$ with $H_R(t)\subset Q(t)$ for every $t\in {\mathbb {R}}$ such that

  • 1. for every $R\ge R_1$ we can find $S(R)\ge R_0$ such that $\{\Vert Px\Vert \le S(R)\}\cap Q(t)\subset H_R(t)$ for every $t\in {\mathbb {R}}$, and moreover $\lim _{R\rightarrow \infty } S(R)=\infty$,

  • 2. for every $R\ge R_1$ we have $H_R(t)\subset \{\Vert Px\Vert \le R\}$ for every $t\in {\mathbb {R}},$

  • 3. for every $R\ge R_0$ and $t\in {\mathbb {R}}$, $S(t,s)Q(s)\setminus H_R(s)\subset Q(t)\setminus H_R(t)$, for every $s\le t$.

• (H3)$_{\textrm{NA}}$ The process $S(\cdot ,\cdot )$ is generalized pullback asymptotically compact.

The candidate for the unbounded pullback attractor is the non-autonomous set ${\mathcal {J}}(\cdot )$ given by

$$\begin{aligned} {\mathcal {J}}(t)=\bigcap _{s\le t}\overline{S(t,s)Q(s)}. \end{aligned}$$

The rest of this section is devoted to the proof that assuming (H1)$_{\textrm{NA}}$–(H3)$_{\textrm{NA}}$ this set satisfies the requirements of Definition 12. We also establish its relation with the time dependent maximal kernel and its section. To this end we first define the time dependent maximal kernel as the family of those complete non-autonomous solutions $u:{\mathbb {R}}\rightarrow X$ which are bounded in the past.

Definition 16

The set ${\mathcal {K}}$ is called a maximal kernel if

$$\begin{aligned} {\mathcal {K}}= & {} \{ u(\cdot )\,:\ \text {there exists}\ \ T\in {\mathbb {R}}\ \, \text {such that}\ \, \sup _{s\in (-\infty ,T]}\Vert u(s)\Vert \le C_u\ \, \text {and}\\{} & {} \quad S(t,s)u(s) = u(t)\, \ \text {for every}\, \ t\ge s\} \end{aligned}$$

It is clear that if the assertion of the above definition holds for some $T\in {\mathbb {R}}$ then it also holds for every ${\overline{T}} < T$. The continuity of the process S with respect to time also implies that this assertion also holds for every ${\overline{T}} > T$. We continue with the definition of the maximal kernel section.

Definition 17

The non-autonomous set $\{{\mathcal {K}}(t) \}_{t\in {\mathbb {R}}}$ is called a maximal kernel section if

$$\begin{aligned} {\mathcal {K}}(t) = \{ u(t) \,:\ u\in {\mathcal {K}} \}\ \ \text {for every}\ \ t\in {\mathbb {R}}. \end{aligned}$$

Clearly, for a continuous process this is an invariant set, namely

Observation 2

If $S(\cdot ,\cdot )$ is a continuous process, then ${\mathcal {K}}(t) = S(t,s){\mathcal {K}}(s)$ for every $s\in {\mathbb {R}}$ and $t\ge s$.

At the moment we do not yet know if either of the sets ${\mathcal {J}}(t)$ or ${\mathcal {K}}(t)$ are nonempty. We establish, however, then they must coincide. This is a non-autonomous version of Theorem 1.

Theorem 9

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$. Then for every $t\in {\mathbb {R}}$ ${\mathcal {J}}(t)={\mathcal {K}}(t)$.

Proof

The proof is analogous to the proof of Theorem 1—the autonomous counterpart of the result. Take $t\in {\mathbb {R}}$. First we prove the inclusion ${\mathcal {K}}(t)\subset {\mathcal {J}}(t)$. We suppose that $u(t)\in {\mathcal {K}}(t)$, then we can find $C\in {\mathbb {R}}^+$ such that $\Vert u(s)\Vert \le C$ for every $s\le t$. Let $B=\{x\in X\, : \ \Vert x\Vert \le C\}$. By $(H1)_{\textrm{NA}}$ we know that for every $\tau \in {\mathbb {R}}$ there exists $s\le \tau$ such that $S(\tau ,s)B\subset Q(\tau )$. Then, taking any $\tau \le t$ we obtain

$$\begin{aligned} u(t)=S(t,\tau )u(\tau ) = S(t,\tau )S(\tau ,s)u(s)\in S(t,\tau )S(\tau ,s)B\subset S(t,\tau )Q(\tau ). \end{aligned}$$

So, for every $\tau \le t$, $u(t)\in S(t,\tau )Q(\tau )$, and hence $u(t)\in {\mathcal {J}}(t)$.

To prove the equality, take $u_0\in {\mathcal {J}}(t)$. Then there exists a sequence $\{y_n\}$ such that $y_n\in Q(t-n)$ and $S(t,t-n)y_n \rightarrow u_0$ as $n\rightarrow \infty$. The convergent sequence $\{S(t,t-n)y_n\}$ is contained in Q(t), whence there exists $R\ge R_0$ such that $\{S(t,t-n)y_n\}\subset H_R(t)$.

Notice that for $s\in [t-n,t]$ also $S(s,t-n)y_n\in H_R(s)$, because if $S(s,t-n)y_n\in Q(s)\setminus H_R(s)$, then it would be $S(t,t-n)y_n=S(t,s)S(s,t-n)y_n\in Q(t)\setminus H_R)(t)$. In particular it must be $y_n\in H_R(t-n)$. So $S(s,t-n)y_n\in H_R(s)\cap S(s,t-n)H_R(t-n)=L_n(s)$, and, for each $s\le t$ this sequence of sets is nested. By Lemma 1 and $(H3)_{\textrm{NA}}$, for each s one can take a subsequence of indexes, still denoted by n such that $S(s,t-n)y_n$ is convergent and the limit is always in $H_R(s)$. In particular, for $s=t-1$ we have $S(t-1,t-n)y_n \rightarrow u_1$ and $S(t,t-n)y_n = S(t,t-1)S(t-1,t-n)y_n \rightarrow S(t,t - 1)u_1$ and hence $S(t,t-1)u_1 = u$ with $u_1\in H_R(t-n)$. Passing to the subsequence in each step of the iterative procedure we are able to construct the sequence $u_n \in H_R(t-n)$ such that $S(t-n+1,t-n)u_n = u_{n-1}$, which allows us to define the solution $u(\cdot )$ by taking $u(r) = S(r,t-n)u_n$ for $t\in [t-n,t-n+1]$. As $u(r) \in H_R(r)$ for every $r\le t$ it follows that there exists a constant C such that $\sup _{s\in (-\infty , t]}\Vert u(s)\Vert \le C$ and the proof is complete. $\square$

Now, we state the non-autonomous version of Lemma 3. This result also implies that $P{\mathcal {J}}(t) = E^+$ for every $t\in {\mathbb {R}}$ and hence sets ${\mathcal {J}}(t)$ are nonempty.

Lemma 13

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$, for every $t\in {\mathbb {R}}$ it holds that for every $p\in E^+$, there exists a $q\in E^-$, such that $p+q\in {\mathcal {J}}(t)$.

Proof

Analogously as in autonomous case we pick $p\in E^+$ and define $B=\{x\in E^+\, :\, \Vert x\Vert <R+1\}$ for appropriately large R such that $p\in H_R(\tau ) \subset B$ for every $\tau \in {\mathbb {R}}$, which is possible by items 1 and 2 of $(H2)_{NA}$. Then $\text {deg}(I,B,p)=1$. Now we pick $t\in {\mathbb {R}}$ and we choose $s>0$. We define continuous mapping

$$\begin{aligned}{}[0,1]\times {\overline{B}}\ni (\theta ,p)&\longmapsto P(S(t,t-\theta s) p) \in E^+. \end{aligned}$$

By item 2. of $(H2)_{NA}$, since $\delta B=\{x\in E^+\,:\ \Vert x\Vert =R+1\} \subset Q(\tau )\setminus H_R(\tau ),$ for every $\tau \in {\mathbb {R}}$, then $S(t,t-\theta s)\delta B\subset Q(t)\setminus H_R(t)$ so $p\notin P(S(t,t-\theta s)\delta B)$ for every $\theta \in [0,1]$. By the homotopy invariance of the degree it follows that $\text {deg}(PS(t,t-s),B,p)=1$ whence for every sequence $s_n\rightarrow -\infty$ we can find $p_n \in E^+$ and $q_n\in E^-$ such $y_n=p+q_n=S(t,t-s_n)p_n\in S(t,t-s_n)Q(t-s_n).$ As in the autonomous case we can find $R'$ such that $y_n \in L_n=S(t,t-s_n)H_{R'}\cap H_{R'} := L_n$, where $L_n$ is a decreasing sequence of sets. We use Lemma 1 and $(H3)_{\text {NA}}$, to deduce that $y_n\rightarrow y$ for a subsequence with $Py=p$. Since $y_n\in S(t,t-s_n)Q(t-s_n)$, it follows that $y\in {\mathcal {J}}(t).$ $\square$

We provide the result that the non-autonomous set ${\mathcal {J}}(\cdot )$ is attracting in every ball.

Theorem 10

Let $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$. Let $t\in {\mathbb {R}}$ and $R\ge R_1.$ We take $B\in B(X)$ such that there exists a $t_1\le t$ that for every $s\le t_1$ there holds $S(t,s)B\cap \{\Vert Px\Vert \le R\} \not = \emptyset$. Then we have

$$\begin{aligned} \lim _{s\rightarrow -\infty } \textrm{dist}(S(t,s)B\cap \{\Vert Px\Vert \le R\},{\mathcal {J}}(t))=0 \end{aligned}$$

Proof

To prove the attraction we proceed in a standard way, i.e. for contradiction we choose the sequences $\{x_n\}\subset B$ and $s_n\rightarrow -\infty$ such that $S(t,s_n)x_n\in S(t,s_n)B\cap \{\Vert Px\Vert \le R\}$ and $\textrm{dist}(S(t,s_n)x_n,{\mathcal {J}}(t))>\varepsilon$ for every n and for some $\varepsilon >0.$

By $(H1)_{\textrm{NA}}$ we know that for every $n\in {\mathbb {N}}$ there exists $k(n) \ge n$ such that $S(s_n,s_k)x_k \in Q(s_n)$, then $y_k=S(t,s_k)x_k\in S(t,s_n)Q(s_n)\subset Q(t)$. Since $\Vert P(S(t,s_k)x_k)\Vert \le R$ for every k, by $(H2)_{\textrm{NA}}$ there exists ${\overline{R}}\ge R_0$ and such that the sequence $\{y_{k(n)}\}_{n\in {\mathbb {N}}}\subset H_{{\overline{R}}}(t)$. We define the sets $L_n=S(t,s_n)Q(s_n) \cap H_{{\overline{R}}}(t)$, these sets are nested, and $y_{k(n)}\in L_n$ for every n. By Lemma 1 and $(H3)_{\textrm{NA}}$, we know that for a subsequence, we must have $y_{k(n)}\rightarrow y$, and by definition of ${\mathcal {J}}(t)$, it must be $y\in {\mathcal {J}}(t)$, which gives a contradiction. $\square$

We end the chapter with the result of minimality of $\{ {\mathcal {J}}(t) \}_{t\in {\mathbb {R}}}$, which is the last property of the unbounded pullback attractor which we need to verify.

Theorem 11

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$, then the non-autonomous set $\{ {\mathcal {J}}(t) \}_{t\in {\mathbb {R}}}$ is the unbounded pullback attractor of the process $S(\cdot ,\cdot )$.

Proof

It only remains to verify the minimality in Definition 12. To this end, suppose that there exists a non-autonomous closed set $\{ {\mathcal {M}}(t) \}_{t\in {\mathbb {R}}}$ which satisfies property (3) of Definition 12, and for a certain $t\in {\mathbb {R}}$, there exist an $u\in {\mathcal {J}}(t)$ such that $u\notin {\mathcal {M}}(t)$. By Theorem 9, we know that the orbit $\bigcup _{s\le t} \{ u(s) \}$ is bounded. Since $u = u(t) = S(t,r) u(r) \subset S(t,r) (\bigcup _{s\le t} \{ u(s) \})$ we know that there exists some $R\ge R_0$ such that $u(t) \in S(t,r) (\bigcup _{s\le t} \{ u(s) \}) \cap \{ \Vert Px\Vert \le R \}$ and hence the latter sets are nonempty for every $r\le t$. Then

$$\begin{aligned} \lim _{r\rightarrow -\infty } \text {dist}(S(t,r) u(r),{\mathcal {M}}(t))\le & {} \lim _{r\rightarrow -\infty } \text {dist}\left( S(t,r)\left( \bigcup _{s\le t} \{u(s)\}\right) \cap \{ \Vert Px\Vert \le R \},{\mathcal {M}}(t)\right) \\= & {} 0, \end{aligned}$$

whence it must be $\text {dist}(u(t),{\mathcal {M}}(t))=0$, so $u=u(t)\in {\mathcal {M}}(t)$, since ${\mathcal {M}}(t)$ is closed, and the proof of minimality is complete. $\square$

We conclude the section withe the result on $\sigma$-compactness of ${\mathcal {J}}(t)$.

Lemma 14

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$. For every $t\in {\mathbb {R}}$ and for every closed and bounded set B the set $B \cap {\mathcal {J}}(t)$ is compact.

Proof

Since $B \cap {\mathcal {J}}(t)\subset H_R(t) \cap {\mathcal {J}}(t)$ for some $R\ge R_0$ it is enough to prove that $H_R(t) \cap {\mathcal {J}}(t)$ is relatively compact. The proof follows the lines of the proof of Theorem 4—the corresponding result for the autonomous case. We take a sequence $\{u_n\}\subset H_R(t)\cap {\mathcal {J}}(t).$ Then we can take a sequence $t_n\rightarrow -\infty$, and $x_n\in {\mathcal {J}}(t_n)$ with $u_n=S(t,t_n)x_n$. Then $x_n\in H_R(t_n)$, so $u_n\in S(t,t_n)H_R(t_n)\cap H_R(t)$. By Lemma 1 and $(H3)_{\text {NA}}$ we obtain the desired result. $\square$

3.3 Structure of the Unbounded Pullback Attractor

We begin with the definition of the kernel section in the non-autonomous case.

$$\begin{aligned} {\mathcal {I}}_b(t) = \{ u(t)\,: \ \text {such that}\ \ \sup _{s\in {\mathbb {R}}}\Vert u(s)\Vert \le C_u\ \ \text {and}\ \ S(r,s)u(s) = u(r)\ \ \text {for every}\ \ r\ge s\}. \end{aligned}$$

Clearly ${\mathcal {I}}_b(t) \subset {\mathcal {J}}(t) = {\mathcal {K}}(t)$, i.e. the kernel section is the subset of the maximal kernel section (which contains those points, through which there pass solutions bounded in the past but possibly unbounded in the future). Moreover $S(s,t){\mathcal {I}}_b(t) = {\mathcal {I}}_b(s)$ for every $s\ge t$, i.e. kernel sections are invariant. In the autonomous case the corresponding set, ${\mathcal {I}}_b = {\mathcal {J}}_b$ was constructed as the $\alpha$-limit of bounded sets in the unbounded attractor. Since, as it seems to us, such construction is no longer possible in the non-autonomous case, we provide an alternative way to obtain ${\mathcal {I}}_b(t)$ from ${\mathcal {J}}(t)$. Since the non-autonomous set $\{{\mathcal {J}}(t)\}_{t\in {\mathbb {R}}}$ is invariant we can define the inverse mapping $(S(t,s))^{-1}:{\mathcal {J}}(t)\rightarrow 2^{{\mathcal {J}}(s)}$ for $t>s$. We will use the notation $(S(t,s))^{-1} = S(s,t)$ for $t>s$. Note that, as we do not assume the backward uniqueness, if we consider S(s, t) on the whole space X, its image can go beyond ${\mathcal {J}}(s)$, and, moreover S(s, t) (even as considered as mapping from ${\mathcal {J}}(t)$ to ${\mathcal {J}}(s)$) can be multivalued, From the invariance we have, however, the guarantee that for every $u\in {\mathcal {J}}(t)$ the set S(s, t)u is nonempty. We define the following non-autonomous set.

$$\begin{aligned} {\mathcal {J}}_b(t)=\bigcup _{R\ge R_0} \bigcap _{\tau \ge t}S(t,\tau )(H_R(\tau ) \cap {\mathcal {J}}(\tau )) \end{aligned}$$

In the next results we will prove that ${\mathcal {J}}_b = {\mathcal {I}}_b$, and it is nonempty.

Lemma 15

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$. For every $t\in {\mathbb {R}}$, the set ${\mathcal {J}}_b(t)$ is nonempty.

Proof

We will prove the result using the Cantor intersection theorem. First, we see that the inverse image $S(\tau ,t)^{-1}$ of the closed set $H_R(\tau )\cap {\mathcal {J}}(\tau )$ is closed, since the process $S(\cdot ,\cdot )$ is continuous. We also observe that for every $\tau \ge t$, we have $S(t,\tau )(H_R(\tau )\cap {\mathcal {J}}(\tau ))\subset H_R(t)\cap {\mathcal {J}}(t)$, a compact set by Lemma 14, then so the sets $S(t,\tau )(H_R(\tau )\cap {\mathcal {J}}(\tau ))$ are compact. They are also nested: indeed, if $\tau _2>\tau _1\ge t$ and $x\in S(t,\tau _2)(H_R(\tau _2)\cap {\mathcal {J}}(\tau _2))$, then $S(\tau _1,t)x\in H_R(\tau _1)$, and, as we are taking inverse image in the set ${\mathcal {J}}(\cdot )$, also $S(\tau _1,t)x\in {\mathcal {J}}(\tau _1).$ $\square$

Lemma 16

Assuming $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$, for every $t\in {\mathbb {R}}$, ${\mathcal {J}}_b(t)={\mathcal {I}}_b(t).$

Proof

We take first $u\in \bigcup _{R\ge R_0} \bigcap _{\tau \ge t}S(t,\tau )(H_R(\tau ) \cap {\mathcal {J}}(\tau ))$, so there exists $R\ge R_0$ such that for every $\tau \ge t$, $S(\tau ,t)u\in H_R(\tau ) \cap {\mathcal {J}}(\tau )$. Since $u\in {\mathcal {J}}(t)$, then there exists a backwards bounded solution through u at time t. Thus, there exists a global bounded solution through u at time t.

To prove the opposite inclusion, since u(t) is bounded for every $t\in {\mathbb {R}}$, there exists $R\ge R_0$, such that $u(t)\in H_R$ for every $t\in {\mathbb {R}}$, and $\sup _{\tau \le t} \Vert u(\tau )\Vert \le C_u$. Since u is an orbit, for $\tau \ge t$, $u(\tau )=S(\tau ,t)u(t)\in H_R(\tau )\cap {\mathcal {J}}(\tau ),$ so $u(t)\in S(t,\tau )(H_R(\tau )\cap {\mathcal {J}}(\tau ))$ for every $\tau \ge t$. $\square$

As a consequence of above results we will get the following corollary

Corollary 3

For any $R\ge R_0$ there holds

$$\begin{aligned} \lim _{\tau \rightarrow \infty }\textrm{dist}(S(t,\tau ) (H_R(\tau )\cap {\mathcal {J}}(\tau )), {\mathcal {J}}_b(t)) = 0 \end{aligned}$$

As in the autonomous case, we can observe that if $u\in {\mathcal {J}}(t)\setminus {\mathcal {J}}_b(t)$ for a certain $t\in {\mathbb {R}}$, then $\lim _{\tau \rightarrow \infty }\Vert S(\tau ,t)u\Vert =\infty$. The proof is similar to the autonomous case Lemma 6

Lemma 17

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$, and let $u\in {\mathcal {J}}(t)\setminus {\mathcal {J}}_b(t)$ for a certain $t\in {\mathbb {R}}$. Then $\lim _{\tau \rightarrow \infty }\Vert S(\tau ,t)u\Vert =\infty$.

Remark 3

In above results we decompose the unbounded attractor into backward bounded part and backward unbounded part. It would be worthwhile to study the concept of unbounded uniform attractors and their decomposition into fibers (which could be backward bounded or unbounded) as well as the relation with unbounded pullback attractors just as it has been done for their classical counterparts in [1, 12, 20]. In particular it would be interesting to extend the theory of uniform attractors to the case when the hull of the non-autonomous part can be unbounded.

3.4 Pullback Behavior of Bounded Sets

In the autonomous case, in Lemma 2 we provided the classification of all bounded sets in three classes. Unfortunately, in non-autonomous case such classification in no longer valid in pullback sense. It is very easy to construct the process $S(\cdot ,\cdot )$ and a bounded set B such that $S(t,s_n)B\subset H_R(t)$ and $S(t,r_n)B\subset Q(t)\setminus H_R(t)$ for sequences $s_n\rightarrow -\infty$ and $r_n\rightarrow -\infty$. In the concept of pullback $\omega$ limits it is natural to operate not on single bounded sets but on non-autonomous bounded sets $\{ B(t) \}_{t\le T}$ defined for every time t less or equal to some given T.

Definition 18

Let $\{B(t)\}_{t\le T}$ be a non-autonomous bounded set in X (i.e. $B(t)\in {\mathcal {B}}(X)$ for every $t\le T$). We define the unbounded pullback $\omega$-limit set as

$$\begin{aligned} \omega (t,B(\cdot )):=\{y\in X \,:\ \text {there exist}\ s_n\rightarrow -\infty \ \text {and}\ u_n\in B(s_n) \text { such that } y=\lim _{s_n\rightarrow -\infty }S(t,s_n)u_n\}. \end{aligned}$$

Observation 3

Let $\{B_1(t)\}_{t\le T_1}$ and $\{B_2(t)\}_{t\le T_2}$ be a two families of subsets of X such that $B_1(t) = B_2(t)$ for every $t\le T_3,$ where $T_3 \le \min \{ T_1,T_2\}$. Then for every $t\in {\mathbb {R}}$ the sets $\omega (t,B_1(\cdot ))$ and $\omega (t,B_2(\cdot ))$ are equal.

The following characterization of $\omega$ limit sets remains valid in unbounded non-autonomous setting.

Lemma 18

Let $\{B(t)\}_{t\le T}$ be a non-autonomous set in X. The following characterization holds

$$\begin{aligned} \omega (t,B(\cdot ))= \bigcap _{s\le t}\overline{\bigcup _{\tau \le s}S(t,\tau )B(\tau ) .} \end{aligned}$$

Proof

In the proof we will denote set $\omega _1(t,B(\cdot )) := \bigcap _{s\le t}\overline{\bigcup _{\tau \le s}S(t,\tau )B(\tau ) }$. Let $x\in \omega (t,B(\cdot )).$ There exist sequences $s_n\rightarrow -\infty$ and $u_n\in B(s_n)$ such that $S(t,s_n)u_n\rightarrow x.$ We have the inclusion $\{S(t,s_n)u_n\}_{n\le n_0}\subset \bigcup _{\tau \le s}S(t,\tau )B(\tau )$ for $n_0$ such that $s_n\le s$ for any $n\ge n_0.$ So $x\in \overline{\bigcup _{\tau \le s}S(t,\tau )B(\tau )}$ for any $s\le t$ and consequently $x\in \omega _1(t,B(\cdot )).$ Now suppose that $x\in \omega _1(t,B(\cdot )).$ Then for every $n\in {\mathbb {N}}$ there exist $s_n\le n$ and $y_n\in S(t,s_n)B(s_n)$ such that $\left\| {x - y_n }\right\| \le \frac{1}{n}.$ As $y_n \in S(t,s_n) B(s_n)$ we can find $u_n\in B(s_n)$ such that $\left\| {x - S(t,s_n)u_n}\right\| \le \frac{1}{n}.$ This implies the existence of sequences $s_n\rightarrow -\infty ,$ and $u_n\in B(s_n)$ such that $S(t,s_n)u_n\rightarrow x.$ We deduce that $x\in \omega (t,B(\cdot )),$ which ends the proof. $\square$

The following result shows that pullback $\omega$-limit sets are always positively invariant.

Lemma 19

Let $\{B(t)\}_{t\le T}$ be a non-autonomous set in X. We have $S(\tau ,t)\omega (t,B(\cdot )) \subset \omega (\tau ,B(\cdot ))$ for every $\tau \ge t$.

Proof

If $y\in \omega (t,B(\cdot ))$ then there exist $s_n\rightarrow -\infty$ and $u_n\in B(s_n)$ such that $y = \lim _{n\rightarrow \infty }S(t,s_n)u_n$. From continuity of $S(\tau ,t)$ we see that $S(\tau ,t)y =\lim _{n\rightarrow \infty }S(\tau ,s_n)u_n$ whence the assertion follows. $\square$

In the next results, which hold for sets which are backward bounded, we establish some properties of unbounded pullback $\omega$-limit sets. To this end we define

$$\begin{aligned} \widetilde{{\mathcal {B}}} = \left\{ \{B(t)\}_{t\le T}\, :\ B(t) \in {\mathcal {B}}(X)\ \text {for every}\ t\le T\ \text {and}\ \bigcup _{t\le T}B(t)\in {\mathcal {B}}(X)\right\} . \end{aligned}$$

Theorem 12

Let conditions $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$ hold. Assume that $\{B(s)\}_{s\le T} \in \widetilde{{\mathcal {B}}}$. Then $\omega (t,B(\cdot ))\subset {\mathcal {J}}(t)$ for every $t\in {\mathbb {R}}$.

Proof

Since $\bigcup _{s\le T}B(s)$ is bounded then for time $r\in {\mathbb {R}}$ there exists a time $t_1(r)\le r$ such that

$$\begin{aligned} S(r,\tau )\left( \bigcup _{s\le T}B(s)\right) \subset Q(\tau ) \end{aligned}$$

for every $\tau \le t_1(r)$. We take $y\in \omega (t,B(\cdot ))$, then there exists a sequence $s_n\rightarrow -\infty$ and $u_n\in B(s_n)$ such that $y=\lim _{s_n\rightarrow -\infty }S(t,s_n)u_n$. For every $r\le t$ $y=\lim _{s_n\rightarrow -\infty }S(t,r)S(r,s_n)u_n$. There exists $n_0(r)$ such that $S(r,s_n)u_n \in Q(r)$ for $n\ge n_0(r)$. Hence $y\in \overline{S(t,r)Q(r)}$ and the proof is complete. $\square$

As a simple consequence of the above lemma and Lemma 14 we obtain the following corollary.

Corollary 4

Let conditions $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$ hold. Assume that $\{B(s)\}_{s\le T} \in \widetilde{{\mathcal {B}}}$. Then for every $t\in {\mathbb {R}}$ and $C\in {\mathcal {B}}(X)$ the set $\omega (t,B(\cdot ))\cap C$ is relatively compact.

Remark 4

Let $B(\cdot )\in \widetilde{{\mathcal {B}}}.$ If for some $t\in {\mathbb {R}}$ and $R>0$ there exist $t_1\le t$ such that for every $s\le t_1$ the intersection $S(t,s)B(s) \cap \{\left\| {Px}\right\| \le R \}$ is nonempty, then there exist ${\widehat{R}}\ge R_1$ such that for every $\tau <t$ there exists $\tau _1$ such that, the intersection $S(\tau ,s)B(s) \cap \{\left\| {Px}\right\| \le {\widehat{R}} \}$ is nonempty, for every $s\le \tau _1.$ If we additionally assume that the image of a bounded set $B \in {\mathcal {B}}(X)$ through S(t, s) must be bounded then for every $\tau >t$ there exists ${\widehat{R}}(\tau )$ and $\tau _1$ such that $S(\tau ,s)B(s)\cap \{\left\| {Px}\right\| \le {\widehat{R}}\}$ is nonempty for every $s\le \tau _1$.

Proof

Note that for some ${\widehat{R}}$ and some $t_2\le t_1$, the set $S(t,s)B(s)\cap H_{{\widehat{R}}}(t)$ is nonempty for every $s\le t_2.$ We can deduce that for every $\tau \le t$ there exists $\tau _1(\tau )$ such that $S(\tau ,s)B(s)\cap H_{{\widehat{R}}}(\tau )$ is nonempty for every $s\le \tau _1.$ Indeed from assumption (H1)$_{\textrm{NA}}$ it follows that $S(\tau ,s)B(s)\subset S(\tau ,s)(\cup _{s\le T}B(s)) \subset Q(\tau )$ for every $s \le \tau _1$ for some $\tau _1.$ Then if for $s \le \tau _1$ we would have $S(\tau ,s)B(s)\subset Q(\tau )\setminus H_{{\widehat{R}}}(\tau )$ then by assumption (H2)$_{\textrm{NA}}$ we would also have $S(t,s)B(s)\subset Q(t)\setminus H_{{\widehat{R}}}(t)$ which would be a contradiction. By assumption (H2)$_{\textrm{NA}}$ we have $H_{{\widehat{R}}} (t)\subset \{\left\| {Px}\right\| \le {\widehat{R}} \}$ for every $t\in {\mathbb {R}}$, so $S(\tau ,s)B(s) \cap \{\left\| {Px}\right\| \le {\widehat{R}} \}$ is nonempty. We consider the case for $\tau > t$. We know that there exists $\tau _1$ such that for every $s\le \tau _1$ there exists $u_s\in B(s)$ with $S(t,s)u_s \in Q(t)\cap \{ \Vert Px\Vert \le R\}$, a bounded set. The image of this set via $S(\tau ,t)$ is bounded and the assertion follows. $\square$

The next two results concern the non-emptiness and attraction in bounded sets by pullback $\omega$-limit set. They both need that S(t, s)B(s) intersects some ball in $E^+$ at some time t for sufficiently small s. Using the above remark we deduce the non-emptiness and attraction of $\omega$-limit sets not only at this time but also at other times, in the past and in the future. Note that for the attraction in the future we need the additional assumption that the image of bounded set via S(t, s) is a bounded set. This assumption is needed to deduce from the non-emptiness of intersection $S(t,s)B(s) \cap H_{R}$ that also the intersection $S(\tau ,s)B(s)\cap H_{{\widehat{R}}}(\tau )$ is nonempty for some ${\widehat{R}}$.

Lemma 20

Assume the conditions $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$. Let $\{B(s)\}_{s\le T} \in \widetilde{{\mathcal {B}}}$ be a non-autonomous set such that there exist $R>0$ and $t\in {\mathbb {R}}$ and $t_1 < t$ such that the intersection $S(t,s)B(s)\cap \{ \Vert Px\Vert \le R \}$ is nonempty for every $s\le t_1.$ Then $\omega (\tau ,B(\cdot ))$ is nonempty for every $\tau \in {\mathbb {R}}.$

Proof

Let $\tau \le t.$ By Remark 4 and assumption (H2)$_{\text {NA}},$ there exist ${\widehat{R}}\ge R_1$ and $\tau _1\le \tau$ such that, we have $S(\tau ,s)B(s)\cap H_{{\widehat{R}}}(\tau )\ne \emptyset ,$ for every $s \le \tau _1.$ For any $s_n\le \tau _1$ and $s_n\rightarrow -\infty$ we can find $u_n$ such that $u_n\in B(s_n)$ and $y_n = S(\tau ,s_n)u_n \in H_{{\widehat{R}}}(\tau )$. Moreover for every n we can find $k(n) > n$ such that $S(s_n, s_{k(n)})u_{k(n)} \in Q(s_n)$. Now $y_{k(n)} = S(\tau ,s_{k(n)})u_{k(n)} \in S(\tau ,s_n)Q(s_n)$. Now $y_{k(n)} \in L_n,$ where $L_n = S(\tau ,s_n)Q \cap H_{{\widehat{R}}} = S(\tau ,s_n)H_{{\widehat{R}}}(s_n) \cap H_{{\widehat{R}}}(\tau ).$ From Lemma 1 and assumption $(H3)_{\text {NA}}$ from $y_{k(n)}$ we can pick a subsequence which converges to some $y\in X.$ So $\omega (\tau ,B(\cdot ))$ is nonempty for every $\tau \le t.$ For $\tau >t$ by Lemma 19 we have $S(\tau ,t) \omega (t,B(\cdot ))\subset \omega (\tau ,B(\cdot )).$ So as $\omega (t,B(\cdot ))$ is nonempty the set $\omega (\tau ,B(\cdot ))$ is also nonempty. $\square$

Theorem 13

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$ and let $t\in {\mathbb {R}}$. Suppose that $\{B(s)\}_{s\le T} \in \widetilde{{\mathcal {B}}}$ is such that for some $R > 0$ there exists $t_1\le t$ such that $S(t,s)B(s)\cap \{\Vert Px\Vert \le R\}\ne \emptyset$ for every $s\le t_1$. Then

$$\begin{aligned} \lim _{s\rightarrow -\infty }\textrm{dist}(S(t,s)B(s)\cap \{\Vert Px\Vert \le R\},\omega (t,B(\cdot )))\rightarrow 0. \end{aligned}$$

Proof

We suppose that there exists a sequence $s_n\rightarrow -\infty$ and $u_n\in B(s_n)$ such that $\Vert P(S(t,s_n)u_n)\Vert \le {R}$ and for some $\varepsilon >0$, we have dist$(S(t,s_n)u_n, \omega (t,B(\cdot )))>\varepsilon$. Since $\bigcup _{s\le T}B(s)$ is bounded, there exists k(n) such that $S(s_n,s_k)u_k\in Q(s_k)$. By (H2)$_{\textrm{NA}}$ we can find ${\widehat{R}}$ such that $\{S(t,s_k)u_k\}_{k\in {\mathbb {N}}}\subset H_{{\widehat{R}}}(t)$, and for every k,. Then $y_{k(n)}=S(t,s_n)S(s_n,s_{k(n)})u_{k(n)}\in S(t,s_n)Q(s_n)\cap H_{{\widehat{R}}}(t)=L_n$, and this is a nested sequence of sets, so by (H3)$_{\textrm{NA}}$ and Lemma 1 there exists a subsequence such that $y_k\rightarrow y$ for some $y\in H_{{\widehat{R}}}(t)$. Since $u_{k(n)}\in B(s_{k(n)})$ and $s_{k(n)}\rightarrow -\infty$ we have that $y\in \omega (t,B(\cdot ))$ so we arrive to a contradiction. $\square$

Lemma 21

Under assumptions of the previous lemma there exists ${\widehat{R}}$ such that for every $\tau < t$ we have

$$\begin{aligned} \lim _{s\rightarrow -\infty }\textrm{dist}(S(\tau ,s)B(s)\cap \{\Vert Px\Vert \le {\widehat{R}}\},\omega (\tau ,B(\cdot )))\rightarrow 0. \end{aligned}$$

If additionally we assume that S(t, s)B is bounded for every bounded set B then for every $\tau > t$ there exists ${\widehat{R}}(\tau )$ such that

$$\begin{aligned} \lim _{s\rightarrow -\infty }\textrm{dist}(S(\tau ,s)B(s)\cap \{\Vert Px\Vert \le {\widehat{R}}(\tau )\},\omega (\tau ,B(\cdot )))\rightarrow 0. \end{aligned}$$

Proof

The proof follows from the same argument as the previous lemma, which is possible by Remark 4 as intersection in the statement of the Lemma are nonempty and Hausdorff semidistance is well defined. $\square$

Lemma 22

Assume (H1)$_{\textrm{NA}}$-(H3)$_{\textrm{NA}}.$ For $\{B(s)\}_{s\le T} \in \widetilde{{\mathcal {B}}},$ the unbounded pullback $\omega$-limit sets are invariant, that is $S(\tau ,t) \omega (t,B(\cdot ))= \omega (\tau ,B(\cdot )).$

Proof

Inclusion $S(\tau ,t) \omega (t,B(\cdot ))\subset \omega (\tau ,B(\cdot ))$ is asserted in Lemma 19. Let $y\in \omega (\tau ,B(\cdot )).$ There exist sequences $s_n \rightarrow -\infty$ and $u_n\in B(s_n)$ such that $\lim _{n\rightarrow \infty } S(\tau ,t ) S(t,s_n)u_n = y.$ Arguing as in the proof of Lemma 20, for a subsequence we have $S(t,s_n)u_n \rightarrow x$ with some $x\in \omega (t,B(\cdot ))$ and it must be that $S(\tau ,t)x = y$ which ends the proof. $\square$

In order to relate the pullback behavior of bounded sets with ${\mathcal {J}}_b(t)$ we need to define the second universe of non-autonomous bounded sets. This time the sets do not have to be backward bounded, but their evolution must stay in $H_R(\cdot )$ at every time and for sufficiently small initial time.

$$\begin{aligned} \widehat{{\mathcal {B}}}&=\{\{B(s)\}_{s\le T} \, : \ B(s)\in {\mathcal {B}}(X)\ \text {and there exists} \ R\ge R_0 \ \text {such that for every}\ t\in {\mathbb {R}}\\&\quad \text {there exists}\ t_1(t)\le T \ \text { such that } \ S(t,s)B(s)\subset H_R(t) \ \text {for every}\ s\le t_1\} \end{aligned}$$

Theorem 14

Assume $(H1)_{\textrm{NA}}-(H3)_{\textrm{NA}}$. For every $B(\cdot )\in \widehat{{\mathcal {B}}}$ we have the following inclusion:

$$\begin{aligned} \omega (t,B(\cdot ))\subset {\mathcal {J}}_b(t) \end{aligned}$$

Proof

Take $y\in \omega (t, B(\cdot ))$, then there exists a sequence $s_n\rightarrow -\infty$ and $u_n\in B(s_n)$ such that $\lim _{s_n\rightarrow -\infty }S(t,s_n)u_n=y$. Pick $s\le t$. There exists $n_0(s)$ such that for every $n\le n_0$ we have $S(s,s_n)u_n\in H_R(s)\subset Q(s)$. We deduce that $u\in {\mathcal {J}}(t)$. It remains to show that the solution starting from y at time t is forward bounded. We take $r\ge t$,

$$\begin{aligned} S(r,t)u=\lim _{s_n\rightarrow -\infty }S(r,t)S(t,s_n)u_n=\lim _{s_n\rightarrow -\infty }S(r,s_n)u_n \end{aligned}$$

and $S(r,s_n)u_n\in H_R(r)$ for every sufficiently large n, so the limit also belongs to $H_R(r)$ and the proof is complete. $\square$

Lemma 23

Under assumptions of previous lemma $\{\omega (r,B(\cdot ))\}_{r\in {\mathbb {R}}}$ are nonempty, compact and invariant sets which pullback attract $B(\cdot )$ at the time r.

Proof

The compactness follows from the compactness of ${\mathcal {J}}_b(t)$ and closedness of pullback $\omega$-limits. To prove the nonemptiness we take a sequence of times $\{s_n\}_{n\in {\mathbb {N}}}$ going to $-\infty$ and $u_n\in B(s_n)$, such that $y_n=S(t, s_n)u_n\in H_R(t)$. We will prove that $y_n$ is relatively compact. Indeed, for every $n\in {\mathbb {N}}$, there exists $k(n)>n$ such that $S(s_n,s_{k(n)})B(s_{k(n)})\subset H_R(s_n)$, whence $y_{k(n)}=S(t,s_{k(n)})u_{k(n)}\in S(t,s_n)H_R(s-n)\cap H_R(t)=L_n$. This is a nested sequence of sets, so by Lemma 1 and (H3)$_{\textrm{NA}}$, we obtain a subsequence convergent to some $y\in \omega (t,B(\cdot ))$. The attraction follows in a standard way. For contradiction take a sequence $u_n\in B(s_n)$, $s_n\rightarrow -\infty$ such that dist$(S(t,s_n)u_n,\omega (t,B(\cdot ))>\varepsilon$. With the same method as to see the non-emptiness we obtain that there exists a subsequence of $\{S(t,s_n)u_n\}_{n\in {\mathbb {N}}}$ such that converges to y, so this $y\in \omega (t,B(\cdot ))$ and we arrive to a contradiction. From Lemma 19 we have the positive invariance. For the negative invariance, we take $y\in \omega (t,B(\cdot ))$, so there exists a sequence $\{s_n\}_{n\in {\mathbb {N}}}$ and $u_n\in B(s_n)$ such that $y=\lim _{s_n\rightarrow -\infty }S(t,s_n)u_n$. We take $\tau <t$, and we write $y=\lim _{s_n\rightarrow -\infty }S(t,\tau )S(\tau , s_n)u_n$. With the same method as in the proof of non-emptiness we see that there exists a subsequence $\{S(\tau ,s_{\nu })u_{\nu }\}\subset \{S(\tau , s_n)u_n\}_{n\in {\mathbb {N}}}$ which converges to some $x\in X$, and $x\in \omega (\tau , B(\cdot ))$. Then $S(t,\tau )x=\lim _{s_{\nu }\rightarrow -\infty }S(t,\tau )S(\tau ,s_{\nu })u_{\nu }=\lim _{s_{\nu }\rightarrow -\infty }S(t,s_{\nu })u_{\nu } = y$ and the proof is complete. $\square$

4 Unbounded Attractors for Problems Governed by PDEs

4.1 Problem Setting and Variation of Constant Formulas

We present here the framework which fits in the formalism presented in previous Section. While it is not in the highest possible generality, its trait of novelty with respect to [6, 9] relies in the fact that its estimates are based on the Duhamel formula rather than in the energy inequalities which follow from testing the equation of the problem by appropriate functions. Let X be a Banach space with a norm $\Vert \cdot \Vert$ and let $A:X\supset D(A) \rightarrow X$ be a linear, closed and densely defined operator. Assume moreover, that the operator $-A$ is sectorial and has compact resolvent. Then, each point in $\sigma (A)$, the spectrum of A, is the eigenvalue, and this set of eigenvalues is discrete. Assume that $\sigma (A) \cap \{ \lambda \in {\mathbb {C}}\,:\ \text {Re}\, \lambda = 0 \} = \emptyset$. Then, denote by P by the spectral projection associated with the part of the spectrum $\sigma (A)\cap \{ \lambda \in {\mathbb {C}}\,:\ \text {Re}\, \lambda > 0 \}$. The range of P is finite dimensional, this will be the space $E^+$, and the range of $I-P$ will be $E^-$, a closed subspace of X. The restriction of A to the range of P is a bounded linear operator. Moreover, for some positive numbers $\gamma _0,\gamma _1,\gamma _2$, the following inequalities hold

$$\begin{aligned} \begin{aligned}&\Vert e^{A(t-s)}\Vert \le M e^{\gamma _0(t-s)}\quad \text {for}\ \ \ t\ge s,\\&\Vert e^{A(t-s)}(I-P)\Vert \le M e^{-\gamma _2(t-s)}\quad \text {for}\ \ \ \ t\ge s,\\&\Vert e^{A(t-s)}P\Vert \le M e^{\gamma _1(t-s)}\quad \text {for}\ \ \ \ t\le s, \end{aligned} \end{aligned}$$

(5)

cf. [12, page 147]. We will consider the following operator equation

$$\begin{aligned} u'(t) = Au(t) + f(t,u), \end{aligned}$$

(6)

with the initial data $u(t_0) = u_0 \in X$. We assume that f is bounded, that is, $\Vert f(t,u)\Vert \le C_f$ for every $u\in X$ and $t\in {\mathbb {R}}$. We also need to make the assumptions on f which guarantee that the above problem has the unique solution $u:[t_0,\infty ) \rightarrow X$ given by the following variation of constants formula

$$\begin{aligned} u(t)=e^{A(t-\tau )}u(\tau ) +\int _\tau ^t e^{A(t-s)}f(s,u(s))ds\ \ \text {for} \ t\geqslant \tau , \end{aligned}$$

(7)

such that $u\in C([t_0,T];X)$ for every $T\ge t_0$. We stress again, that while we do not pursue the highest generality here, it is enough to assume that $f:{\mathbb {R}}\times X\rightarrow X$ is continuous and $f(t,\cdot ):X\rightarrow X$ is Lipschitz continuous on bounded sets of X with the constant independent on t, that is if only $\Vert v\Vert ,\Vert w\Vert \le R$, then

$$\begin{aligned} \Vert f(t,v)-f(t,w)\Vert \le C(R) \Vert v-w\Vert . \end{aligned}$$

For the details of the proof of the solution existence, uniqueness, and its globality in time see for example [12, Chapter 6.7] or [7, Chapters 2 and 3]. Moreover, the solutions constitute the continuous process $S(t,\tau )$ in X, such that for a bounded set $B\in {\mathcal {B}}(X)$ the sets $S(t,\tau )B$ are bounded in the space which is compactly embedded in X, and hence relatively compact in X for $t>\tau$, c.f. for example [7, Chapter 3.3], where the proof of compactness is done for the autonomous case. Thus, assumption (H3)$_{\textrm{NA}}$, and for autonomous case (H3), is satisfied.

If u(s) is a solution to the above problem on some interval $[\tau ,t]$ then we denote $p(s)=Pu(s)$ and $q(s)=(I-P)u(s)$. Thus, q and p satisfy

$$\begin{aligned} p(t)&=e^{A(t-\tau )}p(\tau ) +\int _\tau ^t e^{A(t-s)}Pf(s,p(s)+q(s))ds\ \ \text {for}\ \ t\geqslant \tau , \end{aligned}$$

(8a)

$$\begin{aligned} q(t)&=e^{A(t-\tau )}q(\tau ) +\int _{\tau }^te^{A(t-s)}(I-P)f(s,p(s)+q(s))ds\ \ \text {for}\ \ t\geqslant \tau . \end{aligned}$$

(8b)

4.2 Estimates Which Follow from Boundedness of f and Their Consequences

We begin with the estimate for q. From (8b) we deduce in a straightforward way that

$$\begin{aligned} \Vert q(t)\Vert \le M e^{-\gamma _2(t-\tau )}\Vert q(\tau )\Vert + \frac{M C_f}{\gamma _2} (1-e^{-\gamma _2 (t-\tau )}), \end{aligned}$$

(9)

for $t\ge \tau \ge t_0$. This is enough to guarantee (H1) and its non-autonomous version (H1)$_{\text {NA}}$. Indeed, one can take, in autonomous case

$$\begin{aligned} Q = \overline{\bigcup _{t\ge 0}S(t)\left\{ \Vert (I-P)u\Vert \le \frac{MC_f}{\gamma _2}+1 \right\} }, \end{aligned}$$

and in non-autonomous case

$$\begin{aligned} Q(t) = \overline{\bigcup _{s\le t}S(t,s)\left\{ \Vert (I-P)u\Vert \le \frac{MC_f}{\gamma _2}+1 \right\} }. \end{aligned}$$

Then (H1) and (H1)$_{\text {NA}}$ hold with $D_1 = \frac{MC_f}{\gamma _2}+1$ and $D_2 = M\left( \frac{MC_f}{\gamma _2}+1\right)$. We continue with the estimates for p. First, we have the following upper bound

$$\begin{aligned} \Vert p(t)\Vert \le Me^{\gamma _0(t-\tau )}\Vert p(\tau )\Vert + \frac{MC_f}{\gamma _0} (e^{\gamma _0(t-\tau )}-1), \end{aligned}$$

(10)

valid for $t\ge \tau \ge t_0$. Moreover (8a) implies that

$$\begin{aligned} p(\tau )=e^{A(\tau -t)}p(t) +\int _t^\tau e^{A(\tau -s)}Pf(s,p(s)+q(s))ds, \end{aligned}$$

(11)

for $t\ge \tau \ge t_0$, whence

$$\begin{aligned} \Vert p(\tau )\Vert \le Me^{\gamma _1 (\tau -t)}\Vert p(t)\Vert + \frac{MC_f}{\gamma _1}. \end{aligned}$$

This means that

$$\begin{aligned} \Vert p(t)\Vert \ge e^{\gamma _1(t-\tau )} \left( \frac{1}{M}\Vert p(\tau )\Vert - \frac{C_f}{\gamma _1}\right) . \end{aligned}$$

(12)

Clearly, if the projection p of the initial data is sufficiently large, namely $\Vert p(t_0)\Vert > \frac{MC_f}{\gamma _1}$, then $\Vert p(t)\Vert$ tends exponentially to infinity as $t\rightarrow \infty$. This is not enough, however, to ensure (H2) and its non-autonomous counterpart (H2)$_{\text {NA}}$. The technical difficulty lies in the fact that, although real parts of all eigenvalues of A on $E^+$ are positive, this does not have to hold for $A+A^\intercal$, the symmetric part of A. For simplicity we associate A on $E^+$ with the matrix being its representation in some basis of $E^+$ and vectors $p\in E^+$ with their representations in this basis. Denoting the Euclidean norm and the associated matrix norm by $|\cdot |$, for $p\in E^+$, the finite dimensional space, one has the equivalence $C_1\Vert p\Vert \le |p|\le C_2\Vert p\Vert$. Now one can rewrite the variation of constants formula (8a) as the following non-autonomous ODE

$$\begin{aligned} p'(t) = Ap(t) + P f(t,p(t)+q(t)). \end{aligned}$$

Then consider N, a symmetric and positive definite matrix which is the unique solution of the Lyapunov equation $A^\intercal N + NA = I.$ This N is given by the formula

$$\begin{aligned} N = \int _0^\infty e^{-t(A+A^\intercal )}\, dt. \end{aligned}$$

Now

$$\begin{aligned} \frac{d}{dt}(p^\intercal (t) N p(t))&= p^\intercal (t) (A^\intercal N + NA)p(t) + 2(P f(t,p(t)+q(t)))^\intercal N p(t)\\&= |p(t)|^2 + 2(P f(t,p(t)+q(t)))^\intercal N p(t). \end{aligned}$$

We deduce that

$$\begin{aligned} \frac{d}{dt}(p^\intercal (t) N p(t))\ge C_1^2\Vert p(t)\Vert ^2 - 2C_2^2 C_f |N| \Vert p(t)\Vert = \Vert p(t)\Vert (C_1^2\Vert p(t)\Vert - 2C_2^2 C_f |N|). \end{aligned}$$

This means that if only

$$\begin{aligned} \Vert p(t)\Vert > \frac{2C_2^2 C_f |N|}{C_1^2}, \end{aligned}$$

then the quadratic form $p^\intercal (t) N p(t)$ is strictly increasing. Now, as N is positively defined, there exist positive constants $D_1, D_2$ such that $D_1^2\Vert p\Vert ^2 \le p^\intercal N p \le D_2^2\Vert p\Vert ^2$. It follows that (H2) and its non-autonomous version (H2)$_{\text {NA}}$ hold with

$$\begin{aligned} R_0&> \frac{2C_2^2 C_f |N|}{C_1^2}, \quad R_1 = \frac{D_2}{D_1}R_0,\quad S(R) = \frac{D_1}{D_2}R,\quad \\ H_R&= Q \cap \{ u \in X\, :\ (Pu)^\intercal N (Pu) \le D_1^2 R^2\}. \end{aligned}$$

Observe, that (12) imply that if the problem is autonomous also (H4) holds. We have thus verified (H1)–(H4) of Sect. 2 and (H1)$_{\text {NA}}$–(H3)$_{\text {NA}}$ of Sect. 3, which implies by Theorem 11 the existence of unbounded pullback attractor, and, for the autonomous problem, the existence of the unbounded attractor by Theorem 3.

4.3 Thickness of Unbounded Attractor

In this section we derive the estimates which guarantee that the thickness in $E^-$ of the unbounded attractor tends to zero as $p\in E^+$ tends to infinity, or in the language of the multivalued inertial manifold, that $\lim _{\Vert p\Vert \rightarrow \infty }\text {diam}\, \Phi (p) = 0$. For simplicity we deal only with the autonomous case. The fact that such thickness tends to zero guarantees, by Theorem 4 that the unbounded attractor ${\mathcal {J}}$ attracts the bounded sets not only in the sense

$$\begin{aligned}&\lim _{t\rightarrow \infty } \textrm{dist}(S(t)B \cap \{ \Vert Pu\Vert \le R\},{\mathcal {J}} ) = 0\ \ \text {if only}\ B,R\ \ \text {are such that}\\&\quad \text {the sets}\ \ S(t)B\cap \{ \Vert Pu\Vert \le R\}\ \ \text {are nonempty for every sufficiently large}\ t, \end{aligned}$$

but also in the sense

$$\begin{aligned} \lim _{t\rightarrow \infty } \textrm{dist}(S(t)B ,{\mathcal {J}} ) = 0. \end{aligned}$$

In order to obtain the desired result we need to assume that the projection $I-P$ of the nonlinearity f decays to zero as the projection P or the argument tends to infinity. We make the following assumption which makes precise what rate of this decay is needed.

• (Hf1) The function $f:X\rightarrow X$ has the form $f(u) = f_0 + f_1(u)$, where $f_0\in X$ and there exists $K>0$ such that if $\Vert Pu\Vert \ge K$, then

  $$\begin{aligned} \Vert (I-P)f_1(u)\Vert \le H(\Vert Pu\Vert ) \end{aligned}$$

  where $H:[K,\infty )\rightarrow (0,\infty )$ is nonincreasing, $\lim _{r\rightarrow \infty } H(r) = 0$ and either

  $$\begin{aligned} H(r) \le \frac{D}{r^\alpha }\ \ \text {with}\ \ \alpha>0\ \ \text {and}\ \ D>0\ \ \text {for}\ \ r\ge K, \end{aligned}$$

  (13)

  or

  $$\begin{aligned} {[}K,\infty )\ni r \mapsto r^{\frac{\gamma _2}{\gamma _1}-\varepsilon }H(r)\in {\mathbb {R}}\ \ \text {is nondecreasing for} \ \ \text {for some}\ \ \varepsilon \in \left( 0,\frac{\gamma _2}{\gamma _1}\right) .\qquad \quad \end{aligned}$$

  (14)

Theorem 15

If, in addition to the assumptions of Sect. 4.1 we assume (Hf1), then

$$\begin{aligned} \lim _{t\rightarrow \infty } \textrm{dist}(S(t)B ,{\mathcal {J}} ) = 0\ \ \text {for every}\ \ B\in {\mathcal {B}}(X). \end{aligned}$$

and

$$\begin{aligned} \lim _{\Vert p\Vert \rightarrow \infty }\textrm{diam}\, \Phi (p) = 0, \end{aligned}$$

more precisely if (13) holds then there exists constants $\beta >0$ (depending on $\gamma _0, \gamma _1, \gamma _1, \alpha$) and $M_1 > 0$ such that for sufficiently large $\Vert p\Vert$

$$\begin{aligned} \textrm{diam}\, \Phi (p) \le M_1 \frac{1}{\Vert p\Vert ^\beta }, \end{aligned}$$

and if (14) holds, there exists constants $M_2, M_3 > 0$ such that

$$\begin{aligned} \textrm{diam}\, \Phi (p) \le M_2 H\left( M_3 \Vert p\Vert {^\frac{\gamma _1}{\gamma _0}}\right) , \end{aligned}$$

Remark 5

The proof for the case (13) with the use of the energy estimates instead of the Duhamel formula and $f_0 = 0$ appears in [9, Theorem 6.2]. The main new contribution of the above result is allowing also for the case (14) which makes it possible to consider very slow decay of H, such as $H(s) \le \frac{C}{\ln \, s}$.

Remark 6

From the course of the proof it is possible to derive the exact values of the constants $M_1, M_2, M_3$, and $\beta$. Particular interest lies in the decay rate $\beta$. Namely, if $\gamma _2 > \gamma _1\alpha$, then $\beta = \frac{\gamma _1 \alpha }{\gamma _0}$, if $\gamma _2 < \gamma _1\alpha$, then $\beta = \frac{\gamma _2}{\gamma _0}$, and if $\gamma _2 < \gamma _1\alpha$ then $\beta$ could be taken as any positive number less than $\frac{\gamma _2}{\gamma _0}$. Moreover, an obvious modification of the proof leads in this last case to the decay rate $\beta =\frac{\gamma _2}{\gamma _0}$ with a logarithmic correction.

Proof

As 0 is in the resolvent of A we can find ${\overline{u}}\in X$ the unique solution of $A {\overline{u}} = f_0$. Let u be the solution of (6) with the initial data $u_0$ such that

$$\begin{aligned} \Vert Pu_0\Vert \ge \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) \end{aligned}$$

(15)

Denote $v = u-{\overline{u}}$. Then v solves the equation

$$\begin{aligned} v'(t) = Av(t) + f_1(v(t)+{\overline{u}}). \end{aligned}$$

The problem governed by this equation has the unbounded attractor ${\mathcal {J}}$ and then ${\overline{u}} + {\mathcal {J}}$ is the unbounded attractor for the original problem. We denote $Pv(t) = p(t)$ and $(I-P)v(t) = q(t)$. These functions satisfy the equations

$$\begin{aligned} p(t)&=e^{A(t-\tau )}p(\tau ) +\int _\tau ^t e^{A(t-s)}Pf_1(p(s)+q(s)+{\overline{u}})ds\ \ \text {for}\ \ t\geqslant \tau \ \ \end{aligned}$$

(16a)

$$\begin{aligned} q(t)&=e^{A(t-\tau )}q(\tau ) +\int _{\tau }^te^{A(t-s)}(I-P)f_1(p(s)+q(s)+{\overline{u}})ds\ \ \text {for}\ \ t\geqslant \tau . \end{aligned}$$

(16b)

As $\Vert f_1(u)\Vert \le C_f + \Vert f_0\Vert$, analogously as in Sect. 4.2 from (16a) we obtain

$$\begin{aligned} e^{\gamma _1 t} \left( \frac{1}{M}\Vert P(u_0-{\overline{u}})\Vert - \frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) \le \Vert p(t)\Vert \ \ \text {for}\ \ t\ge 0. \end{aligned}$$

Then $\Vert p(t)+P{\overline{u}}\Vert = \Vert P(p(t)+q(t)+{\overline{u}})\Vert \ge K e^{\gamma _1 t} \ge K$ for $t\ge 0$. Now, from (16b) it follows that

$$\begin{aligned} \Vert q(t)\Vert \le Me^{-\gamma _2 (t-\tau )}\Vert q(\tau )\Vert + Me^{-\gamma _2 t}\int _\tau ^t e^{\gamma _2 s} H(\Vert p(s) + P{\overline{u}}\Vert )\, ds. \end{aligned}$$

(17)

We proceed separately for (13) and (14). If (13) holds then

$$\begin{aligned} \Vert q(t)\Vert \le Me^{-\gamma _2 (t-\tau )}\Vert q(\tau )\Vert + MDe^{-\gamma _2 t}\int _\tau ^t e^{\gamma _2 s} \frac{1}{\Vert p(s) + P{\overline{u}}\Vert ^\alpha }\, ds. \end{aligned}$$

But since

$$\begin{aligned} \frac{1}{\Vert p(s) + P{\overline{u}}\Vert ^\alpha } \le \frac{e^{-\gamma _1\alpha s}}{K^\alpha }, \end{aligned}$$

we deduce that

$$\begin{aligned} \Vert q(t)\Vert \le Me^{-\gamma _2 (t-\tau )}\Vert q(\tau )\Vert + \frac{MD}{K^\alpha }e^{-\gamma _2 t}\int _\tau ^t e^{(\gamma _2-\gamma _1\alpha ) s}\, ds. \end{aligned}$$

Taking $\tau = 0$ we obtain

$$\begin{aligned} \Vert q(t)\Vert \le Me^{-\gamma _2 t}\Vert q(0)\Vert + \frac{MD}{K^\alpha }e^{-\gamma _2 t}\int _0^t e^{(\gamma _2-\gamma _1\alpha ) s}\, ds. \end{aligned}$$

Now if $\gamma _2 > \gamma _1\alpha$ then

$$\begin{aligned} \Vert q(t)\Vert \le Me^{-\gamma _2 t}\Vert q(0)\Vert + \frac{MD}{K^\alpha (\gamma _2-\gamma _1\alpha )}e^{-\gamma _1\alpha t} \le M e^{-\gamma _1\alpha t}\left( \frac{D}{K^\alpha (\gamma _2-\gamma _1\alpha )}+\Vert q(0)\Vert \right) . \end{aligned}$$

If $\gamma _2 = \gamma _1\alpha$, then

$$\begin{aligned} \Vert q(t)\Vert&\le Me^{-\gamma _2 t}\Vert q(0)\Vert + \frac{MD}{K^\alpha }e^{-\gamma _2 t}t \le M\max \left\{ \Vert q(0)\Vert , \frac{D}{K^\alpha }\right\} e^{-\gamma _2t}(1+t) \\&\le M\max \left\{ \Vert q(0)\Vert , \frac{D}{K^\alpha }\right\} \frac{e^\varepsilon }{\varepsilon e} e^{-(\gamma _2-\varepsilon )t}\ \ \text {for small}\ \ \varepsilon >0. \end{aligned}$$

Finally, if $\gamma _2 < \gamma _1\alpha$, then

$$\begin{aligned} \Vert q(t)\Vert \le Me^{-\gamma _2 t}\left( \Vert q(0)\Vert + \frac{D}{K^\alpha (\gamma _1\alpha -\gamma _2)}\right) . \end{aligned}$$

That shows the exponential attraction as $t\rightarrow \infty$ towards the finite dimensional linear manifold ${\overline{u}}+R(P) = {\overline{u}}+E^+$ for the projection P of the initial data outside a large ball given by (15), for f that satisfies (Hf) with (13). Now consider (14). As H is nonincreasing, we deduce, for $\tau =0$ in (17)

$$\begin{aligned} \Vert q(t)\Vert \le Me^{-\gamma _2 t}\Vert q(0)\Vert + Me^{-\gamma _2 t}\int _0^t e^{\gamma _2 s} H(Ke^{\gamma _1 s})\, ds. \end{aligned}$$

It follows that

$$\begin{aligned} \Vert q(t)\Vert&\le Me^{-\gamma _2 t}\Vert q(0)\Vert + Me^{-\gamma _2 t}\int _0^t e^{\gamma _2 s} (Ke^{\gamma _1 s})^{-\frac{\gamma _2}{\gamma _1}+\varepsilon }(Ke^{\gamma _1 s})^{\frac{\gamma _2}{\gamma _1}-\varepsilon }H(Ke^{\gamma _1 s})\, ds\\&\le Me^{-\gamma _2 t}\Vert q(0)\Vert + Me^{-\gamma _2 t}(Ke^{\gamma _1 t})^{\frac{\gamma _2}{\gamma _1}-\varepsilon }H(Ke^{\gamma _1 t})\int _0^t e^{\gamma _2 s} (Ke^{\gamma _1 s})^{-\frac{\gamma _2}{\gamma _1}+\varepsilon }\, ds\\&= Me^{-\gamma _2 t}\Vert q(0)\Vert + Me^{-\gamma _2 t}e^{\gamma _2t}e^{-\varepsilon \gamma _1 t}H(Ke^{\gamma _1 t})\int _0^t e^{\varepsilon \gamma _1 s} \, ds \\&\le M\left( e^{-\gamma _2 t}\Vert q(0)\Vert + \frac{1}{\varepsilon \gamma _1}H(Ke^{\gamma _1 t})\right) . \end{aligned}$$

Hence, for the case (14) we get the attraction towards the finite dimensional linear manifold ${\overline{u}}+R(P) = {\overline{u}}+E^+$ as $t\rightarrow \infty )$ this time with the rate given by $H(Ke^{\gamma _1 t})$.

Now let $\{u(t)\}_{t\in {\mathbb {R}}}$ be the solution in the unbounded attractor and let $u(t) = p(t) + q(t)$. Then, by (12) either there exists $\tau \in {\mathbb {R}}$ such that $\Vert p(\tau )\Vert > \frac{MC_f}{\gamma _1}$ and then $\lim _{t\rightarrow \infty }\Vert p(t)\Vert = \infty$ or we must have $\Vert p(t)\Vert \le \frac{MC_f}{\gamma _1}$ for every $t \in {\mathbb {R}}$. Moreover, also from (12), we deduce that for every solution in the unbounded attractor it must be

$$\begin{aligned} \limsup _{\tau \rightarrow -\infty }\Vert p(\tau )\Vert \le \frac{MC_f}{\gamma _1}. \end{aligned}$$

This means that if only $u\in {\mathcal {J}}$ and $\Vert Pu\Vert > \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) + 1$ then there exists $v\in {\mathcal {J}}$ with $\Vert Pv\Vert = \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) + 1$ and $t>0$ such that $v = S(t)u$. From (10) we deduce that

$$\begin{aligned} \Vert Pu\Vert \le Me^{\gamma _0 t}\left( \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) + 1 + \frac{C_f}{\gamma _0}\right) , \end{aligned}$$

(18)

whence

$$\begin{aligned} e^{-\gamma _0 t} \le M\left( \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) + 1 + \frac{C_f}{\gamma _0}\right) \frac{1}{\Vert P u\Vert }. \end{aligned}$$

We have proved that in the case (13) there exist constants $C, \kappa >0$ such that

$$\begin{aligned} \Vert (I-P) (u - {\overline{u}})\Vert \le C e^{-\kappa t}. \end{aligned}$$

Combining the two above estimates leads us to

$$\begin{aligned} \Vert (I-P) (u - {\overline{u}})\Vert \le C M^{\frac{\kappa }{\gamma _0}}\left( \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) + 1 + \frac{C_f}{\gamma _0}\right) ^{\frac{\kappa }{\gamma _0}} \frac{1}{\Vert P u\Vert ^{\frac{\kappa }{\gamma _0}}}. \end{aligned}$$

On the other hand, if (14) holds then we have proved that there exist constants $C_1, C_2 > 0$ such that

$$\begin{aligned} \Vert (I-P) (u - {\overline{u}})\Vert \le C_1 e^{-\gamma _2 t} + C_2 H(Ke^{\gamma _1 t}). \end{aligned}$$

Combining this bound with (18) leads to

$$\begin{aligned}&\Vert (I-P) (u - {\overline{u}})\Vert \le C_1 M^{\frac{\gamma _2}{\gamma _0}}\left( \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) + 1 + \frac{C_f}{\gamma _0}\right) ^{\frac{\gamma _2}{\gamma _0}} \frac{1}{\Vert P u\Vert ^{\frac{\gamma _2}{\gamma _0}}}\\&\quad + C_2 H\left( KM^{-\frac{\gamma _1}{\gamma _0}}\left( \Vert P{\overline{u}}\Vert + M \left( K+\frac{C_f+\Vert f_0\Vert }{\gamma _1}\right) + 1 + \frac{C_f}{\gamma _0}\right) ^{{-\frac{\gamma _1}{\gamma _0}}} \Vert Pu\Vert {^\frac{\gamma _1}{\gamma _0}}\right) . \end{aligned}$$

It is not hard to check that for sufficiently large $\Vert Pu\Vert$ the second term in the above estimate dominates over the first term, which completes the proof. $\square$

4.4 The Case of Small Lipshitz Constant: Unbounded Attractors and Inertial Manifolds

In the previous section we have proved, that, provided the $(I-P)$ projection of the nonlinearity f(u) tends to zero with appropriate rate as long as $\Vert Pu\Vert$ tends to infinity, the thickness of the unbounded attractor also tends to zero and it attracts bounded sets not only in bounded sets, but also on the whole space.

In this section we consider another situation when the attraction holds on the whole space, namely the nonlinearity f is assumed to be Lipschitz with sufficiently small constant. We will also assume that f does not depend on time directly, leaving the non-autonomous case, for now, open.

We will make the following assumption: one for the graph transform method and one for the Lyapunov–Perron method

(Hf2)$_{\text {GT}\bigcup \text {LP}}$:

The function $f:X\rightarrow X$ satisfies

$$\begin{aligned} \Vert f(u) - f(v) \Vert \le L_f \Vert u-v\Vert \ \ \text {for}\ \ u,v\in X, \end{aligned}$$

with

(Hf2)$_{\text {GT}}$:

either $M=1$ and $L_f < {\left\{ \begin{array}{ll}&{} \frac{\gamma _1\gamma _2}{\gamma _1+\gamma _2} \ \ \text {if}\ \ \gamma _1 \ge \gamma _2,\\ &{}\frac{\gamma _1+\gamma _2}{4}\ \ \text {if}\ \ \gamma _1 \le \gamma _2,\end{array}\right. }$ for the graph transform method,

(Hf2)$_{\text {LP}}$:

or $M\ge 1$ is arbitrary and the following three inequalities hold with some $\kappa > 0$

$$\begin{aligned}&L_f \le \frac{\gamma _1+\gamma _2}{M} \frac{\kappa }{(M+\kappa )(1+\kappa )},\qquad L_f < \frac{\gamma _1+\gamma _2}{M} \frac{1}{2(1+\kappa )}, \end{aligned}$$

(19)

$$\begin{aligned}&\frac{M^2L_f}{\gamma _2+\gamma _1 - 2ML_f(1+\kappa )} + \frac{M^2L_f}{\gamma _2+\gamma _1 - ML_f(1+\kappa )} < 1, \end{aligned}$$

(20)

$$\begin{aligned}&ML_f+\frac{M^2L_f^2 (1+\kappa )(1+M)}{\gamma _1 + \gamma _2 - ML_f(1+\kappa )} < \gamma _2. \end{aligned}$$

(21)

for the Lyapunov–Perron method.

We will prove that under one of the above assumptions, i.e. if the Lipschitz constant $L_f$ is sufficiently small, then all solutions are exponentially attracted to a graph of a certain function $\Sigma :E^+\rightarrow E^-$, the inertial manifold. We will construct it independently by the two methods: the geometric approach by means of the graph transform (see, for example [24], or the monograph [30] for its realization for the dissipative case) and the analytic approach by the Lyapunov–Perron method (see [10, 11, 19]). Although the graph transform method works only if $M=1$ in (5), and the Lyapunov–Perron method works for arbitrary $M \ge 1$ we present both of them, due to the intuitive geometric construction and higher bound present in the graph transform approach.

Remark 7

In (Hf2)$_{GT}$ we have presented the explicit bound for $L_f$, while in (Hf2)$_{LP}$ it is given implicitly, and the restrictions involve $\kappa$, the Lipschitz constant of $\Sigma$. Clearly for a given fixed $\kappa > 0$ the value $L_f = 0$ satisfies all bounds, so one can find maximal $L_{f}(\kappa , \gamma _1, \gamma _2, M)$ such that all three bounds hold for $L_f \in [0,L_{f}(\kappa , \gamma _1, \gamma _2, M))$. The next goal is to find $\kappa = \kappa (\gamma _1, \gamma _2, M)$ such that $L_{f}(\kappa (\gamma _1, \gamma _2, M), \gamma _1, \gamma _2, M) = \max _{\kappa > 0} L_{f}(\kappa , \gamma _1, \gamma _2, M)$. performed this optimization for $M=1$ for several values of $\gamma _1, \gamma _2$. The obtained bound for $L_f$ is presented in the following table.

	$\gamma _1 = 0.1$	$\gamma _1 = 1$	$\gamma _1= 10$
$\gamma _2 = 0.1$	$L_f^{LP} = 0.044, L_f^{GT} = 0.050$	$L_f^{LP} = 0.084, L_f^{GT} = 0.090$	$L_f^{LP} = 0.098, L_f^{GT} = 0.099$
$\gamma _2 = 1$	$L_f^{LP} = 0.242, L_f^{GT} = 0.275$	$L_f^{LP} = 0.441, L_f^{GT} = 0.500$	$L_f^{LP} = 0.845, L_f^{GT} = 0.909$
$\gamma _2 = 10$	$L_f^{LP} = 2.228, L_f^{GT} = 2.525$	$L_f^{LP} = 2.427, L_f^{GT} = 2.750$	$L_f^{LP} = 4.413, L_f^{GT} = 5.000$

Visibly, the bound of the graph transform method is always higher, which means that it allows to choose the Lipschitz constant with more freedom. We stress, however, that we expect that all the obtained bounds are still not sharp: according to [31, 32] the sharp bound cannot be higher than $\frac{\gamma _1+\gamma _2}{2}$, and this value can be obtained with the use of the energy inequalities.

We begin with a lemma.

Lemma 24

Let A be a linear densely defined operator with $-A$ being sectorial and having compact resolvent. Assume that P and $I-P$ are complementary spectral projections satisfying (5) with P being finite dimensional. Let $f:X\rightarrow X$ be bounded ($\Vert f(u)\Vert \le C_f$ for every $u\in X$) and Lipschitz on bounded sets ($\Vert f(u)-f(v)\Vert \le C(R)\Vert u-v\Vert$ for every $u,v\in X$ with $\Vert u\Vert ,\Vert v\Vert \le R$). Assume that there exists a Lipschitz function $\Sigma :E^+\rightarrow E^-$ and the constant $\delta >0$ such that for every bounded set $B\in {\mathcal {B}}(X)$ we can find a constant $C(B) > 0$ with

$$\begin{aligned} \textrm{dist} (S(t)B, \textrm{graph}\, \Sigma ) \le C(B) e^{-\delta t}\ \ \text {for every}\ \ t\ge 0. \end{aligned}$$

(22)

Then, we have the equality ${\mathcal {J}} = \textrm{graph}\, \Sigma$, and the attraction by the unbounded attractor is exponential

$$\begin{aligned} \textrm{dist} (S(t)B,{\mathcal {J}}) \le C(B) e^{-\delta t}\ \ \text {for every}\ \ t\ge 0. \end{aligned}$$

Proof

By the minimality in Theorem 3 we must have

$$\begin{aligned} {\mathcal {J}} \subset \text {graph} \Sigma . \end{aligned}$$

But, as by Lemma 9 the set ${\mathcal {J}}$ coincides with a graph of a multifunction $\Psi$ function over $E^+$ with nonempty values, it follows that for every p there exists exactly one q such that $p+q = {\mathcal {J}}$. Hence it must be ${\mathcal {J}} = \text {graph}\, \Sigma$, the unbounded attractor coincides with the graph of the Lipshitz function over $E^+$. In other words, multivalued inertial manifold is single-valued and Lipschitz. $\square$

Remark 8

In fact in the next two subsections we prove more than attraction of S(t)B by the graph of $\Sigma$, i.e. we demonstrate, using the two methods, that if $u_0\in B \in {\mathcal {B}}(X)$, then

$$\begin{aligned} \Vert \Sigma (PS(t)u_0) - (I-P)S(t)u_0 \Vert \le C(B)e^{-\delta t}. \end{aligned}$$

Clearly, this estimate implies (22).

Remark 9

We actually do not need f to be Lipschitz with the constant satisfying the bound on given in (Hf2) on the whole space. Indeed, the proof that uses the graph transform method in Sect. 4.4.1 uses only the lipschitzness of f on Q, the bounded in $E^-$ absorbing set (which is included in an infinite strip in $E^+$ given by $\{ \Vert (I-P)x\Vert \le D_2 \}$) and the proof that uses the Lyapunov–Perron method in Sect. 4.4.2 needs only the lipschitzness of f on a certain infinite in $E^+$ strip $\{ \Vert (I-P)x \Vert \le \text {CONST} \}$. Hence for both methods it is sufficient if f is Lipschitz with sufficiently small constant on a certain infinite strip in $E^+$ which is bounded in $E^-$.

4.4.1 Graph Transform: Case of $M=1$

The key concept behind the graph transform are cones: we will say that points $u_1 = p_1 + q_1$ and $u_2 = p_2 + q_2$ are in the positive cone with respect to each other if $\Vert q_1-q_2\Vert \le \kappa \Vert p_1-p_2\Vert$. If the opposite inequality $\Vert q_1-q_2\Vert > \kappa \Vert p_1-p_2\Vert$ holds, then the points $u_1, u_2$ are in the negative cone with respect to each other.

Lemma 25

Assume, in addition to assumptions of Sect. 4.1 that (Hf2)$_{\text {GT}\cup \text {LP}}$ holds with

$$\begin{aligned} L_f < \frac{\kappa }{(1+\kappa )^2}(\gamma _1 + \gamma _2) \ \ \text {with a constant}\ \ \kappa > 0. \end{aligned}$$

If $u_1, u_2 \in Q$ are in the positive cone with respect to each other, then $S(t)u_1, S(t)u_2$ are also in the positive cone with respect to each other.

Proof

We will denote $p_1(s) = PS(s)u_1$, $p_2(s) = PS(s)u_2$, $q_1(s) = (I-P)S(s)u_1$, $q_2(s) = (I-P)S(s)u_2$ Assume, for contradiction, that $S(t)u_1, S(t)u_2$ are in the negative cone with respect to each other. Then there exists $\tau \in [0,t)$ such that $\Vert q_1(\tau ) - q_2(\tau )\Vert = \kappa \Vert p_1(\tau ) - p_2(\tau )\Vert$ and $\Vert q_1(s) - q_2(s)\Vert > \kappa \Vert p_1(s) - p_2(s)\Vert$ for $s\in (\tau ,t]$. We deduce from (8a) and (8b) that

$$\begin{aligned} p_1(s)-p_2(s)&=e^{A(s-\tau )}(p_1(\tau )-p_2(\tau )) \nonumber \\&\quad +\int _\tau ^s e^{A(s-r)}P(f(p_1(r)+q_1(r))-f(p_2(r)+q_2(r)))dr, \end{aligned}$$

(23a)

$$\begin{aligned} q_1(s)-q_2(s)&=e^{A(s-\tau )}(q_1(\tau )-q_2(\tau ))\nonumber \\&\quad +\int _{\tau }^se^{A(s-r)}(I-P)(f(p_1(r)+q_1(r))-f(p_2(r)+q_2(r)))dr. \end{aligned}$$

(23b)

for every $s\in (\tau ,t]$. We need to estimate the difference of q from above and difference of p from below. Using (5) we directly obtain

$$\begin{aligned} \Vert q_1(s)-q_2(s)\Vert\le & {} e^{-\gamma _2(s-\tau )}\Vert q_1(\tau )-q_2(\tau )\Vert \\{} & {} +L_f\int _{\tau }^s e^{-\gamma _2(s-r)}(\Vert p_1(r)-p_2(r)\Vert + \Vert q_1(r)-q_2(r)\Vert )dr. \end{aligned}$$

Moreover, (23a) implies that

$$\begin{aligned} p_1(\tau )-p_2(\tau )= & {} e^{A(\tau -s)}(p_1(s)-p_2(s)) \\{} & {} +\int _s^\tau e^{A(\tau -r)}P(f(p_1(r)+q_1(r))-f(p_2(r)+q_2(r)))dr, \end{aligned}$$

whence, by (5),

$$\begin{aligned} \Vert p_1(\tau )-p_2(\tau )\Vert\le & {} e^{\gamma _1(\tau -s)}\Vert p_1(s)-p_2(s)\Vert \\{} & {} +L_f\int _\tau ^s e^{\gamma _1(\tau -r)}(\Vert p_1(r)-p_2(r)\Vert +\Vert q_1(r)-q_2(r)\Vert )dr. \end{aligned}$$

This means that

$$\begin{aligned}{} & {} e^{\gamma _1(s-\tau )}\Vert p_1(\tau )-p_2(\tau )\Vert -L_f\int _\tau ^s e^{\gamma _1(s-r)}(\Vert p_1(r)-p_2(r)\Vert +\Vert q_1(r)-q_2(r)\Vert )dr\\{} & {} \quad \le \Vert p_1(s)-p_2(s)\Vert . \end{aligned}$$

Combining the two bounds yields

$$\begin{aligned}&e^{\gamma _1(s-\tau )}\kappa \Vert p_1(\tau )-p_2(\tau )\Vert -L_f\kappa \int _\tau ^s e^{\gamma _1(s-r)}(\Vert p_1(r)-p_2(r)\Vert +\Vert q_1(r)-q_2(r)\Vert dr\\&\quad < e^{-\gamma _2(s-\tau )}\Vert q_1(\tau )-q_2(\tau )\Vert +L_f\int _{\tau }^s e^{-\gamma _2(s-r)}(\Vert p_1(r)-p_2(r)\Vert + \Vert q_1(r)-q_2(r)\Vert )dr. \end{aligned}$$

Using the fact that $\Vert q_1(\tau ) - q_2(\tau )\Vert = \kappa \Vert p_1(\tau ) - p_2(\tau )\Vert$ and $\Vert q_1(s) - q_2(s)\Vert > \kappa \Vert p_1(s) - p_2(s)\Vert$ for $s\in (\tau ,t]$ we deduce

$$\begin{aligned}{} & {} \left( e^{\gamma _1(s-\tau )}-e^{-\gamma _2(s-\tau )}\right) \Vert q_1(\tau )-q_2(\tau )\Vert \\{} & {} \quad < L_f\int _\tau ^s (\kappa e^{\gamma _1(s-r)}+e^{-\gamma _2(s-r)})\left( 1+\frac{1}{\kappa }\right) \Vert q_1(r)-q_2(r)\Vert dr. \end{aligned}$$

Let $s=\tau +h$ for $h\in [0,t-\tau )$. Then

$$\begin{aligned}{} & {} \left( e^{\gamma _1h}-e^{-\gamma _2h}\right) \Vert q_1(\tau )-q_2(\tau )\Vert \\{} & {} \quad < \left( 1+\frac{1}{\kappa }\right) L_f\int _\tau ^{\tau +h} (\kappa e^{\gamma _1(\tau +h-r)}+e^{-\gamma _2(\tau +h-r)})\Vert q_1(r)-q_2(r)\Vert dr. \end{aligned}$$

Using the mean value theorem for integrals we deduce that there exists $\theta (h) \in (0,1)$ such that

$$\begin{aligned}{} & {} \frac{e^{\gamma _1h}-e^{-\gamma _2h}}{h} \Vert q_1(\tau )-q_2(\tau )\Vert \\{} & {} \quad < \left( 1+\frac{1}{\kappa }\right) L_f (\kappa e^{\gamma _1((1-\theta )h)}+e^{-\gamma _2((1-\theta )h)})\Vert q_1(\tau +\theta h)-q_2(\tau +\theta h)\Vert . \end{aligned}$$

Passing with h to zero yields

$$\begin{aligned} (\gamma _1 + \gamma _2) \Vert q_1(\tau )-q_2(\tau )\Vert \le \frac{(1+\kappa )^2}{\kappa }L_f \Vert q_1(\tau )-q_2(\tau )\Vert , \end{aligned}$$

a contradiction since we must have $q_1(\tau ) \ne q_2(\tau )$. $\square$

Remark 10

The fact that $M=1$ is required only in the above lemma which establishes the invariance of the positive cones. The rest of the argument on this section does not require this restriction on M. Hence, if it would be possible to obtain the invariance of the positive cone for $M>1$, the graph transform argument would work for the general M. For an ODE case this could be obtain by introducing the appropriate change of coordinates both in (then finite dimensional) spaces $E^+$ and $E^-$. For our case such change of coordinates is possible only in the finite dimensional space $E^+$. Hence we leave the question if it is possible to adapt the graph transform argument to the case of general M, for now, open.

Now, choose $\Sigma _0:E^+\rightarrow E^-$, the Lipshitz function with the constant $\kappa$ and denote the graph of $\Sigma _0$ as $X\supset \text {graph}\, \Sigma _0=\{ p+\Sigma _0(p)\,:\ p\in E^+ \}$.

Lemma 26

Assume that $\Sigma _0:E^+\rightarrow E^-$ is a continuous function with $\textrm{graph}\, \Sigma _0 \subset Q$, the absorbing and positively invariant set bounded in $E^-$. For every $t>0$ and for every $p\in E^+$ there exists $q\in E^-$ such that $p+q \in S(t)(\textrm{graph}\, \Sigma _0)$.

Proof

The proof follows the lines of the argument in Lemma 3. Choose $p\in E^+$ and $t>0$ and consider the continuous mapping $H(\theta ,p) = PS(\theta t)(p+\Sigma _0(p))$. Then $H(0,p) = p$. Now we will construct the appropriate set on which we will consider the degree. Since (H2) holds, there exists $R\ge R_0$ such that $\{x\in E^+ \,:\ \Vert x\Vert \le \Vert p\Vert +1 \} \subset H_R$. Define $B = \{ x\in E^+\, :\ \Vert x\Vert < R + 1\}$, and since, by (H2) again, $p \in B$ it follows that $\text {deg}(H(0,\cdot ),B,p) = 1$. As, by (H2), $\partial B = \{ x\in E^+\, :\ \Vert x\Vert = R + 1 \} \subset Q\setminus H_R$ we deduce that $p \not \in H(\theta ,\partial B)$ for every $\theta \in [0,1]$. Hence, by the homotopy invariance of the Brouwer degree, we deduce that $\text {deg}(PS( t)(p+\Sigma _0(p)),B,p) = 1$, whence there exists ${\overline{p}}\in B$ such that $PS(t)({\overline{p}}+\Sigma _0({\overline{p}})) = p$. It is enough to take $q = (I-P))PS(t)({\overline{p}}+\Sigma _0({\overline{p}}))$ to get the assertion of the lemma.

$\square$

Previous two lemmas imply that if $\Sigma _0$ is a $\kappa$-lipschitz function with a graph in Q, then for every t there exists the $\kappa$-lipschitz function $\Sigma _t:E^+\rightarrow E^-$ such that

$$\begin{aligned} S(t)(\text {graph}\, \Sigma _0) = \{ p+\Sigma _t(p)\,:\ p\in E^+ \} = \text {graph}\, \Sigma _t. \end{aligned}$$

Lemma 27

Assume that $\Sigma _0:E^+\rightarrow E^-$ is $\kappa$-Lipschitz with $\text {graph}\, \Sigma _0 \subset Q$, the absorbing and positively invariant set bounded in $E^-$. Moreover assume that

$$\begin{aligned} L_f\left( 1+\frac{1}{\kappa }\right) < \gamma _2. \end{aligned}$$

Then there exist constants $\delta >0$ and $C>0$ such that for every $p\in E^+$ and every $t_1> t_2 >0$ we have

$$\begin{aligned} \Vert \Sigma _{t_1}(p) - \Sigma _{t_2}(p) \Vert \le Ce^{-\delta t_2}. \end{aligned}$$

In consequence there exists a $\kappa$-Lipschitz function $\Sigma :E^+\rightarrow E^-$ such that $\Sigma _t(p) \rightarrow \Sigma (p)$ as $t\rightarrow \infty$ for every $p\in E^+$.

Proof

There exists $p_1, p_2 \in E^+$ such that $(p+\Sigma _{t_1}(p)) = S(t_2)(p_1+\Sigma _{t_1-t_2}(p_1))$ and $(p+\Sigma _{t_2}(p)) = S(t_2)(p_2+\Sigma _{0}(p_2))$. Assume that $\Sigma _{t_1}(p) \ne \Sigma _{t_2}(p)$. This means that points $(p,\Sigma _{t_1}(p))$ and $(p,\Sigma _{t_2}(p))$ are in the negative cone with respect to each other and hence, by Lemma 25 for every $t\in [0,t_2]$ we have

$$\begin{aligned}{} & {} \Vert (I-P)(S(t)(p_1+\Sigma _{t_1-t_2}(p_1)) - S(t)(p_2+\Sigma _{0}(p_2))) \Vert \\{} & {} \quad > \kappa \Vert P(S(t)(p_1+\Sigma _{t_1-t_2}(p_1)) - S(t)(p_2+\Sigma _{0}(p_2)))\Vert . \end{aligned}$$

From the Duhamel formula (8b) we obtain

$$\begin{aligned}&(I-P)(S(t)(p_1+\Sigma _{t_1-t_2}(p_1))-(S(t)(p_2+\Sigma _{0}(p_2)))) =e^{At}(\Sigma _{t_1-t_2}(p_1)-\Sigma _0(p_2)) \\&\quad +\int _{0}^{t}e^{A(t-r)}(I-P)(f(S(t)(p_1+\Sigma _{t_1-t_2}(p_1))-f(S(t)(p_2+\Sigma _{0}(p_2))))dr \end{aligned}$$

It follows that

$$\begin{aligned}&\Vert (I-P)(S(t)(p_1+\Sigma _{t_1-t_2}(p_1))-(S(t)(p_2+\Sigma _{0}(p_2))))\Vert \le e^{-\gamma _2 t_2}\Vert \Sigma _{t_1-t_2}(p_1)-\Sigma _0(p_2)\Vert \\&\quad +L_f\left( 1+\frac{1}{\kappa }\right) \int _{0}^{t_2}e^{-\gamma _2 (t_2-r)}\Vert (I-P)(S(t)(p_1+\Sigma _{t_1-t_2}(p_1))-(S(t)(p_2+\Sigma _{0}(p_2))))\Vert dr. \end{aligned}$$

We are in position to use the Gronwall lemma, whence

$$\begin{aligned}{} & {} \Vert (I-P)(S(t)(p_1+\Sigma _{t_1-t_2}(p_1))-(S(t)(p_2+\Sigma _{0}(p_2))))\Vert \\{} & {} \quad \le \Vert \Sigma _{t_1-t_2}(p_1)-\Sigma _0(p_2)\Vert e^{L_f\left( 1+\frac{1}{\kappa }\right) t}, \end{aligned}$$

for $t\in [0,t_2]$. In consequence

$$\begin{aligned} \Vert \Sigma _{t_1}(p) - \Sigma _{t_2}(p) \Vert \le \Vert \Sigma _{t_1-t_2}(p_1)-\Sigma _0(p_2)\Vert e^{\left( -\gamma _2 + L_f\left( 1+\frac{1}{\kappa }\right) \right) t_2}, \end{aligned}$$

which yields the assertion. $\square$

We denote the graph of $\Sigma$ by $\text {graph}\, \Sigma = \{ p+\Sigma (p)\, :\ p\in E^+ \}$.

Theorem 16

Assume that $f:X\rightarrow X$ is bounded, i.e. $\Vert f(u)\Vert \le C_f$ for every $u\in X$ with $C_f>0$ and let f satisfy (Hf2)$_{\text {GT}}$. Let moreover A be a linear densely defined operator with $-A$ being sectorial and having compact resolvent. Assume that P and $I-P$ are complementary spectral projections satisfying (5) with P being finite dimensional. Let $B\in {\mathcal {B}}(X)$ be a bounded set. There exists a constant C(B) and $\delta >0$ such that

$$\begin{aligned} \textrm{dist}(S(t)B, \textrm{graph}\, \Sigma ) \le C(B) e^{-\delta t}. \end{aligned}$$

Proof

Without loss of generality we may assume that $B\subset Q$. Choose $u_0 = p_0+q_0 \in B$. Denote $p(r) = PS(r)u_0$ and $q(r) = (I-P)S(r)u_0$ for $r\ge 0$. Now fix $t\ge 0$ and let $s\ge t$. We need to estimate the difference $\Sigma _s(p(t)) - q(t).$ To this end observe that there exists a point $p_1 + \Sigma _{s-t}(p_1) \in \text {graph}\, \Sigma _{s-t}$ such that $S(t)(p_1 + \Sigma _{s-t}(p_1)) = p(t) + \Sigma _s(p(t))$. Then either $\Sigma _s(p(t)) = q(t)$, or, if it is not the case, then points $p(t) + \Sigma _s(p(t))$ and $p(t) + q(t)$ are at their negative cones and hence

$$\begin{aligned} \Vert (I-P)S(r)(p_1 + \Sigma _{s-t}(p_1)) - q(r)\Vert > \kappa \Vert P S(r)(p_1 + \Sigma _{s-t}(p_1)) - p(r) \Vert \ \ \text {for}\ \ r\in [0,t]. \end{aligned}$$

We use the Duhamel formula (8b), whence, proceeding analogously to the argument in the proof of the previous Lemma, we obtain

$$\begin{aligned}&\Vert (I-P)S(r)(p_1 + \Sigma _{s-t}(p_1)) - q(r)\Vert \\&\quad \le e^{-\gamma _2 r} \Vert \Sigma _{s-t}(p_1) - q_0\Vert \\&\qquad + L_f\left( 1+\frac{1}{\kappa }\right) \int _0^r e^{-\gamma _2 (r-\tau )}\Vert (I-P)S(\tau )(p_1 + \Sigma _{s-t}(p_1)) - q(\tau )\Vert \, d\tau . \end{aligned}$$

Now the Gronwall lemma implies that

$$\begin{aligned}{} & {} \Vert (I-P)S(r)(p_1 + \Sigma _{s-t}(p_1)) - q(r)\Vert \\{} & {} \quad \le e^{\left( -\gamma _2 + L_f\left( 1+\frac{1}{\kappa }\right) \right) r}\Vert \Sigma _{s-t}(p_1) - q_0\Vert \ \ \text {for every}\ \ r\in [0,t]. \end{aligned}$$

In particular

$$\begin{aligned} \Vert \Sigma _s(p(t)) - q(r)\Vert \le e^{\left( -\gamma _2 + L_f\left( 1+\frac{1}{\kappa }\right) \right) t}\Vert \Sigma _{s-t}(p_1) - q_0\Vert \le C(B) e^{-\delta t}. \end{aligned}$$

We can pass with s to infinity, whence

$$\begin{aligned} \Vert \Sigma (p(t)) - q(r)\Vert \le C(B) e^{-\delta t}, \end{aligned}$$

which implies the assertion. $\square$

Remark 11

We have two bounds on $L_f$. One that follows from the condition on the invariance of the cones

$$\begin{aligned} L_f < \frac{\kappa }{(1+\kappa )^2}(\gamma _1+\gamma _2), \end{aligned}$$

and the second one from the condition of the attraction of bounded sets by the limit graph

$$\begin{aligned} L_f < \frac{\kappa }{1+\kappa }\gamma _2. \end{aligned}$$

Hence we need

$$\begin{aligned} L_f < \min \left\{ \frac{\kappa }{1+\kappa }\gamma _2, \frac{\kappa }{(1+\kappa )^2}(\gamma _1+\gamma _2) \right\} . \end{aligned}$$

A simple calculation shows, that if $\kappa \ge \frac{\gamma _1}{\gamma _2}$ then $\frac{\kappa }{1+\kappa }\gamma _2 \ge \frac{\kappa }{(1+\kappa )^2}(\gamma _1+\gamma _2)$ and if $\kappa \le \frac{\gamma _1}{\gamma _2}$ then $\frac{\kappa }{1+\kappa }\gamma _2 \le \frac{\kappa }{(1+\kappa )^2}(\gamma _1+\gamma _2)$. It is then enough to maximize $\frac{\kappa }{(1+\kappa )^2}(\gamma _1+\gamma _2)$ over the interval $\kappa \in [\frac{\gamma _1}{\gamma _2},\infty )$ and $\frac{\kappa }{1+\kappa }\gamma _2$ over the interval $\kappa \in [0,\frac{\gamma _1}{\gamma _2}]$. Now

$$\begin{aligned} \max _{\kappa \in [0,\frac{\gamma _1}{\gamma _2}]} \frac{\kappa }{1+\kappa }\gamma _2 = \frac{\gamma _1\gamma _2}{\gamma _1+\gamma _2}, \end{aligned}$$

and

$$\begin{aligned} \max _{\kappa \in [\frac{\gamma _1}{\gamma _2},\infty )} \frac{\kappa }{(1+\kappa )^2}(\gamma _1+\gamma _2) = {\left\{ \begin{array}{ll}&{} \frac{\gamma _1\gamma _2}{\gamma _1+\gamma _2} \ \ \text {if}\ \ \frac{\gamma _1}{\gamma _2} \ge 1,\\ &{}\frac{\gamma _1+\gamma _2}{4}\ \ \text {if}\ \ \frac{\gamma _1}{\gamma _2} \le 1. \end{array}\right. } \end{aligned}$$

This means that

$$\begin{aligned} \max _{\kappa \in [0,\infty )} \min \left\{ \frac{\kappa }{1+\kappa }\gamma _2, \frac{\kappa }{(1+\kappa )^2}(\gamma _1+\gamma _2) \right\} = {\left\{ \begin{array}{ll}&{} \frac{\gamma _1\gamma _2}{\gamma _1+\gamma _2} \ \ \text {if}\ \ \frac{\gamma _1}{\gamma _2} \ge 1,\\ &{}\frac{\gamma _1+\gamma _2}{4}\ \ \text {if}\ \ \frac{\gamma _1}{\gamma _2} \le 1. \end{array}\right. } \end{aligned}$$

This motivates (Hf2)$_{\text {GT}}$. In other words, if $\gamma _1\ge \gamma _2$, the optimal upper bound on $L_f$ is given by the half of the harmonic mean of these numbers, and in the opposite case it is given by the half of their arithmetic mean.

4.4.2 Lyapunov–Perron Method: Case of General $M\ge 1$

The arguments to obtain the results of this subsection very closely follow the lines of the proof of [11, Theorem 2.1] where they are done in a general, non-autonomous setup for the case or arbitrary gap, not necessarily the gap at which the real parts of the eigenvalues change sign. We repeat some parts of the arguments after [11, Theorem 2.1] only for the sake of exposition completeness, and to make clear how the limitations on $L_f$ in (Hf2)$_{\text {LP}}$ enter the argument. We will consider the metric space

$$\begin{aligned} \mathcal{L}\mathcal{B}(\kappa )&= \left\{ \Sigma \in C({\mathbb {R}}\times E^+; E^-)\,:\ \sup _{t\in {\mathbb {R}}}\Vert \Sigma (t,p_1)-\Sigma (t,p_2)\Vert \le \kappa \Vert p_1-p_2\Vert ,\right. \\&\quad \left. \Sigma (t,0) = 0\ \text {for every}\ t\in {\mathbb {R}}\ \ \text {and}\ \ \Vert \Sigma (t,p)\Vert \le \frac{2MC_f}{\gamma _2}\ \text {for every}\ t\in {{\mathbb {R}}}, p\in E^+ \right\} , \end{aligned}$$

equipped with the metric $\Vert \Sigma _1-\Sigma _2\Vert _{\mathcal{L}\mathcal{B}} = \sup _{t\in {\mathbb {R}}}\sup _{p\in P, p\ne 0}\frac{\Vert \Sigma _1(t,p) - \Sigma _2(t,p)\Vert }{\Vert p\Vert }$.

We need to translate the solution of the problem in order to guarantee that the nonlinearity is zero for a zero argument. We know that ${\mathcal {J}}_b$, the family of global and bounded solutions in the unbounded attractor is nonempty, let $\{ {\overline{u}}(t)\}_{t\in {\mathbb {R}}} \in {\mathcal {J}}_b$. Then, if the function u(t) is the solution of the original problem, the function $v(t) = u(t)-{\overline{u}}(t)$ solves the translated problem governed by the equation

$$\begin{aligned} v'(t) = Av(t) + f(v(t) + {\overline{u}}(t))-f({\overline{u}}(t)). \end{aligned}$$

(24)

Denoting $g(t,v) = f(v + {\overline{u}}(t))-f({\overline{u}}(t))$ observe that $g(t,0) = 0$ and $g(t,\cdot )$ is Lipschitz with the same constant as f. Note that the problem is now non-autonomous, if we assume that the equation $-A{\overline{u}} = f({\overline{u}})$ has a solution, then we could translate u(t) by this solution and obtain the autonomous translated problem, which would make the argument simpler. We proceed without this assumption. Using the representation $Pv(t) = p(t)$ and $(I-P)v(t) = q(t)$ we have the following Duhamel formulas

$$\begin{aligned} p(t)&=e^{A(t-\tau )}p(\tau ) +\int _\tau ^t e^{A(t-s)}Pg(s,p(s)+q(s))ds\ \ \text {for}\ \ t\geqslant \tau , \end{aligned}$$

(25a)

$$\begin{aligned} q(t)&=e^{A(t-\tau )}q(\tau ) +\int _{\tau }^te^{A(t-s)}(I-P)g(s,p(s)+q(s))ds\ \ \text {for}\ \ t\geqslant \tau . \end{aligned}$$

(25b)

For a given $\Sigma \in \mathcal{L}\mathcal{B}(\kappa )$ and $p_0\in E^+$ it is possible to solve backwards in time the following ODE

$$\begin{aligned} p'(t) = Ap(t) + g(t,p(t)+\Sigma (t,p(t)))\ \text {for}\ t\in (-\infty ,\tau ]\ \text {with}\ p(\tau ) = p_0, \end{aligned}$$

(26)

and the solution satisfies (25a) with $q(s) = \Sigma (s,p(s))$. We define the following Lyapunov–Perron function, G, which, as we will show in the next lemma, is a contraction on $\mathcal{L}\mathcal{B}(\kappa )$ for sufficiently small $L_f$.

$$\begin{aligned} G(\Sigma )(\tau ,p_0) = \int _{-\infty }^\tau e^{A(\tau -s)} (I-P)g(s,p(s)+\Sigma (s,p(s))\, ds. \end{aligned}$$

Lemma 28

Assume (Hf2)$_{\text {LP}}$ in addition to assumptions of Sect. 4.1. The mapping $G:\mathcal{L}\mathcal{B}(\kappa )\rightarrow \mathcal{L}\mathcal{B}(\kappa )$ is a contraction and hence has a unique fixed point $\Sigma ^*\in \mathcal{L}\mathcal{B}(\kappa )$.

Proof

For a given $p_0\in E^+$ and $\Sigma \in \mathcal{L}\mathcal{B}(\kappa )$ we observe, that since $\Vert g(s,u)\Vert \le 2 C_f$ for every $s\in {{\mathbb {R}}}$ and $u\in X$, then

$$\begin{aligned} \Vert G(\Sigma )(\tau ,p_0)\Vert \le \frac{2M C_f}{\gamma _2}\ \ \text {for every}\ \ \tau \in {{\mathbb {R}}}. \end{aligned}$$

We now estimate the growth of p in (26). Fix $\tau \in {{\mathbb {R}}}$. From (25a) and from (5) we obtain for $t\le \tau$

$$\begin{aligned} \Vert p(t)\Vert \le Me^{\gamma _1(t-\tau )}\Vert p_0\Vert + ML_f(1+\kappa )\int _{t}^\tau e^{\gamma _1(t-s)} \Vert p(s)\Vert \, ds. \end{aligned}$$

The Gronwall lemma implies that

$$\begin{aligned} \Vert p(t)\Vert \le M e^{(ML_f(1+\kappa )-\gamma _1)(\tau -t)} \Vert p_0\Vert . \end{aligned}$$

(27)

Take $p_0^1, p_0^2 \in E^+$ and $\Sigma _1, \Sigma _2 \in \mathcal{L}\mathcal{B}(\kappa )$. We denote the solution of (26) corresponding to $p_0^1$ taken at time $\tau$ and $\Sigma _1$ by $p^1$, and the one corresponding to $p_0^2$ taken at time $\tau$ and $\Sigma _2$ by $p^2$. Then

$$\begin{aligned}&\Vert G(\Sigma _1)(\tau ,p_0^1) - G(\Sigma _2)(\tau ,p_0^2)\Vert \\&\quad \le M\int _{-\infty }^\tau e^{\gamma _2 (s-\tau )}L_f (\Vert p^1(s)-p^2(s)\Vert \\&\quad \qquad + \Vert \Sigma _1(p^1(s))-\Sigma _2(p^2(s)\Vert )\, ds \\&\le M L_f \left( (1+\kappa )\int _{-\infty }^\tau e^{\gamma _2 (s-\tau )} \Vert p^1(s)-p^2(s)\Vert \, ds\right. \\&\quad \qquad \left. +M \Vert \Sigma _1 - \Sigma _2\Vert _{\mathcal{L}\mathcal{B}} \Vert p_0^2\Vert \int _{-\infty }^\tau e^{(ML_f(1+\kappa )-\gamma _1-\gamma _2)(\tau -s)} \, ds\right) \\&\quad \le M^2 L_f\Vert \Sigma _1 - \Sigma _2\Vert _{\mathcal{L}\mathcal{B}}\Vert p_0^2\Vert \int _{-\infty }^\tau e^{(ML_f(1+\kappa )-\gamma _1-\gamma _2)(\tau -s)} \, ds\\&\quad \qquad + ML_f(1+\kappa ) \int _{-\infty }^\tau e^{\gamma _2 (s-\tau )} \Vert p^1(s)-p^2(s)\Vert \, ds . \end{aligned}$$

Note from the second bound in (19) we have $2ML_f(1+\kappa ) < \gamma _1+\gamma _2$. It follows that

$$\begin{aligned}&\Vert G(\Sigma _1)(\tau ,p_0^1) - G(\Sigma _2)(\tau ,p_0^2)\Vert \nonumber \\&\quad \le \frac{M^2 L_f \Vert p_0^2\Vert }{\gamma _1+\gamma _2-ML_f(1+\kappa )}\Vert \Sigma _1 - \Sigma _2\Vert _{\mathcal{L}\mathcal{B}} + ML_f(1+\kappa ) \nonumber \\&\qquad \times \int _{-\infty }^\tau e^{\gamma _2 (s-\tau )} \Vert p^1(s)-p^2(s)\Vert \, ds . \end{aligned}$$

(28)

On the other hand, from (25a) and (5) we deduce that

$$\begin{aligned}&\Vert p^1(s)-p^2(s)\Vert \le M e^{\gamma _1(s-\tau )}\Vert p^1_0-p_0^2\Vert \\&\quad +M\int _s^\tau e^{\gamma _1(s-r)}(\Vert g(r,p^1(r)+\Sigma _1(r,p^1(r)))\\&\quad -g(r,p^2(r)+\Sigma _2(r,p^2(r)))\Vert dr, \end{aligned}$$

whence

$$\begin{aligned} \Vert p^1(s)-p^2(s)\Vert&\le M e^{\gamma _1(s-\tau )}\Vert p^1_0-p_0^2\Vert +ML_f\int _s^\tau e^{\gamma _1(s-r)}((1+\kappa )\Vert p^1(r)-p^2(r)\Vert \\&\quad +\Vert \Sigma _1-\Sigma _2\Vert _{\mathcal{L}\mathcal{B}(\kappa )}\Vert p^2(r)\Vert )dr. \end{aligned}$$

After a straightforward calculation which uses (27) it follows that

$$\begin{aligned} \Vert p^1(s)-p^2(s)\Vert&\le M e^{\gamma _1(s-\tau )}\Vert p^1_0-p_0^2\Vert +\frac{M}{1+\kappa }\Vert \Sigma _1-\Sigma _2\Vert _{\mathcal{L}\mathcal{B} }\Vert p_0^2\Vert e^{(ML_f(1+\kappa )-\gamma _1)(\tau -s)} \\&\quad + ML_f(1+\kappa )\int _s^\tau e^{\gamma _1(s-r)}\Vert p^1(r)-p^2(r)\Vert dr. \end{aligned}$$

The Gronwall inequality implies

$$\begin{aligned} \Vert p^1(s)-p^2(s)\Vert&\le M e^{(ML_f(1+\kappa )-\gamma _1)(\tau -s)}\Vert p^1_0-p_0^2\Vert \\&\quad +\frac{M}{1+\kappa }\Vert \Sigma _1-\Sigma _2\Vert _{\mathcal{L}\mathcal{B} }\Vert p_0^2\Vert e^{(2ML_f(1+\kappa )-\gamma _1)(\tau -s)}. \end{aligned}$$

Substituting this last inequality to (28) we deduce

$$\begin{aligned}&\Vert G(\Sigma _1)(\tau ,p_0^1) - G(\Sigma _2)(\tau ,p_0^2)\Vert \le \frac{M^2L_f(1+\kappa )}{\gamma _1+\gamma _2 - ML_f(1+\kappa )} \Vert p^1_0-p_0^2\Vert \\&\quad + \left( \frac{M^2L_f}{\gamma _2+\gamma _1 - 2ML_f(1+\kappa )} + \frac{M^2L_f}{\gamma _2+\gamma _1 - ML_f(1+\kappa )}\right) \Vert \Sigma _1-\Sigma _2\Vert _{\mathcal{L}\mathcal{B} }\Vert p_0^2\Vert . \end{aligned}$$

Hence, we need

$$\begin{aligned} \frac{M^2L_f(1+\kappa )}{\gamma _1+\gamma _2 - ML_f(1+\kappa )} \le \kappa , \frac{M^2L_f}{\gamma _2+\gamma _1 - 2ML_f(1+\kappa )} + \frac{M^2L_f}{\gamma _2+\gamma _1 - ML_f(1+\kappa )} < 1, \end{aligned}$$

the first inequality is needed for the Lipschitz condition on $G(\Sigma )$ with a constant $\kappa$ and the second one for the contraction on G. The second inequality is exactly (20). We can rewrite the first condition as

$$\begin{aligned} L_f \le \frac{\gamma _1+\gamma _2}{M} \frac{\kappa }{(M+\kappa )(1+\kappa )}, \end{aligned}$$

the first bound in (19), and the proof is complete. $\square$

Remark 12

Different to the framework of unbounded attractors, in the general framework of inertial manifolds, where we have freedom to choose the gap, the last restriction in (Hf2)$_{\text {LP}}$, namely (21), needed for the exponential attraction by the Lipschitz graph, in contrast to (19) and (20), is usually easy to obtain by taking the sufficiently high eigenvalue at the gap. Hence it makes sense to compare the bound on $L_f$ which follows only from (19) and (20) between the graph transform and Lyapunov–Perron methods. As in [11], the quantity on the left hand side of (20) is estimated as follows

$$\begin{aligned} \frac{M^2L_f}{\gamma _2+\gamma _1 - 2ML_f(1+\kappa )} + \frac{M^2L_f}{\gamma _2+\gamma _1 - ML_f(1+\kappa )} \le \frac{2M^2L_f}{\gamma _2+\gamma _1 - 2ML_f(1+\kappa )}. \end{aligned}$$

(29)

Hence, the sufficient condition for (20) is

$$\begin{aligned} {2M^2L_f} < \gamma _2+\gamma _1 - 2ML_f(1+\kappa ), \end{aligned}$$

which is equivalent to

$$\begin{aligned} L_f < \frac{\gamma _1+\gamma _2}{M}\frac{1}{2(M+1+\kappa )}. \end{aligned}$$

We need to take the lowest of this bound and the ones that follow from (19), i.e.

$$\begin{aligned} L_f&< \frac{\gamma _1+\gamma _2}{M} \min \left\{ \frac{1}{2(M+1+\kappa )}, \frac{\kappa }{(M+\kappa )(1+\kappa )}, \frac{1}{2(1+\kappa )}\right\} \\&= \frac{\gamma _1+\gamma _2}{M} \min \left\{ \frac{1}{2(M+1+\kappa )}, \frac{\kappa }{(M+\kappa )(1+\kappa )}\right\} . \end{aligned}$$

Comparison of the two functions of $\kappa$ reveals that there exists $\kappa _0(M)$ such that for $\kappa \in (0,\kappa _0)$ the second bound is sharper, while for $\kappa >\kappa _0$ the first one is sharper. Moreover the first bound is a strictly decreasing function of $\kappa$. If $\kappa =\kappa _0$ both bounds coincide. Moreover, the $\kappa$ at which the second bound achieves maximum is always larger than $\kappa _0$. Hence we need to take $\kappa = \kappa _0$ for the optimal bound. This means that the optimal choice of $\kappa$ from the point of view of (19) and (20) (with the non-sharp bound (29))) is

$$\begin{aligned} \kappa = \frac{2M}{M+1+\sqrt{(M+1)^2+4M}}, \end{aligned}$$

We have obtained the restriction on $L_f$ of type $G(M) L_f < \gamma _1 + \gamma _2$. The similar restriction $\max \{M^2+2M+\sqrt{8M^3},3M^2+2M\} L_f < \gamma _1+\gamma _2$ is obtained in [11] but our bound, although the path to obtain it is exactly the same as in [11], is a little bit sharper due to the optimization with respect to $\kappa$, as the following table shows (note, however, that improved bounds are given in [11, Remark 2.4]). The numbers in the table are the lower bounds for $\frac{\gamma _1+\gamma _2}{L_f}$. Note that for the graph transform, the best possible bound in Lemma 25 is obtained for $\kappa =1$. We expect that all presented bounds are still not sharp: the last column gives the sharp bound for $M=1$ obtained in [31, 32] with the use of the energy inequalities.

	Bound of [11]	Remark 12	Graph transform	Sharp bound of [31, 32]
$M=1$	5.829	4.829	4	2
$M=2$	16	14.247	–	–
$M=4$	56	45.613	–	–
large M	$(3M^2 + o(M^2))$	$(2M^2 + o(M^2))$	–	–

This reveals, that while Lyapunov–Perron method with the chosen metrics $\mathcal{L}\mathcal{B}(\kappa )$ can be used for any $M\ge 1$ it gives the bounds which are tentatively nonoptimal, and the graph transform method, which needs the invariance of the cones and hence can be used only for $M=1$, gives the better bound. Note that in one step of the proof, namely in (29) we used the rough estimate $\gamma _2+\gamma _1 - ML_f(1+\kappa ) > \gamma _2+\gamma _1 - 2ML_f(1+\kappa )$. The numerical calculation of the bound for $M=1$ without this estimate leads to the optimal value $\kappa = 1/2$ and the bound $4.5 L_f < \gamma _1+\gamma _2$ which is better than the one in the above table but still more rough than the one from the graph transform.

Now each point $w = Pw + (I-P)w$ in the phase space lies ’over’ some point in the graph of $\Sigma ^*(t,\cdot )$, this point is given by $Pw + \Sigma ^*(t,Pw)$. So, for the solution v(t) (we denote $p(t) = Pv(t)$ and $q(t) = (I-P)v(t)$) one can define its vertical distance in $E^-$ from $\Sigma ^*(t,\cdot )$ as $\Vert \xi (t)\Vert$ where

$$\begin{aligned} \xi (t) = (I-P)v(t) - \Sigma ^*(t,Pv(t)). \end{aligned}$$

(30)

We prove that this distance exponentially tends to zero as the difference between the initial and final time tends to infinity, uniformly on bounded sets of initial data. Here, since the argument formula by formula exactly follows the lines of the corresponding proof of [11, Theorem 2.1], we only state the result.

Lemma 29

Assume (Hf2)$_{\text {LP}}$ in addition to assumptions of Sect. 4.1 and let $v:[t_0,\infty )\rightarrow X$ be the solution of (24). If $\xi (t)$ is given by (30), then

$$\begin{aligned} \Vert \xi (t)\Vert \le M\Vert \xi (\tau )\Vert e^{(t-\tau )\left( -\gamma _2 + ML_f+\frac{M^2L_f^2 (1+\kappa )(1+M)}{\gamma _1 + \gamma _2 - ML_f(1+\kappa )}\right) } \ \ \text {for}\ \ t\ge \tau \ge t_0. \end{aligned}$$

We summarize the results of this section in a theorem

Theorem 17

Assume that $f:X\rightarrow X$ is bounded, i.e. $\Vert f(u)\Vert \le C_f$ for every $u\in X$ with $C_f>0$ and let f satisfy (Hf2)$_{\text {LP}}$. Let moreover A be a linear densely defined operator with $-A$ being sectorial and having compact resolvent. Assume that P and $I-P$ are complementary spectral projections satisfying (5) with P being finite dimensional. There exists a constant $\delta > 0$ and a Lipschitz function $\Sigma :E^+ \rightarrow E^-$ such that for every $u_0 \in X$

$$\begin{aligned} \Vert (I-P)S(s)u_0 -\Sigma (PS(s)u_0)\Vert \le M\left( \Vert u_0\Vert + \frac{3MC_f}{\gamma _2}\right) e^{-\delta s}\ \ \text {for}\ \ s\ge 0, \end{aligned}$$

and in consequence for every $B\in {\mathcal {B}}(X)$ there exists a constant $C(B)>0$ such that

$$\begin{aligned} \textrm{dist}\, (S(s)B,\textrm{graph}\, \Sigma ) \le C(B)e^{-\delta s}. \end{aligned}$$

Proof

By (21) then there exists $\delta > 0$ such that

$$\begin{aligned} \Vert \xi (t)\Vert \le M\Vert \xi (\tau )\Vert e^{-\delta (t-\tau )}\ \ \text {for}\ \ t\ge \tau . \end{aligned}$$

By the definition of $\xi (\cdot )$ we deduce

$$\begin{aligned} \Vert (I-P)v(t) - \Sigma ^*(t,Pv(t))\Vert \le M\Vert (I-P)v(\tau ) - \Sigma ^*(\tau ,Pv(\tau ))\Vert e^{-\delta (t-\tau )}. \end{aligned}$$

But, exploring the relation between the function v, the solution of (24), and the solution of the original problem, we obtain

$$\begin{aligned}{} & {} \Vert (I-P)u(t) - (I-P){\overline{u}}(t) - \Sigma ^*(t,Pv(t))\Vert \\{} & {} \quad \le M\Vert (I-P)u(\tau ) - (I-P){\overline{u}}(\tau ) - \Sigma ^*(\tau ,Pv(\tau ))\Vert e^{-\delta (t-\tau )}. \end{aligned}$$

From (9) and the bound in the definition of $\mathcal{L}\mathcal{B}(\kappa )$ we deduce

$$\begin{aligned} \Vert (I-P)S(t-\tau )u(\tau ) - (I-P){\overline{u}}(t) - \Sigma ^*(t,Pv(t))\Vert \le M\left( \Vert u(\tau )\Vert + \frac{3MC_f}{\gamma _2}\right) e^{-\delta (t-\tau )} \end{aligned}$$

Take $t=0$ and $\tau =-s$ for $s\ge 0$. Then, for any initial data $u_0\in X$, remembering that ${\overline{u}}(0) = {\overline{u}}$ is any chosen point in ${\mathcal {J}}_b$, we deduce

$$\begin{aligned} \Vert (I-P)S(s)u_0 - (I-P){\overline{u}} - \Sigma ^*(0,P(S(s)u_0-{\overline{u}}))\Vert \le M\left( \Vert u_0\Vert + \frac{3MC_f}{\gamma _2}\right) e^{-\delta s} \end{aligned}$$

Defining $\Sigma :E^+\rightarrow E^-$ as $\Sigma (p) = (I-P){\overline{u}}+\Sigma ^*(0,p-P{\overline{u}})$, and observing that this is a $\kappa$-Lipschitz function we obtain the assertion. Note that $\text {graph}\, \Sigma = {\overline{u}} + \text {graph}\, \Sigma ^*(0,\cdot )$. $\square$

4.4.3 Lipschitz Constant Outside a Cylinder

Before we pass to the results of this section, we remind a useful norm inequality [16, 22]. Namely, the following estimate is valid in Banach spaces for nonzero x, y

$$\begin{aligned} \left\| \frac{x}{\Vert x\Vert } - \frac{y}{\Vert y\Vert }\right\| \le \frac{2\Vert x-y\Vert }{\max \{\Vert x\Vert ,\Vert y\Vert \}}. \end{aligned}$$

(31)

In this section we will need the assumptions on f as in Sect. 4.1, that is, in addition to the assumptions which guarantee the solution existence and uniqueness, we require that $\Vert f(u)\Vert \le C_f$ for every $u\in X$. This guarantees the unbounded attractor existence and characterization by ${\mathcal {J}} = \bigcap _{t\ge 0}\overline{S(t)Q}$ where Q is positively invariant absorbing set such that $Q\subset \{ \Vert (I-P)x\Vert \le D_2 \}$. We reinforce these assumptions with the lipschitzness of f for a large projection P of an argument, that is we require that

$$\begin{aligned} \Vert f(u)-f(v)\Vert \le L_f \Vert u-v\Vert \ \ \text {for}\ \ \Vert Pu\Vert , \Vert Pv\Vert \ge R_{cut}, \end{aligned}$$

for some $R_{cut}>0$ with $L_f$ sufficiently small, such that the requirement for the existence of the inertial manifold which follows from the Lyapunov–Perron method or graph transform method holds for the nonlinearity with the Lipshitz constant $5L_f$. This constant

$$5L_f$$

follows from the explicit construction of

$$\tilde{f}$$

being the extension of

$$f$$

that we present below. In the Hilbert space setting, by the Kirszbraun-Valentine theorem, it is possible to extend

$$f$$

to the whole space without increasing the Lipschitz constant. We remark here that in fact it is sufficient to assume

$$\begin{aligned} \Vert f(u)-f(v)\Vert \le L_f \Vert u-v\Vert \ \ \text {for}\ \Vert Pu\Vert , \Vert Pv\Vert \ge R_{cut}\ \ \text {and}\ \Vert (I-P)u\Vert , \Vert (I-P)v\Vert \le A,\nonumber \\ \end{aligned}$$

(32)

where A is the constant (different for the graph transform and Lyapunov–Perron methods) such that if f is Lipschitz with sufficiently small Lipschitz constant on a strip $\{\Vert (I-P)x\Vert \le A\}$, then the inertial manifold exists and coincides with the unbounded attractor. Define

$$\begin{aligned} {\widetilde{f}}(u) = {\left\{ \begin{array}{ll} f(u)\ \ \text {if}\ \ \Vert Pu\Vert \ge R_{cut},\\ \frac{\Vert Pu\Vert }{R_{cut}}f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) \ \ \text {otherwise}. \end{array}\right. } \end{aligned}$$

Lemma 30

If $\Vert f(u)\Vert \le C_f$ for every $u\in X$ then also $\Vert {\widetilde{f}}(u)\Vert \le C_f$ for every $u\in X$. If for every $u,v\in X$ with $\Vert Pu\Vert , \Vert Pv\Vert \ge R_{cut}$ we have $\Vert f(u)-f(v)\Vert \le L_f \Vert u-v\Vert$ for every $u,v \in \{ \Vert (I-P)x\Vert \le A \}$ then, possibly by increasing $R_{cut}$ in the definition of ${\widetilde{f}}$, we have $\Vert {\widetilde{f}}(u)-{\widetilde{f}}(v)\Vert \le 5L_f \Vert u-v\Vert$ for every $u,v \in \{ \Vert (I-P)x\Vert \le A \}$.

Proof

It is enough to prove the Lipschitzness. take $u,v \in X$. If $\Vert Pu\Vert \ge R_{cut}$ and $\Vert Pv\Vert \ge R_{cut}$ then the assertion is clear. If $\Vert Pu\Vert \ge R_{cut}$ and $\Vert Pv\Vert < R_{cut}$ then

$$\begin{aligned} \Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert \le \left\| f(u) - \frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pv}{\Vert Pv\Vert }R_{cut}+(I-P)v\right) \right\| . \end{aligned}$$

We estimate

$$\begin{aligned}&\Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert \le \left\| f(u) - \frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) \right\| \\&\quad + \left\| \frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) -\frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pv}{\Vert Pv\Vert }R_{cut}+(I-P)v\right) \right\| . \end{aligned}$$

It follows that

$$\begin{aligned}&\Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert \le \left\| f(u) - f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) \right\| \\&\quad + \left\| f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) - \frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) \right\| \\&\quad + \frac{\Vert Pv\Vert }{R_{cut}} \left\| f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) -f\left( \frac{Pv}{\Vert Pv\Vert }R_{cut}+(I-P)v\right) \right\| . \end{aligned}$$

Continuing, we obtain

$$\begin{aligned} \Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert&\le L_f\left\| Pu - \frac{Pu}{\Vert Pu\Vert }R_{cut}\right\| + \left\| f\left( \frac{u}{\Vert u\Vert }R_{cut}+(I-P)u\right) \right\| \left( 1- \frac{\Vert Pv\Vert }{R_{cut}}\right) \\&\quad + L_f\frac{\Vert Pv\Vert }{R_{cut}} \left( \Vert (I-P)(u-v)\Vert + R_{cut}\left\| \frac{Pu}{\Vert Pu\Vert }-\frac{Pv}{\Vert Pv\Vert }\right\| \right) . \end{aligned}$$

Hence, after calculations

$$\begin{aligned} \Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert&\le L_f \left( \Vert Pu\Vert - R_{cut}\right) + L_f\left( R_{cut}- \Vert Pv\Vert \right) \\&\quad + \frac{\left\| f\left( (I-P)u\right) \right\| }{R_{cut}}\left( R_{cut}- \Vert Pv\Vert \right) \\&\quad + L_f\Vert u-v\Vert + L_f\Vert Pv\Vert \left\| \frac{Pu}{\Vert Pu\Vert }-\frac{Pv}{\Vert Pv\Vert }\right\| . \end{aligned}$$

Using (31) we obtain

$$\begin{aligned} \Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert&\le 2L_f \Vert u-v\Vert + \frac{C_f}{R_{cut}}\Vert u-v\Vert + 2L_f\frac{\Vert Pv\Vert }{\Vert Pu\Vert } \left\| u-v\right\| \\&\le \left( 4L_f + \frac{C_f}{R_{cut}}\right) \Vert u-v\Vert . \end{aligned}$$

Now consider the case $\Vert Pu\Vert \le R$ and $\Vert Pv\Vert \le R$. Then, assuming that $\Vert Pu\Vert \ge \Vert Pv\Vert$

$$\begin{aligned} \Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert&\le \left\| \frac{\Vert Pu\Vert }{R_{cut}}f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) \right. \\&\quad \left. - \frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pv}{\Vert Pv\Vert }R_{cut}+(I-P)v\right) \right\| \\&\le \left\| \frac{\Vert Pu\Vert }{R_{cut}} f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) - \frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) \right\| \\&\quad + \left\| \frac{\Vert Pv\Vert }{R_{cut}} f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) - \frac{\Vert Pv\Vert }{R_{cut}}f\left( \frac{Pv}{\Vert Pv\Vert }R_{cut}+(I-P)v\right) \right\| \\&\le \left\| f\left( \frac{Pu}{\Vert Pu\Vert }R_{cut}+(I-P)u\right) \right\| \frac{\Vert Pu\Vert -\Vert Pv\Vert }{R_{cut}} \\&\quad + L_f \frac{\Vert Pv\Vert }{R_{cut}} \left( \Vert (I-P)(u-v)\Vert + R_{cut}\left\| \frac{Pu}{\Vert Pu\Vert }- \frac{Pv}{\Vert Pv\Vert }\right\| \right) . \end{aligned}$$

Proceeding in a similar way as for the previous case we obtain

$$\begin{aligned} \Vert {\widetilde{f}}(u) - {\widetilde{f}}(v)\Vert \le \left( L_f + \frac{C_f}{R_{cut}}\right) \Vert u-v\Vert + 2L_f \frac{\Vert Pv\Vert }{\Vert Pu\Vert } \Vert P(u-v)\Vert , \end{aligned}$$

and the assertion follows. $\square$

We denote by $\{S^*(t)\}_{t\ge 0}$ the semiflow governed by the equation

$$\begin{aligned} u'(t) = Au(t) + {\widetilde{f}}(u(t)). \end{aligned}$$

(33)

We observe that with our assumptions on f the problem governed by this equation has the unbounded attractor. Moreover, since the constant $C_f$ is the same for f and ${\widetilde{f}}$ we can take the same $D_1$ and $D_2$ in (H1) both for the problem with f and with ${\widetilde{f}}$ (although the absorbing and positively invariant sets Q may, in general, differ for both problems). If $L_f$ is sufficiently small then, by arguments of Sect. 4.4.1 or 4.4.2 the problem governed by (33) has the inertial manifold which attracts exponentially all bounded sets. We denote this manifold by $\Sigma :E^+\rightarrow E^-$.

Lemma 31

For every $R_{cut}>0$ there exists $R > 0$ such that if $\Vert Pu_0\Vert \ge R$ then $\Vert S(t)u_0\Vert \ge \Vert P S(t) u_0\Vert \ge R_{cut}$ for every $t\ge 0$, and hence we have the equality $S(t)u_0 = S^*(t)u_0$ for every $t\ge 0$.

Proof

From (12) it follows that if $\Vert Pu_0\Vert \ge R$ then

$$\begin{aligned} \Vert PS(t)u_0\Vert \ge e^{\gamma _1 t}\left( \frac{R}{M} - \frac{C_f}{\gamma _1}\right) . \end{aligned}$$

Hence we need $\frac{R}{M} - \frac{C_f}{\gamma _1} \ge R_{cut},$ i.e. it suffices to take any $R \ge MR_{cut} + \frac{MC_f}{\gamma _1}$. By increasing R if necessary we enforce that $S(R) \ge R_{cut}$. $\square$

We define two sets $B_0 = \{ v\in X:\ \Vert (I-P)v\Vert \le D_2, \Vert Pv\Vert < R\}$ and $B_1 = \{ v\in X:\ \Vert (I-P)v\Vert \le D_2, \Vert Pv\Vert = R\}$ and consider the set $B_0 \cup \bigcup _{t\ge 0}S(t)B_1$. We will prove that the thickness in $E^-$ of this set tends to zero as $\Vert Pu\Vert$ tends to infinity and that this set is attracting. Hence, it satisfies the assumption (A1) needed for Theorem 4 to hold. We begin from the result which states that the thickness of this set tends to zero.

Lemma 32

Under all assumptions of this section we have

$$\begin{aligned} \lim _{\Vert p\Vert \rightarrow \infty } \text {diam}\left( \left( \bigcup _{t\ge 0}S(t)B_1\right) \cap \{x\in X: Px=p\} \right) = 0 \end{aligned}$$

Proof

First we observe that for every $u_0 \in B_1$ and every $t\ge 0$ we have $\Vert PS(t)u_0\Vert \ge R_{cut}$ and hence $S(t)u_0 = S^*(t)u_0$. Now if $v = S(t)u_0$ with $u_0 \in B_1$, then using Remark 8 we deduce

$$\begin{aligned} \Vert \Sigma (Pv) - (I-P)v\Vert \le C(B_1)e^{-\delta t} \end{aligned}$$

We know that for $u_0 \in B_1$ we have $\Vert Pu_0\Vert = R$. Hence from (10) it follows that

$$\begin{aligned} \Vert P S(t) u_0\Vert \le e^{\gamma _0 t}M\left( R + \frac{C_f}{\gamma _0} \right) . \end{aligned}$$

Hence, for a given value of $\Vert p\Vert \ge R_{cut}$ the necessary condition for $PS(t)u_0$ to be equal to p is

$$\begin{aligned} \ln \Vert p\Vert \le \gamma _0 t + \ln \left( M\left( R + \frac{C_f}{\gamma _0} \right) \right) , \end{aligned}$$

or, equivalently,

$$\begin{aligned} t \ge \frac{1}{\gamma _0}\left( \ln \Vert p\Vert - \ln \left( M\left( R + \frac{C_f}{\gamma _0} \right) \right) \right) := T_1(p), \end{aligned}$$

We calculate

$$\begin{aligned}&\textrm{diam }\left( \left( \bigcup _{t\ge 0}S(t)B_1\right) \cap \{x\in X: Px=p\} \right) \nonumber \\&\quad = \textrm{diam }\left( \left( \bigcup _{t \ge T_1(p)}S(t)B_1 \right) \cap \{x\in X: Px=p\} \right) \nonumber \\&\quad \le 2 \sup \left\{ \Vert \Sigma (p) - (I-P)v\Vert : v\in \bigcup _{t \ge T_1(p)}S(t)B_1, Pv=p \right\} \le 2 C(B_1)e^{-\delta T_1(p)}\nonumber \\&\quad = 2 C(B_1)\Vert p\Vert ^{- \frac{\delta }{\gamma _0}} \left( M\left( R + \frac{C_f}{\gamma _0} \right) \right) ^\frac{\delta }{\gamma _0}, \end{aligned}$$

(34)

and the proof is complete. $\square$

In the next result we establish that the graph of the inertial manifold for the modified problem is included in the set $B_0 \cup \bigcup _{t\ge 0}S(t)B_1$. This is needed as a preparatory step to demonstrate that this set is attracting.

Lemma 33

Under all assumptions of this section the following inclusion holds

$$\begin{aligned} \text {graph}\, \Sigma \subset B_0 \cup \bigcup _{t\ge 0}S(t)B_1. \end{aligned}$$

Proof

Denote by $Q^*$ the positively invariant and absorbing set for the modified semiflow $S^*$. Since $\text {graph}\, \Sigma \subset Q^* \subset \{ \Vert (I-P)v\Vert \le D_2 \}$ we have $\Vert \Sigma (p)\Vert \le D_2$ for every p. Let $p \in E^+$. If $\Vert p\Vert < R$ then $p+\Sigma (p) \in B_0$ and the assertion holds. Alternatively consider the global solution of $S^*$ passing through $p+\Sigma (p)$ at some time $t > 0$. Denote this solution by v(s), clearly $\Vert (I-P)v(s)\Vert \le D_2$ for every $s \in {\mathbb {R}}$. For this solution (12) implies that

$$\begin{aligned} \Vert Pv(0)\Vert \le Me^{-\gamma _1 t} \Vert p\Vert + \frac{MC_f}{\gamma _1}. \end{aligned}$$

So, for sufficiently large t we deduce that $\Vert Pv(0)\Vert \le \frac{MC_f}{\gamma _1} + 1 \le R$. From continuity of the mapping $t\mapsto \Vert Pv(t)\Vert$ we can choose $t^*$ such that $\Vert Pv(t^*0)\Vert = R$. Hence the function $v:[t^*,t] \rightarrow X$ is the solution of the original S with $v(t^*) \in B_1$. This means that $v(t) \in S(t-t^*)B_1$ and the proof is complete. $\square$

We are ready to prove that the set $B_0 \cup \bigcup _{t\ge 0}S(t)B_1$ is attracting, whence it satisfies all assumptions of Theorem 4.

Lemma 34

Under all assumptions of this section we have

$$\begin{aligned} \lim _{t\rightarrow \infty }\text {dist}\, \left( S(t) B, B_0 \cup \bigcup _{t\ge 0}S(t)B_1\right) = 0\ \ \text {for every}\ \ B\in {\mathcal {B}}(X). \end{aligned}$$

Proof

Take $B \in {\mathcal {B}}(X)$. Then there exists $t_1>0$ such that $S(t_1)B \subset Q$. If $t\ge t_1$ then

$$\begin{aligned} S(t)B&= S(t-t_1)[ [(S(t_1)B)\cap \{\Vert Px\Vert<R\}] \cup [(S(t_1)B)\cap \{ \Vert Px\Vert \ge R \}] \\&= S(t-t_1)((S(t_1)B)\cap \{\Vert Px\Vert<R\}) \cup S(t-t_1)((S(t_1)B)\cap \{\Vert Px\Vert \ge R\})\\&\subset S(t-t_1)(\{\Vert Px\Vert <R\}\cap Q) \cup S(t-t_1)((S(t_1)B)\cap \{\Vert Px\Vert \ge R\}). \end{aligned}$$

Now because for the initial data $v_0$ such that $\Vert Pv_0\Vert \ge R$ we have $\Vert Pv(t)\Vert \ge R_{cut}$ for every $t\ge 0$, we can write

$$\begin{aligned} S(t)B \subset S(t-t_1)(\{\Vert Px\Vert <R\}\cap Q) \cup S^*(t-t_1)((S(t_1)B)\cap \{\Vert Px\Vert \ge R\}). \end{aligned}$$

Hence

$$\begin{aligned}&\text {dist}\, \left( S(t) B, B_0 \cup \bigcup _{t\ge 0}S(t)B_1\right) \\&\quad \le \max \left\{ \text {dist}\, \left( S(t-t_1)(\{\Vert Px\Vert <R\}\cap Q), B_0 \cup \bigcup _{t\ge 0}S(t)B_1\right) , \right. \\&\qquad \left. \text {dist}\, \left( S^*(t-t_1)((S(t_1)B)\cap \{\Vert Px\Vert \ge R\}), B_0 \cup \bigcup _{t\ge 0}S(t)B_1\right) \right\} . \end{aligned}$$

Now assume that $v_0 \in \{\Vert Px\Vert <R\}\cap Q$. It is clear that for every $s\ge 0$ we have $S(s)v_0 \in Q$ and hence $\Vert (I-P)S(s)v_0\Vert \le D_1$. If $\Vert PS(s)v_0\Vert < R$ then $S(s)v_0 \in B_0$. Otherwise $\Vert PS(s)v_0\Vert \ge R$ and there exists $t^* \in [0,s]$ such that $\Vert PS(t^*)v_0\Vert = R$. This means that $S(t^*)v_0 \in B_1$ and $S(s)v_0 = S(s-t^*)S(t^*)v_0 \in S(s-t^*)B_1$. We have proved that $S(t-t_1)(\{\Vert Px\Vert <R\}\cap Q) \subset B_0 \cup \bigcup _{t\ge 0}S(t)B_1$. Hence

$$\begin{aligned}&\text {dist}\, \left( S(t) B, B_0 \cup \bigcup _{t\ge 0}S(t)B_1\right) \\&\quad \le \text {dist}\, \left( S^*(t-t_1)((S(t_1)B)\cap \{\Vert Px\Vert \ge R\}), B_0 \cup \bigcup _{t\ge 0}S(t)B_1\right) \\&\quad \le \text {dist}\, \left( S^*(t-t_1)((S(t_1)B)\cap \{\Vert Px\Vert \ge R\}), \text {graph}\, \Sigma \right) \\&\quad \le C((S(t_1)B)\cap \{\Vert Px\Vert \ge R\})e^{\delta t_1} e^{-\delta t}, \end{aligned}$$

where the last two estimates follow from the facts that $\text {graph}\, \Sigma \subset B_0 \cup \bigcup _{t\ge 0}S(t)B_1$ and $(S(t_1)B)\cap \{\Vert Px\Vert \ge R\}$ is a bounded set. The proof is complete. $\square$

Hence $B_0 \cup \bigcup _{t\ge 0}S(t)B_1$ satisfies all assumptions of Remark 1 and Theorem 1. We can use this last result to deduce the main theorem of this section.

Theorem 18

Under assumptions of this section, in particular if in addition to the assumptions which guarantee the existence of the unbounded attractor ${\mathcal {J}}$, the function f is Lipshitz outside a ball in $E^+$ (i.e. (32) holds) with sufficiently small Lipschitz constant, then ${\mathcal {J}} \subset B_0 \cup \bigcup _{t\ge 0}S(t)B_1$, and

$$\begin{aligned} \lim _{t\rightarrow \infty } \text {dist}\, (S(t)B,{\mathcal {J}}) = 0\ \ \text {for every}\ \ B\in {\mathcal {B}}(X). \end{aligned}$$

Moreover

$$\begin{aligned} \lim _{\Vert p\Vert \rightarrow \infty } \text {diam}\, ({\mathcal {J}}\cap \{x\in X\,:\ Px=p\} ) = 0. \end{aligned}$$

Using the estimate (34) we can provide the exact bound on the unbounded attractor thickness, namely

$$\begin{aligned} \text {dist}(\Phi (p),\{\Sigma (p)\}) \le \frac{C}{\Vert p\Vert ^{\frac{\delta }{\gamma _0}}}\ \ \text {as}\ \ \Vert p\Vert \ge R, \end{aligned}$$

i.e. the (maximal) distance between the multivalued inertial manifold of the nonmodified (original) problem and the (Lipschitz) inertial manifold of the modified problem tends to zero polynomially as $\Vert p\Vert$ tends to infinity.

4.5 Dynamics at Infinity

In this section we give a few comments on the dynamics of (12) at infinity. The assumptions of this section are that of Sect. 4.1. If we take the set $B\in {\mathcal {B}}(X)$ such that $\inf _{u\in B}\Vert Pu\Vert > \frac{MC_f}{\gamma _1}$. Then, by (12) it follows that

$$\begin{aligned} \Vert S(t)u_0\Vert \ge C(B)e^{\gamma _1 t} \ \ \text {for every}\ \ u_0\in B. \end{aligned}$$

(35)

This means that the set B satisfies assertion (1) of Lemma 2 for every $R > 0$. Hence, one can define its $\omega$-limit set at infinity $\omega _\infty (B)$, and this $\omega$-limit set is attracting at infinity in the sense of Lemma 12. We will construct the problem for which the set $\omega _\infty (B)$ is invariant. To this end, define $\frac{Pu(t)}{\Vert Pu(t)\Vert }:=x(t)$. With this definition the set $\omega _\infty (B)$ has the form

$$\begin{aligned} \omega _\infty (B) = \left\{ x \in E^+\,:\ \ \Vert x\Vert = 1, x_n(t_n) \rightarrow x, x_n(0) = \frac{Pu^n_0}{\Vert Pu^n_0\Vert }, u^n_0\in B \right\} \end{aligned}$$

Since u(t) satisfies (6), its projection Pu(t) satisfies the ODE

$$\begin{aligned} (Pu(t))' = A(Pu(t)) + Pf(u(t)), \end{aligned}$$

which is non-autonomous due do the presence of the term P(u(t)). It is straightforward to verify that the function x(t) satisfies the following ODE un the unit sphere in $E^+$

$$\begin{aligned} x'(t) = Ax(t) - (Ax(t),x(t))x(t)+ \frac{Pf(u(t))}{\Vert Pu(t)\Vert } - \left( \frac{Pf(u(t))}{\Vert Pu(t)\Vert },x(t)\right) x(t). \end{aligned}$$

Since $\Vert f(u)\Vert \le C_f$ and by the estimate (35) we deduce

$$\begin{aligned} \left| \frac{Pf(u(t))}{\Vert Pu(t)\Vert } - \left( \frac{Pf(u(t))}{\Vert Pu(t)\Vert },x(t)\right) x(t)\right| \le \frac{2C_f}{C(B)}e^{-\gamma _1 t}. \end{aligned}$$

So we can define the following asymptotically autonomous problem on the unit sphere in $E^+$

$$\begin{aligned} x'(t) = Ax(t) - (Ax(t),x(t))x(t)+ g(t), \end{aligned}$$

with $\Vert g(t)\Vert \le \frac{2C_f}{C(B)}e^{-\gamma _1 t}$. Using the results on the asymptotically autonomous problems [23, 26] we will prove that the set $\omega _{\infty }(B)$, a compact set in the unit sphere in $E^+$ is invariant with respect to the limit autonomous system

$$\begin{aligned} y'(t) = Ay(t) - (Ay(t),y(t))y(t), \end{aligned}$$

(36)

and hence the dynamics at infinity can be described by means of the properties of the operator A only. In fact, this dynamics can be described by representing A in the Jordan form. This is done by the change of basis matrix P and we obtain the new system

$$\begin{aligned} z'(t) = P^{-1}APz(t) - (P^{-1}APz(t),z(t))z(t). \end{aligned}$$

This system is the projection on the unit sphere of the ODE

$$\begin{aligned} z'(t) = P^{-1}APz(t), \end{aligned}$$

the solutions of which can be found explicitly: each Jordan block gives rise to an invariant set, and all the invariant sets with non-equal values of $\text {Re}\, \lambda$ are connected with the connections ordered in the direction of increasing $\text {Re}\, \lambda$. The dynamics on the invariant sets related with given value of $\text {Re}\, \lambda$ depends on the structure of Jordan blocks associated with $\text {Re}\, \lambda$ and can be possibly recurrent. We continue with the lemma on the invariance of $\omega _{\infty }(B)$.

Lemma 35

The set $\omega _{\infty }(B)$ is invariant with respect to the system (36).

Proof

Consider $x\in \omega _{\infty (B)}$. This means that $x_n(t_n)\rightarrow x$ for some $t_n\rightarrow \infty$. Take $t\in {\mathbb {R}}$, $t\ne 0$, either positive or negative number. Then, as $x_n(t_n+t)$ (which is always well defined for n large enough) is always on the unit sphere, for a subsequence we have $x_n(t_n+t)\rightarrow x_1$ with $x_1\in \omega _\infty (B)$. Define functions $f_n:[0,|t|]\rightarrow E^+$ as

$$\begin{aligned} f_n(s) = {\left\{ \begin{array}{ll} x_n(t_n+s) \ \ \text {if}\ \ t> 0,\\ x_n(t_n+t+s)\ \ \text {if}\ \ t< 0. \end{array}\right. } \end{aligned}$$

These functions are equibounded and equicontinuous, so, for a subsequence they converge uniformly to some function f(s). If $t>0$, then

$$\begin{aligned} x_n(t_n+t)&= x_n(t_n) + \int _{t_n}^{t_n+t} Ax_n(s) - (Ax_n(s),x_n(s))x_n(s)+ g(s)\, ds \\&= x_n(t_n) + \int _{0}^{t} A f_n(s) - (Af_n(s),f_n(s))f_n(s)+ g(s+t_n)\, ds. \end{aligned}$$

Passing to the limit from the Lebesgue dominated convergence theorem we obtain

$$\begin{aligned} x_1 = x + \int _{0}^{t} A f(s) - (Af(s),f(s))f(s)\, ds, \end{aligned}$$

with $f(0) = x$ and $f(t) = x_1$. As f solves (36) the assertion for $t>0$ is proved. If $t<0$ then

$$\begin{aligned} x_n(t_n)&= x_n(t_n+t) + \int _{t_n+t}^{t_n} Ax_n(s) - (Ax_n(s),x_n(s))x_n(s)+ g(s)\, ds \\&= x_n(t_n+t) + \int _{0}^{-t} A f_n(s) - (Af_n(s),f_n(s))f_n(s)+ g(s+t_n+t)\, ds. \end{aligned}$$

Again, by the Lebesgue dominated convergence theorem

$$\begin{aligned} x = x_1 + \int _{0}^{-t} A f(s) - (Af(s),f(s))f(s)\, ds, \end{aligned}$$

with $f(0) = x_1$ and $f(-t) = x$. Again f solves (36) whence we have the assertion for $t<0$ and the proof is complete. $\square$