Learning Dynamics by Reservoir Computing (In Memory of Prof. Pavol Brunovský)

Abstract

We study reservoir computing, a machine learning method, from the viewpoint of learning dynamics. We present numerical results of learning the dynamics of the logistic map, one of the typical examples of chaotic dynamical systems, using a 30-node reservoir and a three-node reservoir. When the learning is successful, an attractor that is smoothly conjugate to the logistic map to be learned is observed in the phase space of the reservoir. Inspired by this numerical result, we introduce a degenerate reservoir system and use it to mathematically confirm this observation. We also show that reservoir computing can learn information about dynamics not included in the training data, which we believe is a remarkable feature of reservoir computing compared to other machine learning methods. We discuss this feature in connection with the above observation that there is a smooth conjugacy between the attractor in the reservoir and the dynamics to be learned.

1 Introduction

In this paper, we study reservoir computing, a type of machine learning, from the viewpoint of dynamical systems. Reservoir computing is based on recurrent neural networks (abbreviated as RNNs) with inputs and outputs. An RNN consists of a large number of artificial neurons and their mutual interactions, and can be thought of as a dynamical system with many degrees of freedom. More precisely, each artificial neuron has its own dynamics, and the interaction between related neurons is represented by a directed graph. In other words, each neuron evolves by itself while being influenced by other neurons via the input edges of the graph, and the state of each neuron is propagated to other neurons via the output edges.

Machine learning using RNNs generally requires a large amount of computation because it attempts to perform tasks by optimizing the weights of the interactions between the nodes in the RNN and the nodes in the input and output layers. Reservoir computing, while using such RNNs, can greatly reduce the computational cost of learning by maintaining most of the interaction weights between the nodes and adjusting only those from the nodes of the RNN to the output layer. Reservoir computing was introduced independently by Jaeger and Haas [2] and Maas et al. [4]. See also Jaeger [1].

The purpose of this paper is to study how a reservoir computing system learns dynamics. We consider a dynamical system as a learning target, feed the time series generated by the target dynamical system into a reservoir, and let the reservoir computing system learn its dynamics by observing how well the output of the reservoir system predicts the dynamical system to be learned. The main feature of this research is that it takes the dynamical system viewpoint, considering the reservoir computing system itself as a dynamical system and investigating the dynamical structure of its phase space, including attractors, invariant manifolds, fixed points, their stable and unstable manifolds, and bifurcations. With such an approach, we hope to understand the essential mechanism by which reservoir computing learns dynamics. In this study, we will mainly use numerical computations, but we will also present a theoretical result to clarify the essential mechanism.

As will be discussed later, reservoir computing exhibits two types of dynamical systems: one is a semi-direct product system consisting of the dynamics of the target system to be learned and the dynamics of the reservoir with an input from the target, and another an autonomous dynamical system only on the phase space of the reservoir. The former corresponds to the learning stage, where the time series generated by the target dynamics is fed to the reservoir system. The latter corresponds to the prediction stage after successful learning, where the reservoir system evolves by itself and is expected to predict (mimic) the target dynamics.

In this paper, the logistic map, which is a typical example of chaotic dynamical systems, is used as the target dynamical system for learning. The main numerical results of this paper can be summarized as follows:

• 1. At the learning stage, the semi-direct product system has an attractor in its phase space that is (seemingly smoothly) conjugate to the chaotic dynamics of the logistic map.

• 2. After successful learning, the autonomous reservoir system at the prediction stage also retains an attractor that appears to be smoothly conjugate to the chaotic dynamics of the target.

• 3. Even a reservoir system consisting of only three nodes can learn the chaotic dynamics of the logistic map reasonably well.

• 4. The phase space of the autonomous reservoir has fixed points outside the attractor, which coincide with the phase space structure of the logistic map outside the chaotic dynamics.

• 5. Bifurcation diagrams of the autonomous reservoir system by modifying hyper parameters of the reservoir computation reproduce the essential bifurcation features of the logistic map without using its parameter dependence.

Note that the last two items show that the reservoir computing of dynamics can predict information beyond the training data of the dynamics to be learned. We believe that this is a remarkably unique feature of reservoir computing of dynamics, and we will discuss this in more details at the end of this paper.

For the theoretical study of reservoir computing, we consider a kind of “degenerate" reservoir system as a singular limit of the reservoir computing system used for numerical study. For this degenerate reservoir system, the main theoretical result is as follows:

Theorem 1

The degenerate reservoir system at learning, defined to be smooth, has an attractor $\Sigma$ that is smoothly conjugate to the chaotic attractor of the logistic map. If the projection of $\Sigma$ to the reservoir phase space is injective, then there exists an output map from $\Gamma$, the projection image of $\Sigma$, to the phase space of the logistic map. In addition, there exists an induced dynamical system on $\Gamma$ which can be interpreted as an autonomous degenerate reservoir system after learning, such that the autonomous degenerate reservoir on $\Gamma$ is smoothly conjugate to the chaotic attractor of the logistic dynamics by the output map.

For a precise statement of this theorem as well as related information, see Sect. 4.

There are several works devoted to studying reservoir computing for learning dynamics, such as [1,2,3, 5,6,7,8]. However, to the best of the authors’ knowledge, there is no extensive study on learning dynamics of logistic maps by reservoir computing, even though the logistic map is one of the simplest and most studied examples of chaotic dynamics. In this paper, we study the dynamical aspects of learning of a reservoir computing system by choosing the logistic map as the target of learning and taking full advantage of the low-dimensionality of the dynamics to be learned.

This paper is organized as follows: In Sect. 2, we first briefly describe the general framework of reservoir computing, and then describe the specific architecture for learning dynamics of our reservoir computing system. We also give the definitions of “success" and “failure" in learning, which are particularly suitable for the logistic map. In Sect. 3, we present numerical results on learning logistic maps, and show that the reservoir actually succeeds to reproduce the dynamics of the logistic map. We also present results for three-dimensional reservoirs, which are much lower in dimension than usual reservoirs that are usually expected to have hundreds or thousands of nodes. As explained in Sect. 3.4, the low dimensionality of the three-node reservoir allows us to study its phase space structure in detail.

In Sect. 4 we attempt to understand theoretically how the dynamics can be successfully learned by reservoir computing. Specifically, based on the numerical results of Sect. 3, we introduce a degenerate reservoir computing system, which gives us a mathematical mechanism that indicates how a reservoir system behaves after learning. Finally, in Sect. 5, we summarize the results and discuss future research topics, including a discussion on the remarkable feature from a dynamical system viewpoint of reservoir computing compared to other machine learning methods.

2 What Is Reservoir Computing: Our Setting

2.1 General Scheme of Reservoir Computing

In this subsection, we give a general formulation of reservoir computing, where the reservoir is an RNN consisting of N nodes, having K input nodes and L output nodes. We also consider feedback from the output layer. Our formulation below is based on [1].

For $K\in \mathbb {N}_{0}=\mathbb {N}\cup \{0\}, N,L \in \mathbb {N}$, consider a reservoir whose internal variable is given by $r \in \mathbb {R}^{N}$, along with an input variable $u \in \mathbb {R}^{K}$ and output variable $\eta \in \mathbb {R}^{L}$. The connection weights inside the reservoir are given by the weight matrix $W \in M_{N, N}(\mathbb {R})$, those from the input layer to the reservoir are given by $W^{\text {in}} \in M_{N, K}(\mathbb {R})$, and those from the reservoir to the output layer are $W^{\text {out}} \in M_{L, K+N+L}(\mathbb {R})$. The feedback weights from the output layer back to the reservoir are given by $W^{\text {fb}} \in M_{N, K}(\mathbb {R})$.

Using these notations, the time evolution rule of the reservoir computing system is given as follows:

$$\begin{aligned} r(t + 1) = \varPhi (W^{\text {in}}u(t + 1) +Wr(t) +W^{\text {fb}}\eta (t)) =:F(u(t + 1), r(t), \eta (t)). \end{aligned}$$

Note that we are considering the discrete time evolution of reservoir computing, namely, we assume $t\in \mathbb {N}_{0}$. Continuous time evolution given by an ODE system is also widely used in the literature.

The function $\varPhi :\mathbb {R}^{N}\rightarrow \mathbb {R}^{N}$ is called the activation function. In this paper, for simplicity, we consider the activation function to be a component-wise hyperbolic tangent function, $\varPhi (r)={\overline{\tanh }}(r)=(\tanh (r_1),\dots ,\tanh (r_N))^{\mathsf {T}}$ with $r=(r_1,\dots , r_N)^{\mathsf {T}}$.

In general, supervised machine learning using neural networks is achieved by the following steps:

• Step 1 Optimize the weight matrices ($W^{\text {in}}$, W, $\dots$) based on the given inputs and feedback from training data.

• Step 2 Using the network determined in Step 1, obtain outputs from a new input, which is expected to perform the given task in a desired manner.

For reservoir computing, unlike general RNNs, only $W^{\text {out}}$ is determined at the learning step (Step 1), while $W^{\text {in}}$, W, and $W^{\text {fb}}$ are randomly chosen from a class of matrices and are fixed from the beginning. Therefore, we must clarify the class of matrices from which we take these weight matrices.

In [1], a type of reservoir systems called an echo state network (ESN for short) is introduced, for which W is taken to satisfy the so-called echo state property (ESP for short). In this paper, we consider W chosen from a broader class of matrices; see Sect. 2.2 for a precise definition.

Once the output weight matrix $W^{\text {out}}$ is obtained after learning in Step 1, the output in Step 2 is given by

$$\begin{aligned} \eta (t + 1) = \varPsi (W^{\text {out}} [u(t + 1), r(t + 1), \eta (t)]) =:G(u(t + 1), r(t + 1), \eta (t)). \end{aligned}$$

Here, $\varPsi :\mathbb {R}^{L} \rightarrow \mathbb {R}^{L}$ is also an activation function, which is taken to be the identity in this paper as the simplest choice.

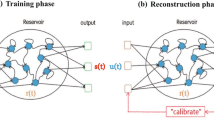
Figure 1 shows the reservoir computing architecture based on the scheme above.

Fig. 1

Schematic picture of general reservoir computing. The circles in the figure represent neurons or nodes of the RNN ($K=2$, $N=10$, $L=3$). The weight matrices W, $W^{\text {in}}$, $W^{\text {fb}}$ are randomly chosen and fixed, and only $W^{\text {out}}$ is determined at the learning stage. The activation functions $\varPhi$ and $\varPsi$ are not shown here

2.2 Setting of Our Reservoir Computing for Learning Dynamics

In this subsection, we define the reservoir architecture and the algorithms for forecasting the time series generated by a chaotic dynamical system. The scheme is mainly based on [1, 2], with some modifications. We consider a set of time series data $\left\{ x(t) \right\} _{}^{}$ generated from a real one-dimensional, discrete time, chaotic dynamical system $x(t+1) = f(x(t))$. For numerical computations in this paper, we choose the logistic map as the target dynamical system:

$$\begin{aligned} x(t+1) = f(x(t)) = ax(t)(1-x(t)) \end{aligned}$$

defined on the interval $I=[0,1]$, with the parameter a chosen to be $a=3.7$ unless otherwise stated. This is a sample choice for a and has no special meaning. For fixed $N \in \mathbb {N}; R, b \ge 0$, consider an N-node RNN as the reservoir with variable $r(t) \in \mathbb {R}^{N}$, having output variable $\eta (t) \in \mathbb {R}^{1}$. We do not use input throughout this paper, and the training data at the learning stage are used via feedback. Therefore, our reservoir computing system for learning is given by

$$\begin{aligned} r(t+1)= & {} {\overline{\tanh }}(Wr(t) + {\varvec{w^{\text {fb}}}}x(t)),\\ x(t+1)= & {} f(x(t)) = ax(t)(1-x(t)). \end{aligned}$$

Here, W of the reservoir is taken from

$$\begin{aligned} W \in \left\{ X \in M_{N, N}(\mathbb {R}) \big | \rho (X) = R,\ X_{ij} \ge 0 \ (i, j = 1, \dots ,N) \right\} , \end{aligned}$$

where $\rho (X)$ is the spectral radius of X, while the feedback weight is from

$$\begin{aligned} {\varvec{w^{\text {fb}}}}\in \left\{ x \in \mathbb {R}^{N} \big | |x_{i}| = b \ (i = 1, \dots ,N) \right\} . \end{aligned}$$

Both W and ${\varvec{w^{\text {fb}}}}$ are chosen randomly and fixed, and $\mathbf {w^{\text {out}}}\in M_{1, N}(\mathbb {R})$ is determined by learning. Note that we do not assume the condition $\rho (W) < 1$, which is often used as a replacement for the echo state property [1]. This is an important point for the numerical experiments given in Sect. 3.1. In addition, we do not assume the sparseness of W either, though this is commonly done in the literature.

Once the output weight $\mathbf {w^{\text {out}}}$ is obtained after learning, the output $\eta (t)$ is calculated as $\eta (t)=\mathbf {w^{\text {out}}}r(t)$. Therefore, each neuron in the reservoir and the output layer evolves according to the following equations (see Fig. 2):

$$\begin{aligned} r(t + 1)= & {} {\overline{\tanh }}(Wr(t) + {\varvec{w^{\text {fb}}}}\eta (t)),\\ \eta (t + 1)= & {} \mathbf {w^{\text {out}}}r(t + 1), \end{aligned}$$

or for short,

$$\begin{aligned} r(t + 1) = {\overline{\tanh }}(Wr(t) + {\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)), \end{aligned}$$

which means the reservoir, after learning, evolves by itself.

Fig. 2

Schematic picture of our setting of reservoir computing of this paper. See also the caption of Fig. 1

Using this setting, the algorithms for learning and prediction are described as follows:

• Step 0: Preparation Choose $N \in \mathbb {N}, R, b \ge 0$, and take

  $$\begin{aligned} W \in&\left\{ X \in M_{N, N}(\mathbb {R}) \big | \rho (X) = R,\ X_{ij} \ge 0\ (i, j = 1, \ldots ,N) \right\} , \end{aligned}$$

  (1)
  $$\begin{aligned} {\varvec{w^{\text {fb}}}}\in&\left\{ x \in \mathbb {R}^{N} \big | |x_{i}| = b\ (i = 1, \ldots ,N) \right\} \end{aligned}$$

  (2)

  randomly and then fix them. Also choose $T_{0}, T_{1}, T_{2} \in \mathbb {N}\ (T_{0}< T_{1} < T_{2})$ and x(0), r(0) appropriately, according to the task.

• Step 1: Learning ($t = 0, \ldots , T_{1}$)

  1-1::

  Update the internal state of the reservoir with the following rule during $t=0,\dots , T_{1}$:

  $$\begin{aligned} x(t + 1)&= f(x(t)), \end{aligned}$$

  (3)

  $$\begin{aligned} r(t + 1)&= {\overline{\tanh }} (Wr(t) + {\varvec{w^{\text {fb}}}}x(t)). \end{aligned}$$

  (4)

  1-2::

  Determine $\mathbf {w^{\text {out}}}$ so as to minimize the error between $\left\{ \mathbf {w^{\text {out}}}r(t) \right\} _{t=T_0+1}^{T_1}$ and $\left\{ x(t) \right\} _{t=T_0+1}^{T_1}$, as explained below.

• Step 2: Prediction ($t = 0, \dots , T_{2}$) With a possible reset of the initial values x(0), r(0), we perform the following steps:

  • 2-1: 1-step prediction ($t = T_0+1, \dots , T_{1}$) Using $\mathbf {w^{\text {out}}}$ determined in 1-2, obtain $\left\{ \mathbf {w^{\text {out}}}r(t) \right\} _{t=T_0+1}^{T_1}$ by iterating the equation

    $$\begin{aligned} x(t + 1)&= f(x(t)),\end{aligned}$$

    (5)
    $$\begin{aligned} r(t + 1)&= {\overline{\tanh }} (Wr(t) + {\varvec{w^{\text {fb}}}}x(t)) \end{aligned}$$

    (6)

    with the true data x(t) being fed at each iteration. The output time series $\left\{ \mathbf {w^{\text {out}}}r(t) \right\} _{t=T_0+1}^{T_1}$ is expected to closely mimic the target time series $\left\{ x(t) \right\} _{t=T_0+1}^{T_1}$.

  • 2-2: reservoir prediction ($t = T_1 + 1, \dots , T_2$) If step 2-1 is successful, obtain $\left\{ \mathbf {w^{\text {out}}}r(t) \right\} _{t=T_1+1}^{T_2}$ by iterating the equation

    $$\begin{aligned} r(t + 1) = {\overline{\tanh }} (Wr(t) + {\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)), \end{aligned}$$

    (7)

    without using any true data x(t). The output $\left\{ \mathbf {w^{\text {out}}}r(t) \right\} _{t=T_0+1}^{T_1}$ is expected to predict the target dynamics.

Some technical remarks are in order.

• In Step 0, W and ${\varvec{w^{\text {fb}}}}$ are set randomly by choosing one random seed. The same random seed always generates the same result.

• Since the domain of the logistic map is the unit interval $I=[0,1]$, which does not contain the origin in its interior, it is sometimes convenient to shift the coordinate of the time series $\left\{ x(t) \right\} _{}^{}$, as noted in [1]. In this paper, we use the shifted time series $\left\{ x(t)-0.5 \right\} _{}^{}$ for the learning and prediction steps, but use $\left\{ x(t) \right\} _{}^{}$ when we show the results in the original coordinates after shifting back.

• In 1-2, $\left\{ r(t) \right\} _{0}^{T_0}$ is not used to determine $\mathbf {w^{\text {out}}}$. This ignores some transient behavior affected by the choice of the initial values x(0) and r(0). $\mathcal {F}$ (see below)).

• We use a standard linear regression to obtain a $\mathbf {w^{\text {out}}}$ in 1-2, namely, we consider minimization of the squared error, which is equivalent to solving the equation $(R^{T}R)(\mathbf {w^{\text {out}}})^{{\mathsf {T}}} = Rx$, where $R :=(r(T_{0} + 1)^{{\mathsf {T}}} \dots r(T_{1})^{\mathsf T})^{{\mathsf {T}}}, \ x :=(x(T_{0} + 1)) \dots x(T_{1}))^{{\mathsf {T}}} .$ We use the Python (NumPy) linear algebra library to solve this equation.

• The main purpose of 2-1 (one-step prediction) is to set the initial condition $r(T_{1})$ of the reservoir reasonably for 2-2 (reservoir prediction). If the one-step prediction does not give good results, we do not perform the reservoir prediction. In addition, because we feed the true data $\left\{ x(t) \right\} _{t=T_0+1}^{T_1}$ each time to generate $\left\{ r(t) \right\} _{t=T_0+1}^{T_1}$ in 2-1, the one-step prediction may be a good test for the chosen $\mathbf {w^{\text {out}}}$ (see also Sect. 3.2).

• The results of 2-2 (reservoir prediction) may not give a good result for predicting the time series of the target dynamics at each time. Nevertheless, we can consider that the results give a good prediction of the target dynamics in some sense. This point will be discussed in the next subsection.

The following should be noted from the viewpoint of dynamical system theory:

• In 1-1 and 2-1, the Equations (3) and (4) form a semi-direct product dynamical system:

  $$\begin{aligned} \mathcal {F} := (f, F) : \mathbb {R}^{1} \times \mathbb {R}^{N} \rightarrow \mathbb {R}^{1} \times \mathbb {R}^{N};\quad \mathcal {F}(x,r) = (f(x), F(x,r)), \end{aligned}$$

  where f is the target dynamical system (3) and $F:\mathbb {R}^{1} \times \mathbb {R}^{N} \rightarrow \mathbb {R}^{N}$ is the time evolution map (4) for the reservoir variable.

• At 2-2, the equation (7) defines an autonomous dynamical system $\tilde{F}: \mathbb {R}^{N} \rightarrow \mathbb {R}^{N}$, namely

  $$\begin{aligned} r(t + 1) = {\overline{\tanh }}(Wr(t) + {\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)) =: \tilde{F}(r(t)). \end{aligned}$$

In what follows, $\mathcal {F} : \mathbb {R}^{1} \times \mathbb {R}^{N} \rightarrow \mathbb {R}^{1} \times \mathbb {R}^{N}$ is called the “semi-direct product reservoir" and its phase space is the “semi-direct product reservoir space", while the phase space of $\tilde{F} : \mathbb {R}^{N} \rightarrow \mathbb {R}^{N}$ is called the “reservoir space".

2.3 Definition of Success for Prediction of the Logistic Dynamics

Fig. 3

Example of successful reservoir prediction for the logistic map. $N=30$, $R = 4.1$, $b = 1.1$. a $\left( \mathbf {w^{\text {out}}}r(t), \mathbf {w^{\text {out}}}r(t+1) \right)$-plot. b One-step prediction. c Reservoir prediction

Fig. 4

Example of failure for the resolver prediction for a logistic map. $N=30$, $R = 4.1$, $b = 1.1$. a $\left( \mathbf {w^{\text {out}}}r(t), \mathbf {w^{\text {out}}}r(t+1) \right)$-plot. b One-step prediction. Note that, though the one-step prediction in b is quite successful, the prediction of the dynamics in a is not quite successful, since there is a gap or a “hole" around 0.7, which is in fact around the unstable fixed point $1-1/\alpha \approx 0.73$ of the logistic map. In this sense, we consider this example to be a “failure", and that evaluation by a one-step prediction alone cannot capture this failure

Fig. 5

Another example of failure where the reservoir prediction shows a periodic orbit of period 7. $N=30$, $R = 4.1$, $b = 1.1$

Chaotic dynamical systems have sensitive dependence on initial conditions, and hence a tiny difference in the initial conditions can grow exponentially fast under the time evolution. Therefore, even if learning of the reservoir is successful, it is impossible to predict the target chaotic time series accurately for a long time by the reservoir system after learning. We therefore study the prediction of the dynamics by the reservoir not by the accuracy of the time series prediction but by the accuracy of capturing the essential feature of the dynamics.

One general method to judge whether learning is successful is to evaluate the error between x(t) and $\mathbf {w^{\text {out}}}r(t)$ at each time of the one-step prediction (with the initial values different from those used in Step 1-1) in the setting of Sect. 2.2. In this paper, the experiment is done for a known dynamical system. Therefore, the success or failure judgment based on the error between $f(\mathbf {w^{\text {out}}}r(t))$ and $\mathbf {w^{\text {out}}}r(t+1)$ can be considered at the reservoir prediction stage.

In this paper, we are more interested in the “learning dynamics" than a faithful prediction of the time series. For this, it is more convenient to plot the two-dimensional output data $(\mathbf {w^{\text {out}}}r(t), \mathbf {w^{\text {out}}}r(t+1))$ and compare the plotted points with a graph of the target dynamical system, the logistic map. Even if the time series prediction is not good due to the chaotic nature of the dynamics, the output data can still be very close to the graph of the target dynamics, which means the reservoir can learn and predict the target dynamics very well. See Fig. 3 for the difference between the time series prediction and a prediction of the dynamics.

However, it is not sufficient to look at the closeness of the output data points with a graph of the target dynamics, since there may be cases where learning of the dynamics is not successful, even if the output data points are very close to the graph of the target dynamics. More specifically, we perform a prediction of the time series $\left\{ x(t)\right\}$ generated by the logistic map $x(t+1) = a x(t)(1-x(t))=:f(x(t))$ ($a = 3.7$), and obtain results like those shown in Figs. 3, 4 and 5 among others. If the results are like Fig. 3, we may consider it to be a “success". However, other cases such as Figs. 4 and 5 are also frequently observed, for the same architecture and algorithms as for the results in Fig. 3 but with different W, ${\varvec{w^{\text {fb}}}}$ chosen in Step 0 of Algorithm 1. For these examples, the results of the one-step prediction are equally successful as in Fig. 3, and hence the difference arises at the reservoir prediction stage.

Based on the above observation, for the numerical experiments in Sect. 3, we define “success" and “failure" as satisfying the following two respective criteria (that are specific to the logistic maps):

• 1. The average error of $|\mathbf {w^{\text {out}}}r(t+1) - f (\mathbf {w^{\text {out}}}r(t)) |$ over $T_{1}+1\le t \le T_{2}-1$ is less than $\varepsilon =10^{-1.6}$.

• 2. After an additional waiting time, which we set as $k=200$ iterations, there is no “hole" in the data points around the fixed point $1-1/a\approx 0.73$ of the logistic map, meaning that every subinterval of equal length of $H=[0.65, 0.75]$ divided into $m=10$ pieces contains at least one data point $\mathbf {w^{\text {out}}}r(t) \ (T_{1}+k \le t \le T_{2})$.

Note that the parameters $\varepsilon$, k, H, m in the above two conditions are rather arbitrary, and $\varepsilon =10^{-1.6}$, $k=200$, $H=[0.65, 0.75]$, and $m=10$ are simply our choice in this paper.

Although the examples in Figs. 4 and 5 violate the second condition of the above and are classified as “failures", they are interesting in their own right. For instance, Fig. 5 suggests stable periodic points of period 7, and indeed the logistic map with $a=3.702$, close to our value of $a=3.7$, has a stable periodic point of period 7. See also Sect. 5.1 for a further discussion.

3 Numerical Study for the Logistic Maps

In this section, we present the results of numerical experiments on learning the dynamics of the logistic map by reservoir computing. Recall from Sect. 2.2 that our N-node reservoir system at the stage of learning is given by

$$\begin{aligned} \begin{array}{rcl} r(t+1) &{}=&{} {\overline{\tanh }}(Wr(t) + {\varvec{w^{\text {fb}}}}x(t)),\\ x(t+1) &{}=&{} f(x(t)) = ax(t)(1-x(t)). \end{array} \end{aligned}$$

(8)

The parameter of the logistic map is fixed to be $a=3.7$ throughout this section. The weight matrices W and ${\varvec{w^{\text {fb}}}}$ are taken from

$$\begin{aligned} W\in & {} \left\{ X \in M_{N, N}(\mathbb {R}) \big | \rho (X) = R,\ X_{ij} \ge 0 \ (i, j = 1, \dots ,N) \right\} ,\\ {\varvec{w^{\text {fb}}}}\in & {} \left\{ x \in \mathbb {R}^{N} \big | |x_{i}| = b \ (i = 1, \dots ,N) \right\} , \end{aligned}$$

where $\rho (X)$ is the spectral radius of X. We use $R:=\rho (W)$ and $b :=| w^{\text {fb}}_{i} |$ as hyper parameters. These weight matrices are chosen randomly from these classes and fixed for each computation. Note that we first choose a random seed to ensure a random choice for the weights.

Once learning is done following the algorithm in Sect. 2.2, we use

$$\begin{aligned} r(t+1) = {\overline{\tanh }}(Wr(t) + {\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)) \end{aligned}$$

(9)

for the prediction of the dynamics. This is an autonomous dynamical system on the reservoir space $\mathbb {R}^N$.

3.1 Successful Learning of Logistic Dynamics

Our first study is to find an appropriate setting of the reservoir for learning dynamics, namely values for the hyper parameters R and b that ensure successful learning of the logistic map. For this purpose, we set the number of reservoir nodes to be $N=30$, and choose 200 pairs of $(W, {\varvec{w^{\text {fb}}}})$ for each fixed R and for b. Using the criteria for success and failure of learning given in Sect. 2.3, we count the number of successes for each choice of $(W, {\varvec{w^{\text {fb}}}})$. The results are given by Fig. 6, showing a particularly high success rate for large values of $\rho (W)$, almost $100\%$ success at around $R=5.5$ and $b=0.7$, which contrasts with the usual choices of W of $\rho (W)<1$.

Fig. 6

Heat map for the success rate of learning. The color indicates the number of successes. $N=30$, $R\in [0.5,7.5]$, $b\in [0.1,2.5]$

Note that the zero “success" rate at $R\ge 5.5$ and $b\ge 1.3$ is an artifact related to the definition of success given in Sect. 2.3, based on the choice of the parameters for criterion 2, such as H and/or m.

3.2 Numerical Verification of the Conjugacy of the Dynamics

Recall that we are interested in an accurate prediction of the dynamics, rather than the time series, and for this purpose it is more convenient to view the results of a computation in comparison with the graph of the logistic map, as explained in Sect. 2.3. For those results classified as successes, we study the phase space structure of the reservoir system at the prediction stage, whose results are shown in Fig. 7a–c, all with $R = 5.0$, $b = 1.3$. Figure 7a is the $\left( \mathbf {w^{\text {out}}}r(t), \mathbf {w^{\text {out}}}r(t+1) \right)$-plot of the output time series compared with the graph of the logistic map, which confirms the success of the prediction of the dynamics.

To explore the reservoir phase space, we have applied a principal component analysis (PCA for short) to this example. There is a set of points in the reservoir space that looks like a one-dimensional curve segment, as shown in Fig. 7b, since it lies in an almost two-dimensional plane, as suggested from the contribution rate of the first principal component of about $94.8\%$ and that of the second of $5.2\%$, the total of these being almost $100\%$; see also Fig. 7c. Note that numerically this set of points can be regarded as an attractor of the reservoir dynamics (9).

Fig. 7

Example of success of the prediction of dynamics by reservoir computing. $N=30$, $R = 5.0$, $b = 1.3$. a $\left( \mathbf {w^{\text {out}}}r(t), \mathbf {w^{\text {out}}}r(t+1) \right)$-plot in comparison with a graph of the logistic map with $a=3.7$. b Result of PCA. Projection of the attractor in the reservoir space into the three-dimensional PCA subspace. c Similar to b, but a projection to the two-dimensional PCA subspace

The “attractor" obtained numerically as a curve segment can be coordinated by $\mathrm{PC}_1$, the first principal component, as suggested by Fig. 7c. Let $\pi _{1}:\mathbb {R}^{30} \rightarrow \mathbb {R}$ be the projection to $\mathrm{PC}_1$. We then plot the points $\left\{ (\pi _1(r(t)), \mathbf {w^{\text {out}}}r(t-1)) \right\}$, whose result is given in Fig. 8. From this, we see that there is a one-to-one correspondence between $\pi _1(r(t))$ and $\mathbf {w^{\text {out}}}r(t-1)$ via a (seemingly smooth) injective map, say $\varphi :\mathbb {R}\rightarrow \mathbb {R}$. This map $\varphi$ gives a bijection from the attractor in the reservoir space to the x-space, namely the phase space of the logistic map, and is compatible with both of the dynamics. Therefore, it shows a (numerically obtained) smooth conjugacy between the attractor of the reservoir at the prediction stage and the logistic dynamics.

Figure 9 shows a numerical calculation of the Lyapunov spectrum of the reservoir dynamics. Only one of the 30 Lyapunov exponents is positive, and it is close to the Lyapunov exponent of the logistic map, which may be understood from the existence of a smooth conjugacy between the reservoir dynamics and the logistic map.

Fig. 8

$\left( \pi _{1}(r(t)), \mathbf {w^{\text {out}}}r(t-1) \right)$-plot. This strongly suggests a smooth conjugacy between the attractor of the reservoir system (9) at the prediction stage and the logistic map

Fig. 9

Numerically computed Lyapunov spectrum. Finite time Lyapunov exponents are plotted, which seem to converge at $T=100$. There is only one positive Lyapunov exponent that is close to that of the logistic map with $a=3.7$

3.3 Numerical Results for a Three-Node Reservoir

In the previous two subsections, we have dealt with reservoir systems with 30 nodes. Similar experiments have been conducted for reservoirs with smaller numbers of nodes. We have found a reservoir system with only three nodes that can learn the dynamics of a logistic map quite successfully. In the rest of this section, we focus on such three-node reservoirs and discuss their dynamics in more detail.

Fig. 10

Heat map for the success rate of three-node reservoirs. The setting is the same as that of Fig. 6 except for $N=3$

Fig. 11

Example of successful prediction by a three-node reservoir. $R = 4.5$, $b = 0.9$. a $\left( \mathbf {w^{\text {out}}}r(t), \mathbf {w^{\text {out}}}r(t+1) \right)$-plot. b Attractor in the three-dimensional reservoir space

Fig. 12

Fixed points $P_j^\pm \ (j=1,2,3,4)$ found in the three-dimensional reservoir space, and the origin O as an additional fixed point. Because $P^{-}_{2}$, $P^{-}_{3}$, $P^{-}_{4}$ lie in a very small region and can be hardly distinguished in a, an enlargement of the region close to the corner point $(-1,-1,-1)$ is presented in b. The same applies to $P^{+}_{2}$, $P^{+}_{3}$, $P^{+}_{4}$ due to the symmetry with respect to O

In this subsection, we first show the performance of the three-node reservoir with respect to the hyper parameters R and b. The results are shown in Fig. 10 and demonstrate that learning by three-node reservoirs can be successful to some extent. An example of a successful reservoir space with $N=3$ is shown in Fig. 11.

3.4 Phase Space Structure of the Three-Node Reservoir

Taking advantage of the three-dimensionality of the reservoir space, we explore the dynamical structure of the phase space directly by computing fixed points and their properties. Note first that, since the image of the $\tanh$ function is $(-1,1)$, a reservoir phase space restricted to the cube $D :=\left[ -1, 1\right] ^{3}$ is sufficient for three-node reservoirs.

First, we search the fixed points of the three-node reservoir system in Fig. 11, given by (9), namely

$$\begin{aligned} r(t+1) = \tilde{F}(r(t)) = {\overline{\tanh }}(Wr(t)+ {\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)). \end{aligned}$$

Specifically, we used the Python (Scipy) optimization library to search for the zeros of $\tilde{F}({\varvec{x}})-{\varvec{x}}$. For the initial values of the search, we randomly selected 1000 points from D. From the numerical computation we found eight fixed points,

$$\begin{aligned} P^{\pm }_{1}&= \pm (0.99279, 0.12238, 0.03424),\\ P^{\pm }_{2}&= \pm (0.99518, 0.99991, 0.99999),\\ P^{\pm }_{3}&= \pm (0.99878, 0.99966, 0.99998),\\ P^{\pm }_{4}&= \pm (0.99980, 0.99794, 0.99991), \end{aligned}$$

shown in Fig. 12a. Note that, from the expression of $\tilde{F}$, these fixed points are located symmetrically about the origin. The two sets of three fixed points $P^{\pm }_{2}$, $P^{\pm }_{3}$, $P^{\pm }_{4}$ are all very close to the corner points $(\pm 1,\pm 1,\pm 1)$, respectively. See Fig. 12b for a magnified picture. The origin is a trivial fixed point, although it was not detected by the numerical computation, and hence we have nine fixed points in total.

Table 1 shows how many initial points, out of 1000, are attracted to each fixed point by this numerical computation. The number suggests the stability information of the fixed points, namely, the points $P^{\pm }_{2}$ seem stable and others seem unstable. Indeed, the linear stability analysis shows that $P^{\pm }_{2}$ are linearly stable, while all the others are unstable.

Table 1 Number of initial points that are attracted to each fixed point

Figure 13 is a further enlargement of Fig. 12b. The circle is $P^{-}_{2}$, the triangle is $P^{-}_{3}$, and the cross is $P^{-}_{4}$. It can be seen that $P^{-}_{4}$ lies in the middle of the attractor (hereafter referred to as $\Gamma ^{-}$) in the reservoir space).

Fig. 13

Detail near $P^{-}_{2},P^{-}_{3},P^{-}_{4}$ The circle is $P^{-}_{2}$, the triangle $P^{-}_{3}$, the cross $P^{-}_{4}$, while the curve is the attractor $\Gamma ^{-}$ shown in 11b

The unstable manifold of each fixed point $P^{-}_{i} \ (i = 1,\dots ,4)$ can be simply computed numerically as follows: Take 50 initial points $r^{i}_{j}(0) \ (j = 1,\dots ,50)$ randomly from a small cube centered at $P^{-}_{i}$ and let them evolve under $\tilde{F}$ for 12 iterations to obtain a total of 650 points $\left\{ r^{i}_{j}(t) \big | t=0,\dots ,12; j = 1, \dots ,50 \right\}$, that are then plotted. The resulting figure may be an approximation of each unstable manifold, as shown in Fig. 14. It can be considered that $P^{-}_{3}$ correspond to the origin as the unstable fixed point of the logistic map, and $P^{-}_{4}$ is the fixed point corresponding to $1-1/a$. It is observed that the unstable manifold of $P^{-}_3$ is attracted on one side to $\Gamma ^-$ and on the other side to $P^{-}_2$. See Sect. 5.1 for the relation of this structure to the logistic map.

Fig. 14

a–d are unstable manifolds of $\tilde{F}$ for $P^{-}_{1}$, $P^{-}_{2}$, $P^{-}_{3}$, and $P^{-}_{4}$, respectively. In b–d, the points that appear to extend vertically from $P^{-}_{2}$, $P^{-}_{3}$, $P^{-}_{4}$ roughly correspond to the set of initial points, from which the unstable manifolds are numerically obtained. For reference, we also show in each figure the unstable subspace $\mathbb {E}^{u}(P^{-}_{i})$ at $P^{-}_{i}$

3.5 Bifurcation Structure of the Three-Node Reservoir

In this subsection, we study the bifurcation of the reservoir system after learning. Recall that we have two hyper-parameters, $R=\rho (W)$ and $b=|{\varvec{w^{\text {fb}}}}_{i}|$. We study the bifurcation of the three-node reservoir system when one of them is varied. More precisely, consider the following two kinds of perturbed families of the autonomous reservoir (9), after successful learning:

$$\begin{aligned} r(t+1)= & {} {\overline{\tanh }}((1+\mu )Wr(t) + {\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)), \end{aligned}$$

(10)

$$\begin{aligned} r(t+1)= & {} {\overline{\tanh }}(Wr(t) + (1+\nu ){\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)), \end{aligned}$$

(11)

where W, ${\varvec{w^{\text {fb}}}}$, $\mathbf {w^{\text {out}}}$ are all fixed with $R=5.0$, $b=1.5$. The bifurcation parameter is $\mu$ or $\nu$, respectively. Figures 15 and 16 show the corresponding bifurcation diagrams, both of which are remarkably similar to that of the logistic map family shown in Fig. 17. See a further discussion in Sect. 5.

Fig. 15

Bifurcation diagram of (10) parametrized by $\mu$ (spectral radius of the weight matrix of the reservoir)

Fig. 16

Bifurcation diagram of (11) parametrized by $\nu$ (size of the feedback weight)

Fig. 17

Bifurcation diagram of the logistic map family parametrized by a

4 Mechanism for Successful Learning of the Reservoir

Based on the results of reservoir computing for the logistic maps given in Sect. 3, here we present a mathematical mechanism that may explain the successful learning of reservoir computing.

The following is observed for successful learning of reservoir computing of the logistic maps in Sect. 3:

• 1. The reservoir dynamics at the prediction stage, after successful learning, has an attractor in its reservoir phase space, that looks like a smooth curve segment (Figs.7b, 11).

• 2. The reservoir dynamics on the attractor is smoothly conjugate to the logistic map (Fig. 8).

Furthermore, it should be noted that, in the three-node reservoir case, the attractor at the prediction stage lies in a very small region near $(-1,-1,-1)$, one of the corner points of the reservoir phase space $(-1,1)^3$, see Fig. 11.

Fig. 18

Numerical prediction of time series by the degenerate reservoir: a One-step prediction, b Prediction of dynamics

Recall that the learning stage of reservoir computing of the logistic maps is governed by the semi-direct product system

$$\begin{aligned} r(t+1)={\overline{\tanh }}(Wr(t)+{\varvec{w^{\text {fb}}}}x(t)), \quad x(t+1)=ax(t)(1-x(t)), \end{aligned}$$

(12)

where the variable r(t) takes values very close to ${\mathbf{v}}=(-1,-1,-1)$, as observed above (Fig. 11). It may therefore make sense to consider the following “singular limit" of (12):

$$\begin{aligned} r(t+1)={\overline{\tanh }}(W{{\mathbf {v}}}+{\varvec{w^{\text {fb}}}}x(t)), \quad x(t+1)=ax(t)(1-x(t)). \end{aligned}$$

(13)

This is a degenerate reservoir computing system in the sense that the RHS of the first equation of (13) does NOT depend on the reservoir variable r(t). Nevertheless, numerical computation shows that such a degenerate reservoir can learn the logistic dynamics well and predict it successfully, as seen in Figs. 18 and 19.

Fig. 19

Prediction of the logistic map by the degenerate reservoir

As an abstract setting, let us consider a dynamical system $f:M\rightarrow M$ on a phase space M as a target dynamics to be learned, and let a map $F:M\times Y\rightarrow Y$ be the reservoir map at learning. Here, we consider $N=\dim Y\gg \ell =\dim M$. These maps define a semi-direct product system

$$\begin{aligned} {{\mathcal {F}}}=(f,F) : M\times Y \rightarrow M\times Y\ ;\ (x,r)\mapsto (f(x), F(x,r)) \end{aligned}$$

(14)

corresponding to the learning stage of reservoir computing.

In Sect. 3, the map f corresponds to the logistic map, M to $\mathbb {R}$ or the interval [0, 1], and F to the map given by

$$\begin{aligned} F(x, r)={\overline{\tanh }}(Wr+{\varvec{w^{\text {fb}}}}x) \end{aligned}$$

with $Y=\mathbb {R}^N$, where N is the number of neurons in the reservoir.

In the case of the degenerate reservoir system given above, the map F(x, r) loses the dependence on r, and hence it depends only on x, namely, $F_0(x)$. The corresponding semi-direct product system becomes

$$\begin{aligned} {{\mathcal {F}}}_0=(f,F_0) : M\times Y \rightarrow M\times Y\ ;\ (x,r)\mapsto (f(x), F_0(x)). \end{aligned}$$

(15)

In this section, we shall assume the space M to be a compact smooth manifold, Y to also be a smooth manifold, and the maps f, F, $F_0$ to all be smooth on their domain manifolds.

4.1 Learning by the Degenerate Reservoir

First, observe that for any initial point (x(0), r(0)), its image under the degenerate reservoir (15) is

$$\begin{aligned} (x(1),r(1))= {{\mathcal {F}}}_0(x(0),r(0))=(f(x(0)),F_0(x(0))), \end{aligned}$$

which does not depend on r(0) but only on x(0). Hence, for all $t\ge 1$, the point (x(t), r(t)) lies in the subset of $M\times Y$ given by

$$\begin{aligned} \Sigma = \mathrm{Im}({{\mathcal {F}}}_0) = \{(f(x),F_0(x))\mid x\in M\}\subset M\times Y. \end{aligned}$$

Remark 2

As noted above, for any initial point (x(0), r(0)) and for any $t\ge 1$, the point (x(t), r(t)) lies on $\Sigma$, which therefore may be considered as an “attractor" of the degenerate reservoir system (15) at the learning stage.

Let

$$\begin{aligned} \Delta = \mathrm{Graph}(F_0) = \{(x,,F_0(x))\mid x\in M\}\subset M\times Y \end{aligned}$$

be the graph of $F_0$, while its image be given by

$$\begin{aligned} \Gamma = \mathrm{Im}(F_0) = \{F_0(x)\mid x\in M\}\subset Y. \end{aligned}$$

Note that $\Gamma =p(\Delta )=p(\Sigma )$ for the standard projection $p:M\times Y \rightarrow Y$.

In what follows, we assume:

Hypothesis 3

The map $F_0:M\rightarrow Y$ is injective.

This implies that the map $F_0$ is bijective onto its image $\Gamma$, and hence it is a diffeomorphism between M and $\Gamma$. Let $\gamma :\Gamma \rightarrow M$ be its inverse map. Then we have the following:

Theorem 4

Under the above Hypothesis 3, the map ${\tilde{F}}:\Gamma \rightarrow Y$ is defined by

$$\begin{aligned} {{\tilde{F}}}(r)=F_0(f(\gamma (r))). \end{aligned}$$

Then $\Gamma$ is invariant under ${\tilde{F}}$, namely $\tilde{F}(\Gamma )\subset \Gamma$, and the dynamical system ${\tilde{F}}$ on $\Gamma$ is smoothly conjugate to f on M by $\gamma :\Gamma \rightarrow M$.

(Proof)   Since $\Gamma =\mathrm{Im}(F_0)$, its invariance under ${\tilde{F}}$ is trivial. For any $r\in \Gamma$, there is a unique $x\in M$ with $F_0(x)=r$ under the Hypothesis 3. By definition, $\gamma (r)=x$, and hence

$$\begin{aligned} (\gamma \circ {{\tilde{F}}})(r)= \gamma (F_0(f(\gamma (r))))=\gamma (F_0(f(x)))=f(x)=(f\circ \gamma )(r), \end{aligned}$$

which shows the conjugacy $\gamma \circ {{\tilde{F}}}=f\circ \gamma$ on $\Gamma$. (end)

4.2 Relation to the Numerical Computation

For the degenerate reservoir system (13) satisfying the Hypothesis 3, we expect that the results of the numerical computation in Sect. 3 for the reservoir system (12), which can be considered as a (singular) perturbation of (13), may be explained by Theorem 4.

In fact, Fig. 20 shows the numerically obtained attractors of (12) and (13) at the learning stage. Note that the attractor of (13) is explicitly given by $\Sigma$.

Fig. 20

Attractors at the learning stage of (12), colored red and labeled as non-degenerate, and (13), colored black and labeled as degenerate. $N=3$. The plots are projected onto the $(r_1,x)$-plane for visualization purpose

Figure 21 shows the projection of the attractors of (12) and (13) at the learning stage into the reservoir space. For (13), it corresponds to $\Gamma$. Both figures show that the sets $\Sigma$ and $\Gamma$ of the degenerate reservoir (13) at the learning stage are very close to the attractor of (12) at the learning stage and its projection to the reservoir space, as expected from Theorem 4.

Fig. 21

Attractors of (12) and (13) in the reservoir space at the learning stage. $N=3$

Fig. 22

Conjugacy

Moreover, after computing the output vector ${{\mathbf {w}}}^\mathrm{out}$, the numerically computed conjugacy map between the autonomous reservoir system at the prediction stage, namely,

$$\begin{aligned} r(t+1)={\overline{\tanh }}(Wr(t)+{\varvec{w^{\text {fb}}}}\mathbf {w^{\text {out}}}r(t)) \end{aligned}$$

(16)

on its attractor in the reservoir space and the logistic map is shown in Fig. 22, together with the theoretical conjugacy map $\gamma :\Gamma \rightarrow M=[0,1]$ given in Theorem 4, which are also very close. Note that the theoretical output map $\gamma :\Gamma \rightarrow M$ is the inverse of $F_0$ on $\Gamma$, namely $x(t)=\gamma (r(t+1))$ is equivalent to $r(t+1)=F_0(x(t))$, which leads to

$$\begin{aligned} r(t+1)= & {} F_0(\mathbf {w^{\text {out}}}r(t))\approx F_0(x(t))=F_0(f(x(t-1)))\\= & {} F_0(f(\gamma (r(t))))=\tilde{F}(r(t)), \end{aligned}$$

explaining the closeness of the autonomous reservoir dynamics $\tilde{F}$ for (13) and the perturbed reservoir dynamics for (12) at the prediction stage.

These numerical results strongly support that Theorem 4 explains the mechanism of successful learning of reservoir computing, by showing that there exist

• 1. An attractor (corresponding to $\Sigma$ in the case of the degenerate reservoir) of the reservoir computing system at the learning stage that is diffeomorphic to the phase space of the target dynamics,

• 2. An attractor (corresponding to $\Gamma$ in the case of the degenerate reservoir) of the reservoir system at the prediction stage, which is close to the projection into the reservoir space of the attractor at the learning stage,

• 3. A smooth conjugacy (corresponding to $\gamma$ in the case of the degenerate reservoir) between the reservoir system on its attractor at the prediction stage and the target dynamics.

5 Concluding Remarks

5.1 Remarkable Features of Reservoir Computing from the Viewpoint of Machine Learning

In Sect. 3.4, we have seen in Fig. 14 that the reservoir dynamics at the prediction stage carries not only the dynamics on the attractor, which seems smoothly conjugate to the target dynamics of the logistic map, but also an unstable fixed point outside the attractor, from which one side of its one-dimensional unstable manifold is connected to the attractor, while the other side is connected to another stable fixed point away from these two and the attractor. This structure of connecting orbits among attractor and fixed points resembles, in the logistic map, the configuration of its chaotic attractor, an unstable fixed point at the origin, and negative infinity. To be more precise, for the logistic map, the chaotic attractor A is the interval $[a^2(4-a)/16,a/4]\approx [0.256,0.925]$ for $a=3.7$. There are unstable fixed points, one of which is $1-1/a\approx 0.73$, which is in the attractor A, and the other is at the origin O. Any points inside the open interval (0, 1) are attracted to A under iteration, while those outside [0, 1] tend toward $-\infty$. Therefore, one side of the unstable manifold of the unstable fixed point O is connected to A, while the other side is connected to $-\infty$, which is exactly the same connecting orbit structure as in Fig. 14.

Note that the learning of reservoir computing uses only chaotic time series from the logistic map which are supported strictly inside the interval (0, 1). Nevertheless, the reservoir dynamics after successful learning seems to reproduce information about the target dynamics far beyond the region of the phase space covered by the time series used for learning. Therefore, we may say that the reservoir can learn information about the dynamics of the target system that is not covered by the training data. Note that a similar observation is reported by [3] for the Lorenz system.

Similar observation can be made for bifurcation. In Sect. 3.5, we have seen in Figs. 15 and 16 that the bifurcation diagram of the autonomous reservoir system at the prediction stage is very similar to that of the logistic map family in Fig. 17. The reservoir is trained using only the time series data corresponding to the parameter value $a=3.7$ of the logistic mapping family, but once successfully trained, the reservoir system exhibits qualitatively the same bifurcation features such as periodic windows, band splitting, etc. that are not included in the time series data used for learning. Therefore, it can also be said that the reservoir computing can learn information about the bifurcation of the target system that is not included in the training data. Thus, to the best of the authors’ knowledge, it has not yet been reported that reservoir computing can reproduce not only dynamics but also bifurcation features.

We remark that this observation may shed light on the results of reservoir computing that are classified as “failures", as in Figs.4 and 5 in Sect. 2.3. Note that Fig. 4 suggests stable periodic points of period 7, while Fig. 5 shows band splitting, neither of which appear at the parameter value of $a=3.7$ in the logistic map family, but at close parameter values, e.g., $a=3.702$ for the former and around $a=3.67$ for the latter; see Fig. 23. This may indicate that the reservoir sometimes learns not the target dynamics but dynamics close to the target, though we do not yet understand why such confusion may happen.

Fig. 23

Part of the bifurcation diagram of the logistic map family over the parameter range $3.65\le a \le 3.75$

We consider that these observations may be explained by the mathematical mechanism of the successful reservoir computing discussed in Sect. 4; more specifically, the reservoir after successful learning reproduces an attractor in the reservoir phase space that is smoothly conjugate to the original target dynamics.

In the case of the logistic map, the essential feature of the dynamics is the folding of the interval to itself, and therefore, the reservoir system obtained by successful learning of the logistic map also carries such a geometric mechanism of the folding of a one-dimensional curve. A natural extension of the domain of definition of the folding dynamics on the curve will inevitably create an unstable fixed point on (the extension of) the curve that must be outside the attractor of the folding dynamics. Also, a natural deformation of the folding dynamics may be obtained by shifting the image of the curve by folding, which creates a similar bifurcation structure to that of the logistic map family.

Note that, in view of Theorem 4 and related discussion in Sect. 4, such a reproduction mechanism of successful reservoir computing can be expected not only for the logistic map but also for a broader class of dynamics.

We consider that this is an important and remarkable feature of reservoir computing as a machine learning method for dynamics. Firstly, machine learning methods using RNNs, including reservoir computing, are regarded as suitable for learning dynamics, while those using feed-forward neural networks, such as deep learning, are not, simply because RNNs are dynamical systems by themselves. Reservoir computing, compared to other machine learning methods using RNNs, is characterized as a method that optimizes only the output weights while learning. This makes reservoir computing very easy to handle and computationally inexpensive. It also helps to clarify the structure of learning by reservoir computing from a mathematical viewpoint in the sense that it allows separation of the dynamical roles of the RNN and the input/output nodes. As a result, we can view reservoir computing at the learning stage as a semi-direct product dynamical system, and that at the prediction stage as an autonomous dynamical system. This viewpoint is essential for the formulation in Sect. 4 to explain the mechanism of successful learning in reservoir computing. In other words, it may be very difficult to obtain a similar mechanism of successful learning in terms of an attractor in the phase space of an RNN that is smoothly conjugate to the original dynamics to be learned at the stages of learning and prediction.

Therefore, we believe that reservoir computing is unique among machine learning methods in that it can reproduce essentially an exact copy of the target dynamics in its reservoir phase space, and as a result, it can obtain dynamical information, including information beyond the training data.

5.2 Discussion

In this paper, we have discussed learning by reservoir computing from dynamical system viewpoints. Numerical computation suggests that reservoir computing after successful learning reconstructs an attractor on which the reservoir system at the prediction stage is smoothly conjugate to the target dynamics of learning. This can be explained mathematically by Theorem 4 for a degenerate reservoir system which is thought of as a singular limit of the original reservoir system.

Unfortunately, such a view has not been verified for reservoir computing in general, other than the degenerate reservoir in Sect. 4. The degenerate reservoir system is introduced by the observation that the attractor of the reservoir system in Sect. 3 is located within a very tiny region of the reservoir phase space, which may be approximated as a constant vector, but such a situation is not the case in general. The reason for this approximation by a constant vector may be due to the strong contraction of the reservoir system in the direction of the reservoir variable, namely $\left\| \frac{\partial F}{\partial r}(x,r)\right\|$ being very small, which should be closely related to the so-called “echo state property" [1]. It is strongly hoped that there is some other mathematical mechanism, other than the degenerate reservoir, that can explain how successful reservoir computing behaves dynamically for a broader class of reservoir systems.

Another future direction may be to extend the study in this paper to a greater variety of dynamics for learning. In the literature, there have been many dynamical systems studied in relation to reservoir computing, such as the MacKay–Glass equation [1, 2], the Lorenz system [3, 6, 8, 9], the Rössler system [9], the Kuramoto-Shivashinsky equation [6, 9], and others. There are, however, very few results similar to those reported in this paper, and there has been no explicit study of the structure of the reservoir attractor at the prediction stage in relation to the target dynamics, such as the smooth conjugacy. We are continuing to study reservoir computing for other dynamical systems along the lines of this paper and hope to report the results in the near future.