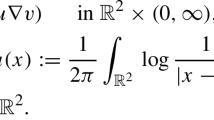Traveling Fronts in a Reaction–Diffusion Equation with a Memory Term

Abstract

Based on a recent work on traveling waves in spatially nonlocal reaction–diffusion equations, we investigate the existence of traveling fronts in reaction–diffusion equations with a memory term. We will explain how such memory terms can arise from reduction of reaction–diffusion systems if the diffusion constants of the other species can be neglected. In particular, we show that two-scale homogenization of spatially periodic systems can induce spatially homogeneous systems with temporal memory. The existence of fronts is proved using comparison principles as well as a reformulation trick involving an auxiliary speed that allows us to transform memory terms into spatially nonlocal terms. Deriving explicit bounds and monotonicity properties of the wave speed of the arising traveling front, we are able to establish the existence of true traveling fronts for the original problem with memory. Our results are supplemented by numerical simulations.

1 Introduction

The study of traveling fronts in scalar reaction–diffusion equations with a bistable nonlinearity is a classical topic and there is a rich literature concerning the existence, uniqueness, and asymptotic stability of such fronts, see e.g. [1, 4, 10, 13] and the references therein. The last three references are actually devoted to scalar, spatially nonlocal, parabolic equations of the form

$$\begin{aligned} {\dot{u}} = L u + F(u) + G\big (u, {{\mathbb {J}}}S(u)\big ), \quad t>0 , \ x\in {{\mathbb {R}}}, \end{aligned}$$

(1.1)

where traveling fronts of the form $u(t,x)= {\mathcal {U}}(x{-}c t) \in {{\mathbb {R}}}$ are investigated. In particular, [10] (which was strongly inspired by [4]) studies the case $Lu=Du_{xx}$, assumes that $G(u,\cdot ):{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ and $S:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ are monotonously increasing and that ${{\mathbb {J}}}$ is a convolution with a smooth, nonnegative kernel $J\ge 0$, i.e. $({{\mathbb {J}}}f)(x)=(J{*}f) (x)=\int _{{\mathbb {R}}}J(x{-}y)f(y)\;\!\mathrm {d}y$. In [27] traveling waves in scalar conservation laws with nonlocal dispersion terms were studied by relying on the result from [4]. The paper [1] considers the case $G\equiv 0$ and $Lu ={\mathrm D}^\alpha _\theta u$, which is a Riesz-Feller operator with $\alpha \in {]1,2]}$ and $|\theta | \le \min \{\alpha ,2{-}\alpha \}$. In all cases, the nonlinearity F is of bistable type such that (1.1) has exactly three homogeneous steady states $u\equiv u_\alpha$ with $\alpha \in \{-,{\mathrm{m}},+\}$, where $u_\pm$ are stable while the middle state $u_{\mathrm{m}}$ is unstable.

In [1, 4, 10] it is shown that, under suitable technical assumptions, Eq. (1.1) admits traveling fronts $u(t,x)={\mathcal {U}}(x{-}c t)$ with ${\mathcal {U}}(\xi )\rightarrow u_\pm$ for $\xi \rightarrow \pm \infty$, and that these solutions are even stable up to translation. The crucial tool for the analysis in these papers are comparison principles involving sub- and supersolutions that are flexible enough to survive nonlocal operators with positive kernels and monotone operators. The only non-monotonicity occurs in the local function $u \mapsto F(u)$.

All the above-mentioned papers treat the case that the nonlocality is in space, such that the equation is local in time. Here we treat a similar type of equation but allow for memory terms (nonlocality in time), namely the equation

$$\begin{aligned} {\dot{u}}(t,x) = D u_{xx}(t,x) + F(u(t,x)) + \int _0^\infty {\widehat{\Gamma }}(\tau ) \, u(t{-}\tau ,x) \;\!\mathrm {d}\tau , \quad t>0 , \ x\in {{\mathbb {R}}}, \end{aligned}$$

(1.2)

with an integrable, nonnegative memory kernel ${\widehat{\Gamma }}$. Note that here the full history $u(\tau ,\cdot )$ with $\tau \in ]-\infty ,0]$ needs to be specified as initial condition in order to solve for the solution $u(t,\cdot )$ with $t>0$. In (1.2) a more general, nonlinear memory kernel of the type $G\big (u, {\widehat{\Gamma }}{*} S( u(\tau ,x))\big )$ could be treated as well (cf. Sect. 3.5), but we avoid this complexity to keep the main arguments simple. Of course, memory terms of this type destroy any kind of comparison principles, so the ideas in [1, 4, 10] cannot be applied directly. Traveling fronts in parabolic equations with discrete time delay are treated in [28], but not including the bistable case considered here.

However, introducing the auxiliary wave speed $\texttt {v}\in {{\mathbb {R}}}$, we look at a corresponding equation with spatial nonlocality, namely

$$\begin{aligned} {\dot{u}}(t,x) = D u_{xx}(t,x) + F(u(t,x)) + \int _0^\infty {\widehat{\Gamma }}(\tau )\, u(t, x{+}\texttt {v}\tau ) \;\!\mathrm {d}\tau , \quad t>0 , \ x\in {{\mathbb {R}}}.\nonumber \\ \end{aligned}$$

(1.3)

According to [1, 4, 10], this nonlocal equation has now traveling fronts if the function $F_\gamma : u \mapsto F(u) + \gamma u$ with $\gamma =\int _0^\infty {\widehat{\Gamma }}(\tau )\;\!\mathrm {d}\tau$ is a bistable nonlinearity and the associated fronts will have a wave speed $\texttt {c}=\texttt {C}(\texttt {v})$. In [4, 27] the (spatial kernel) J is assumed to satisfy $J\in {\mathrm{C}}^1({{\mathbb {R}}})$ with $J'\in {\mathrm{L}}^1({{\mathbb {R}}})$ and the evenness condition $J(-s)=J(s)$. Since we have the leading diffusion term $Du_{xx}$ we can generalize to the case needed for us, namely ${\widehat{\Gamma }}(\tau )=0$ for $\tau <0$ for having causality in (1.2). Otherwise we only need ${\widehat{\Gamma }} \in {\mathrm{C}}^0({[0,\infty [})$, ${\widehat{\Gamma }}(\tau )\ge 0$, and $\int _0^\infty (1{+}\tau ){\widehat{\Gamma }}(\tau )\;\!\mathrm {d}\tau < \infty$, which still matches the assumptions in [10]. In particular, exponential sums as in (1.5) are allowed.

The main observation is now that in the special case $\texttt {v}=\texttt {C}(\texttt {v})$ the traveling wave $u(t,x)={\mathcal {U}}(x{-}\texttt {v}t)$ of (1.3) also solves the original memory equation (1.2), see Proposition 2.1. Hence, existence of traveling fronts for the memory equation (1.2) will be established by providing conditions that guarantee that the function $\texttt {v}\mapsto \texttt {C}(\texttt {v})$ has a fixed point. Indeed, we again use the comparison principles devised in [4, 10] for the spatially nonlocal equation (1.3) to derive continuity of $\texttt {C}$ and certain monotonicities. After providing suitable a priori estimates for the front speeds (see Theorem 2.5), our main result Theorem 2.8 shows that the memory equation (1.2) has always a traveling front if $F_\gamma : u \mapsto F(u) + \gamma u$ is a bistable nonlinearity. Unfortunately, we are not able to transfer the asymptotic stability result of [10, Thm. 5.1] to the traveling fronts in the memory equation (1.2). In Corollary 2.10 we provide bounds on the associated wave speed in terms of the wave speed of the local equation with nonlinearity $F_\gamma$.

In Sect. 3 we discuss several derivations of the memory equation from classical reaction–diffusion systems. In all cases, the memory appears by a coupling to ODEs or PDEs acting locally in $x \in {{\mathbb {R}}}$ but induce memory through its internal dynamics. The simplest case occurs in the coupled PDE-ODE system considered extensively in [17]:

$$\begin{aligned} {\dot{u}} = Du_{xx} + F(u) + \sum _{i=1}^{n_{\mathrm{m}}} a_i w_i, \qquad \dot{w}_i = - \lambda _i w_i + b_i u \ \text { for }i=1,\ldots ,n_{\mathrm{m}}, \end{aligned}$$

(1.4)

where $a_i, \ b_i$, and $\lambda _i$ are fixed real parameters with $\lambda _i>0$. Clearly, the linear ODEs can be solved by $w_i(t)=\int _0^\infty \mathrm {e}^{-\lambda _i \tau } b_i u(t{-}\tau )\;\!\mathrm {d}\tau$, and we obtain (1.2) with

$$\begin{aligned} {\widehat{\Gamma }}(\tau )= \sum _{i=1}^{n_{\mathrm{m}}} \mathrm {e}^{-\lambda _i \tau } a_i b_i, \quad \text { giving }\gamma =\int _0^\infty \!{\widehat{\Gamma }}(\tau )\;\!\mathrm {d}\tau = \sum _{i=1}^{n_{\mathrm{m}}} \frac{a_ib_i}{\lambda _i} . \end{aligned}$$

(1.5)

For the details about the connection between (1.4) and (1.2) we refer to Sect. 3.1.

We emphasize that our theory is applicable also in cases where some of the products $a_ib_i$ are negative, as long as ${\widehat{\Gamma }}$ is nonnegative. We also discuss possible nonlinear couplings that still allow for the application of [10].

A second motivation for deriving memory equations is the study of traveling pulses and fronts in situations where the coefficients in the system are rapidly oscillating, thus modeling a periodic heterogeneous medium on a microscopic scale. In the following, the homogenization parameter $\varepsilon >0$ denotes the ratio between the characteristic length scales of the microscopic and macroscopic structure. A typical system considered in Sect. 3.2 is the heterogeneous FitzHugh-Nagumo system

$$\begin{aligned} \begin{aligned} {\dot{u}}&=\big ( {{\mathbb {D}}}_{\mathrm u}(\tfrac{1}{\varepsilon }x) u_x\big )_x + F(\tfrac{1}{\varepsilon }x, u) + \alpha \big (\tfrac{1}{\varepsilon }x \big ) w, \\ \dot{w}&= \big ( \varepsilon ^2 {{\mathbb {D}}}_{\mathrm w}(\tfrac{1}{\varepsilon }x) w_x\big )_x - {\widehat{\lambda }} \big (\tfrac{1}{\varepsilon }x \big )w + \beta \big (\tfrac{1}{\varepsilon }x \big ) u, \end{aligned} \end{aligned}$$

(1.6)

where all dependence on $\tfrac{1}{\varepsilon }x$ is assumed to be 1-periodic. Of course, exact traveling waves cannot exist, but one still expects periodically modulated pulses and fronts traveling through the heterogeneous medium. Indeed, there exists a vast literature on the study of traveling fronts for reaction–diffusion equations in continuous periodic media, e.g. [3, 19], fronts in discrete periodic media [9, 16], and fronts in perforated domains [18]. We refer to [29] for a review including references to earlier works. Most of the latter results share a common approach based on comparison principles, and so do we. However, our approach also allows for systems of reaction–diffusion equations.

In [23] reaction–diffusion systems are studied and exponential averaging is used to show that traveling wave solutions can be described by a spatially homogeneous equation and exponentially small remainders. The approach based on center-manifold reduction in [6] applies to traveling waves in parabolic equations and, moreover, the authors prove the existence of a generalized oscillating wave that converges to a limiting wave. We point out that all previously mentioned articles study limit problems of “one-scale” nature, in contrast to [17] and the present work where traveling pulses in “two-scale FitzHugh–Nagumo systems” are investigated, see Sect. 3.3. According to Theorem 3.1, the solutions $(u_\varepsilon ,w_\varepsilon )$ of (1.6) converge to the solution (U, W) of the two-scale system

$$\begin{aligned} \begin{aligned} {\dot{U}}(t,x)&= D_{\mathrm u}^\text {eff} \,U_{xx}(t,x) + \int _{{\mathbb {T}}}F(y, U(t,x))\;\!\mathrm {d}y + \int _{{\mathbb {T}}}\alpha (y) W(t,x,y) \;\!\mathrm {d}y, \\ \dot{W}(t,x,y)&= \big ( {{\mathbb {D}}}_{\mathrm w}(y) W_y(t,x,y)\big )_y - {\widehat{\lambda }} (y)W(t,x,y) + \beta (y) U(t,x), \end{aligned} \end{aligned}$$

(1.7)

where the microscopic variable y lies in the circle ${{\mathbb {T}}}={{\mathbb {R}}}_{\!/{{\mathbb {Z}}}}$. The importance of the two-scale system (1.7) is that the microscopic variable y decouples from the macroscopic space variable x such that this system admits exact traveling waves of the form $(U(x{-}ct),W(x{-}ct,y))$. Moreover, the coupling from U to W and its feedback are local in $x\in {{\mathbb {R}}}$ and hence can be captured in spatially local memory terms as in (1.3).

The paper is structured as follows. In Sect. 2 we develop our existence result for traveling fronts for the memory equation (1.2), see Theorem 2.8 which relies on the comparison principle in the spirit of [1, 4, 10] and on new a priori bounds for the front speed c in Theorem 2.5. In Sect. 3 we first present the derivation of memory equations from coupled, but homogeneous systems, and secondly we show that two-scale homogenization can be used to derive effective two-scale limits, which again lead to the same memory equation. Finally, Sect. 4 compares the abstract theory with numerical results in the special case that F is the classical bistable cubic polynomial $-u(u{-}a)(u{-}1)$ with $a\in {]0,1[}$ and the memory kernel is simply given by ${\widehat{\Gamma }}(\tau )=\gamma \,\mathrm {e}^{-\tau }$ with $\gamma =-\beta >0$.

2 Existence of Traveling Fronts

We first describe the setup and the assumptions for our theory in Sect. 2.1. In Sect. 2.2 we introduce the spatially nonlocal equation with the auxiliary speed $\texttt {v}$ and show that for traveling fronts these equations are related. The main technical part are Sects. 2.3 and 2.4 where we exploit the comparison principles developed in [4, 10]. The main results are presented in Sect. 2.5, where we also discuss potential generalizations.

2.1 Setup of the Memory Equation and Assumptions

In all of Sect. 2 we study the Nagumo-type reaction–diffusion equation (cf. [20, 24]) with linear memory term in the form

$$\begin{aligned} {\dot{u}}(t,x) = D u_{xx}(t,x) + F(u(t,x)) + \gamma \int _0^\infty \Gamma (\tau ) u(t{-}\tau ,x) \;\!\mathrm {d}\tau . \end{aligned}$$

(2.1)

Here, the nonnegative memory kernel $\Gamma$ is normalized, and hence satisfies

$$\begin{aligned} \Gamma \in {\mathrm{C}}^0({[0,\infty [}), \quad \Gamma (\tau )\ge 0 \text { for all }\tau \ge 0, \quad \int _0^\infty \Gamma (\tau )\;\!\mathrm {d}\tau =1. \end{aligned}$$

(2.2)

To formulate the precise conditions on the bistable nonlinearity F we introduce the tilted function

$$\begin{aligned} F_\gamma (u)= F(u)+ \gamma u \quad \text {for } u\in {{\mathbb {R}}}. \end{aligned}$$

Hypotheses (H)

(H1):

We have $F\in {\mathrm{C}}^2({{\mathbb {R}}})$ and there exists $\gamma _*>0$ such that for all $\gamma \in [0,\gamma _*]$ the function $F_\gamma$ has exactly three zeros, which we assume to be $u_-^\gamma< u_{\mathrm{m}}^\gamma < u_+^\gamma$ and which satisfy $F_\gamma '(u_-^\gamma )<0$, $F'(u^\gamma _{\mathrm{m}})>0$, and $F_\gamma '(u^\gamma _+)< 0$.

(H2):

The memory kernel $\Gamma$ satisfies (2.2) and $\widehat{g}_1:=\int _0^\infty \Gamma (\tau )\tau \;\!\mathrm {d}\tau <\infty$.

The assumptions imply that the three constant functions $u(t,x)= u^\gamma _\alpha$ with $\alpha \in \{-,{\mathrm{m}},+\}$ are indeed trivial solutions for (2.1). The solutions $u_\pm ^\gamma$ will be stable, while the middle solution $u^\gamma _{\mathrm{m}}$ is unstable. Our aim is to show the existence of nontrivial traveling fronts $u(t,x)={\mathcal {U}}(x{-}c t)$ connecting the two stable levels $u^\gamma _\pm$, namely ${\mathcal {U}}(\xi )\rightarrow u^\gamma _\pm$ for $\xi \rightarrow \pm \infty$. Of course, then also a reflected traveling front $u(t,x) = {\mathcal {U}}^\text {refl} (x{-}c^\text {refl}t)$ exists satisfying ${\mathcal {U}}^\text {refl}(\xi )\rightarrow u^\gamma _\mp$ for $\xi \rightarrow \pm \infty$. Indeed, using the reflection symmetry $x \rightarrow -x$ of (2.1) gives ${\mathcal {U}}^\text {refl}(\xi ) ={\mathcal {U}}({-}\xi )$ and $c^\text {refl}= - c$.

2.2 Traveling Waves for the Auxiliary Equation

The works in [1, 4, 10] allow for nonlocal terms in the reaction–diffusion equation, but only for spatial nonlocality and not for temporal one. However, for traveling waves space and time coincide up to a scaling, so we look at an auxiliary problem, where we choose a corresponding spatial nonlocality. For this we have to choose an auxiliary wave speed $\texttt {v}$ and arrive at the auxiliary problem with spatial nonlocality:

$$\begin{aligned} \dot{{\widetilde{u}}}(t,x) = D {\widetilde{u}}_{xx}(t,x) + F({\widetilde{u}}(t,x)) + \gamma \int _0^\infty \! \Gamma (\tau ) \, {\widetilde{u}}(t,x{+} \texttt {v}\tau ) \;\!\mathrm {d}\tau . \end{aligned}$$

(2.3)

The basis of our theory is the following simple proposition that connects the existence of traveling waves for the original problem with that of the auxiliary one.

Proposition 2.1

If (2.3) has a bounded traveling-wave solution ${\widetilde{u}}(t,x)={\mathcal {U}}( x{-}\texttt {c}t)$ and the wave speed $\texttt {c}$ matches the auxiliary speed $\texttt {v}$ occurring as a parameter in (2.3), then $u(t,x)= {\mathcal {U}}( x{-}\texttt {v}t)$ is also a solution of (2.1).

Proof

Obviously, the partial derivatives and the local function F(u) in (2.3) and (2.1) coincide, so it remains to match the integral terms. The straightforward calculation

$$\begin{aligned} \int _0^\infty \!\Gamma (\tau )\, {\widetilde{u}}(t,x{+}\texttt {v}\tau ) \;\!\mathrm {d}\tau&= \int _0^\infty \!\Gamma (\tau )\, {\mathcal {U}}(x{+}\texttt {v}\tau -\texttt {c}t ) \;\!\mathrm {d}\tau \\&\overset{\texttt {v}=\texttt {c}}{=} \int _0^\infty \! \Gamma (\tau ) \, {\mathcal {U}} (x - \texttt {v}(t{-}\tau )) \;\!\mathrm {d}\tau = \int _0^\infty \! \Gamma (\tau ) \,u(t{-}\tau ,x) \;\!\mathrm {d}\tau , \end{aligned}$$

relying strongly on $\texttt {c}= \texttt {v}$, turns the spatial nonlocality into a temporal memory. This gives the desired result. $\square$

The above result does not specify the form of the traveling wave, hence it is applicable to traveling pulses, traveling fronts, or to (quasi-)periodic wave trains.

2.3 Comparison Principles for the Auxiliary Equation

We are now in a position to apply the general theory for nonlocal parabolic equations as developed in [1, 10] to our auxiliary problem (2.3) for $\gamma \in [0,\gamma _*]$. For this, we define the nonlinear operator $u\mapsto {\mathcal {A}}_{\gamma ,\texttt {v}}[u]$ via

$$\begin{aligned} {\mathcal {A}}_{\gamma ,\texttt {v}}[u](x)&:= D u_{xx}(x) + F(u(x)) + \gamma \int _0^\infty \! \Gamma (\tau ) \, u(x{+} \texttt {v}\tau ) \;\!\mathrm {d}\tau \end{aligned}$$

(2.4)

in the notation of [10]. We first observe the relation ${\mathcal {A}}_{\gamma ,\texttt {v}}[\lambda {\varvec{1}}] = F_\gamma (\lambda ){\varvec{1}}$ for all $\lambda \in {{\mathbb {R}}}$, where ${\varvec{1}}$ denotes the constant function $u(x) = 1$. Moreover, the Fréchet derivative reads

$$\begin{aligned} \big ({\mathcal {A}}'_{\gamma ,\texttt {v}}[u](\varphi )\big )(x) = D \varphi _{xx}(x) +F'(u(x))\varphi (x) + \gamma \int _0^\infty \!\Gamma (\tau ) \, \varphi (x{+} \texttt {v}\tau ) \;\!\mathrm {d}\tau . \end{aligned}$$

Hence, we obtain $\big ({\mathcal {A}}'_{\gamma ,\texttt {v}}[u{+}v]({\varvec{1}})\big )(x) - \big ({\mathcal {A}}'_{\gamma ,\texttt {v}}[u]({\varvec{1}})\big )(x) = F'(u(x){+}v(x))- F'(u(x))$. With this and the assumption $F\in {\mathrm{C}}^2({{\mathbb {R}}})$ from (H1), the two assumptions (A1) and (A3) in [10, Sect. 2] are satisfied.

The crucial and nontrivial assumption (A2) in [10] concerns the strong comparison principle and is the content of part (I) of the following proposition. As the existence result for traveling fronts relies on the even stronger, quantitative version (C2) in [10] we add this version in part (II). To formulate it we introduce the notion of super- and subsolutions for (2.3): We call $u^*$ a supersolution and $u_*$ a subsolution if the relations ${\dot{u}}^* - {\mathcal {A}}_{\gamma ,\texttt {v}}[u^*]\ge 0$ and ${\dot{u}}_* -{\mathcal {A}}_{\gamma ,\texttt {v}}[u_*]\le 0$ hold for all $(t,x)\in {]0,\infty [}{\times }{{\mathbb {R}}}$, respectively.

Proposition 2.2

(Strong comparison principles) Let the Hypotheses (H1)–(H2) and $\gamma \in [0,\gamma _*]$ hold.

• (I) If $u^*$ is a bounded supersolution and $u_*$ is a bounded subsolution of (2.3) such that $u^*(0, \cdot ) \ge u_*(0, \cdot )$ and $u^*(0, \cdot ){-} u_*(0, \cdot ) \not \equiv 0$, then we have $u^*(t, \cdot ) \gneqq u_*(t, \cdot )$ for all $t> 0$.

• (II) There exists a positive continuous function $\eta :{]0,\infty [}{\times }{[0,\infty [} \rightarrow {]0,\infty [}$ such that for all $u_*$ and $u^*$ as in (I) we have the quantitative maximum principle as follows:

  $$\begin{aligned} u^*(t,x)-u_*(t,x)\ge \eta (t,|x|) \int _0^1 \! \big (u^*(0,y){-}u_*(0,y)\big ) \;\!\mathrm {d}y \quad \text {for all }(t,x)\in {]0,\infty [}{\times }{[0,\infty [}. \end{aligned}$$

Proof

We follow some ideas in the proof of [10, Thm. 5.1] for establishing condition (C2). By assumption the difference $w(t,x) := u^*(t,x) - u_*(t,x)$ satisfies $w(0,\cdot ) \ge 0$ and

$$\begin{aligned} {\dot{w}} \ge D w_{xx} + F(u^*) - F(u_*) + {{\mathbb {J}}}w \quad \text {with}\quad ({{\mathbb {J}}}w)(t,x) := \gamma \int _0^\infty \!\Gamma (\tau ) w(t,x{+}\texttt {v}\tau ) \;\!\mathrm {d}\tau . \end{aligned}$$

Step 1 We show by contradiction that the inequality $\dot{{\widetilde{w}}} \ge D {\widetilde{w}}_{xx} + {{\mathbb {J}}}{\widetilde{w}}$ implies ${\widetilde{w}} \ge 0$. For this, we set $K := 4\gamma _* {+}4D$ with $\gamma _*$ from (H1). By assuming ${\widetilde{w}}\ngeq 0$, there exist $\delta >0$ and $T>0$ such that ${\widetilde{w}}(t,x) > - \delta \mathrm {e}^{Kt}$ for $t\in [0,T [$ and $\inf _{x\in {{\mathbb {R}}}} {\widetilde{w}}(T,x) = -\delta \mathrm {e}^{KT}$. Without loss of generality, we may assume ${\widetilde{w}}(T,0) < -\frac{3}{4} \delta \mathrm {e}^{KT}$.

Next we define the comparison function $\varphi _\sigma (t,x) := -(\frac{1}{2}+ \sigma z(x))\, \delta \mathrm {e}^{Kt}$ with $z(x)=\frac{1+3x^2}{1+x^2}$, where the parameter $\sigma > 0$ will be fixed later. On the one hand, using $z\ge 1$ we have, for $\sigma \ge \frac{1}{2}$, the estimate

$$\begin{aligned} \textstyle \varphi _\sigma (t,x) \le -\big (\frac{1}{2} + \frac{1}{2}\,1\big ) \, \delta \,\mathrm {e}^{Kt} = -\delta \mathrm {e}^{Kt} \le {\widetilde{w}}(t,x) \end{aligned}$$

for all $t \in [0,T]$ and $x\in {{\mathbb {R}}}$. On the other hand, using $z(0)=1$ for $\sigma = 1/4$ we find

$$\begin{aligned} \textstyle \varphi _{1/4}(T,0) =-\big (\frac{1}{2} + \frac{1}{4} 1\big ) \, \delta \,\mathrm {e}^{KT} = -\frac{3}{4} \delta \mathrm {e}^{KT} > {\widetilde{w}}(T,0) . \end{aligned}$$

We define $\sigma _*$ as follows:

$$\begin{aligned} \sigma _*:=\inf \Sigma \quad \text {with } \Sigma := \big \{\, \sigma >0 \, \big | \, \forall \, (t,x)\in [0,T]{\times }{{\mathbb {R}}}:\ \varphi _\sigma (t,x) \le {\widetilde{w}}(t,x) \,\big \} \end{aligned}$$

and observe that the above estimates imply $\sigma _*\in {]\frac{1}{4},\frac{1}{2}]}$. By continuity, we see that $\Sigma$ is closed, hence $\sigma _*\in \Sigma$, which implies $\sigma _*>\frac{1}{4}$. Using $z(x)> 2$ for $|x|> 1$, for all $\sigma \ge \frac{1}{4}$ we have $\varphi _\sigma (t,x) < -(\frac{1}{2}+\frac{1}{4} 2) \delta \mathrm {e}^{K t}\le {\widetilde{w}}(t,x)$. Hence, for $\sigma \in {[\frac{1}{4},\sigma _*[} \subset {{\mathbb {R}}}\setminus \Sigma$ there exists $(t_\sigma , x_\sigma ) \in [0,T] {\times }[-1,1]$ such that $\varphi _\sigma (t_\sigma , x_\sigma ) \ge {\widetilde{w}}(t_\sigma , x_\sigma )$.

By the continuity of w and $(\sigma ,t,x)\mapsto \varphi _\sigma (t,x)$ and by compactness of $[0,T] {\times }[-1,1]$, we hence find $(t_*,x_*) \in [0,T] {\times }[-1,1]$ such that $\varphi _{\sigma _*}(t_*,x_*) \ge {\widetilde{w}}(t_*,x_*)$. Obviously, we have $t_*>0$, but $t=T$ may be possible. However $\sigma _*\in \Sigma$ means $\varphi _{\sigma _*}(t,x) \le {\widetilde{w}}(t,x)$ for all $(t,x)\in [0,T]{\times }{{\mathbb {R}}}$. Thus, we conclude ${\widetilde{w}}(t_*,x_*)= \varphi _{\sigma _*}(t_*,x_*)$, ${\widetilde{w}}_x(t_*,x_*)= \partial _x\varphi _{\sigma _*}(t_*,x_*)$,

$$\begin{aligned} {\widetilde{w}}_{xx}(t_*,x_*) \ge \partial ^2_x\varphi _{\sigma _*}(t_*,x_*), \quad \text {and } \left\{ \begin{array}{cl}\dot{{\widetilde{w}}}(t_*,x_*)= {\dot{\varphi }}_{\sigma _*}(t_*,x_*) &{}\text {for }t_*\in {]0,T[}, \\ \dot{{\widetilde{w}}}(t_*,x_*)\le {\dot{\varphi }}_{\sigma _*}(t_*,x_*) &{}\text {for }t_*= T. \end{array}\right. \end{aligned}$$

Using (H2) (nonnegativity of $\Gamma$) and $\gamma \in [0,\gamma _*]$ together with the inequalities (i) $\frac{3}{4} \le \frac{1}{2}+ \sigma _*z(x_*)$ and (ii) $\frac{1}{2}+\sigma _* z(x)\le 2$ for all $x \in {{\mathbb {R}}}$, the following chain of inequalities for the particular point $(t_*,x_*)$ holds:

$$\begin{aligned} -\tfrac{3}{4} \delta K\mathrm {e}^{Kt_*}&\overset{\text {(i)}}{\ge }-\big (\tfrac{1}{2} + \sigma _* z(x_*)\big ) \delta K \mathrm {e}^{Kt_*} = \dot{\varphi }_{\sigma _*}(t_*,x_*) \\&\ge \dot{{\widetilde{w}}}(t_*,x_*) \ge D {\widetilde{w}}_{xx}(t_*,x_*) + \big ({{\mathbb {J}}}{\widetilde{w}}\big )(t_*,x_*) \\&\!\!\! \overset{w\ge \varphi _{\sigma _*}}{\ge }D \partial _x^2\varphi _{\sigma _*}(t_*,x_*) + \textstyle \gamma \int _0^\infty \!\Gamma (\tau ) \, \varphi _{\sigma _*} (t_*,x_*{+}\texttt {v}\tau ) \;\!\mathrm {d}\tau \\&\overset{\text {(ii)}}{\ge }-D \sigma _* z''(x_*)\delta \mathrm {e}^{Kt_*} -2 \gamma \delta \mathrm {e}^{Kt_*} \ge -\big ( 2D+2\gamma _*)\delta \mathrm {e}^{Kt_*} = - \tfrac{1}{2} \delta K \mathrm {e}^{Kt_*}, \end{aligned}$$

where we used $z''(x)\le 4$ and $\sigma _*\le \frac{1}{2}$ and the definition of $K= 4\gamma _*{+}4D$. Thus, we have reached a contradiction and the assertion ${\widetilde{w}} \ge 0$ is proven.

Step 2 By assumption $u_*(t,x)$ and $u^*(t,x)$ are bounded and hence attain values in the bounded interval $[-\texttt {C}_\mathrm {max}, \texttt {C}_\mathrm {max}]$ for some constant $\texttt {C}_\mathrm {max}$. Therefore, we have $F(u^*) - F(u_*) \ge - K_0 w$ with $K_0 := \min _{|u|\le \texttt {C}_\mathrm {max}}|F'(u)| >0$ and conclude

$$\begin{aligned} {\dot{w}} \ge D w_{xx} + F(u^*) - F(u_*) + {{\mathbb {J}}}w \ge D w_{xx} - K_0 w + {{\mathbb {J}}}w . \end{aligned}$$

Defining the function ${\widetilde{w}}(t,x)= \mathrm {e}^{K_0t} w(t,x)$ and using ${{\mathbb {J}}}{\widetilde{w}} = \mathrm {e}^{K_0t} {{\mathbb {J}}}w$ we find $\dot{{\widetilde{w}}} \ge D {\widetilde{w}}_{xx} + {{\mathbb {J}}}{\widetilde{w}}$. Thus, Step 1 implies $w(t,x)= \mathrm {e}^{-K_0t}{\widetilde{w}}(t,x)\ge 0$, which is the weak comparison principle.

Finally, we use that $w(0,\cdot )$ is nonnegative and not identical to 0. Hence, the solution $\psi$ of the linear equation ${\dot{\psi }}=D\psi _{xx} - K_0 \psi$ with $\psi (0,x)=w(0,x)$ is strictly positive, as it is given by $\psi (t,\cdot ) = \mathrm {e}^{-K_0t} H_D(t){*}w(0,\cdot )$, where $H_D(t)$ is the strictly positive heat kernel. We now set $W=\mathrm {e}^{K_0t} (w{-}\psi )$ and obtain $W(0,\cdot )\equiv 0$ and

$$\begin{aligned} \dot{W} =\mathrm {e}^{K_0t}\big (\dot{w} + K_0 w -{\dot{\psi }}- K_0\psi \big ) \ge \mathrm {e}^{K_0t}\big ( Dw_{xx} + {{\mathbb {J}}}w - D\psi _{xx}\big ) \ge D W_{xx}, \end{aligned}$$

where we used ${{\mathbb {J}}}w\ge 0$ because of $w\ge 0$ from above and $\Gamma \ge 0$ from (H2). As in Step 1 (with ${{\mathbb {J}}}=0$) we obtain $W\ge 0$ and conclude

$$\begin{aligned} u^*(t,x) - u_*(t,x)=w(t,x) \ge \psi (t,x)>0 \quad \text {for all } t>0 \text { and }x\in {{\mathbb {R}}}. \end{aligned}$$

This is the desired strong comparison principle (I).

Step 3 To obtain the quantitative strong maximum principle, we simple estimate the function $\psi$ introduced at the end of the previous step. From ${\dot{\psi }}= D \psi _{xx} - K_0\psi$ and $\psi (0,x)=w(0,x)$ we obtain, for all $t>0$ and $x \in {{\mathbb {R}}}$,

$$\begin{aligned} \psi (t,x)&=\mathrm {e}^{-K_0 t} \int _{{\mathbb {R}}}H_D(t,x{-}y)\psi (0,y)\;\!\mathrm {d}y \ge \mathrm {e}^{-K_0 t} \int _0^1 H_D(t,x{-}y)\psi (0,y)\;\!\mathrm {d}y \\&\ge \mathrm {e}^{-K_0 t} \min \big \{\, H_D(t,z) \, \big | \, z\in [x{-}1,x] \,\big \} \int _0^1 w(0,y)\;\!\mathrm {d}y. \end{aligned}$$

With this and $u^*-u_*=w\ge \psi$ we easily obtain

$$\begin{aligned} u^*(t,x)-u_*(t,x)\ge \psi (t,x) \ge \eta (t,|x|) \int _0^1\big ( u^*(0,y){-}u_*(0,y)\big ) \;\!\mathrm {d}y \end{aligned}$$

with $\eta (t,|x|)=\mathrm {e}^{-K_0 t} \frac{1}{(4\pi Dt)^{1/2}} \mathrm {e}^{-(|x|+1)^2/(4Dt)}>0$. Hence, part (II) is established. $\square$

As an important technical tool we obtain the following simple result concerning the speed of traveling fronts.

Proposition 2.3

(Comparison of speeds) Assume that the auxiliary equation (2.3) has a monotone traveling front $u(t,x)={\mathcal {U}}(x{-}ct)$. If there is a monotone traveling-front subsolution $v_*(t,x)=V_*(x{-}c_*t)$ satisfying

$$\begin{aligned} \lim _{\xi \rightarrow -\infty } V_*(\xi )< \lim _{\xi \rightarrow -\infty } {\mathcal {U}}(\xi )< \lim _{\xi \rightarrow +\infty } V_*(\xi ) < \lim _{\xi \rightarrow +\infty } {\mathcal {U}}(\xi ), \end{aligned}$$

(2.5a)

then we have $c\le c_*$. If there is a monotone traveling-front supersolution $v^*(t,x)=V^*(x{-}c^*t)$ satisfying

$$\begin{aligned} \lim _{\xi \rightarrow -\infty } {\mathcal {U}}(\xi )< \lim _{\xi \rightarrow -\infty } V^*(\xi )< \lim _{\xi \rightarrow +\infty } {\mathcal {U}}(\xi ) <\lim _{\xi \rightarrow +\infty } V^*(\xi ), \end{aligned}$$

(2.5b)

then we have $c\ge c^*$.

Proof

It suffices to show the result for the subsolution, since the proof for the supersolutions is analogous.

As the limits of $V_*$ and ${\mathcal {U}}$ at $\xi =\pm \infty$ are strictly ordered, we can shift $V_*$ to the right to make it smaller for $t=0$. More precisely, by (2.5a) we find $R>0$ such that $V_*(\xi ) < {\mathcal {U}}({-}\infty ):= \lim _{\xi \rightarrow -\infty } {\mathcal {U}}(\xi )$ for all $\xi \le -R$ and ${\mathcal {U}}(\xi ) > V_*(\infty )$ for $\xi \ge R$. With this and the monotonicities we obtain $V_*(\xi {-}2R)\le V_*(\infty )< {\mathcal {U}}(\xi )$ for all $\xi \ge R$, and for $\xi \le R$ we have $\xi {-}2R\le -R$ and find $V_*(\xi {-}2R)< {\mathcal {U}}({-}\infty )\le {\mathcal {U}}(\xi )$.

With this, we set $u^*(t,x)={\mathcal {U}}(x{-}ct)$ and $u_*(t,x)=V_* (x{-}2R{-}c_*t)$ and find $u^*(0,x) = {\mathcal {U}}(x) > V_* (x{-}2R) =u_*(0,x)$. The comparison principle in Proposition 2.2 now implies

$$\begin{aligned} u^*(t,x)={\mathcal {U}}(x{-}ct)> V_*(x{-}\xi {-} c_*t)=u_*(t,x) \quad \text { for all } t\ge 0 \text { and }x\in {{\mathbb {R}}}. \end{aligned}$$

(2.6)

Now we assume $c> c_*$, insert $x= \frac{1}{2}(c{+}c_*)t$ into (2.6), and take the limit $t\rightarrow \infty$. This leads to $\lim _{\xi \rightarrow -\infty } {\mathcal {U}}(\xi ) \ge \lim _{\xi \rightarrow +\infty } V_*(\xi )$, which contradicts the middle assumption in (2.5a). Hence the assumption $c>c_*$ is false and $c\le c_*$ is established. $\square$

2.4 Existence of Traveling Fronts for the Auxiliary Equation

We are now in the position to formulate our result concerning the existence of traveling fronts in the auxiliary equation (2.3). The proof will be a direct application of the corresponding result [10, Thm. 5.1] for spatially nonlocal equations. We obtain a two-parameter family ${\mathcal {U}}_{\gamma ,\texttt {v}}$ of traveling fronts depending on the auxiliary speed $\texttt {v}\in {{\mathbb {R}}}$ and the strength $\gamma \in [0,\gamma _*]$ of the nonlocal term.

Proposition 2.4

Let the Hypotheses (H1) and (H2) hold and let $\gamma \in [0,\gamma _*]$. Then, for all $\texttt {v}\in {{\mathbb {R}}}$ there exists a unique (up to translation) traveling-front solution

$$\begin{aligned} \widetilde{u}(t,x) ={\mathcal {U}}_{\gamma ,\texttt {v}}\big (x{-} \texttt {c}t\big )\text { solving} (2.3) \text { with wave speed } \texttt {c}= \texttt {C}(\gamma ,\texttt {v}), \end{aligned}$$

which is characterized by (where $\xi = x{-} \texttt {c}t$)

$$\begin{aligned}&{-} \texttt {c}\,{\mathcal {U}}'_{\gamma ,\texttt {v}}(\xi ) = D\,{\mathcal {U}}''_{\gamma ,\texttt {v}}(\xi ) + F({\mathcal {U}}_{\gamma ,\texttt {v}}(\xi )) + \gamma \int _0^\infty \Gamma (\tau ) \, {\mathcal {U}}_{\gamma ,\texttt {v}}(\xi {+}\texttt {v}\tau ) \;\!\mathrm {d}\tau , \end{aligned}$$

(2.7a)

$$\begin{aligned}&{\mathcal {U}}_{\gamma ,\texttt {v}}(\xi )\rightarrow u_-^\gamma \ \text { for }\xi \rightarrow -\infty \quad \text { and } \quad {\mathcal {U}}_{\gamma ,\texttt {v}}(\xi )\rightarrow u^\gamma _+ \ \text { for }\xi \rightarrow +\infty . \end{aligned}$$

(2.7b)

These traveling fronts satisfy the properties

$$\begin{aligned} {\mathcal {U}}_{\gamma ,\texttt {v}} \in {\mathrm{C}}^2({{\mathbb {R}}}), \quad {\mathcal {U}}_{\gamma ,\texttt {v}}'(\xi ) > 0 \text { on } {{\mathbb {R}}}, \quad {\mathcal {U}}'_{\gamma ,\texttt {v}}(\xi ) \rightarrow 0 \text { as } |\xi |\rightarrow \infty . \end{aligned}$$

(2.8)

Moreover, they are globally asymptotically stable in the following sense: There exists $\kappa > 0$ such that for all solutions u of (2.3) satisfying

$$\begin{aligned} \forall \, x\in {{\mathbb {R}}}: u_-^\gamma \le u(0,x) \le u^\gamma _+ , \qquad \liminf _{x\rightarrow +\infty } u(0,x) > u^\gamma _{\mathrm{m}}, \quad \limsup _{x\rightarrow -\infty } u(0,x) < u^\gamma _{\mathrm{m}}, \end{aligned}$$

(2.9)

there exist constants $\xi$ and K (depending on $u(0,\cdot )$) such that

$$\begin{aligned} \Vert u(t,\cdot ) - {\mathcal {U}}_{\gamma ,\texttt {v}}(\,\cdot \, {-} \texttt {c}t {+} \xi ) \Vert _{\mathrm{L^\infty ({{\mathbb {R}}})}} \le Ke^{-\kappa t} \quad \text {for } t\ge 0 . \end{aligned}$$

(2.10)

Proof

For the evolution equation ${\dot{u}} = Du_{xx} + G(u,J{*}S(u))$ in [10, Eqn. (5.1)], we distinguish the cases $\texttt {v}=0$ and $\texttt {v}\ne 0$. In the former case, there is no nonlocal term, and we set $G(u,p)=F(u) + \gamma u$ and $J\equiv 0$. In the latter case we identify the quantities

$$\begin{aligned} G(u,p) = F(u) + \gamma |\texttt {v}|\, p , \quad S(u) = u , \quad J(y) = \frac{1}{|\texttt {v}|} \,\Gamma \big ( {-}\frac{y}{\texttt {v}} \big ), \end{aligned}$$

where $\Gamma (\tau )=0$ for $\tau < 0$ is assumed. In particular, we have $J\ge 0$, $\int _{{\mathbb {R}}}J(y) \;\!\mathrm {d}y =1$, and $(J*u)(x)= \int _{{\mathbb {R}}}J(x{-}y)u(y)\;\!\mathrm {d}y = \int _0^\infty \Gamma (\tau ) u(x{+}\texttt {v}\tau )\;\!\mathrm {d}\tau$.

It remains to verify the Assumptions (D1)–(D4) of [10, Thm. 5.1], which are shown to hold for $\texttt {v}=0$ (rather trivially) as well as for $\texttt {v}\ne 0$:

(D1):

Clearly, the operator ${\mathcal {A}}_{\gamma ,\texttt {v}}$ defined in (2.4) is translation invariant, ${\mathcal {A}}_{\gamma ,\texttt {v}} [u(\,\cdot \,{+}h)](x) = {\mathcal {A}}_{\gamma ,\texttt {v}} [u(\cdot )](\,\cdot \,{+}h)$ for all $h \in {{\mathbb {R}}}$. The desired properties of the function $F_\gamma : u \mapsto F(u)+\gamma u$ characterized by ${\mathcal {A}}_{\gamma ,\texttt {v}}(\lambda {\varvec{1}}) =F_\gamma (\lambda ){\varvec{1}}$ follow directly from (H1).

(D2):

The condition (D2) in [10, Sec. 5.1] on J is stronger than our condition (H2) on $\Gamma$ because it additionally asks $J \in {\mathrm{C}}^1({{\mathbb {R}}})$ and $\int _{{\mathbb {R}}}|J'(y)|\;\!\mathrm {d}y < \infty$. However, a close inspection of the proof of [10, Thm. 5.1] reveals that these additional conditions are not needed in our case $D>0$. Indeed, (D2) is used to derive (C2) and (C4) there. However, (C2) is the strong comparison principle, which holds according to Proposition 2.2(II), while (C4) follows from classical parabolic regularity theory because of $D>0$.

(D3):

The function $G(u,p)= F(u)+\gamma |\texttt {v}| p$ and $S(u)=u$ are “smooth” with $\partial _p G(u,p) = \gamma \ge 0$ and $S'(u) = 1 > 0$. A check of [10] shows that “smoothness in (D3)” means that G and S are ${\mathrm{C}}^1$ functions and that [10, Eqn. (4.3)] in (C3) can be deduced. The latter follows from our assumption $F\in {\mathrm{C}}^2({{\mathbb {R}}})$ in (H1).

(D4):

This holds because of $D>0$.

Therefore, [10, Thm. 5.1] yields the desired existence of traveling fronts. Because we have $D>0$ we immediately obtain ${\mathcal {U}}\in {\mathrm{C}}^2({{\mathbb {R}}})$ by using (2.7a). $\square$

The comparison principle is not only useful for establishing existence and uniqueness of traveling fronts. It will also be essential to derive qualitative properties of the function $(\gamma ,\texttt {v}) \mapsto \texttt {C}(\gamma ,\texttt {v})$. We first derive upper and lower bounds for $\texttt {C}$ and then its continuity, which will be crucial to construct traveling fronts for the memory equation (2.1). The ideas of the proof follow [10, Lem. 3.2 & Thm. 3.5], but they are much more explicit, thus providing realistic bounds by assuming reasonable bounds for $F_\gamma$. In Fig. 1 we display the way in which $F_\gamma$ needs to be estimated.

Theorem 2.5

(Bounds on the front speed) Let the Hypotheses (H1) and (H2) hold and fix $\gamma \in [0,\gamma _*]$ and $\texttt {v}\in {{\mathbb {R}}}$. Assume further that $F_\gamma$ satisfies the estimates

$$\begin{aligned} \begin{aligned}&F_\gamma (u) \ge -\Phi _* \text { for } u\in [u^\gamma _-,u^\gamma _{\mathrm{m}}]\quad \text {and} \quad F_\gamma (u) \le \Phi ^* \text { for } u\in [u^\gamma _{\mathrm{m}},u^\gamma _+],\\&\exists \, a_*,b_*\in [u^\gamma _{\mathrm{m}},u^\gamma _+]\ \exists \, \alpha _*>0: \quad a_*< b_* \ \text { and } \ F_\gamma (u) \ge \alpha _*(u{-}a_*) \text { for } u \in [a_*,b_*], \\&\exists \, a^*,b^*\in [u^\gamma _-,u^\gamma _{\mathrm{m}}]\ \exists \, \alpha ^*>0: \quad b^*< a^* \ \text { and } \ F_\gamma (u) \le \alpha ^*(u{-}a^*) \text { for } u \in [b^*,a^*]. \end{aligned}\nonumber \\ \end{aligned}$$

(2.11)

Then, the speed $\texttt {c}=\texttt {C}(\gamma ,\texttt {v})$ of the traveling front ${\mathcal {U}}_{\gamma ,\texttt {v}}$ satisfies

$$\begin{aligned} \texttt {v}\ge 0:\quad&-\max \Big \{ \Big (\frac{\Phi ^*D}{b^*{-}a^*} \Big )^{1/2} ,\, \frac{\Phi ^*\gamma \widehat{g}_1\texttt {v}}{\alpha ^*(b^*{-}a^*)} \Big \} - \gamma \widehat{g}_1\texttt {v}\le \texttt {C}(\gamma ,\texttt {v}) \le \Big (\frac{\Phi _*D}{u^\gamma _+{-}u^\gamma _{\mathrm{m}}} \Big )^{1/2} , \end{aligned}$$

(2.12a)

$$\begin{aligned} \texttt {v}\le 0:\quad&- \Big (\frac{\Phi ^*D}{u^\gamma _{\mathrm{m}}{-}u^\gamma _-} \Big )^{1/2} \le \texttt {C}(\gamma ,\texttt {v}) \le \max \Big \{ \Big (\frac{\Phi _*D}{b_*{-}a_*} \Big )^{1/2} ,\, \frac{\Phi _*\gamma \widehat{g}_1|\texttt {v}|}{\alpha _*(b_*{-}a_*)} \Big \} + \gamma \widehat{g}_1|\texttt {v}| \end{aligned}$$

(2.12b)

with $\widehat{g}_1=\int _0^\infty \tau \Gamma (\tau ) \;\!\mathrm {d}\tau >0$ from (H2).

Fig. 1

We show how $F_\gamma$ needs to be estimated from above and below to obtain the upper and lower bounds in Theorem 2.5 for the speed of traveling fronts ${\mathcal {U}}_{\gamma ,\texttt {v}}$ for the nonlocal equation (2.3)

Proof

We construct suitable traveling fronts as subsolutions $V_*$ and supersolutions $V^*$ with speeds $c_*$ and $c^*$, respectively. The comparison principle for the travel speeds in Proposition 2.3 gives the desired result $c^*\le \texttt {c}\le c_*$.

Choosing a small $\delta >0$ and a positive slope $m>0$, we set $\xi _*:=(a_*{-}u^\gamma _-)/m>0$ and $\lambda _*: = m/(b_*{-}a_*)$ and define the function $V_*$ in the specific form

$$\begin{aligned} V_*(\xi )=\left\{ \begin{array}{ll} u^\gamma _- -\delta m&{}\quad \text {for } \xi \le -\delta ,\\ u^\gamma _- +m \xi &{}\quad \text {for } \xi \in [-\delta ,\xi _*], \\ b_*- (b_*{-}a_*)\, \mathrm {e}^{-\lambda _* (\xi -\xi _*)}&{}\quad \text {for }\xi \ge \xi _*. \end{array} \right. \end{aligned}$$

Hence, we have $V_*\in {\mathrm{C}}^0({{\mathbb {R}}})$ and $V_*\in {\mathrm{C}}^1({{\mathbb {R}}}\setminus \{-\delta \})$. Actually $V_*$ could be smoothed out in $I_\delta :=[-2\delta ,-\delta /2]$ such that it lies in ${\mathrm {C}}^2({]{-}\infty ,\xi _*[})$ with $V''_*(\xi )\ge 0$ for $\xi < \xi _*$. Similarly, the jump in $\xi \mapsto V''_*(\xi )$ at the point $\xi =\xi _*$ with limits $V''_*(\xi _*{-}0)=0$ and $V''(\xi _*{+}0)=-m^2/(b_*{-}a_*)$ can be smooth out in a continuous and monotone fashion in an interval ${]\xi _*{-}\varepsilon ,\xi _*{+}\varepsilon [}$ such that the changes on $V_*$ are only of order $\varepsilon$ as well. These smoothenings will not destroy the property of a subsolution derived below.

A main observation is the monotonicity $V'_*(\xi )\ge 0$ and that $V_*$ and ${\mathcal {U}}_{\gamma ,\texttt {v}}$ satisfy the ordering conditions (2.5a) for the limits at $\xi =\pm \infty$. It remains to be shown that there is a speed $c_*$ such that $u_*(t,x)=V_*(x{-}c_*t)$ is a subsolution. To obtain this, we proceed as follows (using $\xi =x{-}c_*t$):

$$\begin{aligned} {\dot{u}}_*(\xi ) -{\mathcal {A}}_{\gamma ,\texttt {v}}[u_*](\xi )&= -c_*V'_*(\xi ) -DV''_*(\xi ) - F_\gamma \big ( V_*(\xi )\big ) - {\mathcal {L}}_{\gamma ,\texttt {v}}[V_*](\xi ) \\ \text { with }{\mathcal {L}}_{\gamma ,\texttt {v}}[w](\xi )&:= \gamma \int _0^\infty \Gamma (\tau ) \big ( w(\xi {+}\texttt {v}\tau ) - w(\xi ) \big ) \;\!\mathrm {d}\tau . \end{aligned}$$

For $\texttt {v}\ge 0$ we have ${\mathcal {L}}_{\gamma ,\texttt {v}}[V_*]\ge 0$ because of the monotonicity of $V_*$ and the nonnegativity of $\Gamma$. Hence, we can drop $-{\mathcal {L}}_{\gamma ,\texttt {v}}[V_*]$ when showing that $u_*$ is a subsolution.

For $\texttt {v}<0$ we estimate $0\le -{\mathcal {L}}_{\gamma ,\texttt {v}}[V_*](\xi )$ from above by considering two regimes for $\xi$ separately: For $\xi \le -\delta$ we have ${\mathcal {L}}_{\gamma ,\texttt {v}}[V_*](\xi )=0$ since $V_*$ is constant on ${]{-}\infty ,-\delta ]}$. For $\xi > -\delta$ we use $V'_*(\xi )\in [0,m]$ and obtain

$$\begin{aligned} 0\le -{\mathcal {L}}_{\gamma ,\texttt {v}}[V_*](\xi ) \le -\gamma \int _0^\infty \Gamma (\tau )\, \texttt {v}\tau m \,\;\!\mathrm {d}\tau = g_\texttt {v}m \quad \text {with } g_\texttt {v}:= \gamma \widehat{g}_1\max \{-\texttt {v},0\} . \end{aligned}$$

We derive the conditions that m and $c_*$ have to satisfy in order to guarantee that $V_*$ is indeed a subsolutions. For this we estimate ${\dot{u}}_*(\xi ) -{\mathcal {A}}_{\gamma ,\texttt {v}}[u_*](\xi )$ from above on the separate domains and collect the corresponding conditions:

$$\begin{aligned} \xi < -\delta :\,&- c_*\cdot 0 - D\cdot 0 - F_\gamma \big ( u^\gamma _- {-}\delta m\big ) - 0 \ \le 0 , \\ \xi \in {]{-}\delta ,\xi _*[}:\,&- c_*\cdot m - D\cdot 0 + \qquad \Phi _* \quad + m \,g_\texttt {v}\le 0 , \\ \xi > \xi _*: \,&(b_*{-}a_*)\big ( ({-}c_* \lambda _*+\lambda _*^2D + \alpha _*) \mathrm {e}^{-\lambda _*( \xi -\xi _*)} - \alpha _* \big ) + m\,g_\texttt {v}\le 0. \end{aligned}$$

The first condition is always true because $F_\gamma (u)>0$ for $u < u^\gamma _-$. For the second condition we simply choose $c_*\ge \Phi _*/m + g_\texttt {v}$, where m is still to be determined.

Hence, it remains to analyze the third condition. For $\texttt {v}\ge 0$, the last term vanishes and the terms multiplying $\alpha _*$ are nonpositive. Hence, it suffices to take $c_* \ge \lambda _* D= m D/(b_*{-}a_*)$. Together with $c_*\ge \Phi _*/m$ we can choose m optimally and find that $c_*= \big ( \Phi _*D/(b_*{-}a_*)\big )^{1/2}$ guarantees that $V_*$ is a subsolution. Surprisingly, the result does not depend on the slope $\alpha _*>0$, hence we may optimize $a_*$ and $b_*$ by pushing them to their limits $u^\gamma _{\mathrm{m}}$ and $u^\gamma _+$, respectively. Thus, we obtain the upper estimate for c in (2.12a).

For $\texttt {v}<0$ the term $m g_\texttt {v}>0$ can only be compensated by $\alpha _*(b_*{-}a_*)$. Setting $m= \theta \alpha _*(b_*{-}a_*)/g_\texttt {v}$ we can rewrite the third condition in the form

$$\begin{aligned} \textstyle \alpha _*(b_*{-}a_*)\Big ( \big (-c_*\frac{\theta }{g_\texttt {v}} +\frac{\alpha _*\theta ^2D}{g_\texttt {v}^2} +1\big )\,\mathrm {e}^{-\lambda _*( \xi -\xi _*)} - 1 + \theta \Big ) \le 0. \end{aligned}$$

Together with the second condition it remains to satisfy

$$\begin{aligned} c_* \ge \max \big \{ \tfrac{1}{\theta }\,\tfrac{\Phi _* g_\texttt {v}}{\alpha _*(b_*{-} a_*)} + g_\texttt {v}\, , \, \theta \,\tfrac{\alpha _* D}{g_\texttt {v}} + g_\texttt {v}\big \} . \end{aligned}$$

For $g_\texttt {v}^2 \Phi _* < \alpha _*^2 (b_*{-}a_*) D$ we find an optimal $\theta \in {]0,1[}$, whereas otherwise the first term in the maximum dominates and $\theta =1$ gives the smallest bound for $c_*$. This establishes the upper estimate in (2.12b).

To obtain the lower estimates, we construct a supersolution in a completely analogous fashion. We emphasize that now we need to estimate $-{\mathcal {L}}_{\gamma ,\texttt {v}}[V^*]$ from below. Since we still have $(V^*)'(\xi )>0$, we find $-{\mathcal {L}}_{\gamma ,\texttt {v}}[V^*] (\xi ) \ge 0$ for $\texttt {v}\le 0$, which is now the easy case leading to the simple lower bound in (2.12b). For $\texttt {v}>0$ we then use $-{\mathcal {L}}_{\gamma ,\texttt {v}}[V^*](\xi )\ge - \texttt {v}\gamma \widehat{g}_1 \, m$ and obtain the lower bound in (2.12a). $\square$

Lemma 2.6

Let the Hypotheses (H1) and (H2) hold. Then, the function $\texttt {C}: [0,\gamma _*] {\times }{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ is continuous.

Proof

Consider a sequence $(\gamma _n, \texttt {v}_n)_{n\in {{\mathbb {N}}}}$ with $(\gamma _n, \texttt {v}_n) \rightarrow (\gamma ,\texttt {v})$ as $n\rightarrow \infty$. According to Proposition 2.4, for all $n \in {{\mathbb {N}}}$ there exists a unique traveling front $u_n(t,x) = {\mathcal {U}}_n(x {-} \texttt {c}_n t)$ for (2.3) with $\texttt {c}_n = \texttt {C}(\gamma _n, \texttt {v}_n)$.

Step 1 Uniform bounds for the sequence $(\texttt {c}_n,{\mathcal {U}}_n)$. Since $({\mathcal {U}}_n)_{n \in {{\mathbb {N}}}}$ is a traveling front, we have $u^{\gamma _n}_-< {\mathcal {U}}_n(\xi ) < u^{\gamma _n}_+$. By (H1) and the form $F_\gamma (u)=F(u)+\gamma u$, the mappings $\gamma \mapsto u^\gamma _\pm$ are uniformly continuous and hence bounded, i.e. there exists $U_*>0$ such that $-U_* \le u^\gamma _-< u^\gamma _+ \le U_*$ for all $\gamma \in [0,\gamma _*]$. Hence, $\Vert {\mathcal {U}}_n\Vert _{\mathrm{L^\infty }} \le U_*$ and there exists $R_*>0$ such that $|F(u)|\le R_*$ for all $u\in [-U_*,U_*]$.

Moreover, we can apply the speed bounds for $\texttt {c}_n=\texttt {C}(\gamma _n,\texttt {v}_n)$ from Theorem 2.5 to show that $|\texttt {c}_n|\le C_0$. Indeed, in a neighborhood of the limit $(\gamma ,\texttt {v})$ we can choose the estimating quantities $\Phi _*$, $a_*$, $b_*$, $\Phi ^*$, $a^*$, and $b^*$ uniform for $(\gamma _n,\texttt {v}_n)$ for all $n\ge n_0$.

Next we show that ${\mathcal {U}}_n$ is also bounded in ${\mathrm{H}}^1_\text {loc}({{\mathbb {R}}})$. For this we use Eq. (2.7a) in the form

$$\begin{aligned} -\texttt {c}_n {\mathcal {U}}'_n=D{\mathcal {U}}''_n + h_n \quad \text { with } h_n(\xi )=F({\mathcal {U}}_n(\xi ))+ \gamma _n \int _0^\infty \Gamma (\tau ){\mathcal {U}}_n(\xi {+}\texttt {v}_n \tau ) \;\!\mathrm {d}\tau ,\nonumber \\ \end{aligned}$$

(2.13)

where now $\Vert h_n\Vert _{\mathrm{L^\infty }} \le H_*$ for a suitable constant $H_*$. Moreover, we define the function $\psi _0 \in {\mathrm{C}}^1({{\mathbb {R}}})$ with $\psi _0(x)=(x^2{-}1)^2$ for $|x|\le 1$ and $\psi _0(x)=0$ otherwise, which satisfies the estimate $\psi '_0(x)^2 \le 16 \psi _0(x)$. For arbitrary $\zeta _* \in {{\mathbb {R}}}$ we define the test function $\psi : \xi \mapsto \psi _0(\xi {-}\zeta _*)$ and test equation (2.13) with $\psi {\mathcal {U}}_n$. Setting $\Xi =[\zeta _*{-}1,\zeta _*{+}1]$ this leads to the estimate

$$\begin{aligned} \Delta _{n,\zeta _*}&:= \int _\Xi D|{\mathcal {U}}'_n|^2\psi \;\!\mathrm {d}\xi = -\int _\Xi D({\mathcal {U}}''_n{\mathcal {U}}_n\psi + {\mathcal {U}}_n {\mathcal {U}}'_n \psi ') \;\!\mathrm {d}\xi \\&\overset{{(2.13)}}{=} \int _\Xi \big ((h_n {+} \texttt {c}_n {\mathcal {U}}'_n){\mathcal {U}}_n \psi - D {\mathcal {U}}_n {\mathcal {U}}'_n\psi ') \;\!\mathrm {d}\xi \\&\le H_*U_*\Vert \psi \Vert _{\mathrm{L^1(\Xi )}} \! + \big \Vert (D\psi )^{1/2}{\mathcal {U}}'_n\big \Vert _{\mathrm{L^2(\Xi )}} \big \Vert \texttt {c}_n (\tfrac{\psi }{D})^{1/2}{\mathcal {U}}_n - (\tfrac{D}{\psi })^{1/2}\psi '{\mathcal {U}}_n\big \Vert _{\mathrm{L^2(\Xi )}} \\&\le \tfrac{16}{15} H_*U_* + \Delta _{n,\zeta _*}^{1/2} \Big ( \big (\tfrac{16}{15 D}\big )^{1/2}C_0U_* + 8D^{1/2} U_* \Big ). \end{aligned}$$

Since $\zeta _*$ was arbitrary and $D\psi (x)\ge D/2$ for $|x|\le 1/2$, we find the uniform estimate

$$\begin{aligned} \sup _{\zeta _*\in {{\mathbb {R}}}} \int _{\zeta _*{-}1/2}^{\zeta _*+1/2} |{\mathcal {U}}'_n(\xi )|^2 \;\!\mathrm {d}\xi \le \tfrac{64}{15D} H_*U_* + \tfrac{8}{D} \big ( \tfrac{16}{15D} C_0^2 U_*^2 + 64 DU_*^2\big ) , \end{aligned}$$

which together with $\Vert {\mathcal {U}}_n\Vert _{\mathrm{L^\infty }}\le U_*$ is the desired uniform bound in ${\mathrm{H}}^1_\text {loc}({{\mathbb {R}}})$.

Inserting the last result into (2.13), we first obtain a uniform bound for ${\mathcal {U}}_n$ in ${\mathrm{H}}^2_\text {loc}({{\mathbb {R}}})$, and inserting again we find $\Vert {\mathcal {U}}''_n\Vert _{\mathrm{L^\infty }} \le C_2 <\infty$ for all $n\in {{\mathbb {N}}}$.

Step 2 Convergent subsequences and passage to the limit We can extract a subsequence (not relabeled) such that $\texttt {c}_n \rightarrow \texttt {c}$ and ${\mathcal {U}}_n \rightharpoonup {\mathcal {U}}$ weakly in ${\mathrm{H}}^1_\mathrm {loc}({{\mathbb {R}}})$. We also fix the translations in such a way that ${\mathcal {U}}_n(0)=u^{\gamma _n}_{\mathrm{m}} \rightarrow u^{\gamma }_{\mathrm{m}}$. Weak convergence in ${\mathrm{H}}^1_\text {loc}({{\mathbb {R}}})$ implies uniform convergence on any compact interval $K\Subset {{\mathbb {R}}}$. Hence, we have ${\mathcal {U}}_n(\xi ) \rightarrow {\mathcal {U}}(\xi )$ for all $\xi \in {{\mathbb {R}}}$ and ${\mathcal {U}}(0)=u^{\gamma }_{\mathrm{m}}$ in particular. Of course, the uniform bounds for ${\mathcal {U}}_n$ imply ${\mathcal {U}}\in {\mathrm{C}}^{1,\text {Lip}}({{\mathbb {R}}})$ with $\Vert {\mathcal {U}}''\Vert _{\mathrm{L^\infty }} \le C_2$. Moreover, since all ${\mathcal {U}}_n$ are nondecreasing, we have ${\mathcal {U}}'(\xi )\ge 0$ as well.

Testing the Eq. (2.7a) with $\Phi \in {\mathrm{C}}^\infty _\mathrm {c}({{\mathbb {R}}})$ and integrating over the arbitrarily chosen compact subset $K \Subset {{\mathbb {R}}}$ with $\mathrm {sppt}\Phi \subset K$ yields

$$\begin{aligned} \int _K -\texttt {c}_n {\mathcal {U}}_n' \Phi \;\!\mathrm {d}\xi = \int _K \bigg ({-} D{\mathcal {U}}_n' \Phi ' + \Big ( F({\mathcal {U}}_n) + \gamma _n\int _0^\infty \! \Gamma (\tau ) {\mathcal {U}}_n(\cdot {+}\texttt {v}_n \tau ) \;\!\mathrm {d}\tau \Big ) \Phi \bigg ) \;\!\mathrm {d}\xi . \end{aligned}$$

Exploiting the continuity of F and the locally uniform convergence ${\mathcal {U}}_n \rightarrow {\mathcal {U}}$, the limit $n\rightarrow \infty$ leads to

$$\begin{aligned} \int _K -\texttt {c}\, {\mathcal {U}}' \Phi \;\!\mathrm {d}\xi = \int _K \bigg (-D{\mathcal {U}}' \Phi ' + \Big ( F({\mathcal {U}}) + \gamma \int _0^\infty \Gamma (\tau ) {\mathcal {U}}(\cdot {+} \texttt {v}\tau ) \;\!\mathrm {d}\tau \Big ) \Phi \bigg ) \;\!\mathrm {d}\xi . \end{aligned}$$

Thus, the pair $(\texttt {c},{\mathcal {U}})$ is a solution of (2.7a), which satisfies ${\mathcal {U}}(0)=u^\gamma _{\mathrm{m}}$.

Step 3 Nontriviality of ${\mathcal {U}}$ We still need to show that ${\mathcal {U}}$ is not equal to the constant solution $u^\gamma _{\mathrm{m}}$. Since we already know that ${\mathcal {U}}$ is monotone, the limits $U_\pm =\lim _{\xi \rightarrow \pm \infty }{\mathcal {U}}(\xi )$ exist. It is easy to see that these limits satisfy $F_\gamma (U_\pm )=0$. Hence, it suffices to show $U_- \lneqq u^\gamma _{\mathrm{m}}$ and $U_+ \gneqq u^\gamma _{\mathrm{m}}$. For this, it is sufficient, to find a $\delta >0$ such that ${\mathcal {U}}'_n(0)\ge \delta$, which implies ${\mathcal {U}}'(0)\ge \delta >0$.

To show this, we consider the case $\texttt {v}_n\le 0$ and estimate ${\mathcal {U}}_n$ from above on ${]{-}\infty ,0]}$, while the case $\texttt {v}_n\ge 0$ is treated analogously by estimating ${\mathcal {U}}_n$ from below on ${[0,\infty [}$. Because of $\gamma _n\rightarrow \gamma$, we find $f_*>0$ such that $F_{\gamma _n}(u) \le -\frac{f_*}{u^{\gamma _n}_{\mathrm{m}}{-} u^{\gamma _n}_-} (u{-}u^{\gamma _n}_-)(u^{\gamma _n}_{\mathrm{m}}-u)\le 0$ holds for all $u\in [u^{\gamma _n}_-, u^{\gamma _n}_{\mathrm{m}}]$ and $n \in {{\mathbb {N}}}$. Hence, using ${\mathcal {U}}'_n\ge 0$ and $\texttt {v}_n\le 0$ we obtain

$$\begin{aligned} D{\mathcal {U}}''_n&= - \texttt {c}_n {\mathcal {U}}'_n - F({\mathcal {U}}_n) - \gamma _n \int _0^\infty \Gamma (\tau ){\mathcal {U}}_n(\xi {+}\texttt {v}_n \tau ) \;\!\mathrm {d}\tau \nonumber \\&\ge -|\texttt {c}_n|{\mathcal {U}}'_n -F_{\gamma _n}({\mathcal {U}}_n) \ge -(|\texttt {c}|{+}1){\mathcal {U}}'_n + \frac{f_*}{u^{\gamma _n}_{\mathrm{m}}{-} u^{\gamma _n}_-} ({\mathcal {U}}_n{-}u^{\gamma _n}_-)\, (u^{\gamma _n}_{\mathrm{m}}{-} {\mathcal {U}}_n). \end{aligned}$$

(2.14)

With this, we can compare the curve ${\mathcal {C}}_n:\xi \mapsto ({\mathcal {U}}_n(\xi ),{\mathcal {U}}'_n(\xi ))$ in the phase plane for $(U,U')$ with the curve $\widetilde{C}_n$ generated by the solution $\widetilde{U}_n$ of the ODE $D U'' = -(|\texttt {c}|{+}1)U' + \frac{f_*}{u^{\gamma _n}_{\mathrm{m}}{-} u^{\gamma _n}_-} (U{-}u^{\gamma _n}_-)\, (u^{\gamma _n}_{\mathrm{m}}{-} U)$, satisfying $\widetilde{U}'_n\ge 0$ and $(\widetilde{U}_n(\xi ),\widetilde{U}'_n(\xi )) \rightarrow (u^{\gamma _n}_-,0)$ for $\xi \rightarrow -\infty$.

The function ${\mathcal {U}}_n$ has the expansion ${\mathcal {U}}_n(\xi )=u^\gamma _- + d_n\mathrm {e}^{\lambda _n\xi }(1{+}o(1))$ for $\xi \rightarrow -\infty$ with $d_n>0$, where $\lambda _n$ is the positive root of the characteristic equation $D\lambda ^2 +\texttt {c}_n \lambda +F'(u^{\gamma _n}_-)=0$. Hence, the former curve ${\mathcal {C}}_n$ leaves the point $(u^{\gamma _n}_-,0)$ to the right with positive slope $\lambda _n>0$, i.e. $U' =\lambda _n(U{-}u^{\gamma _n}_-)+$h.o.t. Similarly, the curve ${\widetilde{ C}}_n$ generated by the solution $\widetilde{U}_n$ has the expansion $U' ={\widetilde{\lambda }}_n(U{-}u^{\gamma _n}_-)+$h.o.t., where ${\widetilde{\lambda }}_n$ is the positive root of $D\lambda ^2 -(|\texttt {c}|{+}1) \lambda -f_* =0$. Because of $\texttt {c}_n\ge -(|\texttt {c}|{+}1)$ and $F'(u^{\gamma _n}_-)\le -f_* <0$ we have $\lambda _n> {\widetilde{\lambda }}_n>0$, which implies that the curve ${\mathcal {C}}_n$ lies above $\widetilde{C}_n$ in a neighborhood of $(u^{\gamma _n}_-,0)$.

Because of the comparison (2.14) we know that ${\mathcal {C}}_n$ must stay above $\widetilde{C}_n$ until both curves hit the line $U=u^{\gamma _n}_{\mathrm{m}}$. Thus, choosing $\widetilde{\xi }_n$ such that $\widetilde{U}_n(\widetilde{\xi }_n) = u^{\gamma _n}_{\mathrm{m}} = {\mathcal {U}}_n(0)$ and $\widetilde{U}_n(\xi )< u^{\gamma _n}_{\mathrm{m}}$ for $\xi \le \widetilde{\xi }_n$, we obtain ${\mathcal {U}}'_n(0)\ge \widetilde{U}'_n(\xi _n)$, see also Fig. 2. By simple scaling we see that $\widetilde{U}_n$ has the form

$$\begin{aligned}&\widetilde{U}_n(\xi )= u^{\gamma _n}_- + \big (u^{\gamma _n}_{\mathrm{m}} {-} u^{\gamma _n}_-\big )\,Y(\kappa (\xi {-}\xi _n)) \ \text { where } Y''+Y'- \sigma Y(1{-}Y)=0 , \\&\kappa =\frac{|\texttt {c}|{+}1}{D}, \quad \sigma = \frac{f_* \,D}{(|\texttt {c}|{+}1)^2}, \quad Y(-\infty )=0,\quad Y(0)=1, \quad Y'(\xi )>0. \end{aligned}$$

With this, we arrive at the desired result

$$\begin{aligned} {\mathcal {U}}'_n(0) \ge \widetilde{U}'_n(\xi _n)= \big (u^{\gamma _n}_{\mathrm{m}} {-} u^{\gamma _n}_-\big )\, \kappa \, Y'(0) \ge \frac{1}{2} \big (u^{\gamma }_{\mathrm{m}} {-} u^{\gamma }_-\big )\,\kappa \, Y'(0) =:\delta >0. \end{aligned}$$

In summary we have shown that the limit pair $(\texttt {c},{\mathcal {U}})$ satisfies the ODE (2.7a) as well as the boundary conditions (2.7b). Hence, by the uniqueness in Proposition 2.4 we conclude $\texttt {c}= \texttt {C}(\gamma ,\texttt {v})$, and the desired continuity of $\texttt {C}$ follows from $(\gamma _n,\texttt {v}_n)\rightarrow (\gamma ,\texttt {v})$ and $\texttt {c}_n = \texttt {C}(\gamma _n,\texttt {v}_n) \rightarrow \texttt {c}= \texttt {C}(\gamma ,\texttt {v})$. Indeed, the convergence along the chosen subsequence converts into convergence of the full sequence, because the limit of any convergent subsequence of $(\texttt {c}_n,{\mathcal {U}}_n)$ is uniquely determined. $\square$

Fig. 2

Phase plane for $(U,U')$ displaying the stream plot of the ODE $U''+\texttt {c}\,U'+ f_* (U{-}u^{\gamma _n}_-) ( u^{\gamma _n}_{\mathrm{m}} {-}U)=0$ together with the (red) curve ${\mathcal {C}}_n: \xi \mapsto ({\mathcal {U}}_n(\xi ),{\mathcal {U}}'_n(\xi ))$ lying above the unstable manifold of $(u^{\gamma _n}_-,0)$ (black curve) (Color figure online)

2.5 Traveling Fronts for the Memory Equation

According to Proposition 2.1, we obtain a traveling front for the memory equation (2.1) by finding $\texttt {v}\in {{\mathbb {R}}}$ such that $\texttt {v}=\texttt {C}(\gamma ,\texttt {v})$. To guarantee existence of such solutions, we derive suitable bounds and monotonicity properties for the wave speed function $\texttt {C}$, where again the comparison principle for sub- and supersolutions is useful, see Propositions 2.2 and 2.3 . We recall our choice that all traveling fronts ${\mathcal {U}}_{\gamma ,\texttt {v}}$ are increasing functions, i.e. they satisfy ${\mathcal {U}}_{\gamma ,\texttt {v}}(-\infty )=u^\gamma _- \lneqq u^\gamma _+ = {\mathcal {U}}_{\gamma ,\texttt {v}}(\infty )$.

Lemma 2.7

(Monotonicity of $\texttt {C}$) For all $\gamma , {\widetilde{\gamma }} \in [0,\gamma _*]$ and all $\texttt {v},{\widetilde{\texttt {v}}} \in {{\mathbb {R}}}$, we have the following implications:

$$\begin{aligned}&(a) \qquad \qquad \texttt {v}\le {\widetilde{\texttt {v}}}&\qquad \Longrightarrow \quad \texttt {C}(\gamma ,\texttt {v})&\ge \texttt {C}(\gamma ,{\widetilde{\texttt {v}}}) ; \end{aligned}$$

(2.15)

$$\begin{aligned}&(b) \ \gamma \le {\widetilde{\gamma }} \text { and } \max \{ u^\gamma _-,u^{{\widetilde{\gamma }}}_-\}\ge 0&\qquad \Longrightarrow \quad \texttt {C}(\gamma ,\texttt {v})&\ge \texttt {C}({\widetilde{\gamma }} , \texttt {v}) . \end{aligned}$$

(2.16)

Proof

Throughout the proof we set $u_{\gamma ,\texttt {v}}(t,x)={\mathcal {U}}_{\gamma ,\texttt {v}} \big ( x{-}\texttt {C}(\gamma , \texttt {v})t\big )$ and insert one traveling front into the parabolic equation for the other front, thus obtaining a super- or a subsolution. Then, Proposition 2.3 provides a comparison of the wave speeds.

Ad (a). We insert $u_{\gamma ,{\widetilde{\texttt {v}}}}$ into the equation for $u_{\gamma ,\texttt {v}}$ and obtain

$$\begin{aligned} {\dot{u}}_{\gamma ,{\widetilde{\texttt {v}}}} {-} {\mathcal {A}}_{\gamma ,\texttt {v}}[u_{\gamma ,{\widetilde{\texttt {v}}}}]&= \underbrace{{\dot{u}}_{\gamma ,{\widetilde{\texttt {v}}}} {-}{\mathcal {A}}_{\gamma ,{\widetilde{\texttt {v}}}}[u_{\gamma ,{\widetilde{\texttt {v}}}}]}_{=0} \ + \ P\big (x- \texttt {C}(\gamma , {\widetilde{\texttt {v}}})t \big ) \nonumber \\ \text {with }P(\xi )&=\gamma \int _0^\infty \!\Gamma (\tau )\;\!\big ({\mathcal {U}}_{\gamma ,{\widetilde{\texttt {v}}}}(\xi {+}{\widetilde{\texttt {v}}}\tau ) {-} {\mathcal {U}}_{\gamma ,{\widetilde{\texttt {v}}}}(\xi {+}\texttt {v}\tau )\big ) \;\!\mathrm {d}\tau . \end{aligned}$$

(2.17)

Using $\Gamma (\tau )\ge 0$, $\gamma \ge 0$, $\texttt {v}\le {\widetilde{\texttt {v}}}$, and ${\mathcal {U}}'_{\gamma ,{\widetilde{\texttt {v}}}}(\xi ) > 0$ (cf. (2.8)) we obtain $P\in {\mathrm{C}}^0({{\mathbb {R}}})$ and strict positivity $P(\xi )>0$ for all $\xi \in {{\mathbb {R}}}$. Thus, we find ${\dot{u}}_{\gamma ,{\widetilde{\texttt {v}}}} -{\mathcal {A}}_{\gamma ,\texttt {v}}[u_{\gamma ,{\widetilde{\texttt {v}}}}]\ge 0$, i.e. $u_{\gamma ,{\widetilde{\texttt {v}}}}$ is a supersolution of ${\dot{u}} = {\mathcal {A}}_{\gamma ,\texttt {v}}[u]$, whereas $u_{\gamma ,\texttt {v}}$ is a (sub)solution.

However, for applying Proposition 2.3 we need a monotone traveling supersolution $v^*:(t,x)\mapsto V^*(x{-}\texttt {C}(\gamma ,{\widetilde{\texttt {v}}})t)$ with strictly higher limits than $u_{\gamma ,\texttt {v}}$, see (2.5b). We now show that $v^*_\varepsilon :=\varepsilon + u_{\gamma ,{\widetilde{\texttt {v}}}}$ provides also supersolutions for all $\varepsilon \in {]0,\varepsilon _0[}$.

Indeed, a simple calculation (with $\xi =x- \texttt {C}(\gamma , {\widetilde{\texttt {v}}})t$) shows

$$\begin{aligned} \dot{v}^*_\varepsilon -{\mathcal {A}}_{\gamma ,\texttt {v}}[ v^*_\varepsilon ]= P(\xi ) + \phi _\varepsilon (\xi ) \quad \text {with } \phi _\varepsilon (\xi ) = F_\gamma ({\mathcal {U}}_{\gamma ,{\widetilde{\texttt {v}}}}(\xi ))- F_\gamma (\varepsilon {+}{\mathcal {U}}_{\gamma ,{\widetilde{\texttt {v}}}}(\xi )). \end{aligned}$$

On the one hand, from ${\mathcal {U}}_{\gamma ,{\widetilde{\texttt {v}}}}(\xi ) \rightarrow u^\gamma _\pm$ for $\xi \rightarrow \pm \infty$ and $F'_\gamma (u^\gamma _\pm ) <0$ (see (H1)) we easily find $\varepsilon _0>0$ and $\Xi >0$ such that $\phi _\varepsilon (\xi )\ge 0$ for $\varepsilon \in [0,\varepsilon _1]$ and $|\xi |\ge \Xi$. On the other hand, we have $|\phi _\varepsilon (\xi )| \le C_F \varepsilon$ because $F_\gamma$ is ${\mathrm{C}}^1$ on $[u^\gamma _-, \varepsilon _1{+}u^\gamma _+]$. The strict positivity of P implies $c_{P,\Xi }:=\min \big \{\, P(\xi ) \, \big | \, \xi \in [-\Xi ,\Xi ] \,\big \} >0$, whence we find $P(\xi )+ \phi _\varepsilon (\xi )\ge 0$ for all $\xi \in {{\mathbb {R}}}$ for all $\varepsilon \in [0,\varepsilon _0]$ with $\varepsilon _0=\min \{ \varepsilon _1,c_{P,\Xi }/C_F\}$.

In summary, Proposition 2.3 applies to $v^*_{\varepsilon _0/2}$, and the estimate $\texttt {v}\le {\widetilde{\texttt {v}}}$ in (2.15) follows.

Ad (b). Assume $u^\gamma _-\ge 0$ such that $u_{\gamma ,\texttt {v}}(t,x)\ge u^\gamma _-\ge 0$. We insert this solution into the equation for $u_{{\widetilde{\gamma }},\texttt {v}}$ and obtain

$$\begin{aligned} {\dot{u}}_{\gamma ,\texttt {v}} {-} {\mathcal {A}}_{{\widetilde{\gamma }},\texttt {v}}[u_{\gamma ,\texttt {v}}] = \underbrace{{\dot{u}}_{\gamma ,\texttt {v}} {-}{\mathcal {A}}_{\gamma ,\texttt {v}}[u_{\gamma ,\texttt {v}}]}_{=0} + (\gamma {-}{\widetilde{\gamma }}) \int _0^\infty \!\Gamma (\tau )\;\! u_{\gamma ,\texttt {v}}(t,x{+}\texttt {v}\tau ) \;\!\mathrm {d}\tau . \end{aligned}$$

(2.18)

Since the integral is nonnegative, the assumption $\gamma \le {\widetilde{\gamma }}$ implies that $u_{\gamma ,\texttt {v}}$ is a subsolution whereas $u_{\gamma ,{\widetilde{\texttt {v}}}}$ is a (super)solution. Hence, (2.16) follows via Proposition 2.3 applied to $v_*^\varepsilon = u_{\gamma ,\texttt {v}}- \varepsilon$ for sufficiently small $\varepsilon >0$, see part (a).

If $u^\gamma _-< 0$ we have $u^{{\widetilde{\gamma }}}_-\ge 0$ by assumption (2.16). Interchanging the role of $\gamma$ and ${\widetilde{\gamma }}$ in (2.18), we see that $u_{\gamma ,{\widetilde{\texttt {v}}}}$ is a supersolution of ${\dot{u}} = {\mathcal {A}}_{\gamma ,\texttt {v}}[u]$ and (2.15) follows again. $\square$

Having collected all preliminary estimates, we can prove the existence of traveling fronts for the original memory equation (2.1). Moreover, we are able to give bounds on the corresponding wave speed.

Theorem 2.8

(Main existence result) Let the Hypotheses (H1) and (H2) hold. Then, for all $\gamma \in [0,\gamma _*]$ the equation $\texttt {c}= \texttt {C}(\gamma ,\texttt {c})$ has a unique solution $\texttt {c}_\gamma$, and thus there exists a unique (up to translation) traveling-front solution $u(t,x) = \overline{\mathcal {U}}_\gamma (x{+}\texttt {c}_\gamma t)$ for the memory equation (2.1), where $\overline{\mathcal {U}}_\gamma$ satisfies the properties (2.7) and (2.8).

Proof

For a fixed $\gamma \in [0,\gamma _*]$ the function $\texttt {v}\mapsto \texttt {C}(\gamma ,\texttt {v})$ is continuous and non-increasing according to Lemma 2.6 and relation (2.15), respectively. Thus, there is a unique solution to $\texttt {v}= \texttt {C}(\gamma ,\texttt {v})$, which we call $\texttt {c}_\gamma$. According to Proposition 2.4 there is a unique (up to translation) traveling front $\overline{\mathcal {U}}_\gamma :={\mathcal {U}}_{\gamma ,\texttt {c}_\gamma }$ for the auxiliary equation (2.3) with $\texttt {v}=\texttt {c}_\gamma$.

Because of $\texttt {v}=\texttt {c}_\gamma = \texttt {C}(\gamma ,\texttt {c}_\gamma )$ we can return to the memory equation using Proposition 2.1, and the result is established. $\square$

Remark 2.9

(Stability of traveling fronts) It is not clear whether the traveling fronts constructed above are also stable in the memory equation (2.1). The exponential stability (2.10) of the traveling fronts in the auxiliary nonlocal equation (2.3) cannot be transferred to the memory equation, because there one would need a much more advanced stability concept involving the history of the solution as well. Thus, the stability, which is observed numerically in the special case treated in Sect. 4, remains an open problem.

Next we combine the available estimates and monotonicity of the wave speed $\texttt {C}(\gamma , \texttt {v})$ to give bounds on $\texttt {c}_\gamma$. Before doing so, we recall the classical result that for the local equation, i.e. $\texttt {v}=0$, the sign of the wave speed $\texttt {C}(\gamma ,0)$ is opposite to the sign of

$$\begin{aligned} {\mathcal {F}}(\gamma ):=\int _{u^{\gamma }_-}^{u^\gamma _+} F_\gamma (u) \;\!\mathrm {d}u. \end{aligned}$$

Indeed, to see this, we multiply (2.7a) by ${\mathcal {U}}'$ and integrate over ${{\mathbb {R}}}$ leading to

$$\begin{aligned} - \texttt {C}(\gamma ,0) \int _{{\mathbb {R}}}{\mathcal {U}}'_{\gamma ,0}(\xi )^2 \;\!\mathrm {d}\xi = \lim _{R\rightarrow \infty } \Big (\frac{D}{2} {\mathcal {U}}'_{\gamma ,0}(\xi )^2 \Big )\Big |_{-R}^R + \int _{{\mathbb {R}}}F_\gamma ({\mathcal {U}}_{\gamma ,0}(\xi )){\mathcal {U}}'_{\gamma ,0}(\xi )\;\!\mathrm {d}\xi = {\mathcal {F}}(\gamma ). \end{aligned}$$

In particular, for ${\mathcal {F}}(\gamma )=0$, we obtain $\texttt {C}(\gamma ,0)=0$, which means that a standing wave exists. Obviously this implies $\texttt {c}_0=0$, i.e. also the memory equation (2.1) has the same standing wave solution as the local equation with nonlinearity $F_\gamma$.

Corollary 2.10

(Bounds on the wave speed) Let the assumptions (H1) and (H2) hold and let $F_\gamma$ satisfy (2.11), then for all $\gamma \in [0,\gamma _*]$, we have the following bounds for the speeds $\texttt {c}_\gamma$ of the traveling front $\overline{\mathcal {U}}_\gamma$ for the memory equation (2.1):

$$\begin{aligned} \begin{aligned} {\mathcal {F}}(\gamma )\le 0&\quad \Longrightarrow \quad 0 \le \texttt {c}_\gamma \le \texttt {C}(\gamma ,0) \le \Big ( \frac{\Phi _* D}{u^\gamma _+{-}u^\gamma _{\mathrm{m}}}\Big )^{1/2} , \\ {\mathcal {F}}(\gamma ) \ge 0&\quad \Longrightarrow \quad 0 \ge \texttt {c}_\gamma \ge \texttt {C}(\gamma ,0) \ge - \Big ( \frac{\Phi ^* D}{u^\gamma _{\mathrm{m}} {-}u^\gamma _-}\Big )^{1/2} . \end{aligned} \end{aligned}$$

(2.19)

Proof

Since $\texttt {v}\mapsto \texttt {C}(\gamma , \texttt {v})$ is non-increasing and continuous, we easily see that the solution $\texttt {c}_\gamma$ of $\texttt {v}=\texttt {C}(\gamma ,\texttt {v})$ always lies between 0 (not included) and $\texttt {C}(\gamma ,0)$ (possibly included). This provides the first two estimates in both lines of (2.19). The last estimate (in both lines) is a direct consequence of (2.12) with $\texttt {v}=0$. $\square$

3 Derivation of Memory Equations from Local PDEs

Equations with memory can be derived from local models if so-called internal variables w are eliminated. Changes in the main variable u induce instantaneous changes in w, but the internal dynamics of the w system leads to the delayed back-coupling from w. This effect stays local in space, if the diffusion in the variable w can be neglected.

3.1 Parabolic Equation Coupled to Linear ODEs

For the modeling of pulse propagation in nerves, one often uses the coupling between a parabolic equation and ODEs, see e.g. [7, Eqn. (0.1)] for the Hodgkin–Huxley equation and [11, 24] for the FitzHugh–Nagumo-like equations, which corresponds to the case $m_{\mathrm w}=1$ in the following model:

$$\begin{aligned} {\dot{u}} = Du_{xx} + F(u) + \sum _{i=1}^{m_{\mathrm w}} a_i w_i, \qquad \dot{w}_i = - \lambda _i w_i + b_i u \ \text { for }i=1,\ldots ,m_{\mathrm w}, \end{aligned}$$

(3.1)

where $a_i, \ b_i$, and $\lambda _i$ are fixed real parameters with $\lambda _i>0$. Clearly, the linear ODEs can be solved locally in space by $w_i(t,x)=w_i(0,x)\mathrm {e}^{-\lambda _it} + \int _0^t \mathrm {e}^{-\lambda _i(t{-}\tau )} b_i u(\tau ,x)\;\!\mathrm {d}\tau$. Assuming that there is infinite history (which is compatible with our search for traveling fronts that exist for all time) we may also write $w_i(t,x)=\int _0^\infty \mathrm {e}^{-\lambda _i \tau } b_i u(t{-}\tau ,x)\;\!\mathrm {d}\tau$. With this we obtain the memory equation (2.1) with the specific kernel

$$\begin{aligned} \Gamma (\tau )= \frac{1}{\gamma }\sum _{i=1}^{m_{\mathrm w}} \mathrm {e}^{-\lambda _i \tau } a_i b_i \quad \text { with }\gamma = \sum _{i=1}^{m_{\mathrm w}} \frac{a_ib_i}{\lambda _i} . \end{aligned}$$

(3.2)

Clearly, our theory is applicable also in cases where some of the products $a_ib_i$ are negative, as long as $\Gamma$ is nonnegative, e.g. $\mathrm {e}^{-2\tau }- 2\mathrm {e}^{-3\tau } + \mathrm {e}^{-4\tau }=(\mathrm {e}^{-\tau }{-}\mathrm {e}^{-2\tau })^2$. Thus, we need a positive feedback $a_ib_i$ for several species i, but we may also allow for a negative feedback $a_jb_j$ for some components if they are not too big. For our theory, there is no need to give a precise connection between the memory equation (1.2) and the PDE-ODE system (3.1). The only thing we need is the “formal” connection established so far and allowing to apply Proposition 2.1 for traveling waves. Nevertheless it is possible to connect the two initial-value problems (1.2) and (3.1) if we impose suitable compatibility conditions between the history $(u_\text {hist}(\tau )\big )_{\tau <0}$ in the former and $(w_i(0))_{i=1,\ldots ,m_{\mathrm w}}$ in the latter, namely

$$\begin{aligned} w_i(0,x)=b_i\int _{-\infty }^0 \mathrm {e}^{\lambda _i \tau }u_\text {hist}(\tau ,x)\;\!\mathrm {d}\tau \quad \text {for all } i\in \{1,\ldots ,m_{\mathrm w}\} \text { and }x \in \Omega . \end{aligned}$$

With this and the definition of $\Gamma$ in (3.2) we find, for $t>0$,

$$\begin{aligned} \sum _{i=1}^{m_{\mathrm w}} a_i w_i(t)&= \sum _{i=1}^{m_{\mathrm w}} a_i \mathrm {e}^{-\lambda _i t} w_i(0) + \int _0^t \mathrm {e}^{-\lambda _i(t{-}\tau )} a_ib_i u(\tau ,x)\;\!\mathrm {d}\tau \\&=\int _{-\infty }^0 \!\!\gamma \Gamma (t{-}\tau ) u_\text {hist}(\tau ,x) \;\!\mathrm {d}\tau + \int _0^t \!\!\gamma \Gamma (t{-}\tau )u(\tau ,x)\;\!\mathrm {d}\tau = \int _0^\infty \!\! \gamma \Gamma (\widetilde{\tau }) u(t{-}\widetilde{\tau },x ) \;\!\mathrm {d}\widetilde{\tau }. \end{aligned}$$

For systems of the type (3.1) the existence of traveling waves, in particular pulses, is studied in [17] in detail, even in cases where Hypothesis (H2) is violated, i.e. $\Gamma$ may change sign. The latter is necessary to handle non-monotone fronts and pulses. Therefore, the assumptions in [17] are more general with respect to the types of traveling waves (e.g. pulses, non-monotone fronts) under consideration.

However, when studying only traveling fronts, the assumptions of the present article are much more general, since (H2) does not require any assumptions on the (exponential) structure of $\Gamma$. In particular, we believe that our approach may be generalized to nonlinear coupling terms as in Sect. 3.5, whereas the approach in [17] relies on the linear structure of the equations for $w_i$. Moreover, the present approach allows to calculate bounds on the wave speed, see Theorem 2.5 and Corollary 2.10.

3.2 The Two-Scale Homogenization Model

A significant body of work (cf. [3, 6, 9, 18, 19, 23, 29]) considers the propagation of waves in periodic media. If the period of the oscillating coefficient is very small one can perform a homogenization and consider traveling waves in the homogenized system. However, often the diffusion coefficients of some of the species are very small as well, which leads to a coupled system of the form

$$\begin{aligned} \left. \begin{aligned} {\dot{u}}&= \mathop {\mathrm {div}}\nolimits \big ( {{\mathbb {D}}}_{\mathrm u}(\tfrac{1}{\varepsilon }x)\nabla u\big ) + f_{\mathrm u}(\tfrac{1}{\varepsilon }x, u,w)\\ \dot{w}&=\mathop {\mathrm {div}}\nolimits \big (\varepsilon ^2 {{\mathbb {D}}}_{\mathrm w}(\tfrac{1}{\varepsilon }x) \nabla w\big ) + f_{\mathrm w}(\tfrac{1}{\varepsilon }x, u,w) \end{aligned} \right\} \quad t>0,\ x\in \Omega . \end{aligned}$$

(3.3)

Here the functions ${{\mathbb {D}}}_{\mathrm u}$, ${{\mathbb {D}}}_{\mathrm w}$, $f_{\mathrm u}(\cdot ,u,w) \in {{\mathbb {R}}}^{m_{\mathrm u}}$, and $f_{\mathrm w}(\cdot , v,w)\in {{\mathbb {R}}}^{m_{\mathrm w}}$ are assumed to be 1-periodic in each component of $y=\frac{1}{\varepsilon }x\in {{\mathbb {R}}}^d$.

It is shown in [22] that under suitable conditions on the diffusion matrices ${{\mathbb {D}}}_{\mathrm u}$ and ${{\mathbb {D}}}_{\mathrm w}$ and the reaction terms $f_{\mathrm u}$ and $f_{\mathrm w}$ the solutions $(u_\varepsilon ,w_\varepsilon )$ to the initial value problem converge in the limit $\varepsilon \rightarrow 0$ to solutions (U, W) of the following two-scale model. For this we denote by ${{\mathbb {T}}}^d={{\mathbb {R}}}^d/{{\mathbb {Z}}}^d$ the d-dimensional torus obtained by identifying the opposite sides of the unit cube. While the fast diffusion of the variable $u_\varepsilon$ guarantees that the limit U only depends on the macroscopic variable $x \in \Omega$, the limit W of the solutions $w_\varepsilon$ is a two-scale function depending also on the microscopic variable $y\in {{\mathbb {T}}}^d$:

$$\begin{aligned} {\dot{U}}(t,x)&= \mathop {\mathrm {div}}\nolimits _x\big ( {{\mathbb {D}}}_{\mathrm u}^\text {eff}\nabla _x U(t,x)\big ) + \int _{{{\mathbb {T}}}^d} f_{\mathrm u}(y, U(t,x),W(t,x,y)) \;\!\mathrm {d}y&\text {in }\Omega , \end{aligned}$$

(3.4a)

$$\begin{aligned} \dot{W}(t,x,y)&=\mathop {\mathrm {div}}\nolimits _y\big ({{\mathbb {D}}}_{\mathrm w}(y) \nabla _y W(t,x,y)\big ) + f_{\mathrm w}(y, U(t,x),W(t,x,y))&\text {in }\Omega {\times }{{\mathbb {T}}}^d. \end{aligned}$$

(3.4b)

Here ${{\mathbb {D}}}_{\mathrm u}^\text {eff}$ is the effective diffusion tensor obtained by classical homogenization, see e.g. [5]. The main point in this theory is that it is not possible to replace the slowly diffusing component $w^\varepsilon$ by its macroscopic average. We rather need to keep track of the microscopic distribution of the $w^\varepsilon$ relative to the underlying periodic microstructure. This is exactly done by the function W depending on x and y.

The original theory in [22] and [26] was developed for bounded Lipschitz domains $\Omega \subset {{\mathbb {R}}}^d$. We show in “Appendix A” how the result can be generalized to equations posed on the full space $\Omega ={{\mathbb {R}}}^d$, which is needed to treat traveling waves. For this one introduces the weighted Lebesgue spaces

$$\begin{aligned} {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d)&:= \Big \{\, u \in {\mathrm{L}}^2_\mathrm {loc}({{\mathbb {R}}}^d) \; \Big | \; \Vert u \Vert ^2_{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d)}} := \int _{{{\mathbb {R}}}^d} \varrho (x) |u(x)|^2 \;\!\mathrm {d}x< \infty \,\Big \} , \nonumber \\ {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d)&:= \Big \{\, U \in {\mathrm{L}}^2_\mathrm {loc} ({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d) \; \Big | \; \Vert U \Vert _{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d\times {{\mathbb {T}}}^d)}}^2 := \int _{{{\mathbb {R}}}^d\times {{\mathbb {T}}}^d} \varrho (x) |U(x,y)|^2 \;\!\mathrm {d}x \;\!\mathrm {d}y < \infty \,\Big \} , \end{aligned}$$

(3.5)

where for a radius $R>0$ we set $\varrho (x)=1/\cosh (|x|/R)$. With this and the natural conditions on ${{\mathbb {D}}}_{\mathrm u}$, ${{\mathbb {D}}}_{\mathrm w}$, $f_{\mathrm u}$, and $f_{\mathrm w}$ we derive the following result in “Appendix A”.

Theorem 3.1

(Two-scale homogenization) Let $(u_\varepsilon , w_\varepsilon )_{\varepsilon >0}$ denote a sequence of solutions to the initial value problem (3.3) on $\Omega ={{\mathbb {R}}}^d$ with initial conditions $(u_\varepsilon ^0,w_\varepsilon ^0)=(u_\varepsilon (0,\cdot ), w_\varepsilon (0,\cdot ))$ that form a bounded sequence in ${\mathrm{L}}^\infty ({{\mathbb {R}}}^d)^{m_{\mathrm u}+m_{\mathrm w}}$ and converge as follows:

$$\begin{aligned} u_\varepsilon ^0 \rightarrow U^0 \text { in } {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d) \quad \text {and}\quad w_\varepsilon ^0 {{\,\mathrm{\xrightarrow {2s}}\,}}W^0 \text { in } {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d) , \end{aligned}$$

then the solution $(u_\varepsilon , w_\varepsilon )$ converges to the solution (U, W) of the two-scale system (3.4),

where $\widetilde{U} \in {\mathrm{L}}^2([0,T] \times \Omega ; {\mathrm{H}}^1({{\mathbb {T}}}^d))$ with $\int _{{{\mathbb {T}}}^d} \widetilde{U} \;\!\mathrm {d}y = 0$ denotes the corrector function.

The major advantage of the two-scale model (3.4) is that it is again homogeneous in the macroscopic spatial variable $x\in {{\mathbb {R}}}^d$, while the periodic structure is restricted to the microscopic variable $y\in {{\mathbb {T}}}^d$. Thus, we have a coupling that is local in $x\in {{\mathbb {R}}}^d$ from $U(s,x)\in {{\mathbb {R}}}^{m_{\mathrm u}}$ to $W(s,x,\cdot )\in {\mathrm{H}}^1({{\mathbb {T}}}^d)^{m_{\mathrm w}}$. At later times $t>s$ the internal parabolic evolution of $W(t,x,\cdot )$ via (3.4b) leads to a delayed feedback of U(s, x) for all $s<t$ of memory type.

In particular, it is possible to look for exact traveling waves for (3.4) in the form

$$\begin{aligned} (U(t,x),W(t,x,y))= ({\mathcal {U}}(x{-}\texttt {c}t), {\mathcal {W}}(x{-}\texttt {c}t,y)) \in {{\mathbb {R}}}^{m_{\mathrm u}+m_{\mathrm w}}. \end{aligned}$$

Transforming these two-scale solutions back into the one-scale form (called folding in [21, 22]) one obtains periodically oscillating traveling waves, namely

$$\begin{aligned} ({\widetilde{u}}_\varepsilon (t,x), {\widetilde{w}}_\varepsilon (t,x))= ({\mathcal {U}}(x{-}\texttt {c}t), {\mathcal {W}}(x{-}\texttt {c}t,\frac{1}{\varepsilon }x)) \end{aligned}$$

that provide the correct first-order approximation of the true solutions $(u_\varepsilon ,w_\varepsilon )$, see Fig. 4 for a plot of such solutions.

3.3 Reduction to a Scalar Equation

Here we give an explicit example for deriving a scalar memory equation from a two-scale system with $(u,w) \in {{\mathbb {R}}}^1{\times }{{\mathbb {R}}}^1$. We start by looking at a specific case for the full time-dependent system (3.4), namely the FitzHugh-Nagumo case where U and W are scalar and are defined on the real line $\Omega = {{\mathbb {R}}}$. Moreover, we assume linear couplings with $f_{\mathrm u}(y,U,W) = \Phi (y,U) + \alpha (y)W$ and $f_{\mathrm w}(y,U,W) = - {\widehat{\lambda }}(y) W + \beta (y)U$:

$$\begin{aligned} {\dot{U}}(t,x)\quad&= D_{\mathrm u}U_{xx}(t,x) +\int _{{{\mathbb {T}}}} \Phi (y,U(t,x) )\;\!\mathrm {d}y + \int _{{{\mathbb {T}}}} \alpha (y) W(t,x,y)\;\!\mathrm {d}y, \end{aligned}$$

(3.6a)

$$\begin{aligned} \dot{W}(t,x,y)&= \left( {{\mathbb {D}}}_{\mathrm w}(y) W_{y}(t,x,y) \right) _y - {\widehat{\lambda }} (y)W(t,x,y) + \beta (y)U(t,x) , \end{aligned}$$

(3.6b)

where ${{\mathbb {T}}}={{\mathbb {T}}}^1={{\mathbb {R}}}_{\!/{{\mathbb {Z}}}}$. All functions $\Phi$, $\alpha$, $\beta$ and ${\widehat{\lambda }}$ are assumed to be continuous. In general, the coupling parameters $\alpha (y)$ and $\beta (y)$ may change sign, while the microscopic diffusion coefficient ${{\mathbb {D}}}_{\mathrm w}(y)$ and the damping factor ${\widehat{\lambda }}$ are assumed to be strictly positive. The solution $\psi (t,y)$ of the linear equation ${\dot{\psi }}=({{\mathbb {D}}}(y)\psi _y)_y - {\widehat{\lambda }} (y)\psi$, $\psi (0,\cdot )=\psi ^0$ has the semigroup representation $\psi (t,y)=\int _{{\mathbb {T}}}H(t,y,\widetilde{y}) \psi ^0(\widetilde{y})\;\!\mathrm {d}\widetilde{y}$, where the Green’s function $H(t,y,\widetilde{y})$ is strictly positive for $t>0$ by the maximum principle for linear parabolic equations, see e.g. [12, Thm. 12, p. 376].

By introducing the effective nonlinearity $F(U):= \int _{{\mathbb {T}}}\Phi (y,U)\;\!\mathrm {d}y$ and expressing W as a linear functional over the history of U via (3.6b), we obtain a Nagumo equation with memory kernel:

$$\begin{aligned} \begin{aligned}&{\dot{U}}(t,x) = U_{xx}(t,x) + F(U(t,x)) + \int _0^{\infty }\! {\widehat{\Gamma }}(\tau ) U(t{-}\tau ,x)\;\!\mathrm {d}\tau \\&\text {with } {\widehat{\Gamma }}(\tau )= \int _{{{\mathbb {T}}}} \int _{{{\mathbb {T}}}} H(\tau ,y,\widetilde{y}) \alpha (\widetilde{y}) \beta (y) \;\!\mathrm {d}y \;\!\mathrm {d}\widetilde{y} . \end{aligned} \end{aligned}$$

(3.7)

Thus, using $H> 0$ a sufficient condition for ${\widehat{\Gamma }}(\tau )\ge 0$ in our Hypothesis (H2) is given by $\alpha (y), \beta (y)\ge 0$ for all $y \in {{\mathbb {T}}}$ or vice versa $\alpha (y),\beta (y)\le 0$.

Remark 3.2

(On the positivity of ${\widehat{\Gamma }}$) The given conditions on $\alpha$ and $\beta$ are far from optimal. Indeed, writing ${{\mathbb {L}}}\psi =-({{\mathbb {D}}}_{\mathrm w}\psi _y)_y + {\widehat{\lambda }} \psi$ we find a complete orthonormal set $(\psi _n)_{n\in {{\mathbb {N}}}}$ in ${\mathrm{L}}^2({{\mathbb {T}}})$ of eigenfunctions, i.e. ${{\mathbb {L}}}\psi _n =\lambda _n \psi _n$ with $0<\lambda _1\le \lambda _2 \le \cdots \le \lambda _n \rightarrow \infty$.

Expanding the coupling coefficients $\alpha (y)=\sum _{{\mathbb {N}}}a_n\psi _n(y)$ and $\beta (y)=\sum _{{\mathbb {N}}}b_n\psi _n(y)$, we find ${\widehat{\Gamma }}(\tau )=\sum _{n=1}^\infty \mathrm {e}^{-\lambda _n \tau } a_n b_n$, and conclude that the property $a_nb_n\ge 0$ for all $n\in {{\mathbb {N}}}$ is sufficient. Hence, setting $\alpha (y)=\beta (y)=\psi _n(y)$ and noticing that, by the Sturm-Liouville property, the function $\psi _n$ has $\lfloor \frac{n-1}{2} \rfloor$ zeros, we have constructed an example for $\alpha$ and $\beta$ that change sign and still satisfy ${\widehat{\Gamma }}(\tau )\ge 0$.

However, it is not even necessary that all of the products $a_nb_n$ are nonnegative, see the arguments after (3.2). In [17] the explicit choices $\alpha (y)= - \sum _{n=1}^{m_*} \psi _n(y)$ and $\beta (y)=\sum _{n=1}^{m_*} \sigma _n \psi _n(y)$ were made, and different signs for $\sigma _n$ are explicitly allowed.

3.4 A Homogenization Example

In the spirit of Remark 3.2 we consider the two-scale system (3.6) in a specific example fulfilling all the assumptions of our theory. For the operator ${{\mathbb {L}}}W := -W_{yy} + W$ we have the eigenfunctions $\psi _{2n}(y) = \sqrt{2} \sin (2\pi n y)$ with eigenvalues $\lambda _{2n} =1{+}(2\pi n)^2$. We set

$$\begin{aligned} \alpha (y) = \psi _2(y) + \psi _4(y) \quad \text {and}\quad \beta (y) = \psi _2(y) + 10 \, \psi _4(y) - \psi _6(y) . \end{aligned}$$

Hence, Hypothesis (H2) is satisfied with $\gamma =\int _0^\infty {\widehat{\Gamma }}(\tau )\;\!\mathrm {d}\tau = 1/\lambda _2 + 10/\lambda _4 \approx 0.08763> 0$. Notice that the coupling coefficients $\alpha (\cdot )$ and $\beta (\cdot )$ do not change sign simultaneously. For the cubic function, we choose $F(u) = -u(u{-}0.25)(u{-}1)$. For this choice of parameters, the two-scale solution (U, W) is depicted in Fig. 3, where the microscopic average of the component W vanishes, since the constant eigenfunction $\psi _1(y)=1$ is not activated because of $\langle \psi _1,\beta \rangle =0$. However, the periodic oscillations of W on the micro-scale are captured by the two-scale limit.

Fig. 3

The front (U, W) of the two-scale system (3.6) moves from right to left in x. Left: U and average $\int _{{\mathbb {T}}}W(t,x,y) \;\!\mathrm {d}y$. Right: the W(t, x, y)-component in (x, y)-plane

We can compare the solution (U, W) of our two-scale limit system with the solution $(u_\varepsilon , w_\varepsilon )$ of the original system (3.4) with rapidly oscillating coefficients. In Fig. 4 one can observe that the $\varepsilon$-periodic coupling coefficients induce $\varepsilon$-periodic oscillations of the solutions. Whereas the amplitude of the oscillations of the component $w_\varepsilon$ is of order O(1), the positive diffusion $D_{\mathrm u}$ reduces the amplitude of the oscillations of the component $u_\varepsilon$ to order $O(\varepsilon )$, such that it vanishes in the limit $\varepsilon \rightarrow 0$. Notice that the component $w_\varepsilon$ also changes sign. Overall, the effective behavior of the oscillating solution $(u_\varepsilon ,w_\varepsilon )$ is nicely captured by the two-scale limit (U, W).

Fig. 4

Solutions $(u_\varepsilon , w_\varepsilon )$ of the original system (3.4): left $\varepsilon {=} 2.5$, right $\varepsilon {=} 0.25$

3.5 Possible Generalizations

For mathematical conciseness we have decided to restrict ourselves to memory terms with a simple linear structure. However, as our theory is mainly based on the quite general work in [10] it is clear that the results can be generalized in several ways.

First, the integral memory can be replaced by discrete time delays in the form such that the equation reads

$$\begin{aligned} {\dot{u}}(t,x) = D u_{xx}(t,x) + F(u(t,x)) + \sum _{j=1}^{j_*} \gamma _j u(t{-}\tau _j,x). \end{aligned}$$

(3.8)

Assuming $\gamma _j>0$ and setting $\gamma =\sum _{j=1}^{j_*} \gamma _j$, we obtain the memory equation (2.1) with a $\Gamma (\tau )=\sum _{j=1}^{j_*} \frac{\gamma _j}{\gamma } \, \delta _{\tau _j}(\tau )$. We refer to [28] for a general approach to traveling waves in reaction–diffusion equations involving linear and nonlinear delay terms.

Secondly, further generalizations can be obtained by looking at nonlinear couplings to ODEs, thus generalizing the coupled system (3.1):

$$\begin{aligned} {\dot{u}}= Du_{xx} +F(u)+ \sum _{i=1}^{m_{\mathrm w}} A_i(u,w_i), \qquad \dot{w}_i = - \lambda _i w_i + B_i(u), \end{aligned}$$

(3.9)

where the coupling functions $A_i:{{\mathbb {R}}}^2\rightarrow {{\mathbb {R}}}$ and $B_i:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ are assumed to be smooth functions with derivatives satisfying $\partial _u A(u,w_i)\le 0$, $\partial _{w_i} A_i(u,w_i)\ge 0$, and $B'_i(u)\ge 0$. Again we can express $w_i(t,x)$ as memory functional depending on u(s, x) for $s \in {]{-}\infty ,t[}$. Hence, (3.9) can be written in the form

$$\begin{aligned}&{\dot{u}}(t,x)= Du_{xx}(t,x) +F(u(t,x))+ \sum _{i=1}^{m_{\mathrm w}} A_i\big (u(t,x), {\mathsf {I}}\Gamma _i{*}B_i(u(\cdot ,x))(t) \big ), \\&\text {where } {\mathsf {I}}\Gamma _i{*}h(t)= \int _0^\infty \mathrm {e}^{-\lambda _i \tau } h(t{-}\tau ) \;\!\mathrm {d}\tau . \end{aligned}$$

Hence we have a memory in time, which is local in the space variable $x\in {{\mathbb {R}}}$. As in Sect. 2.2 we can introduce an auxiliary wave speed $\texttt {v}$ and turn the memory terms into spatially nonlocal terms. Because of our assumptions on $A_i$ and $B_i$ we are exactly in the setting of [10, Eqn. (1.14)]. Thus, it is expected that the methods developed here can be extended to such nonlinear couplings.

Thirdly, it seems possible to generalize the theory to handle multidimensional traveling waves in a cylindrical domain $\Omega ={{\mathbb {R}}}{\times }\Sigma$ as in [14], but now with memory terms.

$$\begin{aligned} {\dot{u}}(t,x,y)&= D\big (u_{xx}(t,x,y)+\Delta _y u(t,x,y)\big )\\&\quad +\, F(y,u(t,x,y))+ \gamma \int _0^\infty \Gamma (\tau ) u(t{-}\tau ,x,y) \;\!\mathrm {d}\tau&\text {for } t>0,\ (x,y)\in {{\mathbb {R}}}{\times }\Sigma , \\ 0&= u(t,x,y)&\text {for }t>0,\ (x,y)\in {{\mathbb {R}}}{\times }\partial \Sigma . \end{aligned}$$

However, then the “bistability” Hypothesis (H1) has to be formulated in terms of the elliptic problem $u \mapsto D\Delta _y u +F(u)+ \gamma u$ in $\Sigma$, which should have exactly three solutions $u^\gamma _\alpha \in {\mathrm{H}}^1_0(\Sigma )$ with appropriate properties.

4 Applications to the Cubic Case

In this section we study the classical FitzHugh-Nagumo system with a bistable cubic nonlinearity, namely

$$\begin{aligned} {\dot{u}} = u_{xx} +F(u) -\beta w, \qquad \dot{w} = -w+u ,\quad F(u)=-u(u{-}a)(u{-}1), \end{aligned}$$

(4.1)

where $a\in {]0,1[}$. Concerning traveling fronts, this system is equivalent to the memory equation

$$\begin{aligned} {\dot{u}}(t,x) = u_{xx}(t,x) +F(u(t,x) ) -\beta \int _0^\infty \mathrm {e}^{-\tau } u(t{-}\tau ,x) \;\!\mathrm {d}\tau . \end{aligned}$$

(4.2)

For general solutions, the equations (4.1) and (4.2) are equivalent for suitable initial conditions as discussed in Sect. 3.1. In particular, our previous parameter $\gamma$ is given by $\gamma =-\beta$, such that our theory developed above only applies for $\beta \le 0$. However, in the numerical simulations documented below, we are free to choose $\beta >0$ as well.

We first observe that the nonlinearity

$$\begin{aligned} F_{-\beta }(u)=-u(u{-}a)(u{-}1) - \beta u \end{aligned}$$

has a bistable structure if and only if $\beta < (1{-}a)^2/4$ and then

$$\begin{aligned} u^{-\beta }_-=0,\quad u^{-\beta }_{\mathrm{m}} = \frac{1{+}a}{2} - \frac{1}{2}\sqrt{(1{-}a)^2-4\beta }, \quad u^{-\beta }_+ = \frac{1{+}a}{2} + \frac{1}{2}\sqrt{(1{-}a)^2-4\beta }. \end{aligned}$$

In [20], the wave speed of the local model ${\dot{u}}=u_{xx}+F_{-\beta }(u)$ is calculated explicitly:

$$\begin{aligned} \texttt {C}^\mathrm {FN}(-\beta ,0):= \frac{1}{\sqrt{2}}\big ( 2u^{-\beta }_{\mathrm{m}}- u^{-\beta }_+\big ) = \frac{1}{2\sqrt{2}} \Big ( 1{+}a - 3\sqrt{(1{-}a)^2-4\beta }\, \Big ). \end{aligned}$$

In the case $\beta =0$ there is no coupling between the ODE and the PDE and $\texttt {c}_0=\texttt {C}^\mathrm {FN}(0,0)= (2a{-}1)/{\sqrt{2}}$ is explicitly given.

For $a\in {]\frac{1}{2},1[}$, which we assume from now on, the function $\beta \mapsto \texttt {C}^\mathrm {FN}({-}\beta ,0)$ changes sign at

$$\begin{aligned} \beta _0(a) = \tfrac{1}{9} \big ( 2a^2{-}5a {+} 2 \big ) \in {]{-}\tfrac{1}{9} ,0[}. \end{aligned}$$

With $\texttt {C}^\mathrm {FN}(0,0)=(2a{-}1)/{\sqrt{2}}>0$, we obtain $\texttt {C}^\mathrm {FN}(-\beta ,0)>0$ for $\beta \in {]\beta _0(a),\frac{1}{4}(1{-}a)^2]}$ and $\texttt {C}^\mathrm {FN}(-\beta ,0)<0$ for $\beta < \beta _0(a)$.

From this, we see that we can apply our existence theory in Theorem 2.8 and obtain a unique traveling front for the FitzHugh-Nagumo system (4.1), or equivalently for the memory equation (4.2) for all $\beta \le 0$. This front connects the values $u^{-\beta }_-=0$ and $u^{-\beta }_+$, and using Corollary 2.10 it travels with the speed $\texttt {c}_{-\beta }$ satisfying the bound

$$\begin{aligned} \begin{array}{ll} 0\le \texttt {c}_{-\beta } \le \texttt {C}^\mathrm {FN}({-}\beta ,0) &{} \quad \text {for } \beta \in [ \beta _0(a),0], \\ \texttt {C}^\mathrm {FN}({-}\beta ,0) \le \texttt {c}_{-\beta } \le 0&{} \quad \text {for } \beta \le \beta _0(a). \end{array} \end{aligned}$$

For numerical simulations we choose $a=0.6$ determine $\texttt {c}_{-\beta }$ on the whole bistable regime $\beta \le (1{-}a)^2/4=0.04$. For this case, we have $\texttt {c}_0=\texttt {C}^\mathrm {FN}(0,0)=0.2/\sqrt{2}\approx 0.1414$ and

$$\begin{aligned} \texttt {C}^\mathrm {FN}(-\beta ,0)= \frac{1}{2\sqrt{2}}\big (1.6-3\sqrt{0.4^2-4\beta }\,\big ) \approx 0.566-2.12\sqrt{0.04{-}\beta } \end{aligned}$$

as upper or lower bound for $\texttt {c}_{-\beta }$. Moreover, we know that $\texttt {C}^\mathrm {FN}({-}\beta ,0)$ changes sign at $\beta _0(0.6)= -0.28/9\approx -0.0311$.

To determine the speed of the traveling front numerically, we solve the coupled system (4.1) starting from front-like initial data with the correct plateau $(u,w) =(u^{-\beta }_+,u^{-\beta }_+)$ for large x and $(u,w) =(0,0)$ for small x. The solution rapidly stabilizes into the front and the speed $\texttt {c}_{-\beta }$ can be measured. The numerical simulations nicely confirm the bounds on the wave speed $\texttt {c}_{-\beta }$ in Corollary 2.10. For all $\beta < \beta _0(0.6) \approx -0.0311$, Fig. 5 shows $\texttt {C}(-\beta , 0) \le \texttt {c}_{-\beta } \le 0$.

Fig. 5

The region $\beta \in [-5,-0.03]$ was sampled with $\beta$-steps of size 0.01 to find $\texttt {c}_{-\beta } \in [\texttt {C}^\mathrm {FN}(-\beta ,0),0]$.

Fig. 6

The region $\beta \in [-0.06,0.04]$ was sampled with $\beta$-steps of size 0.001 to compare $\texttt {c}_{-\beta }$ and $\texttt {C}(-\beta ,0)$ in the upper figure. As the two graphs differ only little, the lower figure displays $c_{-\beta } - \texttt {C}(-\beta ,0)$, where the sign changes at $\beta =\beta _0(0.6)\approx -0.0311$ and $\beta =0$ are clearly visible

For $\beta \in [\beta _0(0.6),0]$ Fig. 6 shows $0 \le \texttt {c}_{-\beta } \le \texttt {C}^\mathrm {FN}(-\beta ,0)$ as predicted by the theory. For positive $\beta \in {]0,0.04[}$ Theorem 2.8 does not apply, however, the comparison argument in (2.17) predicts the reverse relation $\texttt {c}_{-\beta } \ge \texttt {C}^\mathrm {FN}(-\beta ,0) \ge 0$, which is confirmed in the simulations, which also show that $\texttt {c}_{-\beta }$ and $\texttt {C}^\mathrm {FN}(-\beta ,0)$ only differ less than a percent in relative size for all $\beta \in [-0.06,0.03]$. Moreover, the identities $\texttt {c}_{-\beta }=\texttt {C}^\mathrm {FN}(-\beta ,0)$ are confirmed for $\beta =\beta _0(0.6)$ and $\beta =0$.

Two-Scale Convergence in Weighted Sobolev Spaces

The aim of this appendix is to explain how the result in Theorem 3.1 for $\Omega ={{\mathbb {R}}}^d$ can be derived by generalizing the theory for bounded Lipschitz domains $\Omega \subset {{\mathbb {R}}}^d$ as developed in [22, 26]. To this end we introduce a few notations from two-scale convergence and two-scale homogenization as developed in [2, 8, 21, 25]. For arbitrary (bounded or unbounded) Lipschitz domains $\Omega \subseteq {{\mathbb {R}}}^d$, we set

$$\begin{aligned} {\mathcal {T}}_\varepsilon : {\mathrm{L}}^2(\Omega ) \rightarrow {\mathrm{L}}^2({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d); \quad ({\mathcal {T}}_\varepsilon u)(x,y) := u_\mathrm {ex} \left( \varepsilon \left[ \tfrac{x}{\varepsilon } \right] + \varepsilon y \right) , \end{aligned}$$

where $u_\mathrm {ex} \in {\mathrm{L}}^2({{\mathbb {R}}}^d)$ is obtained by extension with 0 on ${{\mathbb {R}}}^d \backslash \Omega$ and $[z] \in {{\mathbb {Z}}}^d$ denotes the integer part for any $z \in {{\mathbb {R}}}^d$. We define weak and strong two-scale convergence via

We briefly recall the mathematical setting for the $\varepsilon$-problem (3.3) such that the two-scale system (3.4) is rigorously justified. The fourth order diffusion tensors ${{\mathbb {D}}}_{\mathrm i}\in \mathrm {Lin}({{\mathbb {R}}}^{d {\times }m_{\mathrm i}}; {{\mathbb {R}}}^{d {\times }m_{\mathrm i}})$ are uniformly elliptic and bounded, i.e. there exist constants $M, \mu > 0$ such that

$$\begin{aligned} {{\mathbb {D}}}_{\mathrm i}(y) \xi : \xi \ge \mu |\xi |^2 \quad \text {and}\quad |{{\mathbb {D}}}_{\mathrm i}(y) \xi | \le M |\xi | \quad \text {for all } \xi \in {{\mathbb {R}}}^{d{\times }m_{\mathrm i}} \text { and } {\mathrm i}\in \{{\mathrm u},{\mathrm w}\}, \end{aligned}$$

and they are not necessarily symmetric. For the reaction terms we assume boundedness $f_{\mathrm i}(\cdot ,u,w) \in {\mathrm{L}}^\infty ({{\mathbb {T}}}^d)$ and global Lipschitz continuity, i.e. there exists $L>0$ such that for $u_1,u_2 \in {{\mathbb {R}}}^{m_{\mathrm u}}$ and $w_1,w_2 \in {{\mathbb {R}}}^{m_{\mathrm w}}$

$$\begin{aligned} |f_{\mathrm i}(y,u_1,w_1) - f_{\mathrm i}(y,u_2,w_2)| \le L(|u_1 {-} u_2| + |w_1 {-} w_2|) \quad \text {for } {\mathrm i}\in \{{\mathrm u},{\mathrm w}\} . \end{aligned}$$

In addition to the weighted Lebesgue spaces ${\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d)$ and ${\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d)$ from (3.5), we also define the weighted Sobolev spaces ${\mathrm{H}}^1_\varrho ({{\mathbb {R}}}^d)$ and ${\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d; {\mathrm{H}}^1({{\mathbb {T}}}^d))$ via

$$\begin{aligned} {\mathrm{H}}^1_\varrho ({{\mathbb {R}}}^d)&:= \Big \{\, u \in {\mathrm{H}}^1_\mathrm {loc}({{\mathbb {R}}}^d) \; \Big | \; \Vert u \Vert _{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d)}} + \Vert \nabla u \Vert _{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d)}}< \infty \,\Big \} , \\ {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d; {\mathrm{H}}^1({{\mathbb {T}}}^d))&:= \Big \{\, U \in {\mathrm{L}}^2_\mathrm {loc}({{\mathbb {R}}}^d; {\mathrm{H}}^1({{\mathbb {T}}}^d)) \; \Big | \; \Vert U \Vert _{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d)}} + \Vert \nabla _y U \Vert _{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d)}} < \infty \,\Big \} . \end{aligned}$$

Our choice $\varrho (x)=1/\cosh (|x|/R)$ gives $\varrho , \varrho ^{-1} \in {\mathrm{L}}^1_\mathrm {loc}({{\mathbb {R}}}^d)$, which implies that the weighted Lebesgue and Sobolev spaces are Banach spaces, see e.g. [15, Thm. 1]. Moreover, introducing the scalar product $(u,v)_{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d)}} := (\sqrt{\varrho } u , \sqrt{\varrho } v )_{\mathrm{L^2({{\mathbb {R}}}^d)}}$ yields that they are also separable Hilbert spaces. The proof of Theorem 3.1 follows along the lines of [22, Thm. 4.1] and [26, Thm. 2.1.1, Thm. 2.2.1] with the following modifications.

• The definition of the periodic unfolding operator

  $$\begin{aligned} {\mathcal {T}}_\varepsilon : {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d) \rightarrow {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d {\times }{{\mathbb {T}}}^d); \quad ({\mathcal {T}}_\varepsilon v)(x,y) := v \left( \varepsilon \left[ \tfrac{x}{\varepsilon } \right] + \varepsilon y \right) \end{aligned}$$

  is immediate and the notion of two-scale convergence follows analogously. Notice that the assumptions on the weight function imply the unfolding estimate

  $$\begin{aligned} \Vert {\mathcal {T}}_\varepsilon \varrho - \varrho \Vert _{\mathrm{L^\infty ({{\mathbb {R}}}^d{\times }{{\mathbb {T}}}^d)}} \le \varepsilon \sqrt{d} \Vert \nabla \varrho \Vert _{\mathrm{L^\infty ({{\mathbb {R}}}^d)}} \le \varepsilon \sqrt{d} /R. \end{aligned}$$

  Hence, we obtain the upper bound for unfolded functions $v \in {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d)$

  $$\begin{aligned} \Vert {\mathcal {T}}_\varepsilon v \Vert _{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d {\times }{{\mathbb {T}}}^d)}} \le C^*_\varepsilon \Vert v \Vert _{\mathrm{L^2_\varrho ({{\mathbb {R}}}^d)}} \quad \text {with}\quad C^*_\varepsilon = \big ( 1 - \varepsilon \sqrt{d}/R \big )^{-1/2} . \end{aligned}$$

• The standard compactness results for two-scale convergence [2, 21, 25] also hold for weighted spaces, since they are, in particular, separable Banach spaces and the Banach–Alaoglu Theorem is applicable.

• The definition of the gradient folding operator $\mathcal {G}^\mathrm {slow}_\varepsilon$ (cf. [22, Def. 3.5]) needs to be adapted as follows: In the case of slow diffusion of order $O(\varepsilon ^2)$, we define for $W \in {\mathrm{L}}^2_\varrho ({{\mathbb {R}}}^d; {\mathrm{H}}^1({{\mathbb {T}}}^d))$ the one-scale function $\mathcal {G}^\mathrm {slow}_\varepsilon W := {\hat{w}}_\varepsilon \in {\mathrm{H}}^1_\varrho ({{\mathbb {R}}}^d)$, which is given by the Lax–Milgram lemma as the unique solution of the elliptic problem

  $$\begin{aligned} \int _{{{\mathbb {R}}}^d} \big [ \sqrt{\varrho } {\hat{w}}_\varepsilon - \mathcal {F}_\varepsilon \left( \sqrt{\varrho } W\right) \big ] \cdot \sqrt{\varrho } \varphi + \big [ \varepsilon \sqrt{\varrho } \nabla {\hat{w}}_\varepsilon - \mathcal {F}_\varepsilon \left( \sqrt{\varrho } \nabla _y W\right) \big ] : \varepsilon \sqrt{\varrho } \nabla \varphi \;\!\mathrm {d}x = 0 \end{aligned}$$

  for all $\varphi \in {\mathrm{H}}^1_\varrho ({{\mathbb {R}}}^d)$.

• For the slowly diffusing species $w_\varepsilon$, we choose the test function $\varphi ^\mathrm {slow}_\varepsilon = \varrho \left( w_\varepsilon {-} \mathcal {G}^\mathrm {slow}_\varepsilon W \right)$ and continue as in [22, 26]. For species $u_\varepsilon$ undergoing diffusion of order O(1), we proceed analogously (cf. [26, Def. 1.2.7]) and choose the test function $\varphi ^\mathrm {stand}_\varepsilon = \varrho \left( u_\varepsilon -\mathcal {G}^\mathrm {stand}_\varepsilon U \right)$.

With these modifications for $\Omega ={{\mathbb {R}}}^d$, the proofs in [22, Thm. 4.1] and [26, Thm. 2.1.1, Thm. 2.2.1] can be easily adapted, and the proof of Theorem 3.1 is complete.