Skip to main content
SpringerLink
Log in

Dynamics of Suspension Bridge Equation with Delay

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

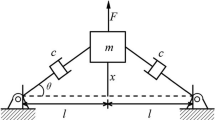
Long-time dynamics of the solutions for the suspension bridge equation with constant and time-dependent delays have been investigated, but there are no works on suspension bridge equation with state-dependent delay. Thus, we first consider the existence of pullback attractor for the non-autonomous suspension bridge equation with state-dependent delay by using the contractive function methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

There is no data were used to support this study.

References

  1. Fitzgibbon, W.E.: Semilinear functional differential equations in Banach space. J. Differ. Equ. 29, 1–14 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  2. Travis, C.C., Webb, G.F.: Existence and stability for partial functional differential equations. Transactions of AMS 200, 395–418 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  3. Wu, J. H., Theory and Applications of Partial Functional Differential Equations, Springer, New York, 1996

    Book  MATH  Google Scholar 

  4. Ruess, W. M.: Existence of solutions to partial differential equations with delay. In: Theory and applications of nonlinear operators of accretive monotone type, Lecture Notes Pure Appl. Math. vol. 178, pp. 259–288 (1996)

  5. Kunisch, K., Schappacher, W.: Necessary conditions for partial differential equations with delay to generate \(C_{0}-\)semigroups. J. Differential Equations 50, 49–79 (1983)

    Article  MATH  Google Scholar 

  6. Rezounenko, A.V.: Partial differential equations with discrete distributed state-dependent delays. J. Math Anal Appl. 326, 1031–1045 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Rezounenko, A. V., Differential equations with discrete state-dependent delay: uniqueness and well-posedness in the space of continuous functions, Nonlinear Anal. TMA, 70 (2009), 3978–3986

    Article  MathSciNet  MATH  Google Scholar 

  8. Chueshov, I., Rezounenko, A.: Finite-dimensional global attractors for parabolic nonlinear equations with state-dependent delay, Commun. Pure. Appl. Anal. 14, 1685–1704 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chueshov, I. and Rezounenko, A., Dynamics of second order in time evolution equations with state-dependent delay, Nonlinear Anal. 123–124 (2015), 126–149

    Article  MathSciNet  MATH  Google Scholar 

  10. Lazer, A.C., McKenna, P.J.: Large-amplitude periodic oscillations in suspension bridge: Some new connections with nonlinear analysis. SIAM Rev. 32, 149–155 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  11. An, Y.K.: On the suspension bridge equations and the relevant problems. Doctoral Thesis (2001)

  12. Humphreys, L. D., Numerical mountain pass solutions of a suspension bridge equation. Nonlinear Anal. (TMA) 28(1997), 1811–1826

    Article  MathSciNet  MATH  Google Scholar 

  13. Ma, Q.Z., Zhong, C.K.: Existence of strong solutions and global attractors for the coupled suspension bridge equations. J. Differential Equations 246, 3755–3775 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  14. Zhong, C. K. Ma, Q. Z. and Sun, C. Y., Existence of strong solutions and global attractors for the suspension bridge equations, Nonlinear Anal. 67(2007), 442–454

    Article  MathSciNet  MATH  Google Scholar 

  15. Ma, Q. Z. Wang, S. P. and Chen, X. B., Uniform compact attractors for the coupled suspension bridge equations, Appl. Math. Comput. 217(2011), 6604–6615

    MathSciNet  MATH  Google Scholar 

  16. Bochicchio, I., Giorgi, C., Vuk, E.: Long-term damped of the extensible suspensiom bridge. Internat. J. Differential Equations. 2010, 1–19 (2010)

    MATH  Google Scholar 

  17. Kang, J. R., Long-time behavior of a suspension bridge equatons with past history, Appl. Math. Comput. 265(2015), 509–529

    MathSciNet  MATH  Google Scholar 

  18. Park, J. Y.: Long-time behavior for suspension bridge equations with time delay, Z. Angew. Math. Phys. 69(45), 1–12, (2018)

    MathSciNet  MATH  Google Scholar 

  19. Wang, S. P. and Ma, Q. Z., Existence of pullback attractors for the non-autonomous suspension bridge equation with time delay, Discrete Contin. Dyn. Syst. Ser. B. 25 (4)(2020), 1299–1316

    MathSciNet  MATH  Google Scholar 

  20. Wang, S. P. and Ma, Q. Z., Uniform attractors for the non-autonomous suspension bridge equation with time delay, J. Inequal. Appl. 180(2019), 1–17

    MathSciNet  Google Scholar 

  21. Wang, S.P., Ma, Q.Z.: Strong pullback attractors of the non-autonomous suspension bridge equation with variable delay. Math. Probl. Eng. Art. ID 1930369, 1–12 (2019)

    Google Scholar 

  22. Chueshov, I., Dynamics of Quasi-Stable Dissipative Systems, Springer, New York, 2015

    Book  MATH  Google Scholar 

  23. Hartung, F., Krisztin, T., Walther, H-O., Wu, J. H.: Chapter 5 Functional Differential Equations with State-dependent Delays: Theory and Applications. In: Handbook of Differential Equations: Ordinary Differential Equations. North-Holland, vol. 3, pp. 435–545 (2006)

  24. Caraballo, T. Lukaszewicz, G. and Real, J., Pullback attractors for asymptotically compact non-autonomous dynamical systems, Nonlinear Anal. 64(2006), 484–498

    Article  MathSciNet  MATH  Google Scholar 

  25. Khanmamedov, A. Kh., Global attractors for a non-autonomous von Karman equations with nonlinear interior dissipation, J. Math. Anal. Appl. 318(2006), 92–101

    Article  MathSciNet  MATH  Google Scholar 

  26. Carvalho, A.N., Langa, J., Robinson, J.: Attractors for Infinite-Dimensional Non-Autonomous Dynamics Systems, Applied Mathematical Sciences, vol. 182. Springer, New York (2013)

    Book  MATH  Google Scholar 

  27. Chueshov, I.D.: Introduction to the theory of infinite-dimensional dissipative systems, acta, Kharkov, 1999, English translation (2002). http://www.emis.de/momographs/Chueshov/

  28. Walther, H.-O.: The solution manifold and \(C^{1}-\)smoothness for differential equations withstate-dependent delay. J. Differential Equations 195(1), 46–65 (2003)

    Article  Google Scholar 

  29. Walther, H-O., On Poisson’s stste-dependent delay, Discrete Contin. Dyn. Syst. 33(2013), 365–379

    Article  MathSciNet  MATH  Google Scholar 

  30. Chueshov, I., Lasiecka, I.: Von Karman Evolution Equations. Well-Posedness and Long Time Dynamics. In: Springer monographs in mathematics, Springer, New York (2010)

  31. Temam, R. (1997) Infinite dimensional dynamical dystems in mechanics and physics, 2nd edn. Springer, Berlin

    Book  MATH  Google Scholar 

Download references

Acknowledgements

We thank the referees for their insightful comments and suggestions all of which improved the presentation.

Author information

Authors and Affiliations

  1. College of Mathematics and Statistics, LongDong University, Qingyang, 745000, Gansu, China

    Suping Wang & Xukui Shao

  2. College of Mathematics and Statistics, Northwest Normal University, Lanzhou, 730070, Gansu, China

    Qiaozhen Ma

Authors
  1. Suping Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qiaozhen Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xukui Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Suping Wang.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Foundation term: This work is partly supported by the NSFC (11961059,11761062), Doctor research funding of LongDong University (XYBY1803), Innovation Fund for Higher Education of Gansu Province, (No 2021B-270)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, S., Ma, Q. & Shao, X. Dynamics of Suspension Bridge Equation with Delay. J Dyn Diff Equat 35, 3563–3588 (2023). https://doi.org/10.1007/s10884-022-10130-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-022-10130-9

Keywords

Mathematics Subject Classification

Search

Navigation