1 Introduction

First order coupled mode equations (CMEs) are used to describe a class of wavepackets in periodic structures [2, 3, 5, 9,10,11, 15]. They are modulation equations for the envelopes of asymptotically broad and small wavepackets. They were first studied in nonlinear optical fiber gratings, see e.g. [2, 3]. A rigorous justification of such an approximation was performed in [15] and [11] for the one dimensional cubic nonlinear wave equation. In [9] the authors derived and justified CMEs as modulation equations for the d-dimensional periodic Gross–Pitaevskii equation. These CMEs have the form

$$\begin{aligned} \begin{aligned} \mathrm{i}(\partial _tA_j+v_g^{(j)}\cdot \nabla A_j) + \sum _{r=1}^N \kappa _{jr} A_r + N_j(\vec {A})=0, \ j = 1,\dots ,N, \end{aligned} \end{aligned}$$
(1.1)

where for \(j,r\in \{1,\dots ,N\}\)

$$\begin{aligned} N_j(\vec {A})&:=\sum _{(m,n,o)\in \{1,\dots ,N\}^3} \gamma _j^{(m,n,o)}A_{m}{\overline{A}}_{n}A_{o},\\ \gamma ^{(m,n,o)}_j&\in {\mathbb {C}}, \kappa _{jr}\in {\mathbb {C}}, v_g^{(j)}\in {\mathbb {R}}^d, \end{aligned}$$

and where the matrix \(\kappa =(\kappa _{jr})_{j,r=1}^N\) is Hermitian. This system (although only for the setting with \(\kappa =0\)) was first derived in [10]. Like with all modulation equations, the application of CMEs is not limited to the Gross–Pitaevskii equation. It applies to wavepackets centered around N Bloch waves (N-wave mixing) with nonzero group velocities in models with nonlinearities that are cubic at lowest order.

The aim of this paper is to prove the existence of localized time harmonic solutions

$$\begin{aligned} \vec {A}(x,t)=e^{-\mathrm{i}\omega t} \vec {B}(x), \ |\vec {B}(x)|\rightarrow 0 \text { as } |x|\rightarrow \infty , \end{aligned}$$
(1.2)

with \(\omega \) in a gap of the linear spatial operator of (1.1). Such solutions are often called (standing) gap solitons. A necessary condition for the existence of a spectral gap is \(\kappa \ne 0\). Hence, gap solitons cannot be obtained in the setting of [10]. We prove the existence of gap solitons in an asymptotic region near a spectral edge point \(\omega _0\). The result can be interpreted as a bifurcation from the zero solution at the spectral edge.

The equation for \(\vec {B}\) is

$$\begin{aligned} \omega \vec {B}- L(\nabla )\vec {B}+\vec {N}(\vec {B})=0, \end{aligned}$$
(1.3)

where

$$\begin{aligned} L(\nabla )=\begin{pmatrix} -\mathrm{i}v_g^{(1)}\cdot \nabla &{} &{} \\ &{} \ddots &{} \\ &{} &{} -\mathrm{i}v_g^{(N)}\cdot \nabla \end{pmatrix} - \kappa . \end{aligned}$$

Our proof is constructive in that we use an asymptotic approximation of a solution \(\vec {B}\) at \(\omega = \omega _0+O(\varepsilon ^2), \varepsilon \rightarrow 0\). The approximation is a modulation ansatz with a slowly varying envelope modulating the bounded linear solution at the spectral edge \(\omega _0\). The envelope is shown to satisfy a \(d-\)dimensional nonlinear Schrödinger equation (NLS) with constant coefficients. We prove that for sufficiently smooth PT symmetric (parity time symmetric) solutions of the NLS there are solutions \(\vec {B}\) of (1.3) at \(\omega = \omega _0+O(\varepsilon ^2)\) which are close to the asymptotic ansatz. The proof is carried out in Fourier variables in \(L^1({\mathbb {R}}^d)\). It is based on a decomposition of the solution in Fourier variables according to the eigenvectors of \(L(\mathrm{i}k)\in {\mathbb {C}}^{n\times n}\) and on a nested Banach fixed point argument. The reduced bifurcation equation is a perturbed stationary nonlinear Schrödinger equation (NLS). Solitary waves are then found via a persistence argument starting from solitary waves of the unperturbed NLS. The persistence holds in a symmetric subspace thanks to a spectral stability result of Kato.

The chosen approach is similar to that used in [6,7,8]. Unlike in these papers, where \(L^2\)-based spaces were used, we work here in \(L^1\) in Fourier variables. This avoids the unfavorable scaling property of the \(L^2\) norm of functions with an asymptotically slow dependence on x, namely \(\Vert f(\varepsilon \cdot )\Vert _{L^2({\mathbb {R}}^d)}=\varepsilon ^{-d/2}\Vert f\Vert _{L^2({\mathbb {R}}^d)}\). The \(L^1-\)approach was first used in this context for the bifurcation of time harmonic gap solitons in the one dimensional wave equation in [13].

The question of the existence of solitary waves of CMEs has previously been addressed only in one dimension in [2], where an explicit family of gap solitons was found for CMEs describing the asymptotics of wavepackets in media with infinitesimally small contrast. These gap solitons are parametrized by the velocity \(v\in (-1,1)\) (after a rescaling). In [4] a numerical continuation was used to construct gap solitons also in one dimensional CMEs for finite contrast periodic structures. It was shown in [9] that for (1.1) in dimensions \(d>1\) a spectral gap of \(L(\nabla )\) does not exist for N odd and for \(N=2\). Next, a gap was found in a special case of (1.1) with \(d=2, N=4\) and standing gap solitons were computed numerically for this case. Here we assume the presence of a spectral gap and prove the existence of standing gap solitons of the form (1.2) for \(\omega \) asymptotically close to the spectrum under the condition that the spectral edge is given by an isolated extremum of the dispersion relation.

The rest of the paper consists firstly of a formal derivation of the effective NLS equation for the modulation ansatz in Sect. 2. Next, in Sect. 3 we state and prove the main approximation result. Finally, Sect. 4 presents a numerical example of a solution \(\vec {B}\) and a numerical verification of the convergence of the asymptotic error.

2 Formal Asymptotics of Gap Solitons

The formal asymptotics of localized solutions of (1.3) were performed already in [9]. We repeat here the calculation for readers’ convenience.

The spectrum of \(L(\nabla )\) can be determined using Fourier variables. We employ the Fourier transform

$$\begin{aligned} {\widehat{f}}(k):=({\mathcal {F}} f)(k):=(2\pi )^{-d/2}\int _{{\mathbb {R}}^d}f(x)e^{-\mathrm{i}k\cdot x}\, \mathrm{d}x \end{aligned}$$

with the inverse formula \(f(x)=({\mathcal {F}}^{-1} {\widehat{f}})(x)=(2\pi )^{-d/2}\int _{{\mathbb {R}}^d}{\widehat{f}}(k)e^{\mathrm{i}k\cdot x}\, \mathrm{d}k\). The spectrum of \(L(\nabla )\) is

$$\begin{aligned} \sigma (L(\nabla ))=\cup _{j \in \{1,\dots ,N\}}\lambda _j({\mathbb {R}}^d), \end{aligned}$$

where \(\lambda _j(k)\) is the eigenvalue of \(L(\mathrm{i}k)\in {\mathbb {C}}^{N\times N}\) for each \(k\in {\mathbb {R}}^d\), i.e.

$$\begin{aligned} L(\mathrm{i}k) \vec {\eta }^{(j)}(k)= \lambda _j(k)\vec {\eta }^{(j)}(k) \end{aligned}$$

for some \(\vec {\eta }^{(j)}(k) \in {\mathbb {C}}^N\setminus \{0\}\). Because \(L(\mathrm{i}k)^*=L(\mathrm{i}k)\) for all \(k\in {\mathbb {R}}^d\), we have \(\lambda _j:{\mathbb {R}}^d\rightarrow {\mathbb {R}}\). The mapping \(k\mapsto (\lambda _1(k),\dots ,\lambda _N(k))^T\) is the dispersion relation of (1.1).

The central assumptions of our analysis are

  1. (A.1)

    The spectrum \(\sigma (L(\nabla ))\subset {\mathbb {R}}\) has a gap, denoted by \((\alpha ,\beta )\) with \(\alpha <\beta \).

  2. (A.2)

    \(\omega _0\in \{\alpha ,\beta \}\) and for some \(j_0 \in {\mathbb {N}}, k_0 \in {\mathbb {B}}\) we have

    $$\begin{aligned} \omega _0=\lambda _{j}(k) \quad \text {if and only if } (j,k)=(j_0,k_0). \end{aligned}$$

As mentioned in the introduction, assumption (A.1) implies that if \(d\geqslant 2\), then \(N\geqslant 4\) and N even. Assumption (A.2) means that the spectral edge \(\omega _0\) is defined by one isolated extremum of the eigenvalue \(\lambda _{j_0}\) and that this is separated at \(k=k_0\) from all other eigenvalues.

We make the following asymptotic ansatz for a gap soliton at \(\omega = \omega _0 +\varepsilon ^2\omega _1\notin \sigma (L(\nabla ))\), where \(\varepsilon >0\) is a small parameter and \(\omega _1=O(1)\) (as \(\varepsilon \rightarrow 0\)),

$$\begin{aligned} \vec {B}_{\text {app}}(x):=\varepsilon C(\varepsilon x)e^{\mathrm{i}k_0\cdot x}\vec {\eta }^{(j_0)}(k_0). \end{aligned}$$
(2.1)

In Fourier variables this is

$$\begin{aligned} \widehat{\vec {B}}_{\text {app}}(k)=\varepsilon ^{1-d}{\widehat{C}}\left( \frac{k-k_0}{\varepsilon }\right) \vec {\eta }^{(j_0)}(k_0). \end{aligned}$$
(2.2)

Substituting (2.2) and \(\omega =\omega _0+\varepsilon ^2\omega _1\) into the Fourier transform of the left hand side of (1.3), we get

$$\begin{aligned} \begin{aligned}&(\omega _0+\varepsilon ^2\omega _1)\widehat{\vec {B}}_{\text{ app }} - L(\mathrm {i}k)\widehat{\vec {B}}_{\text{ app }}+\widehat{\vec {N}}(\vec {B}_\mathrm {app})\\ {}&\quad =\varepsilon (\omega _0+\varepsilon ^2\omega _1-\lambda _{j_0}(k))\eta ^{(j_0)}(k_0) {\widehat{C}}\left( \frac{k-k_0}{\varepsilon }\right) \\ {}&\qquad +\varepsilon ^3 \vec {N}(\eta ^{(j_0)}(k_0))({\widehat{C}}*\widehat{{\overline{C}}}*{\widehat{C}})\left( \frac{k-k_0}{\varepsilon }\right) \\ {}&\quad =\varepsilon ^3\left[ \left( \omega _1 - \left( \frac{k-k_0}{\varepsilon }\right) ^TG_0\frac{k-k_0}{\varepsilon }\right) {\widehat{C}}\left( \frac{k-k_0}{\varepsilon }\right) \right. \\ {}&\qquad \left. + \Gamma ({\widehat{C}}*\widehat{{\overline{C}}}*{\widehat{C}})\left( \frac{k-k_0}{\varepsilon }\right) \right] \vec {\eta }^{(j_0)}(k_0) - \vec {\Theta }(k),\end{aligned} \end{aligned}$$

where

$$\begin{aligned} G_0:=\frac{1}{2}D^2 \lambda _{j_0}(k_0), \quad \Gamma :=\vec {\eta }^{(j_0)}(k_0)^*\widehat{\vec {N}}(\vec {\eta }^{(j_0)}(k_0)), \end{aligned}$$

(with \(v^*\) being the Hermitian transpose of a vector \(v\in {\mathbb {C}}^N\)) and where

$$\begin{aligned} \begin{aligned} \vec {\Theta }(k):&=\varepsilon ^3 \left( \lambda _{j_0}(k)-\omega _0-\left( \frac{k-k_0}{\varepsilon }\right) ^TG_0\frac{k-k_0}{\varepsilon }\right) \vec {\eta }^{(j_0)}(k_0){\widehat{C}}\left( \frac{k-k_0}{\varepsilon }\right) \\ {}&\quad + \varepsilon ^3 \left( \widehat{\vec {N}}(\vec {\eta }^{(j_0)}(k_0)) - \vec {\eta }^{(j_0)}(k_0)^*\widehat{\vec {N}}(\vec {\eta }^{(j_0)}(k_0))\vec {\eta }^{(j_0)}(k_0))\right) ({\widehat{C}}*\widehat{{\overline{C}}}*{\widehat{C}})\left( \frac{k-k_0}{\varepsilon }\right) \end{aligned} \end{aligned}$$

is small as implicitly shown in Sect. 3.

A necessary condition for the smallness of the residual corresponding to \(\vec {B}_{\text {app}}\) is the vanishing of the square brackets. This is equivalent to

$$\begin{aligned} \omega _1 C + \nabla ^T(G_0 \nabla C) + \Gamma |C|^2C=0 \end{aligned}$$
(2.3)

for \(C:{\mathbb {R}}^d\rightarrow {\mathbb {C}}\). Equation (2.3) is the effective nonlinear Schrödinger equation (NLS) for the envelope C.

3 The Bifurcation and Approximation Result

Under assumptions (A.1-A.2) and the following assumption (A.3) we prove the bifurcation result below.

  1. (A.3)

    The kernel of the Jacobian J corresponding to the NLS equation, as defined in (3.22), is \((n+1)\)-dimensional (i.e. generated only by the continuous invariances of the NLS).

We define next the space \(L^1_s({\mathbb {R}}^d)\) for \(s\geqslant 0\) as

$$\begin{aligned} L^1_s({\mathbb {R}}^d):=\{f\in L^1({\mathbb {R}}^d): (1+|\cdot |)^s f \in L^1({\mathbb {R}}^d))\}. \end{aligned}$$

For vector valued functions \(f:{\mathbb {R}}^d\rightarrow {\mathbb {C}}^N\) we write \(f \in L_s^1({\mathbb {R}}^d)\) if \(f_j\in L_s^1({\mathbb {R}}^d)\) for each \(j=1,\dots ,N\).

The space of continuous functions \(f:{\mathbb {R}}^d\rightarrow {\mathbb {C}}\) satisfying the asymptotics \(f(x)\rightarrow 0\) as \(|x|\rightarrow \infty \) is denoted by \(C_0({\mathbb {R}}^d)\). We equip the space with the supremum norm.

Theorem 1

Choose \(\omega _0\) such that (A.1) and (A.2) are satisfied. Let \((\alpha ,\beta )\subset {\mathbb {R}}\) be the spectral gap from (A.1) and let \(\omega _1\in {\mathbb {R}}\) be such that \(\text {sign}(\omega _1)=1\) if \(\omega _0=\alpha \) and \(\text {sign}(\omega _1)=-1\) if \(\omega _0=\beta \). If C is a PT-symmetric (i.e. \(C(-x)=\overline{C(x)}\)) solution of (2.3) with \({\widehat{C}}\in L^1_{4}({\mathbb {R}}^d)\) and such that (A.3) holds, then there are constants \(c_1,c_2,\varepsilon _0>0\) such that for each \(\varepsilon \in (0,\varepsilon _0)\) there is a solution \(\vec {B}\) of Eq. (1.3) with \(\omega =\omega _0+\varepsilon ^2\omega _1\) which satisfies \(\widehat{\vec {B}}\in L^1_{2}({\mathbb {R}}^d)\) and

$$\begin{aligned} \left\| \widehat{\vec {B}}-\varepsilon ^{1-d}{\widehat{C}}\left( \frac{\cdot -k_0}{\varepsilon }\right) \vec {\eta }^{(j_0)}(k_0)\right\| _{L^1({\mathbb {R}}^d)}\leqslant c_1\varepsilon ^2. \end{aligned}$$

In particular,

$$\begin{aligned} \left\| \vec {B}-\varepsilon C(\varepsilon \cdot )\vec {\eta }^{(j_0)}(k_0)e^{\mathrm{i}k_0\cdot }\right\| _{C_0({\mathbb {R}}^d)}\leqslant c_2\varepsilon ^2. \end{aligned}$$

The constants \(c_1\) and \(c_2\) depend polynomially on \(\Vert {\widehat{C}}\Vert _{L^1_4({\mathbb {R}}^d)}\).

Clearly, due to \(\widehat{\vec {B}}\in L^1({\mathbb {R}}^d)\) the lemma of Riemann-Lebesgue implies the decay \(\vec {B}(x)\rightarrow 0\) as \(|x|\rightarrow \infty \).

The existence of a PT-symmetric solution C is satisfied, e.g., if \(G_0\) is definite and \(\text {sign}(\Gamma )=-{{\,\mathrm{sign}\,}}(\omega _1)\). Due to the extremum of \(\lambda _{j_0}\) at \(k=k_0\) we have then that \(\Gamma \) is positive/negative if \(D^2\lambda {j_0}(k_0)\) is positive/negative definite respectively. Hence, the NLS is of focusing type and after a rescaling of the x variables it supports a real, positive, radially symmetric solution with exponential decay at infinity (Townes soliton).

Note that the condition on \(\text {sign}(\omega _1)\) implies

$$\begin{aligned} \omega =\omega _0+\varepsilon ^2 \omega _1 \notin \sigma (L(\nabla )). \end{aligned}$$

We proceed with the proof of Theorem 1. Like in Sect. 2 we work here in Fourier variables. We employ a Lyapunov-Schmidt-like decomposition. For each \(k\in {\mathbb {R}}^d\) we split the solution \(\widehat{\vec {B}}(k)\in {\mathbb {C}}^N\) into the component proportional to the eigenvector \(\vec {\eta }^{(j_0)}(k)\) and the \(l^2({\mathbb {C}}^N)-\)orthogonal complement. We define the projections

$$\begin{aligned} P_k:{\mathbb {C}}^N\rightarrow \text {span}{\vec {\eta }^{(j_0)}(k)}, \vec {v} \mapsto (\vec {\eta }^{(j_0)}(k)^*\vec {v})\vec {\eta }^{(j_0)}(k) \end{aligned}$$

and

$$\begin{aligned} Q_k:=I-P_k. \end{aligned}$$

Then

$$\begin{aligned} \widehat{\vec {B}}(k) = \widehat{\vec {B}}_P(k)+\widehat{\vec {B}}_Q(k), \end{aligned}$$

where

$$\begin{aligned} \widehat{\vec {B}}_P(k)=P_k\widehat{\vec {B}}(k)=:\psi (k)\vec {\eta }^{(j_0)}(k), \ \widehat{\vec {B}}_Q(k)=Q_k\widehat{\vec {B}}(k). \end{aligned}$$

We aim to construct a solution \(\widehat{\vec {B}}\) with \(\psi \) approximated by the envelope in our ansatz, i.e. by \(\varepsilon ^{1-d}{\widehat{C}}\left( \tfrac{\cdot -k_0}{\varepsilon }\right) \). We choose for \(\psi \) a decomposition according to the support

$$\begin{aligned} \psi (k)=\varepsilon ^{1-d}{\widehat{D}}\left( \tfrac{k-k_0}{\varepsilon }\right) +\varepsilon ^{1-d}{\widehat{R}}\left( \tfrac{k-k_0}{\varepsilon }\right) , \end{aligned}$$
(3.1)

where

$$\begin{aligned} \text {supp}{\widehat{D}}\subset B_{\varepsilon ^{r-1}}:=\left\{ k\in {\mathbb {R}}^d:|k|<\varepsilon ^{r-1}\right\} , \ \text {supp}{\widehat{R}}\subset B_{\varepsilon ^{r-1}}^c:={\mathbb {R}}^d\setminus B_{\varepsilon ^{r-1}} \end{aligned}$$

with \(r\in (0,1)\). At the moment r is a free parameter; it will be specified below. We also define

$$\begin{aligned} \widehat{\vec {B}}_D(k) := \varepsilon ^{1-d}{\widehat{D}}\left( \tfrac{k-k_0}{\varepsilon }\right) \vec {\eta }^{(j_0)}(k), \quad \widehat{\vec {B}}_R(k):= \varepsilon ^{1-d}{\widehat{R}}\left( \tfrac{k-k_0}{\varepsilon }\right) \vec {\eta }^{(j_0)}(k) \end{aligned}$$

such that

$$\begin{aligned} \widehat{\vec {B}}_P=\widehat{\vec {B}}_D+\widehat{\vec {B}}_R. \end{aligned}$$

In the ansatz in (3.1) we wish to find the component \({\widehat{D}}\) close to \(\chi _{B_{\varepsilon ^{r-1}}} {\widehat{C}}\) and the component \({\widehat{R}}\) small. The component \(\widehat{\vec {B}}_D\) is then approximated by \(\widehat{\vec {B}}_\mathrm{app}\) in (2.2). If also \(\widehat{\vec {B}}_Q\) is small, then the whole constructed solution \(\widehat{\vec {B}}\) is close to \(\widehat{\vec {B}}_\mathrm{app}\).

The Fourier transform of (1.1) is

$$\begin{aligned} \omega \widehat{\vec {B}}(k) - L(\mathrm{i}k)\widehat{\vec {B}}(k) + \widehat{\vec {N}}(\widehat{\vec {B}})(k)=0, \ k\in {\mathbb {R}}^d. \end{aligned}$$
(3.2)

For the selected ansatz Eq. (3.2) becomes

$$\begin{aligned} \varepsilon ^{1-d}(\omega _0+\varepsilon ^2\omega _1-\lambda _{j_0}(k))\left( {\widehat{D}}\left( \tfrac{k-k_0}{\varepsilon }\right) +{\widehat{R}}\left( \tfrac{k-k_0}{\varepsilon }\right) \right) +\vec {\eta }^{(j_0)}(k)^*\widehat{\vec {N}}(\widehat{\vec {B}})(k)&=0, \end{aligned}$$
(3.3)
$$\begin{aligned} Q_k\left( (\omega _0+\varepsilon ^2\omega _1)I-L(\mathrm{i}k)\right) Q_k\widehat{\vec {B}}_Q(k) + Q_k\widehat{\vec {N}}(\widehat{\vec {B}})(k)&=0. \end{aligned}$$
(3.4)

Because \(\omega _0\in \sigma (L(\mathrm{i}k_0))\), the inverse of the matrix \((\omega _0+\varepsilon ^2\omega _1)I-L(\mathrm{i}k)\) is not bounded uniformly in \(\varepsilon \). In a neighborhood of \(k_0\) the norm of the inverse blows up as \(\varepsilon \rightarrow 0\). However,

$$\begin{aligned} M_k:=Q_k\left( (\omega _0+\varepsilon ^2\omega _1)I-L(\mathrm{i}k)\right) Q_k \end{aligned}$$

is invertible uniformly in \(\varepsilon \) due to assumption (A.2).

We separate the explicit part of (3.4) by writing

$$\begin{aligned} \widehat{\vec {N}}(\widehat{\vec {B}})(k)=\widehat{\vec {N}}(\widehat{\vec {B}}_P)(k)+(\widehat{\vec {N}}(\widehat{\vec {B}})(k)-\widehat{\vec {N}}(\widehat{\vec {B}}_P)(k)) \end{aligned}$$

and

$$\begin{aligned} \widehat{\vec {B}}_Q=\widehat{\vec {B}}_{Q,1}+\widehat{\vec {B}}_{Q,2}, \end{aligned}$$

where \(\widehat{\vec {B}}_{Q,1}\) solves the explicit part, i.e.

$$\begin{aligned} \widehat{\vec {B}}_{Q,1}(k) = -M_k^{-1} Q_k\widehat{\vec {N}}(\widehat{\vec {B}}_P)(k). \end{aligned}$$
(3.5)

The system to solve is thus

$$\begin{aligned} \varepsilon ^{1-d}(\omega _0+\varepsilon ^2\omega _1-\lambda _{j_0}(k))\left( {\widehat{D}}\left( \tfrac{k-k_0}{\varepsilon }\right) + {\widehat{R}}\left( \tfrac{k-k_0}{\varepsilon }\right) \right) +\vec {\eta }^{(j_0)}(k)^*\widehat{\vec {N}}(\widehat{\vec {B}})(k)&=0 \end{aligned}$$
(3.6)
$$\begin{aligned} M_k\widehat{\vec {B}}_{Q,2}(k) + Q_k(\widehat{\vec {N}}(\widehat{\vec {B}})(k)-\widehat{\vec {N}}(\widehat{\vec {B}}_P)(k))&=0. \end{aligned}$$
(3.7)

Our procedure for constructing a solution can be sketched as follows.

  1. (1)

    For any \({\widehat{D}},{\widehat{R}}\in L^1({\mathbb {R}}^d)\) Eq. (3.5) produces a small \(\widehat{\vec {B}}_{Q,1}\) (because \(\Vert \widehat{\vec {B}}_P\Vert _{L^1}=O(\varepsilon )\)).

  2. (2)

    For any \({\widehat{D}},{\widehat{R}}\in L^1({\mathbb {R}}^d)\) and \(\widehat{\vec {B}}_{Q,1}\) from step 1 we solve (3.7) by a fixed point argument for a small \(\widehat{\vec {B}}_{Q,2}\).

  3. (3)

    For any \({\widehat{D}}\in L^1({\mathbb {R}}^d)\) and for \(\widehat{\vec {B}}_{Q}\) from steps 1 and 2 we solve (3.6) with \(k\in B_{\varepsilon ^{r}}(k_0)^c\) for a small \({\widehat{R}}\) by a fixed point argument.

  4. (4)

    With the components obtained in the above steps we find a solution \({\widehat{D}}\in L_2^1({\mathbb {R}}^d)\) of (3.6) with \(k\in B_{\varepsilon ^{r}}(k_0)\) close to a \({\widehat{C}} \in L^1_2({\mathbb {R}}^d)\) (with C a solution of (2.3)) - provided such a C exists. In addition C needs to satisfy a certain symmetry, the PT-symmetry. Also here a fixed point argument is used - roughly speaking for the difference \({\widehat{D}}-{\widehat{C}}\).

  5. (5)

    The error \(\Vert \widehat{\vec {B}}- \widehat{\vec {B}}_\mathrm{app}\Vert _{L^1({\mathbb {R}}^d)}\) is \(O(\varepsilon ^2)\) if \({\widehat{C}}\) decays fast enough, namely if \({\widehat{C}}\in L^1_4({\mathbb {R}}^d)\).

Lemma 1

If \({\widehat{D}}\in L^1({\mathbb {R}}^d)\), \({\widehat{R}}\in L^1_{s_R}({\mathbb {R}}^d)\) for some \(s_R\geqslant 0\), and \(\text {supp}{\widehat{D}}\subset B_{\varepsilon ^{r-1}},\) \(\text {supp}{\widehat{R}}\subset B_{\varepsilon ^{r-1}}^c\), then there are constant \(c_1,c_2>0\) such that for all \(\varepsilon >0\) small enough

$$\begin{aligned} \Vert \widehat{\vec {B}}_P\Vert _{L^1({\mathbb {R}}^d)}\leqslant c_1 \varepsilon \left( \Vert {\widehat{D}}\Vert _{L^1(B_{\varepsilon ^{r-1}})}+\varepsilon ^{(1-r)s_R}\Vert {\widehat{R}}\Vert _{L_{s_R}^1(B_{\varepsilon ^{r-1}}^c)}\right) \end{aligned}$$

and

$$\begin{aligned} \Vert \widehat{\vec {N}}(\widehat{\vec {B}}_P)\Vert _{L^1({\mathbb {R}}^d)}\leqslant c_2 \varepsilon ^3\left( \Vert {\widehat{D}}\Vert _{L^1(B_{\varepsilon ^{r-1}})}+\varepsilon ^{(1-r)s_R}\Vert {\widehat{R}}\Vert _{L_{s_R}^1(B_{\varepsilon ^{r-1}}^c)}\right) ^3. \end{aligned}$$

Proof

Because \(\Vert {\widehat{f}}(\varepsilon ^{-1}(\cdot -k_0))\Vert _{L^1({\mathbb {R}}^d)}=\varepsilon ^d\Vert {\widehat{f}}\Vert _{L^1({\mathbb {R}}^d)}\), we have

$$\begin{aligned} \begin{aligned} \Vert \widehat{\vec {B}}_P\Vert _{L^1({\mathbb {R}}^d)}&\leqslant c\varepsilon \left( \Vert {\widehat{D}}\Vert _{L^1({\mathbb {R}}^d)} + \int _{{\mathbb {R}}^d}(1+|\kappa |)^{-s_R}(1+|\kappa |)^{s_R}|{\widehat{R}}(\kappa )|\, \mathrm{d}\kappa \right) \\&\leqslant c\varepsilon \left( \Vert {\widehat{D}}\Vert _{L^1({\mathbb {R}}^d)} + \sup _{\kappa \in B_{\varepsilon ^{r-1}}^c}(1+|\kappa |)^{-s_R}\Vert {\widehat{R}}\Vert _{L_{s_R}^1(B_{\varepsilon ^{r-1}}^c)}\right) \\&\leqslant c_1 \varepsilon \left( \Vert {\widehat{D}}\Vert _{L^1(B_{\varepsilon ^{r-1}})}+\varepsilon ^{(1-r)s_R}\Vert {\widehat{R}}\Vert _{L_{s_R}^1(B_{\varepsilon ^{r-1}}^c)}\right) . \end{aligned} \end{aligned}$$

The estimate for \(\Vert \widehat{\vec {N}}(\widehat{\vec {B}}_P)\Vert _{L^1({\mathbb {R}}^d)}\) follows by Young’s inequality for convolutions. \(\square \)

  1. (1)

    \(\mathbf{Component \ \widehat{\vec {B}}_{Q,1}}\)

Because \(\widehat{\vec {B}}_{Q,1}=-M_k^{-1}Q_k\widehat{\vec {N}}(\widehat{\vec {B}}_P)(k)\), we get from Lemma 1 the estimate

$$\begin{aligned} \Vert \widehat{\vec {B}}_{Q,1}\Vert _{L^1({\mathbb {R}}^d)}\leqslant c \varepsilon ^3 (\Vert {\widehat{D}}\Vert _{L^1({\mathbb {R}}^d)}+\Vert {\widehat{R}}\Vert _{L^1({\mathbb {R}}^d)})^3. \end{aligned}$$
(3.8)
  1. (2)

    \(\mathbf{Component \ \widehat{\vec {B}}_{Q,2}}\)

With \(\widehat{\vec {B}}_{Q,1}\) from above (and \({\widehat{D}},{\widehat{R}}\) given) component \(\widehat{\vec {B}}_{Q,2}\) satisfies

$$\begin{aligned} \widehat{\vec {B}}_{Q,2}(k) = M_k^{-1}Q_k\left( \widehat{\vec {N}}(\widehat{\vec {B}}_P)(k)-\widehat{\vec {N}}(\widehat{\vec {B}}_P+\widehat{\vec {B}}_{Q,1}+\widehat{\vec {B}}_{Q,2})(k) \right) =:\vec {G}(\widehat{\vec {B}}_{Q,2})(k). \end{aligned}$$

Due to the cubic structure of \(\vec {N}\) we have

$$\begin{aligned}&\Vert \vec {G}(\widehat{\vec {B}}_{Q,2})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c \Vert \widehat{\vec {B}}_{Q,1}+\widehat{\vec {B}}_{Q,2}\Vert _{L^1({\mathbb {R}}^d)}\big (\Vert \widehat{\vec {B}}_{P}\Vert _{L^1({\mathbb {R}}^d)}\\&\quad +\Vert \widehat{\vec {B}}_{Q,1}\Vert _{L^1({\mathbb {R}}^d)}+\Vert \widehat{\vec {B}}_{Q,2}\Vert _{L^1({\mathbb {R}}^d)}\big )^2.\end{aligned}$$

For \(\widehat{\vec {B}}_{Q,2} \in B_{\varepsilon ^\eta }, \eta >0\) we have

$$\begin{aligned} \Vert \vec {G}(\widehat{\vec {B}}_{Q,2})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c(\Vert {\widehat{D}}\Vert _{L^1},\Vert {\widehat{R}}\Vert _{L^1}) (\varepsilon ^5 + \varepsilon ^{2+\eta } + \varepsilon ^{1+2\eta }+ \varepsilon ^{3\eta }). \end{aligned}$$

Hence, \(\vec {G}:B^{(L^1)}_{c_0\varepsilon ^5}\rightarrow B^{(L^1)}_{c_0\varepsilon ^5}\) for some \(c_0(\Vert {\widehat{D}}\Vert _{L^1},\Vert {\widehat{R}}\Vert _{L^1})>0\), where \(B^{(L^1)}_\alpha := \{\vec {v}\in L^1({\mathbb {R}}^d):\Vert \vec {v}\Vert _{L^1({\mathbb {R}}^d)}\leqslant \alpha \}.\) The constants c and \(c_0\) depend polynomially on \(\Vert {\widehat{D}}\Vert _{L^1}\) and \(\Vert {\widehat{R}}\Vert _{L^1}\).

Similarly, we obtain the contraction (for \(\varepsilon >0\) small enough)

$$\begin{aligned} \Vert \vec {G}(\widehat{\vec {B}}^{(1)}_{Q,R})-\vec {G}(\widehat{\vec {B}}^{(2)}_{Q,R})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c\varepsilon ^2\Vert \widehat{\vec {B}}^{(1)}_{Q,R}-\widehat{\vec {B}}^{(2)}_{Q,R}\Vert _{L^1({\mathbb {R}}^d)}, \end{aligned}$$

if \(\widehat{\vec {B}}^{(1)}_{Q,R},\widehat{\vec {B}}^{(2)}_{Q,R}\in B^{(L^1)}_{c_0\varepsilon ^5}\). Hence, for \(\varepsilon >0\) small enough we have a unique solution \(\widehat{\vec {B}}_{Q,2}\in B^{(L^1)}_{c_0\varepsilon ^5}\) of \(\widehat{\vec {B}}_{Q,2} =\vec {G}(\widehat{\vec {B}}_{Q,2})\), i.e.

$$\begin{aligned} \Vert \widehat{\vec {B}}_{Q,2}\Vert _{L^1({\mathbb {R}}^d)}\leqslant c_0(\Vert {\widehat{D}}\Vert _{L^1},\Vert {\widehat{R}}\Vert _{L^1})\varepsilon ^5. \end{aligned}$$
(3.9)
  1. (3)

    \(\mathbf{Component \ \widehat{\vec {B}}_R}\)

For any \({\widehat{D}}\in L^1({\mathbb {R}}^d)\) and with the above estimate on \(\widehat{\vec {B}}_{Q}\) we look for a small \({\widehat{R}}\). The support of \({\widehat{R}}\) is \(B_{\varepsilon ^{r-1}}^c\), whence for \(k\in {\mathbb {R}}^d\setminus B_{\varepsilon ^r}(k_0)\) we can divide in (3.6) by \(\omega _0+\varepsilon ^2\omega _1-\lambda _{j_0}(k)\) and obtain

$$\begin{aligned} {\widehat{R}}\left( \frac{k-k_0}{\varepsilon }\right) = \varepsilon ^{d-1}\nu (k) \vec {\eta }^{(j_0)}(k)^*\widehat{\vec {N}}(\widehat{\vec {B}})(k), \quad k \in {\mathbb {R}}^d\setminus B_{\varepsilon ^r}(k_0) \end{aligned}$$

with

$$\begin{aligned} \nu (k):=(\lambda _{j_0}(k)-\omega _0-\varepsilon ^2\omega _1)^{-1}. \end{aligned}$$

Since \(\nabla \lambda _{j_0}(k_0)=0\), we have \(|\lambda _{j_0}(k)-\omega _0|>c\varepsilon ^{2r}\) for all \(k\in {\mathbb {R}}^d\setminus B_{\varepsilon ^r}(k_0)\) and hence \(|\nu (k)|\leqslant c\varepsilon ^{-2r}\). In order to exploit the localized nature of \(\widehat{\vec {B}}_D\) and the smallness of \(\widehat{\vec {B}}_Q\), we write for \(\kappa :=\tfrac{k-k_0}{\varepsilon }\)

$$\begin{aligned} {\widehat{R}}(\kappa )=H({\widehat{R}})(\kappa ), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} H({\widehat{R}})(\kappa ):&=\varepsilon ^{d-1}\nu (k_0+\varepsilon \kappa )\left[ h(k_0+\varepsilon \kappa )^{-1}h(k_0+\varepsilon \kappa )\vec {\eta }^{(j_0)}(k_0+\varepsilon \kappa )^*\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \kappa )\right. \\&\qquad \left. +\vec {\eta }^{(j_0)}(k_0+\varepsilon \kappa )^*\left( \widehat{\vec {N}}(\widehat{\vec {B}})(k_0+\varepsilon \kappa )-\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \kappa )\right) \right] \end{aligned} \end{aligned}$$
(3.10)

with \(h(k):=\left( 1+\tfrac{|k-k_0|}{\varepsilon }\right) ^{s_D}\). Using \(\sup _{k\in \text {supp}\widehat{\vec {B}}_R}|h(k)^{-1}|\leqslant c\varepsilon ^{(1-r)s_D}\), the cubic form of \(\widehat{\vec {N}}\) and the fact that \(\left( {\widehat{D}}\left( \tfrac{\cdot -k_0}{\varepsilon }\right) *\widehat{{\overline{D}}}\left( \tfrac{\cdot +k_0}{\varepsilon }\right) *{\widehat{D}}\left( \tfrac{\cdot -k_0}{\varepsilon }\right) \right) (k_0+\varepsilon \kappa ) = \varepsilon ^{2d}({\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}})(\kappa )\), we get

$$\begin{aligned} \begin{aligned} \Vert H({\widehat{R}})\Vert _{L^1({\mathbb {R}}^d)}&\leqslant c_1\varepsilon ^{2-2r+(1-r)s_D}\Vert (1+|\cdot |)^{s_D}({\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}})(\cdot )\Vert _{L^1({\mathbb {R}}^d)}\\&\qquad + c_2\varepsilon ^{-2r-1}\left( \Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)}+\Vert \widehat{\vec {B}}_Q\Vert _{L^1({\mathbb {R}}^d)}\right) \\&\times \qquad \left( \Vert \widehat{\vec {B}}_D\Vert _{L^1({\mathbb {R}}^d)}+\Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)}+\Vert \widehat{\vec {B}}_Q\Vert _{L^1({\mathbb {R}}^d)}\right) ^2. \end{aligned} \end{aligned}$$

Since \(\Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)}\leqslant c \varepsilon \Vert {\widehat{R}}\Vert _{L^1({\mathbb {R}}^d)}\), \(\Vert \widehat{\vec {B}}_D\Vert _{L^1({\mathbb {R}}^d)}\leqslant c \varepsilon \Vert {\widehat{D}}\Vert _{L^1({\mathbb {R}}^d)}\), and \(\Vert \widehat{\vec {B}}_Q\Vert _{L^1({\mathbb {R}}^d)}\leqslant c(\Vert {\widehat{D}}\Vert _{L^1},\Vert {\widehat{R}}\Vert _{L^1})\varepsilon ^3\) (with a polynomial c), we have

$$\begin{aligned} \begin{aligned}&\Vert H({\widehat{R}})\Vert _{L^1({\mathbb {R}}^d)}\\&\quad \leqslant c\varepsilon ^{2-2r}\left( \varepsilon ^{(1-r)s_D}\Vert {\widehat{D}}\Vert ^3_{L^1_{s_D}({\mathbb {R}}^d)} + \Vert {\widehat{R}}\Vert _{L^1({\mathbb {R}}^d)}^3+ \Vert {\widehat{R}}\Vert _{L^1({\mathbb {R}}^d)}^2 + \Vert {\widehat{R}}\Vert _{L^1({\mathbb {R}}^d)} + \varepsilon ^2\right) \end{aligned} \end{aligned}$$

with c depending polynomially on \(\Vert {\widehat{D}}\Vert _{L^1}\) and \(\Vert {\widehat{R}}\Vert _{L^1}\).

If \({\widehat{D}}\in L^1_{s_D}({\mathbb {R}}^d)\), \(s_D\geqslant 0\), then there is a constant c depending polynomially on \(\Vert {\widehat{D}}\Vert _{L^1_{s_D}({\mathbb {R}}^d)}\) such that

$$\begin{aligned} \Vert H({\widehat{R}})\Vert _{L^1({\mathbb {R}}^d)}\leqslant c(\Vert {\widehat{D}}\Vert _{L^1_{s_D}})\varepsilon ^\alpha , \quad \alpha :=\min \{4-2r,(2+s_D)(1-r)\} \end{aligned}$$
(3.11)

for all R with \(\Vert {\widehat{R}}\Vert _{L^1({\mathbb {R}}^d)}\leqslant c\varepsilon ^\alpha \) and all \(\varepsilon >0\) small enough. Hence \(H:B^{(L^1)}_{c\varepsilon ^\alpha }\rightarrow B^{(L^1)}_{c\varepsilon ^\alpha }\) for some \(c>0\) if \(\varepsilon >0\) is small enough and if \({\widehat{D}}\in L^1_{s_D}({\mathbb {R}}^d)\).

Similarly, we get the contraction property of H on \(B^{(L^1)}_{c\varepsilon ^\alpha }\) for \(\varepsilon >0\) small enough. The constructed fixed point \({\widehat{R}}\in B^{(L^1)}_{c\varepsilon ^\alpha }\) yields for any \(s_D\geqslant 0\)

$$\begin{aligned} \Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)} \leqslant c(\Vert {\widehat{D}}\Vert _{L^1_{s_D}})\varepsilon ^{\alpha +1}. \end{aligned}$$
(3.12)
  1. (4)

    \(\mathbf{Component \ \widehat{\vec {B}}_D}\)

Finally, we consider the component \(\widehat{\vec {B}}_D\). For \(k\in \text {supp}(\widehat{\vec {B}}_D)= B_{\varepsilon ^r}(k_0)\) we rewrite (3.6) as follows. We add and subtract \(\widehat{\vec {N}}(\widehat{\vec {B}}_D)\) like in (3.10), we Taylor expand \(\lambda _{j_0}(k)\) at \(k=k_0\), and we use the variable \(\kappa =\varepsilon ^{-1}(k-k_0)\). This leads to

$$\begin{aligned} (\omega _1-\kappa ^T G_0\kappa ){\widehat{D}}(\kappa )+\chi _{B_{\varepsilon ^{r-1}}}(\kappa )\Gamma ({\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}})(\kappa )=\rho ({\widehat{D}})(\kappa ), \end{aligned}$$
(3.13)

where

$$\begin{aligned} \begin{aligned} \rho ({\widehat{D}})(\kappa )&= \chi _{B_{\varepsilon ^{r-1}}}(\kappa )\left[ \Gamma ({\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}})(\kappa ) -\varepsilon ^{d-3} \vec {\eta }^{(j_0)}(k_0+\varepsilon \kappa )^*\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \kappa )\right] \\&\qquad +\varepsilon ^{-2}\left[ \delta (k_0+\varepsilon \kappa ){\widehat{D}}(\kappa ) + \varepsilon ^{d-1}\chi _{B_{\varepsilon ^{r-1}}}(\kappa ) \vec {\eta }^{(j_0)}(k_0+\varepsilon \kappa )^*\right. \\&\qquad \left. \left( \widehat{\vec {N}}(\widehat{\vec {B}})(k_0+\varepsilon \kappa )-\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \kappa )\right) \right] \end{aligned} \end{aligned}$$

and \(\delta (k):=\lambda _{j_0}(k)-\omega _0-\frac{1}{2}(k-k_0)^TD^2\lambda _{j_0}(k_0)(k-k_0)\).

Next, we write \(\rho =\rho _1+\rho _2+\rho _3\), where

$$\begin{aligned} \begin{aligned} \rho _1({\widehat{D}})(\kappa )&:=\chi _{B_{\varepsilon ^{r-1}}}(\kappa )\left[ \Gamma ({\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}})(\kappa ) -\varepsilon ^{d-3} \vec {\eta }^{(j_0)}(k_0+\varepsilon \kappa )^*\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \kappa )\right] ,\\ \rho _2({\widehat{D}})(\kappa )&:= \varepsilon ^{-2} \delta (k_0+\varepsilon \kappa ){\widehat{D}}(\kappa ),\\ \rho _3({\widehat{D}})(\kappa )&:= \varepsilon ^{d-3}\chi _{B_{\varepsilon ^{r-1}}}(\kappa ) \vec {\eta }^{(j_0)}(k_0+\varepsilon \kappa )^*\left( \widehat{\vec {N}}(\widehat{\vec {B}})(k_0+\varepsilon \kappa )-\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \kappa )\right) . \end{aligned} \end{aligned}$$

For \(\rho _1\) we get

$$\begin{aligned} \begin{aligned} \rho _1({\widehat{D}})(\kappa )&=\varepsilon ^{-2d}\sum _{{\mathop {j\in \{1,\dots ,N\}}\limits ^{m,n,o\in \{1,\dots ,N\}}}}\gamma _j^{(m,n,o)}\int _{B_{2\varepsilon ^r}}\int _{B_{\varepsilon ^r}(k_0)}\left( {\overline{\eta }}_j^{(j_0)}(k_0+\varepsilon \kappa ) \right. \\&\qquad \left. \times \eta _m^{(j_0)}(k_0+\varepsilon \kappa -s){\overline{\eta }}_n^{(j_0)}(s-t)\eta _o^{(j_0)}(t)-\Gamma \right) \\ {}&\qquad \times {\widehat{D}}\left( \kappa -\frac{s}{\varepsilon }\right) \widehat{{\overline{D}}}\left( \frac{s-t+k_0}{\varepsilon }\right) {\widehat{D}}\left( \frac{t-k_0}{\varepsilon }\right) \, \mathrm {d}t \, \mathrm {d}s\\&=\sum _{{\mathop {j\in \{1,\dots ,N\}}\limits ^{m,n,o\in \{1,\dots ,N\}}}}\gamma _j^{(m,n,o)}\int _{B_{2\varepsilon ^{r-1}}}\int _{B_{\varepsilon ^{r-1}}}\left( {\overline{\eta }}_j^{(j_0)}(k_0+\varepsilon \kappa ) \right. \\&\quad \times \left. \eta _m^{(j_0)}(k_0+\varepsilon (\kappa -{\tilde{s}})){\overline{\eta }}_n^{(j_0)}(k_0+\varepsilon ({\tilde{s}}-{\tilde{t}})) \right. \\ {}&\quad \left. \times \eta _o^{(j_0)}(k_0+\varepsilon {\tilde{t}}) -\Gamma \right) {\widehat{D}}\left( \kappa -{\tilde{s}}\right) \widehat{{\overline{D}}}\left( {\tilde{s}}-{\tilde{t}}\right) {\widehat{D}}\left( {\tilde{t}}\right) \, \mathrm {d}{\tilde{t}} \, \mathrm {d}{\tilde{s}}. \end{aligned} \end{aligned}$$

Because \(\Gamma =\sum _{m,n,o,j\in \{1,\dots ,N\}}\gamma _j^{(m,n,o)}{\overline{\eta }}_j^{(j_0)}(k_0)\eta _m^{(j_0)}(k_0){\overline{\eta }}_n^{(j_0)}(k_0)\eta _o^{(j_0)}(k_0)\), we get

due to the Lipschitz continuity of \(k\mapsto \eta ^{(j_0)}(k)\). Hence, by Young’s inequality for convolutions,

$$\begin{aligned} \Vert \rho _1({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c\varepsilon \Vert {\widehat{D}}\Vert _{L^1_1({\mathbb {R}}^d)}^3. \end{aligned}$$
(3.14)

For \(\rho _2\) we note that \(|\delta (k_0+\varepsilon \kappa )|\leqslant c\varepsilon ^3|\kappa |^3\) for \(\kappa \in B_{\varepsilon ^{r-1}}\) and \(\varepsilon >0\) small enough. We estimate

$$\begin{aligned} \Vert \rho _2({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)}&\leqslant c\varepsilon \int _{B_{\varepsilon ^{r-1}}}|\kappa |^3|{\widehat{D}}(\kappa )|\, \mathrm{d}\kappa \leqslant c\varepsilon \sup _{\kappa \in B_{\varepsilon ^{r-1}}}|\kappa |^\beta \int _{{\mathbb {R}}^d}|\kappa |^{3-\beta }|{\widehat{D}}(\kappa )|\, \mathrm{d}\kappa \nonumber \\&\leqslant c\varepsilon ^{1-\beta (1-r)}\Vert {\widehat{D}}\Vert _{L^1_{3-\beta }({\mathbb {R}}^d)} \end{aligned}$$
(3.15)

for any \(\beta \in [0,3)\).

Finally, we estimate \(\rho _3\). Note that \(\widehat{\vec {N}}(\widehat{\vec {B}})(k_0+\varepsilon \cdot )-\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \cdot )\) appears also in (3.10). We have

$$\begin{aligned} \begin{aligned}&\Vert \widehat{\vec {N}}(\widehat{\vec {B}})(k_0+\varepsilon \cdot )-\widehat{\vec {N}}(\widehat{\vec {B}}_D)(k_0+\varepsilon \cdot )\Vert _{L^1({\mathbb {R}}^d)}\\&\quad \leqslant \varepsilon ^{-d}\left( \Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)}+\Vert \widehat{\vec {B}}_Q\Vert _{L^1({\mathbb {R}}^d)}\right) \left( \Vert \widehat{\vec {B}}_D\Vert _{L^1({\mathbb {R}}^d)}+\Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)}+\Vert \widehat{\vec {B}}_Q\Vert _{L^1({\mathbb {R}}^d)}\right) ^2\\&\quad \leqslant c_1(\Vert {\widehat{D}}\Vert _{L^1_{s_D}})\varepsilon ^{-d}\left( (\varepsilon ^{\alpha +3}+\varepsilon ^5)\Vert {\widehat{D}}\Vert ^2_{L^1({\mathbb {R}}^d)}+(\varepsilon ^{2\alpha +3}+\varepsilon ^7)\Vert {\widehat{D}}\Vert _{L^1({\mathbb {R}}^d)}+\varepsilon ^{3\alpha +3}+\varepsilon ^9\right) \\&\quad \leqslant c_2(\Vert {\widehat{D}}\Vert _{L^1_{s_D}})(\varepsilon ^{\alpha +3-d}+\varepsilon ^{5-d}) \end{aligned} \end{aligned}$$

for \(\varepsilon >0\) small enough, where we have made use of (3.8), (3.9), (3.12), the fact that \(\Vert \widehat{\vec {B}}_D\Vert _{L^1}\leqslant \varepsilon \Vert {\widehat{D}}\Vert _{L^1}\) and the estimate \(\Vert {\widehat{R}}\Vert _{L^1}\leqslant c(\Vert {\widehat{D}}\Vert _{L^1_{s_D}})\varepsilon ^\alpha \). The dependence of \(c_1\) and \(c_2\) on \(\Vert {\widehat{D}}\Vert _{L^1_{s_D}}\) is polynomial. As a result

$$\begin{aligned} \Vert \rho _3({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c(\Vert {\widehat{D}}\Vert _{L^1_{s_D}})(\varepsilon ^{\alpha }+\varepsilon ^{2}). \end{aligned}$$
(3.16)

The whole right hand side of (3.13) is thus estimated as

$$\begin{aligned} \Vert \rho ({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c(\Vert {\widehat{D}}\Vert _{L^1_{s_D}},\Vert {\widehat{D}}\Vert _{L^1_{3-\beta }}) \left( \varepsilon ^{1-\beta (1-r)}+\varepsilon ^{\alpha }\right) \end{aligned}$$

for any \(\beta \in [0,3)\). Once again, the constant c depends polynomially on its arguments.

In order to solve (3.13) for \({\widehat{D}}\) below (using a fixed point argument), we need to consider \(\rho \) as an in-homogeneity. The linearized operator to be inverted in the iteration is of second order such that in Fourier space it acts from \(L^1_2({\mathbb {R}}^d)\) to \(L^1({\mathbb {R}}^d)\). For that reason we need to choose \(s_D=2\) and \(\beta \geqslant 1\) above. The choice \(s_D=2, \beta =1, r=1/2\) leads to \(\alpha =2\) and \(1-\beta (1-r)=1/2\), i.e. \(\Vert \rho ({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c \varepsilon ^{1/2}\) provided \({\widehat{D}}\in L^1_{2}({\mathbb {R}}^d)\). For \(s_D=2,\beta =1\) the largest value of \( \min \{1-\beta (1-r),\alpha \}\) is 4/5 attained at \(r=4/5\). Hence, with \(r=4/5\) we get the best possible estimate

$$\begin{aligned} \Vert \rho ({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c(\Vert {\widehat{D}}\Vert _{L^1_{2}}) \varepsilon ^{4/5}. \end{aligned}$$

This order determines the accuracy of the approximation and turns out to be insufficient. It leads to \( \Vert \widehat{\vec {B}}-\widehat{\vec {B}}_{\text {app}}\Vert _{L^1({\mathbb {R}}^d)}\leqslant c\varepsilon ^{9/5}\) instead of \(c\varepsilon ^2\).

Clearly, the leading order term in the residual \(\rho \) is caused by the error from the Taylor expansion of \(\lambda _{j_0}\). We introduce a refined ansatz for \({\widehat{D}}\) in order to make this error of higher order. Note that Eq. (3.13) is a perturbation of the NLS (2.3). Writing

$$\begin{aligned} f_\mathrm{NLS}(C):=\omega _1 C + \nabla ^T(G_0\nabla C) + \Gamma |C|^2C, \end{aligned}$$

Eq. (3.13) is

$$\begin{aligned} \chi _{B_{\varepsilon ^{r-1}}}\widehat{f_\mathrm{NLS}(D)} = \rho ({\widehat{D}}). \end{aligned}$$
(3.17)

We search for D close to a solution C of the NLS, i.e. of \(f_\mathrm{NLS}(C)=0\). For that we need to look for \({\widehat{D}}\) in a vicinity of

$$\begin{aligned} {\widehat{C}}^{(\varepsilon )}:=\chi _{B_{\varepsilon ^{r-1}}}{\widehat{C}}. \end{aligned}$$

We choose the following ansatz

$$\begin{aligned} {\widehat{D}}(\kappa )=\left( 1+\varepsilon \frac{D^3\lambda _{j_0}(k_0)(\kappa ,\kappa ,\kappa )}{6(\omega _1-\kappa ^TG_0\kappa )}\right) {\widehat{C}}^{(\varepsilon )}(\kappa )+{\widehat{d}}(\kappa ), \end{aligned}$$
(3.18)

where \(D^3\lambda _{j_0}(k_0)(\kappa ,\kappa ,\kappa )\) is the third order term in the Taylor expansion of \(\varepsilon ^{-3}\lambda _{j_0}(k_0+\varepsilon \kappa )\) and where \(\text {supp}({\widehat{d}}) \subset B_{\varepsilon ^{r-1}}\). We look for a solution with a small \({\widehat{d}}\).

We also define

$$\begin{aligned} {\widehat{D}}_0:={\widehat{C}}^{(\varepsilon )}+{\widehat{d}}, \quad \nu (\kappa ):=\frac{D^3\lambda _{j_0}(k_0)(\kappa ,\kappa ,\kappa )}{6(\omega _1-\kappa ^TG_0\kappa )}, \end{aligned}$$

such that \({\widehat{D}}={\widehat{D}}_0+\varepsilon \nu {\widehat{C}}^{(\varepsilon )}\). With this notation Eq. (3.17) reads

$$\begin{aligned} \chi _{B_{\varepsilon ^{r-1}}}\widehat{f_\mathrm{NLS}(D_0)} = \rho ({\widehat{D}}) + \chi _{B_{\varepsilon ^{r-1}}}\left( \widehat{f_\mathrm{NLS}(D_0)}-\widehat{f_\mathrm{NLS}(D)}\right) =:{\tilde{\rho }}({\widehat{D}}). \end{aligned}$$
(3.19)

Compared to \(\rho \) the right hand side \({\tilde{\rho }}\) is smaller as we show next. It is

$$\begin{aligned} {\tilde{\rho }}({\widehat{D}})=\rho _1({\widehat{D}})+\rho _3({\widehat{D}})+{\tilde{\rho }}_2({\widehat{D}}), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\tilde{\rho }}_2({\widehat{D}})(\kappa )&= \varepsilon ^{-2} \left( \lambda _{j_0}(k_0+\varepsilon \kappa )-\omega _0-\varepsilon ^2\kappa ^TG_0\kappa \right) {\widehat{D}}(\kappa )-\varepsilon (\omega _1-\kappa ^TG_0\kappa )\nu (\kappa ){\widehat{C}}^{(\varepsilon )}(\kappa )\\&\qquad + \chi _{B_{\varepsilon ^{r-1}}}(\kappa )\Gamma \left[ {\widehat{D}}_0*\widehat{{\overline{D}}_0}*{\widehat{D}}_0-{\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}}\right] (\kappa )\\&= \varepsilon ^{-2} \left( \lambda _{j_0}(k_0+\varepsilon \kappa )-\omega _0-\varepsilon ^2\kappa ^TG_0\kappa -\frac{\varepsilon ^3}{6} D^3\lambda _{j_0}(k_0)(\kappa ,\kappa ,\kappa )\right) {\widehat{C}}^{(\varepsilon )}(\kappa )\\&\qquad +\varepsilon ^{-2} \left( \lambda _{j_0}(k_0+\varepsilon \kappa )-\omega _0-\varepsilon ^2\kappa ^TG_0\kappa \right) \left( \varepsilon \nu (\kappa ){\widehat{C}}^{(\varepsilon )}(\kappa )+ {\widehat{d}}(\kappa )\right) \\&\qquad + \chi _{B_{\varepsilon ^{r-1}}}(\kappa )\Gamma \left[ {\widehat{D}}_0*\widehat{{\overline{D}}_0}*{\widehat{D}}_0-{\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}}\right] (\kappa ). \end{aligned} \end{aligned}$$

To estimate \({\tilde{\rho }}_2\) note that the first Taylor expansion error term (i.e. the first line) can be estimated in \(L^1({\mathbb {R}}^d)\) by \(c\varepsilon ^2\Vert {\widehat{C}}^{(\varepsilon )}\Vert _{L^1_4({\mathbb {R}}^d)}\leqslant c\varepsilon ^2\Vert {\widehat{C}}\Vert _{L^1_4({\mathbb {R}}^d)}\). For the second Taylor expansion error note first that \(|\nu (\kappa )|\leqslant c(1+|\kappa |)\) for all \(\kappa \in {\mathbb {R}}^d\) such that

$$\begin{aligned}&\Vert \varepsilon ^{-2} \left( \lambda _{j_0}(k_0+\varepsilon \cdot )-\omega _0-\varepsilon ^2(\cdot )^TG_0(\cdot )\right) (\varepsilon \nu {\widehat{C}}^{(\varepsilon )}+ {\widehat{d}})\Vert _{L^1({\mathbb {R}}^d)}\\&\quad \leqslant c\left( \varepsilon ^2\Vert {\widehat{C}}\Vert _{L^1_4({\mathbb {R}}^d)} + \varepsilon \int _{{\mathbb {R}}^d}|\kappa |^3|{\widehat{d}}(\kappa )|\, \mathrm{d}\kappa \right) . \end{aligned}$$

Just like in (3.15) we get

$$\begin{aligned} \varepsilon \int _{{\mathbb {R}}^d}|\kappa |^3|{\widehat{d}}(\kappa )|\, \mathrm{d}\kappa \leqslant c\varepsilon ^{1-\beta (1-r)}\Vert {\widehat{d}}\Vert _{L^1_{3-\beta }({\mathbb {R}}^d)} \end{aligned}$$

for any \(\beta \in [0,3)\). Once again, we need to choose \(\beta \geqslant 1\) in order for \({\tilde{\rho }}_2:{\widehat{d}}\mapsto {\tilde{\rho }}_2({\widehat{d}})\) to be a mapping from \(L^1_2({\mathbb {R}}^d)\) to \(L^1({\mathbb {R}}^d)\). With \(\beta =1\) and \(r=1/2\) we get \(1-\beta (1-r)=1/2\).

The last term in \({\tilde{\rho }}_2\) is

$$\begin{aligned} \begin{aligned}&\chi _{B_{\varepsilon ^{r-1}}}\Gamma \left[ {\widehat{D}}_0*\widehat{{\overline{D}}_0}*{\widehat{D}}_0-{\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}}\right] \\&\quad =\chi _{B_{\varepsilon ^{r-1}}}\Gamma \left[ ({\widehat{D}}-\varepsilon \nu {\widehat{C}}^{(\varepsilon )})*(\widehat{{\overline{D}}}-\varepsilon \nu \widehat{{\overline{C}}}^{(\varepsilon )})*({\widehat{D}}-\varepsilon \nu {\widehat{C}}^{(\varepsilon )})-{\widehat{D}}*\widehat{{\overline{D}}}*{\widehat{D}}\right] . \end{aligned} \end{aligned}$$

In the \(L^1\)-norm this can be estimated using Young’s inequality by

$$\begin{aligned} c\left( \varepsilon \Vert {\widehat{C}}\Vert _{L^1_1({\mathbb {R}}^d)}\Vert {\widehat{D}}\Vert ^2_{L^1({\mathbb {R}}^d)}+\varepsilon ^2\Vert {\widehat{C}}\Vert ^2_{L^1_1({\mathbb {R}}^d)}\Vert {\widehat{D}}\Vert _{L^1({\mathbb {R}}^d)}+\varepsilon ^3\Vert {\widehat{C}}\Vert ^3_{L^1_1({\mathbb {R}}^d)}\right) . \end{aligned}$$

In summary, with the above choice of \(\beta \) and r we get

$$\begin{aligned}&\Vert {\tilde{\rho }}_2\Vert _{L^1({\mathbb {R}}^d)}\leqslant c\left( \varepsilon ^{1/2}\Vert {\widehat{d}}\Vert _{L^1_2}+\varepsilon ^2 \Vert {\widehat{C}}\Vert _{L^1_4({\mathbb {R}}^d)}\right. \nonumber \\&\quad \left. +\varepsilon \Vert {\widehat{C}}\Vert _{L^1_1({\mathbb {R}}^d)}\Vert {\widehat{D}}\Vert ^2_{L^1({\mathbb {R}}^d)}+\varepsilon ^2\Vert {\widehat{C}}\Vert ^2_{L^1_1({\mathbb {R}}^d)}\Vert {\widehat{D}}\Vert _{L^1({\mathbb {R}}^d)}+\varepsilon ^3\Vert {\widehat{C}}\Vert ^3_{L^1_1({\mathbb {R}}^d)}\right) .\end{aligned}$$
(3.20)

The terms \(\rho _1\) and \(\rho _3\) are estimated in (3.14) and (3.16). As discussed above, we seek \({\widehat{D}}\) in \(L^1_2({\mathbb {R}}^d)\) and hence we set \(s_D=2\) in (3.11). This yields \(\alpha =2\) and

$$\begin{aligned} \Vert \rho _3({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c(\Vert {\widehat{D}}\Vert _{L^1_2})\varepsilon ^2. \end{aligned}$$

In summary, for any \({\widehat{C}}\in L^1_4({\mathbb {R}}^d)\) fixed (with C being a solution of the NLS), the right hand side of (3.19) is estimated as

$$\begin{aligned} \Vert {\tilde{\rho }}({\widehat{D}})\Vert _{L^1({\mathbb {R}}^d)}\leqslant c \left( \varepsilon + \Vert {\widehat{d}}\Vert _{L^1_2}\varepsilon ^{1/2} + (\Vert {\widehat{d}}\Vert _{L^1_2}^2+\Vert {\widehat{d}}\Vert _{L^1_2}^3)\varepsilon \right) . \end{aligned}$$
(3.21)

We proceed with a fixed point argument for the correction d. In order to obtain a differentiable function (to use the Jacobian of the NLS), we write \(f_\mathrm{NLS}\) in real variables. Writing \(D=D_R+\mathrm{i}D_I, C=C_R+\mathrm{i}C_I\), \(d=d_R+\mathrm{i}d_I\), and \({\tilde{\rho }} = {\tilde{\rho }}_R+\mathrm{i}{\tilde{\rho }}_I\), we define

$$\begin{aligned} F_\mathrm{NLS}(D_R,D_I):=\begin{pmatrix}{{\,\mathrm{Re}\,}}(f_\mathrm{NLS}(D_R+\mathrm{i}D_I))\\ {{\,\mathrm{Im}\,}}(f_\mathrm{NLS}(D_R+\mathrm{i}D_I))\end{pmatrix}, \end{aligned}$$

the Jacobian

$$\begin{aligned} J:=DF_\mathrm{NLS}(C_R,C_I) \end{aligned}$$
(3.22)

as well as the Fourier-truncation of the Jacobian

$$\begin{aligned} {\widehat{J}}_\varepsilon :=\chi _{B_{\varepsilon ^{r-1}}} {{\mathcal {F}}}\left( DF_\mathrm{NLS}(C_R^{(\varepsilon )},C_I^{(\varepsilon )})\right) , \end{aligned}$$

where \(\widehat{C_R}^{(\varepsilon )}:=\chi _{B_{\varepsilon ^{r-1}}} \widehat{C_R}, C_R^{(\varepsilon )}:={{\mathcal {F}}}^{-1}(\widehat{C_R}^{(\varepsilon )})\) and \(\widehat{C_I}^{(\varepsilon )}:=\chi _{B_{\varepsilon ^{r-1}}} \widehat{C_I}\), \(C_I^{(\varepsilon )}:={{\mathcal {F}}}^{-1}(\widehat{C_I}^{(\varepsilon )})\). \({\widehat{J}}_\varepsilon \) has the form

$$\begin{aligned} \begin{aligned} {\widehat{J}}_\varepsilon =&\chi _{B_{\varepsilon ^{r-1}}} (\omega _1 +\kappa ^T G_0 \kappa ) \text {Id}_{2\times 2} \\&+ \chi _{B_{\varepsilon ^{r-1}}} \Gamma \begin{pmatrix} 3\widehat{C_R}^{(\varepsilon )}*\widehat{C_R}^{(\varepsilon )}* + \widehat{C_I}^{(\varepsilon )}*\widehat{C_I}^{(\varepsilon )}* &{} 2\widehat{C_R}^{(\varepsilon )}*\widehat{C_I}^{(\varepsilon )}* \\ 2\widehat{C_R}^{(\varepsilon )}*\widehat{C_I}^{(\varepsilon )}* &{} 3\widehat{C_I}^{(\varepsilon )}*\widehat{C_I}^{(\varepsilon )}* + \widehat{C_R}^{(\varepsilon )}*\widehat{C_R}^{(\varepsilon )}* \end{pmatrix}. \end{aligned} \end{aligned}$$

With this notation (3.19) reads

$$\begin{aligned} {\widehat{J}}_\varepsilon \widehat{\vec {d}}=W(\widehat{\vec {d}}), \end{aligned}$$

where

with \(\widehat{\vec {C}}^{(\varepsilon )}:=(\widehat{C_R}^{(\varepsilon )},\widehat{C_I}^{(\varepsilon )})^T\) and \(\vec {{\tilde{\rho }}}:=({\tilde{\rho }}_R,{\tilde{\rho }}_I)^T\).

The aim is to construct a small fixed point \(\widehat{\vec {d}}\in L^1_{s_D}({\mathbb {R}}^d)\) of \({\widehat{J}}_\varepsilon ^{-1}W\). The difficulty is that the inverse of \({\widehat{J}}_\varepsilon \) is not bounded uniformly in \(\varepsilon \). This is due to the presence of the \(d+1\) zero eigenvalues of J caused by the d spatial shift invariances and the phase invariance of the NLS, see assumption (A.3). The distance of the essential spectrum of \({\widehat{J}}_\varepsilon \) from zero is \(|\omega _1|\) due to the choice of \(\text {sign}(\omega _1)\). To eliminate the zero eigenvalues, we work in a symmetric subspace of \(L^1_{s_D}({\mathbb {R}}^d)\) in which the invariances do not hold. A natural symmetry is the PT-symmetry. Hence, we consider the fixed point problem

$$\begin{aligned} \widehat{\vec {d}}={\widehat{J}}_\varepsilon ^{-1} W(\widehat{\vec {d}}) \end{aligned}$$

in the space

$$\begin{aligned} \begin{aligned} X_{s_D}^\text {sym}:=&\{\widehat{\vec {d}}\in L^1_{s_D}({\mathbb {R}}^d): \text {supp}(\widehat{\vec {d}})\subset B_{\varepsilon ^{r-1}}, d(-x)=\overline{d(x)} \ \forall x \in {\mathbb {R}}^d\}\\ =&\{\widehat{\vec {d}}\in L^1_{s_D}({\mathbb {R}}^d): \text {supp}(\widehat{\vec {d}})\subset B_{\varepsilon ^{r-1}}, {{\,\mathrm{Im}\,}}(\widehat{d_R})=-{{\,\mathrm{Re}\,}}(\widehat{d_I\, \, })\}. \end{aligned} \end{aligned}$$

Note that \({\widehat{J}}_0,{\widehat{J}}_\varepsilon :L^1_{q}({\mathbb {R}}^d)\rightarrow L^1_{q-2}({\mathbb {R}}^d)\) for any \(q\geqslant 2\). Because of assumption (A.3) \({\widehat{J}}_0^{-1}\) is bounded in \(X_{s_D}^\text {sym}\) for any \(s_D\geqslant 2\). Since \({\widehat{J}}_\varepsilon \) is a perturbation of \({\widehat{J}}_0\), we still need to ensure that 0 is not an eigenvalue of \({\widehat{J}}_\varepsilon \). For that we use a spectral stability result of Kato, see [12, Theorem IV.3.17]. Applied to our problem in the Banach space \(X_{s_D-2}^\text {sym}, s_D\geqslant 2\) with the domain of \({\widehat{J}}_0\) being \(D({\widehat{J}}_0)=X_{s_D}^\text {sym}\), it reads:

Assume \({\widehat{J}}_\varepsilon -{\widehat{J}}_0\) is \({\widehat{J}}_0\)-bounded, i.e. \(\text{ domain }({\widehat{J}}_0)\subset \text{ domain }({\widehat{J}}_\varepsilon -{\widehat{J}}_0)\) and for some \(a,b\geqslant 0\) is

$$\begin{aligned} \Vert ({\widehat{J}}_\varepsilon -{\widehat{J}}_0)\widehat{\vec {d}}\Vert _{L^1_{s_D-2}} \leqslant a\Vert \widehat{\vec {d}}\Vert _{L^1_{s_D-2}}+b\Vert {\widehat{J}}_0\widehat{\vec {d}}\Vert _{L^1_{s_D-2}} \text { for all } \widehat{\vec {d}}\in X_{s_D}^\text {sym}. \end{aligned}$$
(3.23)

If for some \(\zeta \in \rho ({\widehat{J}}_0)\)

$$\begin{aligned} a\Vert ({\widehat{J}}_0-\zeta )^{-1}\Vert _{L^1_{s_D-2}\rightarrow L^1_{s_D}}+b\Vert {\widehat{J}}_0({\widehat{J}}_0-\zeta )^{-1}\Vert _{L^1_{s_D-2}\rightarrow L^1_{s_D-2}}<1, \end{aligned}$$
(3.24)

then \(\zeta \in \rho ({\widehat{J}}_\varepsilon )\) and

$$\begin{aligned} \begin{aligned} \Vert ({\widehat{J}}_\varepsilon -\zeta )^{-1}\Vert _{L^1_{s_D-2}\rightarrow L^1_{s_D}}\leqslant&\Vert ({\widehat{J}}_0-\zeta )^{-1}\Vert _{L^1_{s_D-2}\rightarrow L^1_{s_D}}\left( 1-a\Vert ({\widehat{J}}_0-\zeta )^{-1}\Vert _{L^1_{s_D-2}\rightarrow L^1_{s_D}}\right. \\&\left. -b\Vert {\widehat{J}}_0({\widehat{J}}_0-\zeta )^{-1}\Vert _{L^1_{s_D-2}\rightarrow L^1_{s_D-2}}\right) ^{-1}. \end{aligned} \end{aligned}$$

We check now (3.23) and (3.24) for \(\zeta =0\). For \(\widehat{\vec {d}}\in X_{s_D}^\text {sym}\) one has

$$\begin{aligned} \begin{aligned} \Vert ({\widehat{J}}_\varepsilon -{\widehat{J}}_0)\widehat{\vec {d}}\Vert _{L^1_{s_D-2}} =&|\Gamma |\left\| \left( \widehat{C_R}^{(\varepsilon )}*\widehat{C_R}^{(\varepsilon )}-\widehat{C_R}*\widehat{C_R}\right) *(3\widehat{d_R}+\widehat{d_I\, \, })\right. \\&+\left( \widehat{C_I}^{(\varepsilon )}*\widehat{C_I}^{(\varepsilon )}-\widehat{C_I}*\widehat{C_I}\right) *(3\widehat{d_I\, \, }+\widehat{d_R})\\&\left. +2\left( \widehat{C_R}^{(\varepsilon )}*\widehat{C_I}^{(\varepsilon )}-\widehat{C_R}*\widehat{C_I}\right) *(\widehat{d_R}+\widehat{d_I\, \, })\right\| _{L^1_{s_D-2}}. \end{aligned} \end{aligned}$$

Writing \(\widehat{C_{R,I}}^{(\varepsilon )}=:\widehat{C_{R,I}}+\widehat{\gamma _{R,I}}^{(\varepsilon )}\), it is \(\text {supp}(\widehat{\gamma _{R,I}}^{(\varepsilon )})\subset B_{\varepsilon ^{r-1}}^c\). The difference \(({\widehat{J}}_\varepsilon -{\widehat{J}}_0)\widehat{\vec {d}}\) consists of terms that are linear or quadratic in \(\widehat{\gamma _{R,I}}^{(\varepsilon )}\); for instance terms like \(\widehat{\gamma _{R}}^{(\varepsilon )}*\widehat{C_{R}}^{(\varepsilon )}*\widehat{d_{R}}\) or \(\widehat{\gamma _{I}}^{(\varepsilon )}*\widehat{C_{R}}^{(\varepsilon )}*\widehat{d_I\, \, }\). Because

$$\begin{aligned} \begin{aligned} \Vert \widehat{\gamma _{R,I}}^{(\varepsilon )}\Vert _{L^1_{s_D-2}}&=\int _{B_{\varepsilon ^{r-1}}^c} (1+|\kappa |)^{s_D-2}|\widehat{\gamma _{R,I}}(\kappa )|\, \mathrm{d}\kappa \\&\leqslant \sup _{|\kappa |>\varepsilon ^{r-1}}\frac{1}{(1+|\kappa |)^2}\Vert \widehat{\gamma _{R,I}}^{(\varepsilon )}\Vert _{L^1_{s_D}}\leqslant c\varepsilon ^{2(1-r)}\Vert \widehat{\gamma _{R,I}}^{(\varepsilon )}\Vert _{L^1_{s_D}}, \end{aligned} \end{aligned}$$

Young’s inequality for convolutions yields

$$\begin{aligned} \Vert ({\widehat{J}}_\varepsilon -{\widehat{J}}_0)\widehat{\vec {d}}\Vert _{L^1_{s_D-2}} \leqslant c(\Vert {\widehat{C}}\Vert _{L^1_{s_D}})\varepsilon ^{2(1-r)}\Vert \widehat{\vec {d}}\Vert _{L^1_{s_D-2}} \end{aligned}$$

with c depending polynomially on \(\Vert {\widehat{C}}\Vert _{L^1_{s_D}}\). Conditions (3.23) and (3.24) for \(\zeta =0\) are thus satisfied with \(a=c\varepsilon ^{2(1-r)}\) and \(b=0\) if \(\varepsilon >0\) is small enough and if \({\widehat{C}}\in L^1_{s_D}({\mathbb {R}}^d)\).

For the fixed point problem we use \(s_D=2\) and \(r=1/2\) and show firstly that if \({\widehat{C}} \in X_{4}^\text {sym}\), then there is some \(c>0\) such that for all \(\varepsilon >0\) small enough

$$\begin{aligned} {\widehat{J}}_\varepsilon ^{-1}W:B_{c\varepsilon }^{2,\text { sym}}\rightarrow B_{c\varepsilon }^{2,\text { sym}}, \end{aligned}$$
(3.25)

where \(B_{c\varepsilon }^{2,\text { sym}}\) is the \(c\varepsilon \)-ball in \(X_{2}^\text {sym}\), i.e.

$$\begin{aligned} B_{c\varepsilon }^{2,\text { sym}}:=\{\varphi \in X_{2}^\text {sym}: \Vert \varphi \Vert _{L^1_{2}}\leqslant c\varepsilon \}. \end{aligned}$$

Note that the requirement \({\widehat{C}}\in L^1_4\) is dictated by (3.20).

Secondly, we prove that \({\widehat{J}}_\varepsilon ^{-1}W\) is contractive provided \({\widehat{C}}\in \{{\widehat{f}}\in L^1_{4}({\mathbb {R}}^d): {{\,\mathrm{Im}\,}}(\widehat{f_R})=-{{\,\mathrm{Re}\,}}(\widehat{f_I}) \}\). We start by showing \({\widehat{J}}_\varepsilon :X_{2}^\text {sym}\rightarrow X_{0}^\text {sym}\). The loss of 2 in the weight is due to the second order nature of the operator J, i.e. due to the factor \(\kappa ^TG_0\kappa \) in Fourier variables. The entries \(\omega _1+\kappa ^TG_0\kappa \) clearly preserve the PT-symmetry. For the convolution terms we have, for instance

$$\begin{aligned} {{\,\mathrm{Im}\,}}(\widehat{C_R})=-{{\,\mathrm{Re}\,}}(\widehat{C_I}) \ \Rightarrow \ {{\,\mathrm{Im}\,}}(\widehat{C_R}^{(\varepsilon )})=-{{\,\mathrm{Re}\,}}(\widehat{C_I}^{(\varepsilon )}) \ \Rightarrow \ C^{(\varepsilon )}(-x)=\overline{C^{(\varepsilon )}(x)} \ \forall x. \end{aligned}$$

Hence \(C_R^{(\varepsilon )^2}d_R, C_I^{(\varepsilon )^2}d_R\), and \(C_R^{(\varepsilon )}C_I^{(\varepsilon )}d_I\) are even and \(C_I^{(\varepsilon )^2}d_I, C_R^{(\varepsilon )^2}d_I\), and \(C_R^{(\varepsilon )}C_I^{(\varepsilon )}d_R\) are odd such that the \(PT-\)symmetry is preserved also by the convolution terms. In end effect, \({{\,\mathrm{Im}\,}}(({\widehat{J}}_\varepsilon \widehat{\vec {d}})_1)=-{{\,\mathrm{Re}\,}}(({\widehat{J}}_\varepsilon \widehat{\vec {d}})_2)\). Hence, \({\widehat{J}}_\varepsilon :X_{2}^\text {sym}\rightarrow X_{0}^\text {sym}\) and for \({\widehat{J}}_\varepsilon ^{-1}\) we get \({\widehat{J}}_\varepsilon ^{-1}:X_{0}^\text {sym}\rightarrow X_{2}^\text {sym}\).

Next, we show that \(W:B_{c\varepsilon }^{2,\text { sym}}\rightarrow B_{c\varepsilon }^{0,\text {sym}}\) if \({\widehat{C}} \in X_{4}^\text {sym}\). The term \(\rho \) is estimated in (3.21) and dictates the order \(\varepsilon ^1\).

The difference \(F_\mathrm{NLS}(\widehat{\vec {C}}^{(\varepsilon )}+\widehat{\vec {d}})-{\widehat{J}}_\varepsilon \widehat{\vec {d}}\) consists of terms quadratic in \(\widehat{\vec {d}}\) and hence is bounded in \(L^1({\mathbb {R}}^d)\) by \(c_1(\Vert \widehat{\vec {d}}\Vert _{L^1({\mathbb {R}}^d)}^2+\Vert \widehat{\vec {d}}\Vert _{L^1({\mathbb {R}}^d)}^3)\). In summary,

$$\begin{aligned} \Vert W(\widehat{\vec {d}})\Vert _{L^1({\mathbb {R}}^d)} \leqslant c_2 (\varepsilon + \varepsilon ^{1/2}\Vert \widehat{\vec {d}}\Vert _{L^1_2({\mathbb {R}}^d)} + \Vert \widehat{\vec {d}}\Vert _{L^1_2({\mathbb {R}}^d)}^2+\Vert \widehat{\vec {d}}\Vert _{L^1_2({\mathbb {R}}^d)}^3) \leqslant c \varepsilon \end{aligned}$$

if \(\Vert \widehat{\vec {d}}\Vert _{L^1_2({\mathbb {R}}^d)} \leqslant c\varepsilon \) and \(\varepsilon >0\) is small enough. Due to the boundedness of \({\widehat{J}}_\varepsilon ^{-1}: X_{0}^\text {sym}\rightarrow X_{2}^\text {sym}\) we thus have (3.25).

The contractive property of \({\widehat{J}}_\varepsilon ^{-1}W\) in \(B_{c\varepsilon }^{2,\text { sym}}\) is now clear due to the quadratic nature of \(F_\mathrm{NLS}(\widehat{\vec {C}}^{(\varepsilon )}+\widehat{\vec {d}})-{\widehat{J}}_\varepsilon \widehat{\vec {d}}\).

We conclude that if the solution C of the NLS (2.3) satisfies \({\widehat{C}}\in \{{\widehat{f}}\in L^1_{4}({\mathbb {R}}^d): {{\,\mathrm{Im}\,}}(\widehat{C_R})=-{{\,\mathrm{Re}\,}}(\widehat{C_I}) \}\), then there is \(c>0\) such that for all \(\varepsilon >0\) small enough the constructed solution D of (3.13) satisfies

$$\begin{aligned} {\widehat{D}} \in \{{\widehat{f}}\in L^1_{2}({\mathbb {R}}^d): {{\,\mathrm{Im}\,}}(\widehat{f_R})=-{{\,\mathrm{Re}\,}}(\widehat{f_I\, \, }) \} \end{aligned}$$

and due to (3.18)

$$\begin{aligned} \Vert {\widehat{D}}-\chi _{B_{\varepsilon ^{-1/2}}}{\widehat{C}}\Vert _{L^1_2({\mathbb {R}}^d)}\leqslant c(\Vert {\widehat{C}}\Vert _{L^1_4({\mathbb {R}}^d)})\varepsilon . \end{aligned}$$
(3.26)

Here we have also used \(\Vert \varepsilon \nu \chi _{B_{\varepsilon ^{-1/2}}}{\widehat{C}}\Vert _{L^1_2}\leqslant c\varepsilon \Vert {\widehat{C}}\Vert _{L^1_3}\).

This allows us to estimate \(\widehat{\vec {B}}_D-\widehat{\vec {B}}_{\text {app}}\). We have

$$\begin{aligned} \begin{aligned} \Vert \widehat{\vec {B}}_D-\widehat{\vec {B}}_{\text {app}}\Vert _{L^1({\mathbb {R}}^d)}\leqslant&\varepsilon ^{1-d}\left\{ \left\| \left( {\widehat{D}}\left( \frac{\cdot -k_0}{\varepsilon }\right) -{\widehat{C}}\left( \frac{\cdot -k_0}{\varepsilon }\right) \right) \vec {\eta }^{(j_0)}(k_0) \right\| _{L^1(B_{\varepsilon ^{r}}(k_0))}\right. \\&+\left\| {\widehat{D}}\left( \frac{\cdot -k_0}{\varepsilon }\right) \left( \vec {\eta }^{(j_0)}(\cdot )-\vec {\eta }^{(j_0)}(k_0)\right) \right\| _{L^1(B_{\varepsilon ^{r}}(k_0))}\\&\left. +\left\| {\widehat{C}}\left( \frac{\cdot -k_0}{\varepsilon }\right) \vec {\eta }^{(j_0)}(k_0)\right\| _{L^1(B^c_{\varepsilon ^{r}}(k_0))} \right\} \end{aligned} \end{aligned}$$

Next we use (3.26), the Lipschitz continuity of \(\vec {\eta }^{(j_0)}\), and the estimate \(\Vert {\widehat{C}}\Vert _{L^1(B^c_{\varepsilon ^{r-1}})}\leqslant \varepsilon ^{(1-r)s_C}~\Vert {\widehat{C}}\Vert _{L^1_{s_C}({\mathbb {R}}^d)}\) for all \(s_C\geqslant 0\). This produces at \(r=1/2\)

$$\begin{aligned} \begin{aligned} \Vert \widehat{\vec {B}}_D-\widehat{\vec {B}}_{\text{ app }}\Vert _{L^1({\mathbb {R}}^d)}\leqslant&c\left( \varepsilon ^2 + \varepsilon ^2\Vert {\widehat{D}}\Vert _{L^1_1({\mathbb {R}}^d)}+ \varepsilon ^{1+s_C/2}\Vert {\widehat{C}}\Vert _{L^1_{s_C}({\mathbb {R}}^d)} \right) \\ \leqslant&c\left( 1+\Vert {\widehat{D}}\Vert _{L^1_1({\mathbb {R}}^d)}+\Vert {\widehat{C}}\Vert _{L^1_4({\mathbb {R}}^d)}\right) \varepsilon ^2\end{aligned} \end{aligned}$$

if \(s_C=4\).

We can now summarize the error estimate

$$\begin{aligned} \begin{aligned} \Vert \widehat{\vec {B}}-\widehat{\vec {B}}_{\text {app}}\Vert _{L^1({\mathbb {R}}^d)}&\leqslant \Vert \widehat{\vec {B}}_D-\widehat{\vec {B}}_{\text {app}}\Vert _{L^1({\mathbb {R}}^d)} +\Vert \widehat{\vec {B}}-\widehat{\vec {B}}_D\Vert _{L^1({\mathbb {R}}^d)} \\&\leqslant \Vert \widehat{\vec {B}}_D-\widehat{\vec {B}}_{\text {app}}\Vert _{L^1({\mathbb {R}}^d)} + \Vert \widehat{\vec {B}}_Q\Vert _{L^1({\mathbb {R}}^d)}+ \Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)}. \end{aligned} \end{aligned}$$

The components \(\widehat{\vec {B}}_Q\) and \(\widehat{\vec {B}}_R\) are estimated in (3.8), (3.9), and (3.12). Having now estimated \(\Vert {\widehat{R}}\Vert _{L^1}\) in terms of \(\Vert {\widehat{C}}\Vert _{L^1}\) and \(\Vert {\widehat{D}}\Vert _{L^1}\) in terms of \(\Vert {\widehat{C}}\Vert _{L^1_2}\), we get for \(r=1/2\) and \(s_D=2\)

$$\begin{aligned} \Vert \widehat{\vec {B}}_Q\Vert _{L^1({\mathbb {R}}^d)}\leqslant c_1(\Vert {\widehat{C}}\Vert _{L^1_2({\mathbb {R}}^d)}) \varepsilon ^{3}, \qquad \Vert \widehat{\vec {B}}_R\Vert _{L^1({\mathbb {R}}^d)}\leqslant c_2(\Vert {\widehat{C}}\Vert _{L^1_2({\mathbb {R}}^d)}) \varepsilon ^3, \end{aligned}$$

where \(c_1\) and \(c_2\) depend polynomially on \(\Vert {\widehat{C}}\Vert _{L^1_2({\mathbb {R}}^d)}\). Hence, the estimate in Theorem 1 is proved.

4 Numerical Example of Bifurcating Gap Solitons for \(d=2\)

In [9] it is shown that assumption (A.1), i.e. the existence of a spectral gap is satisfied for \(N=4\) in the symmetric case

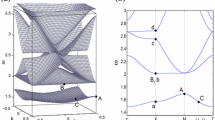
$$\begin{aligned} \begin{aligned}&v_g^{(1)}=-v_g^{(2)}=:v,v_g^{(3)}=-v_g^{(4)}=:w, \\&\kappa _{12}=\kappa _{34}=:\alpha _1,\\&\kappa _{14}=\kappa _{32}=:\alpha _2,\\&\kappa _{13}=\kappa _{42}=:\alpha _3,\\&\kappa _{jj}=0, j=1,\dots ,4 \end{aligned} \end{aligned}$$
(4.1)

provided \(|\alpha _1|^2>2(|\alpha _2|^2+|\alpha _3|^2)\). In the following example we choose \(v=(0,1)^T, w=(1,0)^T\), \(\alpha _1=2,\) and \(\alpha _2=\alpha _3=1\). The dispersion relation \(\omega _j:{\mathbb {R}}^2\rightarrow {\mathbb {R}}, j=1,\dots ,4\) of (1.1) is plotted in Fig. 1. The gap appears even though the sufficient condition \(|\alpha _1|^2>2(|\alpha _2|^2+|\alpha _3|^2)\) is not satisfied.

Fig. 1
figure 1

Dispersion relation of (1.1) for the example in Sect. 4

Full size image
Fig. 2
figure 2

Asymptotic approximation \(B_{\text {app},1}\) and the numerical solution \(B_1\) (real and imaginary part) at \(\varepsilon =0.05\)

Full size image
Fig. 3
figure 3

Convergence of the asymptotic error in \(\varepsilon \)

Full size image

We see that the second eigenvalue \(\lambda _2\) has an isolated maximum at \(k=k_0:=0\). The corresponding frequency is \(\omega _0:=\lambda _2(0)=0\). The eigenvector corresponding to \(\lambda _2(0)\) is \(\vec {\eta }_{j_0}(0)=\tfrac{1}{\sqrt{2}}(1,1,-1,-1)^T\).

We use the following special case of the coefficients \(\gamma _j^{(m,n,o)}\) in (1.3)

$$\begin{aligned} \begin{aligned} 1&=\gamma _{j}^{(j,j,j)}=\gamma _j^{(j,i,i)}=\gamma _j^{(i,i,j)}, \quad i,j=1,\dots ,4,\\&= \gamma _1^{(3,2,4)}= \gamma _1^{(4,2,3)}= \gamma _2^{(3,1,4)}= \gamma _2^{(4,1,3)}\\&= \gamma _3^{(1,4,2)}= \gamma _3^{(2,4,1)}= \gamma _4^{(1,3,2)}= \gamma _4^{(2,3,1)},\\&\quad \gamma _j^{(m,n,o)}=0 \text { otherwise.} \end{aligned} \end{aligned}$$
(4.2)

Clearly, coefficients (4.1) and (4.2) allow symmetric solutions with \(B_2=\overline{B_1}\) and \(B_4=\overline{B_3}\). We do not make a direct use of this symmetry in our computations. We construct the approximation \(\vec {B}_\mathrm{app}\) of a solution of (1.3) at \(\omega = \omega _0+\varepsilon ^2\omega _1\) for six values of \(\varepsilon \): 0.2, 0.1, 0.05, 0.025, 0.0125, and 0.00625. The coefficients of the effective NLS (2.3) are \(G_0=-0.25~ I_{2x2}\) and \(\Gamma = 2.25\) and we choose \(\omega _1=1\). A real C radially symmetric was chosen in this example. It was computed using the shooting method for the NLS in polar variables.

Using the numerical Petviashvili iteration [1, 14], we also produce a numerical approximation of a solution \(\vec {B}\) at \(\omega = \omega _0+\varepsilon ^2\). The Petviashvili iteration is a fixed point iteration in Fourier variables with a stabilizing normalization factor. The initial guess of the iteration was chosen as \(\vec {B}_\mathrm{app}\). Note that although \(\vec {B}_\mathrm{app}\) can be real (if a real solution C of the NLS is chosen), Eq. (1.3) does not allow real solutions \(\vec {B}\) due to the term \(\mathrm{i}\nabla \vec {B}\) and due to the realness of \(\alpha _1,\alpha _2,\) and \(\alpha _3\) and of \(\gamma _j^{(m,n,o)}\). Nevertheless, if \(\vec {B}_\mathrm{app}\) is real, there must be a solution \(\vec {B}\) with \(\text {Im}(\vec {B})=O(\varepsilon ^2)\). Figure 2 shows \(\vec {B}_\mathrm{app}\) and \(\vec {B}\) for \(\varepsilon =0.05\).

The numerical parameters for the Petviashvili iteration were selected as follows: we compute on the domain \(x\in [-3/\varepsilon , 3/\varepsilon ]^2\) with the discretization given by 160x160 grid points, i.e. \(dx_1=dx_2=3/(80\varepsilon )\). Note that because \(k_0=0\), the relatively coarse discretization for small values of \(\varepsilon \) does not matter (there are no oscillations to be resolved).

For each \(\varepsilon \) we evaluate the asymptotic error \(E:=\Vert \vec {B}-\vec {B}_\mathrm{app}\Vert _{C_0}\). Figure 3 shows the convergence of the error in \(\varepsilon \). Clearly, \(E(\varepsilon )\sim c\varepsilon ^2\), which confirms the convergence rate proved in our theorem.