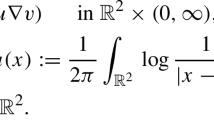Abstract
We consider positive classical solutions of
in the super-fast diffusion range \(m<-1\). Our main interest is in smooth positive initial data \(v_0=v(\cdot ,0)\) which decay as \(x\rightarrow +\infty \), but which are possibly unbounded as \(x\rightarrow -\infty \), having in mind monotonically decreasing data as prototypes. It is firstly proved that if \(v_0\) decays sufficiently fast only in one direction by satisfying
and some \(c>0\), then the so-called proper solution of (\(\star \)) vanishes identically in \({\mathbb {R}}\times (0,\infty )\), and accordingly no positive classical solution exists in any time interval in this case. Complemented by some sufficient criteria for solutions to remain positive either locally or globally in time, this condition for instantaneous extinction is shown to be optimal at least with respect to algebraic decay of the initial data. This partially extends some known nonexistence results for (\(\star \)) (Daskalopoulos and Del Pino in Arch Rat Mech Anal 137(4):363–380, 1997) in that it does not require any knowledge on the behavior of \(v_0(x)\) for \(x<0\). Next focusing on the phenomenon of extinction in finite time, we show that in this respect a mass influx from \(x=-\infty \) can interact with mass loss at \(x=+\infty \) in a nontrivial manner. Namely, we shall detect examples of monotone initial data, with critical decay as \(x\rightarrow +\infty \) and exponential growth as \(x\rightarrow -\infty \), that lead to solutions of (\(\star \)) which become extinct at a finite positive time, but which have empty extinction sets. This is in sharp contrast to known extinction mechanisms which are such that the corresponding extinction sets coincide with all of \({\mathbb {R}}\).
Similar content being viewed by others
References
Aronson, D.G.: Regularity properties of flows through porous media: the interface. Arch. Rat. Mech. Anal. 37, 1–10 (1970)
Aronson, D.G.: The porous medium equation. Nonlinear diffusion problems, Lect. 2nd 1985 Sess. C.I.M.E. Montecatini Terme/Italy 1985. Lect. Notes Math. 1224, 1–46 (1986)
Aronson, D.G., Caffarelli, L.A.: The initial trace of a solution of the porous medium equation. Trans. Am. Math. Soc. 280, 351–366 (1983)
Bénilan, Ph., Crandall, M.G., Pierre, M.: Solutions of the porous medium equation in \({\mathbb{R}}^N\) under optimal conditions on initial values. Indiana Univ. Math. J. 33, 51–87 (1984)
Blanchet, A., Bonforte, M., Dolbeault, J., Grillo, G., Vázquez, J.L.: Asymptotics of the fast diffusion equation via entropy estimates. Arch. Rat. Mech. Anal. 191, 347–385 (2009)
Bonforte, M., Dolbeault, J., Grillo, G., Vázquez, J.L.: Sharp rates of decay of solutions to the nonlinear fast diffusion equation via functional inequalities. Proc. Nat. Acad. Sci. 107, 16459–16464 (2010)
Bonforte, M., Segatti, A., Vázquez, J.L.: Non-existence and instantaneous extinction of solutions for singular nonlinear fractional diffusion equations. Calc. Var. Part. Diff. Equ. 55: 68 (2016)
Brézis, H., Friedman, A.: Nonlinear parabolic equations involving measures as initial conditions. J. Math. Pures Appl. 62, 73–97 (1983)
Dahlberg, B.E.J., Kenig, C.E.: Nonnegative solutions of the porous medium equation. Commun. Part. Differ. Equ. 9, 409–437 (1984)
Daskalopoulos, P., del Pino, M.: On nonlinear parabolic equations of very fast diffusion. Arch. Rat. Mech. Anal. 137(4), 363–380 (1997)
Daskalopoulos, P., del Pino, M.: On the Cauchy problem for \(u_t=\Delta \log u\) in higher dimensions. Math. Ann. 313(2), 189–206 (1999)
Daskalopoulos, P., Kenig, C.E.: Degenerate Diffusions. Initial Value Problems and Local Regularity Theory. EMS Tracts in Mathematics. European Mathematical Society, Zürich (2007)
Daskalopoulos, P., Sesum, N.: On the extinction profile of solutions to fast diffusion. J. Reine Angew. Math. 622, 95–119 (2008)
Diaz, G., Diaz, J.I.: Finite extinction time for a class of non-linear parabolic equations. Commun. Part. Differ. Equ. 4, 1213–1231 (1979)
Esteban, J.R., Rodriguez, A., Vázquez, J.L.: A nonlinear heat equation with singular diffusivity. Commun. Part. Differ. Equ. 13, 985–1039 (1988)
Fila, M., King, J.R., Winkler, M.: Rate of convergence to Barenblatt profiles for the fast diffusion equation with a critical exponent. J. Lond. Math. Soc. 90, 167–183 (2014)
Fila, M., Vázquez, J.L., Winkler, M.: A continuum of extinction rates for the fast diffusion equation. Commun. Pure Appl. Anal. 10, 1129–1147 (2011)
Fila, M., Vázquez, J.L., Winkler, M., Yanagida, E.: Rate of convergence to Barenblatt profiles for the fast diffusion equation. Arch. Rat. Mech. Anal. 204, 599–625 (2012)
Fila, M., Winkler, M.: Optimal rates of convergence to the singular Barenblatt profile for the fast diffusion equation. Proc. R. Soc. Edinburgh Sect. A 146, 309–324 (2016)
Galaktionov, V.A., Peletier, L.A.: Asymptotic behaviour near finite-time extinction for the fast diffusion equation. Arch. Rat. Mech. Anal. 139, 83–98 (1997)
Galaktionov, V.A., Vázquez, J.L.: Continuation of blowup solutions of nonlinear heat equations in several space dimensions. Commun. Pure Appl. Math. 50(1), 1–67 (1997)
Grillo, G., Muratori, M., Punzo, F.: The Porous Medium Equation with Large Initial Data on Negatively Curved Riemannian Manifolds. arXiv:1609.06498
King, J.R.: Self-similar behaviour for the equation of fast nonlinear diffusion. Phil. Trans. R. Soc. Lond. A 343, 337–375 (1993)
Ladyzenskaja, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasi-linear Equations of Parabolic Type. AMS, Providence (1968)
Luckhaus, S., Dal Passo, R.: A degenerate diffusion problem not in divergence form. J. Differ. Equ. 69, 1–14 (1987)
Peletier, M.A., Zhang, H.: Self-similar solutions of a fast diffusion equation that do not conserve mass. Differ. Int. Equ. 8, 2045–2064 (1995)
Pierre, M.: Nonlinear fast diffusion with measures as data. In: Nonlinear Parabolic Equations: Qualitative Properties of Solutions (Rome, 1985). Pitman Res. Notes Math. Ser. Longman Sci. Tech. Harlow 149, 179–188 (1987)
Rodriguez, A., Vázquez, J.L.: A well-posed problem in singular Fickian diffusion. Arch. Rat. Mech. Anal. 110(2), 141–163 (1990)
Tomi, F.: Über semilineare elliptische Differentialgleichungen zweiter Ordnung. Math. Z. 111, 350–366 (1969)
Vázquez, J.L.: Darcy’c Law and the theory of shrinking solutions of fast diffusion equations. SIAM J. Math. Anal. 35(4), 1005–10284 (2004)
Vázquez, J.L.: Smoothing and Decay Estimates for Nonlinear Diffusion Equations. Equations of Porous Medium Type. Oxford Lecture Series in Mathematics and its Applications, pp. 33. Oxford University Press, Oxford (2006)
Wiegner, M.: A degenerate diffusion equation with a nonlinear source term. Nonlin. Anal. TMA 28, 1977–1995 (1997)
Winkler, M.: Conservation of boundary decay and nonconvergent bounded gradients in degenerate diffusion problems. Adv. Differ. Equ. 13, 27–54 (2008)
Winkler, M.: Spatially monotone homoclinic orbits in nonlinear parabolic equations of super-fast diffusion type. Math. Ann. 355(2), 519–549 (2013)
Acknowledgements
The author would like to sincerely thank the anonymous reviewer for numerous detailed remarks and suggestions which substantially supported improvement of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Winkler, M. One-Dimensional Super-Fast Diffusion: Persistence Versus Extinction Revisited—Extinction at Spatial Infinity. J Dyn Diff Equat 30, 331–358 (2018). https://doi.org/10.1007/s10884-017-9577-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-017-9577-3