Periodic Solutions of a Class of Non-autonomous Discontinuous Second-Order Differential Equations

Abstract

We consider the second-order discontinuous differential equation y^″ + η sgn(y) = 𝜃y + α sin(βt) where the parameters η, 𝜃, α, and β are real. The main goal is to discuss the existence of periodic solutions. Under explicit conditions, the number of such solutions is given. Furthermore, for each of these periodic solutions, an explicit formula is provided.

Appendix

Consider Eq. (1) with β = 1, η = −𝜃 = 1/25 > 0:

$$y^{\prime\prime}+(1/25)\operatorname{sgn}(y)=-(1/25)y+\alpha\sin(t). $$

From Lemmas 6.1 and 6.2, the solution satisfying

$$y(0)= 0, y^{\prime}(0)=(1/5)\tan{\left( k\pi/10\right)}-(25/24)\alpha $$

with $k\in {\mathbb {N}}\setminus \{0\}$, is

$$y_{[k]}(t)=\cos{\left( t/5\right)}+\tan{\left( k\pi/10\right)} \sin{\left( t/5\right)}-1-(25/24)\alpha\sin(t). $$

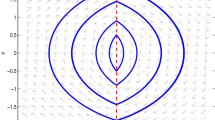
By Lemma 6.4, the condition η ⋅ tan (kπ/10) > 0 is satisfied only when tan (kπ/10) > 0. This gives us the restriction on k ∈{1, 2, 3, 4}. For each k, there is a positive number $\alpha ^{*}_{k}=\min \{K_{1}^{(k)},K_{2}^{(k)},K_{3}^{\theta ,(k)}\}$. We will denote $\alpha ^{*}=\min \{\alpha _{i}^{*}\hspace {0.15cm} | \hspace {0.15cm} i = 1,2,3,4\}$. Some calculations give us $\alpha ^{*}=K_{3}^{\theta ,(1)}\cong 0.048537$. For |α| < α^∗, we have the following configurations for the solution on [0, kπ], with k = 1, 2, 3, 4 and k = 6, 7, 8, 9 (Fig. 11).

Fig. 11

Examples of 2kπ–periodic solutions on [0, kπ] for k ∈{1,2,3,4}. When k ∈{6,7,8,9} the respective solutions are such that y^′(0) < 0 and it does not generate a solution of the discontinuous equation

Fig. 12

A simple singular 2π-periodic solution (dashed curve) on [0, π]

Fig. 13

Examples of 2kπ–periodic solutions on [0, kπ] for k ∈{6,7,8,9}. When k ∈{1,2,3,4}, the respective solutions are such that y^′(0) < 0 and it does not generate a solution of the discontinuous equation

Observe that for k = 6, 7, 8, 9, the solution is such that y^′(0) < 0 and the necessary conditions of Lemma 6.3 are not met. For k = 1, there is a value α for which we obtain a simple singular 2π–periodic solution. This value is given by the condition x(π/2) = 0 and is α = (24/25)(sec(π/10) − 1). See Fig. 12.

Now, if we consider η = 𝜃 = − 1/25 < 0, the solution satisfying the initial conditions

$$y(0)= 0, y^{\prime}(0)=-(1/5)\tan{\left( k\pi/10\right)}-(25/24)\alpha $$

with $k\in {\mathbb {N}}\setminus \{0\}$, is

$$y_{[k]}(t)=-\cos{\left( t/5\right)}-\tan{\left( k\pi/10\right)} \sin{\left( t/5\right)}+ 1-(25/24)\alpha\sin(t). $$

By Lemma 6.4, the condition η ⋅ tan (kπ/10) > 0 is satisfied only when tan (kπ/10) < 0. This gives us the restriction on k ∈{6, 7, 8, 9}. For each k, there is a positive number $\alpha ^{*}_{k}=\min \{K_{1}^{(k)},K_{2}^{(k)},K_{3}^{\theta ,(k)}\}$. We will denote $\alpha ^{*}=\min \{\alpha _{i}^{*}\hspace {0.15cm} | \hspace {0.15cm} i = 6,7,8,9\}$. Some calculations give us $\alpha ^{*}=K_{3}^{\theta ,(1)}\cong 0.048537$. For |α| < α^∗, we have the following configurations for the solution on [0, kπ], with k = 6, 7, 8, 9 and k = 1, 2, 3, 4:

Observe that for k = 1, 2, 3, 4, the solution is such that y^′(0) < 0 and the necessary conditions of Lemma 6.3 are not met (Fig. 13).