Influence of indium and selenium co-doping on structural and thermoelectric properties of Bi₂Te₃ alloys

Abstract

The melt-grown, indium and selenium co-doped Bi₂Te₃ single-crystal system is studied with a purpose to improve and analyze the thermoelectric performance in the low and near room-temperature range (10–400 K). The influence of co-dopants on the crystalline perfection, symmetry, dislocation, and single-crystal quality is investigated using high-resolution X-ray diffraction. The surface morphological features show the existence of small-angle grain boundaries, white patches, and tilt boundaries. Degenerate type of semiconducting behavior is seen in all the samples over the entire temperature range. The existence of small polarons is experimentally inferred from temperature-dependent electrical resistivity. Measurement of Seebeck coefficient confirms p- to n-type transition in the crystals doped with indium and selenium. The total thermal conductivity at 11 K was decreased by 3.4 times in (Bi_0.98In_0.02)₂Te_2.7Se_0.3 as compared to pristine sample. Therefore, this novel co-doped indium and selenium Bi₂Te₃ single-crystal combination is viable to use as a competitor for low and near-room-temperature thermoelectric applications.

1 Introduction

About 70% of the energy produced in the world is dissipated into the environment, mainly as waste heat. Thermoelectricity is one of the cost effective and sustainable ways to convert this waste heat into usable thermal energy [1]. Thermoelectric generators (TEG), which are silent solid-state devices with no moving parts, can collect the waste heat from automobile exhaust, industry (steel plant), etc. and utilize the same for other applications. The efficiency of thermoelectric materials is experimentally measured with the help of the dimensionless figure of merit ZT, given by $ZT=\frac{{S}^{2}T}{{\rm K}\rho }$, where $S$ is the Seebeck coefficient, ${\rm K}$ is the total thermal conductivity, $\rho$ is the electrical resistivity, and T is the temperature [2].

It is very challenging to increase the electrical conductivity and simultaneously decrease the thermal conductivity of a material to enhance the ZT values [3]. Currently one of the most promising narrow bandgap semiconductor single-crystal bismuth tellurides owns the such unique thermoelectric properties with low thermal conductivity at temperatures around 300 K or lower [4]. Bismuth telluride shows limiting solidification near its melting point (576 °C). As a result, good-quality single crystals can be grown by melt growth technique. The intrinsic point defects formed during crystal growth function as negatively charged antisite disorders like Bi_Te and Bi_Se [5]. As a result, there is a formation anionic vacancy such as V_Te and Vse, carrying positive charges. However, the role of these point defects in governing the thermoelectric properties of the doped bismuth chalcogenide compounds is not well understood. The parameters like electrical resistivity, thermal conductivity, and Seebeck coefficient need to be decoupled from each other. As there is an increase in this quantum confinement, band of electron energy structure tends to be narrower, which results in the greater values of electrical conductivity, Seebeck coefficient, and effective mass. The variation in the degenerate valley maximizes the entropy per carrier within the electronic bands. Additionally, the level of resonance also takes crucial role in optimizing the values of thermoelectric parameters. The insertion of dopants to the parent compound matrix results in the distortion of the Fermi level. As a result, there is an enhancement in the effective mass of the charge carriers without the deterioration of carrier concentration [6,7,8].

Bismuth chalchogenides are promising materials for thermoelectric applications due to their high-power factor ($\frac{{S}^{2}}{\rho }$), However, their high thermal conductivity is a point of concern. Single doping has been proved to be useful in improving the thermoelectric performance in recent years [9,10,11,12]. Prompted by these investigations and in continuation with our ongoing research on co-doped bismuth chalchogenide single crystals [13,14,15], we report here the synthesis and growth of In and Se co-doped Bi₂Te₃ single crystals.

Adam et al. [16] have used the traditional melting process,for preparing polycrystalline bulk samples of the Bi₂(Se_1−xTe_x)₃ system with x = 0.0–0.9. Te atoms were successfully and affordably substituted for Se atoms to produce Bi₂Se₃/Bi₂Te₃. Numerous studies have been conducted by Ibrahim et al. on the physical characteristics of Cu(II)-Schiff base complexes and metal-Schiff base complexes, including their electric and optical characteristics. Bi₂Se₃ bulk alloys [17] created using mono-temperature melting procedure and used as source materials to form thin films on non-conductive ultra-cleaned glass substrates. Shokr et al. [18] adopted annealing process to generate polycrystalline solid solutions of (Bi_1−xSb_x)₂Se₃ (x = 0, 0.025, 0.050, 0.075, and 0.100). Sb_2−xBi_xTe₃ prepared by melting process shows peak power factor value of about 24.7 W/cm K² and the highest figure of merit of 1.14 [19]. Polycrystalline samples of (Bi_0.95Sb_0.05)₂Se₃ were created by Ibrahim et al. by melting method at 1273 K [20].

Indium contributes maximum number of resonant levels to the electronic bands of BiTe [21,22,23,24]. Se can achieve a high level of substitution at the site of Te due to their comparable chemical and physical properties. This serves as a motivation for doping with both In and Se. In our previous work, we have achieved the reduction of thermal conductivity due to co-doping of Sn and In in polycrystalline Bi₂Se₃ [25]. When the bismuth telluride-based compounds are used for low-temperature power generation, intrinsic excitation becomes the major limitation. To widen the band gap, selenium alloying can be adopted, which is a practical solution to suppress the bipolar conduction [26]. Point defects, antisite defects, and vacancies generated by different doping and alloying reduce the thermal conductivity of Bi₂Te₃ by shifting the phonon density of states.

Bi₂Te₃ and its alloys are the most important class of thermoelectric materials because they have the highest known efficiency at low temperatures (< 300 K), whereas the silicon-based alloys are usually used in high-temperature thermoelectric applications (> 600 K). The market for temperature control is dominated by Bi₂Te₃ solid-state devices. Peltier cooling is becoming increasingly appealing as the demand to eliminate greenhouse-gas refrigerants grows, especially in small systems where the efficiencies are equivalent to conventional refrigerant-based coolants. With the accuracy in assessing the band structures, the interest in topological insulators of bismuth and its alloys has revealed new insights into the complicated electronic structure. Despite being the most popular and well-known functional material, silicon’s thermoelectric material efficiency is unfortunately inferior to that of Bi₂Te₃. The silicon-germanium alloys are not commonly used due to their high price and low ZT values [27, 28].

To the best of our knowledge, doping on Bi₂Se3 and Bi₂Te₃ has been thoroughly explored, but simultaneous doping and composite for these compounds have received the least attention. We previously reported the low-temperature thermoelectric characteristics of the polycrystalline sample series of (Bi_1−xSn)₂Te_2.7Se_0.3, (Bi_1−xIn)₂Se_2.7Te_0.3, and (Bi_1−x In)₂Se_2.7Te_0.3. As per continuation of the previous study, indium and selenium co-doped bismuth telluride single crystals are grown by melt growth technique. To investigate structural features, high-resolution X-ray diffraction and powder X-ray diffraction techniques were employed. Thermoelectric properties including electrical resistivity, thermal conductivity, and Seebeck coefficient have been explored in the temperature range of 10–400 K. In the current study, it was observed that thermal conductivity of the system decreases drastically due to the co-doping. Hence, Bi₂Te₃ with indium and selenium co-doped single-crystal system may be a good candidate for low and near room-temperature thermoelectric applications.

2 Experimental details

2.1 Single-crystal growth and characterization

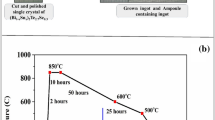
The stoichiometric ratio of the precursors metallic powder of indium (99.9%), bismuth (99.99%), tellurium (99.99%), and selenium (99.995%) was subjected to intense grinding using a pestle and agate mortar for 2 h. The ground mixture powder was introduced into quartz ampoule of 200 mm length mm and 14 mm diameter. The vacuum sealing was carried out at 10⁻³ Torr in an argon atmosphere. Ampoule containing sample was tied to the motor of the crystal puller. The sample was heated and cooled in eight segments in the range of 30–850 °C, utilizing a programmable furnace attached to the crystal puller. The pulling of ampoule was carried out at the rate of 2 mm/hour at the transition temperature of 600 °C. The temperature profile chart and the schematic diagram of process of melt growth are shown in our previously reported article [12, 14]. The grown ingot of bismuth telluride is shown in Fig. 1.

Fig. 1

Melt-grown ingot of Bi₂Te₃ single crystal

The structural studies were performed using powder X-ray diffractometer (Rigaku ultima IV, radiation source Cu Kα, wavelength 1.54 Å, resolution 0.02, PDXL Software, semiconductor detector) on finely powdered (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples between 20° and 80° at the scan rate of 2°/min. High-resolution X-ray diffraction (HRXRD) investigation was done on 2 × 2 × 1 mm³ slashed crystal surface using “Diffractometer D8 Bruker” (Cu Kα source, double crystal monochromator Global mirror, 1 D speed detector, resolution 1.5 × 10⁻⁴_, Diffrac Suit Software, semiconductor detector ) to obtain information about the crystalline perfection, symmetry, dislocation, single-crystal quality, and the influence of dopants on the inner plane structure of the single crystals. The surface morphological features of the single crystals were analyzed by field emission scanning electron microscope (FESEM) using “Carl Zeiss Sigma” (3 detectors, 20–120 µm range with a step-up voltage capable of 30 kV) at the particle scale of 1 µm with a 35 kX magnification. The chemical composition of the single crystals was examined by energy-dispersive X-ray analysis (EDS) utilizing EVO MA18 with Oxford EDS (X-act). The carrier concentration and mobility at ambient temperature were evaluated using Van der Pauw method (“Keithley meter 6220” with an input current 50 mA, and the magnetic field of 6000 Gauss). All the crystal were cut into a rectangular parallelopiped shape with size of about ∼ 1.5 × 1.0 × 6.0 mm³ for the transport measurements. The melt-grown single-crystal ingot of dimension 2 × 5 mm² (shown in Fig. 1) is used for the measurements. The ingot formed is of anisotropic in nature.

The crystal plane corresponding to larger surface area was identified as “ab” plane (perpendicular to “c” axis). Hence, this plane has been used to investigate thermoelectric properties of all the samples of (Bi_1−xIn_x)₂Te_2.7Se_0.3 [29]. The thermoelectric properties such as electrical resistivity, thermal conductivity, and Seebeck coefficient are measured along ab plane. Due to corresponding variation in these three parameters, the thermoelectric figure of merit is focused on ab plane only rather than other planes such as ac and bc. Hence, this plane of the area in the single crystal has been used to investigate thermoelectric properties of all the samples of (Bi_1−xIn_x)₂Te_2.7Se_0.3. Electrical resistivity, thermal conductivity, and Seebeck coefficient of (Bi_1−xIn_x)₂Se_2.7Te_0.3 were measured utilizing physical property measurement system (PPMS) (Quantum design) in the temperature range 10–400 K.

3 Results and discussion

3.1 Powder X-ray diffraction

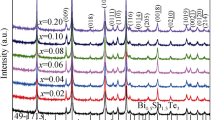
Figure 2 shows the XRD patterns of pristine Bi₂Te₃ and co-doped (Bi_1−xIn_x)₂Te_2.7Se_0.3 samples. The peak (015) at about 28° is found to be the highest in all the samples. The doping of selenium into the matrix of bismuth telluride follows the “Vegards law” [30, 31]. The peak broadening observed at 27.34° is due to the changes in the ionic radii between the host lattice and the dopants. Figure 3 shows that, with the exception of (Bi_0.96In_0.04)₂Te_2.7Se_0.3, there is a modest shift in the peak indicated above towards higher angle theta. The peaks shift is mostly brought on by grain reflation and the considerable strain from the dopants’ energy result in a lattice irregularity. Indium ion doping in the radius of bismuth ion has reached saturation. The bifurcation effect is observed at angles 28°, 40°, 55°, 65° corresponds to sharing of lattice points on the face of the existing crystal [32, 33]. The XRD peak patterns are fitted using “EXPO 2014” software (Fig. 4) [34]. Hence, there is an uneven lattice strain in the compound (Bi_0.96In_0.04)₂Te_2.7Se_0.3. This causes backward shift of XRD peak patterns in the samples. The crystallite size has been estimated using the Williamson–Hall formula.

Fig. 2

XRD peak patterns of a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single-crystal samples

Fig. 3

The shifting of XRD (015) peak for the powdered melt-grown a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single-crystal samples

Fig. 4

The Rietveld refinement plots of melt-grown a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single-crystal samples

$$\beta cos\theta = \left( {\frac{{0.9\lambda }}{D}} \right) + 4\varepsilon sin\theta,$$

(1)

“where β is the full width at half maximum intensity, $\lambda$ is the X-ray wavelength, ε is the strain, and D is the crystallite size.” As a function of co-doping of indium and selenium, there is a steady decrease in the crystallite size (Table 1). The produced characteristic reliability factors such as profile factor (R_p), weighted profile factor (R_wp), expected profile factor (R_ep), and goodness of fit (χ²) are presented in Table 1. The R_p, R_wp, and R_ep values are found to quiet higher due to the simultaneous occupation of Bi in the site of Te (1) and Te (2) [35, 36]. The refined XRD patterns show that the crystal has a hexagonal structure with R$\stackrel{-}{3}$m space group symmetry. The compound chemical phases of all the samples were revealed using “Profex 3.14” software, and the results are given in Table 2. The table shows that supplementary phases Bi–Se, In–Te, and In–Se were found in all the doped samples. Although there are binary phases, amounting to 10–15%, influence of resonant levels on the thermoelectric response of Bi₂Te₃ warrants further exploration. Indium on the Bismuth site and Selenium on Tellurium site can modify the density of states (DOS) by the influence of the resonant levels through interactions between the dopants and the host. Hence, there is a need to discuss conductivity and thermoelectric figure of merit of these samples [37].

Table 1 Characteristic reliability factors such as Profile factor (R_p), Weighted profile factor (R_wp), Expected profile factor (R_ep), Goodness of fit (χ² ), crystallite size, lattice parameters (a, b, and c), and lattice strain information obtained from the powder XRD analysis of melt-grown (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

Table 2 The different phases of melt-grown (Bi_1−xIn_x )₂Te_2.7Se_0.3 single-crystal samples.

3.2 High-resolution X-ray diffraction (HRXRD)

Figure 5 indicates the inner plane scanned θ–2θ plot in the 2θ range of 5°–90°, scanned at the rate of 2°/min. The (006) plane is found to be the highest oriented phase in the Bi₂Te₃ and Bi₂Te_2.7Se_0.3 single crystal, whereas the (0015) plane is found to be the highest oriented one in the (Bi_1−xIn_x)₂Te_2.7Se_0.3 (x = 0.02 and 0.04) samples. This difference may be due to the variation in the recrystallization and anisotropic nature of the crystal [38]. The sharpness of the peaks indicates a reasonable degree of crystallinity, with low grain boundaries and growth along the ‘c’ direction [39].

Fig. 5

The θ−2θ HRXRD scan of the melt-grown a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single-crystal samples

The θ–2θ scan for the inner (015) plane in the range 20°–80° measured at the scan rate of 2°/min is shown in Fig. 6. The figure shows that the crystal growth has taken place in the (015) plane. This is in good agreement with the powder XRD diffraction of the outer plane (015) and confirms the growth along the ‘c’ direction [40]. The particle size and the lattice strain of the single crystals are given in the Table 3, which agree with the powder XRD data. The lattice strain for (Bi_0.98In_0.02)₂Te_2.7Se_0.3 is highest due to the substitution of selenium and indium in the Bi₂Te₃ matrix, insufficient surface tellurium atoms are available to complete the fifth and sixth levels of the quintuple stalk layer [41].

Fig. 6

The θ−2θ HRXRD scan for (015) plane of the melt-grown a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single-crystal samples

Table 3 The HRXRD data of the melt-grown (Bi_1−xIn_x)₂Te_2.7Se_0.3 single crystals

Azimuthal scan (∅ scan) has been performed in the range − 180° to 180° at the rate of 2°/min for the (015) plane, which has shown three peaks corresponding to three-fold symmetry of notifying the in-plane orientation, in which the variation in the intensity of the peak may be attributed to the disorder in the in-plane direction at some region of the crystals (Fig. 7). The interval between the two peaks of all the samples is found to be 120° with some random variation in shifting. There are some inadequate tellurium atoms present on the surface of the crystal to complete each stalking of quintuple layer to maintain the fully terminated surface state. As a result, many stalking faults are introduced in the quintuple layer during the melt growth of indium and selenium-doped bismuth telluride. As a result, there exist selenium, tellurium vacancies and the intercalation of Bi–In atoms in the wander-walls gap which creates local strain fields in the crystal [42].

Fig. 7

The HRXRD ϕ scan for (015) plane of the melt-grown a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single-crystal samples

Figure 8 represents the rocking curve scan for the (0015) plane in the 2θ range 18°–24° at the rate of 2°/min. The rocking curve provides information about the perfection of single crystals. There is a gradual shift in the rocking curve to the higher 2θ side as the doping concentration increases. The unexpected backward 2θ change of the rocking curve of (Bi_0.96In_0.04)₂Te_2.7Se_0.3 is mainly due to the small tilt angles formed by the indium super stoichiometric behavior with bismuth ion [43]. The rocking curves of all the samples match well with the simulated curve of the Lorentzian non-linear fitting. As evidence, the R² and FWHM (β) values are presented in Table 3, which shows the perfect single-crystalline nature of the samples. The sample doped with In (x = 0.02) has a small secondary peak in the rocking curve, which indicates the presence of low-angle grain boundary due to the presence of misorientation in the crystal domains and mosaic orientation [44].

Fig. 8

The HRXRD rocking curve scan for (0015) plane of a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In _0.04)₂Te_2.7Se_0.3 single-crystal samples

The dislocation densities calculated using Eqs. 2 and 3 are given in the Table 3 [45, 46].”

$${D}_{s}=\frac{{\omega }^{2}}{4.35{b}_{s}^{2}},$$

(2)

$${D}_{e}=\frac{{\omega }^{2}}{4.35{b}_{e}^{2}},$$

(3)

where $\omega$ is the full width at half maximum intensity of the rocking curve, b_s is the screw dislocation constant which comes out to be 15.0 nm, and b_e is the edge dislocation constant which comes out to be 2.1 nm. However, some white patches are seen on the surface of the compound (indium doped, x = 0.04) due to the sublimation of tellurium (Fig. 9d). [47]. It is assumed that ordered surface morphological low-angle grain boundaries of (Bi_1−xIn_x)₂Te_2.7Se_0.3 significantly affect the carrier conduction. Moreover, the selenium doping also forms minor interfaces during the crystal growth has the potential for a localized high-strain field, which can act as a carrier transport barrier.

Fig. 9

The FESEM images of melt-grown a Bi₂Te₃ b Bi₂Te_2.7Se_0.3 c (Bi_0.98In_0.02)₂Te_2.7Se_0.3 d (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single-crystal samples

3.3 Field emission scanning electron microscopy (FESEM) and energy-dispersive X-ray analysis of spectra (EDS)

Figure 9 shows surface morphological features on the interface of the grown single crystals. From the nanoscale to the macroscale, surface morphology and topography are crucial characteristics of materials. These characteristics result from the chemical makeup, structure, and manufacturing processes of these materials. Materials can be identified by particular elements of their surface morphology, which have an impact on final surface characteristics including porosity, flatness, and volatilization of the samples. The utilization of chalcogenides in various thermoelectric material applications, therefore, requires knowledge of their surface morphology and topography.

EDS image of Bi₂Te₃ shown in Fig. 10A (a) indicates only the presence of bismuth and tellurium, whereas Fig. 10A (b) depicts the presence of element selenium along with bismuth and Te. Figure 10A (c) and (d) confirms the presence of indium. The expected and observed atomic % of the elements are presented in Table 4. There is a slight variation in the expected and observed atomic percentage due to the volatilization of selenium. The data acquired at the interface specify that the observed Bi atomic percentage is homogenous whereas the Te atomic percentage is varying significantly. Hence, there could be any significant change in the thermoelectric performance of the prepared compounds. The EDS mapping provided in the Fig. 10B shows the homogeneity in the grown single crystals [48].

Fig. 10

A: EDS images of (a) Bi₂Te₃ (b) Bi₂Te_2.7Se_0.3 (c) (Bi_0.98In_0.02)₂Te_2.7Se_0.3 (d) (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single crystals B: The EDS mapping of (Bi_1−xIn_x)₂Te_2.7Se_0.3 single crystal

Table 4 Elemental composition of the melt-grown (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

3.4 Electrical Resistivity

Figure 11 depicts the temperature-dependent electrical resistivity of indium and selenium co-doped Bi₂Te₃ single crystal in the range 10–400 K. Overall, the electrical resistivity increases with increasing temperature in all the samples indicating a degenerate semiconducting behavior, so that these materials seem to act more like a metal than a semiconductor. Due to the presence of electron from one donor atom close to the next atom, there is an overlapping of different wave functions providing the communication between the fifth electrons of all the donor atoms. Hence, all the samples exhibit low electrical resistivity at 10 K [43]. Under this state of degeneracy, the energy band over the quantum states are occupied by the fifth electron of the donor atom. There is an overlap of conduction band with the donor band gives rise to a composite band [49]. A hump-like feature is observed near 150 K in all the samples because of the interaction of dopants indium and selenium with bismuth and tellurium, respectively, which leads to the formation of percolation passages resulting in spatial redistribution of the impurity atoms. Further excessive number of antisite defects Bi_(In) on Te_(Se) are formed [50, 51]. The curves exhibit a metal-semiconductor electrical resistivity transition at 300 K, due to the overlapping of half-filled 6p and the fully filled 6s bands in the Bi₂Se₃ compound, whereas the electrical resistivity decreases with rise of temperature beyond 300 K showing semiconducting behavior because of the exceeding of thermally excited carriers as compared to the ionized impurity carriers. As a result, the mobility of the carriers seems to be reducing with the rise in temperature, which leads to the decrease of electrical resistivity. The defects are controlled by the positively charged vacancies. Te and Se act as electron donor atoms and exhibit n-type electrical conduction. The holes between grains reduce the direct connection of the grains and prevent electrical conduction that occurs due to direct contact between the grains. Thus, it has been found that increase in electrical resistivity with temperature for all the compounds. However, the electrical resistivity decreases with rise of temperature beyond 300 K showing semiconducting behavior because of the exceeding of thermally excited carriers as compared to the ionized impurity carriers [52,53,54,55]. By observing the trend of increasing electrical resistivity with doping, it is realized that doping on these single crystals can induce both charge scattering and lattice vibrations [24]. The compound doped with indium (x = 0.02) shows the highest electrical resistivity due to the suppression of the bond between bismuth and tellurium by a small quantity of indium where it leads to the formation of antisite defects Bi (In)-Te, Bi (In)-Se. A similar behavior has also been observed in our previous work [56].

Fig. 11

The temperature-dependent electrical resistivity of the melt-grown pristine and (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

3.5 Seebeck Coefficient

Temperature-dependent Seebeck coefficients of the pristine and doped samples are shown in Fig. 12. The Seebeck coefficient is found to be positive for Bi₂Te₃, Bi₂Te_2.7Se_0.3, and (Bi_0.96In_0.04)₂Te_2.7Se_0.3 single crystals in the temperature range 10–400 K. As the temperature increases, there is additional thermal energy in the single crystals which increases the lattice vibrations. Indium and selenium are used as acceptor and donor impurities, respectively. The dopant indium attempts to increase the hole concentration, whereas selenium maintains the high carrier mobility and density of states. As a result, there is a recombination of free electrons with the unfilled covalent bond. This leads to a saturation like behavior of the Seebeck coefficient above 300 K [57, 58]. The bipolar conduction increases slightly in compound having larger dopant concentration.

Fig. 12

Temperature-dependent Seebeck coefficient of the melt-grown pristine and (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

At high temperature, the intrinsic carrier concentration may be comparable to the dopant concentration and the conduction of electrons occur by both electrons and holes [59]. On the other hand, (Bi_0.98In_0.02)₂Te_2.7Se_0.3 has shown the n-type semiconducting behavior which could be attributed to partially substitution of tellurium by selenium, which decreases the p-type charge conduction monotonically and increases the n-type charge conduction [21, 60]. The change in carrier’s type with Te content could be attributed to the bound dangling creation at grain boundaries due to the Te vacancies that act as an electron source. Similar transitions from n-type to p-type and vice versa have been observed in our previous work [20]. Due to defects controlled by the positive charged vacancies in Se serving as electron donors and (ii) Bi antisite defects, the 0.02 doped Bi₂Te₃ combination exhibits n-type electrical conduction. The electronegativity and atom size discrepancies between Bi and the cation (Se, Te) diminish with the partial substitution of Te by Se, which improves the antisite defects and boosts the electron density [56]. Due to the random distribution of low-angle grains, there is a variation of orientations in various parts of the granular samples. Hence, the carriers have to be pass through several potential barriers leading to simultaneous energy filtering and carrier localization. This leads to a variation in the trend of the temperature dependence of the Seebeck coefficient as a function of composition [58]. The density of states, effective mass, and Hall mobility values are presented in Table 5 [59]. It is observed that there is a slight difference in the coefficient of theoretical and experimental carrier concentrations, which occurs because the crystal lattice is acted upon by the external forces of the dopants like indium and selenium. The valence electrons existing in different quantum states are scattered over distinct energy levels with different velocities.

Table 5 Experimental (n_Exp), theoretical carrier concentration (n_Th); experimental (µ_Exp), theoretical (µ_Th) carrier mobility; experimental (γ_Exp), theoretical (γ_Th) carrier scattering factor; effective mass (m^*), weighted mobility (µ_w), of the (Bi_1−xIn_x)₂Te_2.7Se_0.3 single crystals

The Fermi energy is calculated using the formula [60]:

$${E}_{F}=-\frac{{\pi }^{2}{{{k}_{B}}^{2}}_{ }^{ }T}{3eS}.$$

(4)

Negative Fermi-energy values indicate that its levels are within the bulk valence band due to the existence of the Dirac point on the surface of the single crystals [61]. The low-angle grain boundaries play a critical role in the presence of different mean-free paths of carriers and phonons due to the combined effect of dislocation scattering and carrier scattering. As a result, it has been observed that there is an increase in the electrical resistivity and reduction in lattice thermal conductivity [62, 63].

3.6 Thermal conductivity

Figure 13 shows the total thermal conductivity (K) measured in the temperature range 10–400 K. All the samples have exhibited the characteristic phonon peak at low temperatures (near about 11 K) due to the combined effect of electron–phonon and electron-impurity scattering. The exponential drop in thermal conductivity is due to phonon–phonon scattering, especially the Umklapp process [beyond 11 K] [64, 65]. The highest (28.00 W/mK) and the lowest (7.0 W/mK) values of K have been observed in pristine and the single crystal doped with indium 0.02. To understand the mechanisms of thermal conduction, the electronic thermal conductivity and lattice thermal conductivity [Figs. 14 and 15] have been calculated using the Wiedemann–Franz formula

Fig. 13

Total thermal conductivity and electronic thermal conductivity of the melt-grown pristine and (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

Fig. 14

Lattice thermal conductivity of the melt-grown pristine and (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

Fig. 15

Electronic thermal conductivity of the melt-grown pristine and (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples.

$${K}_{e}=\frac{{L}_{o}T}{\rho },$$

(9)

where T is the temperature, ${L}_{o}$ is the Lorenz number for degenerate semiconductor and is calculated using the relation [${L}_{0}=1.5+\text{exp}\left(\frac{\left|-S\right|}{116}\right)$] (Fig. 16) [45]. We observe that the K_l exhibits a reduction with doped indium content in the single crystals. The added dopants distort the lattice of Bi₂Se₃, which generates local vibrations that scatter the high-frequency phonons. The reduction in lattice thermal conductivity is achieved by the dislocation and distortions produced by the indium and selenium doping. This encourages the scattering of mid- and strong wavelength phonons. Hence, there is a systematic reduction in lattice thermal conductivity at 11 K [66,67,68]. In addition, selenium doping also forms minor interfaces during the crystal growth which helps reduce the lattice thermal conductivity. In this study, we have achieved 3.4 times reduction in total thermal conductivity in the (Bi_0.98In_0.02)₂Te_2.7Se_0.3 samples as compared to that of the pristine at 11 K, though there is a small cross-over between Bi₂Te₃ and Bi₂Te_2.7Se_0.3. The significant decrease in thermal conductivity results from the multiple textures, lattice distortions, and dislocations that Indium and Tellurium induce on phonon transport. These effects distinctly cause the scattering of mid- and long-wavelength phonons across a broad wavelength spectrum to lower the thermal conductivity. To put it briefly, the multiscale hierarchical textures and lattice defects created by doping effectively restrict the movement of various frequency phonons, reducing the contribution of lattice thermal conductivity to thermal conductivity.

Fig. 16

Lorenz number of the melt-grown pristine and (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

The presence of volume/lattice faults is highly correlated with thermal conductivity. Therefore, volume defects like cracks and lines scatter the mid- and long-wavelength phonons, whereas atomic defects like lattice defects or vacancies scatter shorter wavelength phonons. Hence, the region ~ 50 K where the thermal conductivity changes for two alloys Reduced lattice thermal conductivity is caused by lattice disorder acting as a scattering center for low/mid-energy phonons. Estimates of the dislocation density and strain from structural investigations also showed that indium and selenium doping increase dislocation and cause problems in the Bi₂Te₃ lattice. The 0.02 and 0.04 dopants exhibit extremely stressed lattices and large dislocation densities, which are validated by HRXRD study. This might result in a significant decrease in the heat conductivity of the lattice [69]. Our previously reported polycrystalline (Bi_1−xIn_x)₂Te_2.7Se_0.3 samples have shown lower thermal conductivity values as compared to the single crystals because the poly crystalline materials have large number of grain boundaries that scatter both phonons and electrons [66].

3.7 Quality factor (B), thermoelectric power factor (PF) and figure of merit (ZT)

The temperature-dependent power factor (PF = S²/ρ) and thermoelectric figure of merit [$ZT=\frac{{S}^{2}T}{{\rm K}\rho }$] have been calculated for the grown single crystals from 10 to 400 K. The highest value of power factor 3074 µW/mK² has been found in Bi₂Te₃, which is 5.12 times greater than our previously reported polycrystalline Bi₂Te₃ samples (Fig. 17) [48]. The maximum ZT value ~ 0.26 is noticed in Bi₂Te₃ single crystal at 350 K (Fig. 18). Comparison of Electrical resistivity, Thermal conductivity, Seebeck coefficient, and ZT values of some reported Thermoelectric systems is shown in Table 6 [26, 70,71,72]. Thermoelectric characteristics of melt-grown indium- and selenium-doped bismuth telluride are the focus of the current investigation. Crystal structure of Bi₂Te₃-based alloys tends to be more organized, resulting in the greatest value of band gap, as demonstrated by Tang et al. The lattice thermal conductivity is found to decrease drastically because of the induced alloying dispersion. Doped bismuth telluride grown via bridgeman method shows a monotonically increasing electrical resistivity with temperature (Yashmita et al.); however, p-type specimen shows a considerably faster rise in resistivity with temperature than the n-type. Present compound exhibits the similar behavior. Kim et al. generated Sb- and Se-co-doped Bi₂Te₃ thermoelectric nanocomposites by combining the atom-by-atom assembly of multi-walled carbon nanotubes and Al₂O₃ nano-powders. In contrast, co-doping bismuth telluride is a major focus of this study. The bandgap of Bi₂Te₂Se alloys may be effectively widened by alloying, which reduces the bipolar effect at elevated temperatures. The multiscale phonon scattering decreases the heat conductivity of the lattice, and bipolar conduction also decreases thermal conductivity, but the presence of antisite defect in our co-doped samples makes a significant decrease in the thermal conductivity in the temperature range of 40–350 [26, 70,71,72].

Table 6 Comparison of electrical resistivity, thermal conductivity, seebeck coefficient, and ZT values of some reported thermoelectric systems with present compound

Fig. 17

The Power factor of the the melt-grown pristine and (Bi_1−xIn_x)₂Se_2.7Te_0.3 single-crystal samples

Fig. 18

The ZT of the the melt-grown pristine and (Bi_1−xIn_x)₂Se_2.7Te_0.3 single-crystal samples

Figure 19 exhibits the quality factor (B) of the (Bi_1−xIn_x)₂Te_2.7Se_0.3 single crystals at 350 K. The intrinsic thermoelectric properties can be defined by the dimensionless thermoelectric quality factor using

Fig. 19

The quality factor of the melt-grown pristine and (Bi_1−xIn_x)₂Te_2.7Se_0.3 single-crystal samples

$$ B = \frac{{8\pi \left( {2m_{e} } \right)^{{\frac{3}{2}}} k_{B} ^{{\frac{7}{2}}} }}{{3eh^{3} }}\frac{{\mu _{w} T^{{\frac{5}{2}}} }}{{k_{L} }} = 4.33 \times 10^{{ - 10}} \left( {\frac{{\mu _{w} T^{{\frac{5}{2}}} }}{{k_{L} }}} \right). $$

(5)

The highest B value of about 15 × 10⁻⁴ V⁻¹ is obtained for (Bi_0.96In_0.04)₂Te_2.7Se_0.3 crystals at 350 K, due to its highest weighted mobility and the lowest lattice thermal conductivity.

4 Conclusion

The thermoelectric performance of (Bi_1−xIn_x)₂Te_2.7Se_0.3 single crystals grown by melt growth technique has been studied in the temperature range 10–400 K. Structural investigation such as powder XRD and HRXRD show that the single crystals have hexagonal structure with $R\stackrel{-}{3}$ m space group symmetry. Surface morphological features indicate the absence of small-angle grain boundaries in Bi₂Te₃. By observing the increase in electrical resistivity trend of the doped samples, it is realized that doping on single crystal can induce both charge scattering and lattice vibrations on phonons. The p- to n-type transformation observed in co-doped samples attributes to partial substitution of tellurium by selenium. 3.4 times reduction of total thermal conductivity has been achieved by co-doping in the (Bi_0.98In_0.02)₂Te_2.7Se_0.3 sample as compared to that of pristine at 11 K. Thus, indium- and selenium-co-doped Bi₂Te₃ single crystal can be used as potential candidate for low and near room-temperature thermoelectric applications.