The influence of concentration variation on the spectroscopic behavior of Sm³⁺-doped zinc–lead-phosphates glasses for orange and reddish-orange light-emitting applications: experimental and Judd–Ofelt approach

Abstract

A spectroscopy study was performed to investigate the absorption and emission behavior of zinc–lead phosphate-doped Sm³⁺ glasses sample. The parameters, density, ρ, molar volume, V_m, samarium ion concentration N, and mean samarium ion separation, R were calculated. The absorption peaks were assigned and discussed. The band gap and Urbach’s energies analysis were illustrated. The emission spectra and the emission lifetime decay were studied. The CIE diagram coordinate (0.393, 0.601) of the sample’s emission was very close to the TV standard value. The oscillator strength f_cal and f_exp were calculated using Judd–Ofelt theory, and the model parameter trend was found to be Ω₄ > Ω₂ > Ω₆ which indicates high glasses rigidity. The Absorption and emission cross-sections were studied and illustrated. The obtained optical parameters, absorption, and emission behaviors introduce the samples under investigation as a candidate for orange and reddish-orange photonic applications.

1 Introduction

Nowadays, phosphate glasses attract many researchers due to their low melting temperature and low optical dispersion. The advantages of high lanthanide solubility led to a low refractive index and high transparency [1]. In addition, the Phosphate glasses have lower phonon energy than other glasses families [2]. Furthermore, its chemical stability can be enhanced by having metal oxides including, Li₂O, Al₂O₃, and many more. All such glasses are worthy of use for radiation shielding purposes [3]. Also, phosphate glasses outperform silicate glasses in terms of being suitable for high concentrations of rare earth ions doping for LED devices and other optical materials applications [4, 5].

Adding PbO to the phosphate glasses enhances their moisture resistance. PbO makes more stable glasses than alkali or alkaline earth oxide modifiers because of its dual function. However, PbO has been investigated by many researchers using it with PbO₄ structural unit as a former or with PbO₆ structural unit as a modifier for the glasses compositions [6]. Besides that, adding the PbO to the glasses compositions increases their density and index of refraction, which influences the optical characterization of the glasses compositions [7]. The insertion of the PbO additionally helps in lowering the energy of the associate phonon and nonirradiative energy loss [8]. Through researchers who work in environmental applications prefer to use phosphate glasses in the treatments of certain hazardous wastes [9].

Moreover, researchers have been interested in trivalent rare-earth-doped materials because of their unique emission characterization, and they are considered potential candidates for their use in LED devices, laser materials, and optical sensors. For decades, among various lanthanide ions, Samarium (Sm³⁺) ions with the 4f⁵ state have been investigated. Sm³⁺ ions display a significant orange-red emission in the visible spectrum and absorb strongly in the UV–Visible field [10]. The line-shaped emission of Sm³⁺ ions-doped luminous materials is appealing because the emitting light has a high color purity [11]. Interestingly, the investigation for new orange-red emission phosphors in Sm³⁺-doped glasses has high curiosity [12], for different applications like temperature sensors [13], and phosphors for white light-emitting diodes (LEDs) [14], and white light-emitting diodes (WLEDs) [15,16,17].

As a result, given the importance of locating suitable phosphates glass that could theoretically be used to manufacture tunable yellow to orange-reddish phosphor-dependent LED technology, an analysis based on UV–Visible absorption and emission spectroscopy, and decay time profile measurements of Sm³⁺-doped P₂O₅–PbO–ZnO glasses will be conducted in this work.

2 Experimental procedure

2.1 Chemicals

P₂O₅, PbO, and ZnO, (Laboratory Rasayan Sd Fine-Chem. Limited), and Sm₂O₃ (Sisco research Lab. India) were used in powder form.

2.2 Glasses sample preparation

The melt-quenching method was used to prepare the glasses samples. The mixtures of the precursors (35 g) were carefully mixed in porcelain crucibles and introduced into an electrical furnace at 1000 ± 10 °C for 1 h with a spin of the melt every 30 min to achieve a high homogeneity. The melt was cast using a special design stainless steel template (4 cm × 1 cm × 2 mm) and remained sintered for 30 min at 300 °C in a muffle furnace. As of the last stage, the samples were allowed to cool to room temperature at 30 °C/h cooling rates. The samples were labeled as, PPbZS0 (Sm₂O₃ 0 mol%) to PPbZS6 (Sm₂O₃ 2.61 mol%).

Using the Archimedes method, the glass density, (ρ), was calculated where the liquid density of xylene ρ = 0.863 g/cm³. The glass molar volume, V_m, was estimated from the mutual density. The experiment was repeated many times, and an average value of the density was recorded [18].

A spectrophotometer, (JASCO, Model V-570 Japan), was used to carry out the optical absorption of highly smoothed and polished samples in the range of 200–900 nm with 2 nm resolution.

3 Results and discussion

3.1 Physical properties

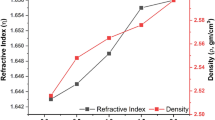
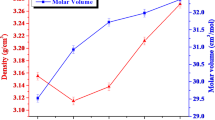
Table 1 illustrates the obtained density (ρ) and molar volume (V_m). It is apparent from this table that the density values increase as the Sm₂O₃ content % increases from 3.999 g/cm³ for the PPBZS0 sample to 4.102 g/cm³ for the PPbZS6 sample. It is also noticed that the molar volume values decrease as the Sm₂O₃ content increases, from 63.53 cm³/mol for the PPBZS0 sample to 62.53 cm³/mol for the PPbZS6 sample. The change in the density and the molar volume indicate the change that occurred in the glass network. Low P₂O₅ density (string P₂O₅, PbO, ZnO = 2.39, 9.53, 5.606 g/cm³ correspondingly) may have been replaced with greater Sm₂O₃ density (string (Sm₂O₃) = 8.347 g/cm³), increasing density values. The possibility of increasing density values may be attributed to the change in the glasses 3-dimensional matrix that may break the bridging oxygen in glasses network, resulting in non-bridging oxygens (NBOs) as the Sm₂O₃ content % increases (NBOs) [19,20,21].

Table 1 The glass composition [P₂O₅–Pbo–ZnO–Sm₂O₃], in mole fraction, glass density, ρ, molar volume, V_m, samarium ion concentration N, and mean samarium ion separation, R

The Sm³⁺ ions concentration, N, and the average separation of samarium ions, R, are change with the density of glass and the Sm₂O₃ content %, x, and they could be calculated using the formulas below [18, 22,23,24]:

$$N = 2\left[ {\left( {\frac{\rho x}{{M_{{{\text{wt}} - {\text{Sm}}_{2} {\text{O}}_{3} }} }}} \right)N_{A} } \right]$$

(1)

$$R = N^{{ - \frac{1}{3}}}$$

(2)

where N_A is the Avogadro’s number and M_wt is defined as molecular weight. As the content % of Sm₂O₃ in the glass framework increases and the isolation of the samarium reduces, the concentration of Sm³⁺ ions increases, as shown in Table 1 and Fig. 1.

Fig. 1

The glass density, ρ, molar volume, V_m, samarium ion concentration N, and mean samarium ion separation, R against Sm₂O₃ content mol. %

Figure 2 displays the UV–Vis spectrum of zinc–lead phosphate doped with Sm₂O₃ glass. The presence of a small quantity of Sm₂O₃ in base glass (PPbZS1) contributes to an increase in absorbance strength with an increase in Sm₂O₃ content %, and intensity increase at these bands 210, 219, 227, 231, 245, 254, 378, 414, 484, 951, 1094, 1253, 1402, 1505, 1536, and 1983 nm is shown in Fig. 2. The incorporation of zinc ions in alkali lead phosphate glasses causes a variety of exciting physical and chemical changes, which are directly dependent on how zinc ions are incorporated in the glass network. According to various Authors [25,26,27], zinc ions emerge in glasses as former networks (with tetrahedral coordination) or modifiers (in octahedral coordination), depending on the need of alkali oxide to enhance the existence of these tetrahedral units. The surrounding alkali ions must have added additional negatively surface-charged ions to the planned ZnO₄ tetrahedron. In these settings, the release of alkali ions is reduced therefore, glasses containing tetrahedral coordination should have better chemical stability and physical properties. The addition of ZnO to the host glass increases the oxide's ability to enhance the glass' optical properties and improves its chemical hardness [27, 28]. With regard to the existence of the phosphor color center in the glasses, a variety of ideas on the creation of this optical color center and luminescence center have been suggested as follows: (i) The existence of pentavalent phosphor ion (P⁵⁺) and monovalent phosphor (P¹⁺) and (ii) The presence of P clusters or P colloids [22, 23].

Fig. 2

Absorption UV–VIS spectrum of zinc–lead phosphate doped with Sm₂O₃ glasses spectra

The recorded Ultraviolet–visible absorption bands 210, 219, 227, 231, and 245 of the studied glasses appear to be strongly linked with traces of inevitable Fe contaminations in the used chemicals. The cumulative outcome of UV absorption owing to great P³⁺, Pb²⁺, and Zn²⁺ ions has been reported [29,30,31,32]. The appearance of the ultraviolet bands mostly arises from the iron trace impurities even if it presents at very low concentrations. Paul[33] and Park and Webb [34] identified an ultraviolet peak when traces of P³⁺ ions were added to the lead and zinc glasses. Duffy and Ingram decided that the transfer of this peak is strongly linked to ¹S₀ → ³P₁ [35]. The optical spectra contain different transition bands related to transitions between the ground state 6H_5/2 and higher energy levels (⁴P_1/2, ⁴H_11/2, ⁴H_9/2, ⁴H_7/2, ⁴M_19/2, ⁴I_11/2, ⁴M_15/2, ⁶F_11/2, ⁶F_9/2, ⁶F_7/2, ⁶F_3/2, ⁶H_15/2, and ⁶F_1/2) inside the Sm³⁺ ions' 4P³ electronic configuration. The optical results can be comprehended and interpreted in the following ways:

• I. It can be seen in the distinctive Sm³⁺ glass system's absorption spectra. Fewer transitions were detected for the other glasses and their UV-cut offs are moved to higher wavelengths [36]. Previous hypotheses revealed the detected optical absorption spectra of Sm₂O₃-doped glasses to the presence of metal oxides like PbO, ZnO, and P₂O₅ which make a red shift in the absorption boundaries and decrease the absorption peak strength as detected in the studied samples [25].

• II. Because the excitation from the ⁶H_5/2 ground state to the ⁶H and ⁶F terms is required to allow for a spin (S = 0), the NIR transitions are intense. With the selection criteria J = 0, 1, all transitions in the visible range that involve a magnetic dipole contribution are forbidden spin, and the intensity of the absorption transitions is found to be robust. All the observed transitions in the lower energy range are spin permitted (S = 0), sharp, and intense, ascribed to the 6H5/2 6FJ manifolds with J = 1/2, 3/ 2, 5/2, 7/2, 9/2, and 11/2, respectively [27].

• III. Sundari et al. [37] whereas other authors [18, 20] identified seven strong transitions at 414, 484, 951, 1094, 1253, 1402, 1505, 1536, and 1983 nm concluded that the existence of high Pb²⁺ or high P³⁺ contents % prevents the detection of most of these bands. Some authors [38,39,40] expected that the increase in rare earth ions concentration, both network-modifying and network-forming positions increases.

3.2 Urbach’s analysis and the band gap calculations

Using the absorption spectra, the optical band gap energy ${E}_{\text{opt}}$ could be calculated. The change in the absorption coefficient $\alpha \left(\nu \right)$ with the photon energy ($h\nu$) for direct and indirect transitions can be calculated using the following relation [38]:

$$\alpha \left( \nu \right) = \frac{{B\left( {h\nu - E_{{{\text{opt}}}} } \right)^{r} }}{h\nu }$$

(3)

where r is the index number used to decide the nature of the inter-band electronic transition causing the absorption, B is the band tailing parameter, and hν is the incident photon energy. E_opt values were obtained by extrapolating the linear region of the curves to the zero absorption at (αhν)^1/2 = 0 for indirect allowed transitions ,and the band tailing parameter values were also obtained from the slope of the curves. Figure 3a shows the Tauc’s plot of (αhν)^1/2 as a function of photon energy (hν) for the indirect allowed transitions of the prepared Sm³⁺-doped zinc–lead phosphate glasses. The fundamental absorption edge, optical band gap (E_opt), and the band tailing parameter values of the prepared glasses are calculated and are presented in Table 2. The fundamental absorption edge/cut off wavelength is found to undergo red shift with the addition of Sm₂O₃. Further, it is observed from Table 2 that the indirect band gap values decrease slightly with the increase in Sm³⁺ ion content % resulting in an increase in the bonding defect and non-bridging oxygen. The reduction in band gap values may be due to the increment in non-bridging oxygen or the formation of bridging oxygen as well as the formation of six coordinated phosphate units as Sm₂O₃ content % increases. This structural change causes an increase in the degree of electron localization due to increasing the donor centers in the glass host which in turn increases the band gap values. The optical band gap values are found to be in the range 3.172823–2.633379 eV for all the prepared glasses.

Fig. 3

A Tauc’s plot of (αhν)1/2 as a function of photon energy (hν) for the indirect allowed transitions and (3). B The change of the optical band gab and Urbach energy ∆E with increases of Sm₂O₃ content %

Table 2 The band gab, E_opt, the Urbach energy, ∆E, A and B and C constants, the mean dispersion, Abby number, v, the dispersion energy

The absorption coefficient α(ν) near the absorption band edge exhibits an exponential behavior on the photon energy (hν) and obeys the Urbach empirical relation given by [41]

$$\alpha \left( \nu \right) = \alpha_{o} \exp \left( {\frac{h\nu }{{\Delta E}}} \right),$$

(4)

where ΔE is the Urbach energy and ${\alpha }_{o}$ is a constant. The Urbach's band energy was calculated from the slope of the ln $\alpha \left(\nu \right)$ variation with hv, and the obtained values are shown in Table 2. The Urbach's energy values increase as the Sm³⁺ ion concentration increases, and the calculated values are in the range of 0.515791 eV to 0.64096 eV.

Comparing other glasses compositions, the glass that has higher Sm³⁺ content % showed higher Urbach energy value, indicating the higher possibility of long-range order produced from the smaller number of defects.

On the other side, ΔE values are inversely proportional to E_g values and indicate the disorder and defects in the glasses’ structure. These defects produce spatial states and decrease the optical band gap values [42, 43].

Figure 3a illustrates the Tauc’s plot of (αhν)^1/2 as a function of photon energy ($h\nu$) for the indirect allowed transitions, and Fig. 3b demonstrates the change of the optical band gap and Urbach energy ∆E with the increase of Sm₂O₃ content % [41, 42]

3.3 Determination of optical constants

For a better understanding of the interaction of the light with the material, the optical parameters were investigated. The reflectance (R) was calculated using the following empirical equation [43,44,45,46] taking into account the refractive index real part ($n$) and the extinction coefficient k:

$$R = \frac{{\left( {n - 1} \right)^{2} + k^{2} }}{{\left( {n + 1} \right)^{2} + k^{2} }}$$

(5)

where the appropriate root of the above equation is considered as the refractive index. The extinction coefficient was calculated by

$$k = \frac{\alpha \lambda }{{4\pi }}$$

(6)

Equation (7) gives the solution of Eq. (5) for the refractive index n [44]:

$$n = \frac{{ \pm \left( {1 + R} \right) \pm \sqrt { - k^{2} + 4R + 2k^{2} R - k^{2} R^{2} } }}{ - 1 + R}$$

(7)

As noticed from Fig. 4, the glasses refractive index decreases with the increase of the wavelength while increases with increasing Sm₂O₃ content %. Non-bridging oxygen is considered the main factor affecting the refractive index. In the current composition glass ZnO–PbO–P₂O₅, the glass contains bridging oxygen and non-bridging oxygen as well. By increasing the ZnO content % the bridging oxygen decreases and the non-bridging oxygen increases. The polarizability of ionic bonds is greater than that of bridging oxygen's mostly covalent bonds, resulting in a higher index value. In ZnO–PbO–P₂O₅–Sm₂O₃ glass, a part of the PbO was substituted by Sm₂O₃ where Sm⁺³ ions are partly enclosed in the matrix and act as bridges between the matrix forming groups.

Fig. 4

A The refractive index, n, distribution with the wavelength. B Plotting $\left( {n^{2} - 1} \right)^{ - 1}$ against the photon energy $\left( {h\upsilon } \right)^{2}$ and its fitting

For glass samples doped with Sm₂O₃, Fig. 4 illustrates the wavelength (λ) dependency of refractive index (n).

The normal-dispersion regions of the dispersion curve, known as the anomalous-dispersion branches, reflect a normal dispersion that roughly obeys the empirical Cauchy dispersion equation:[46,47,48]:

$$n = A + \frac{B}{{\lambda^{2} }} + \frac{C}{{\lambda^{4} }}$$

(8)

where A, B, and C denoted as the nonlinear Cauchy’s coefficients. Table 2 summarizes the obtained Cauchy coefficients for the normal-dispersion component of the studied glasses samples. It can be seen that when the Sm₂O₃ content %increased, the Cauchy coefficient A increased (from 1.5199 to 1.67061). The observed increase in coefficient A of the examined glasses in response to the increase of Sm₂O₃ content % reflects the increase in the non-bridging oxygen accompanying with a structural shrinkage.

Figure 5A shows the extinction coefficient as a function of wavelength for the current samples. The extinction coefficient behavior showed more than 6 peaks in the UV and Near IR spectrums and the number of developed peaks increased with Sm₂O₃ content % [43, 47]. The Abbe dispersion number $\left( \upsilon \right)$, the indicator of the glass dispersion, is detected as follows:

$$\nu = \frac{{n_{d} - 1}}{{n_{F} - n_{C} }}$$

(9)

where ${n}_{d}, {n}_{F} \mathrm,{and} {n}_{C} \mathrm{are}$ denoted as the index of refraction for the yellow He d-line, the linear Index of refraction for H₂ F-line, and the index of refraction for H₂ C-line, respectively.

Fig. 5

A the distribution of the extinction coefficient k as a function of wavelength. B The distribution of the real part of the dielectric constant ε’ with the wavelength. C The distribution of the dielectric imaginary part of the ε″

The glass has (${\nu }_{d}$ > 50) and is considered as high dispersion one. According to Table 2, the Abbe’s dispersion numbers increased from 56.581179 to 166.95830 as the Sm₂O₃ content % grew, indicating that the glasses changed from high to low dispersion power as the Sm₂O₃ content % increased.

3.4 Complex dielectric constant

The interaction of the electromagnetic wave (light) with materials produces a fundamental molecular mechanism known as the optical dielectric complex factor ($\varepsilon )$ [43, 49]. The complicated dielectric constant components $\left( {\varepsilon^{\prime}} \right)$ the real part and $\left( {\varepsilon^{\prime\prime}} \right)$ the imaginary part of a material are represented as

$$\varepsilon^{\prime} = n^{2} - k^{2} \,{\text{and}}\,\varepsilon^{\prime\prime} = 2nk$$

(10)

Figure 4b shows the real component of the dielectric constant against wavelength (nm) for the investigated glasses. The dielectric constant decreases with wavelength in all samples and increases with increasing Sm₂O₃ content %. The free carrier concentration of the various sample’s compositions modified in the same way as Sm₂O₃ content %. Figure 4c illustrates $\left( {\varepsilon^{\prime}} \right)$ as a function of the wavelength The optical relaxation time of glasses could be determined using the imaginary dielectric constant [44,45,46,47,48,49]. The index of refraction under the inter-band absorption edge and the normal dispersion of the optical dielectric constant in materials and the energy successfully described by Sellmeier relation[47, 50]:

$$n^{2} - 1 = \frac{{E_{o} E_{d} }}{{E_{o}^{2} - E^{2} }}$$

(11)

where $E, {E}_{0}, {E}_{d}$ are the photon energy in eV, the single oscillator energy, and the material dispersion energy parameter, respectively [51]. Figure 5b shows the fitting of the straight part of the single oscillator parameter against the photon energy and Table 2 illustrates the calculated values of $E_{o}$ and $E_{d}$ for the glass compositions.

3.5 Ion polarizability of the glasses

The estimation of glasses containing the electronic polarizability of ions is subject of the so-called polarizability. The molar refraction was determined using the refractive indices calculated for different compositions, as introduced by Volf [52], Lorentz[53]:

$$R_{m} = \frac{{\left( {n^{2} - 1} \right)}}{{\left( {n^{2} + 2} \right)}}\left( {\frac{M}{\rho }} \right)$$

(12)

where R_m, n, M, and ρ denote the molar refraction, the index of refraction at 587.56 nm, the molecular weight, and the glass density, respectively. The average of the molar refraction is influenced by the glass structure and is increased with the increase of the material's electronic polarizability as the following relationship [54].

$$\alpha_{m} = \left( {\frac{3}{4\pi N}} \right)R_{m}$$

(13)

where N is the Avogadro's number. The obtained values of the $R_{m}$ and $\alpha_{m}$ are illustrated in Table 3 which indicates that the increase of the Sm₂O₃ content % in the samples increases both the R_m and refractive index. Dimitrov and Sakka [22, 55] used the following equation to calculate the average electronic polarizability of oxide ions $\alpha_{0}^{2 - }$,with the general formula X₁A_pO_q–X₂B_rO_s–X₃C_nO_m–X₄G_vO_u, where X is the molar fraction for each oxide.

$$\alpha_{0}^{2 - } \left( n \right) = \frac{{\left[ {\frac{M}{2.52\rho }\left( {\frac{{n^{2} - 1}}{{n^{2} + 2}}} \right) - \sum {\alpha_{cat} } } \right]}}{{\left( {N_{o}^{2 - } } \right)}}$$

(14)

where $\sum {\alpha_{cat} }$ denotes molar cation polarizability and is given by

Table 3 The molar refraction, the molar electronic polarizability, the average electronic polarizability, metallization, and theoretical optical basicity of glass studied

X₁pα_A + X₂rα_B + X₃nα_C + X₄vα_G and $N_{o}^{2 - }$ denotes the number oxide ions in the chemical formula given by X₁q + X₂s + X₃m + X₄u. The molar cation polarizability $\sum {\alpha_{cat} }$ of the glasses is calculated using the data on the polarizability of cations collected in reference [56]. Herzfeld [58] proposed a metallization theory of condensed matter for the boundary condition $\left( {{{R_{m} \rho } \mathord{\left/ {\vphantom {{R_{m} \rho } {M = 1}}} \right. \kern-0pt} {M = 1}}} \right)$, where the refractive index becomes infinite, and estimated by the relation $\left( {{{R_{m} \rho } \mathord{\left/ {\vphantom {{R_{m} \rho } {M > 1}}} \right. \kern-0pt} {M > 1}}} \right)$ (for metallic) and $\left( {{{R_{m} \rho } \mathord{\left/ {\vphantom {{R_{m} \rho } {M < 1}}} \right. \kern-0pt} {M < 1}}} \right)$(for nonmetallic).

$$M\left( n \right) = 1 - \frac{{R_{m} \rho }}{M}$$

(15)

When the term $M\left( n \right)$ tends to be zero the transition to the metal state may occur. From Table 3, $M\left( n \right)$ increases with increasing of Sm₂O₃ content %.

3.6 Optical basicity of the glasses

The glass materials that contain oxides may be classified using the optical basicity and may be computed based on the equation [57]:

$$\Lambda_{{{\text{th}}}} = X_{1} \Lambda_{{{\text{Bi}}_{{2}} {\text{O}}_{{3}} }} + X_{2} \Lambda_{{{\text{ZnO}}}} + X_{3} \Lambda_{{{\text{PbO}}}} + X_{4} \Lambda_{{{\text{Smd}}_{{2}} {\text{O}}_{{3}} }}$$

(16)

where X₁, X₂, X₃, and X₄ are fractions related to the quantity of the oxygen that inserted by each oxide to the glass composition. The constants $\Lambda$₁, $\Lambda$₂, $\Lambda$₃, and $\Lambda$₄ are basicity of every oxide in the composition, where the P₂O₅ has a basicity of 0.33, ZnO has a basicity of 1.13 [58], PbO has a basicity of 1.17 [59], and Sm₂O₃ has a basicity of 1.3081 [60]. Table 3 shows the estimated values of optical basicity for the studied glasses which found to be increase with increasing Sm₂O₃ content %.

4 The emission spectra and emission lifetime measurements

Figure 6 shows the emission spectra observed for the studied samples at room temperature ranging from 500 to 750 nm. Four transition bands are related to the (4f³ → 4f³) transitions from the ⁴G_5/2 level to the ⁶H_5/2 at approximately (563 nm), ⁶H_7/2 at approximately at (601 nm), ⁶H_9/2 at approximately (648 nm), and finally ⁶H_11/2 at approximately (710 nm) levels in the emission spectra. The transition at (601 nm) produces the most powerful emission, which is strong orange-reddish color [21]. On other hand, KFP03Sm shows the highest emission strengths, with intensity decreasing as Sm³⁺ concentration increases.

Fig. 6

The emission spectra recorded for Sm³⁺-doped KFP glasses

The nonradioactive emission takes place at higher concentrations and the energy is lost [22]. The transition ⁴G_5/2 → ⁶H_9/2 is highly responsive to the host environment, while the transition ⁴G_5/2 → ⁶H_11/2 is considered as purely electric dipole (ED), and the transition ⁴G_5/2 to ⁶H_5/2 is considered as purely magnetic dipole (MD), which is insensitive to the host environment.

The ratio ED/MD is used to evaluate the immediate symmetry of the RE of the surrounding ions [23]. For the KFP01Sm, KFP03Sm, KFP05Sm, KFP10Sm, KFP15Sm, and KFP20Sm glasses, the emission intensity ratio (ED (⁴G_5/2 → ⁶H_9/2) / MD (⁴G_5/2 → ⁶H_5/2)) is determined to be 3.32, 3.30, 3.17, 3.15, 3.09, and 3.00, respectively. The Sm³⁺ ions are spread inside the noninversion symmetry or asymmetric locations, based on this behavior. The local asymmetric environment decreases as the concentration of Sm³⁺ ion in the KFP glass composition increases. Figure 7 shows the energy level system for excitation and emission processes for the Sm³⁺.

Fig. 7

Energy level scheme of Sm³⁺ excitation and emission processes

The effect of the emission transitions represents by the CIE 1931 chromaticity diagram in Fig. 8. The values of the X and Y (X,Y) coordinates (the black point) are located very close to the national slandered value of television system (0.67, 0.33) [61]. The 563 nm emission peak have coordinates (0.394, 0.603) orange (Blue point), the 601 nm emission peak have coordinates (0.631, 0.368) reddish-orange (green point), and the peaks at 648 nm and 710 nm have the approximately same coordinates (0.731, 0.270) Red (Aqua point).

Fig. 8

CIE 1931 chromaticity diagram for studied samples

The emission lifetime measurements were performed for samples 1, 2, 3, and 6 using spectrofluorometer (Model FS5, Edinburgh Instruments, UK) equipped with a flash Xenon lamp and Fluoracle® software. Figure 9 Illustrates the unfitted emission lifetime at 598 nm excited with 403 nm wavelength using 100 Hz flash lamp where the inset shows the sample 1 fitted data. The measured data were fitted using the formula [62]:

$$I\left( t \right) = B_{i } \exp \left( {\frac{ - t}{{t_{1} }}} \right) + B_{j } \exp \left( {\frac{ - t}{{t_{2} }}} \right) + B_{k } \exp \left( {\frac{ - t}{{t_{3} }}} \right)$$

(17)

where I(t), B_i, B_j, B_k are the emission intensity at any time (t), B_i, B_j, B_k are the pre-exponential weight factors, and t₁, t₂, and t₃ are the three decay time components. These values were obtained from the Fluracle® fitting software and are demonstrated in Table 4.

Fig. 9

The unfitted emission lifetime at 598 nm excited with 403 nm wavelength using 100 Hz flash lamp, the inset shows the sample PPbZS1 fitted data

Table 4 The three decay time components t₁, t₂, and t₃ and the constants B_i, B_j, and B_k

The three-time decay components t₁, t₂, and t₃ indicate that the emission lifetime decay contains three decays process. t₁ is the fast decay component. t₂ is the intermediate component and t₃ is the slow decay component [63]. It is apparent from Table 4 that there is a significant difference between the values of the three decay components and all of them decrease with the increase of the Sm⁺³ ions concentration.

5 Oscillator strengths and Judd–Ofelt parameters

Several studies have produced estimates of the Judd–Ofelt (JO) parameters Ω_λ (where λ = 2, 4, 6), which increase our knowledge about the glass structure and the influence of the surrounding environments with the glass host materials [64]. Least square fittings results of the calculated oscillation strength (f_cal) and the experimental oscillation strength (f_exp) are listed in Table 5 and can be estimated using the formula [65, 66]:

$$F_{\exp } = \frac{{2.303 mc^{2} }}{{N\pi e^{2} }}\int {\varepsilon \left( \upsilon \right) {\text{d}}\upsilon = 4.318*10^{ - 9} } \int {\varepsilon \left( \upsilon \right) {\text{d}}\upsilon }$$

(18)

and

$$F_{{{\text{cal}}}} = \frac{{8 \pi^{2} mc\upsilon }}{{3h \left( {2J + 1} \right)}} \frac{{\left( {n^{2} + 2} \right)^{2} }}{9n}* \mathop \sum \limits_{\lambda = 2, 4, 6} \Omega_{\lambda } \left( {\left. {\Psi J} \right\|\left. {U^{\lambda } } \right\|\Psi^{\prime}J^{\prime}} \right)^{2}$$

(19)

where m is mass of the electron, N is Avogadro’s number, c is light velocity, e is a charge of the electron, ε(υ) is molar absorptivity (cm⁻¹), and $\int \varepsilon \left(\upsilon \right) d\upsilon$ is the area under the absorption curve. The calculated oscillator strengths F_cal are determined from the equation above [66].

Table 5 Measured and calculated absorption line strengths and J–O parameters Ω_λ of Sm³⁺ in (P₂O₅–PbO–ZnO–Sm₂O₃) glasses

Where the parameters ℏ, c, m, υ, and n are the Plank’s constant, the light velocity, the mass of electron, the wave number, and the refractive index, respectively. Taking into consideration that the term $\frac{{({n}^{2}+2)}^{2}}{9n}$ is denoted as the spatial electric field correction provided by Lorentz, $\Psi J$ is denoted as ground state, ${\Psi }^{^{\prime}}{J}^{^{\prime}}$ is denoted as excited state, and the function $\left\| {U^{\lambda } } \right\|^{2}$ is denoted as the double square of the matrix elements of the operator. The (JO) Ω_λ (where λ = 2, 4, 6) are capable to estimate. The importance of estimating those parameters is improve the information about the rare earth surrounds, and the bonding of the rare earth with their surrounding media which provide a wider picture for the influence of the host materials with Sm³⁺ [67, 68] Glass samples with higher hardness and viscosity have higher Ω₄ and Ω₆ values. The ratio Ω_4/ Ω₆ is denoted as the (X factor) or known as the spectroscopic quality factor. The materials with higher spectroscopic factor values (greater than 1) suggest effective stimulated emission and superior glass stability which give the opportunity for the glass structure as a candidate for optoelectronics and photonics [64, 68]. Table 6 shows the samples features of the Judd–Ofelt parameters based on the results obtained from the preliminary analysis in Table 6. The arrangement Ω₄ > Ω₂ > Ω₆ is the trend of the Judd–Ofelt parameters which is in correlations with pervious obtained analysis for in Sm³⁺ doped TeO₂–SrO–ZnO–Nb₂O₅–B₂O₃ [64]_, Li₂O–B₂O₃ [69], 70, PbO–P₂O₅ [70], P₂O₅–Na₂O–Al₂O₃–B₂O₃–ZnF₂[71], PbF–P₂O₅ [41]. From Table 6, it can be concluded that higher Ω₂ values mean more deformation originated from the change of the structure, bigger modifier volume, and superior Samarium-Oxygen bond formed more field strength [70]. Meanwhile, higher Ω₄ and Ω₆ values lead to estimate a higher inflexible and rigid glass samples [68]. Moreover, the fitting is needed between the both oscillator strengths, the Calculated ${F}_{cal},$ and the xperimental ${F}_{\text{exp}}$, and the fitting quality can be estimated from the root mean square (r.m.s.) based on the equation [72, 73]:

$$r.m.s. = \left( {\mathop \sum \limits_{p} \frac{{\left( { f_{{{\text{cal}}}} - f_{\exp } } \right)^{2} }}{p - 3}} \right)^{1/2}$$

(20)

where p is the number of the absorption transitions. In Fig. 5, there is a clear trend of increasing the refractive index for each transition with the increasing of the Sm₂O₃ content %.

Table 6 Electric (S_ED) dipole strength, electric (A_ED) and magnetic (A_MD) radiative transition probabilities, branching ration (β_r), and radiative lifetime (τ_r) for Er-doped zinc-borate glass

Other important parameters can be estimated using the obtained calculated refractive index and the Judd–Ofelt parameter such as A, ${\sigma }_{P}^{E}$, Δλ_eff, β, and τ which are expressed as the probability of transition, the cross-section of the emission, the width of band, the branching ratio, and radiative lifetime, respectively [66]. From previous studies the branching ratio β is considered as the mean factor in the laser material design and used to estimate the intensity of the radiative transitions emission of an excited state [66, 74] and describes the stimulated emission possibilities for a certain transition. The branching ratio r is calculated as follows [75]:

$$\beta_{r} = \frac{{A_{{{\text{Rad}}}} }}{{A_{T} }}$$

(21)

$$A_{{{\text{Rad}}}} = \frac{{64\pi^{4} \upsilon^{3} n\left( {n^{2} + 2} \right)^{2} e^{2} }}{{27hC^{2} \left( {2J + 1} \right)}} \left[ {\mathop \sum \limits_{\lambda = 2,4,6} \Omega_{\lambda } \left( {\left. {aJ} \right\|\left. {U^{\lambda } } \right\|bJ^{\prime}} \right)^{2} } \right]$$

(22)

$$A_{T} = \sum {A_{{{\text{Rad}}}} }$$

(23)

where A_Rad and A_T are known as the probability of the electric field dipole spontaneous emission between the two states excited bJ' and the lower aJ state, and the total probability of all transitions, respectively. The value of the branching ratio β is more than 0.5 and is essential to produce a laser [66]. According to the findings, the ⁶H_5/2 → ⁶F_5/2 emission transition for the samples has a greater branching ratio (0.5) and then has a potential to use for laser material design.

The radiative lifetime’s $\tau$ is estimated from the inverse of the probability of the electric field dipole spontaneous emission and is unaffected by the energy of the phonon of the host matrix [66, 74]. It is given by inversion of the sum of transition probabilities:

$$\tau = \frac{1}{{A_{T} }}$$

(24)

Table 6 illustrates the parameters obtained from Eqs. (21) to (24).

5.1 Absorption and emission cross-sections

The current glass samples absorption cross-sections ${\sigma }_{a}\left(\lambda \right)$ as a wavelength function can be estimated using the following relation [72, 73],

$$\sigma_{a} \left( \lambda \right) = \frac{{2.303 {\text{OD}} \left( \lambda \right)}}{NL}$$

(25)

where $OD\left(\lambda \right)=log\frac{{I}_{o}}{I}$ , N, and L are considered as the optical experimental absorption density of spectrum, the samarium ions concentration, and the thickness of the sample, respectively.

On the other hand, the Sm3+-doped glass emission cross-section ${\sigma }_{e}\left(\lambda \right)$ is estimated using the relation [72, 73]:

$$\sigma_{e} \left( \lambda \right) = \sigma_{a} \left( \lambda \right)\frac{{Z_{l} }}{{Z_{u} }}\exp \left( {\frac{{E_{zl} - hc\lambda^{ - 1} }}{{K_{B} T}}} \right)$$

(26)

where Z_l and Z_u are denoted as the partition functions for both the lower and upper levels in considering of the optical transition and T is the room temperature.

The difference between the lower energy sublevels of the Stark emission and the lower energy sublevels of the Stark level is known as zero-line energy for the transition E_zl.

Figure 10 illustrates the calculated absorption and emission cross-sections for prepared Sm³⁺ doped glass samples.

Fig. 10

The calculated absorption and emission cross-sections for prepared Sm³⁺-doped glass samples

It can be noticed from Fig. 10 that the stimulated emission cross-section peaks for the Sm³⁺-doped glass samples are varied between 0.496 × 10^–20 and 32.29 × 10^–20 cm⁻² for the studied sample.

The value of ${\sigma }_{P}^{E}$ peak for sample 2.61 mol% is considered the greatest value in the samples series which may refer to two reasons. First is the high value of the ⁶F_9/2 → ⁶H_5/2 [72, 76]. The second is due to the high index of refraction of the glass samples [76]. The full width at half maximum FWHM is considered an important factor to evaluate the gain bandwidth of the optical amplifiers [76] and their values lie between 19.25 and 21.12 nm for the studied samples.

Using the estimated outgoing values for the absorption ${\sigma }_{\text{abs}}\left(\lambda \right)$ and the emission ${\sigma }_{\text{ems}}\left(\lambda \right)$ cross-sections, the gain coefficient ${\sigma }_{\text{gain}}\left(\lambda \right)$ for laser media can be estimated using the relation [72]:

$$\sigma_{{{\text{gain}}}} \left( \lambda \right) = P\sigma_{{{\text{ems}}}} \left( \lambda \right) - \left( {1 - P} \right)\sigma_{{{\text{abs}}}} \left( \lambda \right)$$

(27)

where P is population inversion. The function ${\sigma }_{\text{gain}}\left(\lambda \right)$ was calculated for P = 0 to P = 1 with 0.1 increasing steps and is illustrated in Fig. 11. The gain coefficient ${\sigma }_{\text{gain}}\left(\lambda \right)$ leads to potential operating laser wavelength lines ⁴M_15/2 → ⁶H_5/2, ⁶F_11/2 → ⁶H_5/2, ⁶F_9/2 → ⁶H_5/2, ⁶F_3/2 → ⁶H_5/2, ⁶H_15/2 → ⁶H_5/2, and ⁶F_1/2 → ⁶H_5/2, and it is familiar to laser device systems.

Fig. 11

The predicted optical gain coefficient σ_gain for the prepared glasses

Table 7 illustrates the Emission band positions (λ_P, nm), effective bandwidths (∆λ_eff, nm), radiative transition probabilities (A_R, s⁻¹), peak stimulated emission cross-sections (σ_P, × 10^–22 cm²), and experimental branching ratios (β_exp) of ⁴G_5/2 state for Sm³⁺-doped PPbZ glass matrix with different concentrations.

Table 7 Emission band positions (λ_P, nm), effective bandwidths (∆λ_eff, nm), radiative transition probabilities (A_R, s⁻¹), peak stimulated emission cross-sections (σ_P, × 10^–22 cm²), experimental branching ratios (β_exp) of ⁴G_5/2 state for Sm³⁺-doped PPbZ glass matrix with different concentrations

6 Conclusion

Glass samples with Sm³⁺-doped Lead–Zinc Phosphate were successfully produced. With increasing Sm³⁺ concentration, the glass density, and samarium ion concentration N increase gradually. While the mean samarium ion separation, R, decreases as the Sm³⁺ concentration rises. The absorption spectra showed bands of 210, 219, 227, 231, 245, 254, 378, 414, 484, 951, 1094, 1253, 1402, 1505, 1536, and 1983 nm. The strength of the observed absorption bands appears to grow as the concentration of Sm₂O₃ increases. The bands at 210, 219, 227, 231, 245, and 254 nm are due to the charges move in the ultraviolet bands. That are normally observed in nearly advertisement glasses and are caused by trace iron impurities, even if they are existing in ppm amounts.

With the addition of Sm₂O₃ ion content %, the optical absorption edge/cut off wavelength undergoes a red shift. Furthermore, as the Sm³⁺ ion content % increases, the indirect band gap values fall slightly, leading in an expansion in the bonding defect and non-bridging oxygen. When compared to the other compositions, the glasses with a higher Sm₂O₃ content % have greater Urbach energy values, indicating the probability of long-range order spatial developing from the smallest amount of defects.

In addition, the Urbach energy values are inversely proportional to the optical band gap values. Four bands are connected with 4f³ → 4f³ transitions from the ⁴G_5/2 level to the ⁶H_5/2 (563 nm), ⁶H_7/2 (601 nm), ⁶H_9/2 (648 nm), and ⁶H_11/2 (710 nm) transitions in the emission spectra. The ⁴G_5/2 → ⁶H_7/2 (601 nm) transition produces the most powerful emission, which is intense orange-reddish in color. Among the various concentrations, 0.3 mol percent Sm³⁺-doped glass matrix (KFP03Sm) exhibits the highest emission intensities, with intensity decreasing as Sm³⁺ concentration increases.

At larger concentrations of Sm³⁺ ions, energy is dropped due to the nonradiative (NR) processes. The rise in the number of NR decay channels, as well as the many closely spaced excited states that lead to quenching are most likely to blame for this occurrence.

The values of the X and Y (X,Y) coordinates (the black point) are located very close to the national slandered value of television system (0.67, 0.33). The 563 nm emission peak has coordinates (0.394, 0.603) orange (Blue point), the 601 nm emission peak has coordinates (0.631,0.368) reddish-orange (green point), and the peaks at 648 nm and 710 nm have approximately the same coordinates (0.731,0.270) Red (Aqua point). The Judd–Ofelt theory indicated that the model parameter trend found to be Ω₄ > Ω₂ > Ω₆ which indicate high glasses rigidity.

The ⁶H_5/2 ⁶F_5/2 emission transition for samples has a greater branching ratio (0.5) and a potential utility for laser design, according to spontaneous emission probability. The optical amplifiers' gain bandwidth properties are 19.25 to 21.127 nm for Sm³⁺ 1.0 to 7 mol. percent, respectively. The samples under examination are introduced as a candidate for orange and reddish-orange photonic application based on the discovered optical characteristics, absorption, and emission behaviors.