Reduction in thermal conductivity and electrical resistivity of indium and tellurium co-doped bismuth selenide thermoelectric system

Abstract

Polycrystalline samples of (Bi_1-xIn_x)₂Se_2.7Te_0.3 (x = 0.00, 0.02, and 0.04) were prepared by the solid-state reaction technique. X-ray diffraction pattern confirms that the polycrystalline samples have a hexagonal structure with spacegroup R $\stackrel{-}{3}$ m. The surface morphologic study reveals the existence of porous behavior in the studied samples due to the volatilization of Selenium. Energy dispersive X-ray analysis validates the expected and observed elemental composition of the samples. Electrical resistivity has shown metallic behavior. Hall effect and Seebeck coefficient measurements indicate the p-type and n-type conduction for the pristine sample Bi₂Se₃ and the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples, respectively. The thermal conductivity and electrical resistivity were found to reduce by 7.5 and 9 times, respectively, for (Bi_0.96In_0.04)₂Se_2.7Te_0.3 compared to the pristine sample Bi₂Se₃.

1 Introduction

One of the best solutions for renewable energy is thermoelectric (TE) materials, which convert waste heat into electricity and vice versa and provide better management for clean and green energy production [1]. The efficiency of thermoelectric material is determined by a dimensionless quantity called the thermoelectric figure of merit (ZT) and is calculated using the formula $ZT=\frac{{S}^{2}T}{\kappa \rho }$, where S is the Seebeck coefficient, κ is the total thermal conductivity, ρ is the electrical resistivity, and T is the absolute temperature [2, 3]. The chalcogenide materials like Bismuth Selenide and Bismuth Telluride are the reliable low-temperature TE materials that are used for Peltier cooling devices. The alloys based on Bismuth Selenide and Bismuth Telluride have been studied extensively as representative materials for thermoelectric applications near room temperature. The most challenging task in search of high-performance TE materials is to simultaneously control the electrical conductivity and thermal conductivity [4].

Adam et al. [5] have obtained the power factor of 131 × 10² μW/mK² for 2D material Bi₂Se_3-xTe_x. Ali et al. [6] have reported Bi₂Te_2.7Se_0.3 tetradymite by the physical vapor deposition method. Kadel et al. [7] have reported Bi₂Se₃ thin film with ZT of 0.096 at 523 K, synthesized by nanoscale route method. Quentin et al. [8] have reported the thermoelectric performance of Cu-doped n-type Bi₂Te₃ with ZT of 0.1 at 300 K. Margarita et al. [9] have reported vapor–solid synthesis of Bi₂Se₃ with the fabrication of graphene layer. Ramezani et al. [10] have introduced the nanoparticle synthesis of Bi₂Se₃ as a novel precursor. Nano flakes of Bi₂Se₃ have been reported with a ZT value of 0.02 at 300 K by Yuho et al. [11]. Single crystal Bi₂Se₃ was reported by Anuj Krishna et al. [12] with ZT of 0.6 at 400 K. Kulsi et al. [13] have reported Ni-doped Bi₂Se₃ with ZT value of 0.22 at 300 K. Enhanced thermoelectric properties of phase-separating bismuth selenium telluride thin films via a two-step method was reported by Masayuki et al. [14]. Jana et al. [15] reported the thermoelectric properties of Bi₂Se₃ thin film with the Seebeck coefficient of 150 μV/K by the vapor–solid technique. Thermoelectric properties of Bi₂Te₃ doped with different copper amounts have been reported by Lognone et al. [16]. From the literature mentioned above, the effects of co-doping are much less studied in the chalcogenide thermoelectric materials in the low and near room temperature range (10–350 K).

Since Bi₂Se₃ is bonded with Van der Waals force between layers, the extra layer should be introduced to stack Bi₂Se₃ superlattice. The introduction of Indium will produce an extra electron to the Bi₂Se₃ lattice, in which an increase in the carrier concentration is expected [17]. The effect of Indium substitution may lead to the localized electronic states in crystal, which would vary the electronic properties of the alloys. In the (Bi_1-xIn_x)₂Se_2.7Te_0.3 system, the Bismuth ions are larger than Indium ions, and the Tellurium ions change the c axis spacing by creating Se_Te vacancies. Hence, the co-doping in Bi₂Se₃ will significantly modify the structural parameters and in turn, the thermoelectric properties [18]. Tellurium can achieve a high level of substitution on the Selenium site due to their similar chemical properties [19]. The doping of Tellurium in the site of Selenium finds an active approach to avoid the intrinsic conduction. Also, it seems to balance the carrier concentration and resultant enhancement of thermoelectric properties in Bi₂Se_3. As an optimization, lattice thermal conductivity can be reduced by intensified scattering of alloys for electrons and phonons [20]. The co-substitution of Bi by In favors the construction on Te_Se antisite defect of Bi₂Se_3. The challenging task is to the decrease in thermal conductivity without deteriorating the electrical conductivity, which motivates us to study co-doping effects in chalcogenides. The present investigation is focused on the thermoelectric properties of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 system in the temperature range 10–350 K. Remarkably, the simultaneous decrease of electrical resistivity and thermal conductivity is observed in the co-doped chalcogenides, and in turn, an enhancement of the ZT value is achieved.

2 Experimental procedure

2.1 Sample preparation

The samples of Bi₂Se₃ and (Bi_1-xIn_x)₂Se_2.7Te_0.3 were synthesized by solid-state reaction technique in which the precursors Bismuth (99.99%), Indium (99.9%), Selenium (99.995%), and Tellurium (99.99%) were added in a stoichiometric ratio and mixed well in an agate mortar for 2 h with an intense grinding. The mixed powder was subjected to pelletization under the compression pressure of 5 tons. The pellets of dimension 10 × 2 × 5 mm³ were obtained. The pellets were sealed in a quartz tube under a vacuum of 10^–6 torr and sintered at 480 °C for 30 h. The grinding is repeated for the sintered pellets to improve the homogeneity in the compounds. The pelletization is repeated and sintered at 250 °C for 15 h.

2.2 Experimental techniques

The X-ray diffraction (XRD) study was carried out by powder X-ray diffractometer (Rigaku Miniflex with Cu Kα) in the angle 2θ range 22°–80° at the rate of 2°/min to confirm the purity, crystallinity, dominated phase, and formation of compounds. The surface morphological features of samples were inspected by field emission scanning electron microscope (Carl Zeiss Sigma) at the particle range of 1 μm with the magnification of 35 kX. The chemical composition of grown samples was examined by energy dispersive X-ray analysis (EDAX) using EVO MA18 with Oxford EDS (X-act).

The carrier concentration, mobility, and Hall coefficient at room temperature were measured by the Van der Pauw technique. The low and near room temperature electrical resistivity was measured in the temperature range 10 – 350 K using the four-point probe method in closed cycle refrigeration. The dc heat pulse technique was used to measure the Seebeck coefficient (S) and thermal conductivity (κ) simultaneously [21].

3 Results and discussion

3.1 X-ray diffraction (XRD) study

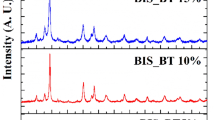
Figure 1 shows the XRD patterns of the samples Bi₂Se₃ and (Bi_1-xIn_x)₂Se_2.7Te_0.3. The highest intensity peak (015) has been observed for the samples Bi₂Se₃, (Bi₀.₉₈In₀.₀₂)₂Se_2.7Te_0.3 and (Bi₀.₉₆In₀.₀₄)₂Se_2.7Te_0.3, whereas the peak (216) is dominated in Bi₂Se_2.7Te_0.3 sample. This could be due to the variation in the recrystallization of the sample during the sintering and anisotropic nature of the crystal [22]. Besides, there is a gradual shifting in the peak position to the lower 2θ angle side, except the sample doped with In (x = 0.04) (Fig. 2). The shift in XRD peak position is due to the insertion of the larger ionic radius atom tellurium onto the smaller ionic radius of Selenium site. The random variation in the sample doped with In (x = 0.04) is because of uneven variation of strain in the sample, which has affected the crystallite size, lattice parameter, and is listed in Table 1. The crystallite size has been calculated using the Williamson Hall formula [23].

$$\beta \cos \theta = \left( {\frac{0.9\lambda }{D}} \right) + 4 \in \sin \theta$$

(1)

Fig. 1

XRD peak patterns of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

Fig. 2

XRD Peak (015) shifting of a Bi₂Se₃, b Bi₂Se_2.7Te_0.3, c (Bi_0.98In_0.02)₂Se₂.₇Te_0.3, and d (Bi₀.₉₆In_0.04)₂Se₂.₇Te_0.3 samples

Table 1 XRD analysis data of (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

where β is full width half maximum intensity, $\uplambda$ is the wavelength of X-ray, ε is the strain, and D is the crystallite size. It is observed that there is a gradual increase in the crystallite size, in line with an increase in the lattice parameter values. The twinning effect is observed at 28° and 45° for all the samples, which corresponds to the sharing of the lattice point on the face of the existing crystal. The XRD peak patterns are fitted by the software “EXPO 2014” which is shown in Fig. 3 [24, 25]. The values of R_p (Profile factor), R_ep (Expected Profile factor), R_wp (Weighted profile factor), and χ² values have been tabulated in Table 1. The refined XRD patterns show that the crystal belongs to the hexagonal crystal system with R $\stackrel{-}{3}$ m space group.

Fig. 3

Rietvield refinement plots of a Bi₂Se₃, b Bi₂Se_2.7Te_0.3, c (Bi_0.98In_0.02)₂Se₂.₇Te_0.3, d (Bi₀.₉₆In_0.04)₂Se₂.₇Te_0.3 samples

3.2 Field emission scanning electron microscopy (FESEM)

Figure 4a shows the surface morphology of the pristine Bi₂Se₃ sample. It is observed that there are growth and shrinkage of the grains in some areas without any sign of impurities. As the Tellurium is inserted into the matrix of Bi₂Se₃, the white patches can be observed in certain areas with some porous behavior, as shown in Fig. 4b and c. Besides, there is an increase in the porosity of the In-doped sample (x = 0.04) due to the volatilization of Selenium during sintering [Fig. 4d]. Partial evaporation of Selenium causes decrease in the concentration of ${V}_{Se}^{..}$. As a result, the electron concentration decreases. Hence there is a variation in the density of the material in all the compounds [26, 27]. The selenium vapor pressure increases during sintering which forms negative gradient of Se precipitates on the surface. The effect of doping of Te has resulted in the agglomeration of the particles [28, 29].

Fig. 4

FESEM images of a Bi₂Se₃, b Bi₂Se_2.7Te_0.3, c (Bi_0.98In_0.02)₂Se_2.7Te_0.3, d (Bi_0.96In_0.04)₂Se_2.7Te_0.3 samples

3.3 Energy dispersive X- ray analysis (EDAX)

The chemical composition of the samples was examined by the EDAX, and the images of the studied samples are shown in Fig. 5. The pristine Bi₂Se₃ sample indicates the presence of Bismuth and Selenium as expected, whereas the Bi₂Se_2.7Te_0.3 sample shows the presence of Tellurium along with the Bismuth and Selenium. For the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples, the presence of Indium in these In-doped samples (Fig. 5c, d) is confirmed. The observed elemental composition of the studied samples matches well with the expected pre-crystal formation, as shown in Table 2.

Fig. 5

EDAX images of a Bi₂Se₃, b Bi₂Se_2.7Te_0.3, c (Bi_0.98In_0.02)₂Se_2.7Te_0.3, and d (Bi_0.96In_0.04)₂Se_2.7Te_0.3 samples

Table 2 The elemental composition data of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

3.4 Electrical resistivity

The temperature-dependent electrical resistivity ρ(T) of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 system is shown in Fig. 6. It is seen that the pristine sample has the highest electrical resistivity among all studied samples, while the In-doped (x = 0.04) sample has the lowest electrical resistivity. It is noticed that there is a gradual decrease in electrical resistivity with the increase in the doping level. Initially, the pristine sample shows the usual semiconductor behavior, in which the resistivity decreases as the temperature increases till 233 K and metallic behavior is observed after 233 K. This could be due to the direct cation–cation interaction of homopolar bonds of Bi-Bi, which changes the bandgap as temperature changes [30]. The donor band of the quantum states are occupied by the fifth electron of donor atom. There is an overlapping of donor band with the conduction band which leads to the composite band. The few of the lower energy states of this band is occupied by electrons, whereas other band energy states are unfilled. The insertion of In into the site of Bi has caused the intrinsic point defect which is dependent on the polarity of the bond [31]. Due to the differences in the electronegativities, there is a suppression of bonding between Bi-Se by In-Se. Hence there is a probability of bonding between In-Se and In-Te rather than Bi-Te and Bi-Se. As a result, electrical resistivity increases, with increase in temperature. Along with this, there is a decrease in ${V}_{Te}^{..}$ and ${V}_{Se}^{..}$ vacancies with the change in the creation of energy lattice defect in mixed crystal Bi_1-xIn_xSe_3-xTe_x. Also, at greater temperature, electrons are captured from the conduction band. The doping of In in Bi₂Se₃ also initiates the volatilization of Se and Te atoms during sintering. Hence the samples Bi₂Se_2.7Te_0.3, (Bi_0.98In_0.02)₂Se_2.7Te_0.3, and (Bi_0.96In_0.04)₂Se_2.7Te_0.3 show degenerate semiconducting behavior [32, 33]. The drastic change in electrical resistivity from pristine to the doped samples is presumably due to impurity band, which makes disorders in the potential energy of the donors [34]. Fermi level is situated in the middle of the band gap, although there is a huge intrinsic vacancy, Bi₂Se₃ has high hole concentration. Fermi level lies just above the valence band, which results in p-type transport behavior in Bi₂Se₃, where the total density of states is varied unconditionally. Deep defect states are basically filled in bulk band in Bi₂Se_3. This probable distortion of density of states occurred due to doping of indium in valence band region. As a result, there is a creation of deep defect states above the valence band. Also, the hybridization of In with Bi is also the reason for deep defect states [35]. The distorted density of states is initiated by the interaction of pristine with the dopant indium atom. This variation in defect states bring the modification in electrical resistivity. Along with the doping of indium, it is observed that tellurium doping leads to an increase in the density of ionized impurities, as the dopants concentration become large due to co-doping. Te has been introduced to increase carrier concentration and scattering of carriers through Se_Te vacancies. The influence of carriers excited by the doping of tellurium results in the increase of electrical conductivity. Se_Te atoms occupy Bi_In vacancies resulting in the formation of antisite defects. These antisite defects produce excess of electrons. They will be excited from valence band to the conduction band easily by the doping of tellurium [36,37,38]. This phenomenon could be enhanced even at the time of sintering. As a result, the antisite defect is formed in the doped and co-doped samples [39]. This leads to the super-stoichiometric behavior of the Bi(In)–Bi(In), which replaces the Se_Te sublattice. The lattice point defect in (Bi_1-xIn_x)₂Se_2.7Te_0.3 is likely to form with the addition of Indium into the matrix [40]. In this case, (Bi_0.96In_0.04)₂Se_2.7Te_0.3 shows 9 times reduction in electrical resistivity value compared to pristine Bi₂Se₃. The antisite defect equation is represented by

$$4Bi_{{Bi}} + 2Bi^{\prime}_{{Se}} + 2e^{\prime} + 7V_{{Se}} + 2V_{{Bi}}^{{1.5}} + (2V_{{Bi}}^{{1.5}} + 3V_{{Se}} ) + 2In + \left( {\frac{3}{2}} \right){\text{Se}}_{2} = 6Bi_{{Bi}} + 2In_{{Bi}}^{X} + + Se_{{Te}}^{X} + 9V^{\prime}_{{Se}} + 9e^{\prime}$$

(2)

Fig. 6

Temperature-dependent electrical resistivity of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

The electrical resistivity at low-temperature (30–200 K) region and near room temperature region (200–350 K) were attempted to fit by variable range hopping model (VRH) and small polaron hopping (SPH) model [41, 42], and the results are shown in Figs. 7 and 8, respectively. The VRH model is given by

$$\rho = \rho_{0} {\exp}\left( {\frac{{T_{0} }}{T}} \right)^{1/4}$$

(3)

Fig. 7

Variation of ln ρ versus 1/T^1/4 for the (Bi_1-xIn_x)₂Se_2.7Te_0.3 compounds

Fig. 8

Linear fitting of SPH model of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 sample

where ${\rho }_{0}$ is the pre-exponential factor, and T₀ is the characteristic temperature. It is seen that temperature-dependent electrical resistivity for all studied samples is satisfactorily described by the VRH model in the temperature range 10–60 K (see Fig. 7). The VRH model is valid when the thermal energy is not enough to excite the electrons to hop to their adjacent neighbors. It is more favorable for the electrons to hop further to find a site with a minor potential difference. The characteristic temperature is given by

$$T_{0} = \left( {\frac{{18\alpha^{3} }}{{k_{B} N\left( {E_{F} } \right)}}} \right)$$

(4)

where N(E_F) is the density of state at the Fermi level, k_B is the Boltzmann constant, and α is the average localization length, calculated using

$$\alpha = \frac{{q^{2} 0.025 \rho }}{\hbar }$$

(5)

It was found to be 0.013 nm⁻¹[43]. Using T₀ obtained from the slope in Fig. 7, N(E_F) is estimated by employing Eq. 4, and the value for each sample is given in Table 3. A clear distinction among the two types of conduction can be made by the pre-exponential factor for the conduction in localized states. In a semiconductor extrinsic regime at sufficiently low temperatures, the charge transport between the localized state in an impurity band allows few charge carriers with hopping from occupied states below the fermi level. Thus, VRH conduction could play a vital role in the charge of transport phenomenon [44, 45]. On the other hand, the temperature-dependent electrical resistivity data for all studied samples are well fitted to the SPH model in the temperature range 200–350 K, and the result is shown in Fig. 8. The SPH model is given by

$$\rho = \rho_{0} T{\exp}\left( {\frac{{E_{A} }}{{k_{B} T}}} \right)$$

(6)

Table 3 Characteristics temperature (T_o), Pre-exponential factor (ρ₀), the Fermi level density of states N(E_F) of (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

where E_A is the activation energy. The activation energy of each compound is calculated using the obtained slope from Fig. 8. Thermally activated hopping polarons are responsible for the conduction mechanism in high-temperature region [46]. Activation energies of Bi₂Se_3, Bi₂Se_2.7Te_0.3, (Bi_0.98In_0.02)₂Se_2.7Te_0.3, and (Bi_0.96In_0.04)₂Se_2.7Te_0.3 are found to be 15 meV, 17 meV, 22 meV, and 15 meV at 300 K, respectively. As the impurities are introduced to the lattice, there is an increase in the activation energy of samples due to the addition of extra energy levels. Electrons will settle within the conduction band, which elevates the Fermi level to higher energy as a result of the co-doping in Bi₂Se₃. This is presumably due to the super-stoichiometry and/or point defects that play a major role in the crystal lattice [47]. The change in the effective mass may be the reason for the unexpected decrease in the activation energy of the In-doped sample with x = 0.04. The activation energy of the presently studied compounds is compared with other reports in Table 4 [48,49,50,51].

Table 4 Comparison of E_A values of some reported compounds

3.5 Seebeck coefficient

The temperature-dependent Seebeck coefficient (S) of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 (x = 0.00, 0.02, and 0.04) system is displayed in Fig. 9. The pristine Bi₂Se₃ sample has the highest Seebeck coefficient value of about 123 μV/K at 350 K and shows p-type semiconductor nature. It is well documented that Selenium is significantly vaporized from the sample during crystal growth, which creates lattice vacancies of V_Se. Similarly, Bi cations produce the anionic lattice vacancies to generate antisite defect Bi_Se. The small crystallites in the crystals are joined by grain boundaries of complex structure, as a result disorders are formed in atomic layers. This will cause a significant change in electronic properties [48, 52, 53]. Hence the carrier scattering effect of grain boundary refinement will produce holes which could be the reason for the p-type nature of the compound Bi₂Se₃ [54]_. The rest of the samples has a negative value of the Seebeck coefficient, indicating the n-type semiconductor nature. This is due to the dopants acting as a donor atom by providing extra electrons. Because of the initial substitution of Tellurium in Se² sites, Bi-(In)-Se² will be replaced by Bi-(In)-Te² bonds. This will lead to the mutual bonding of [-Se-Bi-Te-Bi-Se-]. Therefore, by the continuous substitution of Tellurium, Seebeck coefficient becomes negative. As a result, electrical conductivity increases gradually among the samples [55, 56]. It is observed that there is random variation in the Seebeck coefficient of doped samples, which could be due to the unobvious grain growth of microstructure caused by the carrier scattering effect. The carrier scattering factor is calculated using

$$\gamma = {\text{In}}n + S$$

(7)

Fig. 9

Temperature-dependent Seebeck coefficient of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

where γ is the scattering factor, n is the carrier concentration, and S is the Seebeck coefficient [39]. Moreover, Experimental and theoretical calculation of the carrier scattering factor values are in good matching with each other which are only dependent on carrier concentration and Seebeck coefficient. The value of Seebeck coefficient becomes very negligible compared to the natural logarithm of carrier concentration (n) of each sample. Expectedly, the scattering factors are matching well among theoretical and experimental calculations [57].The Hall measurement was performed using the Van Der Paw method with the input current of 50 mA at 300 K, which confirms the p-type nature of the pristine sample and n-type nature for the doped samples, consistent with the Seebeck coefficient measurements. Theoretical Hall effect calculations can be related to Seebeck coefficients by the formula

$$S\left( T \right) = \frac{{8k_{b}^{2} \pi^{2} m^{*} }}{{3eh^{2} }}\left( {\frac{\pi }{3n}} \right)^{2/3} T$$

(8)

where S(T) is the Temperature-dependent Seebeck coefficient, k_b is the Boltzmann’s constant, m* is the effective mass of electron, e is the charge of an electron, h is the plank’s constant, n is the carrier concentration, and T is the temperature applied [58, 59]. Theoretical values of mobility were calculated using

$$\mu_{H} = \frac{1}{ne\rho }$$

(9)

where $\rho$ is the electrical resistivity ($\Omega m$. Theoretical and experimental carrier concentrations, mobility, and scattering factor values are presented in Table 5. The theoretical and experimental carrier concentration values are in the same range of order 10²²/m³ which exhibits that the hall effect and the Seebeck coefficients are in good agreement with each other. There is a deviation in values of theoretical hall mobility from experimental hall mobility among the samples, which is presumably due to some unavoidable constraints of the experiment. The order of experimental and theoretical carrier concentration (n) values is found to be 10²²/m³ among all the samples. However, there is a variation in the coefficient of n values which could be due to the anisotropic nature of samples (Bi_1-xIn_x)₂Se_2.7Te_0.3. The probable reason for deviation in Hall measurements may be attributed to rapid drop of resistance of four thermal in the direction of high mobility by collective anisotropic orientation, which is a main challenge to measure the precise values of mobility and carrier concentration simultaneously and can be considered as limiting factor for experimental and theoretical deviations [60, 61]. The localization of electron–electron interaction causes co-occurrence of degenerated bulk thermally activated layers with high experimental mobility value in Bi₂Se₃ (21.7 × 10⁻⁴m²/Vs), whereas (Bi_0.96In_0.04)₂Se_2.7Te_0.3 has 1/7 ratio of experimental and theoretical Hall mobility which is due to the increase in the doping density with hopping conduction by small polarons, which resulted in a discrepancy of theoretical Hall mobility values. Besides the electrons in the conduction band are observed to be localized, as there is not much contribution to the Hall voltage, but continue to contribute to the electrical conductivity [62]. The theoretical values of Hall mobility are calculated using Eq. 9. The theoretical values of Hall mobility are dependent on values of carrier concentration and electrical resistivity of a sample, whereas the experimental values are directly obtained by Hall effect instrument Keithley meter 6220″. Besides the uneven variation of effective mass has made a significant effect on Hall mobility. The effective mass is calculated using Eq. 8 and is shown in Table 5. The Fermi energy (E_F) of each compound is calculated by using

$$E_{F} = \frac{3eS}{{\pi^{2} k_{b} T}}$$

(10)

and presented in Table 5.

Table 5 Experimental and theoretical Carrier concentration (n_exp and n_th), Hall mobility (μ_expand μ_th), scattering factor(γ_th and γ_exp), and Fermi Energy (E_F) of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 system at 300 K

3.6 Thermal conductivity

Figure 10 illustrates the temperature-dependent thermal conductivity κ(T) of (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples in the temperature range 10–350 K. The pristine Bi₂Se₃ shows a pronounced phonon peak at around 25 K, which is a common feature for crystalline solids [63, 64]. It is seen that the height of the peak is significantly suppressed with doping at low temperatures, suggesting a substantial enhancement in the phonon scattering. Besides, we found that κ(T) decreases with an increase in Indium content for the (Bi_1-xIn_x)₂Se_2.7Te_0.3 system at high temperatures. These findings are presumably due to the lattice point defects in the crystal caused by the substitution which induces mass and size contrast [65]. As a result, the grain boundary scattering and point defect scattering have a significant effect on thermal transport property at low temperatures. The atomic defects such as vacancies and antisite disorder could also reduce thermal conductivity, as the average wavelength of heat-carrying phonons reduces [66].

Fig. 10

Thermal conductivity of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

The total thermal conductivity for crystalline solids is generally expressed as sum of electronic and lattice contributions. The electronic contribution of heat transport κ_e can be calculated by the Wiedemann–Franz law

$$\kappa_{e} = \frac{{L_{0} T}}{\rho }$$

(11)

where L₀ is the Lorentz number, which is equal to 2.45 × 10^–8 WΩK⁻², and ρ is the electrical resistivity [67, 68]. The lattice component of thermal conductivity (κ_L) is obtained by subtracting the electronic thermal conductivity from the total thermal conductivity (κ). The electronic and lattice thermal conductivity graphs are shown in Fig. 11. By the separation of electronic and lattice contributions of the total thermal conductivity, it is revealed that the major contribution to the measured κ originates from the phononic component rather than charge carriers. A rapid increase in the lattice thermal conductivity at low temperatures is seen. With further increase of temperature, the lattice thermal conductivity decreases due to the predominate phonon–phonon scattering (Umklapp process) [69]. (Bi_0.96In_0.04)₂Se_2.7Te_0.3 exhibits 7.5 times reduction in thermal conductivity value compared to pristine Bi₂Se₃.

Fig. 11

Electronic thermal conductivity and lattice thermal conductivity of (Bi_1-xIn_x)₂Se_2.7Te_0.3 sample

3.7 Power factor (PF) and thermoelectric figure of merit (ZT)

The temperature-dependent power factor is calculated in the temperature range 10–350 K using equation PF = S²/ρ, and is shown in the inset Fig. 12. It is seen that there is an increase in PF as the doping concentration increases. The In-doped samples with x = 0.02, 0.04 show the highest power factor of about 120 μW/mK² at 350 K, which is about twice that of the pristine sample. Correspondingly, the ZT values are calculated as a function of temperature, and the result is shown in Fig. 12. The highest ZT value of about 0.023 was observed for the In-doped samples with x = 0.02 at 350 K, which is about 2.1 times higher than that of the pristine sample. (Bi_0.98In_0.02)₂Se_2.7Te_0.3 and (Bi_0.96In_0.04)₂Se_2.7Te_0.3 show better PF and ZT values, mainly due to the significant reduction in electrical resistivity and thermal conductivity. Hence, the co-doped (Bi_0.96In_0.04)₂Se_2.7Te_0.3, (Bi_0.98In_0.02)₂Se_2.7Te_0.3 compounds are potential candidate for Peltier cooling applications.

Fig. 12

Temperature-dependent figure of merit (ZT) and Power Factor (PF) of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 samples

4 Conclusion

In this work, we report low and near room temperature (10–350 K) thermoelectric properties of the (Bi_1-xIn_x)₂Se_2.7Te_0.3 system. The XRD analysis shows that the crystal structure is hexagonal with space group of $R\stackrel{-}{3}$ m. The surface morphology shows that there is an increase in porosity and volatilization of Selenium in the sample. The sample doped with Indium (x = 0.04) shows a 9 times reduction in electrical resistivity compared to the pristine sample due to the variation in impurity bands. At low temperature, the thermal conductivity was found to reduce by 7.5 times in the In-doped sample with x = 0.04 in comparison with the pristine sample. It is revealed that the phonon–phonon interaction is predominant over the phonon–electron interaction. The Seebeck coefficient and Hall effect measurements confirm the p-type nature for the pristine and n-type nature for the doped samples. The highest ZT values are found to be 0.023 and 0.022 for the In-doped sample with x = 0.02 and 0.04, respectively, with a PF value of about 120 μW/mK² at 350 K. From the present study, it is realized that co-doping reduces thermal conductivity and electrical resistivity. Hence co-doping may be an alternative strategy to improve the thermoelectric performance of Bi₂Se₃, (Bi_0.98In_0.02)₂Se_2.7Te_0.3, and (Bi_0.96In_0.04)₂Se_2.7Te_0.3 systems._. By suitable optimization, In-doped Bi₂Se_2.7Te_0.3 can be used for low and near room temperature TE applications.