Introduction

To obtain favorable ferroelectric materials, the polar order must be controlled. Therefore, the chemical compositions, structures, and fabrication processes are designed. Ferroelectric polar order well develops and micron-scale domains form in normal ferroelectrics [1]. In a solid solution of morphotropic-phase-boundary compositions, polar order can be miniaturized down to tens of nanometers, leading to the formation of lamellarlike nanodomains, and high piezoelectric coefficients can be obtained [2, 3]. Furthermore, by introducing local chemical inhomogeneities [4,5,6,7], size of polar order is reduced to a few nanometers [8, 9]. This can be the origin of relaxor ferroelectricity, that is, a high dielectric constant and a unique dependence on frequency and temperature [10].

Lead zirconate titanate (Pb(Zrx,Ti1−x)O3: PZT) is a well-known ferroelectric compound, which has been widely used for commercial applications because of the high piezoelectric constant [11]. For x < 0.53, it is in a tetragonal ferroelectric phase with the space group of P4mm at 300 K [12, 13], while it is in a rhombohedral ferroelectric phase for 0.53 < x < 0.95 [13,14,15]. In both cases, long-range polar order develops and size of ferroelectric domain is often hundreds of nanometers or larger [16, 17]. For x close to 0.53, crystal symmetry down to a monoclinic phase [13] and size of ferroelectric domain is reduced [16, 17]. The lamellar like nanodomains typically have width of tens of nanometers and length of hundreds of nanometers, which indicates that long-range polar order is still retained.

Distribution of polar order in individual unit cells can be visualized by precise measurement of atomic positions using Scanning transmission electron microscopy (STEM) [18]. Furthermore, if lattice parameters of the unit cells were correctly measured, relationship between the polar order and the lattice parameters can be established, which should lead to better understanding of structure formation mechanism. However, measurement of accurate lattice parameters is not a trivial task owing to errors caused by image distortions that derive from sample drift and scanning system of the microscope [19, 20], and errors in measured lattice parameters are usually as much as 2–3% if no any corrections are adapted [21]. Recently, we have established the distortion correction scheme [21] and have demonstrated that error in lattice parameters be reduced to approximately 0.1% in a good case [22].

Artificial superlattices have been used to obtain structures and/or properties that are not expected for bulk crystalline materials [23, 24], and fabrication of composition-modulated artificial superlattices have also been reported for PZT [25,26,27,28,29]. However, relationship between distribution of polar order and lattice parameters has not been clarified in the atomic scale. Therefore, in the present study, we applied the aforementioned distortion-corrected atomic-scale STEM to examine the distributions of polar order and lattice parameter of unit cells in the Pb(Zr0.65Ti0.35)O3/Pb(Zr0.30Ti0.70)O3 (PZT65/PZT30) superlattice [30]. In addition, based on the understanding of the polar order and the lattice parameters, first-principles calculations were carried out to discuss a possible structure formation mechanism.

Materials and methods

Thin film growth and electrical property evaluations

PZT65/PZT30 superlattices were fabricated on SrRuO3(001)/Pt-grown Si substrates with a ZrO2 buffer layer (KRYSTAL, Inc., Japan) via multiple-target radio-frequency sputtering. PZT30 and PZT65 layer thicknesses were approximately 4 nm, and the total film thickness was approximately 800 nm (Fig. 1a) [30]. Additional details concerning thin film growth were reported in Ref. [30]. X-ray diffraction profile was measured using SmartLab (Rigaku Co. Japan.) at a tube voltage of 40 kV and a tube current of 40 mA. Measurement methods of the polarization–electric field (P–E) hysteresis loop, relative permittivity, and converse transverse piezoelectric constant (e31,f) were described in Ref. [30]. A thin foil for cross-sectional electron microscopy was prepared with a focused ion beam (Quanta 200i, FEI Co. Japan Ltd., Japan), at a 30 kV acceleration voltage. Final milling at 2 kV was performed to remove damaged surface layers.

Figure 1
figure 1

PZT65/PZT30 superlattice. a Schematic of the film structure, and b cross-sectional annular-dark field scanning transmission electron microscopy (STEM) image of the film. A (001)-oriented SrRuO3/Pt/ZrO2/Si substrate was used. STEM energy-dispersive spectroscopy map for the superlattice. c STEM image, d Pb-L map, e O-K map, f Zr-L map, and g Ti-K map.

Full size image

Electron microscopy

Transmission electron microscopy (TEM) and Scanning TEM (STEM) was performed with JEM-2100 and JEM-ARM200CF instruments (JEOL Ltd., Japan) at the Ultramicroscopy Center at Kyushu University. The acceleration voltages were 200 kV. TEM images and selected-area diffraction patterns were recorded with an Orius SC200D charge-coupled-device camera (Gatan Inc., USA) and a TemCam complementary-metal-oxide semiconductor camera (TVIPS GmbH, Germany). STEM images were recorded with a DigiScanII™ (Gatan Inc., USA). Annular-dark-field STEM images were acquired using a probe-forming aperture with a 26-mrad semi-angle and a detection angle range of 90–370 mrad. Ten frames were sequentially recorded and averaged using rigid and non-rigid registration methods with the SmartAlign plug-in (HREM Research Inc., Japan) [31] in DigitalMicrograph™ (Gatan Inc., USA) to enhance the signal-to-noise ratio. Individual 1024 × 1024 pixel frames were obtained using 2 s pixel dwell times and a 500 s flyback. The Pb-ion and Zr/Ti-ion column positions were identified with two-dimensional Gaussian function peak-fitting of averaged images [32]. Lattice parameters were calculated based on the Pb-ion column positions. To evaluate lattice parameters accurately, distortions in the STEM images caused by specimen drift and the instrument were corrected with two-step affine transformations [22]. Element distributions were acquired via energy-dispersive X-ray spectroscopy using twin silicon drift detectors (JEOL Ltd., Japan) in the JEM-ARM200CF microscope.

Density functional theory calculation

First-principles density-functional theory calculations were performed using VASP [33]. Projector-augmented wave potentials [34] were used under a local-density approximation [35], where Pb-6s, 6p, and 5d, Ti-3s, 3p, 3d, and 4s, Zr-4s, 4p, 5d, and 5s, and O-2s and 2p orbitals were treated as valence states. The cut-off energy for the plane-wave basis set was 400 eV, and a 6 × 6 × 6 k-point mesh generated with the Monkhorst–Pack [36] scheme was used. Electronic structures were iteratively optimized self-consistently until the energy difference was less than 10−4 eV. During structural optimizations, lattice parameters were fixed, Pb and Zr/Ti ions were fixed at specific positions for a given displacement vector. While, O ion positions were allowed to relax, and were iteratively optimized until all force norms had become less than 0.02 eV/Å.

Results and discussion

Microstructure and interface structure

An approximately 800-nm-thick PZT film was grown on a SrRuO3/Pt/ZrO2/Si substrate (Fig. 1b). Energy-dispersive X-ray spectroscopy maps acquired in the middle of the film (Fig. 1c–g) showed that approximately 4-nm-thick Zr-rich PZT65 and Ti-rich PZT30 layers were alternately grown, which confirmed formation of the composition-modulated superlattice as was also reported in Ref. [30]. STEM images of the PZT/SrRuO3 interface revealed that lattice defects were introduced several atomic layers above the interface (Fig. 2a). Inverse Fast fourier transform (FFT) of the image (Fig. 2b) indicated that there were extra half planes as pointed by arrows, showing that misfit dislocations were introduced and their Burger’s vector is a[100]. This can be attributed to a lattice mismatch between SrRuO3 (with pseudo-cubic lattice parameter a = 392.8 pm [28, 37]) and the PZT (lattice parameter a = 397.8 pm in PZT30 [12]). As lattice mismatch was relaxed by the introduction of the misfit dislocations, PZT65/PZT30 superlattice well above the interface was less affected by the substrate. Ferroelectric domain structures were not observed in middle of the film from Dark-field (DF) TEM images of the superlattice (Fig. 2c), which was consistent with the absence of diffraction spot splitting in the selected-area diffraction pattern (Fig. 2d). The horizontal stripe contrast in the DF TEM image was caused by the superlattice, and the vertical line contrast was most probably attributed to lattice defects, such as threading dislocations or sub grain boundaries reported previously [27].

Figure 2
figure 2

Interface and microstructure of the PZT65/PZT30 superlattice. a Annular-dark field scanning transmission electron microscopy (STEM) image of the superlattice/SrRuO3 interface and b inverse FFT (Fast Fourier Transform) of the image that was calculated using the 100 and \(\overline{1}00\) components (surrounded by dotted circles) in the FFT pattern as shown in the inset. c Dark-field TEM image and d a selected-area diffraction pattern acquired from the superlattice. The diffraction pattern was acquired with a zone of axis of [010] for the perovskite-type unit cell in both PZT65 and PZT30 layers.

Full size image

Atomic-scale STEM observation

Before moving to atomic-scale STEM analysis of the superlattice, accuracy in lattice parameters measured by the present method was examined using Si substrate as a reference. From two atomic-scale annular-dark-field STEM images, lattice parameters, a100 (a along [100]), a001 (a along [001]), and cell angle α, were calculated [Fig. S1Footnote 1].

For the first image, a100 = 545.1 ± 6.7 pm, a001 = 545.1 ± 7.1 pm, and α = 89.96° ± 0.89° on average of 1225, 1226, and 1186 unit cells, respectively, and a100 = 545.1 ± 5.2 pm, a001 = 545.2 ± 5.4 pm, and α = 90.03° ± 0.77° on average of 1280, 1280, and 1240 unit cells, respectively, for the second image. Differences of the average a100 and a001 measured from the STEM from those measured by XRD (Fig. S1 (i)) were 2.0 pm (0.37%), 2.1 pm (0.39%), respectively. Given that the XRD lattice parameter was a true value, errors in the STEM lattice parameters were less than 0.4%. Also, as Si is a cubic crystal, α should be 90°. Therefore, error of the average α measured from the STEM was as small as 0.1°.

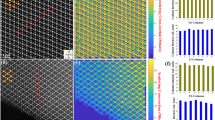
Figure 3a displays a typical atomic-scale annular-dark-field STEM image taken from the superlattice. The brightest contrast represents Pb–ion columns, while the next brightest corresponds to Zr/Ti ion columns. In Fig. 3b, the map of Pb ionic displacements in individual unit cells is derived from the image. For clarity, the displacement vectors are shown in color for magnitudes greater than 10 pm and in gray those smaller than 10 pm. Note that ionic displacement along the Y direction could not be considered in the present study, as the STEM image was projected along the Y direction. Consequently, a gray arrow signifies either a small displacement magnitude or a large magnitude close to the + Y or − Y direction. Figure 3b depicts areas of colored arrows interspersed among gray-arrow regions. Furthermore, these colored arrows exhibit a variety of colors and directions. These findings suggest the coexistence of nano-scale polar and nonpolar regions or the presence of nano-scale polar regions oriented in different polar directions. In either scenario, it is evident that long-range polar order was disrupted and confined within a nanometer scale. It is worth noting the observation of a ferroelectric hysteresis loop for the superlattice (Fig. S2 (see foot note 1)) [30], supporting the presence of polar order. Further discussion on the relation between the disruption of long-range polar order and the ferroelectric P − E loop can be found in the Supplementary Information (see foot note 1). Additionally, data on dielectric and piezoelectric properties measured from the superlattice are also provided in the Supplementary Information (see foot note 1) [30]. Although defining the sizes of nano-scale polar regions was challenging due to their irregular shapes, it was apparent that long-range polar order was disrupted. In Fig. 3b, the majority of colored arrows point upward, whereas another dataset (Fig. 3c, d) demonstrates a majority of the colored arrows directed leftward. The narrowness of the regions studied via STEM imaging precludes discussion about the preferential polar-order direction across the entire film.

Figure 3
figure 3

Pb ionic displacements in the PZT65/PZT30 superlattice. a Atomic-scale annular-dark field scanning transmission electron microscopy image of the superlattice. b Map of the Pb ionic displacements relative to the center of Zr/Ti sublattice. The arrows tails are set at Pb sites, their color and direction indicate the displacement direction, and their length shows the displacement magnitude. The arrow length corresponds to a 30-pm magnitude shown at the top left. c Another atomic-scale annular-dark field scanning transmission electron microscopy image measured from a different region and d Pb ionic displacement calculated from the image in c. Dotted lines in b and d show the locations of interfaces between PZT65 and PZT30 layers, which was deduced from the out-of-plane lattice parameter map as will be later shown in Fig. 4b.

Full size image

Next, lattice parameter distributions were examined. Figure 4 a–c shows maps of in-plane lattice parameter (ax), out-of-plane lattice parameter (az), and cell angle (β) calculated from the STEM image in Fig. 3a. Vertical stripe was observed in the az map corresponded to alternating PZT30 and PZT65 layers as confirmed in Fig. 1f, g. As ionic radius of Zr4+ is larger than that of Ti4+, regions of larger and smaller az corresponded to PZT65 and PZT30, respectively. To compare average lattice parameters, ax, az, and β in the PZT65 and PZT30 layers, corresponding regions were selected as shown in Fig. 4d–i. In the PZT65, ax = 402.3 ± 6.8 pm on average of 795 unit cells, az = 405.8 ± 6.1 pm on average of 810 unit cells, and β = 90.07° ± 1.38° on average of 795 unit cells, respectively (Fig. 4d–f). While, in the PZT30, ax = 402.0 ± 8.0 pm on average of 660 unit cells, az = 396.3 ± 7.0 pm on average of 671 unit cells, and β = 90.09° ± 1.64° on average of 656 unit cells, respectively (Fig. 4g–i). Difference of the average ax and az between PZT65 and PZT30 was 0.3 pm (0.08%) and 9.5 pm (2.3%), respectively. As the difference in ax (0.08%) was smaller than the magnitude of an expected error (0.4%), it can be said that ax was similar in the PZT65 and the PZT30. Whereas, the difference in az (2.3%) was significantly larger than the magnitude of an expected error (0.4%), it can be said that ax was different in the PZT65 and the PZT30. The similar in-plane lattice parameters (ax) were due to mutual lattice constraint, and the different out-of-plane lattice parameters (az) were due to the relaxation of crystal lattice along the Z-axis direction. In addition, difference of average β in between the PZT65 and PZT30 was 0.02°, and they were within ± 0.1° from 90°. This suggests that the PZT65 and PZT30 layers connected without significant rotation nor tilt of crystal lattice, and shape of unit cell was rectangular.

Figure 4
figure 4

Lattice parameter distributions in the PZT65/PZT30 superlattice. Maps of lattice parameters a ax, b az, and c β for the entire image in Fig. 3a. d ax, e az, and f β maps in the PZT65 layers, and g ax, h az, and i β maps in the PZT30 layers, respectively.

Full size image

Structure of unit cell

Unit cell structures of PZT65 and PZT30 are summarized and are compared with stable structures in bulk crystalline forms [12, 14] in Fig. 5. Average ax, az, and β values in the superlattice were calculated from the high-magnification STEM image (Fig. S4) (see foot note 1) by the same way as in Fig. 4. The average values were: ax = 403.5 pm, az = 398.1 pm, and β = 89.9° from 206 unit cells in PZT30, and ax = 404.0 pm, az = 410.6 pm, and β = 90.1° from 124 unit cells in PZT65, respectively. It was assumed that ax = ay because the in-plane x and y directions were equivalent. Shape of PZT65 unit cell in the superlattice was rectangular, which was unusual because it is rhombohedral in the bulk form. Shape of unit cell in the PZT30 superlattice a (= b) was also rectangular, which is the same case as in the bulk PZT30. An important difference between the superlattice and the bulk is that c axis was shorter than a (b) axis in the superlattice, whereas c axis was longer in the bulk. In addition, it was unusual that Pb ionic displacement directions was not fixed to specific directions in the superlattice, in contrast to that the displacement direction is fixed to \(\left\langle {{001}} \right\rangle\) in bulk PZT30 and \(\left\langle {{111}} \right\rangle\) in bulk PZT65.

Figure 5
figure 5

Structures of unit cells in the PZT65 and PZT30 layers. Boxes and bold arrows indicate unit cells and polarization directions, respectively.

Full size image

Density functional theory calculations

First-principles calculations were performed to obtain an insight on preferred Pb ionic displacement directions in unit cells. Although average composition is Pb(Zr0.30Ti0.70)O3 (PZT30) or Pb(Zr0.65Ti0.35)O3 (PZT65) in the superlattice, individual perovskite-type single unit cells should be classified into either PbZrO3 (PZ) or PbTiO3 (PT) single unit cells. Therefore, the energy landscapes for the Pb displacement vectors were calculated for PT or PZ single unit cells. Based on the results in Fig. S4, the lattice parameters a = b = 0.4038 nm, c = 0.3981 nm, α = β = γ = 90.0° were used for the PT and PZ unit cells in PZT30, while a = b = 0.4038 nm, c = 0.4106 nm, α = β = γ = 90.0° were used for PT and PZ unit cells in PZT65. Because shape of the unit cells was rectangular, the energy landscapes were mirror symmetric with respect to the (001), (100), (010), (110), and (\(1\overline{1}0\)) planes. Therefore, the landscapes were calculated only for the irreducible portions of the entire sphere and then duplicated via mirror symmetries on the reducible portions.

In three-dimensional energy landscapes Fig. 6a–d, the unit cells centers were set at the origins and Pb positions (i.e., displacement-vector end points) were indicated by colored circles, where the color indicates the relative energy Erel. The Erel value was defined as the energy difference for a unit cell having Pb at a certain position relative to that for Pb at the center. The energy landscapes differed (Fig. 7a–d), indicating that PZ and PT in PZT30 and PZT65 had different dependences on the preferred displacement vectors. Displacement magnitudes of 20 and 24 pm were stable for PZT30 and PZT65, respectively.

Figure 6
figure 6

Energy landscape for PT and PZ unit cells in the PZT30 and PZT65 superlattice. Three-dimensional map of relative energy versus displacement vector for a PT in PZT30, b PZ in PZT30, c PT in PZT65, and d PZ in PZT65.

Full size image
Figure 7
figure 7

Stereographic projection of the energy landscape for PT and PZ unit cells in the PZT30 and PZT65 superlattice. Projection for a PT in PZT30, b PZ in PZT30, c PT in PZT65, and d PZ in PZT65. e Corresponding figure showing displacement vectors. The same data with an energy scale bar in a wider window is shown in Fig. S5 (see foot note 1).

Full size image

A stereographic projection at the 20 pm (PZT30) or 24 pm (PZT65) displacement is shown in (Fig. 7a–d). For both PT and PZ in PZT30, displacement along the \(\left\langle {{001}} \right\rangle\) (c) direction was not stable (Fig. 7a, b), which was attributed to a shorter c-axis in PZT30 unit cells. For PT in PZT30 (Fig. 7a), the energy was low in the regions covering [111]–[110]–[\(11\overline{1}\)] and [\(\overline{1}11\)]–[\(\overline{1}10\)]–[\(\overline{1}1\overline{1}\)]. Displacement along \(\left\langle {{111}} \right\rangle\)  was the most stable, with an energy difference as small as 2 meV relative to the \(\left\langle {{110}} \right\rangle\) case. This indicated that various displacement directions near \(\left\langle {{111}} \right\rangle\) and \(\left\langle {{110}} \right\rangle\) could coexist. For PZ in PZT30 (Fig. 7b), displacement along \(\left\langle {{111}} \right\rangle\) became more stable. This is a similar behavior to Pb ion in rhombohedral bulk PZT (0.53 < x < 0.95). For PT in PZT65 (Fig. 7c), displacement directions close to the c-axis (\(\left\langle {{001}} \right\rangle\)) were stable, which is consistent with bulk PZT for x < 0.53. This is reasonable because the rectangular unit-cell shape as well as the longer c axis in PZT65 in the superlattice are similar features to those for bulk PZT (x < 0.53). Finally, displacement directions close to \(\left\langle {{111}} \right\rangle\) were stable for PZ in PZT65 (Fig. 6d), similar to that for PZ in PZT30. Here, we summarize the results and briefly discuss on preferred Pb ionic displacement directions in unit cells. For PZ, \(\left\langle {{111}} \right\rangle\) direction was commonly preferred in PZT65 and PZT30 in the superlattice, irrespective of the different shapes of unit cell. Because Zr4+ ion is sufficiently large and the Zr ion is strongly bound with six neighboring O ions, forming ZrO6 octahedron, Pb tends to displace away from Zr–O bonds that are parallel to \(\left\langle {{100}} \right\rangle\). Thus, ionic size has a stronger effect in PZ. On the other hand, in PT, preferred displacement directions were different for PZT65 and PZT30. Because Ti4+ ion is smaller and some Ti–O bonds can be weakened, leading to a Ti–ion offset from the center of TiO6 octahedron. Pb ionic displacement is parallel to the Ti-offset direction that is also parallel to the long axis [38]. Thus, unit cell shape has a stronger effect in PT.

Discussion

Based on the understanding of preferred displacement directions in unit cells as discussed above, Pb ionic displacements in the superlattice is discussed. In the PZT30 layer, 30 and 70% of unit cells are PZ and PT, respectively. Pb ions in PZ tend to displace along \(\left\langle {{111}} \right\rangle\) and those in PT tend to displace along \(\left\langle {{111}} \right\rangle\) and \(\left\langle {{110}} \right\rangle\). Because of the competition between different preferred directions in PZ and PT, long-range polar order was disrupted. In the PZT65 layer, 65 and 35% of unit cells are PZ and PT, respectively. Long-range polar order should also be disrupted in the PZT65 layer, because Pb ions in PZ tend to displace along \(\left\langle {{111}} \right\rangle\) while those in PT tend to displace along \(\left\langle {{001}} \right\rangle\). Moreover, competition of the preferred displacement directions also takes place in the interface between the neighboring PZT30 and PZT65 layers, which should play a role to disrupt long-range polar order.

One may speculate that the disruption of long-range polar order observed in our study is attributed to the so-called size effect, given the small thickness of individual layers (4 nm). For instance, in the well-studied perovskite-type ferroelectric material BaTiO3, a transition from a tetragonal to a cubic phase occurs, leading to the disappearance of ferroelectricity when the particle size is smaller than a critical value [39]. If the same scenario had held for the present PZT superlattice, and if ferroelectricity had vanished due to the size effect, ax should have been identical to az, and the magnitudes of Pb-ion displacements should have been zero. However, our observations in Fig. 4a, b suggest otherwise, indicating that unit cell behaviors in the present superlattice cannot be solely explained by the size effect.

This conclusion is further supported by comparisons with references [28, 29]. In Ref. [28], ferroelectric domains were observed in a superlattice with an individual layer thickness of 20 nm, whereas they were not observed in a superlattice with a thinner individual layer of 5 nm. Conversely, in Ref. [28], a–c domains typical of the tetragonal phase of PZT were observed in a (3 nm PZT60/5 nm PZT40) superlattice, while ferroelectric domains were not observed in a superlattice with a thicker 8 nm layer thickness. These contrasting findings indicate that the development and disruption of ferroelectric polar order are influenced by multiple factors beyond individual layer thickness alone.

Long-range polar order might be disrupted in the PZT65/PZT35 (111) superlattice of 5-nm-thick individual layers [29] and the PZT60/PZT40 superlattice of 8-nm-thick individual layers [28]. In Ref. [28], the absence of ferroelectric domains in the superlattice of 8-nm-thick individual layers was confirmed in piezoelectric force microscopy (PFM) image as well as polarization-voltage measurement, which is consistent with that the PZT65/PZT30 superlattice examined in the present study exhibited the ferroelectricity [30]. These results support the presence of ferroelectric polar order, although their development to a long range is disrupted. It is considered that nano-scale polar order can be aligned by applying a sufficiently large external electric field. Interestingly, bright, and dark nano-scale contrast was observed outside the scanned box in the PFM image in the superlattice of 8-nm-thick individual layers [28]. It is speculated that the bright and dark contrast may correspond to nano-scale polar order.

Conclusion

In Summary, precise ionic displacements and accurate lattice parameters were measured using distortion-corrected atomic-resolution STEM, and first-principles calculations were conducted for composition-modulated PZT65/PZT30 superlattice in the present study. The ionic-displacement measurement clarified that long-range polar order was disrupted and nano-scale polar order was formed. The lattice-parameter measurements revealed that in-plane lattice parameters were similar in the PZT65 and PZT30 layers due to mutual lattice constraint, while out-of-plane parameters were different by lattice relaxation. It was also found that shape of unit cell was unusual in the superlattice. Shape of unit cell was rectangular in the PZT65 layer, which is different from PZT65 bulk. Besides, c axis was shorter than a and b axes in the PZT30 layer, which is in contrast to longer c axis for PZT30 bulk. By taking account of these unusual unit-cell shapes, first-principles calculations revealed that directions of preferred Pb ionic displacements were different in PZ and PT in the PZT65 and PZT30 layers. Competition of the different preferred directions should be a reason for the disruption of long-range polar order.

Supplementary information

Supplementary information for lattice parameter measurements for the Si substrate, P − E hysteresis loop, lattice parameter measurements used for first-principles calculations, and the energy landscape obtained by the first-principles calculation in a wider energy scale can be viewed separately.