Introduction

Lath martensitic steels are used in a wide range of industrial applications including transportation because of their high strength that results from the mutual interaction of dislocations, carbon in solid solution, and grain refinement [1, 2]. Such steels are attracting increasing interest in the automotive industry where martensitic steels are being used as reinforcements for improved crash behavior. They are also being considered for other applications such as pipelines, where there is a need to balance the strength and toughness.

Lath martensite (α′) is known to hold an orientation relationship close to Kurdjumov–Sachs (K–S OR, {111}γ//{110}α′ and < 101 > γ// < 111 > α′) with the parent austenite (γ), resulting in 24 distinct martensite orientations/variants [3, 4]. According to the parallel relationship between the close-packed plane of the parent austenite and martensite, the variants can be categorised into four groups of six, each having a similar habit plane. Therefore, a hierarchical structure appears within a given parent austenite grain during the martensitic transformation, consisting of packets, blocks, and laths. This ultimately leads to an abundance of internal boundaries within the microstructure (i.e., grain refinement) [5,6,7,8], which has a significant influence on the lath martensite properties (e.g., strength and toughness) [9, 10]. However, the extent of the property improvement strongly depends on the boundary network characteristics, namely the population of the boundary of interest and its connectivity.

The nature of the boundary network developed through the martensitic shear transformation considerably differs from that developed through diffusional transformation (i.e., ferrite) [4, 11, 12]. It is largely governed by the crystallography constraints related to the martensitic transformation rather than energy minimisation observed in microstructures developed through the conventional nucleation and growth process. There are well-established approaches to change the network of grain boundary in polycrystalline metals, though these are largely restricted to iterative recrystallisation/recovery processes [13, 14]. However, these approaches cannot be utilised in materials such as steel where the high-temperature austenite structure is not maintained at room temperature due to its transformation upon cooling. Therefore, it is essential to implement new routes to engineer the boundary network developed during the phase transformation.

During the martensitic transformation, all 24 variants are formed with an approximately equal probability within given austenite, leading to a weak overall transformation texture [15]. However, a local variant pairing, a combination of distinct variants having a similar habit plane, appears preferentially during the martensitic transformation to partially accommodate the strain related to the shear transformation [15,16,17,18]. This mostly results in the promotion of specific intervariant boundary/ies within the microstructure (e.g., 60°/[110]) [4, 15, 19]. Therefore, the martensite intervariant boundary network can be controlled by altering the arrangement of variants (i.e., known as variant selection) within a given parent austenite grain during the transformation.

Variant selection is affected by the characteristics of the parent phase (i.e., grain size [20, 21], composition [22, 23], overall texture [24], and substructure developed by deformation [15, 24,25,26,27]), which significantly alters the characteristics of the daughter phase in terms of size, preferred variant nucleation (i.e., on specific parent phase active slip system/s) and ultimately variant groupings to accommodate the strain related to the shear transformation. Deformation in the austenite regime, in the absence of recrystallisation, is a common thermomechanical processing (TMP) route employed to refine the transformed microstructure. This also promotes the formation of specific variant/s (i.e., variant selection) among the 24 variants upon transformation [15, 19]. This, in turn, results in the development of a strong transformation texture [26, 28, 29], which is believed to be the main reason for the enhancement in strength without deteriorating the toughness. In fact, the mechanical properties of steel are strongly related to the overall texture developed through the phase transformation. The presence of rotated cube in the transformed microstructure deteriorates the toughness, as it promotes the cleavage fracture. The austenite hot deformation in the absence of recrystallisation significantly decreases the development of the rotated Cube component in the transformed microstructure and subsequently leads to the development of a strong transformation texture consisting of Copper {112} < 111 > , Brass {110} < 112 > , S {123} < 634 > and Goss {110} < 001 > . This ultimately increases the strength of the material without scarifying the toughness [28, 29]. It is important to emphasise, however, that the change in the variant arrangement in the microstructure is also expected to lead to distinct variants intersection/s, potentially resulting in a different intervariant boundary network. However, there is a lack of understanding of how the variant selection during martensitic transformation in steels changes the network of intervariant boundary (i.e., the relative areas of different types of boundaries and their connectivity).

The aim of the current study was to explore the influence of different thermomechanical processing conditions applied to the high temperature parent austenite phase on the intervariant boundary network in the transformed lath martensite of a low carbon, high strength steel. Here, the steel was subjected to deformation in the non-recrystallisation regime at different strain levels followed by water-quenching to produce a fully martensitic microstructure. The intervariant boundary network of martensite was analysed at different TMP conditions using a stereological interpretation of conventional electron back-scatter diffraction (EBSD) maps to measure the relative areas of boundaries, along with homology metrics to measure the connectivity of certain groups of boundaries within the martensitic microstructure. The outcome of this work will be a framework for the grain boundary engineering of martensitic microstructures to improve properties such as toughness.

Experimental procedure

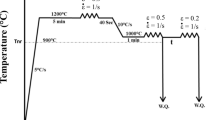
The as-received steel was in the form of a slab with a thickness of 40 mm, having a composition of 0.043 C, 1.68 Mn, 0.2 Si, 0.017 Ti, 0.021 Nb, 0.002 B (in wt%). The as-received slab was subjected to a multi-pass hot rolling process in the temperature range of 1200–1000 °C to obtain a final thickness of 12 mm thick. The exact deformation temperature in this range is not critical at this stage, as long as it occurs when the steel is single-phase austenite. Plane strain compression samples with a dimension of 60 × 30 × 10 mm were machined from the hot-rolled plate where the length was parallel to the rolling direction. Afterward, the samples were subjected to different thermomechanical procedures using a servo-hydraulic thermomechanical treatment simulator apparatus (Servotest, 500 kN). This is an automated testing machine having an induction furnace, a muffle furnace, and a computer data acquisition system. A thermocouple was embedded in the specimen to monitor the temperature throughout the test. Samples were coated with a boron nitride lubricant to minimize the oxidation/decarburation of the surface and the friction between the two sides of sample surface in contact with the compression anvils during deformation. The samples were reheated to 1200 °C at 5 °C/s heating rate and held for 300 s to obtain a fully austenitic microstructure and to dissolve all alloying elements. They were then deformed to a strain of 0.3 at a strain rate of 0.1 s−1 followed by holding for 40 s at 1200 °C to achieve a fully recrystallized austenite microstructure with an average grain size of 92 µm. One sample was immediately water-quenched to attain a martensitic microstructure. Other specimens were cooled at 10 °C/s to 875 °C, which is well below the non-recrystallization temperature (i.e., Tnr =  ~ 900 °C [30], a temperature below which the recrystallization is retarded due to the precipitation) and held for 60 s to homogenise the temperature gradient throughout the specimens. The samples were then subjected to different strains of 0.2, 0.4, 0.6, 0.8, and 1 at a strain rate of 0.1 s−1 followed by water-quenching (Fig. 1).

Figure 1
figure 1

Schematic representation of different thermomechanical routes. Tnr is non-recrystallization temperature

Full size image

The martensitic microstructures produced through different thermomechanical routes were subjected to tempering treatment at a temperature of 450 °C for 2 h. The tempering treatment led to a reduction in the dislocation density of the martensite through recovery, which enhances the confidence index of the electron backscatter diffraction mapping. The plane strain compression samples were then cut along the plane parallel to the deformation direction using a Dscotom 100/10 cutting machine and then mounted using conductive resin.

EBSD samples were initially prepared by standard mechanical grinding using grinding papers ranging from 240 to 1200 grits. The samples were further mechanically polished by diamond suspensions with sizes of 9, 3, and 1 µm, followed by a colloidal silica slurry. EBSD mapping was undertaken on a field emission gun Quanta 3D FEI scanning electron microscope. The instrument was equipped with a fully automated EBSD device. The voltage and current of the electron beam for all samples were 20 kV and 4 nA, respectively. TSL software was employed for the data acquisition and post-processing steps. Multiple EBSD maps were acquired for each thermomechanically processed sample using a step size of 0.15 μm with a hexagonal grid, covering an area of 43,200 μm2. Here, the lath martensitic crystal structure was considered as body-centred cubic (bcc) due to very low carbon content in the steel (~ 0.04 wt%) [4]. The average confidence index mostly changed between 0.57 and 0.70. The size of prior austenite grain, as well as block and packet sizes of martensitic microstructure at different TMP conditions, was measured using linear intercept technique [31].

Multiple cleaning steps were conducted to extract the boundary line segments using different cleaning functions in the TSL software. The raw data were initially subjected to dilation clean-up to remove any ambiguous data. It is followed by assigning an orientation to a given grain by averaging the orientations of the constituent pixels using the single orientation function. Then, the boundary reconstruction function was employed to smooth ragged/uneven grain boundaries using a deviation limit of 2× the step size (2 × 0.15 = 0.30 µm) and collect all-grain boundary line segments. The extracted boundary data were employed to compute the 5-parameter grain boundary character distribution through stereological interpretation of the data (known as five-parameter analysis [32,33,34]) and measure the intervariant boundary network connectivity of the martensitic microstructure for different TMP conditions through the homology metrics approach described elsewhere [4].

To reconstruct the prior austenite grain orientations from the EBSD data, an automated computer program called ARPGE was utilized. This program has been written in Python code, in which the parent austenite orientations are calculated using one of the known orientation relationships from the daughter phase (i.e., martensite) orientations [35]. The EBSD maps were then displayed by TSL software to reveal the prior austenite grain boundaries. In the current study, the prior austenite grain structure reconstruction was performed through quadruplets method considering Kurdjumov–Sachs orientation relationship using APRGE software version 2020. The initial tolerance angle value was 3° and 6° for nucleation and growth steps, respectively. These values were increased by 2° at each cycle of the reconstruction. The same values were set during the reconstruction process for each austenite state. When the tolerance angle for nucleation or growth exceeds a limit (i.e., 15° and 20°, respectively), the reconstruction was stopped.

Results

In the current thermomechanical procedure, the deformation was applied at 2 temperatures of 1200 °C and 875 °C. The former promoted static recrystallization during post-deformation annealing, forming equiaxed austenite grains. The latter resulted in the formation of pancaked/elongated austenite grains, as the deformation was applied below the Tnr temperature, where the recrystallization process was retarded through the solute drag and/or precipitation pinning effect [36]. The flow curves revealed very similar characteristics, displaying a power-law work-hardening behavior at a given deformation temperature (Fig. 2). The flow curves at 875 °C also exhibited a steady-state plateau behavior beyond a peak strain of 0.4 (corresponding to 0.7 strain in Fig. 2), suggesting the occurrence of dynamic recovery as the dominant restoration mechanism.

Figure 2
figure 2

The true stress–true strain curves obtained from the samples deformed at two temperature regimes of 1200 °C (Route A) and 875 °C (Route B)

Full size image

Effect of austenite state on the transformation texture

The martensitic microstructure transformed from the recrystallized austenite state (strain-free condition, i.e., Route A) revealed a weak overall texture, with a strength of 2.28 multiples of a random distribution (MRD) (Fig. 3a). The application of deformation in austenite regime below Tnr led to stronger texture in the martensite. At a strain of 0.2, the texture strength was 2.67 MRD, and consisting of rotated Cube rotated Copper, and a relatively weak component along the γ fiber (Fig. 3b). In general, the γ fiber is positioned along {111} < 110 > through {111} < 112 > orientation, having Euler angles of φ1 = 0–90°, ϕ = 54.7° and φ2 = 45° [37, 38]. Further strain below Tnr increased the texture intensity progressively, until reaching a maximum of 5.17 MRD at a strain of 1 (Fig. 3f). The rotated Cube texture strength gradually decreased with an increase in the strain, changing from ~ 2 MRD at a strain 0.2 to ~ 1 MRD at a strain of 0.8 and above. The Goss and rotated Goss components nearly disappeared above a strain of 0.2 (Fig. 3c–f). In summary, the overall texture characteristics were progressively altered towards the formation of a well-defined transformation texture formed from the non-recrystallized austenite, which mostly consisted of the rotated Copper, rotated Brass, and a relatively weak rotated Cube [28, 29].

Figure 3
figure 3

ODFs obtained from the martensitic microstructures transformed from the austenite subjected to deformation below Tnr at different strains a strain-free condition b 0.2, c 0.4, d 0.6, e 0.8 and f 1. ♦, , , ▼, and represent rotated Cube, Goss and rotated Goss, rotated Copper, rotated S and rotated Brass components, respectively

Full size image

The effect of phase transformation on the intervariant boundary plane character distribution

The microstructure of the as-quenched condition had a lath martensitic microstructure, containing a high dislocation density. The application of deformation below the Tnr (~ 900 °C) led to austenite parent grains elongated (pancaked) perpendicular to the plane strain compression direction, which can be clearly observed from the prior austenite grain shapes reconstructed using ARPGE software [35] (Fig. 4). This ultimately transformed to lath martensite upon quenching. Due to very low carbon in the current steel (i.e., 0.04%wt C), it is assumed in the present study that the austenite to martensite transformation follows the K–S OR [4, 15, 19]. Therefore, up to 24 variants can be produced from each individual austenite grain based on cubic system symmetry (Table 1). In general, the 24 variants are classified into four groups consisting of 6 distinct variants, associated with a similar habit plane. The intersection of these 24 variants results in 23 intervariant boundaries, which can be reduced to 16 distinct intervariant boundaries, due to crystal symmetry (Table 1). Therefore, a given parent austenite is subdivided into laths, blocks and packets during the martensitic transformation, which can be distinguished through these distinctive lattice misorientations. Here, a block is defined using intervariant boundaries, which formed through the intersection of two different variants belonging to a specific family having the identical austenite habit plane (e.g., V1–Vi=2–6 in Table 1). A packet is determined by the lattice misorientations that result from the impingement of variants that belonged to two different families (i.e., having distinct habit planes, Table 1). At the strain-free condition (i.e., Route A), the martensite constituents (i.e., lath, block, and packet) were relatively coarse (Fig. 4a). However, the deformation of austenite prior to the martensitic transformation led to the partitioning of prior austenite grains, subsequently refining the martensite constituents (Figs. 4f, 5).

Figure 4
figure 4

Band contrast images and IPF maps of the martensitic microstructures transformed from the austenite subjected to deformation below Tnr at different strains a strain-free condition b 0.2, c 0.4, d 0.6, e 0.8 and f 1 and their corresponding prior austenite microstructure (IPF image) constructed using ARPGE software [35]. The black and red lines in IPF images represent general high angle boundaries and annealing twin boundaries, respectively. PSC represents plane strain compression. The triangle inset in (a) is the colour codes referring to normal direction. The packet and boundary features are demonstrated in IPF map in (a)

Full size image
Table 1 Possible 24 variants generated through phase transformation having the KS orientation relationship
Full size table
Figure 5
figure 5

the effect of strain in austenite below Tnr temperature on the size of packet and block of martensite transformed upon water-quenching

Full size image

The misorientation angle distribution of the lath martensite microstructure for the strain-free condition (i.e., Route A) exhibited three weak peaks in the range of 5–22° and two main peaks in the range of 45–60°, which are consistent with those expected from the K–S orientation relationship. Since the misorientation angles between 23–46° do not represent the misorientations resulting from the K–S OR, they can be considered to be related to the prior austenite grain boundaries (Fig. 6 and Table 1). With an increase in the deformation below Tnr, the misorientation angle distribution of the martensitic microstructure changed significantly. As the deformation increased from 0 to 0.6, there was a slight decrease in the population of misorientation angles in the range of 5–22°. When deformed beyond 0.6, the length fraction of this peak increased and the maxima shifted from ~ 13° to ~ 8°. Interestingly, the length fraction of boundaries with misorientation angles between 23 and 46°, which do not represent any misorientations resulting from the K–S OR (i.e., prior austenite grain boundaries), progressively increased with strain at the expense of the population of boundaries in the 47–60° range (Fig. 6b–f). The distribution in this higher angle range merged to a single maximum at 58° for strains greater than 0.2, and the height of the maximum decreased as the strain increased.

Figure 6
figure 6

The effect of strain in austenite below Tnr temperature on misorientation angle distribution of martensite microstructure transformed upon water-quenching. a ɛ = 0, b ɛ = 0.2, c ɛ = 0.4, d ɛ = 0.6, e ɛ = 0.8 and f ɛ = 1

Full size image

In the strain-free condition (Route A), the highest intervariant length fraction belonged to 60°/[011] with 52.5% followed by 10.5°/[\(0\overline{1 }\overline{1 }\)] and 57.2°/[\(\overline{6 }\overline{2 }\)5] having ~ 10% (Fig. 7a). Interestingly, the first two highest populated intervariant boundaries belonged to the laths within a packet having the same close-packed plane (i.e., V1–V2 and V1–V4, Table 1). Deformation in austenite altered the intervariant boundary fractions, though the trend depended on the intervariant boundary type. The fraction of 60°/[011] intervariant boundaries changed the most, reducing from 52.5% in the strain-free condition (Route A) to 29.5% at a strain of 1 (Fig. 7a). On the other hand, the fraction of some intervariant boundaries slightly increased with the strain (e.g., 10.5°/[\(11\overline{1 }\)] and 60°/[\(11\overline{1 }\)]). A similar trend was also observed for the length of different boundary types per unit area (i.e., µm/µm2) at various strains. It should be noted that the length per unit area of non-KS boundaries progressively increased with an increase in strain (from 0.27 µm/µm2 for the strain-free condition to 0.52 µm/µm2 at the strain of 1) (Fig. 7b).

Figure 7
figure 7

The fraction of total population a and length per area b of interfaces belonging to The K–S OR, comparing intervariant interfaces between V1 and Vi (i = 2–24), for the martensite microstructures formed at different thermomechanical conditions. The data were obtained through the applications available in TSL software. The mean values and standard deviations were determined from the values measured from at least 5 different orientation maps

Full size image

The intervariant boundary plane distribution, irrespective of misorientation, displayed a significant anisotropy with a maxima at (101) having ~ 1.9 MRD for the strain-free condition, meaning that its population is ~ 90% higher than the value expected in a random distribution. The distribution had a minimum at the (001) plane with ~ 0.2 MRD, whereas the intensity of the (111) plane was ~ 0.8 MRD (Fig. 8a). The intervariant boundary plane distribution revealed a similar trend for all deformation conditions, revealing maxima and minima at the positions of (101) and (100), respectively. However, the intensity of the maxima at (101) progressively decreased with an increase in the strain below Tnr and was only ~ 1.1 MRD at the strain of 1 (Fig. 8b–f).

Figure 8
figure 8

The distribution of intervariant boundary planes character of lath martensite at thermomechanical conditions. MRD represents multiples of a random distribution

Full size image

At the 10.5°/[011] misorientation, the intervariant boundary plane character distribution showed multiple maxima around different {110} planes with ~ 6.5 MRD (Fig. 9). The deformation decreased the intensity of these maxima to ~ 4 MRD at a strain of 0.6. At a strain of 0.8, the maximum at the (011) orientation increased to ~ 6 MRD. At a strain of 1, the maxima at (011) were replaced by peaks near the (010) and (001) positions (Fig. 9). At the misorientation angle of 49.5°, a single peak was observed at the {110}||{110} twist position for all thermomechanical processing conditions. Deformation of the austenite did not alter the overall distribution, though it significantly reduced the intensity of the peak from ~ 24 MRD at the strain-free condition to ~ 12 MRD at a strain of 1. The twist boundary population was much larger at a misorientation of 60° (~ 250 MRD in the strain-free condition) and decreased with increased strain until it was ~ 90 MRD at a strain of 1.

Figure 9
figure 9

The distribution of plane normals for boundaries having misorientation angles about [110] axis for martensitic microstructures formed at different thermomechanical conditions

Full size image

The intervariant boundary plane character distribution at 10.5°/[\(11\overline{1 }\)] misorientation displayed multiple distinct peaks, mainly centerd on the (\(\overline{1 }01\)), (\(0\overline{1 }1\)), (\(\overline{1 }\overline{1 }0\)) planes having 10 MRD in the strain-free condition (ɛ = 0) (Fig. 10). The strain did not change the overall distribution, although it affected the peak intensities. The intensity gradually decreased to ~ 8 MRD at a strain of 0.6. Further deformation led to a progressive increase in the peak intensity to ~ 10 MRD and spreading of the peaks towards the {001} positions at the strain of 1. For the 49.5°/[111] misorientation, the majority of interfaces appeared along the zone axis of tilt boundaries (i.e., the great circle perpendicular to the [\(\overline{1 }\overline{1 }1\)] axis) with an intensity of ~ 5.5 MRD in the strain-free condition. The character of the intervariant boundary plane distribution did not change with deformation, though its intensity gradually increased up to a strain of 0.6, beyond which it continuously decreased with further deformation. At 60°/[\(11\overline{1 }\)] misorientation, the distribution maintained its tilt character with ~ 15 MRD at the strain-free condition and progressively increased with the strain, reaching ~ 24 MRD at the strain of 1 (Fig. 10).

Figure 10
figure 10

The distribution of plane normals for boundaries having misorientation angles about [111] axis for martensitic microstructures formed at different thermomechanical conditions

Full size image

The high index misorientations largely revealed multiple peaks spreading around the {110} positions with a mixed character for the strain-free condition. The peaks in these distributions were mostly lower than 7 MRD except for the 57.2°/[\(\overline{3 }\)56] misorientation, which had a maximum of ~ 32 MRD in the strain-free condition. The deformation below Tnr did not alter the distribution characteristics, although it affected the peak intensity. However, the change in the peak intensity did not have a specific trend with deformation for these intervariant boundaries (Fig. 11).

Figure 11
figure 11

The distribution of boundary plane normals with different lattice misorientations associated with the K–S OR for martensitic microstructure transformed at different thermomechanical conditions

Full size image

Discussion

Effect of strain on the intervariant boundary network

The application of deformation in the austenite single-phase regime below the Tnr temperature appears to significantly alter the intervariant boundary network characteristics of lath martensite transformed upon water-quenching. For the strain-free condition, the misorientation angle distribution reveals multiple peaks within a range of 5–22° and 45–60°, with a relatively smaller and nearly constant distribution at other misorientation angles. This is consistent with the misorientations theoretically anticipated from the K–S OR (Table 1). The non-K–S misorientations in the angular range of 23–46° most likely rising from the intersection of variants on either side of prior austenite grain boundaries. Note that with increasing strain, the fraction of these non-K–S boundaries increased (Fig. 6).

The grain boundary network can be influenced by a number of parameters including chemical composition [22, 23, 39, 40], initial grain size [41], crystallographic texture [42], transformation mechanism [43], and thermomechanical processes [14, 42, 44,45,46]. The chemical composition and phase transformation mechanism are ruled out here, as the thermomechanically treated samples have identical composition and all undergo martensitic transformation. In the absence of recrystallization, the deformation does not change the prior austenite grain size, though it alters the austenite grain characteristics, i.e., roughening the austenite grain boundaries, inducing intragranular defects (dislocation substructure) and pancaking the austenite grains (Fig. 4). The latter largely has a geometric effect, limiting the growth of martensite laths, which is expected to refine the microstructure, and increasing grain boundary surface area, promoting martensite nucleation sites. However, the other microstructural changes in the prior austenite grain ultimately influence the subsequent martensitic phase transformation kinetics (i.e., nucleation and growth) and the final martensite transformation texture.

Deformation of austenite below Tnr results in a strong texture depending upon the level of deformation. In the absence of recrystallization, deformation promotes various texture components in austenite, consisting of Copper, S, Brass, and Goss components. Considering the K–S orientation relationship during the austenite to martensite phase transformation, these texture components produce distinct texture orientations, namely transformed Brass, transformed Copper, and rotated Cube [37, 42, 47,48,49]. The resultant texture depends on the chemical composition (i.e., precipitation), finishing temperature and amount of deformation [42, 47, 50, 51]. Here, the chemical composition and austenite finishing temperature are the same for all TMP conditions (875 °C), but the amount of strain changes from 0 to 1. As shown in the current result, the strength of these components gradually increases with an increase in strain from 2.3 MRD in the strain-free condition to 5.2 MRD at a strain of 1 with multiple peaks along the γ-fiber (< 111 > //normal direction, Fig. 3). In a fully ferritic microstructure, the enhancement of the γ-fiber texture promotes the misorientation angles within the range of 0–60° with an approximately equal probability in the distribution [42]. Therefore, the enhancement of the γ-fibre may partly contribute to the increase in the fraction of boundaries with misorientation angles below 46° at the expense of boundaries having higher misorientation angles.

The deformation of austenite also leads to an increase in the martensite start transformation temperature, Ms, due to the enhancement of nucleation sites through the prior austenite grain boundary serration and/or the intragranular defects. The latter largely appears as elongated bands (microbands) and/or equiaxed cells (subgrains) separated by dislocation sub-boundaries. The presence of dislocation sub-boundaries restricts the martensite growth, which proceeds through shear. This ultimately reduces the martensite finish temperature and expands the Ms–Mf range [52]. The expansion of the temperature range of martensitic transformation due to straining affects the strength of the parent austenite, which eventually influences the martensite lath size (i.e., packet and block) [52, 53], as also observed in the current results (Fig. 5).

The formation of substructure features such as subgrains and microbands during deformation fragments each prior austenite grain into several units, as each substructure feature has its own local orientation. The extent of the orientation deviation depends proportionally on the amount of strain [54,55,56]. Therefore, each individual substructural feature can be considered as a parent austenite, which can theoretically transform to 24 K–S variants upon martensitic transformation. Consequently, it is anticipated that the K–S variants set formed in each equiaxed subgrain would be different from those transformed in neighbouring subgrains. Hence, their impingements at the sub-boundaries do not necessarily yield the lattice misorientations anticipated from the ideal K–S orientation relationship. As a result, this leads to enhancement of non-K–S misorientations, to some extent, promoting the boundaries in the range 23–46° at the expense of boundaries with K–S misorientations (i.e., 10–22° and 46–60°) in the transformed product (i.e., martensite). These changes are progressively enhanced with strain in the austenite, due to further fragmentation of the prior austenite grains and greater deviation in orientation between adjacent subgrains (i.e., higher misorientation angles across sub-boundaries), which is aligned with the current observation (Fig. 6). Furthermore, the orientation relationship of lath martensite may deviate from the K–S when nucleating intragranularly on a dislocation substructure and/or propagating through orientation gradients developed within the austenite grain upon deformation. This leads to the broadening of peaks in the disorientation angle distribution, which enhances with the strain (Fig. 6).

The dislocation substructure introduced in the austenite also influences the arrangement of variants forming in a given prior austenite grain through the martensitic transformation. It has been demonstrated that the dense dislocation walls/sub-boundaries developed upon deformation in austenite promote variant selection that depends on the strain [57, 58]. At a low strain level, the variants with habit plane (011)α′ closely parallel to the primary slip plane in parent austenite (i.e., (111)γ) are formed favorably (i.e., V1 through V6, Table 1) [19]. The interaction of the variants that belong to this family is expected to promote the block boundaries such as 10.5°/[011], 49.5°/[011], 60°/[011] and 60°/[111] (Table 1). This is consistent with the current result as all of these boundaries, except 10.5°/[011], and 60°/[011] increase in their length fraction at a strain of 0.2 (Fig. 7). Further deformation appears to also promote other variants whose (011)α′ plane is nearly parallel to the secondary slip plane (1\(\overline{1 }\)1)γ (i.e., V13 through V18, Table 1) as well as variants related to the primary slip plane. Among these 12 variants, V3, V4, V13 and V14 are reported to form more regularly at high strain. Interestingly, the intersection of these 4 variants promotes the intervariant boundaries of 10.5°/[111], 49.5°/[111], and 60°/[111]. The latter represents the block boundary, where two consecutive variants from the same family intersect (i.e., V3– V4 and V13– V14). The other two intervariant boundaries are formed because of the intersection of two variants having distinct habit planes (e.g., V3– V13). This is well-aligned with the current observation as the population of these intervariant boundaries increases with strain. However, the striking observation here is a progressive reduction in the fraction of the 60°/[011] intervariant boundary with the strain. This suggests that the variant selection resulting from deformation of the austenite restricts the formation of variant pairs that yield the 60°/[110] intervariant boundary (i.e., V1– V3, V3–V5, and so on). Instead, it promotes the formation of other variant pairs that stimulate 60°/[111], 10.5°/[011], and 49.5°/[110] intervariant boundaries.

Intervariant boundary plane distribution

The relative areas of grain boundary planes have an inverse correlation to their energies for polycrystalline materials, undergoing normal grain growth during their evolution (i.e., nucleation and growth) [12, 59]. However, the microstructures described here were developed through the martensitic/shear transformation. Therefore, it is expected that these martensitic microstructures display different boundary plane distribution characteristics compared with polycrystalline materials with the bcc crystal structure produced through the grain growth process (e.g., polygonal ferritic microstructure [42]). For example, the grain boundary plane distribution for 60°/[111] displays a peak at the {110} tilt boundary position for martensitic microstructures formed for all current thermomechanical processing conditions. The current result differs from the distribution in polygonal ferrite, in which the peak appears at the {112} tilt boundary position having the minimum energy [4, 12]. The current observation is related to the martensitic/shear crystallographic constrains, which largely stimulate the {110} planes during phase transformation and do not inevitably have the minimum energy setting. The deformation of parent austenite appears to only change the intensity of the peak/s (boundary population) in the distribution rather than the plane character, as shear is dominant transformation mechanism for all thermomechanical conditions used in these experiments.

Connectivity of intervariant boundary network

The homology metrics approach was utilised to parameterize the topology of grain boundary network using Betti numbers, β0 and β1. The parameter β1 represents the continuous and closed paths of the boundaries, and β0 represents the set of boundaries disconnected from the rest of the network [4, 60, 61]. The ratio of β0 and β1 (i.e., β01) denotes the inverse connectivity of the boundary network within a given microstructure. The inverse connectivity of the intervariant boundary network for lath martensite was initially measured as a function of the misorientation angle for different thermomechanical conditions, after removing boundaries with 23–46° misorientation angles (Fig. 12). The excluded boundary range is associated with the prior austenite grain boundary as they are not expected to form considering the K–S orientation relationship (Table 1). The current result reveals that most interfaces with the K–S OR have {110} planes orientation in the lath martensitic microstructure due to displacive phase transformation constraints (Figs. 8–11) [4]. Therefore, the current intervariant boundary network analysis largely represents the connectivity of {110} boundaries. In general, the intervariant {110} boundary network connectivity decreased as the misorientation angle threshold increased for all deformation conditions. This is not surprising as more boundaries were excluded with the misorientation angle threshold (Fig. 12a). In addition, the application of strain mostly reduced the connectivity of intervariant boundaries compared with the strain-free condition (Fig. 12a), which connected to a decrease in their population (Fig. 7).

Figure 12
figure 12

The inverse connectivity of intervariant boundary network structure as a function of misorientation angle threshold for martensitic microstructure transformed at different thermomechanical conditions: a {110} boundaries, b {110} twist boundaries and c {110} symmetric tilt boundaries

Full size image

The boundaries with the misorientation axes of [111] and [110] largely have the tilt and twist characters, respectively, in the martensitic structure (Figs. 9–10). Therefore, boundaries with a given misorientation axis were selected to measure the network of twist or tilt intervariant boundaries. For the boundaries with the misorientation axis of [110] representing {110} twist boundaries, the deformation of the austenite prior to transformation led to a progressive reduction in the intervariant boundary network connectivity so that it became less connected at the strain of 1 than the strain-free condition (Fig. 12b). By contrast, the connectivity of intervariant boundary network as a function of misorientation threshold gradually increased with strain for the misorientation axis of [111], representing {110} tilt boundaries (Fig. 12c). The changes observed in the grain boundary network for different boundary types closely matched with the change in their populations for different thermomechanical processing conditions (Fig. 7).

It has been shown that the boundary network can be controlled to influence material performance (e.g., toughness). For example, by changing the intervariant boundary network in a very similar bainitic lath microstructure in high strength pipeline steels, the 40 J impact transition temperature was reduced from − 20 to − 100 °C [62]. Similar to the current observation, the intervariant boundaries in bainitic structures largely terminate on {110} crystallographic planes, which are also the preferred slip planes for dislocation glide in bcc materials. It is, therefore, expected that close alignment of intervariant boundary planes with the {110} slip planes makes it possible for dislocation to slip in the direction parallel to the intervariant boundary, while intersecting lath boundaries will restrict slip. The degree of general yielding, therefore, depends on the spacing between the intervariant boundaries that limits the slip length. In other words, the reduction in intervariant boundary spacing (higher boundary network connectivity) impedes general yielding/plasticity at the stress concentration, which favours fracture (reducing the toughness) [62]. This suggests that the enhancement of toughness due to the deformation below Tnr can be, to some extent, explained by decreasing the connectivity of the {110} intervariant boundaries (Fig. 12a) together with the change in overall texture [26, 28, 29]. Interestingly, the {110} intervariant boundaries have different character (twist, tilt and mixed), displaying distinct connectivity trends as a result of deformation below Tnr (Fig. 12b–c). In addition, it is not clear yet how the character of intervariant boundary (twist, tilt and mixed) influences the general yielding. This is an area which requires further work. Nevertheless, the decrease in the overall intervariant boundary connectivity is largely due to the reduction in the fraction of {110} twist boundaries with the strain (Fig. 12b).

Conclusion

In the current study, the role of parent austenite deformation in the non-recrystallisation regime on the intervariant boundary network in a lath martensitic microstructure was examined by means of conventional EBSD technique, analysis of the five-parameter boundary character distribution, and of homology metrics. The findings are summarised as follows:

  • The misorientation angle distribution of the lath martensite displayed a bimodal distribution, closely correlated to the K–S orientation relationship. The deformation of parent austenite lessened the population of 60°/[011] intervariant boundaries in proportion to the strain in the austenite.

  • The change in the population of intervariant boundary was mainly attributed to the introduction of a dislocation substructure in the parent austenite through deformation, which promotes the selection of variants whose habit planes (011)α′ are closely parallel to the primary slip plane (111)γ and/or the secondary slip plane (1–11)γ. The interaction of these variants led to the promotion of specific intervariant boundaries (e.g., 60°/[111], 10.5°/[011] and 49.5°/[110]) at the expense of 60°/[011].

  • Local variant selection significantly influenced the intervariant boundary network connectivity in the lath martensite. Generally, the connectivity of boundaries with {110} plane orientation decreased with increasing strain in the austenite. A similar trend was observed for the intervariant boundaries with a {110} twist character, which closely corresponded to the drop in the population of 60°/[110] intervariant boundaries. However, the connectivity of the {110} tilt boundaries progressively increased with strain.

  • The application of deformation in the parent austenite largely altered the population of intervariant boundaries, rather than their character. The distribution of intervariant boundary plane largely displayed anisotropic character for all martensitic microstructures, terminated on {110} planes due to the displacive/shear nature of martensitic phase transformation. However, the extent of anisotropy progressively reduced with the strain.