Introduction

With a great versatility of elements which can occupy the A- and B-site positions, perovskite-type oxides ABO3 offer the possibility of tailoring materials with a variety of properties for specific technological applications (electronic-, ionic- or mixed-conductors, ferro- and piezoelectrics, thermistors, varistors, etc.) [1, 2]. In solid oxide cells (SOCs), which comprise solid oxide fuel cells (SOFCs) and solid oxide electrolysis cells (SOECs), perovskite-type oxides are applied as air electrode materials due to their high electronic and significant ionic conductivities and fast oxygen exchange kinetics [3,4,5,6,7]. SOC air electrode materials, which are optimized for operation temperatures of 650–850 °C, usually contain La3+ and Sr2+ on the A-site and mixed-valence transition metals on the B-site (Co, Fe) [4, 8]. However, the insufficient long-term stability of state-of-the-art SOC air electrodes under application-relevant conditions remains a critical factor and a challenge towards materials development. The degradation mechanism of materials from the La1-xSrxCo1-yFeyO3-δ series frequently involves the surface segregation of Sr [9,10,11] driven (among other factors) by the size-mismatch between the host (La3+) and substituent ion (Sr2+) [12], and the reaction with acidic impurities such as volatile Cr- or Si-species and SO2 [13,14,15,16,17,18,19]. A possible approach towards the improvement of long-term stability is, therefore, the replacement of Sr with different substituents (preferably with smaller ionic radius) and the decrease in the compound basicity [20, 21].

Recently, promising results with regard to fast oxygen exchange kinetics and high stability vs. SO2-poisoning were reported for Sr- and Co-free perovskites from the La1-xCaxFeO3-δ series [7, 22,23,24]. Price et al. reported that the solubility limit of Ca in La1-xCaxFeO3-δ is 38% [25]. In the series La1-xCaxFeO3-δ (0.1 ≤ x ≤ 0.25), La0.8Ca0.2FeO3-δ showed the highest oxygen exchange activity [7, 23] and excellent long-term stability [26]. The results of long-term oxygen exchange measurements and post-test analyses indicated that the improved impurity tolerance of La0.8Ca0.2FeO3-δ is due to lower compound basicity and the island-like formation pattern of secondary phases [20, 26].

In the present study, the solubility of 10–70% of Nd on the A-site of La0.8Ca0.2FeO3-δ is investigated with the aims to further decrease compound basicity and to further improve long-term stability against impurity poisoning, while at the same time (to the greatest possible extent) maintaining the excellent properties of the original compound. With an ionic radius of 1.27 Å Nd3+(XII) is smaller than (but still relatively close to) the ionic radius of La3+(XII), which is 1.36 Å [12]. A-site substitution with Ce3+ or Pr3+ was avoided since both cations are capable of valence changes (3 +/4 +), which may introduce more complex changes in the material properties or lead to problems with phase stability. Sm3+(XII) with an ionic radius of 1.24 Å and rare earth elements with even higher atomic numbers (i.e. even smaller ionic radii) were also considered unfavourable, since these cations may lead to more significant changes in crystal structure and material properties compared to the original compound La0.8Ca0.2FeO3-δ.

The present publication describes the synthesis of the compounds La0.8-xNdxCa0.2FeO3-δ (0.1 ≤ x ≤ 0.7) as well as characterization of the crystal structure and thermal expansion behaviour of the single-phase materials La0.8-xNdxCa0.2FeO3-δ (0.1 ≤ x ≤ 0.6) in comparison with La0.8Ca0.2FeO3-δ. By analysis of XRD data with Rietveld refinement, information on phase purity and structural parameters (space group, bond length and angles, atom positions) was obtained. The thermal expansion behaviour was characterized by dilatometry in a wide range of temperatures (30–1000 °C) and oxygen partial pressures (1 × 10–3 ≤ pO2/bar ≤ 1).

Experimental

Sample preparation

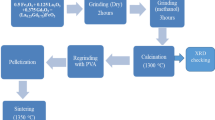
A series of solid solutions La0.8-xNdxCa0.2FeO3-δ (0.1 \(\le\) x \(\le\) 0.7) was synthesised via a citric acid – ethylenediaminetetraacetate (EDTA) sol–gel process starting with stoichiometric amounts of the metal nitrates La(NO3)3.6H2O, Nd(NO3)3.6H2O, Ca(NO3)2.4H2O and Fe(NO3)3.9H2O (all chemicals obtained from Sigma-Aldrich, analytical grade quality). These were mixed with distilled H2O in a stainless steel vessel. Anhydrous citric acid and EDTA (one mole each per mole cations) were added after the metal nitrates were completely dissolved. Subsequently, 25% aqueous NH3 solution was added until pH = 8 was reached and a clear dark red solution was obtained. The temperature was slowly raised to evaporate water and form a gel. Self-ignition and combustion of the dried gel occurred at approximately 500 °C.

The raw ash was crushed in an agate mortar and calcined at 1000 °C for 4 h (5 K min−1 ramps for heating and cooling) in air. According to XRD, single-phase compounds were obtained for La0.8-xNdxCa0.2FeO3-δ with x \(\le\) 0.6. Further increase in the Nd concentration to x = 0.7 led to the formation of the secondary phases CaO and Ca2Fe2O5 (see Supplementary Material, Figure S-1 and Table S-1). The particle size distribution of the calcined powders was determined by use of a CILAS 1064L particle size analyser. After calcination, the d50 values of the powders were in the range of 18.6 \(\le\) d50/µm \(\le\) 22.4. A bench top roll-mill was used to grind the calcined powders until 0.5 \(\le\) d50/µm \(\le\) 0.7 was reached.

For thermal expansion measurements, cylindrical pellets were fabricated by uniaxial pressing. After sintering at 1150 °C for 10 h with heating and cooling rates of 1 K min−1, the samples were approximately 5 mm in diameter and 8 mm long. The relative densities of the sintered samples of La0.8-xNdxCa0.2FeO3-δ with x = 0 [7] and x = 0.3–0.6 (this study) were in the range of 97–99% of the theoretical densities. (Relative densities of La0.8-xNdxCa0.2FeO3-δ with x = 0.1–0.2 were determined with 92% of the theoretical densities; however, since these two samples were not ideally cylindrical, the relative densities may be underestimated.)

X-ray diffraction and electron microscopy

XRD of the calcined powders was performed with a diffractometer (BRUKER-AXS D8 Advance ECO) using a Cu K\(\alpha\) radiation source operated at 40 kV and 25 mA. The diffractograms were recorded at scanning rates of 0.01° s−1. Rietveld refinement was performed by using the commercially available software TOPAS (Bruker) [27]. Lattice parameters were obtained from fits of the reflections’ positions to an orthorhombic unit cell (space group Pnma). Reflection broadening was described by convolution of a Voigt function with a modified pseudo-Voigt function according to Thompson–Cox–Hastings [28].

Sample preparation for the TEM investigation was carried out on a focused ion beam (FIB) microscope FEI NOVA 200 Nanolab. TEM analyses were performed with a TITAN3 G2 60–300 from FEI at 300 kV accelerating voltage in scanning transmission electron microscopy mode (STEM). The microscope is equipped with a CS–probe corrector and a Super-X detector system (FEI). STEM images were acquired with a high-angle annular dark-field (HAADF) and a bright-field (BF) detector. The software packages GMS 3 (Gatan) and Velox 2 (Thermo Fisher Scientific) were used to acquire HAADF images and EDX spectrum images.

The cation stoichiometry (Table 1) was obtained by energy-dispersive X-ray spectroscopy (EDXS) measurements in a scanning electron microscope (Cambridge, STEREOSCAN 250 MK3) equipped with an Oxford Instruments Mod. 6272 detector. To confirm the homogeneity of cation distribution, area scans on polished samples with 10 mm diameters were measured.

Table 1 Cation stoichiometry of compounds from the La0.8-xNdxCa0.2FeO3-δ series; data obtained from SEM–EDX analyses of sintered pellets are compared to theoretical values (in parentheses) calculated from the nominal composition. All values are given in atomic percent
Full size table

Dilatometry and differential scanning calorimetry

The thermal expansion behaviour of the materials was investigated between 30 and 1000 °C with heating rates of 1 K min−1 using a single-rod dilatometer DIL 402/PC4 (NETZSCH). Atmospheres with different oxygen partial pressures in range of 1 × 10–3 ≤ pO2/bar ≤ 1 were obtained by O2-Ar gas mixtures using mass flow controllers (Teledyne HFC-302) at flow rates of 10 l h−1.

Differential scanning calorimetry (DSC) was performed on selected sintered (1100 °C, 2 h, air) and finely ground powders using a High Temperature DSC 404 C Pegasus (NETZSCH). The sample (approximately 20–30 mg) was placed in an 85 µl Pt–Rh crucible. To minimize the influence of adsorbed humidity or CO2, the powders were heated in the calorimeter to 1000 °C, kept in 20% O2 (rest Ar) and cooled to 20 °C before the actual experiments were started. The DSC measurements were performed between 20 and 1000 °C in 20% O2 (rest Ar) with heating and cooling rates of 20 K min−1 and gas flow rates of 50 ml min−1.

Results and discussion

3.1 Crystal structure and cation distribution

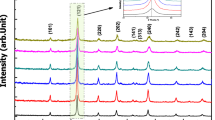
XRD patterns of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6) are shown in Fig. 1a. All reflections were assigned to the orthorhombic GdFeO3 perovskite structure with the space group Pnma (SG#62). With increasing Nd content, the reflections shift towards higher diffraction angles. This effect is shown in detail for the reflections ascribed to the lattice planes (220) and (022) in Fig. 1(b), and for the lattice planes (321), (240), (123) and (042) in Fig. 1(c). The separation of these reflections increases with increasing Nd concentration. Rietveld refinement was performed for all compounds La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6). The lattice parameters of the orthorhombic unit cells are plotted as a function of Nd concentration in Fig. 2a. Linear dependences of the unit cell parameters of the solid solutions on the Nd concentration are observed, following Vegard’s law [29]. No change in space group is observed within the investigated range of compositions (see also the plot of the orthorhombicity, defined as 2(b −  a)/(a + b) [30], in Fig. 2b). The lattice parameters of the Nd-substituted compounds are given in Table 2, which also includes data of the unsubstituted materials LaFeO3 [31], CaFeO3 [32] and NdFeO3 [33], and of La0.8Ca0.2FeO3-δ [7]. Increasing substitution of La3+ with Nd3+ causes a linear decrease in the unit cell volume of La0.8-xNdxCa0.2FeO3-δ (Table 2 and Fig. 2(c)).

Figure 1
figure 1

(a) XRD patterns of calcined powders of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6); plots (b) and (c) show details of (a) with reflections ascribed to the lattice planes (220), (022) in (b) and (321), (240), (123), (042) in (c) indicated with dashed lines

Full size image
Figure 2
figure 2

(a) Lattice parameters of the orthorhombic unit cells (SG: Pnma) of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6), (b) orthorhombicity (defined as 2(b-a)/(a + b) [30]) and (c) unit cell volume as a function of Nd concentration

Full size image
Table 2 Lattice parameters, unit cell volume and tolerance factor of compounds from the La0.8-xNdxCa0.2FeO3-δ series in comparison with similar perovskites
Full size table

Goldschmidt’s tolerance factor t (Table 2), which describes the deviation from the ideal cubic perovskite structure (t = 1) and may be used as an indicator of the relative stability of the structure, was calculated according Eq. 1 [34, 35].

$$t{ = }\frac{{{\text{ x}}_{{\text{A}}} {\text{ r}}_{{\text{A}}} {\text{ + x}}_{{{\text{A}}^{{^{\prime} }} }} {\text{ r}}_{{{\text{A}}^{{^{\prime } }} }} {\text{ + x}}_{{{\text{A}}^{{^{\prime \prime } }} }} {\text{ r}}_{{{\text{A}}^{{^{\prime \prime } }} { }}} {\text{ + r}}_{{\text{O}}} }}{{\sqrt {2} { }\left( {{\text{r}}_{{\text{B}}} {\text{ + r}}_{{\text{O}}} } \right)}}$$
(1)

The variables \({\text{x}}_{{\text{A}}}\), \({\text{x}}_{{{\text{A}}^{\prime } }}\) and \({\text{x}}_{{{\text{A}}^{{^{\prime \prime } }} }}\) represent the occupancy of the A-sites of the perovskite lattice with A = La, A′ = Ca and A′′ = Nd (for example: \({\text{x}}_{{\text{A}}}\) = 0.2, \({\text{x}}_{{{\text{A}}^{\prime } }}\) = 0.2 and \({\text{x}}_{{{\text{A}}^{{^{\prime \prime } }} }}\) = 0.6 in La0.2Nd0.6Ca0.2FeO3-δ). The symbols ri denote the ionic radii of the species i (A- and B-site cations, oxygen). The following ionic radii from [12] were used: r(La3+)(XII) = 1.36 Å; r(Ca2+)(XII) = 1.34 Å, r(Nd3+)(XII) = 1.27 Å, r(Fe3+(high spin))(VI) = 0.645 Å, r(O2−)(VI) = 1.40 Å. As indicated in Table 2, t decreases with increasing Nd concentration from LaFeO3 (t = 0.9543) [31] over La0.7Nd0.1Ca0.2FeO3-δ (t = 0.9498) to CaFeO3 (t = 0.9474), and subsequently to La0.2Nd0.6Ca0.2FeO3-δ (t = 0.9343) and NdFeO3 (t = 0.9232).

As an example for the compounds from the LNCF series, La0.2Nd0.6Ca0.2FeO3-δ was analysed with atomically resolved STEM-EDX regarding the distribution of the cations La, Nd, Ca and Fe. The contrast in the STEM-HAADF image (Fig. 3, upper left image) results from the differences in the atomic numbers of the elements, with heavier elements appearing brighter than lighter ones. Due to the similar atomic numbers of La (57) and Nd (60), it is not possible to distinguish between those two elements solely based on the information from the HAADF image. However, the elemental distributions of La and Nd were determinable with STEM-EDX spectrum images. The elemental maps of La, Nd, Fe and Ca thus obtained are shown in Fig. 3. The Ca map is not as clear as those of La and Nd, due to the relatively low Ca signal intensities in the EDX spectra. However, the elemental distribution maps indicate that the cations are indeed homogeneously distributed on the A- (La, Nd, Ca) and B-sites (Fe) of La0.2Nd0.6Ca0.2FeO3-δ. Similar behaviour is assumed for the elemental distribution in the other compounds from the LNCF series.

Figure 3
figure 3

STEM-HAADF image of La0.2Nd0.6Ca0.2FeO3-δ in [010] zone axis (upper left); STEM-EDX elemental distribution maps of Fe, Fe and Nd, Nd, La and Ca based on net peak intensities after background subtraction

Full size image

Under consideration of these results, the atomic positions of the La-, Nd- and Ca-sites in the Rietveld refinement of the XRD data were set equivalent for all investigated compounds of the LNCF series. As an example, the refined XRD pattern and the crystal structure of La0.2Nd0.6Ca0.2FeO3-δ are shown in Fig. 4a and Fig. 4b. The atomic positions of La0.8-xNdxCa0.2FeO3-δ (0.1 ≤ x ≤ 0.6) are given in Table 3. Table 4 shows bond lengths and bond angles of materials from the LNCF series in comparison with the unsubstituted compounds LaFeO3 [31], CaFeO3 [32], NdFeO3 [33] and the Nd-free analogue La0.8Ca0.2FeO3-δ [7]. Bond lengths and bond angles of La0.8-xNdxCa0.2FeO3-δ (0 ≤ x ≤ 0.6) are also shown as a function of Nd concentration in Fig. 5. Substitution of 10% La with Nd decreases the bond length between Fe and the apical oxygen (Fe1-O1, Fig. 5f), followed by an increase in the bond length from x = 0.1 to 0.3 in La0.8-xNdxCa0.2FeO3-δ (Fig. 5(a)). An increase with different slopes is observed at higher Nd concentrations (x = 0.4 to 0.6). While the bond lengths Fe1-O2 (Fig. 5(b)) decrease with increasing x, the bond lengths Fe1-O2′ show similar trends to those of Fe1-O1 (Fig. 5c, decrease from x = 0 to x = 0.1 and increase with further increase in x). The presence of two different equatorial oxygen positions (O2 and O2′) is due to a distortion of the FeO6 octahedra [31, 33, 36]. Although Fe1-O2 and Fe1-O2′ have different bond lengths, the bond angles of Fe1-O2-Fe1 and Fe1-O2′-Fe1 are equal. The bond angles Fe1-O2-Fe1 and Fe1-O2′-Fe1 (both shown in Fig. 5d), as well as Fe1-O1-Fe1 (Fig. 5e) increase from x = 0 to x = 0.1 and decrease from x = 0.1 to 0.6.

Figure 4
figure 4

(a) XRD pattern of La0.2Nd0.6Ca0.2FeO3-δ (circles) and fit obtained from Rietveld refinement (solid line); the grey line represents the difference plot between measured and calculated data. The high fit quality is indicated by the reliability parameters Rexp = 5.39, Rwp = 7.96 and χ2 = 1.48. (b) Crystal structure of La0.2Nd0.6Ca0.2FeO3-δ oriented along the crystallographic c-axis

Full size image
Table 3 Atomic positions of compounds from the La0.8-xNdxCa0.2FeO3-δ series; all investigated materials crystallize in the orthorhombic space group (Pnma). Atomic positions of Ca and Nd were considered equivalent to those of La
Full size table
Table 4 Bond lengths and bond angles of compounds from the La0.8-xNdxCa0.2FeO3-δ series in comparison with similar perovskites. The numbers in parentheses denote standard deviations in units of the least significant digits
Full size table
Figure 5
figure 5

Bond lengths (a) Fe1-O1, (b) Fe1-O2, (c) Fe1-O2′ and (d) bond angles Fe1-O2-Fe1 (equal to Fe1-O2′-Fe1) and (e) Fe1-O1-Fe1 of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6) as a function of Nd concentration; (f) labelling of the atomic sites using the example of La0.2Nd0.6Ca0.2FeO3-δ oriented along the crystallographic b-axis

Full size image

The high-resolution HAADF image shown in Fig. 6b was used to perform a Fast Fourier Transformation (FFT) (Fig. 6d) to analyse the changes in the crystal structure when substituting Nd with La within the perovskite structure. For this purpose, La0.2Nd0.6Ca0.2FeO3-δ was compared with the Nd-free compound La0.8Ca0.2FeO3-δ. The reciprocal lattice spacings and angles measured from FFTs of La0.2Nd0.6Ca0.2FeO3-δ were compared with values obtained from simulations of electron diffraction patterns via JEMS [37]. Figure 6c depicts the simulated diffraction patterns of La0.8Ca0.2FeO3-δ and La0.2Nd0.6Ca0.2FeO3-δ in [010] zone axis. A comparison of Fig. 6d with the simulations clearly reveals the changes in the crystal structure: spots from the (001), (00-1), (100) and (-100) lattice planes (marked in red squares) appear in the FFT as well as in the diffraction pattern simulation of La0.2Nd0.6Ca0.2FeO3-δ, but are not visible in the simulation of La0.8Ca0.2FeO3-δ. The absence of further diffraction spots in La0.8Ca0.2FeO3-δ (marked with dashed squares) is due to the fact that these reflections can be explained as orders of the inner missing spots.

Figure 6
figure 6

(a) STEM bright-field image of La0.2Nd0.6Ca0.2FeO3-δ. The structure matches the superimposed projection of the unit cell along the [010] zone axis; (b) STEM-HAADF image of La0.2Nd0.6Ca0.2FeO3-δ in [010] orientation; (c) simulated diffraction patterns of La0.8Ca0.2FeO3-δ (left) and La0.2Nd0.6Ca0.2FeO3-δ (right); (d) FFT of the HAADF image shown in (b)

Full size image

3.2 Thermal expansion and phase stability

Thermal expansion coefficients \(\alpha\) of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6) were obtained from the slopes of ΔL/L0 vs. T curves (Figure S-2–S-5) in the temperature regions I (40 \(\le {\text{T}}/^\circ {\text{C}} \le\) 530) and II (530 \(\le {\text{T}}/^\circ {\text{C}} \le\) 990) and different oxygen partial pressures in the range of 1 × 10–3 ≤ pO2/bar ≤ 1 (Table 5 and Fig. 7). A three-dimensional representation of the T- and pO2-dependence of the average \(\alpha\) values (50 \(\le {\text{T}}/^\circ {\text{C}} \le\) 1000) is given in Figure S-6. At constant pO2, the effect of Nd-substitution in the series La0.8-xNdxCa0.2FeO3-δ on the thermal expansion coefficient is relatively small, and the \(\alpha\) values of La0.8-xNdxCa0.2FeO3-δ (0.1 \(\le\) x \(\le\) 0.6) are similar to those of La0.8Ca0.2FeO3-δ [7]. At pO2 = 1 bar, \(\alpha\) of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6) is in the range of (12.8 ± 0.3) × 10–6 K−1 (region I) and (15.3 ± 0.5) × 10–6 K−1 (region II), and at 0.1 bar in the range of (13.0 ± 0.2) × 10–6 K−1 (region I) and (15.7 ± 0.2) × 10–6 K−1 (region II). At lower oxygen partial pressure, i.e. pO2 = 0.01 bar, \(\alpha\) values are (13.4 ± 0.3) × 10–6 K−1 (region I) and (17.4 ± 0.9) × 10–6 K−1 (region II), and at 0.001 bar (13.2 ± 0.3) × 10–6 K−1 (region I) and (18.4 ± 0.4) × 10–6 K−1 (region II). The increase in \(\alpha\) with decreasing pO2 (esp. at 1 × 10–2 and 1 × 10–3 bar) and increasing temperature (esp. in region II) is presumably due to the additional contribution of chemical expansion caused by the formation of oxygen vacancies as observed with similar perovskites [7, 22, 23].

Table 5 Thermal expansion coefficients \({\upalpha }\) of compounds from the La0.8-xNdxCa0.2FeO3-δ series in temperature regions I (40 \(\le {\text{T}}/^\circ {\text{C}} \le\) 530) and II (530 \(\le {\text{T}}/^\circ {\text{C}} \le\) 990) at different oxygen partial pressures
Full size table
Figure 7
figure 7

taken from the literature [7]

Thermal expansion coefficients of La0.8-xNdxCa0.2FeO3-δ (0 ≤ x ≤ 0.6) as a function of Nd concentration for different oxygen partial pressures in temperature regions I (40–530 °C) and II (530–990 °C). Data for the Nd-free compound in temperature regions I (30–750 °C) and II (750–1000 °C) were

Full size image

The \(\alpha\) values of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6), determined in temperature regions I and II at pO2 = 0.1 bar, are similar to those of Nd-free lanthanum calcium ferrites like La0.9Ca0.1FeO3-δ (13.1 × 10–6 K−1 [23]) and La0.75Ca0.25FeO3-δ (15.1 × 10–6 K−1 [22]), but significantly smaller than those of the state-of-the-art SOFC cathode material La0.6Sr0.4CoO3-δ (18.9 × 10–6 K−1 [38]). Further, the thermal expansion coefficients of La0.8-xNdxCa0.2FeO3-δ (0 \(\le\) x \(\le\) 0.6) are relatively close (especially in temperature region I) to those of common solid electrolytes like 8YSZ (10.8 × 10–6 K−1 [39]) or Ce0.9Gd0.1O2-δ (12.5 × 10–6 K−1 [40]).

As previously reported in the literature, the Nd-free compound La0.8Ca0.2FeO3-δ shows a reversible transition from the orthorhombic (SG: Pnma) to the trigonal (SG: R-3c) structural modification at approximately 740 °C [7, 25]. According to DSC measurements, substitution of La with Nd seems to suppress the structural transition in La0.8-xNdxCa0.2FeO3-δ (0.1 \(\le\) x \(\le\) 0.6) (Figures S-7 and S-8). While the DSC curve of La0.8Ca0.2FeO3-δ shows an exothermal peak at approximately 740 °C (previously attributed to the structural transition [7, 25]), no comparable peaks were observed in the DSC curves La0.8-xNdxCa0.2FeO3-δ (0.1 \(\le\) x \(\le\) 0.6).

Summary and conclusions

Single-phase perovskites from the series La0.8-xNdxCa0.2FeO3-δ with 0.1 ≤ x ≤ 0.6 were synthesized and characterized with respect to crystal structure, chemical composition, thermal expansion behaviour and phase stability. All the investigated compounds of the La0.8-xNdxCa0.2FeO3-δ series crystallize in the orthorhombic space group Pnma. High-resolution transmission electron microscopy with energy-dispersive X-ray spectroscopy confirmed the homogeneous distribution of the A-site ions (La3+, Nd3+ and Ca2+) on the example of La0.6Nd0.2Ca0.2FeO3-δ. The thermal expansion coefficients of the materials from the LNCF series are in the range of (13–18) × 10–6 K−1 at 40–990 °C and 1 × 10–3 ≤ pO2/bar ≤ 1. Differential scanning calorimetry indicated that substitution of La with Nd in La0.8-xNdxCa0.2FeO3-δ (0.1 \(\le\) x \(\le\) 0.6) suppresses the transition from the orthorhombic to the trigonal structural modification, which is observed in the Nd-free compound La0.8Ca0.2FeO3-δ.

In future work, the materials from the series La0.8-xNdxCa0.2FeO3-δ will be characterized with regard to oxygen nonstoichiometry and electronic conductivity as a function of temperature and oxygen partial pressure. It would also be of interest to further investigate selected compositions of La0.8-xNdxCa0.2FeO3-δ in terms of long-time stability, especially in comparison with the Nd-free perovskite La0.8Ca0.2FeO3-δ and state-of-the-art SOC air electrode materials from the La1-xSrxCo1-yFeyO3-δ series.