Introduction

In early works on aluminum alloys, after quenching, an enhanced diffusion at room temperature was noticed [1]. However, at this low temperature this could not be explained by the concentration of thermal vacancies. So, vacancy-solute interactions have been already assumed in early studies in the 1950th and 60th as a possible reason for enhanced or delayed hardening response [2, 3], whereas a direct evidence could not be given until the method of positron annihilation entered this field in the 1970th (see [4] and references therein). However, the method of angular correlation used in these early works [4] was not able to distinguish between different kind of traps. Later the method of Positron Annihilation Lifetime Spectroscopy (PALS) has been applied [5, 6]. Nevertheless, these early works were hampered from a poor understanding of the complex interaction of positron trapping to quenched-in vacancies, vacancy-solute-atom complexes and clusters of solute atoms forming immediately after quenching [7]. So, the time of several hours to take one single PALS spectrum could not shed light on these complicated processes immediately starting after quenching when storing the samples at room temperature. However, this problem is evident for all methods where data acquisition takes more than a few minutes.

The Al-Cu 2xxx alloy system has important applications as high-strength light-weight material for the fuselage in aviation (Al-Cu-Mg, Al-Cu-Li), as lean Cu alloys (Al-Mg-Cu) in automotive applications and as cast alloys (Al-Si-Cu) for engine blocks in the transport sector [8]. In Al-Cu alloys without a second alloying element the main hardening precipitates are Guinier-Preston Zones (GP-II) / \(\theta \, ''\) (\(\hbox {Al}_3\)Cu) and \(\theta \, '\)-phase (\(\hbox {Al}_2\)Cu) [9], where the structure-property relationship is to a large extent determined by size, distribution and the crystal structure of the formed precipitates.

The influence of trace elements from the fifth row in the periodic table—namely Cd, In, Sn—was noticed already during 1952-1954 [10, 11]. At that time the main investigation method for structural characterizations has been single crystal X-ray diffraction comparing the obtained signals to changes in the hardness of the samples. A couple of years later the influence of the trace elements Cd, In, Sn on the precipitation behaviour was systematically investigated by Silcock et al. [12, 13]. However, the atomistic mechanisms due to the present trace elements governing the drastic changes in the precipitation sequence going along with a significant hardness increase during artificial ageing (\(150\ldots 200\,^\circ {\text {C}}\)) could not be revealed. Nevertheless, it became clear that at room temperature the formation of GP-I and GP-II zones is suppressed by the addition of Cd/In/Sn, while at elevated temperatures the Cu atoms precipitate preferentially as finely dispersed \(\theta \, '\)-phase particles. This phenomenon is indeed responsible for the increase in hardness or strength. But even 50 years later the interaction between Cu and Cd/In/Sn was still mysterious as stated by Jeanne Silcock [14].

Even nowadays the reason for the modified precipitation sequence altering the hardening behaviour in Al-Cu containing just a few \(100\, {{\mathrm {ppm}}}\) of trace elements is a matter of active research [15, 16]. It has been shown recently that this effect is also found in Al-Mg-Si alloys as well [17,18,19].

To the knowledge of the authors there is only one experimental study giving direct evidence about the interaction of trace elements including In and Sn with vacancies quenched-in from high temperature [20]. This study employed the method of positron lifetime spectroscopy (PALS). However, in this study the purity of the used aluminium was only 4N. Recently, it has been confirmed by the present authors that quenched-in thermal vacancies in high-purity binary alloys (5N5 Al with trace elements) are responsible for the diffusion of solute atoms at room temperature or slightly higher temperatures [21]. The latter study employed PALS, which is sensitive to relevant concentrations of vacancies and vacancies-like defects, but also coincidence Doppler broadening spectroscopy (CDBS), which can deliver information about the atom types attached to vacancies [22,23,24].

Another approach is the calculation of vacancy-solute binding energies by ab-initio methods. This has been done by employing the well known pseudo-potential plane wave code VASP, determining the binding energies of vacancies to many elements in the periodic table including Cd/In/Sn [25]. As discussed in [21] there are still significant discrepancies between experimental studies [20, 26] and ab-inito calculations [25], especially concerning the binding energy of vacancies to Mg-atoms.

From the fifth row elements cadmium has not been investigated in this study due to its low vapor pressure. Hence, it is difficult to properly control the experimental conditions during the heat treatment, i.e. it is difficult to maintain thermodynamic equilibrium. Instead, we investigated one element (Pb), which has been expected to have an even higher vacancy-solute binding energy than In or Sn [25].

In the present publication we study these high-purity alloys by DSC measurements, SAXS and structural investigations employing high-resolution and analytical TEM. The solute-vacancy interaction will be investigated by the methods of positron annihilation spectroscopy (PAS).

Experimental

For casting the alloys very high purity aluminium (5N5) has been used as base material, while the Cu and trace element additions (In, Sn, and Pb) had a nominal purity of 4N. The alloys contain 1.7 at.% Cu and 0.010 at.% (100 ppm) of In, Sn, or Pb. The pure Al-1.7 at% Cu alloy is just called “base alloy” in following.

All alloys were cast in a copper mold so that conically shaped samples of about \(70\, \text {mm}\) in length and \(9 - 11\, \text {mm}\) in diameter were obtained. To avoid any contamination from the casting process the outer most layer (reducing the diameter by \(1\, \text {mm}\)) was removed by a turning machine.

Then, these alloys were cleaned by ethanol and did undergo a homogenisation anneal at 520 \(^\circ {\text {C}}\) for 4 h in air. After cooling inside the furnace and removing them, we cut slices of approximately 1mm thickness.

Following the respective preparation for the different methods, the samples were solution heat treated at 520 \(^\circ {\text {C}}\) for 1 h under flowing Argon if not otherwise stated. The furnaces were well calibrated to ensure a stability of the temperature of less than \(\pm 2\, {\text {K}}\) during solution heat treatment. Following this solution treatment the samples were rapidly quenched into ice water, i.e. cooling to a temperature of \(0\,^\circ {\text {C}}\) within the fraction of a second creating a supersaturated solid solution. After this procedure all samples denoted “as-quenched” have been immediately mounted to e.g. the DSC or they were cooled to \(-80\,^\circ {\text {C}}\) or less and stored there to freeze out the precipitation process. For the small angle X-ray scattering (SAXS) measurements at the synchrotron samples were stored on dry ice throughout transportation and then kept in liquid nitrogen. This way the samples were not exposed to room temperature RT (about \(22\,^\circ {\text {C}}\)) for more than 5 min.

Some samples were naturally aged at RT for the given times. Other samples were artificially aged by exposing them to a temperature of 150 or 200\(\,^\circ {\text {C}}\) for various times.

Vickers hardness testing was done on a tool of the type VMHT by the company Uhl following the norm ISO 6507 using the load level HV0,5. The printed result is the average of 5 single measurements.

The DSC samples were cut as square-shaped samples with a mass of 45 mg. We employed a surface grinding on one side to ensure a good contact with the Al-crucible. The heat-flux DSC measurements were carried out in a Netzsch 204 F1 Phoenix apparatus with a heating rate of 20 K/min in a range from \(-20\,^\circ {\text {C}}\) to \(530\,^\circ {\text {C}}\) under nitrogen atmosphere. To provide equal heat capacities over the temperature range we measured all samples against pure aluminium (5N) as a reference. Finally, for a better visualization the data were corrected for baseline [27] and then shifted by a similar amount.

For TEM-investigations the mentioned slices were prepared by grinding and finally polishing with \(1\mu \)m diamond suspension. The final preparation was done in a combined SEM-focused ion beam (FIB) system of the type Helios NanoLab 660 of FEI-company using the in-situ lift-out method [28]. In order to provide a proper orientation of the sample for the TEM, the specific grain direction of the extraction was determined after a pre-characterization employing EBSD using a Zeiss Gemini system [29].

A Zeiss Libra 200 MC CsSTEM was available for TEM investigations. It is equipped with a monochromator, Cs-corrector in the illumination path, two HAADF-detectors, an in-column energy filter and an EDX-detection system of the Inca-type by Oxford instruments. This system was mainly operated in the STEM-mode, which enables the combination of an image signal with atomic resolution, at the same time giving information about chemical constitution and binding.

For SAXS the samples were prepared as discs having a thickness of about \(100\,\mu {\text {m}}\) by gradually grinding with SiC paper (#500–#2000). SAXS measurements were performed at the mySpot beamline at the Helmholtz-Zentrum-Berlin (HZB) BESSY-II under the proposal 172-OSS91 ST/R. The beam energy was set to 8.7 keV with a spot size of approximately \(100\,\mu {\text {m}}\) and a sample detector distance of about 700 mm. The beamline station was equipped with a furnace, which enabled in situ ageing experiments at 150\(\,^\circ {\text {C}}\). A scattering image was recorded approximately every minute.

For PALS measurements the disc shaped samples were cut as slices from the casted rods and then ground. They had a thickness of about 1 mm. In this study a standard digital positron lifetime spectrometer [30] was used together with a temperature-controlled sample holder. The typical number of counts detected in a single lifetime spectrum is \(4.5 \times 10^6\) counts in total. The instrument resolution function (time resolution) is about 170 ps FWHM (full width of half maximum) when modeled as single Gaussian. A \(^{22}\)Na positron source having an activity of 25 \(\upmu \)Ci is deposited on 6 \(\upmu \)m thick Al foil and, finally, sandwiched between two identical samples. As a reference we used the same pure Al material (5N5) as for casting the alloys. The count rate has been about 500 counts per second. After source and background subtraction this material showed a single lifetime of \(\tau _{\text {b}}=158\,\text {ps}\) (defect-free bulk lifetime), which is in good agreement with [31] and [32]. The nonlinear least square fitting procedure is implemented in the used software LT9 [33]. We can note here that the well known defect-specific positron lifetime for mono-vacancies on the Al-fcc lattice is \(\tau _{{1V}}=240\,{\mathrm {ps}}\) [34, 35]. The estimated detection limits for positron annihilation are considered according to Staab [36] for vacancies in metals.

The sample treatment has been as follows: following solution treatment (2 h) and quenching, the samples were isochronally annealed for 30 min in steps of 10 \({\text {K}}\) in the temperature range up to 327\(\,^\circ {\text {C}}\). The samples were cooled down to RT after each annealing step and then subjected to the next positron lifetime measurement. All measurements have been done without removing the samples from the spectrometer keeping them during the measurement—if not otherwise stated—at RT. So, the first measurement at RT has to be considered with care as discussed in ``Introduction'' section.

Figure 1
figure 1

Hardness curves for Al-1.7 at.% Cu alloys: pure and containing trace elements (100 ppm) as indicated in the legend. bottom: changes in hardness for natural ageing; top: changes in hardness for ageing at 150 and \(200\,^\circ {\text {C}}\)

Full size image

Results

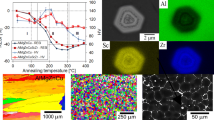
Vickers Hardness Fig. 1 displays the hardening response during natural (bottom) and artificial ageing (top) of the Al-1.7 at.% Cu base alloys with 100 ppm trace elements, as indicated, or without additions.

For natural ageing one immediately recognizes that there are only small deviations for Al-Cu-Pb compared to the pure Al-Cu base alloy (see Fig. 1 bottom): in the presence of lead the hardness increase is slightly retarded with time, while the general time evolution is pretty similar (compare also the DSC results in Fig. 4). However, the presence of 100 ppm Pb obviously hinders the diffusion of copper atoms slightly so that the hardness always lags a bit behind the pure base alloy. This is in agreement with our findings on binary alloys [21], where Pb shows either a very weak binding (below 50 meV) to vacancies or the solubility of Pb in aluminium is below 2 ppm. Natural ageing leads—for both Al-Cu and Al-Cu-Pb—to the formation of Cu clusters and GP-zones, which are typically detected by XRD after a few hours ageing at RT. All methods applied in the following (DSC, TEM) agree with the observed hardening response.

On the other hand, the Al base alloys with In and Sn additions did not show a similar hardness increase, but—compared to the pure base alloy—significantly lower values in their hardness curves over the whole range of natural ageing up to 1000 h (Fig. 1 bottom). A simple guess here is that quenched-in vacancies are immobilised and, thus, the decomposition of the In and Sn containing alloys is prohibited. Additionally, we observe a small difference between In and Sn additions, where the indium containing alloy shows the first significant rise of hardness after about 4 h while this happens for the tin containing alloy after 24 h. However, for the indium containing alloy the hardness stays for all times by a small amount above that containing tin (see Fig. 1 bottom).

Exposing the alloys to an elevated temperature of \(150\,^\circ {\text {C}}\) (Fig. 1 top) and comparing the Al base alloy with and without Pb addition relative changes in hardness are similar to natural ageing: the hardening response of the lead containing alloy is slightly retarded and the hardness reached after 48 h artificial ageing (\(100\,{\text {H}_v}\)) is not much different than after 1000 h of natural ageing.

On the other hand, exposing the In and Sn containing Al-Cu alloys to the same artificial ageing at \(150\,^\circ {\text {C}}\) (Fig. 1 top) we see a fast hardening response and significantly higher values of \(130\,{\text {H}_v}\) compared to 80 and \(70\,{\text {H}_v}\) for natural ageing of alloys containing In and Sn, respectively. We have to note that the same peak hardness is reached but after different ageing times: 4 h for Sn and 48 h for In.

Summarizing the behaviour for artificial ageing at \(150\,^\circ {\text {C}}\), we can state that for the Al base alloy with or without 0.01 at.% Pb the hardness stays nearly constant for the first 2 h and then increases to the level for RT ageing. The In and Sn containing alloys start from a lower hardness level, but show a very rapid hardening response and exceed the base alloy after 4 and 2 h, respectively.

When artificial ageing it performed at 200 instead of \(150\,^\circ {\text {C}}\), the Al-Cu base alloys with In and Sn additions show a very similar but even earlier hardness response, where the Sn containing alloy reaches a slightly higher peak hardness (see Fig. 1—top). However, the peak hardness reached for both alloys after only 2 h stays below that of artificial ageing at \(150\,^\circ {\text {C}}\).

Figure 2
figure 2

DSC curves for Al-1.7 at.% Cu alloy + 100 ppm X (X = Pb, In, Sn) in as-quenched conditions (mounted directly after quenching to ice water from 520\(\,^\circ {\text {C}}\)). The curve displays several exo- and endothermal peaks indicating the formation and dissolution of precipitates containing Cu. The curves have been shifted for better visibility

Full size image
Figure 3
figure 3

DSC curves for Al-1.7 at.% Cu with 0.010 at.% In (straight lines) and 0.010 at.% Sn (dashed lines) measured after different times of RT ageing. The arrow marks the evolution of the endothermal peak corresponding to Cu clustering. Between different ageing times the curves have been shifted for better visibility

Full size image

Differential Scanning Calorimetry The thermograms in Fig. 2 show that the base alloy with 1.7 at.% Cu (red line) just exhibits the typical exo- or endothermal peaks corresponding to the formation of precipitates (clusters, GP zones and later intermetallic phases) or their dissolution (see Baur/Gerold [37] or Hardy [1] for early reviews). Please, note that this measurement of a well-known system just serves as a reference (see [38] for a thorough discussion).

Regarding the lead containing alloy (dark green line) compared to the Al-Cu base alloy only tiny differences are visible in the thermogram of Fig. 2. So, Pb does seem to have only little influence on the precipitation in Al-Cu alloys. However, this is in clear contradiction to the calculated high binding energy of lead atoms to vacancies [25].

Shown in Fig. 2 for Al-Cu-Sn (green) and Al-Cu-In (blue), one can see in comparison to the Al-Cu base alloy that the exothermal GP-I formation peak around \(100\,^\circ {\text {C}}\) is definitely suppressed. It is important to note that also the formation peak of \(\theta \, '\) is significantly shifted by about 100 K to a lower temperature for both additions. However, it is noteworthy that the formation peak of \(\theta \, '\) appears at slightly higher temperature for the In containing alloy compared to the Sn containing.

Regarding the dissolution of the \(\theta \, '\)-phase as well as the formation and dissolution of the stable \(\theta \)-phase for the In and Sn containing alloys there are only tiny deviations of the peak positions. All three mentioned peaks do not deviate much in their position from the pure Al-Cu base alloy.

A small hump visible in the \(\theta \, '\) formation peak might be attributed to different stable variants of \(\theta \, '\) precipitates [39], where the effect appears to be slightly more pronounced for the tin containing alloy.

Figure 4
figure 4

DSC curves for the Al-1.7 at.% Cu alloy without (straight lines) and with Pb trace additions of 100 ppm (dashed lines) measured after ageing for different times at \(150\,^\circ {\text {C}}\) (directly after quenching to ice water from 520\(\,^\circ {\text {C}}\)). The curve displays several exo- and endothermal peaks indicating the formation and re-solution of Cu-precipitates. Between different ageing times the curves have been shifted for better visibility

Full size image

The DSC curves for samples of the base alloy with In and Sn after different times of room temperature ageing are shown in Fig. 3. Both alloys behave similarly under natural ageing conditions. During the first 4 h of natural ageing the Cu diffusion is still significantly suppressed, as shown by the reaction-free regions 50—\(150\,^\circ {\text {C}}\) in the DSC curves, i.e. in comparison to the base alloy the dissolution peak of Cu clusters and /or GP-I zones is missing. After more than 4 h natural ageing a dissolution peak becomes prominent, which indicates that the diffusion of Cu atoms is not totally blocked at room temperature. These peaks shift to higher temperatures for longer ageing times at RT—see arrow in Fig. 3. We attribute this to the fact that larger clusters / GP zones are more stable than smaller ones.

Figure 5
figure 5

DSC curves for Al-1.7 at.% Cu with 0.010 at.% In (straight lines) and 0.010 at.% Sn (dashed lines) measured after different times of ageing at \(150\,^\circ {\text {C}}\). The major endothermal peak between 200 and \(270\,^\circ {\text {C}}\) represents the dissolution of precipitates, which have formed during ageing. After 48 h of ageing at \(150\,^\circ {\text {C}}\) the less pronounced exothermal peak at about \(300\,^\circ {\text {C}}\) is attributed to the formation of \(\theta \, '\) precipitates during ageing. Between different ageing times the curves have been shifted for better visibility

Full size image

Regarding the ageing at elevated temperatures of \(150\,^\circ {\text {C}}\) there are only minor differences between the pure Al-Cu base alloy and the Al-Cu alloy with 100 ppm lead as trace element (straight and dashed curves in Fig. 4). We can detect a major dissolution peak between 200 and \(270\,^\circ {\text {C}}\) in both alloys for all ageing times. Hence, ageing between 2 and 48 h at \(150\,^\circ {\text {C}}\) resulted in the formation of GP-I and -II zones. With increasing ageing time the amplitude of this peak grows and it shifts to higher temperatures. We attribute this to a growth of the precipitates in size and volume fraction.

Figure 6
figure 6

DSC curves for Al-1.7 Cu-0.010 In or Sn at.% measured after various ageing times at \(200\,^\circ {\text {C}}\). The shrinkage in the main exothermal peak at about \(290\,^\circ {\text {C}}\) is associated with the formation of \(\theta \, '\) during ageing. Between different ageing times the curves have been shifted for better visibility

Full size image

This clearly shows the nearly negligible influence of lead on the precipitation sequence in the Al-Cu base alloy. Hence, we can conclude that Pb has only a minor influence on the diffusion of quenched-in vacancies. This is in accordance with our TEM and PALS results.

However, if lead is replaced by the same amount of indium or tin in the alloying process, the picture becomes completely different as shown in Fig. 5. After ageing 1 h at \(150\,^\circ {\text {C}}\) we observe mostly GP-I and GP-II zone dissolution in the DSC thermograms for both alloys.

In the Al-Cu alloy with Sn addition one can notice a small shoulder at about \(240\,^\circ {\text {C}}\), which seems to be missing for the alloy with In addition. This shoulder becomes more pronounced for longer ageing times and seems to appear not until 4 h ageing time in the In containing alloy. This overlapping peak could possibly be attributed to bigger \(\theta \, ''\) structures and/or small \(\theta \, '\), which both seem to be present at those ageing states (see Sec. 3 and [39]). The main \(\theta \, '\) precipitation is observed for ageing times between 24 and 48 h at \(150\,^\circ {\text {C}}\) visible by the clear shrinkage of the \(\theta \, '\) formation peak (see Fig. 5—green lines).

Additionally, we considered a higher artificial ageing temperature of \(200\,^\circ {\text {C}}\) as shown in Fig. 6. In contrast to ageing at \(150\,^\circ {\text {C}}\) we can observe already for the shortest ageing time of 1 h no major GP zone dissolution peak, but rather a relative sharp \(\theta \, '\) formation peak, which shrinks for longer ageing times. This peak is a bit more pronounced for Al-Cu-In.

This is an indication for direct nucleation of \(\theta \, '\) as the dominating phase at \(200\,^\circ {\text {C}}\) ageing temperature resulting in a very rapid hardening response (see Fig. 1): the peak hardness is reached after 2 h, while the maximum hardness stays well below that reached for ageing at \(150\,^\circ {\text {C}}\). Both alloys show very similar thermograms, which is also resembled in the hardening curves in Fig. 1.

Microstructure The maximum solubility for all elements considered here is specified in Table 1. At room temperature the respective solubilities are several orders of magnitude below the given numbers.

Figure 7
figure 7

High-resolution TEM image of the Al-1.7 at% Cu base alloy and the same Al-Cu base alloy containing 100 ppm Sn (inset) after long term natural ageing (\(> 1000\,\)h at RT). In the pure Al-Cu base alloy Guinier-Preston zones of type I (GP-I) are visible (arrows) having sizes between 3 and 6 nm and a high volume density. Due to the vacancy binding by the tin atoms the precipitation of GP-I zones is strongly suppressed (inset)

Full size image

Approaching the melting point of aluminum (\(660\,^\circ {\text {C}}\)) a solubility between 0.091 and 0.026 at.% for cadmium, indium and tin is predicted. For other elements in that region of the periodic table (Sb, Pb and Bi) the data base is poor (see [21] and Table 1).

For all figures presented in this part the samples have been prepared as explained in Sect. 2: solution heat treated and quenched to ice water. So, we only give the ageing times here.

Figure 8
figure 8

STEM darkfield of the Al-Cu base alloy aged at \(150\,^\circ {\text {C}}\) for 48 h. Beside a high density of GP-II zones with a size of about 20–40 nm some \(\theta \, '\) precipitates (large, bright rods) having a size of 100–150 nm are present. The visible \(\theta \, '\) particles—identified by their diffraction patterns—are surrounded by a region depleted of GP-II zones

Full size image
Table 1 Maximum solubility at high temperature of selected elements in aluminium. The data base for Pb does allow only to estimate an upper limit [44]
Full size table

Figure 7 shows a high-resolution TEM image of a naturally aged Al-1.7 at% Cu base alloy, while the inset shows the Al-Cu base alloy containing 100 ppm tin. One can clearly see that in the presence of Sn the formation of GP-I zones is significantly retarded—in accordance with the ageing response in Fig. 1 and the DSC results in Figs. 2 and 3. We assume that this is due to quenched-in vacancies bound to Sn atoms. This mechanism will be discussed intensively in ``Discussion'' section.

Figure 9
figure 9

STEM darkfield of the Al-Cu base alloy with 100 ppm In (a, c, e) and 100 ppm Sn (b, d, f) aged at \(150\,^\circ {\text {C}}\) for 1 h (a, b), 4 h (c, d) and 48 h (e, f). In (a) and (b) we find very small precipitations of the GPI-type. While in the indium alloy (a) In particles could not be detected, in the Sn containing alloy (b) the tin is precipitating in small separate particles. Bright spherical spots can be identified as Sn. Whereas in (c) the indium containing alloy is dominated by GP-II-like precipitates with a size of 20–40 nm, the tin containing alloy in (d) shows additionally larger \(\theta \, '\) particles. In both alloys (c, d) globular precipitations of a few nm size of the trace elements In or Sn, separated from copper based precipitations can be observed. In (e) and (f) there are homogenously distributed \(\theta \, '\) precipitates of 100 —150 nm size in a high density present. In addition one can observe a high number of the smaller GP-II zones (about 50 nm)

Full size image

When the Al-Cu base alloy is aged 48 h at elevated temperatures (\(150\,^\circ {\text {C}}\)), the microstructure looks completely different (see Fig. 8): GP-II zones with a size of about 20–40 nm and some larger \(\theta \, '\) precipitates having a size of 100–150 nm are now present. The \(\theta \, '\) particles are surrounded by regions depleted of GP-II zones, which is an indication of less copper in solution there. Obviously, the growth of \(\theta \, '\) particles has consumed the copper in neighbouring areas.

However, when the Al-Cu base alloy containing 100 ppm In or Sn is aged at the same elevated temperature (\(150\,^\circ {\text {C}}\)) and the same time (48 h), the microstructure changes (see Fig. 9e and f). Now finely distributed \(\theta \, '\) precipitates of 100–150 nm size dominate the microstructure. Both for the indium and tin containing alloys this possibly is the reason for the significantly increased hardness from \(105\, {{\mathrm {H}}_{\mathrm {v}}}\) for the base alloy to \(130\, {{\mathrm {H}}_{\mathrm {v}}}\).

Figure 10
figure 10

STEM images of an Al-Cu base alloy with 100 ppm In in darfield mode (a) and 100 ppm Sn in brigtfield mode (b) after ageing at \(200\,^\circ {\text {C}}\) for 2 h. The microstructure in both alloys is determined by large precipitations (150–200 nm) of the \(\theta \, '\) and \(\theta \) type. Smaller particles (5–10 nm) of the trace elements (In and Sn) are found attached at the plate-like Cu-rich precipitates

Full size image

In Fig. 9a and b we show the microstructure after a shorter ageing time (1 h) at \(150\,^\circ {\text {C}}\) of the In and Sn containing samples, respectively. One can see clearly in comparison to ageing for 48 h that the decomposition of the alloy has just started—visible by plate-like Cu precipitates forming on the \(\{ 100 \}\)-planes and In/Sn precipitates as seen in binary alloys [21].

Figure 9c and d show the effect of intermediate ageing times: 4 h at \(150\,^\circ {\text {C}}\) for In and Sn additions, respectively. The decomposition of the Al-Cu alloys has progressed to a great part now.

While there are obviously differences in the kinetics of Cu diffusion depending on the type of trace element during the first 24 h of ageing at \(150\,^\circ {\text {C}}\), one can clearly notice that the microstructures for the Al-Cu base alloys with indium or tin look pretty similar after 48 h ageing at \(150\,^\circ {\text {C}}\) (see Fig. 9e and f).

Ageing the Al-Cu base alloy with 100 ppm In or Sn at \(200\,^\circ {\text {C}}\) leads to an even more rapid hardening response as shown in Fig. 1. Figure 10a and b show the corresponding microstructures at peak hardness, respectively. It exhibits a dominating \(\theta \, '\) phase with some \(\theta \, ''\) precipitates in the mix. However, the peak hardness observed after ageing at \(150\,^\circ {\text {C}}\) is not reached for this higher temperature.

Figure 11
figure 11

SAXS 2D-scattering pattern for Al-1.7 at.% Cu containing 0.010 at.% In (a) 0.010 at.% Sn (b) measured in-situ during ageing at \(150\,^\circ {\text {C}}\). The samples had been cooled immediately below 200K after quenching to ice water from 520\(\,^\circ {\text {C}}\)

Full size image

Small Angle X-Ray Scattering Fig. 11 shows a series of normalized 2D scattering images during in situ ageing at \(150\,^\circ {\text {C}}\) for the Al-Cu base alloy with In (a) and Sn (b), respectively. It is well known that disc shaped objects like GP zones, \(\theta \, ''\) and \(\theta \, '\) precipitates give rise to streaks in the 2D image of SAXS experiments [45], since the beam size is in the same range as the average grain size and the precipitates are growing with a defined orientation on the \(\{100\}\) planes of the Al matrix [46, 47]. So, by just looking at the evolution of the scattering image (of a grain well oriented with respect to the X-ray beam) we can get an idea of the precipitation kinetics without any modeling of the resulting scattering curves. For the Al-Cu-In alloy (Fig. 11a) one can see the streaks appearing very faintly after about 60 min ageing at \(150\,^\circ {\text {C}}\) and becoming more intense for longer ageing times up to 480 min. In Al-Cu-Sn, on the other hand, the streaks already emerge after only 5 min ageing at \(150\,^\circ {\text {C}}\) and rapidly increase in intensity, which indicates a growth of the volume fraction of the scattering objects. This faster kinetics of the tin containing alloy is in good agreement with the hardness data (Fig. 1) and also becomes evident in our DSC curves (Fig. 5) and TEM investigations (Fig. 9c and d).

This very simple qualitative description of the scattering behaviour serves as a nice tool here to explain the kinetic differences between the two trace additions. A quantitative description of the precipitate morphology is rather challenging and well beyond the scope of this article and will be treated in a separate publication.

Table 2 Literature data by Wolverton [25]: calculated values for vacancy-solute binding energies for selected elements according to ab-initio calculations with VASP employing the LDA-functional
Full size table

Positron Annihilation Spectroscopy As described in ``Introduction'' section, elements from the group Cd/In/Sn (fifth row of the periodic table) are well known to have a significant influence on the precipitation sequence in Al-Cu alloys. One reason seems to be the high vacancy solute binding energy calculated (see Table 2).

Figure 12
figure 12

PALS measurement of pure Al- 1.7 at.% Cu (red) and Al- 1.7 at.% Cu containing 0.01 at.% Pb (dark green), 0.01 at.% In (blue) and 0.01 at.% Sn (light green): All samples have been quenched from \(520\,^\circ {\text {C}}\) and subsequently annealed to the given temperature. Shown is the decomposition of the lifetime spectra. \(I_2\) and \(\tau _2\) are parameters from the nonlinear fitting procedure. For the pure Al- 1.7 at.% Cu alloy between 130 and \(250\,^\circ {\text {C}}\) no data points for \(I_2\) and \(\tau _2\) are displayed, since the spectra did contain only one single component

Full size image

Figure 12 shows the annealing of pure Al- 1.7 at.% Cu and Al- 1.7 at.% Cu containing Pb, In or Sn, each at a concentration of 0.01 at.%. For the pure Al- 1.7 at.% Cu alloy between 130 and \(250\,^\circ {\text {C}}\) no data points for \(I_2\) and \(\tau _2\) are displayed, since the spectra did contain only one single component. Otherwise, the change in average positron lifetime and the decomposition is nearly the same as for the lead containing alloy. This is in accordance with hardening (Fig. 1) and the DSC curves (Fig. 2).

For the indium containing alloy we observe a similar feature as in the corresponding binary Al-In alloy [21]: immediately after quenching the defect characteristic positron lifetime \(\tau _2\) is above the typical value for mono vacancies (240 ps) in the temperature range below \(100\,^\circ {\text {C}}\). This has been explained in a recent publication by the existence of di-vacancy-indium complexes [21].

Between 120 and \(150\,^\circ {\text {C}}\) \(\tau _2\) decreases to a value close to 240 ps probably by the detachment of the second vacancy leaving mostly vacancy-solute pairs behind. So, exclusively single vacancies attached to one solute atoms (here: Indium) are left over [21].

Then, at about \(167\,^\circ {\text {C}}\) a maximum in \(\tau _2\) and \(\tau _{\mathrm {av}}\) is reached. At this point most of the vacancies are going to be released and either move to sinks or agglomerate (increased \(\tau _2\)). At the same time the fraction of trapped positrons and, hence, \(I_2\) decreases [36], since more and more vacancies move to sinks while promoting the precipitation of copper.

Above \(250\,^\circ {\text {C}}\) the characteristic lifetime starts to decrease, while the corresponding intensity \(I_2\) increases again. This is most likely caused by the formation of semi-coherent precipitates such as the \(\theta \, '\) phase, which can also act as a positron trap with a characteristic positron lifetime (\(\tau _2\)). According to ab-inito calculations in [48] the characteristic positron lifetime (here named \(\tau _2\)) of \(\theta \, '\) bulk was calculated to be 178 ps, while a vacancy on the Cu-sublattice would result in 190 ps [48]. This view is supported by the data for the pure Al-Cu alloy showing for temperatures above \(250\,^\circ {\text {C}}\) a characteristic positron lifetime \(\tau _2\) of 180–185 ps. This agrees well with the assumption of trapping to \(\theta \, '\), since this phase is formed according to DSC in this temperature range.

In a similar fashion the PALS spectra of the tin containing sample can be described. Nevertheless, some differences have to be noted. At first, there is no drop in the defect characteristic lifetime \(\tau _2\) , which has been attributed to the separation of the second vacancy. This leads us to the assumption that the separation of di-vacancies from Sn atoms happens already at lower temperatures. Secondly, the maximum of the average positron lifetime and thus, the release of most vacancies is located at a slightly lower temperature of about \(157\,^\circ {\text {C}}\) for Sn. The decrease in \(\tau _2\) and the increase in \(I_2\) above \(300\,^\circ {\text {C}}\) is supposed to have the same reasons as for the Al-Cu base alloy with In.

Discussion

The existing literature divides the influences of trace elements like In or Sn mostly into two mechanisms: (i) the suppression of GP zone formation due to a strong vacancy binding to trace element atoms and (ii) the observed increased hardening response due to preferred \(\theta \, '\) nucleation, where at the same time the precipitates are—in contrast to pure Al-Cu alloys—finely dispersed in the Al matrix [13,14,15, 49, 50].

Ageing at room temperature

The phenomenon of suppressing the formation of GP-I/GP-II zones at room temperature due to quenched-in vacancies attached to trace element atoms is definitely evident form our data (see Sect. 3) and in accordance with the few data found in the literature [20, 21].

Ageing at \(150\,^\circ {\text {C}}\)

At elevated ageing temperatures (\(>100\,^\circ {\text {C}}\) ) the picture looks different. In this case we like to speak of a “conservation of quenched-in vacancies” promoting Cu diffusion. From our PALS data here (see Sect. 3) and in [20, 21] it becomes clear that a significant part of the conserved vacancies is released already at temperatures below \(150\,^\circ {\text {C}}\). Those vacancies plus the existing thermal vacancies then promote the alloy’s decomposition, i.e. the formation of precipitates at \(150\,^\circ {\text {C}}\) in Al-Cu-In/Sn. This results in the observed rapid hardening response during the first hours at \(150\,^\circ {\text {C}}\) (see Fig. 1). The hardening curves show that there are minor differences between indium and tin containing alloys: indium leads, compared to tin, to a slightly retarded hardening response, which can nicely be visualized by the in situ SAXS images (see Fig. 11a) and also TEM (Fig. 9c and d).

Regarding the preferred \(\theta \, '\) formation, we observe only few precipitates during the first hours of ageing (see Fig. 9a and b), while the main formation takes place between 24 and 48 h at \(150\,^\circ {\text {C}}\) (see Fig. 5 for the vanishing \(\theta \, '\) formation peak and compare Fig. 9e and f). We closely connect those observations with the clustering and/or precipitation of the trace elements, since a classical homogenous nucleation of \(\theta \, '\) happens very rarely at this temperature as can be seen in the binary Al-Cu alloy (Fig. 4).

The exact role of the trace element atoms/particles is still unclear to some extent [51] and has been discussed in various other studies [39, 49, 50]. In our TEM investigations we did not find any Sn precipitates for less than 1 h of ageing at \(150\,^\circ {\text {C}}\), while longer times of 4 h at \(150\,^\circ {\text {C}}\) were necessary to precipitate In. Also in the peak aged condition at \(150\,^\circ {\text {C}}\) (30 h and 4 h in case of In and Sn, respectively) only few trace element particles can be observed in the vicinity of the \(\theta \, '\) precipitates. Further evidence for this comes from the PALS data, which indicate the existence of trace element vacancy pairs, which are stable below \(150\,^\circ {\text {C}}\). This again underlines the clear separation of the two mentioned effects at \(150\,^\circ {\text {C}}\): the conservation of vacancies to promote Cu diffusion in general and the trace element agglomerations assisting \(\theta \, '\) nucleation.

Ageing at \(200\,^\circ {\text {C}}\)

At \(200\,^\circ {\text {C}}\) on the contrary, \(\theta \, '\) seems to form much faster and almost exclusively (see Figs. 1 and 6 as well as the TEM images in Fig. 10a and b). As mentioned before, the main reason for this may be highly mobile trace elements, which possibly assist the nucleation of \(\theta \, '\) by lowering the interfacial energy between \(\theta \, '\) precipitates and the matrix and/or the shear strain [52]. From PALS we know that at \(200\,^\circ {\text {C}}\) we are well above the threshold temperature for the vacancies to become released from indium and tin atoms.

On the one hand this explains why the difference between In and Sn at \(150\,^\circ {\text {C}}\) ageing temperature is not observed at \(200\,^\circ {\text {C}}\). On the other hand the solute diffusion is enhanced in this condition and the aforementioned trace element precipitates in direct spatial correlation to the \(\theta \, '\) platelets are much more common.

Another interesting thing to note is the 10–20 % lower peak hardness that is achieved at \(200\,^\circ {\text {C}}\) compared to \(150\,^\circ {\text {C}}\). It seems that for the lower artificial ageing temperature of \(150\,^\circ {\text {C}}\) the mixture of GP-I, \(\theta \, ''\) and \(\theta \, '\) precipitates, still being finely distributed in the matrix, blocks the dislocation movement more effectively.

Conclusion

We have considered the influence of different trace elements on the precipitation sequence in high-purity Al-Cu alloys. The following conclusions can be drawn:

  • Even though Pb atoms are assumed to bind tightly to vacancies [25], we could not observe this effect experimentally by either DSC or TEM nor by PALS (see also [21]). Indeed, compared to the pure Al-Cu alloy, there are only tiny effects visible concerning the hardening response, DSC thermograms, or PALS spectra. Reasons may be either an extremely low solubility or a much weaker vacancy-solute atom binding than calculated. In the first case the solubility has to be smaller than 2 ppm, since this is the lower sensitivity limit for detecting vacancies with PALS (see the discussion in [21] and the limit given in [36]).

  • Al-Cu alloys containing 100 ppm In or Sn show for natural or room temperature ageing that the GP-I and GP-II formation is significantly hindered but not fully suppressed (shown by DSC and TEM).

  • For artificial ageing at elevated temperatures of \(150\,^\circ {\text {C}}\) the Al-Cu-Sn alloy shows a slightly faster ageing response compared to the In containing one (DSC, TEM, SAXS and PALS measurements). We attribute this in the case of indium to a higher threshold for the release of bound vacancies, i.e. a slightly stronger binding of vacancies to In atoms, compared to Sn atoms. This, however, is in contradiction to the results by Hutchinson [20], where aluminium with 4N purity had been alloyed with 300 ppm of trace elements. There, Sn showed a slightly larger binding of about 50 meV compared to In.

  • In the presence of In or Sn as trace elements, ageing Al-Cu alloys at \(200\,^\circ {\text {C}}\) an almost exclusive and direct formation of \(\theta \, '\) precipitates is observed. This is most likely caused at this temperature by the highly mobile trace elements and Cu atoms.

  • For artificial ageing we propose two separate mechanisms in the presence of In or Sn: after quenching thermal vacancies are bound tightly to trace element atoms and, thus, are “conserved”, i.e. they cannot diffuse to sinks and anneal there. At elevated temperatures most of those vacancies are released and promote the copper diffusion necessary to form the observed \(\theta \, '\) precipitates. However, also the trace element atoms In and Sn become mobile and may assist the nucleation of \(\theta \, '\) as single atoms and/or as agglomerates.

The difference between In or Sn as trace element shows up not only in DSC, SAXS and PALS data but also leaves its traces in the formed microstructure as characterized by TEM. However, the finally formed microstructures under ageing at \(150\,^\circ {\text {C}}\) for 48 h become very similar: we find finely distributed particles of both GP-II and \(\theta \, '\). This is identified as the cause for the increased hardness achieved by trace additions In or Sn.

In general, we may say that, provided a sufficient solubility of 100 ppm or more is existing at typical temperatures for the solution heat treatment, trace element additions can significantly influence the precipitation sequence during natural or artificial ageing. However, a second requirement has to be fulfilled: the vacancy-solute binding energy has to be in the range \(150\ldots 300\,{\mathrm {meV}}\) so that the vacancies, which are needed for diffusion, are released at an artificial ageing temperature suitable to jump over the temperature range, where the formation of GP-I/II is taking place. This paves the way to an easy formation of finely dispersed \(\theta \, '\).

For all considered trace elements except Pb the release of the vacancies, bound to the solute atoms In or Sn up to temperatures of 150\(\,^\circ {\text {C}}\), explains their effect on the precipitation sequence in Al-Cu alloys.

For a better prediction of suitable elements experiments with a large range of high-purity binary alloys as well as accurate and reliable ab-initio calculations would be of great help.