Introduction

The high-entropy disordered state of substances (viz. amorphous materials) is typically derived from a melt owing to rapid cooling, which allows avoid kinetically competitive crystallization processes [1]. That is why different melt-quenching (MQ) routes freezing a liquid state for room-temperature conditions are widely used in commercial glass-preparation technologies [2].

However, amorphous state can be also achieved in an alternative way ensuring generation of a large amount of structural defects in a crystal over a critical density. In this view, the high-energy mechanochemical milling (MM) reducing substantially grain sizes of the appeared nanoparticles (NPs) [1] seems to be one of the most promising technological solutions.

More commonly, the appearance of amorphous phase was detected in different substances possessing extensive row of glassy-prone compositions and inter-crystalline equilibriums like over-stoichiometric As–S alloys [2,3,4,5], also referred to (preferentially in biomedical literature) as arsenicals [6]. Recently [7], some of the current authors reported the first results on observation of complete amorphization in semicrystalline As45S55 alloy subjected to MM in a dry mode under protective Ar atmosphere. The amorphous phase possessing double-Tg relaxation originated from intrinsic separation on distinct high- and low-temperature glass components was identified as close to alloy of the same nominal chemical composition. Careful inspection with X-ray powder diffraction (XRPD) related to the first sharp diffraction peak (FSDP) revealed this amorphous phase as extension of MQ As-rich glass-forming structural motifs stretching beyond As2S3 stoichiometry. Generation of amorphous phase in addition to parent crystalline compound, albeit not exactly defined, was also detected in high-temperature polymorph of tetraarsenic tetrasulfide β-As4S4 after dry or wet MM, studied in view of promising anticancer activity [8,9,10,11,12]. Recently, the macroscopic evolution processes associated with intrinsic sub-nanometer free-volume voids were comprehensively studied in this β-As4S4 polymorph subjected to high-energy MM, using different mathematical treatment procedures applied to reconstructed positron annihilation lifetime (PAL) spectra [12]. The identified stages of MM-induced interaction between generated NPs include non-interacting accumulation, adhesion-enhanced aggregation, and irreversible agglomeration.

This work is aimed to characterize the microstructure picture of amorphization in β-As4S4, driven by high-energy ball MM at different rotational speeds, employing experimental methods of intermediate-range structural probing with FSDP-related XRPD, free-volume voids study with PAL spectroscopy, supported by atomic clustering simulation with ab initio quantum-chemical models developed for covalent-bonded glass-forming networks known as CINCA (the cation-interlinking network cluster approach [13]).

Experimental

Commercial arsenic sulfide β-As4S4 (98% in purity, purchased in Sigma-Aldrich, USA) was used as initial precursor for MM. The small pieces of this arsenical were coarse-grained, powdered, and sieved under 200 μm. Then, this powder (3 g) was subjected to MM in a dry mode under protective Ar atmosphere, using planetary ball mill Pulverisette 6 (Fritsch, Germany) loaded with 50 tungsten carbide balls of 10 mm in diameter (the MM conditions being described in more details elsewhere [9]). The overall MM duration was 60 min for each sample at different rotational speed of the planet carrier n, for example, REHE-0 (coarse-grained powdered sample), REHE-100 (n  = 100 min−1), REHE-200 (n  = 200 min−1), REHE-500 (n = 500 min−1), and REHE-600 (n = 600 min−1). Finally, the samples were compressed by compacting inside a stainless steel die under the same 0.7 GPa pressure to prepare disk-like pellets (6 mm in a diameter and 1 mm in a thickness).

The crystal structures of the arsenical pellets were identified by XRPD method, the data being collected in a transmission mode using STOE STADI P diffractometer (STOE & Cie GmbH, Darmstadt, Germany) with linear position-sensitive detector (Cu-Kα1 radiation, curved Ge(111) monochromator) as was described elsewhere [7, 9]. The crystal structure of arsenic sulfide (JCPDS card No. 72-0686) was refined by the Rietveld method with the FullProf.2k (v.5.40) program [14]. The microstructure of crystallites (average apparent crystallite size D, average maximum strain S) was defined within this Rietveld refinement procedure in terms of isotropic line broadening [15].

The identity of amorphous phase appeared at MM was clarified by the FSDP-related XRPD. Processing of the XRPD patterns was performed by STOE WinXPOW 3.03 and PowderCell 2.4 programs, following normalization in respect of the intensity of the maximum peak. These data were used for next profile fitting by WinPLOTR program [16]. The both angular position and full width at half maximum (FWHM) were determined with ± 0.01°–0.04° 2θ accuracy. The FSDP parameters in a reciprocal space (scattering vector Q and width ΔQ) were calculated as:

$$ Q = \, \left( {4\pi /\lambda } \right)\sin \theta , $$
(1)
$$ \Delta Q = \, \left( {4\pi /\lambda } \right)\sin \left( {{\text{FWHM}}/2} \right). $$
(2)

The radius of coordination sphere R (viz. spacing of the FSDP-responsible “quasi-periodicity”) and correlation length L over which this “periodicity” is maintained were obtained as:

$$ R = 2\pi /Q, $$
(3)
$$ L = 2\pi /\Delta Q. $$
(4)

The PAL measurements were performed for pelletized samples using fast–fast coincidence system ORTEC (FWHM = 230 ps) based on two Photonis XP2020/Q photomultiplier tubes coupled to BaF2 scintillator 25.4A10/2 M-Q-BaF-X-N detectors (Scionix, Bunnik, Holland) and ORTEC® electronics (ORTEC, Oak Ridge, TN, USA). The 22Na isotope of low activity (~ 50 kBq) wrapped by Kapton® foil and sealed was used as positron source sandwiched between two pellets. The normal statistics for 1 M annihilation events collected at 22 °C temperature and 35% humidity were employed for reliable PAL measurements. The channel width of 6.18 ps allows total number of channels to be 8000. Three measurements ensure good reproducibility, the source contribution being evidenced at 15% allowing compensation of input from positrons annihilated in the Kapton® foil with 0.372 ns lifetime. The PAL spectra were resolved with good variance of fit into three distinct exponentials, covering channels originated from positrons annihilating in defect-free bulk, trapped in free-volume defects and forming bound positron–electron Ps (positronium) state. This was performed with a help of LT 9.0 program [17], the accuracies in lifetimes τi and component intensities Ii being ± 0.005 ns and ± 0.5%, respectively.

The PAL data were treated using two-state STM (simple trapping model), assuming one kind of free-volume defects for positrons [18, 19], disturbed by slight input from Ps-decaying. This approach allows determination of positron-trapping modes (defect-specific τd and defect-free bulk τb lifetimes, trapping rate in defects κd, and fraction of trapped positrons η) [18,19,20], in addition to Ps-decaying modes (radius of spherical free-volume holes R, fractional free volume fv [21]).

Applicability of such approach is defined by contribution from third component, and, under some circumstances, the PAL data cannot be treated unambiguously. For inhomogeneous solids, where annihilation is expected through positron-Ps channels so that only o-Ps traps are transformed in positron-trapping centers, the formalism of Ps-to-positron trapping conversion [10, 22,23,24,25,26] can be applied to identify free-volume structure. Within this approach referred to as x3–x2-CDA (coupling decomposition algorithm) [22], we deal with x3-term PAL spectrum transformed to generalized x2-term form for reference and NP-modified (nanostructurized) solids, second component involving contributions from all other channels (positron trapping, o-Ps decaying, and p-Ps self-annihilation). This simulation allows resolving additional input with defect-specific τint lifetime and Iint intensity in the second component of x2-term PAL spectrum for NP-modified matrix, provided compensating (τn, In) input in the first component obeys condition of complete inter-channel equilibrium. Parameterization of Ps-to-positron trapping conversion in the modified matrix (conversion direction is defined by In and Iint signs) is achieved accepting (τn, In) and (τint, Iint) as first and second components of x2-term PAL spectrum employing two-state STM [18,19,20]. Trapping modes derived within this approach concern hypothetical NP-modified matrix evolving Ps- and positron-trapping sites, these being defect-specific τint and defect-free bulk τ NPb lifetimes, trapping rate in defects κ NPd , and some trapping sites characteristics, such as signature of trap size in terms of equivalent number of vacancies defined by (τint–τ NPb ) and nature of these traps defined by τint/τ NPb [18].

The geometrically optimized configurations of different network-forming clusters responsible for amorphization in β-As4S4 were simulated with ab initio quantum-chemical algorithm CINCA [13]. These clusters were built by breaking cage-type As4S4 molecule possessing D2d symmetry on distinct fragments linked with network by sulfur-bridging chains S1/2…S1/2. With this aim, we used the HyperChem Release 7.5 program package based on restricted Hartree–Fock self-consistent field method with split-valence double-zeta basis set and single polarization function 6-311G* [27, 28]. The final geometrical optimization and single-point energy calculations for selected atomic clusters were performed employing the Fletcher–Reeves conjugate gradient method until the root-mean-square gradient of 0.1 kcal/(Å mol) was reached. The calculated energies of atomic clusters were corrected on energy of terminated H atoms used to transform the network-forming configurations in molecular self-consistent ones according to the procedure well developed elsewhere [29, 30].

Results and discussion

Recent XRPD results [9] testify that MM-driven nanostructurization in β-As4S4 arsenical is revealed through extensive generation and interaction of different NPs, the character crystallite sizes of which being ~ 30 nm in REHE-0 (non-milled) and REHE-100, slightly depressed in REHE-200 and REHE-500 (~ 19–21 nm), and again increased in REHE-600 sample (up to ~ 26 nm). Noteworthy, the maximum strain shows only growing tendency in this sequence (from 0.0043 to 0.0044 ‰ in REHE-0/100 to 0.0082 ‰ in REHE-600 [9]). So, the MM arsenicals are not affected at low rotational speed (100 min−1). The fragmentation of crystallites prevails at n = 200–500 min−1 that corresponds to the increased surface area due to NPs aggregation in terms of the model [31]. Finally, at n = 600 min−1, the most energetically treated crystallites agglomerate, resulting in partially decreased (but not fully restored) specific surface area [9].

Amorphization by the FSDP-related XRPD

The MM-driven nanonization in the arsenicals at growing rotational speed n is accompanied by progressive appearance of amorphous halos (typical for As–S glasses [32, 33]) in the XRPD patterns near 13°–19°, 26°–34°, and 52°–60° 2θ, superimposed on crystalline reflexes ascribed to β-As4S4 (Fig. 1). According to Fourier-transform formalism [34], the first of these halos can be reproduced in a reciprocal space (in the structure factor determination) as the FSDP, corresponding to a real-space ordering with R “quasi-periodicity” and L correlation length, defined, respectively, by Eqs. (3) and (4).

Figure 1
figure 1

XRPD patterns of β-As4S4-based arsenicals REHE-0 (a) and REHE-600 (b). Experimental (red circles) and calculated (solid line through circles) profiles are given with calculated Bragg positions (green vertical ticks) for β-As4S4 (the difference is shown by blue solid line at the bottom)

Full size image

The FSDP is an obvious manifestation of medium-range order in glass-forming systems [35]; however, its strict microstructure origin remains controversial (see, e.g., [36] and literature therein). Nevertheless, the Gaskell’s concept on crystalline-like order in MQ glasses [37] modified with Wright’s justification on the FSDP as arising from periodicity in the distribution of some “pseudo-planes” for Bragg diffraction (“quasi-periodicity”) separating succession of randomly packed network cages [38] seems convenient for interpretation of crystalline-to-amorphous transition in MM nanoarsenicals. The flattened cage structure of network glasses produces inner equivalent planes at the opposite sides of these cages forming necessary contribution to reciprocal space Fourier component generating the FSDP [38]. Within this model, the FSDP can be ascribed to variations in the underlying cage structure of glass-forming network defined by interlinked polyhedrons forming multiple cycles (like random atomic array within Zachariasen’s diagram [39]). So, the cages keep some elements of interplanar “ordering” in network glasses, character for most stable crystalline counterparts of close chemical compositions.

Detailed inspection of XRPD profile after subtracting the overlapping β-As4S4 reflexes (Fig. 2) allows the FSDP parameterization using Eqs. (1)–(4), these data being gathered in Table 1. With increase in speed n, the FSDP parameters reach saturation, so that the FSDP is indeed sharp (in a reciprocal space) in REHE-600 due to low width of scattering vector ΔQ = 0.23 Å−1 centered at Q = 1.14 Å−1, thus corresponding to R = 5.49 Å in “quasi-periodicity” and L = 27.0 Å in correlation length (in a real space). These parameters are well fitted to monotonic compositional dependence in amorphous As–S as going from MQ As40S60 glass [33], MQ As42S58 glass [33] (both being within glass-forming region in binary As–S system [2,3,4]) and completely amorphized As45S55 alloy [7] toward As-rich compositions. Therefore, it can be assumed that under current MM conditions, we deal with continuous generation of compositionally authentic amorphous phase in β-As4S4 arsenical. The most stabilized amorphous substance appeared in REHE-600 sample differs substantially in its medium-range ordering from stoichiometric MQ As2S3 glass. Within Gaskell–Wright’s microscrystalline concept [37, 38], the smooth shift in the FSDP position to lower Q (respectively, 2θ) with rotational speed n can be treated as domination in the MM products; some structural derivatives arise from cage-type entities of crystalline β-As4S4. Indeed, the most intensive (11\( \bar{1} \)) reflex of this β-As4S4 crystal phase (possessing C2/c space group) corresponds just to interplanar distance \( d_{{(11\bar{1})}} \) = 5.76 Å; that is the highest one within all possible over-stoichiometric As–S polymorphs [7]. Simultaneously, the FSDP becomes sharper with increased n, as it is character to longer correlation lengths L of networks built of these cage-type molecular derivatives (Table 1).

Figure 2
figure 2

Experimental (red points) and calculated (black solid line) XRPD patterns of REHE-600 sample showing the profile fitting of the FSDP at the background of β-As4S4 reflexes (the difference is given by blue solid line at the bottom)

Full size image
Table 1 FSDP parameterization in pelletized β-As4S4 nanoarsenicals as compared with those of near-stoichiometric MQ [33] and MM [7] arsenic sulfides
Full size table

Amorphization by PAL spectroscopy

The PAL spectra of pelletized MM arsenicals are depicted in Fig. 3 with insert showing depressed and right-shifted peaks in a sequence of REHE-0, REHE-200, REHE-500, REHE-600. This depressing and time-enhancing trend correlates with degree of amorphization in these samples as determined from FSDP-related XRPD, and, thus, can be used as indicative of the appeared amorphous phase, whichever its occurrence (composition, sizes, shapes, morphologies, etc.).

Figure 3
figure 3

Comparison of raw PAL spectra of β-As4S4-based REHE-0, REHE-200, REHE-500, and REHE-600 arsenicals (the insert shows depressed and right-shifted peak due to amorphization)

Full size image

The collected PAL spectra were fitted using three unconstrained exponentials, proving a decreasing tendency in mean positron lifetime \( \tau_{{{\text{av}}.}}^{\varSigma} \) as it follows from data gathered in Table 2. Since only low contribution in the PAL spectra arises from third component (no more 3%), we tried to resolve the physically realistic annihilation channels exploring two-state STM [18,19,20] in addition to Ps-decaying modes [21] (Table 3). Despite simplification, it is clearly seen that free-volume changes associated with nanostructurization of β-As4S4 arsenicals due to MM notably differ in dependence on rotational speed n. Under small n (REHE-200), there are no changes in free volumes responsible for positron and Ps trapping (unchanged τ2 and τ3 lifetimes), apart from amount of positron traps, which demonstrates rather growing trend in view of higher I2, thus resulting in increased positron-trapping rate in defects κd. With further n increase resulting in aggregation of NPs and increased specific surface area in REHE-500 pellet, this trapping-enhancing trend is missed, leading to decreased fractional free volumes fv. In contrast, in REHE-600 pellet dominated by agglomerated NPs, the free-volume voids responsible for positron trapping also agglomerate (thus giving increased τ2 and decreased I2), but fractional volume fv increases notably due to both volume and amount of Ps-trapping holes (drastic increase in both τ3 and I3, Table 3).

Table 2 Fitting parameters describing x3-term PAL spectra of pelletized β-As4S4-based arsenicals
Full size table
Table 3 PAL-trapping modes describing x3-term PAL spectra of pelletized β-As4S4-based arsenicals exploring two-state STM and Ps-decaying models
Full size table

Noteworthily, the evolution trends in positron- and Ps-trapping modes in MM β-As4S4 arsenicals are mutually correlated. This allows assuming that at MM with increased rotational speed n, only Ps traps are transformed into positron traps and vice versa. Hence, we can try to parameterize this trapping-conversion process employing the x3–x2-CDA [22,23,24,25,26] for tested MM probes in respect of non-milled (coarse-grained) REHE-0 one, the results being gathered in Table 4. These data clarify that at n = 200–500 min−1, the free-volume changes in MM arsenicals correspond to the scheme of direct Ps-to-positron trapping conversion due to positive both In and Iint intensities.

Table 4 PAL-trapping modes determined within x3–x2-CDA describing nanostructurization in pelletized β-As4S4-based arsenicals in respect of different reference probes
Full size table

In REHE-200 pellet, the spherical Ps traps with R3 = 0.286 nm disappear (see Table 3), being replaced by positron traps with defect-specific lifetime τint = 0.335 ns (see Table 4). These sites can be identified as interfacial free-volume holes between neighboring crystallite grains forming so-called triple junctions (TJs) [10, 22,23,24,25,26, 40]. With known semiempirical correlations for As–S compounds [41,42,43], these positron traps can be ascribed to bi-/tri-atomic vacancies characterized by (τint  −  τ NPb ) = 0.09 ns and τint/τ NPb  = 1.37 (Table 4). These defects are stabilized in preferential crystalline environment, as it follows from τ NPb approaching defect-free bulk lifetime in crystalline arsenic sulfides [41, 44]. Amorphization is inessential in REHE-200 sample, in full respect of low amorphization degree derived from the FSDP-related XRPD.

The MM-driven amorphization is enhanced in REHE-500 sample subjected to MM under higher speed. Despite general direction of free-volume evolution which does not change in this sample, the Ps-to-positron trapping conversion is more suppressed (due to κ NPd  = 1.20 ns−1) as compared with REHE-200 (κ NPd  = 1.59 ns−1). The positron-trapping defects appeared instead of Ps traps with R3= 0.286 nm (Table 3) are characterized by higher volumes in respect of τint = 0.369 ns (Table 4), which can be ascribed rather to quadruple vacancies in As–S alloys [41,42,43]. The chemical environment of these positron-trapping TJs is preferentially amorphous in view of τ NPb  = 0.281 ns, which closely approaches the defect-free bulk lifetime in glassy As–S [41, 42].

Conceptually, despite the same initial state, the studied MM arsenicals are not linked by sole technology (because of changed rotational speeds n, resulting in different structural transformations in the milled substance). Nevertheless, we can apply the developed approach for REHE samples to clarify the microstructural picture of their differentiation, assuming unchanged origin of responsible free-volume elements. The results of such comparison employing x3–x2-CDA for REHE-500 pellet in respect of REHE-200 one are also given in Table 4. It is evident that greater speed n leads to more amorphous structure of MM arsenical, possessing positron-trapping sites with defect lifetime τint = 0.372 ns (proper to multi-atomic vacancies [41,42,43]) appeared instead of Ps traps in an amorphous environment (due to τ NPb = 0.289 ns correlated with bulk lifetime in glassy As–S [41, 42]).

However, the character of trapping conversion changes drastically in REHE-600 pellet, where crystallite agglomeration associated with decreased specific surface area prevails. Both In and Iint intensities occur to be negative (in respect of REHE-0, Table 4), testifying in a favor of positron-to-Ps trapping conversion (which can be considered as inverse Ps-to-positron trapping conversion), associated with more intensive free-volume generation due to increased \( \tau_{{{\text{av}}.}}^{\varSigma } \) = 0.334 ns (see Table 2). The NPs agglomeration under these MM conditions is accompanied by elimination of positron-trapping TJs between contacting crystallites (with defect lifetime τint= 0.338 ns character for bi/tri-atomic vacancies) and appearance of extended Ps-trapping holes. Irrespective of enhanced degree of amorphization, this process prevails mainly in crystalline environment of REHE-600 pellet (due to τ NPb = 0.243 ns close to non-defect bulk lifetimes in crystalline arsenic sulfides [41, 44]).

Again, by assuming that REHE samples are interlinked only by physically correlated states, which can be validated for unchanged origin of respective free-volume elements responsible for their PAL spectra, the difference in free-volume structure can be unambiguously parameterized for REHE-600 pellet taken in respect of REHE-500 as a reference. Within such comparative consideration, it seems that less amount of positron traps with τint= 0.358 ns (corresponding to multiatomic vacancy clusters) are stabilized in REHE-600 pellet affected by MM at n = 600 min−1. These free-volume entities disappear from mixed crystalline–amorphous environment proper to more amorphized REHE-500 sample, as it can be expected from calculated τ NPb = 0.263 ns, which is higher than τb in crystalline, but lower than in glassy As–S alloys [41,42,43,44]).

So in contrast to substances possessing poor glass-forming ability, and thus obeying MM-driven size-dependent pressure-induced amorphization [1] in respect of crystalline destabilization model [45], the directly synthesized β-As4S4-based arsenicals are distinguished by continuous generation of amorphous phase under speed-increased high-energy MM. These findings as it follows from above research (especially, the PAL spectroscopy data on responsible free-volume elements) testify rather in a favor of “shell” kinetic model [46], treated this phenomenon in terms of intensive defect accumulation in parent β-As4S4 crystalline phase. Such defects appear firstly at grain boundaries, and amorphous phase nucleates heterogeneously followed by stretching into interior, thus creating mixed crystalline–amorphous environment for TJs between contacting grains.

These PAL-responsible elements are sketched in Fig. 4. Under MM with n = 200–500 min−1, the NPs aggregation is accompanied by transformation of free-volume entities within Ps-to-positron trapping-conversion scheme. The Ps-trapping holes between loosely packed crystalline–amorphous grains and positron-trapping TJs between β-As4S4 crystallites (depicted in Fig. 4b, c) are character for non-milled REHE-0. Under low amorphization (due to MM at n = 200 min−1), the Ps-holes transform into positron traps in mainly crystalline environment (see Fig. 4c). With increased rotational speed (n = 500 min−1), this process occurs in an amorphous environment (see Fig. 4d). Finally, under highest rotational speed in REHE-600, the NPs agglomeration starts, this process being accompanied by disappearing of TJs between grains in both crystalline (Fig. 4c) and crystalline–amorphous environment (Fig. 4d) into inter-NPs Ps-trapping holes (see Fig. 4b).

Figure 4
figure 4

Schematic view of PAL-responsible free-volume entities in MM β-As4S4-based arsenicals: inter-grain Ps-trapping holes (red-shadowed, a, b) and inter-crystallite positron-trapping TJs (yellow-shadowed, c, d) in preferential crystalline (a, c) and amorphous (b, d) environment (crystalline phase is crosshatched, and amorphous phase is blue-colored)

Full size image

Amorphization by ab initio quantum-chemical CINCA modeling

The cage-type As4S4 molecule character for realgar α-As4S4 structure [44] can be accepted as starting element for MM-driven amorphization of directly synthesized β-As4S4-based REHE arsenicals. This is well confirmed by obviously reduced intensities of all bands corresponding to this molecular unit in the Raman scattering spectra of MM REHE-200 and REHE-600 samples, especially as compared with non-milled REHE-0 and REHE-100 pellets [9].

The optimized configuration of this monomer As4S4 molecule nominating geometrical positions of all atoms which is as follows from CINCA simulation is shown in Fig. 5, the bond distances and angles (which occur to be in an excellent agreement with known experimental data [47]) being given previously in [44]. To estimate network-forming ability of amorphized network, the forming energy of this molecule (Ef = − 0.58 kcal/mol) is defined in respect of the energy of single AsS3/2 pyramidal unit (− 79.404 kcal/mol), as it is typically accepted in CINCA modeling [13]. The network-forming clusters can be derived from this As4S4 molecule by breaking corresponding sulfur atoms, linking them with surrounding environment through S1/2…S1/2 chains. For modeling purpose, these dangling bonds are terminated by hydrogen H atoms (allowing full saturation of covalent bonding), and thus overall forming energies for such molecular self-closed clusters can be simply calculated. By subtracting the energy of H-based terminated atomic groups, the proper energy of network clusters can be recalculated as it is demonstrated in more details elsewhere [13, 29, 30].

Figure 5
figure 5

Geometrically optimized configuration of realgar-type As4S4 molecule and its projection on plane of S atoms (S and As atoms are depicted by yellow and red colors, respectively)

Full size image

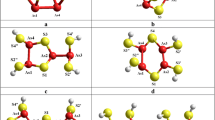
Full structural diversity for starting As4S4 molecule (see Fig. 5), composed of four S and four As atoms linked in D2d symmetry (thus evolving maximum number of short-ring entities, i.e., four pentagons and four hexagons), is described by four types of network clusters formed due to single breaking in (S1) position, two types of double breaking in (S1)–(S3) and (S1)–(S4) positions, and triple breaking in (S1)–(S2)–(S3) positions. The geometrically optimized configurations of these clusters are shown in Fig. 6, the character-forming energies (in respect of the energy of AsS3/2 pyramid) being given in Table 5.

Figure 6
figure 6

Geometrically optimized configurations of some network-forming clusters derived from As4S4 molecule by single breaking in (S1) position (a), double breaking in (S1) and (S3) positions (b), double breaking in (S1) and (S4) positions (c), and triple breaking in (S1), (S2), and (S3) positions (d). The terminated H atoms are denoted by gray circles, S and As atoms are marked as in Fig. 5 (see text for more details)

Full size image
Table 5 Cluster-forming energies Ef determined in respect of the energy of single AsS3/2 pyramid for simulated As4S4-derivative clusters
Full size table

It is seen that destruction of As4S4 molecule due to single breaking in (S1) position (Fig. 5) followed by network polymerization due to two S–H bonds (thus forming As4S5H2 molecular cluster, see Fig. 6a) is energetically plausible. Indeed, this process needs only Ef = − 1.29 kcal/mol energy to be realized (i.e., twice more as forming energy of monomer As4S4 molecule, see Table 5). Under such destruction–polymerization transformation, only three short-ring entities remain, these being two pentagons and one hexagon (Fig. 6a). Previously, such changes in As4S4 clusters were considered by Musgraves et al. [48] to explain the mechanism of photo-induced effects in As-rich arsenicals. Double breaking in (S1)–(S3) and (S1)–(S4) positions (see Fig. 5) followed by network polymerization remains only one short-ring entity in the remnants of As4S4 molecule (i.e., As4S6H4 molecules), this being pentagon (Fig. 6b) or hexagon (Fig. 6c). The former (the pentagon-based As4S4 derivative) was considered in [49] as resulting from broken chemical ordering in arsenic sulfide glasses. Nevertheless, the energetic costs for such transformations seem to be too expensive (see Table 5) to be considered as realistic competitive scheme of MM-driven amorphization of β-As4S4 arsenical. Triple breaking in (S1)–(S2)–(S3) positions (see Fig. 5) destroys all short-ring entities, transforming monomer As4S4 molecule into network of two (As–S) bonds interlinked by homonuclear (As–As) bonds (the corresponding As4S7H6 molecular cluster is shown in Fig. 6d). This destruction–polymerization process needs only Ef = − 1.72 kcal/mol energy, and, correspondingly can be accepted as quite possible for realization in As4S4-based network.

So, in respect of CINCA modeling, the structural matrix of directly synthesized β-As4S4 can be imagined as admixture of crystalline phase composed of monomer cage-type As4S4 molecules and some amount of isocompositional amorphous phase, built of network-forming fragments, mainly single- and triple-broken As4S4 derivatives. This phase equilibrium is responsible for the FSDP-related XRPD in (Fig. 1a) and free-volume distribution governing the PAL spectrum of REHE-0 sample (Fig. 3). The effect of high-energy MM can be identified as destructive action on As4S4 molecules and existing amorphous phase, transforming them into the network of triple-broken As4S4-molecule derivatives. The topologically changed amorphous phase possessing no short-ring entities modifies the FSDP parameters of β-As4S4 arsenicals milled with increasing speed n as shown in Table 1. This structurally inhomogeneous amorphous phase (composed preferentially of single- and triple-broken As4S4 derivatives) is also responsible for modified environment of PAL-detectable free-volume elements (inter-grain Ps-trapping holes and inter-crystallite positron-trapping TJs schematically shown in Fig. 4) in MM β-As4S4 arsenicals.

Conclusions

Continuous generation of amorphous phase in addition to parent crystalline phase was studied in directly synthesized β-As4S4 arsenicals affected by high-energy dry MM at 100–600 min−1 speeds.

In respect of the FSDP-related XRPD and PAL data, the nanocrystalline and amorphous forms coexist among milling products, testifying in favor of solid-state amorphization by “shell” kinetic model. The appeared amorphous phase is identified as compositionally authentic to arsenic monosulfide, but different in intermediate-range ordering from stoichiometric As2S3. The amorphized arsenicals exhibit the XRPD halos typical for glassy As–S with the FSDP positioned near 1.14 Å−1, corresponding to 5.49 Å in a real-space interplanar distance and 27.0 Å in a correlation length, these parameters being in a good accordance with those extrapolated for melt-quenched glassy alloys. The networks of MM arsenicals are assumed to be built of randomly packed cycle-type entities proper to As4S4 cage-like formations. Depressing and time-enhancing trend in the peak of the PAL spectrum is accepted as direct indicative of MM-driven amorphization. Observed trapping-conversion processes are parameterized in respect of non-milled β-As4S4 arsenical employing the x3–x2-CDA. It is shown that at low rotational speed (200 min−1), the positron traps equivalent to bi-/tri-atomic vacancies appear instead of Ps traps. At higher speed (500 min−1), these traps grow to quadruple vacancies sizes, the reduced Ps-to-positron trapping conversion occurring in amorphous environment. Increase in the speed to 600 min−1 is concomitant with void evolution through positron-to-Ps trapping conversion. Despite enhanced amorphization, this process is identified as elimination of positron-trapping triple junctions between neighboring crystallites and appearance of Ps traps in preferentially crystalline environment.

In respect of ab initio quantum-chemical CINCA modeling, the structural matrix of directly synthesized β-As4S4 arsenical is imagined as admixture of crystalline phase composed of monomer As4S4 molecules and some amount of isocompositional amorphous phase, built of network-forming fragments, mainly single- and triple-broken As4S4-molecule derivatives. Effect of high-energy MM is identified as destructive action on monomer As4S4 molecules and existing amorphous phase, transforming them preferentially into the network of triple-broken As4S4-molecule derivatives.