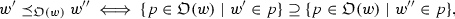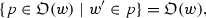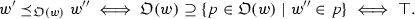Abstract
The semantics of progressive sentences presents a challenge to linguists and philosophers alike. According to a widely accepted view, the truth-conditions of progressive sentences rely essentially on a notion of inertia. Dowty (Word meaning and Montague grammar: the semantics of verbs and times in generative grammar and in Montague’s PTQ, D. Reidel Publishing Company, Dordrecht, 1979) suggested inertia worlds to implement this “inertia idea” in a formal semantic theory of the progressive. The main thesis of the paper is that the notion of inertia went through a subtle, but crucial change when worlds were replaced by events in Landman (Nat Lang Semant 1:1–32, 1992) and Portner (Language 74(4):760–787, 1998), and that this new, event-related concept of inertia results in a possibility-based theory of the progressive. An important case in point in the paper is a proof that, despite its surface structure, the theory presented in Portner (1998) does not implement the notion of inertia in Dowty (1979); rather, it belongs together with Dowty’s earlier, 1977 theory according to which the progressive is a possibility operator.
Similar content being viewed by others
Notes
As one of the anonymous reviewers has pointed out, “the general squishiness of intuitions” about the truth-conditions of progressive sentences is itself something to be explained.
See Vendler (1967) for the origin of the aspectual classification of verbs, verbal phrases, and sentences into states, activities, achievements, and accomplishments.
“The meaning of an accomplishment verb phrase invariably involves the coming about of a particular state of affairs. [...] I maintain that it is impossible to give an adequate semantic analysis of accomplishment verb phrases without providing for the entailment that such a result-state comes about. Yet it is just this entailment that such a result-state comes about which fails when the accomplishment verb phrase appears in the progressive tense. [...] This is the ‘imperfective paradox’.” (Dowty 1977: 261)
Dowty (1979: 147).
By saying “not true” I leave open the possibility that (8) and (9) might not have a truth value at the moment when the coin is snatched, cf. the discussion in Naumann and Piñón (1997). However, the question of truth value gaps will be ignored below.
‘\({{\mathrm{\bigwedge }}}\)’, ‘\({{\mathrm{\bigvee }}}\)’, ‘\(\mathrel {\Rightarrow }\)’, ‘
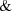 ’ and ‘\(\vee \)’ are the metalinguistic symbols used in this paper for universal and existential quantification, conditional, conjunctive and disjunctive statements, respectively.
’ and ‘\(\vee \)’ are the metalinguistic symbols used in this paper for universal and existential quantification, conditional, conjunctive and disjunctive statements, respectively.While both Dowty (1977) and Dowty (1979) talk freely about events in the explication of the respective theories, there is no formal commitment to events in the theories themselves. The reason for this, as given in Dowty (1977: fn. 7), is that Dowty takes events to be entities reducible to the properties of temporal intervals. On this view, the incorporation of a category of events into the ontology is superfluous.
Dowty (1979: 154).
For the non-final subinterval relation ‘\(\sqsubset \)’, see Formulas (11g) and (16g) in “Appendix A”. Actually, the definition in Dowty (1977) contains the weaker “proper subinterval” relation, but this is probably a harmless simplification because the same definition reprinted in Dowty (1979: 146) uses the non-final subinterval relation.
See Dowty (1979: 147–148).
We will also see a slightly different characterization of inertia worlds below.
As Dowty points it out himself, these characterizations fall short of being definitions. Giving an explicit definition of inertia worlds is one of the main goals in Portner (1998).
Dowty (1979: 148).
As Vlach (1981: 286) points out, “In the natural course of events the [truck] will hit [Mary] and [she] will never cross the street; it would be not only unnatural but a miracle for [Mary] cross the street to become true.”
The theory in Landman (1992) can also be interpreted as a \({{\mathrm{{\Box }}}}\)-type theory from a purely formal point of view. But this is just a byproduct of the fact that the set of possible worlds on which the truth-conditions of the progressive depend is always a singleton set in Landman (1992). This is not so in non-trivially \({{\mathrm{{\Box }}}}\)-type theories such as the one in Dowty (1979).
See “Appendix B”.
The name \({{\mathrm{{\mathsf {NI}}}}}\) is apparently the abbreviation of “No Interruptions.”
Portner (1998) does not contain a dedicated section in which the model theoretic background of the theory is summarized, so we have to infer the missing details from the examples and the explanations in the text.
As I have already mentioned, the domain of the modal base \({{\mathrm{{\mathsf {Circ}}}}}\) will be different in Portner’s (1998) final theory.
“\({{\mathrm{{\mathsf {Prog}}}}}(\varphi )\) is true at a pair of an interval and world \(\langle i,w\rangle \) iff there is an event e in w such that \(T(e)=i\) and for all worlds \(w'\) in \({{\mathrm{{\textsc {Best}}}}}({{\mathrm{{\mathsf {Circ}}}}}, {{\mathrm{{\mathsf {NI}}}}}, e)\), there is an interval \(i'\) which includes i as a nonfinal subinterval, such that \(\varphi \) is true at \(\langle i',w'\rangle \).”
This is also suggested by the fact that in the final theory, interval variables are completely replaced by event variables in the definition of the progressive operator; see Portner (1998: 782).
Portner (1998: 774).
Portner (1998: 782).
This interpretation is also perfectly in accordance with the accepted interpretation of the concept of culmination, even though the event property is often suppressed. However, this is only “loose talk;” as Zucchi (1999) argues convincingly, culminations should always be relativized to an event property parameter: an event does not culminate simpliciter, but always culminates with respect to an event property \(\varphi \). See Zucchi (1999: 185).
Portner (1998: 772).
See the second italicized phrase in the quotation above, and also, e.g.: “the ordering source \({{\mathrm{{\mathsf {NI}}}}}(e)\) provides a definition of what it is for a given event not to be interrupted” (Portner 1998, 777).
Briefly, the Limit Assumption is the condition that for every world \(w\in {\mathcal {W}}\), \({{\mathrm{{\textsc {Best}}}}}\bigl ({{\mathrm{{\mathfrak {B}}}}}(w),{{\mathrm{{\mathfrak {O}}}}}(w)\bigr ) \ne \emptyset \). (See Assumption 1 in “Appendix B”.) For the fact that Portner (1998) subscribes to the Limit Assumption, see Portner (1998: 771).
If \(\mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\cap \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\ne \emptyset \), then \({{\mathrm{{\textsc {Best}}}}}\bigl ({{\mathrm{{\mathfrak {B}}}}}(w),{{\mathrm{{\mathfrak {O}}}}}(w)\bigr ) = \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\cap \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\).
Proof Assume that \(\mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\cap \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\ne \emptyset \), and take any \(w'\in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\cap \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\). According to the definition of the ideality preorder (see Definition 17 in “Appendix B”), for every \(w''\),
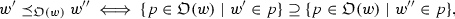
and note that in the case of \(w'\),
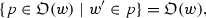
therefore, \(w'\) is at least as ideal as any world \(w''\in {\mathcal {W}}\):
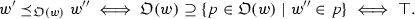
Since \(w'\preceq _{{{\mathrm{{\mathfrak {O}}}}}(w)} w''\) for all \(w''\in {\mathcal {W}}\), and \(\mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\subseteq {\mathcal {W}}\), \(w'\preceq _{{{\mathrm{{\mathfrak {O}}}}}(w)} w''\) for all \(w''\in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\). Therefore the following holds:
$$\begin{aligned} w'\in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\cap \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\mathrel {\Rightarrow }w'\in {{\mathrm{{\textsc {Best}}}}}\bigl ({{\mathrm{{\mathfrak {B}}}}}(w),{{\mathrm{{\mathfrak {O}}}}}(w)\bigr ). \end{aligned}$$To prove the equality, we also have to show that
$$\begin{aligned} w'\not \in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\cap \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\mathrel {\Rightarrow }w'\not \in {{\mathrm{{\textsc {Best}}}}}\bigl ({{\mathrm{{\mathfrak {B}}}}}(w),{{\mathrm{{\mathfrak {O}}}}}(w)\bigr ). \end{aligned}$$If \(w'\not \in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\cap \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\), then \(w'\not \in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\) or \(w'\not \in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\). On the one hand, if \(w'\not \in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\), then \(w'\not \in {{\mathrm{{\textsc {Best}}}}}\bigl ({{\mathrm{{\mathfrak {B}}}}}(w),{{\mathrm{{\mathfrak {O}}}}}(w)\bigr )\). On the other hand, if \(w'\not \in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\), then \(w'\not \in {{\mathrm{{\textsc {Best}}}}}\bigl ({{\mathrm{{\mathfrak {B}}}}}(w),{{\mathrm{{\mathfrak {O}}}}}(w)\bigr )\) because, by the original assumption, there is at least one world \(w''\) in \(\mathop {\bigcap }\limits {{\mathrm{{\mathfrak {O}}}}}(w)\), and this world \(w''\) is strictly more ideal than \(w'\), which means \(w'\) cannot be in the set of the best worlds. \(\square \)
Portner (1998: 779).
See formula (46)b. in Portner (1998: 782).
Portner (1998: 785).
Cf. Portner (1998: 779).
Based on Gendler Szabó’s (2004) example.
Note that this does not mean that an independent notion of inertia could not be combined with events, yielding a genuinely \({{\mathrm{{\Box }}}}\)-type theory of the progressive. On the contrary, this is what happens in, e.g., Asher (1992): Asher has a theory of inertia (more precisely, normalcy) which is independent of his theory of the progressive and, therefore, can fulfill the role that inertia plays in Dowty (1979). I am not discussing Asher’s (1992) theory in the paper, since a detailed discussion of Asher (1992) can be found in Varasdi (2014).
\(\mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\mathop {=}\limits ^{{\mathrm{def}}}\mathop {\bigcap }\limits _{p\in {{\mathrm{{\mathfrak {B}}}}}(w)}p\).
Note that as long as we consider (however big but) finite ordering sources, the Limit Assumption is automatically satisfied (provided that the modal base is consistent).
If we drop the Limit Assumption, the definitions of the modal operators become more complicated: for all \(\alpha \in \textsf {Form}\) and \(u,v,z\in \mathop {\bigcap }\limits {{\mathrm{{\mathfrak {B}}}}}(w)\),

and possibility is defined as the dual of the necessity operator, i.e.,
$$\begin{aligned}{}[ \! [ {{\mathrm{{\Diamond }}}}(\alpha ) ] \! ]^{\mathcal {K}}_{w} = {\mathbf {1}}\mathop {\iff }\limits ^{\mathrm{def}}[ \! [ \lnot {{\mathrm{{\Box }}}}(\lnot \alpha ) ] \! ]^{\mathcal {K}}_{w} = {\mathbf {1}}. \end{aligned}$$
References
Abusch, D. (1985). On verbs and time (Montague Grammar, Semantics, Aspect, Tense). Ph.D. thesis, University of Massachusetts, Amherst.
Asher, N. (1992). A default, truth conditional semantics for the progressive. Linguistics and Philosophy, 15(5), 463–508.
Bennett, M., & Partee, B. (1972). Toward the logic of tense and aspect in English. Technical report, System Development Corporation, Santa Monica, CA.
Bonomi, A. (1997). The progressive and the structure of events. Journal of Semantics, 14, 173–205.
Dowty, D. R. (1977). Towards a semantic analysis of verb aspect and the English ‘imperfective’ progressive. Linguistics and Philosophy, 1(1), 45–77.
Dowty, D. R. (1979). Word meaning and Montague grammar: The semantics of verbs and times in generative grammar and in Montague’s PTQ. Dordrecht: D. Reidel Publishing Company.
Dowty, D. R., Wall, R. E., & Peters, S. (1981). Introduction to montague semantics. Studies in linguistics and philosophy (Vol. 11). Dordrecht: Kluwer Academic Publishers.
Szabó, Z. G. (2004). On the progressive and the perfective. Noûs, 38(1), 29–59.
Kenny, A. (1963). Action, emotion and will. New York: Routledge & Kegan Paul.
Kratzer, A. (1977). What ‘must’ and ‘can’ must and can mean. Linguistics and Philosophy, 1(3), 337–356.
Kratzer, A. (1981). The notional category of modality. In H.-J. Eikmeyer & H. Rieser (Eds.), Words, worlds, and contexts (pp. 38–74). Berlin: Walter de Gruyter.
Kratzer, A. (1991). Modality. In A. von Stechow & D. Wunderlicht (Eds.), Semantics: An international handbook of contemporary research (pp. 639–650). Berlin: Walter de Gruyter.
Landman, F. (1992). The progressive. Natural Language Semantics, 1, 1–32.
Lewis, D. (1981). Ordering semantics and premise semantics for counterfactuals. Journal of Philosophical Logic, 10(2), 217–234.
Montague, R. (1973). The proper treatment of quantification in ordinary English. In J. Hintikka, J. Moravcsik, & P. Suppes (Eds.), Approaches to natural language: Proceedings of the 1970 stanford workshop on grammar and semantics (pp. 221–242). Dordrecht: Reidel.
Naumann, R., & Piñón, C. (1997). Decomposing the progressive. In P. Dekker, M. Stokhof, & Y. Venema (Eds.), Proceedings of the 11th Amsterdam Colloquium (pp. 241–247). Amsterdam: University of Amsterdam.
Nute, D. (1984). Conditional logic. In F. Guenthner & D. M. Gabbay (Eds.), Handbook of philosophical logic (Vol. II, pp. 387–439). Dordrecht: D. Reidel Publishing Company.
Portner, P. (1998). The progressive in modal semantics. Language, 74(4), 760–787.
Thomason, R. (1970). Indeterminist time and truth-value gaps. Theoria, 3, 264–281.
Varasdi, K. (2014). Making progressives: Necessary conditions are sufficient. Journal of Semantics, 31(2), 179–207.
Vendler, Z. (1957). Verbs and times. The Philosophical Review, LXVI, 143–160. (Reprinted in Vendler 1967).
Vlach, F. (1981). The semantics of the progressive. In P. Tedeschi & A. Zaenen (Eds.), Tense and aspect (Vol. 14, pp. 271–292)., Syntax and semantics New York: Academic Press.
Wolfson, B. (2012). Agential knowledge, action and process. Theoria, 78(4), 326–357.
Zucchi, S. (1999). Incomplete events, intensionality and imperfective aspect. Natural Language Semantics, 7(2), 179–215.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: The Language \({\mathcal {L}_{\text {Prog}}}\)
1.1 A. 1 Syntax
We assume a type-theoretic language \({\mathcal {L}_{\text {Prog}}}\) with following basic types (corresponding to events, intervals, and truth-values, respectively):
Types are generated from basic types in the usual way as the smallest set satisfying the following conditions:
The language has nonlogical constants \(\mathbf {Con}_{\sigma }\) and variables \(\mathbf {Var}_{\sigma }\) in every type \(\sigma \); these together constitute the set of \(\sigma \)-type terms \(\mathbf {Term}_{\sigma }\):
The set of variables \(\mathbf {Var}\), constants \(\mathbf {Con}\) and terms \(\mathbf {Term}\) are the collections of variables, constants and terms for every possible type:
We define the set of well-formed expressions recursively as follows. Terms are well-formed expressions:
The following clauses describe the ways in which complex expressions are made out of simpler ones in \({\mathcal {L}_{\text {Prog}}}\):




The set of well-formed expressions of the language consists of the union of the well-formed expressions in all types:
1.2 A. 2 Semantics
In order to interpret the well-formed expressions of \({\mathcal {L}_{\text {Prog}}}\), we assume the following comprehensive frame,
where the respective components are explained in Sect. 3. Based on the set of moments \(\langle {\mathcal {T}},\le \rangle \), the set of intervals are defined as follows:

The domains of the typed expressions of \({\mathcal {L}_{\text {Prog}}}\) are given as follows.
For basic types:
and for complex types:

By a model of \({\mathcal {L}_{\text {Prog}}}\) we understand the following sequence of components:
where \({\mathcal {F}}\) is the frame above; and \([ \! [ \cdot ] \! ]^{\mathcal {{\mathcal {M}}}}_{}:\mathbf {Con}_{\sigma }\rightarrow ({\mathcal {W}}\rightarrow \mathbb {D}_{\sigma })\) is the interpretation function assigning intensions to the non-logical constants in every type \(\sigma \in \mathbf {Type}\). The other components are explained in the text [\({\mathcal {H}}\) and \({\mathsf {Inr}}\) in Sect. 4 on Dowty (1977) and Sect. 5 on Dowty (1979), and \({{\mathrm{{\mathsf {Circ}}}}}\), \({{\mathrm{{\mathsf {NI}}}}}\) in Sect. 7 on Portner (1998)].
As is usual, we use variable assignments to extend the interpretation function \([ \! [ \cdot ] \! ]^{\mathcal {{\mathcal {M}}}}_{}\) to arbitrary terms, where an assignment function \(\theta :\mathbf {Var}_{\sigma }\rightarrow \mathbb {D}_{\sigma }\) assigns values to variables in every type \(\sigma \).
The denotation \([ \! [ \cdot ] \! ]^{\mathcal {{\mathcal {M}}}}_{\theta ,w}\) of a well-formed expression of the language is computed relative to a model \(\mathcal {{\mathcal {M}}}\), variable assignment \(\theta \) and possible world w according to the following clauses.
The denotation of terms (nonlogical constants and variables) are given by clauses (14) and (15):
The denotation of the complex expressions of \({\mathcal {L}_{\text {Prog}}}\) are given by the following clauses (16a)–(16i):







Finally, for every expression \(\alpha \) of type \({{\mathbf {t}}}\), the proposition expressed by \(\alpha \) is given by the following definition:

Appendix B: Kratzer’s Theory of Modality
Since Portner (1998) uses Kratzer’s modal framework (Kratzer 1977, 1981, 1991), I summarize its main points very briefly below. The point of this section is not that of making a historically faithful survey of Kratzer’s theory but, rather, the description of the theoretical means and terminology used in Sect. 7.
For expository purposes in this section, I define a simple propositional language \({\mathcal {L}_K}\) containing two modal operators \({{\mathrm{{\Box }}}}\) and \({{\mathrm{{\Diamond }}}}\) as follows. Let \(\mathbf {Atom}\) be a denumerable set of atomic formulas \(\psi , \psi ', \psi '',\dots \) The set of formulas \(\mathbf {Form}\) is the smallest set satisfying the following clauses:
Having the syntax in place, let us turn to the semantics. The formulas of \({\mathcal {L}_K}\) are interpreted in a model \(\mathcal {K} = \langle {\mathcal {W}}, {{\mathrm{{\mathfrak {B}}}}}, {{\mathrm{{\mathfrak {O}}}}},[ \! [ \cdot ] \! ]^{\mathcal {K}}_{}\rangle \), where \({\mathcal {W}}\) is a nonempty set of possible worlds, \({{\mathrm{{\mathfrak {B}}}}}:{\mathcal {W}}\rightarrow \wp (\wp ({\mathcal {W}}))\) is a function called the modal base, \({{\mathrm{{\mathfrak {O}}}}}:{\mathcal {W}}\rightarrow \wp (\wp ({\mathcal {W}}))\) is a function called the ordering source, and \([ \! [ \cdot ] \! ]^{\mathcal {K}}_{}:\textsf {Atom}\rightarrow ({\mathcal {W}}\rightarrow \{{\mathbf {0}},{\mathbf {1}}\})\) is the interpretation function assigning characteristic functions of propositions—i.e., sets of worlds—to the atomic formulas; intuitively, \([ \! [ \alpha ] \! ]^{\mathcal {K}}_{}\) is the characteristic function of the set of worlds at which \(\alpha \) is true in model \(\mathcal {K}\). The modal base and the ordering source are called conversational backgrounds.
The denotation of a formula not containing \({{\mathrm{{\Box }}}}\) or \({{\mathrm{{\Diamond }}}}\) as main operator is given at a possible world w as follows:
Crucial to the interpretation of the two modal operators \({{\mathrm{{\Box }}}}\) and \({{\mathrm{{\Diamond }}}}\) is the ideality ordering \(\preceq _{{{\mathrm{{\mathfrak {O}}}}}(w)}\) over \({\mathcal {W}}\) induced by \({{\mathrm{{\mathfrak {O}}}}}\) in the following way:
Definition 17
(Ideality preorder) Let the ordering source \({{\mathrm{{\mathfrak {O}}}}}(w)\) be assigned to possible world w. For any \(w',w''\in {\mathcal {W}}\), \(w'\) is said to be at least as good as \(w''\) with respect to \({{\mathrm{{\mathfrak {O}}}}}(w)\), in notation: \(w'\preceq _{{{\mathrm{{\mathfrak {O}}}}}(w)} w''\), if \(w'\) verifies every proposition in \({{\mathrm{{\mathfrak {O}}}}}(w)\) that \(w''\) verifies:

Based on \(\preceq _{{{\mathrm{{\mathfrak {O}}}}}(w)}\), we can define the set of “best worlds” which contains those worlds in the modal base \({{\mathrm{{\mathfrak {B}}}}}(w)\) that verify maximal subsets of the ordering source \({{\mathrm{{\mathfrak {O}}}}}(w)\):Footnote 39
Definition 18
(Best worlds)

As Kratzer points out, there is in general no guarantee that the set of the best worlds is not empty, that is, in the general case she does not subscribe to the Limit Assumption:Footnote 40
Assumption 1
(Limit Assumption) For every world \(w\in {\mathcal {W}}\),
In applications of Kratzer’s theory, the Limit Assumption is usually assumed to hold.Footnote 41 In this case the definition of the modal operators in \({\mathcal {L}_K}\) are as follows.Footnote 42
Definition 19
(\({{\mathrm{{\Box }}}}\) and \({{\mathrm{{\Diamond }}}}\))

Rights and permissions
About this article
Cite this article
Varasdi, K. Worlds, Events, and Inertia. J of Log Lang and Inf 26, 303–332 (2017). https://doi.org/10.1007/s10849-017-9253-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-017-9253-3




 ’ and ‘
’ and ‘ ’, see Formulas (
’, see Formulas (