Introduction

Job scheduling is a major area of interest within the field of production planning. A production organization that can often be observed in practice is the job shop, where each production job has a set of operations to be processed successively. Each operation is processed without interruption by a continuously available production resource (e.g. a machine), and each resource can only process one operation at a time. In the job shop scheduling problem, the objective is to define operation sequences in such a way, that an objective function (e.g., makespan or flow time minimization) is optimized. Another common form is the flow shop, where every job has the same processing order regarding the resources. A specialized form of the flow shop is the permutation flow shop, where the sequencing decision can only be made at the first resource (cf. transfer lines) (Naderi & Ruiz, 2010).

However, in realistic manufacturing environments, further planning parameters must be considered, which can be independent of the production organization. Especially dynamic events such as machine failures endanger baseline schedules and can require re-scheduling procedures. This leads to a loss of time, additional manufacturing costs, missing production goals, customer dissatisfaction and stress for employees (Liu et al., 2017; Mailliez et al., 2021; Shen et al., 2016). Dynamic events can be resource-dependent (internal events such as uncertain setup and processing times, machine failures, uncertain material delivery windows or unplanned rework) or customer-related (external events such as new unplanned orders, order cancellations, changed due dates or order priorities) (Rahmani & Heydari, 2014).

For this reason, there is a need for dynamic or stochastic scheduling methods that take into account uncertainties. Proactive scheduling, also called robust or predictive scheduling, plays a central role in the treatment of dynamic events in advance. Instead of a reactive approach based on subsequent or successive re-scheduling, uncertainties are considered ex ante while generating baseline schedules. These schedules should be as insensitive as possible to disruptions so that re-scheduling situations are prevented (de Vonder et al., 2007; Goren & Sabuncuoglu, 2008; Jorge Leon et al., 1994; Negri et al., 2020).

As critical indicators for proactive schedules, robustness and stability metrics have been studied widely. Robustness R is defined as the difference between expected performance \(P_E\) and real performance \(P_R\) (see Eq. 1)(Jorge Leon et al., 1994), whereby the performance corresponds to the main scheduling objective value (MSOV), e.g. makespan. If the difference is positive, the baseline schedule is too conservative. As a result, resources are not used optimally. If the difference is negative, the baseline schedule is too optimistic. This can lead to overload and time pressure. Due to the nature of minimization problems, an absolute robustness value is also used in some studies (see e.g. Al-Behadili et al.,2019; Goren & Sabuncuoglu, 2008). However, it is then not possible to take precise consideration of conservatism and optimism. The stability S indicates how precisely the operations \(o \in O\) are planned for the resources. A stability measure, often used in other studies, is defined as the sum of absolute deviations between expected operation completion times \(c_{E}\) and real operation completion times \(c_{R}\) (see Eq. 2) (Al-Behadili et al., 2019; Goren & Sabuncuoglu, 2008; Liu et al., 2017; Rahmani & Heydari, 2014).

$$\begin{aligned} R&= P_E - P_R \end{aligned}$$
(1)
$$\begin{aligned} S&= \sum \nolimits _{o \in O} |c_{E}^{o} - c_{R}^{o} | \end{aligned}$$
(2)

Depending on the chosen performance indicator, there is a conflict in balancing robustness and stability: Improving one metric can worsen the other (Goren & Sabuncuoglu, 2008). It has been shown that exact robust-stable scheduling is an NP-complete problem even in single machine environments (Bougeret et al., 2019). Recent studies have demonstrated heuristic methods to generate balanced robust-stable schedules. We identified two main paradigms to measure robustness and stability: using MCE or using surrogate measures. There are also two main ways to to balance robustness and stability: by creating neighborhood solutions or by adding slack times to critical operations (see Section “Literature review”). The problem with these approaches is, that they either do not explicitly optimize robustness and stability or require too much computing time. This can be a crucial hurdle in reactive real-time environments.

In recent years, several researchers have identified DRL as an appropriate optimization method for scheduling problems (see e.g. Kardos et al., 2021; Park et al., 2021). DRL is a machine learning technique to solve decision problems with deep artificial neural networks. Through conditioning, an autonomous virtual agent learns a policy on how to interact with a sequentially influenceable environment in order to achieve objectives and maximize the outcome. The iterative process can be formulated as a Markov Decision Process, which can be summarized as follows: The agent observes an environment state \(S_i\) and applies action \(A_i\). Based on the action effect, the environment is transferred to a new state \(S_{i+1}\) and a reward \(R_i\) is distributed to the agent (Morales & Zaragoza, 2012). As function approximators, deep neural networks are used to represent the policy gradually learned and to predict appropriate actions (output) for given state observations (input) (François-Lavet et al., 2018). Fully trained DRL agents achieve a very good compromise between result quality and computing time (Liu et al., 2020). However, after conducting a systematic literature review, we identify a notable lack of scientific approaches investigating, how DRL can be used to optimize and to balance robustness and stability in dynamic flow shops in the proactive stage. The contribution of this study is a proposal on how modern DRL techniques can be implemented to enable a good trade-off between robustness, stability and computing time (see Section “Trade-off between MSO, robustness and stability”).

This article is organized as follows: First, we present related studies with robust-stable scheduling approaches and highlight research gaps (see Section “Literature review”). After that, we show our method of how DRL can be used to dynamically modify operations by stretching or compressing processing times (see Section “Proposed approach”). We then carry out numerical experiments and benchmark different DRL models and metaheuristics in terms of computing time and result quality. In addition, the robustness/stability trade-off, the behavior and the scalability of DRL agents is examined (see Section “Computational study”). Finally, we summarize our results and present future research questions (see Section “Conclusions and future research”).

Literature review

In recent years, a considerable amount of literature has been published on proactive or reactive scheduling in different problem contexts such as project, production, crew or workforce planning. However, there is a relatively small body of literature that is concerned with pure proactive scheduling in production environments considering robustness and stability. The existing literature was analyzed with respect to the use of slack-based techniques, the use of simulation, the trade-off analysis of robustness and stability and the application of DRL for proactive scheduling problems. An overview of the reviewed papers is given in Table 1.

Dynamic environments and uncertainty modeling

A great deal of previous research has focused on rather simple environments, such as single machine (SM) and parallel machine (PM) environments, flow shops (FS), permutation flow shops (PFS), job shops (JS) or flexible job shops (FJS) (Goren & Sabuncuoglu, 2008; Goren et al., 2011; Liu et al., 2017; Shen et al., 2016; Vieira et al., 2017; Wang et al., 2022; Wu et al., 2020). Few authors have used more complex environments like dual resource JS (DRJS) or dual resource FJS (DRFJS) (Soofi et al., 2021; Xiao et al., 2019). Most researchers considered the minimization of makespan (\(C_{max}\)), flow time (F), total tardiness (T) resp. earliness/tardiness (E/T) as single or separate main scheduling objectives (MSO) (Davenport et al., 2001; Goren & Sabuncuoglu, 2008; Gonzalez-Neira et al., 2021; Jorge Leon et al., 1994; Liu et al., 2017; Rahmani & Heydari, 2014). Furthermore, the minimization of energy consumption (EC), setup time (ST), and idle time (IT) has been considered (Moratori et al., 2010; Sundstrom et al., 2017), some of which were taken into account simultaneously (Moratori et al., 2010; Salmasnia et al., 2014).

The greater part of the literature on proactive scheduling focuses on varying processing times (PT) (Juan et al., 2014; Rahmani & Heydari, 2014; Shen et al., 2016) or machine failures (MF) (Al-Behadili et al., 2019) separately or simultaneously (Negri et al., 2020). Gonzalez-Neira et al. (2021) and Vieira et al. (2017) considered varying setup times (ST) in addition to varying processing times. Sundstrom et al. (2017) considered internal delays (ID). It has been noted that external uncertainties (ex.) such as new job arrivals are only considered in the reactive stage (e.g. Moratori et al., 2010). Since we focus on proactive scheduling approaches, we did no further analysis on the considered external uncertainties. In the literature examined, uncertainties were often modeled by probability distributions (PD) (Al-Behadili et al., 2019; Davenport et al., 2001), intervals (Wang et al., 2022) or scenarios (Rahmani & Heydari, 2014; Soofi et al., 2021; Xiao et al., 2019). A scenario can be defined as a specific production situation from a finite set of possible situations that can occur with a certain probability or under certain conditions and is reflected in various parameters (e.g. processing times). Xiong et al. (2013) determined a failure probability (FB) for every machine considering the machine’s busy time and the total workload of all machines. Negri et al. 2020 used real-time sensor data (RTD) to model machine health conditions.

Table 1 Related work matrix
Full size table

Techniques to generate proactive schedules

One approach to solve a scheduling problem under uncertainty is to explicitly allow the insertion of slack or analyze a schedule’s slack (Davenport et al., 2001; Liu et al., 2017; Moratori et al., 2010; Salmasnia et al., 2014; Sundstrom et al., 2017; Xiong et al., 2013). The idea of slack-based techniques is to add additional time to certain activities, so that the schedule can absorb the effects of the uncertainty and avoid re-scheduling (Davenport et al., 2001; Sundstrom et al., 2017). Davenport et al. (2001) introduced two slack-based techniques: time window slack (TWS) and focused time window slack (FTWS). TWS ensures that each operation will have at least a specified amount of slack. FTWS additionally takes into account where along the temporal horizon the operation is scheduled. Interestingly, the authors claimed that later scheduled operations need more slack to improve robustness. Unlike other studies, Hatami et al. (2018) applied slack-based techniques in backward scheduling. Their approach aims at setting a suitable amount of slack at the beginning of the schedule.

Another approach to generate proactive production schedules is by creating neighborhood solutions and choosing the best neighbor found (Al-Behadili et al., 2019; Goren & Sabuncuoglu, 2008; Shen et al., 2016). Neighbors are feasible solutions that have a small distance in the solution space relative to the initial solution (Shen et al., 2016). In practical scheduling heuristics, neighborhoods are generated by swapping operations in their topological order (Goren & Sabuncuoglu, 2008) or by flipping assigned resources in flexible environments. Up to now, a number of studies adopted a simheuristic approach to generate proactive schedules. Simheuristics integrate simulation into a metaheuristic-driven framework (Juan et al., 2015). Thus, they combine the effectiveness of metaheuristics and the simulation’s capability of uncertainties. Negri et al. (2020) proposed a simheuristic approach that composes a genetic algorithm and a discrete event simulation (DES). Liu et al. (2017) proposed a hybridized evolutionary multi-objective optimization algorithm, where each phenotype of the population is evaluated by a simulation model. Another simheuristic approach was proposed by Gonzalez-Neira et al. (2021). Their approach can be split up into two phases. In the construction phase, a schedule that optimizes earliness/tardiness, is generated. In the second phase, the local search phase, interchanges between jobs are performed and evaluated through MCE. So far, several studies have used exact approaches for robust-stable scheduling (e.g. Davenport et al., 2001; Goren et al., 2011; Rahmani & Heydari, 2014; Salmasnia et al., 2014; Wu et al., 2020). But due to the high computational time required for exact methods, most researchers propose heuristic approaches (see Al-Behadili et al., 2019; Goren et al., 2011; Soofi et al., 2021; Xiao et al., 2019; Wang et al., 2022).

Techniques to evaluate proactive schedules

Most researchers evaluate proactive schedules by using robustness and stability measures described in Section “Introduction”. Rahmani et al. (2014), who model varying processing times through scenarios, evaluated a schedule by the expected robustness over all scenarios. This approach was also applied by Wang et al. (2022), who called it the min-max regret criterion (MMR). Wu et al. (2020) introduced a metric called robust makespan (RMS). RMS is defined as the maximum makespan of a schedule among all scenarios. Soofi et al. (2021) also use RMS and additionally consider the average makespan (AMS) over all scenarios. Gonzalez-Neira et al. (2021) additionally used two qualitative criteria to evaluate the schedule performance and address robustness through expected value (EV) and standard deviation (SD) of the earliness/tardiness. The greater part of the literature on proactive scheduling has utilised simulation to evaluate a schedule’s robustness or stability, such as Leon et al. (1994), Davenport et al. (2001) and Shen et al. (2016). Alternatively, simulation models can be integrated into the optimization algorithm, as described above.

Since simulation experiments require substantial computational times (Goren & Sabuncuoglu, 2008), some studies used surrogate measures for evaluation, such as Goren and Sabuncuoglu (2008), Goren et al. (2011), Liu et al. (2017) or Sundstrom et al. (2017). Surrogate measures are quickly observable metrics that are assumed to correlate well with stochastically ascertainable robustness or stability. Two well-known examples are the average total slack time (Jorge Leon et al., 1994) or sum of variances on the critical path (Goren et al., 2011). Classically, they are used to estimate how susceptible the critical path is to disturbances such as machine breakdowns or varying processing times. The disadvantage is that they only implicitly describe the actual robustness and stability, which can lead to undesirable side effects such as neglecting non-critical operations. Conclusively, surrogate measures have shown low effectiveness compared to simulation-based metrics (Xiao et al., 2017).

Trade-off between MSO, robustness and stability

A number of studies optimized two or more objectives simultaneously. Al-Behadili et al. (2019) proposed an approach that optimizes makespan as MSO, robustness and stability. In general, a schedule is called stable, if the real operations do not deviate from the planned operations of the baseline schedule. It can be measured by the sum of absolute deviations between expected operation completion times and real operation completion times (see Eq. 2) or by using surrogate measures, such as slack-based methods, which do not require simulation and therefore show more computational efficiency (see e.g. Davenport et al., 2001). But there are only few researchers who analyzed the trade-offs between MSO and robustness or between robustness and stability. Xiong et al. (2013) analyzed the trade-off between MSO and robustness. They developed a multi-objective evolutionary algorithm to minimize the estimated makespan and estimated robustness, that generates a set of feasible, pareto-optimal schedules. They suggested involving managers in the decision-making process by allowing them to choose the final schedule based on domain knowledge. In further research, Shen et al. (2016) also proposed a heuristic approach to optimize two MSOs and the robustness over different scenarios. They highlighted that the MSOs and robustness are seriously conflicted, and no solution can simultaneously optimize all three objectives.

Few studies have analyzed the trade-off between robustness and stability. Goren and Sabuncuoglu (2008) analyze the trade-off in a single-machine environment with random machine failures for three different MSO namely makespan, total flow time and total tardiness. They explored the effect on stability if robustness is optimized and vice versa. They discovered that stability is not considered during robustness optimization and that the schedule’s robustness worsens during stability optimization. Thus, the researchers suggested managing the trade-off by optimizing the weighted linear combination of robustness and stability depending on the MSO: In case of makespan minimization as MSO, practitioners should focus on stability optimization and in case of flow time or tardiness minimization, robustness optimization should be prioritized. Liu et al. (2017) managed the trade-off between robustness and stability by developing an algorithm that efficiently creates a set of pareto-optimal schedules. The visualization of these pareto fronts show, that increasing stability leads to lower robustness and vice versa. The paper focuses on the algorithm’s efficiency and draws no further conclusions about the actual trade-off. Sundstrom et al. (2017) systematically evaluated the triangular trade-off between MSO namely energy consumption, robustness and stability. They also used pareto fronts to analyze the trade-off. Each front depicts robustness and stability values for a constant energy consumption and shows the same results as Liu et al. (2017). Further analysis of the corresponding schedules revealed that slack at the end of the schedule would improve the robustness, while stability is improved by slack throughout the schedule (Sundstrom et al., 2017).

DRL-based methods

Recent studies have been utilized DRL for scheduling with uncertainties. However, the usage of DRL in the field of production scheduling is limited to the reactive phase of the approaches, such as in (Minguillon & Stricker, 2020; Shahrabi et al., 2017; Wang et al., 2020). However, examples of robust scheduling with DRL in the proactive phase can be found in other domains (Kenworthy et al., 2021; Su et al., 2018). Kenworthy et al. (2021) used a combination of DRL and Integer Programming (IP) to solve an aircraft crew-scheduling problem. The probabilities in the neural network output layer are used to assign coefficient weights to the variables in the IP. This approach enables an IP with fewer variables and constraints that can deal with stochastic flight durations. Their scheduling objective is to maximize the total amount of buffers. A buffer, in this case, is defined as the amount of time between successive flights of a particular pilot. Su et al. (2018) proposed a hybrid teaching-learning-based optimization algorithm that includes DRL techniques in the teaching phase. They apply their algorithm for aircraft carrier flight deck operations with stochastic durations to maximize the probability of completing within the limitative makespan and minimize the weighted sum of expected makespan and the makespan variance.

Research gaps

The following essential research gaps can be summarized from our literature review:

  1. 1.

    There exist a few exact robust-stable scheduling approaches such as (Davenport et al., 2001; Goren et al., 2011; Rahmani & Heydari, 2014; Salmasnia et al., 2014; Wu et al., 2020) and several heuristic approaches such as (Al-Behadili et al., 2019; Goren et al., 2011; Soofi et al., 2021; Xiao et al., 2019; Wang et al., 2022). To the best of our knowledge, there does not exist an approach that uses DRL in the proactive stage of production planning. We also cannot identify a DRL-based approach that directly balances robustness and stability in general. Since a fully trained DRL agent can be computationally efficient, can handle uncertain environments, and has proven good results in proactive scheduling in other domains, the use of DRL for robust-stable production scheduling should be scientifically investigated.

  2. 2.

    Many researchers used simulations to evaluate robustness and stability (Al-Behadili et al., 2019; Davenport et al., 2001; Soofi et al., 2021; Wu et al., 2020; Xiao et al., 2019), since the effectiveness is higher compared to surrogate measures (Xiao et al., 2017). Thus, there exist several approaches that integrate simulations directly into the heuristic search strategies (Gonzalez-Neira et al., 2021; Liu et al., 2017; Negri et al., 2020). These so called simheuristics improve the verification and validation processes (Juan et al., 2015) and thus, lead to better results. But a major disadvantage of simheuristics is their computational effort (Juan et al., 2015). To ensure stochastic precision in practical cases with a large number of planning objects and uncertainties, a correspondingly high number of MCEs must be carried out. Thus, the real-time applicability of simheuristics is rather low and more research is required too minimize the computational effort to generate proactive schedules without losing insights gained by simulation.

  3. 3.

    A few researchers have analyzed a schedule’s robustness and its stability simultaneously (Al-Behadili et al., 2019; Goren & Sabuncuoglu, 2008; Liu et al., 2017; Sundstrom et al., 2017). The approaches of Goren and Sabuncuoglu (2008) and Liu et al. (2017) suggested two different ways how to manage the trade-off between robustness and stability. To the best of our knowledge, Sundstrom et al. (2017) are the only researchers, who further analyze, how prioritizing robustness and stability influence the schedule itself. Thus, we suggest further research on how proactive schedules are influenced by the trade-off and additionally, if the trade-off is influenced by the MSO.

Proposed approach

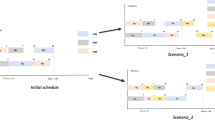
This section describes the core components of our DRL-based method to generate robust-stable schedules proactively. The approach enables a non-iterative method with a metrics-oriented optimization: A DRL agent internalizes the behavior of a stochastic DES and is able to adjust operation processing times without performing computationally intensive MCE step by step. The method is aligned to a dynamic flow shop scenario considering uncertain processing times, machine failure probabilities and uncertain repair times. It is inspired by our industrial partner (see Sections “Deterministic flow shop problem”, “Scenario with uncertainties”). The method comprises the following sequential sub-steps: First, an opening optimization procedure is conducted, where a baseline schedule is generated deterministically without considering robustness and stability. Then, stability, robustness and other metrics are measured within DES-based MCE (see Section “Robustness and stability evaluation”). Based on the stochastic results, a DRL agent modifies the baseline schedule to improve robustness and stability. Here, either operations are extended by additional slack times (stretching) or operations are shortened in their plan duration (compressing) (see Sections “Subsequent robustness and stability optimization”, “DRL design”). Stretching corresponds to conservative planning, while compression corresponds to optimistic planning. For example, the agent can put additional slack times on the critical path of the schedule to stretch operations and catch endangering dynamic events (see Fig. 1).

Fig. 1
figure 1

Illustrated baseline schedule with 3 machines and 3 jobs (input for the proposed DRL-based approach) and proactive schedule with additional slack times (output from the DRL agent)

Full size image
Table 2 Notation for the deterministic baseline problem (flow shop scheduling problem)
Full size table

Deterministic flow shop problem

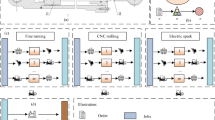
Before describing the dynamic problem with uncertainties and the robustness/stability optimization, the opening procedure’s deterministic baseline problem must be formalized. Inspired by the production organization by our corporate research partner, a flow shop scheduling problem with waiting times and infinite machine buffers is considered. In this setting, every production job has a number of operations equal to the number of machines. As a non-permutation setting, jobs can overtake each other in the production line. As MSO, the operation sequences should be set in such a way that either the makespan or the total flow time without release times is minimized. Due to the alignment as a feasibility study, the problem was simplified to ensure a better transferability of the proposed approach. For example, employees, sequence dependencies or setup operations were not taken into account (Table 2).

Table 3 Metrics for a single simulation run
Full size table

The baseline flow shop model for makespan minimization can be formulated as the following mixed integer linear program:

$$\begin{aligned}&\min C_{max} = \max _{1 \le i \le n} \{ \delta _{i,m} + p_{i,m} \} \end{aligned}$$
(3)
$$\begin{aligned}&\quad \text { s.t.} \nonumber \\ {}&\delta _{i,k}+p_{i,k}\le \delta _{i,k+1} \quad \forall i \in \{1,...,n\}, \forall k \in \{1,...,m-1\} \end{aligned}$$
(4)
$$\begin{aligned}&\epsilon _{i,j,k}(\aleph +p_{j,k})+\delta _{i,k}-\delta _{j,k}\ge p_{j,k} \end{aligned}$$
(5)
$$\begin{aligned}&\quad \forall i \in \{1,...,n\}, \forall j \in \{1,...,n\}, \forall k \in \{1,...,m\} \nonumber \\ {}&(1-\epsilon _{i,j,k})(\aleph +p_{i,k})+\delta _{j,k}-\delta _{i,k} \ge p_{i,k} \end{aligned}$$
(6)
$$\begin{aligned}&\quad \forall i \in \{1,...,n\}, \forall j \in \{1,...,n\}, \forall k \in \{1,...,m\} \nonumber \\ {}&\delta _{i,k} \in {\mathbb {N}} \quad \forall i \in \{1,...,n\}, \forall k \in \{1,...,m\} \end{aligned}$$
(7)
$$\begin{aligned}&\epsilon _{i,j,k} \in \{0,1\} \quad \forall i \in \{1,...,n\}, \forall j \in \{1,...,n\},\nonumber \\ {}&\forall k \in \{1,...,m\} \end{aligned}$$
(8)

Equation 3 represents the objective function for makespan minimization. Equation 4 ensures that an operation of a job can only start, when the preceding operation on the previous machine is completed. Furthermore, wait times between operations are allowed with this modeling. Equations 5, 6 ensure that a machine can only process one operation at a time. For total flow time minimization (without release times), Eq. 3 must be replaced by the following objective function:

$$\begin{aligned} \min F = \sum _{i=1}^{n} \delta _{i,m} + p_{i,m} \end{aligned}$$
(9)

Scenario with uncertainties

To specify a dynamic problem with consideration of uncertainties, the scenario must be explained in more detail: the partner company manufactures custom industrial fittings, where the single production of complete systems involves the non-takted manufacturing steps (1) machining, (2) welding and (3) assembly. For each product category \(PC\in \{1,2\}\) and manufacturing step k, we assume triangularly distributed uncertain processing times \(D_{k,PC}\). Each uncertain processing time is represented as a tuple (a, c, b), where [a, b] are the interval bounds and c is the mode (\(a\le c\le b\)). In this way, asymmetric distributions can also be defined in a compact manner. The expected value E(X) and the standard deviation \(\root 2 \of {V(X)}\) for a triangular distribution tuple X can be defined as follows:

$$\begin{aligned}&E(X) = \frac{ a + b + c }{ 3 } \end{aligned}$$
(10)
$$\begin{aligned}&\root 2 \of {V(X)} = \frac{ \root 2 \of {(a-b)^2 + (b-c)^2 + (a-c)^2} }{ 6 } \end{aligned}$$
(11)

Moreover, each machine has a failure probability \(P(F_k)\). As a simplified modeling, a failure can occur once per operation and requires a repair operation with a triangularly distributed machine-specific repair time \(Q_k\). Equation 12 defines the expected processing time of an operation including a probable machine repair time. This value is used for each operation processing time \(p_{i,k}\) in the deterministic opening procedure to achieve an optimal or near optimal MSOV under realistic conditions (see Section “Action space analysis”).

$$\begin{aligned} E(D_{k,c}) + P(F_k)E(Q_k) \end{aligned}$$
(12)

Robustness and stability evaluation

After generating a baseline schedule deterministically with expected processing times, robustness and stability must be evaluated under stochastic conditions within DES-based MCE. The DES is used to dynamically simulate a baseline schedule according to the operation sequence set by the opening procedure. Dynamic simulation means that random processing times are set according to the processing time distributions and consideration of downtimes. During simulation, operations are started as soon as the previous operation is completed and the machine is available. The start time of an operation set by the opening procedure can therefore also be undershot. According to the formulated baseline problem (see Section “Deterministic flow shop problem”), waiting times between operations and jobs are possible. Moreover, station buffer upper bounds are not taken into account. The DES is designed as a process-based simulation in which each resource is designed as its own asynchronous process. In the beginning, a separate process is started for each machine \(M_1,...,M_m\). A process runs until all associated operations are completed according to the baseline schedule. In each process, the next specified operation is taken from the input buffer as it becomes available. Next, the operation is executed with a randomly set processing time according to the distributions. In addition, a machine failure can occur that must be remedied within the respective repair time. After the operation is completed, it is committed to the next machine’s buffer or final drain. The simulation ends when all processes are finished. In the context of MCE, the simulation is performed multiple times, with dynamic events being triggered randomly in each case. After a simulation run, the metrics described in Table 3 are measured. Considering all simulation experiments, the metrics described in Table 4 can be obtained.

Table 4 Summary metrics for all simulation runs
Full size table

Subsequent robustness and stability optimization

For a better understanding of the proposed DRL-based method, the subsequent dynamic problem is formalized in this section. The optimization model enables stretching and compressing operation durations to absorb dynamic events and to improve robustness and stability simultaneously. To evaluate a proactive schedule candidate PS, the optimization procedure integrates MCE (see Section “Robustness and stability evaluation”) to calculate an aggregated and normalized robustness/stability value \(\Lambda \in {\mathbb {R}}_{>0}\).

$$\begin{aligned}&\min \Lambda = \frac{|PS_{{\overline{R}}} |w}{|BS_{{\overline{R}}} |}+\frac{PS_{{\overline{S}}}(1-w)}{BS_{{\overline{S}}}} \end{aligned}$$
(13)
$$\begin{aligned}&\quad \text { s.t.} \nonumber \\ {}&PS_{p_{i,k}} \in {\mathbb {N}} \quad \forall i \in \{1,...,n\}, \forall k \in \{1,...,m\} \end{aligned}$$
(14)

The lower the \(\Lambda \) value, the better is the linear combination of robustness and stability in comparison to the related baseline schedule BS. Since robustness and stability are competing objectives, a linear weighting is applied using a robustness weight \(w \in [0,1]\) and a stability weight \(1-w\) for balancing (see Eq. 13). Stretching or compressing operations is enabled my manipulating operation plan durations \(p_{i,k}\) in a range as it is allowed by technological constraints. Every operation duration \(PS_{p_{i,k}}\) from the PS is overwritten with regard to improve robustness and stability (see Eq. 14, Fig. 2). The next section describes how a DRL agent can be implemented to solve this dynamic problem, taking into account the logistical specifics of the baseline problem (see Section “Deterministic flow shop problem”).

Fig. 2
figure 2

Stretching an operation before evaluating robustness and stability via MCE. Simplified example with 1 machine and 1 job

Full size image

DRL design

This section describes the general conception of the DRL agent based on the formalized dynamic problem in Section “Subsequent robustness and stability optimization”. We identified two state-of-the-art actor critic DRL algorithms for discrete action spaces: Proximal Policy Optimization (PPO) (see OpenAI, 2022c; Schulman et al., 2017) and Advantage Actor-Critic (A2C) (see Mnih et al., 2016; OpenAI, 2022b), which have been realized using an OpenAI Gym environment (see OpenAI, 2022a) in combination with the Stable-Baselines3 framework (see Stable-Baselines3, 2022). Hyperparameter configuration including neural network architecture and documentation of the training process can be found in Section “DRL policy learning benchmark (PPO vs. A2C)”.

Algorithm 1 illustrates the essential training procedure including reward calculation. An episode always includes as many steps as there are operations in the schedule. The first step refers to the first operation on machine \(M_1\), the last step to the last operation on machine \(M_m\). For each training step, the current state \(\pi \), the chosen action \(\zeta \) and the current modified proactive schedule candidate PS are passed as arguments. The state space contains various features that are intended to describe the baseline schedule and the current proactive schedule structure as generally as possible (see Table 5). Figure 3 shows the discrete action space utilized. It provides three actions applicable for each scheduled operation (i, k). Depending on the action chosen, the operation processing time \(p_{i,k}\) is stretched or compressed to improve robustness and stability.

In the step function essential for the episodic learning, the next operation is first initialized and then modified considering the chosen action, which is also overwritten in the PS candidate. Then, the PS is simulated once in a deterministic manner. In this way, current effects on robustness and stability are measured and updated in a new state space \(\pi ^*\). Based on this, the intermediate reward can be calculated, that is distributed after each step (see Algorithm 2). It is calculated according on how the agent set the processing time per operation. Setting optimistic processing times improves stability, if operations were previously stretched. On the other hand, conservative processing times improve robustness (see Section “Action space analysis”). Stability optimization through action 2 is rewarded directly but results in a penalty due to robustness degradation considering w. On the other hand, robustness improvement only results in a reward, which is slightly higher. In the last episode step, the PS is handed over to the MCE to calculate the robustness/stability value \(\Lambda \) (see Eq. 13). Based on this, a final penalty is distributed, where \(\Lambda \) is multiplied by a large number. This ensures that the final penalty has a significantly greater impact than the intermediate rewards. A value greater than 1 awards a higher penalty that increases linearly with degradation. For a value less than 1, the penalty decreases rapidly as the improvement increases. In this way, combined with appropriate discount factors, we were able to make the agent more greedy and reliable in terms of achievable end results. The specified reward and penalty scores are the result of a successive empirical analysis and will not be explained further.

figure a
figure b
Table 5 DRL observation features with logistical specifics for non-permutation flow shops with waiting times and infinite machine buffers
Full size table
Fig. 3
figure 3

DRL discrete action space with three possible actions for selecting an operation plan duration within the aggregated uncertainty distribution. The actions have been determined by the experiments in Section “Action space analysis”. \(Action\ 1\) corresponds to plan duration \(PD_3\); \(Action\ 2\) corresponds to \(PD_2\); \(Action\ 3\) corresponds to \(PD_4\) (see Appendix Table 9). Illustrated representation not to scale

Full size image

Computational study

Numerical experiments were conducted and discussed to answer the following questions: (1) How does the plan duration affect the trade-off between robustness and stability and how to define the action space (see Section “Action space analysis”)? (2) How well do DRL agents learn a policy to generate robust-stable schedules (see Section “DRL policy learning benchmark (PPO vs. A2C)”)? (3) How is the learned policy reflected in the agent’s decision behavior (see Section “DRL agent behavior analysis”)? (4) How well performs a DRL agent in comparison to a Simulated Annealing with Research Strategy (SARS) approach regarding result quality and computational efficiency (see Section “DRL performance benchmark (PPO vs. SARS)”)? (5) How performs the agent when varying problem size and uncertainty and how are robustness and stability affected (see Section “Scalability investigation”)? The general experimental setup for all experiments including test data description is documented in Section “Experimental setup”.

Experimental setup

The experiments were conducted with the following hardware: GPU: Nvidia Quadro RTX3000 5980MB VRAM; CPU: Intel Core i7-10875H @ 2.3 GHz (16 CPUs); 16384MB RAM. Makespan (\(C_{max}\)) and total flow time (F) minimization were considered as separate MSOs. With respect to the scope, robustness and stability have been considered equally in the experiments (\(w=0.5\)). In fact, the weight w is an independent variable that has an effect on the planning result depending on the MSO Goren and Sabuncuoglu (2008). However, results from equal weighting are discussed in relation to the agent performance (see Section “DRL policy learning benchmark (PPO vs. A2C)”). After intensive research, we could not identify suitable benchmark instances which can be used for our approach and uncertainty modeling without further modification. Furthermore, the uncertainties had to be scalable in order to analyze the degree of uncertainty. Consequently, like other authors (see e.g. Al-Behadili et al., 2019; Goren & Sabuncuoglu 2008; Liu et al., 2017), we generated suitable instances. In addition to instances based on the industrial scenario (see Section “Scenario with uncertainties”), we modified a well-known instance proposed by Taillard (1993) for deterministic flow shop scheduling benchmarks.

  • GMRT5x3. Compact scenario-based test data with 5 jobs and 3 machines.

  • GMRT10x3. Extended scenario-based test data with 10 jobs.

The GMRT instances were utilized to generally analyze the DRL agent learning performance and behavior (cf. initially mentioned experiment questions 1–4). For training and evaluating the DRL agent, 10 training and 10 test instances were generated per data set and per MSO, each with a random number of product categories. The COIN-OR Branch-and-Cut solver V2.10 has been used to generate optimal deterministic baseline schedules. The uncertainties considered for the subsequent proactive optimization method can be found in Appendix Tables 6, 7. According to experiment question 4, the proposed DRL-based approach has been compared against an iterative metaheuristic. Consequently, the number of experiments must be chosen such that the true \(\Lambda \) value of a neighbor is precisely approximated. It had to be prevented that random outliers are confused with local optima. We used the standard deviation of the means to measure the error of yielded \(\Lambda \) values Jacoboni and Lugli (1989). Here we set an upper limit of about \(\sigma _n \approx 0.005\), which corresponds to about \(n=10,000\) experiments and led to reliable results.

In order to indicate the reliability and scalability of the method, the following instances were used:

  • T20x5LV. Modified Taillard instance with 20 jobs, 5 machines and low uncertainty variance (LV).

  • T20x5HV. The same instance with a high uncertainty variance (HV).

According to experiment question 5, it was analyzed how the agent handles more extensive environments with varied uncertainties. In this case, the baseline schedules were generated using the Shortest Processing Time (SPT) dispatching rule. Due to the specifics of our scheduling and uncertainty model, the data was modified as described in Appendix Table 8.

Action space analysis

This analysis addressed the first experiment question and examined the impact of different plan durations (PD) utilizable as \(PS_{p_{i,k}}\) in the subsequent robustness and stability optimization method (see Section “Subsequent robustness and stability optimization”). The aim was to investigate and to specify the scope of the DRL action space (see Section “DRL design”), which is important for a proper policy learning. In particular, it was analyzed which PD leads to which consequences in terms of robustness and stability. Moreover, general conclusions about the conflict between robustness and stability could be drawn. Five PD were considered, where \(PD_1\) is a very optimistic, \(PD_3\) a realistic and \(PD_5\) a very conservative time. All PD are within the bounds of the aggregated processing time distribution of an operation (see Appendix Table 9). Appendix Table 10 and Fig. 4 give a statistical overview of the effects.

What stands out in the results are the very similar trade-off patterns and the associated impact of different PD. According to our observations, \(PD_3\) achieved good stability values for \(C_{max}\) and F minimization. More optimistic or conservative values worsened the stability in all cases. The more conservative \(PD_4\), on the other hand, led to better robustness. With \(PD_5\), even positive robustness was achieved for all baseline schedules. This measurement confirms the conflict in a simultaneous robustness and stability optimization in this case: The more realistic the plan durations, the better the stability. If, on the other hand, the PD are chosen more conservatively, the robustness increases at the expense of stability. This interesting finding may be related to statistical scope per metric. With a single operation, it is most likely that the expected operation duration will occur (scope of stability). However, at the level of the overall schedule (scope of robustness), previously unknown causes lead to overly optimistic planning when expected values are utilized. Future studies should examine these causes in more detail, which would go beyond the scope of this work.

A closer inspection of the figure shows that the robustness values in the F case are significantly more sensitive to the PD chosen and more widely spread, which can also be observed in the different value ranges of the robustness axes. This result can be explained by the fact that the \(C_{max}\) objective function only depends on one value (end time of the last operation), whereby the F objective function contains the end time of each job. Therefore, instead of one, several operations must be considered in the F case. This is an indicator that stretching or compressing operation durations has to be done in a targeted manner. In this case, it is not sufficient to just stretch an operation at the end in order to achieve apparent robustness. Conclusionally, it can be confirmed that a corresponding optimization method for balancing robustness and stability can be utilized by choosing PD dynamically per operation and in a targeted manner. Since we locate the best trade-offs between \(PD_2\) and \(PD_4\), these three PD have been included in the DRL action space. In terms of a feasibility study, this choice of actions may be is appropriate. However, future work should examine the applicability of continuous action spaces, where even more targeted values can potentially be set. Subject to the three selectable actions defined, the agent’s learning and prediction performance are presented and discussed in the next section. How and why the agent selects which action in which situation is examined in Section “DRL agent behavior analysis”.

Fig. 4
figure 4

Different PD and their effect on robustness and stability. Results observed by GMRT5x3 with F and \(C_{max}\) minimization as MSO. In both MSO cases, the robustness/stability conflict becomes transparent. Good stability is obtained with realistic expected values (\(PD_3\)). Good robustness can be achieved with more conservative values (\(PD_4\))

Full size image

DRL policy learning benchmark (PPO vs. A2C)

The purpose of this experiment was to evaluate an A2C and a PPO model to compare two modern DRL algorithms regarding their learning and predicting performance (see experiment question 2). Separate models were trained for F minimization and \(C_{max}\) minimization as MSO. Each model was trained multiple times with GMRT5x3 and GMRT10x3 training samples. After extensive tests, some Stable-Baselines3 standard parameters have been modified to improve policy learning (see Appendix Table 11). During successive modification and identification of proper hyperparameters, PPO was significantly more robust to adjustments. In contrast to A2C, PPO has generally shown good performance even with different settings. A2C sometimes delivered bad results, so choosing a proper parameter setting was very time-consuming. A possible explanation for this might be that A2C is more sensitive to the hyperparameters than PPO.

Figure 5 shows an overview of the agents’ performances quantified by overall reward obtained during the training process for F and \(C_{max}\) minimization as MSO (left graph). In the first training half, all models experienced significant growth, which eventually slowed during the exploitation phase. Independently from the MSO, the learning curves share a similar pattern, where the PPO learning curve has a steeper slope and has significantly higher rewards in the final stages. Another interesting finding is, that both models consistently earn more reward for F minimization in comparison to \(C_{max}\) minimization. This result may be explained by the fact that the weight \(w=0.5\) has an effect on the outcome. According to Goren and Sabuncuoglu (2008), greater priority should be given to stability in the context of \(C_{max}\) minimization. Furthermore, robustness is more insensitive in this case, which can lead to poorer results with this weighting. In summary, the observed difference in performance is complementary to the authors’ recommendation.

Moreover, the obtained predictions (average \(\Lambda \) values) for the fully trained DRL models are visualized in form of a box chart (right graph). Statistical details are added in Appendix Table 12. For all test samples and for both MSO, PPO generally achieved better average \(\Lambda \) values and lower standard deviations. This also reflects the patterns of rewards achieved in the training processes, with the improvement being more pronounced in the F case than in the \(C_{max}\) case. The standard deviation was less than 0.043 in each case, with PPO tending to have slightly less scatter with this metric. Therefore, in some cases, the \(\Lambda \) values deteriorated compared to the baseline schedule. Nevertheless, the average robustness and stability could be improved by the agents, whereby PPO has outperformed A2C. In addition, the PPO model was handier to train and better able to learn policy, because it was more independent of hyperparameters.

The results in this section indicate that DRL is a suitable method for robust-stable scheduling in dynamic manufacturing environments. However, with respect to DRL design and to the reduced and abstracted problem, further investigations must be carried out. First, this study was limited to the manipulation of processing times (stretching or compressing operations). With respect to the large scope, other approaches could not be considered. Consequently, more research is required to analyze and implement other paradigms of robust-stable scheduling, such as generating proactive schedules by creating neighborhood solutions through resource flipping or changing sequences by operation swapping. Second, it must be examined how an agent performs in different environments with different parameters. A related scalability analysis is carried out in Section “Scalability investigation”. In advance, the next section moves on to discuss the behavior of the PPO agent and to answer the question: Which action has been chosen in which situation and what are the consequences?

Fig. 5
figure 5

PPO vs. A2C benchmark for F and \(C_{max}\) minimization as MSO (\(w=0.5\)). Average rewards achieved during training over time (left graph) and best model’s predictions after training (right graph). All models were trained and tested with GMRT5x3 and GMRT10x3 samples. PPO outperforms A2C in terms of obtained rewards and predictions after training (\(\Lambda \) values)

Full size image

DRL agent behavior analysis

The following analysis examines the DRL agent’s decision behavior and draws conclusions about the optimization metrics (see experiment question 3). It was analyzed, which actions based on which observations were chosen by the agent and how did this affect robustness and stability. The fully trained PPO agent was analyzed based on GMRT10x3 instances in the context of F minimization. From 500 episodes, all actions chosen by the agent were compared with the situational state observation.

Looking at Fig. 6, it is apparent that the agent did not choose the actions evenly: Stretching (applying \(PD_4\)) was applied significantly more often, whereby the realistic value (\(PD_3\)) was hardly retained. This result may be explained by the fact that the baseline schedules generated are always too optimistic. This corresponds to the expectation in accordance with the analysis in Section “Action space analysis”: The use of \(PD_3\) always implies a negative robustness. However, these results were predictable, since robustness and stability have to be balanced with \(w=0.5\). On the other side, the application of compressing (applying \(PD_2\)) is particularly interesting. Overall viewed and in comparison to \(PD_3\) and \(PD_4\), \(PD_2\) has a negative impact on robustness and stability. Nevertheless, the agent selected compression in about 15% of all cases.

In a further analysis, we examined in which situations the agent tends to compress operations. For this purpose, we have generated a classification decision tree based on state-action tuples. Techniques based on decision trees are a suitable method to (approximately) explain the behavior of DRL agents (Ding et al., 2020). In order to reduce complexity, stretching actions were not taken into account. Figure 7 shows an excerpt of the first decision tree leaves. Even if the Gini coefficients are relatively even, the essential pattern is emerging that be interpreted as follows: If the agent assumes that (1) an operation will end earlier than planned and (2) that the operation tends to be on the critical path, the operation is compressed by the agent. Such a situation occurs especially, when predecessor operations have already been stretched. Thus, compressing the operation compensates the effect of an “overflow” of the current operation and all successor operations.

At first glance, this behavior seems trivial due to the reward design (see Section “DRL design”), but it may indicate a problem related to the stability metric. The stability metric used in this study and by most authors only considers operation end times (see Eq. 2). And if, in practice, target processing times are shortened in order to cushion other operations, this can lead to stress and pressure. This observation may support the hypothesis that the widely used stability metric is too imprecise. We suggest qualitatively, that stability should be characterized by the fact that re-scheduling procedures can be avoided as often as possible. The more stable the plan, the less often re-scheduling occurs or the less impact re-scheduling causes. In particular, the impact must be suitably quantified.

Fig. 6
figure 6

Actions chosen by the agent (F minimization as MSO in the context of GMRT10x3). The agent stretched most of the operations and compressed them less often. The default expected value (realistic operation duration) was hardly selected

Full size image
Fig. 7
figure 7

Decision process whether operations are compressed (CART decision tree). The agent tends to choose compression when a critical path operation may end earlier than originally planned

Full size image
Fig. 8
figure 8

PPO vs. SARS benchmark for F and \(C_{max}\) minimization as MSO (\(w=0.5\)) in the context of GMTR5x3 and GMRT10x3. In this analysis, average \(\Lambda \) values achieved, scatter and computing time are compared. The computing time is shown on a logarithmic axis. PPO achieves about 2% worse results than SARS, but only requires about 2% computing time

Full size image
Fig. 9
figure 9

PPO performance for F minimization as MSO (\(w=0.5\)) in the context of T20x5LV and T20x5HV data sets. Average rewards achieved during training over time (left graph) and best model’s predictions after training (right graph). Lower uncertainty variances (T20x5LV) lead to better performances during and after training

Full size image

DRL performance benchmark (PPO vs. SARS)

In this experiment we analyzed the PPO agent performance in comparison to a SARS algorithm roughly based on Yu et al. (2021) (see experiment question 4). The SARS algorithm has been implemented as follows: In every iteration, a random operation is randomly stretched or compressed according to the action space options (see Appendix Algorithm 3). The number of cooling steps was set to 50, which already required a computation time of about 8 minutes. This is due to the fact that the step-by-step evaluation performed 10,000 MCE each time, which significantly increased the computing time. All five steps were checked to see whether an improvement had occurred. If not, the current solution has been reverted to the best solution found. This performance analysis examined the relationship between average \(\Lambda \) value achieved, the related scatter in the form of standard deviation, and approximate computation time in seconds.

Figure 8 shows the obtained results summarized for GMRT10x3 and GMRT5x3. Statistical details can be found in Appendix Table 13. What stands out in these results is the dominance of the DRL agent in terms of computing time. The DRL Agent required about 10 seconds to generate a proactive schedule and to evaluate via MCE. Without evaluation, the time could be further reduced to less than one second. The average \(\Lambda \) values and scatter obtained by the PPO agent were only slightly worse in all cases. This can be an indication that the agent needs even better features or training sequences for better generalization. However, this potential for improvement is not considered in detail in this feasibility study. From the graph, it can be seen that in the case of \(C_{max}\) minimization, significantly poorer average results were also achieved with the SARS implementation. This supports the hypothesis that this is an effect of the weight \(w=0.5\) and not attributed to the DRL agent or training process design (see Section “DRL policy learning benchmark (PPO vs. A2C)”). Interestingly, the scattering behaves in the opposite way: Both the agent and the metaheuristic each achieve a better standard deviation in the \(C_{max}\) case. This can be explained by the greater variability of the F objective, which has already been observed and discussed in Section “Action space analysis”. The more operations are stretched in terms of conservative, robust planning, the greater the scattering of the robustness achieved in the F case (see Fig. 4).

Based on the previous findings, these results support the idea that DRL is a viable and efficient method to generate proactive schedules, although there is room for improvement. The greatest advantage of the proposed DRL approach lies in the low computing time. After a proper training, it obtains about 98% of the result quality in about 2% of the time compared to traditional methods such as metaheuristics. This can be explained by the fact, that a DRL agent internalized the behaviour of the stochastic simulation model within the training to infer on robustness and stability. Conventional probabilistic methods such as metaheuristics have no way of storing experiences and hypotheses that lead to the situational selection of suitable actions. Instead, it is necessary to evaluate successively, which takes up a lot of computing time due to the complex MCE.

As mentioned in the previous parts, there are some disadvantages or improvement potentials that can be investigated in further studies. The central research question raised in this section is: How is it possible to outperform metaheuristics in other performance criteria such as mean scores and scatter? In particular, it should be examined whether hyperparameters, training processes, actions, rewards and observations can be further improved. Finally, the scalability of the DRL design is evaluated in the next section.

Scalability investigation

In order to assess the applicability of the proposed approach to other environments, repeated measurements of the learning and prediction performance were conducted (see Fig. 9 and Appendix Table 14). It was analyzed how the agent handles a larger problem input (more machines, more jobs) and how the extent of uncertainties affects robustness and stability. With respect to the large scope, we have focused on F minimization as MSO and PPO as DRL technology. With minor modifications, we were able to make the agent operational for a larger scaled environment. The training duration was increased to 20,000 steps and the final reward was distributed by a factor of ten. This ensured the higher weighting of the final reward compared to the sum of the intermediate rewards.

The charts below illustrate the average reward achieved during training (left graph) and the prediction quality after training completion (right graph). The agents experienced a learning curve in both scenarios (low and high uncertainty) and generated comparatively good proactive schedules after training. What is striking about the training performances is the significantly different reward scores obtained. At higher uncertainty variances (T20x5HV data set), the agent has a significantly lower slope of rewards over time, possibly influenced by the MCE: The greater the impact of uncertainties, the more experiments have to be carried out in order to calculate precise robustness and stability metrics. In addition, it can be assumed that the agent has to explore more during training and also experiences many deterioration effects. Likewise, the fully trained agent generated significantly better proactive schedules in the case of low uncertainty. With regard to the \(\Lambda \) values, better means, less scattering and fewer outliers could be achieved with T20x5LV. Interestingly, the results were even better than in the previous GMRT experiments. This is an indicator that the proposed method can also be scaled to larger flow shops. However, an increase in uncertainty results in a loss of obtainable robustness and stability. Conclusionally, the degree of uncertainty has a greater effect than the number of planning objects such as machines or jobs.

A major disadvantage is still, that an agent must be trained for new situations. Future work should analyze how an agent can be better generalized for a varying number of planning objects. It is particularly important to design the reward and the observation space even more universally. Due to the need for more and more robustness, flexibility and responsiveness in innovative logistic systems (Jafari et al., 2022; Monostori, 2018) this also refers to other scheduling domains and associated MSO. In addition to related production organizations such as flexible job shops or more complex environments such as multi-resource shops, robust-stable scheduling can also be used, for example, in route planning, project management or for crew scheduling. From a mathematical point of view, it is also about allocating resources with tasks on the timeline. Consequently, the robustness and stability metrics defined as well as the design of the action space remain universally applicable. However, the observation space responsible for describing the environmental constraints has to be adapted for each specific problem in an extensive feature engineering process. Moreover, the proactive consideration of other types of dynamic events and especially external events such as new job arrivals is of scientific and practical relevance.

Conclusions and future research

The presented research examined, how DRL can be applied in the proactive stage for robust-stable scheduling to absorb uncertainties in advance. For this purpose, a DRL concept was developed, where scheduled operations were stretched or compressed in their time in order to optimize the competing metrics, robustness and stability. The metrics were collected in the course of DES-based MCE for dynamic flow shops, whereby uncertain processing times and machine repair times were given by triangular distributions. The study was primarily set out to analyze the effectiveness, efficiency and scalability of DRL. After extensive numerical experiments, the findings suggest that DRL, and especially PPO, is a viable method to generate proactive schedules in near real-time. PPO comes about 98% close to SARS, but requires only 2% of its computing time after a successful training. This is a great advantage for the application in time-critical reactive environments. Moreover, it could be shown that the DRL agents can also learn and predict successfully after varying jobs, machines and uncertainties. These findings will be of interest to researchers and practitioners and could be used to develop proactive methods by making them more efficient and intelligent.

The major restriction of this work was proof-of-concept DRL design focusing the proactive stage for F and \(C_{max}\) minimization as MSO. In summary, the following wide range of future research questions can be derived from the limitations of this study:

  • Aggregated robust-stable scheduling. A limitation of the proposed approach is the decomposition of MSOV optimization and proactive planning in two consecutive steps. It could be analyzed which positive and undesirable effects are related to an aggregation of both stages (see Section “Proposed approach”).

  • DRL-based re-scheduling. This article does not include an analysis of how to combine proactive planning and reactive planning. Further work could analyze and develop a hybrid approach of predictive-reactive scheduling considering DRL on one or both stages (see Section “Proposed approach”).

  • Robustness/stability trade-off. The conflict between robustness and stability must be formally explained in more detail (see Section “Action space analysis”).

  • Continuous actions. Future work could improve the agent’s precision by utilizing continuous rather than discrete action spaces (see Section “Action space analysis”).

  • Neighborhood-based scheduling. It would be interesting how robust-stable neighborhood solutions can be generated using DRL (see Section “DRL policy learning benchmark (PPO vs. A2C)”).

  • Balancing robustness and stability. As far as we know, general situational rules for weighting robustness and stability with regard to MSO and practical requirements have not yet been established (see Section “DRL policy learning benchmark (PPO vs. A2C)”).

  • Stability metric improvement. It could be identified that the frequently used stability metric in particular can lead to undesirable effects. Future research should develop methods that focus directly on minimizing re-scheduling situations or associated effects (see Section “DRL agent behavior analysis”)

  • Agent performance improvement. Further investigations could analyze how DRL can obtain even better end results than traditional metaheuristics and how to reduce the prediction scatter (see Section “DRL performance benchmark (PPO vs. SARS)”).

  • Other scheduling contexts. It would be interesting to evaluate the applicability of other scheduling models, MSO or different types of dynamic events (see Section “Scalability investigation”).

  • Agent generalizability. Further research is required to make the agents more reliable and independent of the environment (see Section “Scalability investigation”)

  • Practical application. Due to the scope, no evaluation of practical use could be carried out in this work. In this context, future studies should address in-situ simulations, benchmarks and in-depth analysis of robust-stable methods in practical environments.