Homogeneous inhibition is optimal for the phase precession of place cells in the CA1 field

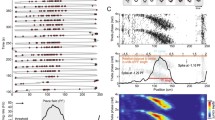
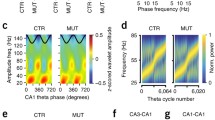
Abstract

Place cells are hippocampal neurons encoding the position of an animal in space. Studies of place cells are essential to understanding the processing of information by neural networks of the brain. An important characteristic of place cell spike trains is phase precession. When an animal is running through the place field, the discharges of the place cells shift from the ascending phase of the theta rhythm through the minimum to the descending phase. The role of excitatory inputs to pyramidal neurons along the Schaffer collaterals and the perforant pathway in phase precession is described, but the role of local interneurons is poorly understood. Our goal is estimating of the contribution of field CA1 interneurons to the phase precession of place cells using mathematical methods. The CA1 field is chosen because it provides the largest set of experimental data required to build and verify the model. Our simulations discover optimal parameters of the excitatory and inhibitory inputs to the pyramidal neuron so that it generates a spike train with the effect of phase precession. The uniform inhibition of pyramidal neurons best explains the effect of phase precession. Among interneurons, axo-axonal neurons make the greatest contribution to the inhibition of pyramidal cells.

Appendix

Equations for currents:

$$\begin{aligned} I_{\text {leak}, j}(V_j) = g_{\text {leak}, j}(V_j - E_{\text {leak}}), \end{aligned}$$

$$\begin{aligned} I_{Na, j}(V_j, h_j) = g_{Na, j} m^2_{\infty } (V_j - E_{Na}), \end{aligned}$$

$$\begin{aligned} I_{K-DR, j}(V_j, n_j) = g_{K-DR, j} n_j (V_j - E_K), \end{aligned}$$

$$\begin{aligned} I_{Ca, j}(V_j, s_j) = g_{Ca, j} s^2_{j} (V_j - E_{Ca}), \end{aligned}$$

$$\begin{aligned} I_{K-AHP, j}(V_j, q_j) = g_{K-AHP, j} q_j (V_j -E_K), \end{aligned}$$

$$\begin{aligned} I_{K-C, j}(V_j, [Ca^{2+}]_j, c_j) = g_{K-C, j} c_j \text {min}(1, \frac{[Ca^{2+}]_j}{250}) (V_j - E_K), \end{aligned}$$

where j $\in$ S, D, S and D denote the soma and dendrite of pyramidal neurons, respectively (Table 2); E is the reversal potential of the currents (Table 3); g is the maximal conductance (Table 2). The equations and parameters for the synaptic currents (Eq. (3)) are given in the next section. All conductances are measured in the units $mS/cm^2$. The potential is measured in the unit mV. $[Ca^{2+}]$ - mM.

The equations for intracellular calcium concentration [Ca2+] are:

$$\begin{aligned} \frac{d[Ca^{2+}]_j}{dt} = -\phi I_{Ca,j} - \beta _{[Ca^{2+}]_j} [Ca^{2+}]_j, \quad j\in {S,D} \end{aligned}$$

Equations for calcium concentration

$$\frac{dy_j}{dt} = \frac{y_{\infty }(U) - y_j}{\tau _y(U)} \quad \text {with} \quad \ U = \begin{cases}V_j, &{} \text{for} \ y_j \ne q_j\\ [Ca^{2+}]_j, &{} \text {for} \ y_j = q_j, \end{cases}$$

where $\phi _{Ca} = 0.13 \ mM \cdot cm^2 \cdot nA^{-1}$ is a scaling constant that converts the inward calcium current into internal calcium concentration, $\beta = 0.075 \ ms^{-1}$.

The gating variables $h_j$ , $n_j$, $s_j$ , $c_j$ , $q_j$ , $j\in \{S,D\}$ are each governed by an equation of a form:

$$\begin{aligned} \frac{dy_j}{dt} = \frac{y_{\infty }(U) - y_j}{\tau _y(U)} \quad \text {with} \quad \ U = {\begin{cases} V_j, &{} \text {for} \ y_j \ne q_j\\ [Ca^{2+}]_j, &{} \text {for} \ y_j = q_j, \end{cases} } \end{aligned}$$

The associated steady state value and time constant are defined in the usual manner

Equations for gate variables

$$\begin{aligned} y_{\infty }(U) = \frac{\alpha _y(U)}{\alpha _y(U) + \beta _y(U)} \quad \text {and} \quad \tau _y(U) = \frac{1}{\alpha _y(U) + \beta _y(U)}, \end{aligned}$$

$$\begin{aligned} \alpha _m(V_j) = \frac{0.32 \cdot (-46.9 - V_j)}{exp((-46.1-V_j)/4)-1}, \quad \beta _m(V_j) = \frac{0.28 \cdot (V_j+19.9)}{exp((V_j+19.9)/5)-1}, \end{aligned}$$

$$\begin{aligned} \alpha _h(V_j) = 0.128 \cdot exp((-43-V_j)/18), \quad \beta _h(V_j) = \frac{4}{exp((-20-V_j)/5)+1}, \end{aligned}$$

$$\begin{aligned} \alpha _n(V_j) = \frac{0.016 \cdot (-24.9 - V_j)}{exp((-24.9-V_j)/5)-1}, \quad \beta _n(V_j) = 0.25 \cdot exp(-1-0.025V_j), \end{aligned}$$

$$\begin{aligned} \alpha _n(V_j) = \frac{1.6}{exp(-0.072(V_j-125))+1}, \quad \beta _n(V_j) = \frac{0.02 \cdot (V_j-111.1)}{exp((V_j-111.1)/5}-1), \end{aligned}$$

$$\begin{aligned} \alpha _c(V_j) = {\left\{ \begin{array}{ll} 2 \cdot exp((-53.5-V_j)/27), &{} \text {if} \ V_j > 50\\ exp[((V_j-70)/11-(V_j+53.5)/27)/18.975] &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \beta _c(V_j) = {\left\{ \begin{array}{ll} 0, &{} \text {if} \ V_j > 50\\ 2 \cdot exp((-53.5-V_j)/27) - \alpha _c(V_j) &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \alpha _q([Ca^{2+}]_j) = \text {min}(0.00002\cdot [Ca^{2+}]_j, 0.01), \end{aligned}$$

$$\begin{aligned} \beta _q = 0.001, \end{aligned}$$

The parameter p is the proportion of the cell area taken by the somatic compartment.

Table 2 Maximal ionic conductances ($mS/cm^2$) Ferguson and Campbell (2009)

Table 3 Values and units of reversal potentials, coupling parameters, and membrane capacitance Ferguson and Campbell (2009)