1 Introduction

Carbyne, a linear carbon chain with sp-hybridization, has recently received a revival of interest due to its extraordinary mechanical, thermal and structure-dependent electronic properties [1, 2]. First-principles calculations reveal exceptional mechanical properties of the material (i.e., specific stiffness, strength, and elastic modulus) outperforming other carbon structures, including diamond [3]. Extremely high thermal stability [4] and thermal conductivity [5] have been reported for carbyne much exceeding the other low definitional carbon systems (e.g., graphene). This material also shows interesting electronic, magnetic and transport properties which can be promising for practical implementation in nanotechnology development [3, 6,7,8].

Due to high reactivity of carbon, it is technologically challenging to create long carbon chains using conventional physical vapor deposition methods such as arc discharge [9, 10], laser ablation [11,12,13] and on-surface synthesis [14, 15]. In this respect, multi-walled carbon nanotubes (CNTs) are found to be the best environment for the bottom-up growth of linear carbon chains [16,17,18,19]. Record-long linear chain (up to 6000 carbon atoms) has already been synthesized using this method [20]. Hydrocarbon precursors are commonly inserted inside the CNTs in order to create carbon chains [21, 22]. However, recent atomistic scale simulations for the catalytic growth of carbyne inside double-walled CNT using hydrocarbon species [23] shows that the purity of carbyne depends on the ratio of hydrogen to carbon in the feedstock. Depending on this ratio, carbon chains with different level of hydrogen termination are obtained and the properties of the resulting structures are determined with the degree of hydrogenation. For example, semiconducting to metallic transition can be obtained by increasing the concentration of terminating hydrogen atoms [23]. These finding indicate the possibility of creating carbyne structures with tunable electronic properties and therefore require detailed research to unveil the potential of such functional systems.

Fig. 1
figure 1

Electronic band structure of pristine (a), hydrogenated (b), fluorinated (c) and double hydrogenated (d) carbyne. Insets show the optimized structures and carbon–carbon bond lengths

Full size image

Here, we use first-principles density functional theory (DFT) calculations in combination with Greens functional formalism to study the effect of hydrogenation and fluorination on the electronic transport properties of carbyne. We found profound structural and electronic changes due to surface functionalization. For example, linear carbon chain with alternating bond order transforms into buckled structure with equidistant C–C spacing, resulting in semiconducting to metallic transition. Surface treatment also increases the current in the system due to delocalization of electronic states along the chain. We also studied the electronic transport properties of partially hydrogenated carbyne and interface structures consisting of pristine and functionalized carbyne. Transmission spectrum and eigenstates analysis are conducted to explain the obtained results.

2 Computational details

The considered systems are studied using DFT within the generalized gradient approximation of Perdew–Burke–Ernzerhof (PBE) [24]. All atoms are described using the norm-conserving and relativistic pseudopotential PseudoDojo with medium basis set. Grimme’s PBE empirical dispersion correction is used to describe van der Waals interactions during the geometry optimizations [25]. Monkhorst–Pack method is used for Brillouin zone integration [26]. The convergence criterion for Hellman–Feynman forces was 0.001 eV/Å and stress tolerance was 0.001 GPa. Periodic boundary condition is applied along the carbon chain and vacuum spacing more than 10 Å is applied in the other directions. Both atomic positions and lattice parameters are relaxed during the simulations. Electronic transport calculations are conducted using the nonequilibrium Green’s function formalism [27]. Electronic current–voltage (I–V) characteristics are calculated using the Landauer–Büttiker formula [28]

$$\begin{aligned} I(V)= & {} \frac{2e}{h}\int _{\mu _{\text {L}}}^{\mu _{\text {R}}}T(E,V)\left[ f(E-\mu _{\text {L}})\right. \nonumber \\&\left. -f(E-\mu _{\text {R}})\right] {\text {d}}E, \end{aligned}$$
(1)

where T(E, V) is the transmission spectrum for the given value of voltage biasing (V), \(f(E,E_F)\) is the Fermi–Dirac distribution function and \(\mu _{\text {L}}\)/\(\mu _{\text {R}}\) is the chemical potential of the left/right electrode. Calculations are conducted using the computational package Atomistix toolkit [29,30,31].

3 Results and discussion

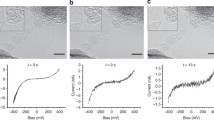
We start with studying structural and electronic properties of the considered systems. It is known that pristine carbyne has two structures: cumulene with double bounds throughout the linear chain and polyyne with alternating single and triple bounds [1]. The former structure shows a metallic nature due to evenly distributed \(\pi\)-electrons, whereas the second system is a semiconductor with a finite band gap at the Brillouin zone edge [1]. The estimated bond length for cumulene is 1.282 Å, whereas polyyne has bond lengths of 1.265 Å and 1.301 Å  [32]. Carbyne favours a poleene configuration due to the Peierls instability [33] with energy difference of 2 meV per carbon atom [3]. In this work, we have conducted simulations for a supercell consisting of 4 carbon atoms using 15 k-point sampling along the chain and 4081 eV density mesh cut-off. Geometry optimization resulted in polyyne structure with alternating bond lengths of 1.264 Å and 1.309 Å (see the inset of Fig. 1a), which are in agreement with the previous DFT predictions [32]. Electronic band structure calculations confirm the semiconducting nature of the system with estimated band gap of 0.408 eV (see Fig. 1a). Both hydrogenation (H-carbyne, see the inset of Fig. 1b) and fluorination (F-carbyne, see the inset of Fig. 1c) resulted in buckled structure with C–C distance of 1.399 Å and 1.411 Å, respectively, for H-carbyne and F-carbyne. Both systems show metallic behavior as revealed in our band structure calculations (see Fig. 1b, c). Such semiconducting-metal transition due to hydrogenation was also reported in Ref. [23]. Semiconducting-metal transition can also be obtained by applying external strain to carbyne [34,35,36] or due to charge transfer between carbyne and host CNT [37]. We also considered the case when two hydrogen atoms are attached to a single carbon atom (see the inset of Fig. 1d). In this case, interatomic distance increases (1.531 Å) and the system becomes an insulator with band gap of 7.52 eV (Fig. 1d). Knowing the fact that PBE exchange-correlation function underestimates semiconducting band gap, we have conducted band structure calculations using hybrid HSE06 [38] functional to have better band gap estimates for the considered structures. The estimated bad gaps are 0.744 eV and 6.874 eV, respectively, for pristine and double hydrogenated carbyne. Hydrogenated and fluorinated samples still show metallic behavior with zero band gap.

Fig. 2
figure 2

a–c Device geometries of pristine (a), hydrogenated (b) and fluorinated (c) carbyne. d I-V characteristics of the considered systems. e Log plot of the ratio of currents obtained for H-carbyne and pristine carbyne as a function of bias voltage

Full size image
Fig. 3
figure 3

Zero-bias device density of states (a) and transmission spectra (b) as a function of electron energy (zero corresponds to Fermi energy) for pristine (solid-black curves), hydrogenated (dashed-red curves) and fluorinated (dotted-blue curves) carbyne

Full size image

Using the optimized geometries, we have constructed a two-probe device geometries consisting of left/right electrodes and an scattering region (see Fig. 2a–c). In all device structures, the size of the scattering region is 10 times larger than the size of the electrodes in order to avoid the influence of the electrodes on the conductivity [39]. The electrodes are modeled as a semi-infinite extension of the simulation supercell (5.148 Å, 4.951 Å and 5.0488 Å for pristine carbyne, H-carbyne and F-carbyne, respectively). 1 \(\times\) 1 \(\times\) 120 k-points are used during the simulations. Since the HSE functional cannot be applied or device geometries in the current version of the ATK software, we used the PBE functional for the electronic transport calculations. Figure 2d shows shows I–V characteristics of pristine (filled-black circles), H-carbyne (open-red circles) and F-carbyne (filled-blue squares) for the range of bias voltage 0–2 V. For pristine carbyne, finite current is obtained along the carbon chain starting from 0.4 V due to the semiconducting behavior of the material. With further increasing the bias voltage, the current increases monotonically. Starting from 1.4 V, we obtained linear dependence of the current on the applied voltage (i.e., Ohmic regime). Since the other two systems are metallic in nature, finite current is obtained for any non-zero voltage and I–V curves show Ohmic character. Both hydrogenated and fluorinated systems show very similar I–V characteristics. Surface functionalization increases the electronic transport in the system significantly. This is shown in Fig. 2e, where we present the ratio of the currents obtained for H-carbyne and pristine carbyne. It is seen from this figure that depending on the applied voltage the current along the carbon chain can be increased by more than an order of magnitude. Enhanced electronic transmission in H-carbyne (i.e., n-alkene) has recently been reported by Garner et al. (see Fig. 3d in Ref. [40]).

Fig. 4
figure 4

Fermi levels of the electrodes as a function of applied voltage

Full size image
Fig. 5
figure 5

Device density of states (a) and transmission spectra (b) as a function of electron energy (zero corresponds to Fermi energy) for bias voltage 1 V. Panels 1–3 show isosurface plots (isovalue 0.25 1/Å\({}^{1.5}\)eV\(^{0.5}\)) of the transmission eigenstates at \(E = -0.4\) eV for pristine (panel 1), hydrogenated (panel 2) and fluorinated (panel 3) carbyne

Full size image
Fig. 6
figure 6

a I–V curves of pristine carbyne (solid-black circles) and carbyne with 1 (open-red circles) and 4 hydrogen atoms (filled-blue squares). b Transmission spectra of the considered samples as a function of electron energy for bias voltage 1.8 V. Panels 1–3 show isosurface plots (isovalue 0.25 1/Å\(^{1.5}\)eV\(^{0.5}\)) of the transmission eigenstates at \(E=0.5\) eV for pristine carbyne (panel 1) and carbyne with 1 (panel 2) and 4 hydrogen atoms (panel 3)

Full size image

To get fundamental understanding of the current enhancement due to surface functionalization of carbyne, we have conducted transmission spectra, device density of states (DDOS) and the transmission eigenstates analysis for the considered systems at different voltage biases. Figure 3 shows the zero-bias DDOS and transmission spectra of the considered systems as a function of electron energy. Due to the semiconducting nature of pristine carbine, we obtained zero density of states and zero transmission in the band gap area (from -0.2 to 0.2 eV). Consequently, we obtained zero electronic current for bias voltages less than 0.4 V (see solid-black circles in Fig. 2d). On the contrary, in the cases of functionalized carbyne (dashed-red and dotted blue curves in Fig. 3), the finite DDOS and transmission near the Fermi level result in finite electronic current through the system even at small bias voltages. With increasing the applied voltage, the Fermi levels of the electrodes change (see Fig. 4) and finite DDOS and, consequently, finite transmission is obtained near the energy zero (i.e., average fermi level). This is shown in Fig. 5 where we plot the DDOS (a) and the transmission spectra (b) as a function of electron energy for all three systems at bias voltage 1 V. The results are present for the range of electron energy from \(-0.5\) to 0.5 eV, which is used for calculating the current [see Eq. (1)] for this voltage value. In this energy range, the largest DDOS is obtained for the pristine carbyne (solid-black curve in Fig. 5a). Despite such large DDOS, the electronic transmission pristine carbyne is much smaller than the ones obtained for the other two systems (Fig. 5b). H-carbyne shows the same transmission as F-carbyne, despite the smaller DDOS. To reveal the peculiarities on the transmission curves, we have calculated transmission eigenstates at different electron energies. Panels 1–3 in Fig. 5 show the isosurface plots of the transmission eigenstates calculated at \(E=-0.4\) eV for which we obtained the largest DDOS for the pristine carbyne. For functionalized systems (panels 2 and 3), the electronic states are extended along the chain, which explains the larger transmission value and, consequently, the larger current across the system. However, in the pristine carbyne (panel 1) the states are localized between carbon atoms with shorter interatomic distance (i.e., triple bonding) and therefore zero transmission is obtained despite largest DDOS. Thus, current enhancement in functionalized carbyne originates from nanoscale charge delocalization along the chain.

Fig. 7
figure 7

I–V curves (a) and asymmetry (b) of the systems consisting of pristine carbyne and H-carbyne (open-red circles) and pristine carbyne and F-carbyne (solid-blue squares). Solid-black circles in a shows I–V curve of pristine carbyne as a reference. Panels 1 and 2 show device geometries

Full size image

Next, we study the effect of partial hydrogenation of the transport properties of carbyne. Figure 6a shows I–V curves of carbyne with single (open-red curve) and 4 (filled-blue squares) hydrogen atoms. The results for the pristine carbyne (solid-black circles) are also present as a reference. These partially hydrogenated systems also show semiconducting behavior which is reflected in the I–V curves as negligible current at small biases (\(\le\) 0.4 V). Slightly enhanced current is obtained in the functionalized systems for bias voltages smaller than 1.2 V. With further increasing the applied voltage, the current in the partially hydrogenated systems becomes smaller. This reduction of the current originates from the nanoscale charge localizations as found in our transmission spectrum analysis. As an example, we show in Fig. 6b transmission spectra of the considered systems at 1.8 V together with transmission eigenstates obtained for electron energy 0.5 eV (panels 1–3). Two transmission eigenvalues are obtained for the given parameters for all three systems. In the case of pristine carbyne, both states are extended along the transmission direction (see panel 1) enhancing the probability of the electrons to cross the system. However, in partially functionalized samples electronic states are localized for one transmission channel (see lower plots in panels 2 and 3). This is the reason for the reduced transmission in functionalized systems at higher voltages.

Finally, we consider interface structures consisting of pristine and fully functionalized carbynes (see insets in Fig. 7b for the device structures). Current rectification is expected in such interfacial systems because of the semiconducting and metallic properties of their constituents. Figure 7a shows the I–V curves of the considered samples (open-red circles and filled-blue squares) together with the results for the pristine carbyne (filled-black circles). There are several distinct features in the I–V curves of the hybrid systems as compared to the one obtained for pristine carbyne. First, the voltage range with zero current reduces (\(\le\) 0.2 V) due to reduced band gap in the electronic structure. Second, the current shows a linear dependence on the voltage starting from small biasing, which is not present in the reference sample. The current enhancement is also obtained in the hybrid systems. Finally, the current for the reverse biasing is larger then the one for the forward biasing, i.e., current rectification is obtained in the hybrid systems. To estimate the rectification level, we have calculated the asymmetry as the ratio of reverse to forward current. Figure 7b shows the asymmetry for both structures. Maximum rectification (> 50%) is obtained for small bias voltage. The asymmetry decreases with increasing the applied bias. Both samples show similar rectification with slightly larger rectification value for the fluorinated system.

4 Conclusions

We have conducted first-principles quantum transport calculations to study the effect of surface functionalization of the electronic transport properties of carbyne. Both hydrogenation and fluorination result in significant structural changes and semiconducting to metallic transition as revealed in our band structure calculations. As a consequence, the current in the functionalized samples becomes larger than the one obtained for pristine carbyne for a given value of the applied voltage. Such current enhancements originates from the extension of the electronic states along the carbon chain. Current rectification is obtained in hybrid systems consisting of pristine and functionalized carbyne due to semiconducting and metallic behaviors of their constituents. These findings can be useful in developing low dimensional carbon structures with tunable electronic properties.