A scheme for the development of a trinary logic unit (TLU) using polarization-based optical switches

Abstract

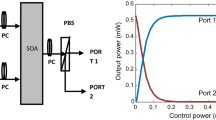
Frequency-encoded optical processors based on multivalued logic (MVL) will play a significant role in future all-optical networks. In this work, basic optical logic gates are designed using a modified trinary system, exploiting the switching action of semiconductor optical amplifiers (SOAs) based on the principle of the nonlinear rotation of the polarization of a probe beam in the presence of a pump beam. A control unit capable of performing OR, AND, and XOR logic operations depending on the frequency of the control signal is then developed. Finally, a trinary logic unit is designed to execute 27 different logic operations. The feasibility of these proposals is confirmed by simulation results. In this approach, each trinary bit, i.e., “trit,” is represented by a unique frequency, which in turn helps to address the noise margin problem that arises in intensity-encoded MVL systems. This scheme can therefore play an important role in errorless optical computing and processing.

Appendix

• (a) The derivation of Eq. (8) [solving from Eqs. (6) and (7)]

From Eq. (6),

$$\frac{{\partial \varphi^{\text{TE}} }}{\partial z} = - \frac{1}{{2v_{\rm g}^{\text{TE}} }}\alpha^{\text{TE}} \varGamma^{\text{TE}} g^{\text{TE}} \left( {z,t} \right).$$

So, $\partial \varphi^{\text{TE}} \left( {z,t} \right) = - \frac{1}{{2v_{\rm g}^{\text{TE}} }}\alpha^{\text{TE}} \varGamma^{\text{TE}} g^{\text{TE}} \left( {z,t} \right)\partial z$.

Integrating both sides yields

$$\int {{\text{d}}\varphi^{\text{TE}} \left( {z,t} \right)} = \int { - \frac{1}{{2v_{\rm g}^{\text{TE}} }}\alpha^{\text{TE}} \varGamma^{\text{TE}} g^{\text{TE}} \left( {z,t} \right){\text{d}}z}.$$

Since the phase variation takes place only along the Z-direction, the partial derivative reduces to the total derivative:

$$\varphi^{\text{TE}} \left( {L,t} \right) = - \frac{1}{{2v_{\rm g}^{\text{TE}} }}\alpha^{\text{TE}} \varGamma^{\text{TE}} g^{\text{TE}} \left( {L,t} \right)L + C_{1},$$

(14)

where L is the length of the SOA and $C_{1}$ is a constant depending upon the initial phase of the mode. Here, we consider that the gain remains constant throughout the length of the SOA.

Now, from Eq. (7),

$$\frac{{\partial \varphi^{\text{TM}} }}{\partial z} = - \frac{1}{{2v_{\rm g}^{\text{TM}} }}\alpha^{\text{TM}} \varGamma^{\text{TM}} g^{\text{TM}} \left( {z,t} \right).$$

So, $\partial \varphi^{\text{TM}} \left( {z,t} \right) = - \frac{1}{{2v_{\rm g}^{\text{TM}} }}\alpha^{\text{TM}} \varGamma^{\text{TM}} g^{\text{TM}} \left( {z,t} \right)\partial z$.

Integrating both sides yields

$$\int {{\text{d}}\varphi^{\text{TM}} \left( {z,t} \right)} = \int { - \frac{1}{{2v_{\rm g}^{\text{TM}} }}\alpha^{\text{TM}} \varGamma^{\text{TM}} g^{\text{TM}} \left( {z,t} \right){\text{d}}z}.$$

Since phase variation takes place only along the Z-direction, the partial derivative reduces to the total derivative:

$$\varphi^{\text{TM}} \left( {L,t} \right) = - \frac{1}{{2v_{\rm g}^{\text{TM}} }}\alpha^{\text{TM}} \varGamma^{\text{TM}} g^{\text{TM}} \left( {L,t} \right)L + C_{2}.$$

(15)

Here we consider that the gain remains constant throughout the length of the SOA.

From Eqs. (14) and (15),

$$\begin{aligned} \varphi^{\text{TM}} \left( {L,t} \right) - \varphi^{\text{TE}} \left( {L,t} \right) & = - \frac{1}{{2v_{\rm g}^{\text{TM}} }}\alpha^{\text{TM}} \varGamma^{\text{TM}} g^{\text{TM}} \left( {L,t} \right)L + C_{2} + \frac{1}{{2v_{\rm g}^{\text{TE}} }}\alpha^{\text{TE}} \varGamma^{\text{TE}} g^{\text{TE}} \left( {L,t} \right)L - C_{1} \\\Delta \varPhi & = \frac{1}{2}\left( {\alpha^{\text{TE}} \varGamma^{\text{TE}} g^{\text{TE}} \left( {L,t} \right) - \alpha^{\text{TM}} \varGamma^{\text{TM}} g^{\text{TM}} \left( {L,t} \right)} \right)L + \left( {C_{2} - C_{1} } \right) \\\Delta \varPhi & = \frac{1}{2}\left( {\alpha^{\text{TE}} \varGamma^{\text{TE}} g^{\text{TE}} \left( {L,t} \right) - \alpha^{\text{TM}} \varGamma^{\text{TM}} g^{\text{TM}} \left( {L,t} \right)} \right)L + \varphi_{0}, \\ \end{aligned}$$

where $\Delta \varPhi$ and $\varphi_{0}$ are the phase difference between the two modes at the output of the SOA and the initial phase difference between the two modes at the input of the SOA, respectively.

• (b) The derivation of Eqs. (11) and (12) [solving from Eqs. (9) and (10)]

From Eq. (11),

$$\frac{{\partial P^{\text{TE}} \left( {z,t} \right)}}{\partial z} = \left[ {\varGamma^{\text{TE}} g^{\text{TE}} \left( {z,t} \right) - \alpha_{\text{int}}^{\text{TE}} } \right]\frac{{P^{\text{TE}} }}{{v_{\rm g}^{\text{TE}} }}.$$

So, $\frac{{\partial P^{\text{TE}} \left( {z,t} \right)}}{{P^{\text{TE}} }} = \left[ {\varGamma^{\text{TE}} g^{\text{TE}} \left( {z,t} \right) - \alpha_{\text{int}}^{\text{TE}} } \right]\frac{1}{{v_{\rm g}^{\text{TE}} }}\partial z$.

Now, integrating both sides yields

$$\int \limits_{{P_{\text{in}}^{\text{TE}} }}^{{P_{\text{out}}^{\text{TE}} }} \frac{{{\text{d}}P^{\text{TE}} \left( {z,t} \right)}}{{P^{\text{TE}} }} = \int \limits_{0}^{L} \left[ {\varGamma^{\text{TE}} g^{\text{TE}} \left( {z,t} \right) - \alpha_{\text{int}}^{\text{TE}} } \right]\frac{{{\text{d}}z}}{{v_{\rm g}^{\text{TE}} }}.$$

Here also, the variation takes place only along the Z-direction, thus the partial derivative reduces to the total derivative:

$$\begin{aligned} \ln \frac{P_{\rm out}^{\rm TE}}{P_{\rm in}^{\rm TE} } & = \left[ {\varGamma^{\rm TE} g^{\rm TE} \left( {L,t} \right) -\alpha_{\rm int}^{\rm TE}} \right]\frac{L}{v_{\rm g}^{\rm TE} } \\ P_{\rm out}^{\rm TE} &= P_{\rm in}^{\rm TE} {\text{e}}^{\left[ {\varGamma^{\rm TE} g^{\rm TE} \left( {L,t} \right) - \alpha_{{\rm int}}^{\rm TE}} \right]\frac{L}{v_{\rm g}^{\rm TE} }}. \\ \end{aligned}$$

From Eq. (12),

$$\begin{aligned} \frac{{\partial P^{\text{TM}} \left( {z,t} \right)}}{\partial z} & = \left[ {\varGamma^{\text{TM}} g^{\text{TM}} \left( {z,t} \right) - \alpha_{\text{int}}^{\text{TM}} } \right]\frac{{P^{\text{TM}} }}{{v_{\rm g}^{\text{TM}} }} \\ \frac{{\partial P^{\text{TM}} \left( {z,t} \right)}}{{P^{\text{TM}} }} & = \left[ {\varGamma^{\text{TM}} g^{\text{TM}} \left( {z,t} \right) - \alpha_{\text{int}}^{\text{TM}} } \right]\frac{1}{{v_{\rm g}^{\text{TM}} }}\partial z. \\ \end{aligned}$$

Integrating both sides yields

$$\begin{aligned} \int \limits_{P_{\rm in}^{\rm TM}}^{P_{\rm out}^{\rm TM}} \frac{{\text{d}}P^{\rm TM} \left( {z,t} \right)}{P^{\rm TM} } & = \int \limits_{0}^{L} \left[ \varGamma^{\rm TM} g^{\rm TM} \left( {z,t} \right) - \alpha_{\rm int}^{\rm TM} \right]\frac{{\text{d}}z}{v_{\rm g}^{\rm TM} } \\ \ln \frac{P_{\rm out}^{\rm TM} }{P_{\rm in}^{\rm TM} } & = \left[ {\varGamma^{\rm TM} g^{\rm TM} \left( {L,t} \right) - \alpha_{\rm int}^{\rm TM} } \right]\frac{L}{v_{\rm g}^{\rm TM} } \\ P_{\rm out}^{\rm TM} & = P_{\rm in}^{\rm TM} {\text{e}}^{{\left[ {\varGamma^{\rm TM} g^{\rm TM} \left( {L,t} \right) - \alpha_{\rm int}^{\rm TM} } \right]\frac{L}{v_{\rm g}^{\rm TM} }}}. \\ \end{aligned}$$