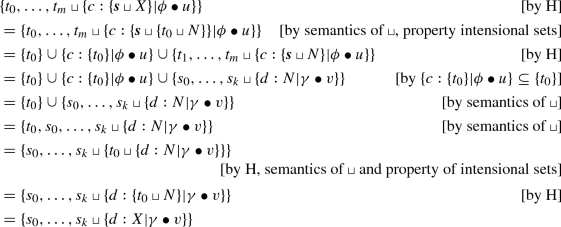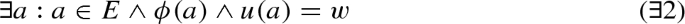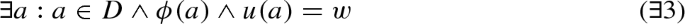Automated Reasoning with Restricted Intensional Sets

Abstract

Intensional sets, i.e., sets given by a property rather than by enumerating elements, are widely recognized as a key feature to describe complex problems (see, e.g., specification languages such as B and Z). Notwithstanding, very few tools exist supporting high-level automated reasoning on general formulas involving intensional sets. In this paper we present a decision procedure for a first-order logic language offering both extensional and (a restricted form of) intensional sets (RIS). RIS are introduced as first-class citizens of the language, and set-theoretical operators on RIS are dealt with as constraints. Syntactic restrictions on RIS guarantee that the denoted sets are finite. The language of RIS, called ${\mathcal {L}}_\mathcal {RIS}$, is parametric with respect to any first-order theory ${\mathcal {X}}$ providing at least equality and a decision procedure for ${\mathcal {X}}$-formulas. In particular, we consider the instance of ${\mathcal {L}}_\mathcal {RIS}$ when ${\mathcal {X}}$ is the theory of hereditarily finite sets and binary relations. We also present a working implementation of this instance as part of the $\{log\}$ tool, and we show through a number of examples and two case studies that, although RIS are a subclass of general intensional sets, they are still sufficiently expressive as to encode and solve many interesting problems. Finally, an extensive empirical evaluation provides evidence that the tool can be used in practice.

Appendices

Rewrite Rules

This section lists all the ${\mathcal {L}}_\mathcal {RIS}$ rewrite rules for $=$, $\ne$, $\in$ and $\notin$ constraints not given in Sect. 3.2, along with the rules for $set$ and $isX$ constraints; rules for $un$ and $disj$ constraints are instead all shown in Sect. 3.2 and are not repeated here. All rules listed in this appendix not dealing with RIS terms are borrowed unaltered from [30].

We adopt the following notational conventions: s, t, u (possibly subscripted) stand for arbitrary ${\mathcal {X}}$-terms; A, B, C, D stand for arbitrary $\mathcal {RIS}$-terms of sort $\textsf {Set}$ (either extensional or intensional, variable or not); ${{\bar{D}}},{{\bar{E}}}$ represent either variables of sort $\textsf {Set}$ or variable-RIS; X, N are variables of sort $\textsf {Set}$ representing extensional sets (not RIS) while x is a variable of sort ${\textsf {X}}$; $\varnothing$ represents either $\emptyset$ or a RIS with empty domain (e.g., $\{\emptyset | \phi \mathbin {\bullet } u\}$); finally, ${{\varvec{X}}}$ represents either the variable X or a set term containing X as its innermost variable set part, i.e., $\{t_1,\dots ,t_n \sqcup X\}$. Note that, when $n=0$, $\{t_1,\dots ,t_n \sqcup X\}$ is just X.

In all rules, variables appearing in the right-hand side but not in the left-hand side are assumed to be fresh variables.

Besides, recall that: a) the rules are given for RIS whose domain is not another RIS (see Appendix A.1 for further details); b) the control term of RIS terms is assumed to be a variable in all cases (see Appendix A.2 for further details); c) $\phi (d)$, $\gamma (d)$, $u(d)$ and $v(d)$ are shorthands for $\phi [x \mapsto d]$, $\gamma [x \mapsto d]$, $u[x \mapsto d]$ and $v[x \mapsto d]$, respectively, where $[x \mapsto d]$ represents variable substitution; and d) we use $=$ and $\in$ in place of $=_{\mathcal {X}}$ and $\in _{\mathcal {X}}$ whenever it is clear from the context. We will also use the symbol $\equiv$ to denote syntactic equality between terms.

1.1 Equality

There is a symmetric rule for each of the following: ($=3$), ($=4$), ($=5$), ($=10$), ($=11$), ($=12$), ($=13$) and ($=14$). That is, these rules apply when the l.h.s. and the r.h.s. are switched.

All other admissible $=$-constraints not covered by the rules are in solved form; hence, they are dealt with as irreducible constraints (see Sect. 4.2).

Remark 8

• Rules ($=1$) and ($=5$) include rules (4) and (5) of Fig. 1 as special cases.

• The condition $A \not \equiv \{ \{d \sqcup D\} | \phi \mathbin {\bullet } u\}$ in rule ($=4$) is motivated by the fact that the case where $A \equiv \{ \{d \sqcup D\} | \phi \mathbin {\bullet } u\}$ is dealt with by rule ($=11$).

• The set part of an extensional set can be also a RIS term. All rules listed in this section still continue to work also in these cases. In particular, rule ($=3$) deals also with constraints of the form $X = \{t_0,\dots , t_n \mathbin {\scriptstyle \sqcup }\{X | \phi \mathbin {\bullet } u\}\}$ where the domain of the RIS is the same variable occurring in the left-hand side of the equality. This constraint is rewritten to $X = \{t_0,\dots , t_n \mathbin {\scriptstyle \sqcup }\{N | \phi \mathbin {\bullet } u\}\}$ where N is a fresh variable. For example, the equality $X = \{a,b \mathbin {\scriptstyle \sqcup }\{x:X | true \mathbin {\bullet } x\}\}$ is rewritten to $X = \{a,b \mathbin {\scriptstyle \sqcup }\{x:N | true \mathbin {\bullet } x\}\}$. Note that, if $N = \emptyset$, then $X = \{a,b\}$, which is clearly a solution of the given constraint.

• Rules ($=12$) and ($=13$) (resp., ($=6$), ($=7$) and ($=8$)) are motivated by the observation that rule ($=14$) (resp., ($=9$)) does not work satisfactory (it loops forever) whenever the same variable X occurs in both sides of the equation. As an example, the rewriting of the simple constraint $\{x : D \mathbin {\bullet } x\} = \{1 \mathbin {\scriptstyle \sqcup }D\}$ does not terminate using rule ($=14$), though it has the obvious solution $D = \{1 \mathbin {\scriptstyle \sqcup }N\}$, N a fresh variable. Thus, rules ($=12$) and ($=13$) (resp., ($=6$), ($=7$) and ($=8$)) are introduced to deal with these special cases. Note that these rules are, in a sense, the analogous of rule ($=3$) which deals with equations of the form $X = \{t_0,\dots , t_n \mathbin {\scriptstyle \sqcup }{{\varvec{X}}}\}$ where the same variable X occurs in both sides of the equation. In turn, rule ($=3$) is a generalization to RIS of rule (6) listed in Fig. 3 of [30].

• In ($=8$) the first six branches consider the cases in which $t_0 \in \{s_0,\dots , s_k\}$, while the next three branches consider the cases in which $t_0 \notin \{s_0,\dots , s_k\}$. Moreover the following mutually exclusive conditions hold for the last three branches:

  $$\begin{aligned}&\phi (n) \wedge u(n) \notin \{s_0, \dots , s_k\} \\&\phi (n) \wedge u(n) = s_j \\&\lnot \phi (n) \end{aligned}$$

  $\square$

1.2 Inequality

There is a symmetric rule for each of the following: ($\ne 4$) and ($\ne 7$). That is, these rules apply when the l.h.s. and the r.h.s. are switched.

All other admissible $\ne$-constraints not covered by the rules are in solved form (see Sect. 4.2).

Remark 9

The fact that $A \ne \{D | \phi \mathbin {\bullet } u\}$ (rule ($\ne 7$)) and $X \ne \{t_0, \dots , t_n \mathbin {\scriptstyle \sqcup }\{D | \phi \mathbin {\bullet } u\}\}$ (rule ($\ne 5$)) are not considered in solved form as it is $X \ne S$ when S is not a RIS term is motivated by the observation that, while determining the satisfiability of $X \ne S$ is immediate, the satisfiability of the inequalities involving RIS depends on D, $\phi$ and $u$ and hence requires further simplification of the constraint. $\square$

1.3 Set Membership

1.4 Not Set Membership

All other admissible $\notin$-constraints not covered by the rules are in solved form (see Sect. 4.2).

Remark 10

(Membership/not membership) Rules ($\in _{1}$) and ($\notin _{1}$) include rules ($\in _{1}$) and ($\notin _{1}$) of Fig. 2 as special cases. $\square$

1.5 Sort Constraints

Remark 11

In Algorithm 1 (see Sect. 3), $SAT _\mathcal {RIS}$ calls $SAT _{\mathcal {X}}$ only once, at the end of the computation. $SAT _{\mathcal {X}}$ is called by passing it the whole collection of ${\mathcal {X}}$ literals previously accumulated in the current formula $\varPhi$ by the repeated applications of the rewrite rules within STEP. Alternatively, and more efficiently, $SAT _{\mathcal {X}}$ could be called repeatedly in the inner loop of the solver, just after the STEP procedure has been called. This would allow possible inconsistencies to be detected as soon as possible instead of being deferred to the last step of the decision procedure. For example, if $\varPhi$ contains the equation $\{1\} = \{2\}$, which is rewritten by STEP as $1 =_{\mathcal {X}} 2$, calling $SAT _{\mathcal {X}}$ just after STEP ends allows the solver to immediately detect that $\varPhi$ is unsatisfiable. Similarly, variable substitutions entailed by equalities possibly returned by $SAT _{\mathcal {X}}$ are propagated to the whole formula $\varPhi$ as soon as possible. $\square$

1.6 Nested RIS Domains

According to the syntax of ${\mathcal {L}}_\mathcal {RIS}$ (see Sect. 2), RIS domains can be a nested chain of RIS, ending in a variable or an extensional set. On the other hand, the rewrite rules presented in Sect. 3.2 and Appendix A apply only to RIS whose domain is not another RIS. We do so because the rewrite rules for the most general case are more complex; thus, they would hinder understanding of the decision procedure.

These more general rules, however, can be easily generated from the rules for the simpler case. In this section we show how this generalization can be done by showing how one of the rules presented in Sect. 3.2, namely rule (7), is adapted to deal with the more general case. All other rewrite rules can be generalized in the same way.

Consider a non-variable RIS whose domain is a nested chain of RIS where the innermost domain is an extensional set. The generalization of rule (7) to a RIS of this form is a follows:

where n and N are two new variables. Note that the first element n of the domain of the outermost RIS is obtained by the recursive application of the same rules for equality, over the domain itself (possibly another RIS) and the extensional set $\{n \mathbin {\scriptstyle \sqcup }N\}$. Note also that when $m = 1$ this rule boils down to rule (7) of Fig. 1.

1.7 Control Terms

As with nested RIS domains, we preferred not to show the rewrite rules when the control term is not a variable, as these rules are somewhat more complex than the others.

According to Definition 3, when the control term is not a variable, then it is an ordered pair of the form (x, y) where both components are variables. Consider the following RIS:

$$\begin{aligned} \{(x,y):\{(1,2),55\} | \phi \mathbin {\bullet } u\} \end{aligned}$$

The problem with this RIS is that (x, y) does not unify with 55, for all x and y. The semantics of RIS stipulates that 55 must not be considered as a possible value on which $\phi$ and $u$ are evaluated.

As this example shows, it is necessary to consider one more case (i.e., one more non-deterministic choice) in each rewriting rule. For example, if in rule (7) we consider a general control term c, and not just a variable, the rule is split into two rules:

Note how the second rule simply skips d.

Now we combine rules (7’) and (7”) to give the full rewrite rule corresponding to rule (7). For this combination to be feasible, however, we need to assume that the parameter language ${\mathcal {L}}_{\mathcal {X}}$ provides two constraints, $pair (t)$ and $npair (t)$, to state that an ${\mathcal {X}}$-term is or is not an ordered pair, respectively. This is guaranteed, for instance, when ${\mathcal {X}}$ is $\mathcal {BR}$.

Source Code of the Bell-LaPadula Case Study

Detailed Proofs

This section contains detailed proofs of the theorems stated in the main text, along with some results that justify some of our claims.

In the following proofs H denotes the current hypothesis.

The following proposition given in the main text supports the claim that many RIS parameters can be avoided by a convenient control term.

Proposition 1

If $\mathbf {p}$ is a vector of existentially quantified variables declared inside an intensional set, then:

$$\begin{aligned}&S = \{x:D_1 | \exists \mathbf {p}(\phi (x,\mathbf {p}) \wedge \mathbf {p}\in D_2 \mathbin {\bullet } u(x,\mathbf {p}))\} \\&\Leftrightarrow S = \{(x,\mathbf {p}):D_1 \times D_2 | \phi ((x,\mathbf {p})) \mathbin {\bullet } u((x,\mathbf {p}))\} \end{aligned}$$

Proof

$\Longrightarrow$)

$\Longleftarrow$) Similar to the previous case. $\square$

Now we prove Proposition 2 from the main text which gives the conditions to eliminate existential quantifiers appearing in RIS filters in relation to functional predicates.

Proposition 2

Let $\phi _q$ be the precondition of a functional predicate $p(x_1,\dots ,x_{n-1},y)$. Let $\phi _r$ be an ${\mathcal {X}}$-formula, and $\mathbf {x}_q$ and $\mathbf {x}_r$ subsets of $x_1,\dots ,x_{n-1}$. Then, given $x_1,\dots ,x_{n-1}$ the following holds:

$$\begin{aligned}&\forall y (\lnot (p(x_1,\dots ,x_{n-1},y) \wedge \phi _r(\mathbf {x}_r,y) )) \\&\Leftrightarrow \lnot \phi _q(\mathbf {x}_q) \vee (\phi _q(\mathbf {x}_q) \wedge \exists z (p(x_1,\dots ,x_{n-1},z) \wedge \lnot \phi _r(\mathbf {x}_r,z))) \end{aligned}$$

$\square$

Proof

Note that:

$$\begin{aligned}&\forall y (\lnot (p(x_1,\dots ,x_{n-1},y) \wedge \phi _r(\mathbf {x}_r,y))) \nonumber \\&\Leftrightarrow \forall y (\lnot p(x_1,\dots ,x_{n-1},y) \vee \lnot \phi _r(\mathbf {x}_r,y)) \end{aligned}$$

(1)

Now we divide the proof into two implications.

$\Longrightarrow$) If $\phi _q(\mathbf {x}_q)$ does not hold the conclusion is proved. Now assume $\phi _q(\mathbf {x}_q)$ holds. Then, $p(x_1,\dots ,x_{n-1},z)$ holds for some z due to the hypothesis and Definition 19. Hence, for (1) to be true, $\phi _r(\mathbf {x}_r,z)$ must be false (because otherwise the disjunction would be true for z). So, in this case we have $\phi _q(\mathbf {x}_q) \wedge p(x_1,\dots ,x_{n-1},z) \wedge \lnot \phi _r(\mathbf {x}_r,z)$, which proves the conclusion.

$\Longleftarrow$) If $\phi _q(\mathbf {x}_q)$ does not hold, then $p(x_1,\dots ,x_{n-1},y)$ does not hold for all y due to the hypothesis and Definition 19, hence the conclusion.

Now assume z is such that $\phi _q(\mathbf {x}_q) \wedge p(x_1,\dots ,x_{n-1},z) \wedge \lnot \phi _r(\mathbf {x}_r,z)$ is true. Then, the conclusion is true for z because $\phi _r(\mathbf {x}_r,z)$ is false. Now consider any $y \ne z$. Given that p is a functional predicate symbol (hypothesis), then we have $\lnot p(x_1,\dots ,x_{n-1},y)$ because p can hold for at most one value of its last parameter (and we know it holds for z). So, the conclusion. $\square$

The following justifies that RIS can be used to encode RUQ.

Proposition 3

$$\begin{aligned} D \subseteq \{x:D | F\} \Leftrightarrow \forall x (x \in D \implies F) \end{aligned}$$

Proof

$\Longrightarrow$)

$\Longleftarrow$)

$\square$

The following proposition supports the claim that to force a RIS to be empty it is enough to consider its filter.

Proposition 4

If D is a non-empty set, then:

$$\begin{aligned} \{x:D | \phi \mathbin {\bullet } u\} = \emptyset \Leftrightarrow \forall x (x \in D \implies \lnot \phi (x)) \end{aligned}$$

Proof

$$\begin{aligned}&\{x:D | \phi \mathbin {\bullet } u\} = \emptyset \\&\Leftrightarrow \{y : \exists d (x \in D \wedge \phi \wedge y = u)\} = \emptyset \\&\Leftrightarrow \forall y (\lnot \exists d (d \in D \wedge \phi \wedge y = u)) \\&\Leftrightarrow \forall y (\forall d (d \notin D \vee \lnot \phi (d) \vee y \ne u(d))) \\&\Leftrightarrow \forall d (d \in D \implies \lnot \phi (d)) \end{aligned}$$

$\square$

The next subsections provide the proofs of the theorems stated in the main text. All these proofs concern the base ${\mathcal {L}}_\mathcal {RIS}$ language, not the possible extensions discussed in Sect. 6 nor those presented in Appendixes A.1 and A.2 .

1.1 Satisfiability of the Solved form (Theorem 1)

Basically, the proof of this theorem uses the fact that, given a pure $\mathcal {RIS}$-formula $\varPhi$ verifying the conditions of the theorem, it is possible to guarantee the existence of a successful assignment of values to all variables of $\varPhi$ using pure sets only, with the only exception of the variables X occurring in terms of the form $X = u$—which are obviously already assigned. In particular, the solved forms involving variable RIS verify the following ($X_i$ are variables; $R_i$ are variables or variable-RIS whose domain is variable $X_i$):

• $t \notin \{X_1 | \phi \mathbin {\bullet } u\}$

• $\{X_1 | \phi \mathbin {\bullet } u\} = \varnothing$

• $\{X_1 | \phi _1 \mathbin {\bullet } u_1\} = \{X_2 | \phi _2 \mathbin {\bullet } u_2\}$

• $un (R_3,R_4,R_5)$

• $R_3 \parallel R_4$

are solved with $X_i = \emptyset$ and $R_i = \emptyset$ for those $R_i$ that are variables.

In the proof we use the auxiliary function $find$:

$$\begin{aligned} find (x,t) = {\left\{ \begin{array}{ll} \emptyset &{} \text {if } t = \emptyset , x \ne \emptyset \\ \{0\} &{} \hbox { if}\ t = x\\ \{1 + n : n \in find (x,y)\} &{} \text {if } t = \{y \mathbin {\scriptstyle \sqcup }\emptyset \} \\ \{1 + n : n \in find (x,y)\} \cup find (x,s) &{} \text {if } t = \{y \mathbin {\scriptstyle \sqcup }s\}, s \ne \emptyset \end{array}\right. } \end{aligned}$$

which returns the set of ‘depths’ at which a given element x occurs in the set t.

Proof

Consider a pure $\mathcal {RIS}$-formula $\varPhi$ in solved form. The proof is basically the construction of a mapping for the variables of $\varPhi$ of sort $\textsf {Set}$ into the interpretation domain $D_\textsf {Set}$ (see Sect. C.2 to see how variables of sort ${\mathcal {X}}$ are managed). The construction is divided into two parts by dividing $\varPhi$ as $\varPhi _= \wedge \varPhi _r$, where $\varPhi _=$ is a conjunction of equalities whose l.h.s is a variable, and $\varPhi _r$ is the rest of $\varPhi$. In the first part $\varPhi _=$ is not considered. A solution for $\varPhi _r$ is computed by looking for valuations¹⁰ of the form:

$$\begin{aligned} X_{i} \mapsto \underbrace{\{\cdots \{}_{n_{i}} \emptyset \}\cdots \} \end{aligned}$$

(2)

fulfilling all $\ne$ and $\notin$ constraints. We will briefly refer to the r.h.s. of (2) as $\{ \emptyset \}^{n_i}$. In particular, RIS domains are mapped onto $\emptyset$ ($n_i = 0$) and the numbers $n_{i}$ for the other variables are computed choosing one possible solution of a system of integer equations and disequations, that trivially admits solutions. Such system is obtained by analyzing the ‘depth’ of the occurrences of the variables in the terms. Then, all the variables occurring in $\varPhi$ only in r.h.s. of equations of $\varPhi _{=}$ are bound to $\emptyset$ and the mappings for the variables of the l.h.s. are bound to the uniquely induced valuation.

In detail, let $X_1,\dots , X_m$ be all the variables occurring in $\varPhi$, save those occurring in the l.h.s. of equalities, and let $X_1,\dots , X_h$, $h \le m$, be those variables occurring as domains of RIS terms. Let $n_1,\dots , n_m$ be auxiliary variables ranging over ${\mathbb {N}}$. We build the system Syst as follows:

• For all $i\le h$, add the equation $n_i=0$.

• For all $h<i\le m$, add the following disequations:

  $$\begin{aligned} \begin{array}{ll} n_i \ne n_j+c &{} \forall X_i \ne t \text { in } \varPhi \text { and } c \in find (X_j,t)\\ n_i \ne c &{} \forall X_i \ne t \text { in } \varPhi \text { and } t \equiv \{\emptyset \}^c\\ n_i \ne n_j+c+1 &{} \forall t \notin X_i \text { in } \varPhi \text { and } c \in find (X_j,t) \\ n_i \ne c+1 &{} \forall t \notin X_i \text { in } \varPhi \text { and } t \equiv \{\emptyset \}^c \end{array} \end{aligned}$$

If $m = h$, then $n_i = 0$ for all $i=1,\dots ,m$ is the unique solution of Syst. Otherwise, it is easy to observe that Syst admits infinitely many solutions. Let:

• $\{n_1=0,\dots , n_h=0, n_{h+1}={\bar{n}}_{h+1},\dots , n_m={\bar{n}}_m\}$ be one arbitrarily chosen solution of Syst.

• $\theta$ be the valuation such that $\theta (X_i)=\{\emptyset \}^{n_i}$ for all $i\le m$.

• $Y_1,\dots , Y_k$ be all the variables of $\varPhi$ which appear only in the l.h.s. of equalities of the form $Y_i=t_i$.

• $\sigma$ be the valuation such that $\sigma (Y_i)=\theta (t_i)$.

We prove that ${\mathcal {R}} \models \varPhi [\theta \sigma ]$ by case analysis on the form of the atoms in $\varPhi$:

• $Y_i=t_i$ It is satisfied, since $\sigma (Y_i)$ has been defined as a ground term and equal to $\theta (t_i)$.

• $X_i\ne t$ If t is a ground term, then we have two cases: if t is not of the form $\{\emptyset \}^c$, then it is immediate that $\theta (X_i)\ne t$; if t is of the form $\{\emptyset \}^c$, for some c, then we have $n_i\ne c$, by construction, and hence $\theta (X_i)\ne t$.

  If t is not ground, then if $\theta (X_i)=\theta (t)$, then there exists a variable $X_j$ in t such that ${\bar{n}}_i={\bar{n}}_j+c$ for some $c\in find (X_j,t)$; this cannot be the case since we started from a solution of Syst.

• $t \not \in X_i$ Similar to the case above.

• $\{X_i | \phi \mathbin {\bullet } u\} = \varnothing$ This means that ${\bar{n}}_i=0$ and $\theta (X_i)=\theta (X_j)=\theta (X_k)=\emptyset$.

• $\{X_i | \phi _1 \mathbin {\bullet } u_1\} = \{X_j | \phi _2 \mathbin {\bullet } u_2\}$ This means that ${\bar{n}}_i={\bar{n}}_j=0$ and $\theta (X_i)=\theta (X_j)=\emptyset$.

• $un (R_i,R_j,R_k)$ Recall that $R_i,R_j,R_k$ can be either variables or variable-RIS whose domain are variables $X_i,X_j,X_k$, respectively. Now, those R that are variables are replaced by a corresponding X and for those that are not the valuation is computed for the domains (which are variables, by construction). For example, if $R_i$ and $R_k$ are variable-RIS and $R_j$ is a variable, we have $un (R_i,X_j,R_k)$, $X_i$ is the domain of $R_i$, $X_k$ is the domain of $R_k$ and the valuation is computed for $X_i$, $X_j$ and $X_k$. Also recall that from item 5 of Definition 16, there are no $\ne$ constraints involving any of the X participating of the $un$ constraint. Then, this means that ${\bar{n}}_i={\bar{n}}_j={\bar{n}}_k=0$ and $\theta (X_i)=\theta (X_j)=\theta (X_k)=\emptyset$.

• $R_i \parallel R_j$ Similar considerations for $R_i$ and $R_j$ to the previous case apply. Then:

  • If $i,j \le h$, then $\theta (X_i)=\theta (X_j)=\emptyset$

  • If $i > h$ (the same if $j > h$), then ${\bar{n}}_i \ne {\bar{n}}_j$ and so $\theta (X_i)=\{ \emptyset \}^{n_i}$ is disjoint from $\theta (X_j)=\{ \emptyset \}^{n_j}$.

$\square$

1.2 Satisfiability of $\varPhi _{\mathcal {S}} \wedge \varPhi _{\mathcal {X}}$ (Theorem 2)

The satisfiability of $\varPhi _{\mathcal {X}}$ is determined by $SAT _{\mathcal {X}}$. Since $SAT _{\mathcal {X}}$ is a decision procedure for ${\mathcal {X}}$-formulas, if $\varPhi _{\mathcal {X}}$ is unsatisfiable, then $SAT _{\mathcal {X}}$ returns $false$; hence, $\varPhi$ is unsatisfiable. If $\varPhi _{\mathcal {X}}$ is satisfiable, then $SAT _{\mathcal {X}}$ rewrites $\varPhi _{\mathcal {X}}$ into an ${\mathcal {X}}$-formula in a simplified form which is guaranteed to be satisfiable w.r.t. the interpretation structure of ${\mathcal {L}}_{\mathcal {X}}$. This rewriting, however, may cause non-set variables in $\varPhi _{\mathcal {X}}$, i.e., variables of sort ${\textsf {X}}$, to get values for which the formula is satisfied. These variables can occur in both $\varPhi _{\mathcal {X}}$ and $\varPhi _{\mathcal {S}}$. Given that, at this point, $\varPhi _{\mathcal {S}}$ is in solved form, variables of sort ${\textsf {X}}$ can only appear in constraints that are in solved form. Specifically, if x is a variable of sort ${\textsf {X}}$, the following are all solved form constraints that may contain x:

• 1. $X = S(x)$ or $X = \{Y | \phi (x) \mathbin {\bullet } u(x)\}$ (i.e., x is a non-local variable in the RIS)

• 2. $\{X | \phi (x) \mathbin {\bullet } u(x)\} = \varnothing$ or $\varnothing = \{X | \phi (x) \mathbin {\bullet } u(x)\}$

• 3. $\{X | \phi _1(x) \mathbin {\bullet } u_1(x)\} = \{Y | \phi _2(x) \mathbin {\bullet } u_2(x)\}$.

• 4. $X \ne S(x)$

• 5. $t(x) \notin {{\bar{D}}}$

• 6. $un ({{\bar{C}}},{{\bar{D}}},{{\bar{E}}})$ and ${{\bar{C}}}$ or ${{\bar{D}}}$ or ${{\bar{E}}}$ are of the form $\{X | \phi (x) \mathbin {\bullet } u(x)\}$

• 7. ${{\bar{C}}} \parallel {{\bar{D}}}$, and ${{\bar{C}}}$ or ${{\bar{D}}}$ are of the form $\{X | \phi (x) \mathbin {\bullet } u(x)\}$

All these constraints remains in solved form regardless of the value bound to x. Hence, $\varPhi$ is satisfiable.

1.3 Termination of $SAT _\mathcal {RIS}$ (Theorem 4)

In order to prove termination of $SAT _\mathcal {RIS}$, we use the rules given in Appendix A for equality, inequality, set membership, and not set membership, and those for union and disjointness given in Figs. 3 and 4 in the main text.

First of all, it is worth noting that the requirement that the set of variables ranging on $\mathcal {RIS}$-terms (i.e., variables of sort $\textsf {Set}$) and the set of variables ranging on ${\mathcal {X}}$-terms (i.e., variables of sort ${\textsf {X}}$) are disjoint sets prevents us from creating recursively defined RIS, which could compromise the finiteness property of the sets we are dealing with. In fact, a formula such as $X = \{D | F(X) \mathbin {\bullet } P\}$, where F contains the variable X, is not an admissible $\mathcal {RIS}$-constraint, since the outer X should be of sort $\textsf {Set}$ whereas the inner X should be of sort ${\textsf {X}}$ (recall that the filter is a ${\mathcal {X}}$-formula). Note that, on the contrary, a formula such as $X = \{D(X) | F \mathbin {\bullet } P\}$ is an admissible formula, which, in many cases, is suitably handled by our decision procedure.

Let a rewriting procedure for $\pi$ be the repeated application of the rewrite rules for a specific $\mathcal {RIS}$-constraint $\pi$ until either the initial formula becomes $false$ or no rules for $\pi$ apply. Following [30], we begin by proving that each individual rewriting procedure, applied to an admissible formula, is locally terminating, that is each call to such procedures will stop in a finite number of steps. For all the rules inherited from CLP($\mathcal {SET}$) we assume the results in [30]. Then, we prove local termination only for the new rules dealing with RIS.

The following are non-recursive rules; thus, they terminate trivially: ($=1$), ($=2$), ($=3$), ($=4$), ($=5$), ($=7$), ($\ne 1$), ($\ne 2$), ($\ne 3$), ($\ne 4$), ($\ne 5$), ($\ne 6$), ($\ne 7$), ($\in _{1}$), ($\in _{3}$), ($\in _{4}$), ($\notin _{1}$), (14), (15), (16), (17), (22), (23) and (24).

Now we consider rules which contain direct recursive calls or calls to other rules of the same rewriting procedure and involve at least one RIS. Figures 8, 9 and 10 show what rewrite rule calls other rewrite rules of the same rewriting procedure, for $=$, $un$ and $\parallel$, respectively. In these figures an arrow from a node to another means that the former calls the later. We only depict these because the other rewriting procedures are simpler. We will pay special attention to the possible loops that can be seen in all three graphs.

Fig. 8

Calls relation between rules of the $=$-rewriting procedure

Fig. 9

Calls relation between rules of the $un$-rewriting procedure

Fig. 10

Calls relation between rules of the $\parallel$-rewriting procedure

• Rule (6) In all branches, the recursive call is made with at least one argument whose size is strictly smaller than the one of the input formula. In particular, in the last branch the size of X will not affect the size of the arguments of the recursive call because X is a variable so it cannot add elements to N, N is a variable itself and X is removed from the recursive call.

• Rule (8) In the first seven branches, the recursive call is made with at least one argument whose size is strictly smaller than the one of the input formula. In the last branch, the recursive call is made with arguments whose size is equal to those of the input formula. Indeed, we remove $t_0$ from the l.h.s. set but we add $u(n)$ while variable X is substituted by the new variable N. However, we now know that $u(n) = s_j$ for some $j \in [0,k]$. Hence, the recursive call will be processed by one of the first seven branches which we know reduce the size of at least one of their arguments.

• Rule (9) We will prove termination of this rule by describing a particular abstract implementation.

• 1. If the set parts of A and B are not RIS, then the results of [30] apply.

• 2. If the set part of either A or B are RIS, then:

  • (a) ‘Empty’ their domains. This means that if one of the RIS is of the form:

    $$\begin{aligned} \{ \{d_1,\dots ,d_k \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\} \end{aligned}$$

    then rewrite this set into:

    $$\begin{aligned} \{u(d_1) \mathbin {\scriptstyle \sqcup }\{ \{d_2,\dots ,d_k \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\}\} \end{aligned}$$

    or

    $$\begin{aligned} \{ \{d_2,\dots ,d_k \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\} \end{aligned}$$

    depending on whether $\phi (d_1)$ holds or not. Continue with this rewriting until all the $d_i$ have been processed. This process will transform the initial RIS into a number of sets of the form:

    $$\begin{aligned} \{u(d_{i_1}),\dots ,u(d_{i_m}) \mathbin {\scriptstyle \sqcup }\{ D | \phi \mathbin {\bullet } u\}\} \end{aligned}$$

    (3)

    with $\{d_{i_1},\dots ,d_{i_m}\} \subseteq \{d_1,\dots ,d_k\}$ and D variable or the empty set.

    Hence, at the end of this process the domains of the RIS so generated are either the empty set or a variable.

  • (b) If the domain of one of the RIS obtained in the previous step is the empty set, then substitute the RIS by the empty set. Then, RIS of the form (3) become $\{u(d_{i_1}),\dots ,u(d_{i_m}) \mathbin {\scriptstyle \sqcup }\emptyset \}$ which is equal to $\{u(d_{i_1}),\dots ,u(d_{i_m})\}$.

    Hence, at the end of this process the domains of the RIS so generated are variables.

  • (c) Substitute the RIS by new variables. Formally (when at both sides there are RIS):

    $$\begin{aligned}&\{t_0,\dots ,t_m \mathbin {\scriptstyle \sqcup }\{ D | \phi \mathbin {\bullet } u\}\} = \{s_0,\dots ,s_k \mathbin {\scriptstyle \sqcup }\{ E | \gamma \mathbin {\bullet } v\}\} \\&\longrightarrow \\&\{t_0,\dots ,t_m \mathbin {\scriptstyle \sqcup }N_1\} = \{s_0,\dots ,s_k \mathbin {\scriptstyle \sqcup }N_2\} \\&{}\wedge N_1 = \{ D | \phi \mathbin {\bullet } u\} \wedge N_2 = \{ E | \gamma \mathbin {\bullet } v\} \end{aligned}$$

    (a)

    Note that might be no more RIS at this point, so there is nothing to substitute.

• 3. Now apply rule ($=9$) only to the first conjunct of (a) as in [30] until it terminates, delaying the processing of the remaining conjuncts in (a). As no RIS are in the first conjunct of (a) the results of [30] apply.

• 4. Once rule ($=9$) applied to the first conjunct terminates, variables $N_i$ are substituted back by the corresponding RIS, thus obtaining equalities of the following forms:

  $$\begin{aligned}&\{ D | \phi \mathbin {\bullet } u\} = \{ E | \gamma \mathbin {\bullet } v\} \\&\{ D | \phi \mathbin {\bullet } u\} = \{\cdot \mathbin {\scriptstyle \sqcup }N\}\\&\{ D | \phi \mathbin {\bullet } u\} = \{\cdot \mathbin {\scriptstyle \sqcup }\{ E | \gamma \mathbin {\bullet } v\}\} \end{aligned}$$

  where D and E are variables (due to the process described in step 2).

  Note that, without RIS, the final formulas returned by ($=9$) would be in solved form as their l.h.s. would be variables.

• 5. As can be seen, by the form of the returned equalities and by Fig. 8, these equalities are processed by some of the rules added to deal with RIS.

So, ($=9$) either terminates as in [30], or calls other rules for equality (which is an added behavior compared to [30]).

• Rule (10) The recursive call is made with one argument whose size is strictly smaller than in the initial formula, since t is removed from the domain of the RIS.

• Rule (11) In the first branch there is no recursion on the same rule because the l.h.s. of the equality constraint is no longer a RIS but an extensional set. In particular, the size of the arguments are the same w.r.t. the initial ones. However, the rules that can be fired in this case (see Fig. 8 and the analysis for the corresponding rules), all reduces the size of at least one of its arguments. In particular, if rules ($=9$) or ($=14$) are called, if they call this rule back, it will be done with strictly smaller arguments. Then, this loop will run a finite number of times.

  In the second branch the recursive call is made with one argument whose size is strictly smaller than in the initial formula, since t is removed from the domain of the RIS.

• Rule (12) The size of the r.h.s. argument of the equality constraint is strictly smaller than the one of the input formula because $t_0$ has been removed. Furthermore, the size of X will not affect the size of the arguments of the recursive call because X is a variable so it cannot add elements to N, N is a variable itself and X is removed from the recursive call.

• Rule (13) Same arguments of previous rule apply.

• Rule (=14) The recursive call is made with one argument whose size is strictly smaller than in the initial formula, since t is removed from the r.h.s. The size of D can affect the size of the arguments of the recursive call only if D is the set part of A. However, this case is processed by one of the following rules: ($=12$) or ($=13$).

• Rule ($\in _{2}$) The recursive call is made with a r.h.s. argument whose size is strictly smaller than the initial one because s is removed from the set.

• Rule ($\notin _{2}$) Same arguments of previous rule apply.

• Rule ($\notin _{3}$) In either branch the recursive call is made with a r.h.s. argument whose size is strictly smaller than the initial one because d is removed from the domain of the RIS.

• Rule (18) In the first branch the recursive call is made with a first argument whose size is strictly smaller than the initial one because t is removed from it. In the second branch, it is both arguments whose sizes are strictly smaller than the initial ones because t is effectively removed from A given that we know that $t \in A$.

  Note that in Fig. 9 this rule may call rule (21), which in turn may call back this rule or rules (19) and (20), thus possibly generating an infinite loop. However, this rule can call (21) only when the first or second argument is a non-variable RIS. In that case, rule (21) removes one element of the domain of the RIS but it does not necessarily reduces the size of the arguments. This may fire the callback to this rule. But this rule reduces the size of its arguments, so after a finite number of calls the loop finishes. This shows how the arrow labeled ($un$-a) in Fig. 9 can be traversed only a finite number of times.

  See below for an analysis of rule (21).

• Rule (19) Symmetric arguments to previous rule apply.

• Rule (20) In all branches the size of the third argument of the recursive call is strictly smaller than the initial one because t is removed from it.

• Rule (21) Consider the non-variable RIS arguments of this rule. The rule transforms these RIS into either extensional sets or new RIS.

  • 1. If all such arguments are transformed into extensional sets, then the rule does not recur on itself (but calls other rules of the $un$ constraint).

  • 2. If all such arguments are transformed into variable RIS, then the rule does not recur on itself (but calls other rules of the $un$ constraint or, possibly, is in solved form).

  • 3. If at least one of such arguments is still a non-variable RIS, then there is a recursive call but the size of that argument is strictly smaller than the initial one. In effect, this case occurs when the initial argument in question is of the following form $\{ x:\{a,b \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\}$ with $a \ne b$ and $\lnot \phi (a)$. That is, the initial argument is a non-variable RIS with at least two elements in its domain but the “first” one does not satisfy the filter. Then, $u(a)$ does not belong to the RIS and so it is equal to $\{ x:\{b \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\}$. Precisely, this last RIS is used as the argument to the recursive call. Hence, at least one argument of the recursive call is strictly smaller than the initial one.

    Nevertheless, if $\phi (a)$ holds, then a is removed from the domain but the RIS becomes the set part of an extensional set with $u(a)$ as its element part. In this case, the size of this argument is equal to the initial one. However, in this case, there is no recursive call but a call to one of rules (18), (19) and (20), which effectively reduce the size of one of its.

Rule (25):

The recursive call is made with a r.h.s. argument whose size is strictly smaller than the initial one because t is removed from the set.

Rule (26):

Symmetric arguments of previous rule apply.

Rule (27):

In either branch the recursive call is made with a r.h.s. argument whose size is strictly smaller than the initial one because d is removed from the domain of the RIS.

Rule (28):

Symmetric arguments of previous rule apply.

Therefore, the loops shown in Fig. 10 end in a finite number of times since rules (25)–(28) reduce the size of at least one of their arguments every time they are called.

Local termination of each individual procedure, however, does not guarantee global termination of $SAT _\mathcal {RIS}$, since the different procedures may be dependent on each other. However, we observe that rewrite rules not involving RIS in their left-hand sides do not construct any new RIS term in their right-hand sides. They simply treat RIS terms as any other term. Hence, the presence of RIS terms do not affect their termination, which has been proved in [30]. Hence, it is enough to consider only the new rules involving RIS terms.

Rules involving RIS generate both $\mathcal {RIS}$- and ${\mathcal {X}}$-formulas. The $SAT _{\mathcal {X}}$ solver solves the ${\mathcal {X}}$-formulas without producing $\mathcal {RIS}$-formulas. Then, for each constraint $\pi$ and each recursive rewrite rule for it, we will analyze what $\mathcal {RIS}$-constraints other than $\pi$ are generated. In this way we will see if there are cycles between rewriting procedures. We proceed by rule inspection.

• 1. Rules ($\ne 5$), ($\ne 6$) and ($\ne 7$) generate $\in$- and $\notin$-constraints.

• 2. Rule ($\in _{3}$) generates $=$-constraints.

• 3. Rules (18), (19) and (20) generate $=$-constraints.

• 4. Rules (25), (26), (27) and (28), generate $\notin$-constraints.

This is depicted in Fig. 11. Hence, as can be seen, there are no loops between the rewriting procedures.

Fig. 11

Calls relation between rewriting procedures

1.4 Equisatisfiability (Theorem 3)

This section contains the detailed proofs on the equisatisfiability of the rewrite rules involving RIS presented in Sect. 3.2 and Appendix A; the equisatisfiability of the remaining rules has been proved elsewhere [30]. Hence, these proofs use the rules considering that the control expression is a variable and that the domain of RIS are not other RIS. These proofs can be easily extended to the more general case.

In the following theorems and proofs, $\phi$, $\gamma$, $u$ and $v$ are shorthands for F(x), P(x), G(x) and Q(x), respectively. Moreover, note that a set of the form $\{P(x) : F(x)\}$ (where pattern and filter are separated by a colon ( : ), instead of a bar (|), and the pattern is before the colon) is a shorthand for $\{y : \exists x (P(x) = y \wedge F(x))\}$. That is, the set is written in the classic notation for intensional sets used in mathematics.

$u$ and $v$ are assumed to be bijective patterns. Recall that all patterns allowed in ${\mathcal {L}}_\mathcal {RIS}$ fulfill this condition. The condition on the bijection of patterns is necessary to prove equisatisfiability for rule (8).

The proof of Theorem 3 rests on a series of lemmas each of which shows that the set of solutions of left and right-hand sides of each rewrite rule is the same. Note that, in all Lemmas, n, $n_i$, N and $N_i$ (for any subscript i) are intended to be implicitly existentially quantified variables. That is, we use the same convention used in the rules w.r.t. introducing new variables.

Lemma 1

(Equivalence of rule ($=1$)) We consider only the following case; all the others covered by this rule are either symmetric or trivial.

$$\begin{aligned} \{x:\emptyset | \phi \mathbin {\bullet } u\} = \emptyset \end{aligned}$$

Proof

$$\begin{aligned}&\{x:\emptyset | \phi \mathbin {\bullet } u\} \\&= \{u(x): x \in \emptyset \wedge \phi (x)\} \\&= \{u(x): false \wedge \phi (x)\} \\&= \{u(x): false \} \\&= \emptyset \end{aligned}$$

$\square$

Proposition 5

$$\begin{aligned} \begin{aligned}&\forall d, D: \\&\{x:\{d \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\} = \{u(d): \phi (d)\} \cup \{u(x): x \in D \wedge \phi (x)\} \end{aligned} \end{aligned}$$

Proof

Taking any d and D, we have:

$$\begin{aligned}&\{x:\{d \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\} \\&= \{u(x): x \in \{d \mathbin {\scriptstyle \sqcup }D\} \wedge \phi (x)\} \\&= \{u(x): (x = d \vee x \in D) \wedge \phi (x)\} \\&= \{u(x): (x = d \wedge \phi (x)) \vee (x \in D \wedge \phi (x))\} \\&= \{u(x): x = d \wedge \phi (x)\} \cup \{u(x): x \in D \wedge \phi (x)\} \\&= \{u(d): \phi (d)\} \cup \{u(x): x \in D \wedge \phi (x)\} \end{aligned}$$

$\square$

Lemma 2

(Equivalence of rule ($=3$)) We will consider only the case where $S \equiv \{c:{{\varvec{X}}} | \phi \mathbin {\bullet } u\}$ with $c \equiv u$, because the other one is proved in [30]:

$$\begin{aligned} \begin{aligned}&\forall X, t_0,\dots ,t_k: \\&X = \{t_0,\dots , t_k \mathbin {\scriptstyle \sqcup }\{c:{{\varvec{X}}} | \phi \mathbin {\bullet } u\}\} \\&\Leftrightarrow X = \{t_0,\dots , t_k \mathbin {\scriptstyle \sqcup }\{c:{{\varvec{X}}}[X/N] | \phi \mathbin {\bullet } u\}\} \end{aligned} \end{aligned}$$

where N is a new variable.

Proof

Taking any $X, t_0,\dots ,t_k$, we have:

Now note that if $c \equiv u$, then:

$$\begin{aligned} \{c:X | \phi \mathbin {\bullet } u\} \subseteq X \end{aligned}$$

If $\{c:X | \phi \mathbin {\bullet } u\} = X$, then:

If $\{c:X | \phi \mathbin {\bullet } u\} \subset X$, then let N be the (proper) subset of X such that $\{c:N | \phi \mathbin {\bullet } u\} = \{c:X | \phi \mathbin {\bullet } u\}$. Hence:

$$\begin{aligned}&X = \{t_0,\dots , t_k\} \cup \{c:\{s_1,\dots ,s_a\} | \phi \mathbin {\bullet } u\} \cup \{c:X | \phi \mathbin {\bullet } u\} \\&\Leftrightarrow X = \{t_0,\dots , t_k\} \cup \{c:\{s_1,\dots ,s_a\} | \phi \mathbin {\bullet } u\} \cup \{c:N | \phi \mathbin {\bullet } u\} \\&\Leftrightarrow X = \{t_0,\dots , t_k\} \cup \{c:\{s_1,\dots ,s_a \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\} \\&\Leftrightarrow X = \{t_0,\dots , t_k\} \cup \{c:{{\varvec{X}}}[N/X] | \phi \mathbin {\bullet } u\} \end{aligned}$$

$\square$

In the following lemma, the case where $R \equiv X$ and $S \equiv X$ is covered in [30]. Besides, given that the case where $R \equiv \{c:{{\varvec{X}}} | \phi \mathbin {\bullet } u\}$ and $S \equiv X$ is covered by the case where $R \equiv \{c:{{\varvec{X}}} | \phi \mathbin {\bullet } u\}$ and $S \equiv \{d:X | \gamma \mathbin {\bullet } v\}$, we will prove only the last one. Indeed, given that $c \equiv u$, $d \equiv v$, we have $\{d:X | \gamma \mathbin {\bullet } v\} \subseteq X$. Then, the last case covers the second case when $\{d:X | \gamma \mathbin {\bullet } v\} = X$. In fact, in this and the following lemma we will write $\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\}$ instead of ${{\varvec{X}}}$, where ${{\varvec{s}}}$ denotes zero or more elements; if ${{\varvec{s}}}$ denotes zero elements, then $\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\}$ is just X.

Lemma 3

(Equivalence of rule ($=6$)) If $c \equiv u$ and $d \equiv v$:

$$\begin{aligned} \begin{aligned}&\forall X, t_0,\dots ,t_m,s_0,\dots ,s_k: \\&\begin{aligned} \{t_0,&\dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\ {}\Leftrightarrow {}&t_0 = s_j \\&\quad {}\wedge \{t_0 \mathbin {\scriptstyle \sqcup }N_1\} = \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin N_1 \\&\quad {}\wedge \{t_0 \mathbin {\scriptstyle \sqcup }N_2\} = \{d:X | \gamma \mathbin {\bullet } v\} \wedge t_0 \notin N_2 \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }N_1\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }N_2\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge t_0 \notin \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin \{d:X | \gamma \mathbin {\bullet } v\} \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge \{t_0 \mathbin {\scriptstyle \sqcup }N\} = \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin N \wedge t_0 \notin \{d:X | \gamma \mathbin {\bullet } v\} \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }N\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge t_0 \notin \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge \{s_j \mathbin {\scriptstyle \sqcup }N\} = \{d:X | \gamma \mathbin {\bullet } v\} \wedge s_j \notin N \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }N\} \\&{}\vee t_0 = s_j \\&{}\quad \wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge \{t_0, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee X = \{t_0 \mathbin {\scriptstyle \sqcup }N\} \wedge \gamma (t_0) \\&{}\quad \wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\} \end{aligned} \end{aligned} \end{aligned}$$

Proof

$\implies )$

By H, $t_0$ must belong the r.h.s. set. We will divide the proof in the following cases each of which corresponds to one of the branches at the r.h.s. Note that the disjunction of all the preconditions covers all possible cases.

• $t_0 \in \{s_0,\dots , s_k\}$, then $t_0 = s_j$, for some j

  • $t_0 \notin \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k\}$

    • $s_j \notin \{t_1, \dots , t_m\}$

      • First branch: $\{t_0 \mathbin {\scriptstyle \sqcup }N_1\} = \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge \{t_0 \mathbin {\scriptstyle \sqcup }N_2\} = \{d:X | \gamma \mathbin {\bullet } v\} \wedge t_0 \notin N_1 \wedge t_0 \notin N_2$.

        

        Since the last equality is H, then the first equality holds.

      • Second branch: $t_0 \notin \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin \{d:X | \gamma \mathbin {\bullet } v\}$

        

        Since the last equality is H, then the first equality holds.

      • Third branch: $\{t_0 \mathbin {\scriptstyle \sqcup }N\} = \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin \{d:X | \gamma \mathbin {\bullet } v\} \wedge t_0 \notin N$.

        

        Since the last equality is H, then the first equality holds.

      • Fourth branch: $t_0 \notin \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge \{s_j \mathbin {\scriptstyle \sqcup }N\} = \{d:X | \gamma \mathbin {\bullet } v\} \wedge s_j \notin N$.

        

        Since the last equality is H, then the first equality holds.

    • $s_j \in \{t_1, \dots , t_m\}$

      Now we consider the fifth branch.

      Given that $s_j = t_0$ and that $s_j \in \{t_1, \dots , t_m\}$, then $t_0 \in \{t_1, \dots , t_m\}$.

      

  • $t_0 \in \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k\}$

    Now we consider the sixth branch.

    Given that $s_j = t_0$ and that $t_0 \in \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k\}$, then $s_j \in \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k\}$.

    

• $t_0 \notin \{s_0,\dots , s_k\}$

  Now we consider the last branch.

  Given that $t_0 \notin \{s_0,\dots , s_k\}$, then necessarily $t_0 \in \{d:X | \gamma \mathbin {\bullet } v\}$, then $t_0 \in X$ and $\gamma (t_0)$ holds. Now, the proof is divided in two cases.

  • $t_0 \in \{t_1,\dots , t_m\} \cup \{{{\varvec{s}}}\} \wedge \phi (t_0)$

    In this case we take $N = X$. Then, $\{t_0 \mathbin {\scriptstyle \sqcup }N\} = \{t_0 \mathbin {\scriptstyle \sqcup }X\} = X$, where the last equality holds because $t_0 \in X$. Now:

    

  • $t_0 \notin \{t_1,\dots , t_m\} \cup \{{{\varvec{s}}}\} \vee \lnot \phi (t_0)$

    In this case we take $N = X \setminus \{t_0\}$, then $X = \{t_0 \mathbin {\scriptstyle \sqcup }N\}$ because $t_0 \in X$. Besides $t_0 \notin N$. Now we start from H.

    

$\Longleftarrow )$

We will consider each branch and will prove that the equality holds.

• First branch.

  

• Second branch.

  

• Third branch.

  

• Fourth branch.

  

• Fifth branch.

  

• Sixth branch.

  

• Seventh (last) branch.

  

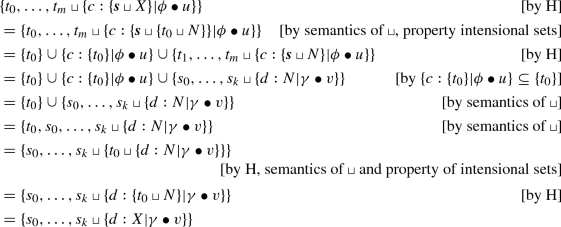
$\square$

Lemma 4

(Equivalence of rule ($=8$)) If $c \not \equiv u$ and $d \not \equiv v$:

$$\begin{aligned} \begin{aligned} \forall X,&t_0,\dots ,t_m,s_0,\dots ,s_k: \\&\begin{aligned} \{t_0,&\dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\ {}\Leftrightarrow {}&t_0 = s_j \\&\quad {}\wedge \{t_0 \mathbin {\scriptstyle \sqcup }N_1\} = \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin N_1 \\&\quad {}\wedge \{t_0 \mathbin {\scriptstyle \sqcup }N_2\} = \{d:X | \gamma \mathbin {\bullet } v\} \wedge t_0 \notin N_2 \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }N_1\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }N_2\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge t_0 \notin \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin \{d:X | \gamma \mathbin {\bullet } v\} \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:X | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge \{t_0 \mathbin {\scriptstyle \sqcup }N\} = \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge t_0 \notin N \wedge t_0 \notin \{d:X | \gamma \mathbin {\bullet } v\} \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }N\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge t_0 \notin \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} \wedge \{s_j \mathbin {\scriptstyle \sqcup }N\} = \{d:X | \gamma \mathbin {\bullet } v\} \wedge s_j \notin N \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }N\} \\&{}\vee t_0 = s_j \\&{}\quad \wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee t_0 = s_j \\&\quad {}\wedge \{t_0, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_{j-1},s_{j+1}, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:X | \gamma \mathbin {\bullet } v\}\} \\&{}\vee X = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge \gamma (n) \wedge t_0 = v(n) \wedge \phi (n) \wedge u(n) \notin \{s_0, \dots , s_k\} \\&\quad {}\wedge t_0 = u(n) \wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\} \\&{}\vee X = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge \gamma (n) \wedge t_0 = v(n) \wedge \phi (n) \wedge u(n) = s_j \\&\quad {}\wedge \{u(n),t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\} \\&{}\vee X = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge \gamma (n) \wedge t_0 = v(n) \wedge \lnot \phi (n) \\&\quad {}\wedge \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\} \end{aligned} \end{aligned} \end{aligned}$$

Proof

The first six branches of this lemma are proved exactly as in the previous lemma, in both directions, because those branches are equal in both lemmas. Hence, we will prove only the last three branches, in both directions.

$\implies )$

In order to prove these branches, we need to recall that $u$ and $v$ are ordered pairs whose first component is the control variable and whose second component is a ${\mathcal {X}}$-term. Then, from now on we will take $u(x) = (x,f_u(x))$ for some term $f_u$ and $v(x) = (x,f_v(x))$, for some term $f_v$.

Besides, all these branches are proved under the assumption as in the previous lemma:

$$\begin{aligned} t_0 \notin \{s_0,\dots , s_k\} \end{aligned}$$

(4)

The first step in the proof is that we can conclude that $t_0$ must belong to the r.h.s. set, by H. Hence, due to (4), $t_0$ must belong to $\{d:X | \gamma \mathbin {\bullet } v\}$, which means that there exists $n \in X$, $\gamma (n)$ holds and $t_0 = v(n)$. Observe that $t_0 = v(n)$ means that $t_0 = (n,f_v(n))$.

Now, note that the following conditions of the branches under consideration are mutually exclusive:

$$\begin{aligned}&\phi (n) \wedge u(n) \notin \{s_0, \dots , s_k\} \\&\phi (n) \wedge u(n) = s_j \\&\lnot \phi (n) \end{aligned}$$

Since $n \in X$, then in the first two cases we have $u(n) \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}$, which implies that $u(n)$ belongs to the l.h.s. set. If $u(n)$ belongs to the l.h.s. set of H, then it must belong to the r.h.s. of H. Then, in the first case we assume $u(n)$ belongs to $\{d:X | \gamma \mathbin {\bullet } v\}$, while in the second we assume is one of the $s_i$.

Hence, in order to prove each branch we will assume the corresponding condition and we will prove the remaining predicates of the conclusion.

• Assume $\phi (n) \wedge u(n) \notin \{s_0, \dots , s_k\}$.

  We will prove that $t_0 = u(n)$ by contradiction. We know that $u(n) \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}$. So:

  

  which is clearly a contradiction. Hence, $t_0 = u(n)$.

  Now we will prove that $\{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:N | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\}$, by dividing the proof in two cases.

  • $t_0 \in \{t_1,\dots , t_m\} \cup \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$

    In this case we take $N = X$. Then, $\{n \mathbin {\scriptstyle \sqcup }N\} = \{n \mathbin {\scriptstyle \sqcup }X\} = X$, where the last equality holds because $n \in X$.

    • $t_0 \in \{t_1,\dots ,t_m\}$

      

    • $t_0 \in \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$. Note that in this case $\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} = \{t_0 \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\}$.

      

  • $t_0 \notin \{t_1,\dots , t_m\} \cup \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$

    In this case we take $N = X \setminus \{n\}$, then $X = \{n \mathbin {\scriptstyle \sqcup }N\}$ because $n \in X$. Besides $n \notin N$. Now we start from H.

    

  The justification of $(\dagger )$ is the following:

  • 1. Note that $\{c:\{n\} | \phi \mathbin {\bullet } u\} = \{u(n)\} = \{t_0\}$ [by assumption of this branch and because in this branch $u(n) = t_0$], then $\{c:\{n\} | \phi \mathbin {\bullet } u\} \setminus \{t_0\} = \emptyset$.

  • 2. $\{d:\{n\} | \gamma \mathbin {\bullet } v\} = \{t_0\}$ [by $\gamma (n) \wedge t_0 = v(n)$], then $\{d:\{n\} | \gamma \mathbin {\bullet } v\} \setminus \{t_0\} = \emptyset$.

  • 3. $t_0 \notin \{c:N | \phi \mathbin {\bullet } u\}$ because if it does then there exists $n' \in N$ such that $\phi (n')$ holds and $t_0 = u(n')$. But, $t_0 = u(n') \Leftrightarrow t_0 = (n',f_u(n'))$. On the other hand $t_0 = (n,f_v(n))$ and so $(n,f_v(n)) = (n',f_u(n'))$ which implies that $n = n'$. But this is impossible because we have $n' \in N$ and $n \notin N$.

  • 4. $\{t_0, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} \setminus \{t_0\} = \{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\}$ [by assumption: $t_0 \notin \{t_1,\dots , t_m\} \cup \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$; and by $t_0 \notin \{c:N | \phi \mathbin {\bullet } u\}$].

  • 5. $\{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\} \setminus \{t_0\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\}$ [by $t_0 \notin \{s_0,\dots , s_k\}$ and $n \notin N$].

• Assume $\phi (n) \wedge u(n) = s_j$.

  We have to prove that $\{u(n),t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\}$. We proceed as with the previous branch. In fact, the first case is identical (note that there we used assumptions that are also available in this branch). In the second case, we take the same value for N and start from H as in the previous branch.

  

  The justification of $(\dagger )$ is the following:

  • 1. $\{d:\{n\} | \gamma \mathbin {\bullet } v\} = \{t_0\}$ [by $\gamma (n) \wedge t_0 = v(n)$], then $\{d:\{n\} | \gamma \mathbin {\bullet } v\} \setminus \{t_0\} = \emptyset$.

  • 2. $t_0 \ne u(n)$ because if not then $t_0 = s_j$ which is in contraction with (4).

  • 3. $t_0 \notin \{c:N | \phi \mathbin {\bullet } u\}$ because if it belongs then there exists $n' \in N$ such that $\phi (n')$ holds and $t_0 = u(n')$. But, $t_0 = u(n') \Leftrightarrow t_0 = (n',f_u(n'))$. On the other hand $t_0 = (n,f_v(n))$ and so $(n,f_v(n)) = (n',f_u(n'))$ which implies that $n = n'$. But this is impossible because we have $n' \in N$ and $n \notin N$.

  • 4. $\{u(n),t_0, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} \setminus \{t_0\} = \{u(n),t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\}$ [by assumption: $t_0 \notin \{t_1,\dots , t_m\} \cup \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$; by $t_0 \ne u(n)$; and by $t_0 \notin \{c:N | \phi \mathbin {\bullet } u\}$].

  • 5. $\{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\} \setminus \{t_0\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\}$ [by $t_0 \notin \{s_0,\dots , s_k\}$ and $n \notin N$].

• Assume $\lnot \phi (n)$.

  We have to prove that $\{t_1, \dots , t_m \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} = \{s_0, \dots , s_k \mathbin {\scriptstyle \sqcup }\{d:N | \gamma \mathbin {\bullet } v\}\}$. We proceed as in the first branch considered in this lemma. In fact, the first case is identical (note that there we used assumptions that are also available in this branch). In the second case, we take the same value for N and proceed in the same way. The only difference is in the first item of the justification of $(\dagger )$ because now we have $\{c:\{n\} | \phi \mathbin {\bullet } u\} = \emptyset$ because $\lnot \phi (n)$.

$\Longleftarrow )$

We will consider only the last three branches and will prove that the equality holds.

Note that when $\phi (n)$ holds then $\{c:\{n\} | \phi \mathbin {\bullet } u\} = \{u(n)\}$; and when $\phi (n)$ does not hold then $\{c:\{n\} | \phi \mathbin {\bullet } u\} = \emptyset$.

• Seventh branch.

  

• Eighth branch.

  

• Ninth branch.

  

The equivalence of rule ($=9$) has been proved previously for any finite set (extensional or intensional) [30].

Lemma 5

(Equivalence of rule ($=10$)) We consider only the following case because the others covered by this rule are similar.

$$\begin{aligned} \begin{aligned}&\forall d, D: \\&\begin{aligned}&\{x:\{d \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\} = \emptyset \\&\Leftrightarrow \lnot \phi (d)\wedge \{x:D | \phi \mathbin {\bullet } u\} = \emptyset \end{aligned} \end{aligned} \end{aligned}$$

Proof

Taking any d and D, we have:

The following lemma proves the equivalence of rule ($7\dag$) which is the extended version of rule ($=11$). This serves as evidence about our claim that all our results are still valid in case the rewrite rules are extended to general control terms and nested RIS domains.

Lemma 6

(Equivalence of rule ($7\dag$))

$$\begin{aligned}&\forall d, D, B: \\&\text {If }c_m \in {\mathcal {V}}: \\&\qquad \{c_m:\{ \dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} | \phi _m \mathbin {\bullet } u_m\} = B \Leftrightarrow \\&\{\dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge n \notin N \\&\quad \wedge (\phi _m(n) \wedge \{u_m(n) \mathbin {\scriptstyle \sqcup }\{c_m:N | \phi _m \mathbin {\bullet } u_m\}\} = B \\&\qquad \vee \lnot \phi _m(n) \wedge \{c_m:N | \phi _m \mathbin {\bullet } u_m\} = B) \\&\vee \\&\{\dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} = \emptyset \\&\quad \wedge B = \emptyset \\&\text {If }c_m \equiv (x_1,x_2): \\&\{c_m:\{ \dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} | \phi _m \mathbin {\bullet } u_m\} = B \Leftrightarrow \\&\{\dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge n \notin N \wedge pair (n)\\&\quad \wedge (\phi _m(n) \wedge \{u_m(n) \mathbin {\scriptstyle \sqcup }\{c_m:N | \phi _m \mathbin {\bullet } u_m\}\} = B \\&\qquad \vee \lnot \phi _m(n) \wedge \{c_m:N | \phi _m \mathbin {\bullet } u_m\} = B)\\&\vee \\&\{\dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge n \notin N \wedge npair (n) \\&\quad \wedge \{c_m:N | \phi _m \mathbin {\bullet } u_m\} = B \\&\vee \\&\{\dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} = \emptyset \\&\quad \wedge B = \emptyset \end{aligned}$$

Proof

Taking any d, D and B, we proceed as follows. The second branch of the first syntactic case and the third of the second syntactic case are trivial. In effect, in these cases the domain of the RIS is the empty set in which case the RIS itself is the empty set and so B must be the empty set as well. From now on we consider the remaining branches of both syntactic cases. In these branches we know that the domain of the RIS is non-empty and so there exists n and N such that:

$$\begin{aligned} \{\dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge n \notin N \end{aligned}$$

holds (n can be any element of the domain and N is the difference between the domain and $\{n\}$). Now we can substitute:

$$\begin{aligned} \{\dots \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi _1 \mathbin {\bullet } u_1\}\dots | \phi _{m-1} \mathbin {\bullet } u_{m-1}\} \end{aligned}$$

by $\{n \mathbin {\scriptstyle \sqcup }N\}$ in the l.h.s.:

$$\begin{aligned} \{c_m:\{n \mathbin {\scriptstyle \sqcup }N\} | \phi _m \mathbin {\bullet } u_m\} = B \end{aligned}$$

Now we consider each syntactic case.

First syntactic case ($c_m \in {\mathcal {V}}$). In this case $c_m$ unifies with n regardless of the kind of term n is. So, we have:

Now assume $\phi _m(n)$, then:

Now assume $\lnot \phi _m(n)$, then:

which finishes the proof of this case.

Second Syntactic Case ($c_m = (x_1,x_2)$). In this case $c_m$ unifies with n only if n is an ordered pair. In this case pair(n) holds and so we can proceed as in the first syntactic case.

On the other hand, if npair(n) holds (thus n is not an ordered pair), then it cannot unify with $c_m$. In this case, $u_m(n)$ cannot belong to the RIS regardless of whether $\phi _m(n)$ holds or not. Hence, B must be equal to $\{c_m:N | \phi _m \mathbin {\bullet } u_m\}$ given that N is the rest of the RIS domain w.r.t. n. $\square$

Remark 12

Note that in rule ($=11$) when B is:

• An extensional set of the form $\{y \mathbin {\scriptstyle \sqcup }A\}$, then the equality in the first disjunct becomes an equality between two extensional sets:

  $$\begin{aligned} \{u(d)\mathbin {\scriptstyle \sqcup }\{x:D | \phi \mathbin {\bullet } u\}\} = \{y \mathbin {\scriptstyle \sqcup }A\} \end{aligned}$$

  which is solved by the rules described in [30]. In turn, the equality in the second disjunct becomes an equality between a RIS and an extensional set:

  $$\begin{aligned} \{x:D | \phi \mathbin {\bullet } u\} = \{y \mathbin {\scriptstyle \sqcup }A\} \end{aligned}$$

  This equality is managed by either rule ($=11$) itself (if D is not a variable) or by rule ($=14$) (if D is a variable).

• A non-variable RIS of the form $\{x:\{e \mathbin {\scriptstyle \sqcup }E\} | \gamma \mathbin {\bullet } v\}$, then the equality in the first disjunct becomes an equality between an extensional set and a non-variable RIS:

  $$\begin{aligned} \{u(d)\mathbin {\scriptstyle \sqcup }\{x:D | \phi \mathbin {\bullet } u\}\} = \{x:\{e \mathbin {\scriptstyle \sqcup }E\} | \gamma \mathbin {\bullet } v\} \end{aligned}$$

  which is managed again by rule ($=11$). In turn, the equality in the second disjunct becomes an equality between a RIS and a non-variable RIS:

  $$\begin{aligned} \{x:D | \phi \mathbin {\bullet } u\} = \{x:\{e \mathbin {\scriptstyle \sqcup }E\} | \gamma \mathbin {\bullet } v\} \end{aligned}$$

  which is managed by the same rule once more.

  Moreover, note that in this case there can be up to four cases (and thus up to four solutions) considering all the possible combinations of truth values of $\phi$ and $\gamma$

• A variable RIS of the form $\{x:E | \gamma \mathbin {\bullet } v\}$, then the equality in the first disjunct becomes an equality between an extensional set and a variable RIS:

  $$\begin{aligned} \{u(d)\mathbin {\scriptstyle \sqcup }\{x:D | \phi \mathbin {\bullet } u\}\} = \{x:E | \gamma \mathbin {\bullet } v\} \end{aligned}$$

  which is managed by rule ($=14$). In turn, the equality in the second disjunct becomes an equality between a RIS and a variable RIS:

  $$\begin{aligned} \{x:D | \phi \mathbin {\bullet } u\} = \{x:E | \gamma \mathbin {\bullet } v\} \end{aligned}$$

  which is no further processed (if D is a variable) or is processed by rule ($=11$) again (if D is not a variable). $\square$

For the following rule we only consider the case where $S \equiv \{c:{{\varvec{X}}} | \phi \mathbin {\bullet } u\}$ because the other one covered by the rule corresponds to results presented in [30]. In this and the following lemma we will write $\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\}$ instead of ${{\varvec{X}}}$, where ${{\varvec{s}}}$ denotes zero or more elements; if ${{\varvec{s}}}$ denotes zero elements, then $\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\}$ is just X.

Lemma 7

(Equivalence of rule ($=12$)) If $c \equiv u$ and $d \equiv v$:

$$\begin{aligned}&\forall X,t_0,t_1,\dots ,t_k: \\&\quad \{d: X | \gamma \mathbin {\bullet } v\} = \{t_0,t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} \\&\quad {}\Leftrightarrow X = \{t_0 \mathbin {\scriptstyle \sqcup }N\} \wedge \gamma (t_0) \wedge \{d:N | \gamma \mathbin {\bullet } v\} = \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} \end{aligned}$$

Proof

In order to simplify the proof, we will not write $u$ and $v$ in the intensional sets because $c \equiv u$ and $d \equiv v$.

$\implies )$

Clearly, $t_0$ must belong to $\{d: X | \gamma \}$, then $t_0 \in X$ and $\gamma (t_0)$ holds.

If $t_0 \in \{t_1,\dots ,t_k\} \cup \{{{\varvec{s}}}\} \wedge \phi (t_0)$ we take $N = X$. In this case we have: $\{t_0 \mathbin {\scriptstyle \sqcup }N\} = \{t_0 \mathbin {\scriptstyle \sqcup }X\} = X$ because $t_0 \in X$. Now we prove the last conjunct:

• $t_0 \in \{t_1,\dots ,t_k\}$

  

• $t_0 \in \{{{\varvec{s}}}\}$. Note that in this case $\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \} = \{t_0 \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \}\}$ because $\phi (t_0)$ holds by assumption.

  

If $t_0 \notin \{t_1,\dots ,t_k\} \cup \{{{\varvec{s}}}\} \vee \lnot \phi (t_0)$ we take N to be $X \setminus \{t_0\}$. Then, $X = \{t_0 \mathbin {\scriptstyle \sqcup }N\}$. Besides, $t_0 \notin N$. Now we will prove the last conjunct by double inclusion.

Take any $x \in \{d:N | \gamma \}$, then $x \in N$ and $\gamma (x)$ holds. Hence, $x \in \{d: X | \gamma \}$ because $N \subseteq X$ [by construction]. Now $x \in \{t_0,t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \}\}$ [by H]. If $x = t_0$, then there is a contradiction with the fact that $x \in N$ because $t_0 \notin N$. So x cannot be $t_0$. If $x = t_i$ ($i \ne 0$), then x trivially belongs to $\{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \}$. Finally, if $x \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \}$, then $\phi (x)$ holds. But $x \in N$ so $x \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \}$.

Now the other inclusion. Take any $x \in \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \}\}$. If $x = t_i$, then $x \in \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \}\}$ and so $x \in \{d: X | \gamma \}$ [by H], which implies $x \in X$ and $\gamma (x)$ holds. Given that $x \ne t_0$ [by $t_0 \notin \{t_1,\dots ,t_k\}$] and $x \in X$, then $x \in N$ [by construction]. Since $x \in N$ and $\gamma (x)$ holds, then $x \in \{d:N | \gamma \}$. If $x \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \}$ then $\phi (x)$ holds and $x \ne t_0$ [by assumption]. Now $x \in \{t_0,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \}\}$ [by $N \subseteq X$]. Then, by H, $x \in \{d: X | \gamma \}$ which means that $x \in X$ and $\gamma (x)$ holds. Since $x \ne t_0$, then $x \in X$ implies $x \in N$. Then, $x \in \{d:N | \gamma \}$.

$\Longleftarrow )$

Lemma 8

(Equivalence of rule ($=13$)) If $c \not \equiv u$ and $d \not \equiv v$:

$$\begin{aligned}&\forall X, t_0,t_1,\dots ,t_k: \\&\quad \{d:X | \gamma \mathbin {\bullet } v\} = \{t_0,t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\} \\&\quad {}\Leftrightarrow X = \{n \mathbin {\scriptstyle \sqcup }N\} \wedge \gamma (n) \wedge t_0 = v(n) \wedge (\phi (n) \implies t_0 = u(n)) \\&\qquad \quad {} \wedge \{d:N | \gamma \mathbin {\bullet } v\} = \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\} \end{aligned}$$

Proof

In order to prove this lemma, we need to recall that $u$ and $v$ are ordered pairs whose first component is the control variable and whose second component is an ${\mathcal {X}}$-term. Then, from now on we will take $u(x) = (x,f_u(x))$ for some term $f_u$ and $v(x) = (x,f_v(x))$, for some term $f_v$.

$\implies )$

Clearly, $t_0$ must belong to $\{d:X | \gamma \mathbin {\bullet } v\}$, which means that there exists $n \in X$, $\gamma (n)$ holds and $t_0 = v(n)$. Observe that $t_0 = v(n)$ means that $t_0 = (n,f_v(n))$.

Now we will prove that $\phi (n) \implies t_0 = u(n)$. So assume, $\phi (n)$ holds but $t_0 \ne u(n)$:

which is clearly a contradiction. Hence, if $\phi (n)$ holds then $t_0 = u(n)$.

Finally, we will prove $\{d:N | \gamma \mathbin {\bullet } v\} = \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\}$ by distinguishing two cases. In the first case, we assume $t_0 \in \{t_1,\dots ,t_k\} \cup \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$, and so we take $N = X$ which guarantees that $X = \{n \mathbin {\scriptstyle \sqcup }N\}$ [by $X = N$ and $n \in X$]. Now we prove the set equality (last conjunct):

• $t_0 \in \{t_1,\dots ,t_k\}$

  

• $t_0 \in \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$. Note that in this case $\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\} = \{t_0 \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\}$.

  

In the second case, we assume $t_0 \notin \{t_1,\dots ,t_k\} \cup \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$, and so we take $N = X \setminus \{n\}$. This means that $X = \{n \mathbin {\scriptstyle \sqcup }N\}$ [by $n \in X$] and $n \notin N$.

Now we proceed by double inclusion. Take any $(x,f_v(x)) \in \{d:N | \gamma \mathbin {\bullet } v\}$, then $x \in N$ and $\gamma (x)$ holds. As $x \in N$ then $x \ne n$ and so $(x,f_v(x)) \ne (n,f_v(n)) = t_0$. Given that $N \subseteq X$, then $(x,f_v(x)) \in \{d:X | \gamma \mathbin {\bullet } v\}$ and so $(x,f_v(x)) \in \{t_0,t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\}$ [by H]. Given that $(x,f_v(x)) \ne t_0$, then $(x,f_v(x)) \in \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}\}$. But $x \ne n$ and so if $(x,f_v(x)) \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }X\} | \phi \mathbin {\bullet } u\}$ then it actually belongs to $\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}$. Hence, $(x,f_v(x)) \in \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\}$.

Now the other inclusion. Take any $x \in \{t_1,\dots ,t_k \mathbin {\scriptstyle \sqcup }\{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}\}$. If $x = t_i$ (for some $i \ne 0$) then $x \ne t_0$, and $x \in \{d:X | \gamma \mathbin {\bullet } v\}$ [by H]. So, we have $n' \in X$ such that $\gamma (n')$ holds and $x = (n',f_v(n'))$. Now if $n' = n$ then we have $x = (n',f_v(n')) = (n,f_v(n)) = t_0$, which is a contradiction with $x \ne t_0$. Hence, $n'$ must be different from n and so $n' \in N$ [by $n' \in X = \{n \mathbin {\scriptstyle \sqcup }N\}$ [by construction] and $n' \ne n$]. Since $n' \in N$ and $\gamma (n')$ holds we have $x = (n',f_v(n')) \in \{d:N | \gamma \mathbin {\bullet } v\}$. Finally, if $x \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}$ then $x = (n',f_u(n'))$ with $n' \in \{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\}$ and $\phi (n')$ holds. If $n' = n$ then $n' \in \{{{\varvec{s}}}\}$ because $n \notin N$, and in this case we would have $t_0 \in \{c:\{{{\varvec{s}}}\} | \phi \mathbin {\bullet } u\}$ because $\phi (n')$ holds, but this a contradiction with the assumption. Hence, $n' \ne n$. On the other hand, $x \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}$ implies that $x = (n',f_u(n')) \in \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}$ [by $N \subseteq X$], which in turn implies $x = (n',f_u(n')) \in \{d:X | \gamma \mathbin {\bullet } v\}$ [by H]. Then, $n' \in X$ and $\gamma (n')$ holds. Now $n' \in X$ iff $n' \in \{n \mathbin {\scriptstyle \sqcup }N\}$ [by construction], but we have proved that $n' \ne n$, so actually $n' \in N$. Therefore, we have $n' \in N$ and $\gamma (n')$ holds, so we have $x = (n',f_u(n')) \in \{d:N | \gamma \mathbin {\bullet } v\}$.

$\Longleftarrow )$

($\dagger$) Note that if $\phi (n)$ does not hold then $\{c:\{n \mathbin {\scriptstyle \sqcup }\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\}\} | \phi \mathbin {\bullet } u\} = \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}$; and if $\phi (n)$ holds then $\{c:\{n \mathbin {\scriptstyle \sqcup }\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\}\} | \phi \mathbin {\bullet } u\} = \{(n,f_u(n))\} \cup \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\} = \{t_0\} \cup \{c:\{{{\varvec{s}}} \mathbin {\scriptstyle \sqcup }N\} | \phi \mathbin {\bullet } u\}$. Besides if $\phi (n)$ holds then $f_u(n) = f_v(n)$ because $t_0 = v(n) = u(n)$. $\square$

Lemma 9

(Equivalence of rule ($=14$))

$$\begin{aligned} \begin{aligned}&\forall D, y, A: \\&\begin{aligned}&\{x:D | \phi \mathbin {\bullet } u\} = \{y \mathbin {\scriptstyle \sqcup }A\} \\&\Leftrightarrow \exists d, E: D = \{d \mathbin {\scriptstyle \sqcup }E\} \wedge \phi (d)\wedge y = u(d)\wedge \{x:E | \phi \mathbin {\bullet } u\} = A \end{aligned} \end{aligned} \end{aligned}$$

Proof

$\implies )$

By H, $y \in \{x:D | \phi \mathbin {\bullet } u\}$; then:

Then, we have proved that $\phi (d)\wedge u(d)= y$ holds.

It remains to be proved the existence of E and $\{x:E | \phi \mathbin {\bullet } u\} = A$. To this end, the proof is divided in two cases.

In the first case we assume $y \notin A$. Hence, take $E = D \setminus \{d\}$, which verifies $D = \{d \mathbin {\scriptstyle \sqcup }E\}$. We will prove $\{x:E | \phi \mathbin {\bullet } u\} = A$ by proving that:

$$\begin{aligned} \{x:E | \phi \mathbin {\bullet } u\} \subseteq A \wedge A \subseteq \{x:E | \phi \mathbin {\bullet } u\} \end{aligned}$$

• $\{x:E | \phi \mathbin {\bullet } u\} \subseteq A$. Take any $w \in \{x:E | \phi \mathbin {\bullet } u\}$; then

  

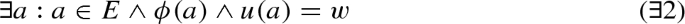
  As $D = \{d \mathbin {\scriptstyle \sqcup }E\}$, then $a \in D$ which implies $w \in \{x:D | \phi \mathbin {\bullet } u\}$ which implies $w \in \{y \mathbin {\scriptstyle \sqcup }A\}$, by H. Since $u$ is a bijective pattern, then $u(a) \ne u(d)$ because $a \ne d$ because $a \in E = D \setminus \{d\}$. Given that $u(d) = y$ [by ($\exists$1)] and $u(a) = w$ [by ($\exists$2)], then $w \ne y$, which implies that $w \in A$.

• $A \subseteq \{x:E | \phi \mathbin {\bullet } u\}$. Take any $w \in A$; then, by assumption of this case, $w \ne y$ $(*)$ and $w \in \{x:E | \phi \mathbin {\bullet } u\}$. Hence:

  

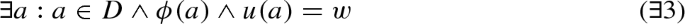
  So, we need to prove that $a \in E$, which by ($\exists$3) will imply that $w \in \{x:E | \phi \mathbin {\bullet } u\}$, which will prove this branch.

  Given that $D = \{d \mathbin {\scriptstyle \sqcup }E\}$ and that $a \in D$, then $a \in E$ iff $a \ne d$. If $a = d$ then $u(a) = u(d)$, then $w = y$ because $u(a) = w$ [by ($\exists$3)] and $u(d) = y$ [by ($\exists$1)]. And if $w = y$ then there is a contradiction with $(*)$. Therefore, $a \ne d$ and so $a \in E$.

In the second case we assume $y \in A$. Hence, take $E = D$, then $\{d \mathbin {\scriptstyle \sqcup }E\} = \{d \mathbin {\scriptstyle \sqcup }D\} = D$ because $d \in D$. If $y \in A$, then $\{y \mathbin {\scriptstyle \sqcup }A\} = A$ [by semantics of $\mathbin {\scriptstyle \sqcup }$]. So, by H, we have:

$\Longleftarrow )$

By H, let d and E be such that:

$$\begin{aligned} D = \{d \mathbin {\scriptstyle \sqcup }E\} \wedge \phi (d)\wedge u(d)= y \wedge \{x:E | \phi \mathbin {\bullet } u\} = A \end{aligned}$$

(5)

Now:

$\square$

The equivalence of the rule for $\ne$ (i.e., rule (9)) is trivial because this rule applies the definition of set disequality which is given in terms of $\in$ and $\notin$.

Lemma 10

(Equivalence of rule ($\in _{4}$))

$$\begin{aligned} \begin{aligned}&\forall D, y: \\&y \in \{x:D | \phi \mathbin {\bullet } u\} \Leftrightarrow \exists d: d \in D \wedge \phi (d)\wedge y = u(d)\end{aligned} \end{aligned}$$

Proof

The proof is trivial since this is the definition of set membership w.r.t. an intensional set. $\square$

Lemma 11

(Equivalence of rule ($\notin _{3}$))

$$\begin{aligned} \begin{aligned}&\forall t, d, D: \\&t \notin \{\{d \mathbin {\scriptstyle \sqcup }D\} | \phi \mathbin {\bullet } u\} \\&\begin{aligned} \Leftrightarrow&\phi (d)\wedge t \ne u(d)\wedge t \notin \{D | \phi \mathbin {\bullet } u\} \\&\vee \lnot \phi (d)\wedge t \notin \{D | \phi \mathbin {\bullet } u\} \end{aligned} \end{aligned} \end{aligned}$$

Proof

$\square$

Concerning the $un$ constraint, since rules (14)–(20) are extensions of the rules presented by [30], the corresponding proofs are trivial. Rule (21) is the only one that truly processes non-variable RIS.

Lemma 12

(Equivalence of rule (21)) If at least one of A, B, C is not a variable nor a variable-RIS:

$$\begin{aligned}&un (A, B, C) \Leftrightarrow un ({\mathcal {S}}(A), {\mathcal {S}}(B), {\mathcal {S}}(C)) \wedge {\mathcal {C}}(A)&\wedge {\mathcal {C}}(B) \wedge {\mathcal {C}}(C) \end{aligned}$$

where ${\mathcal {S}}$ is a set-valued function and ${\mathcal {C}}$ is a constraint-valued function

$$\begin{aligned}&{\mathcal {S}}(\sigma ) = {\left\{ \begin{array}{ll} N_\sigma &{} \hbox { if}\ \sigma \equiv \{ \{d \sqcup D\} | \phi \mathbin {\bullet } u\} \nonumber \\ \sigma &{} \text {otherwise} \end{array}\right. } \\&{\mathcal {C}}(\sigma ) = {\left\{ \begin{array}{ll} N_\sigma = (\{u(d) \sqcup \{ D | \phi \mathbin {\bullet } u\}\} \wedge \phi (d)) &{} \hbox { if}\ \sigma \equiv \{ \{d \sqcup D\} | \phi \mathbin {\bullet } u\} \nonumber \\ \quad {}\vee (N_\sigma = \{ D | \phi \mathbin {\bullet } u\} \wedge \lnot \phi (d)) &{} \\ true &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

Proof

Actually, this rule covers several cases that could have been written as different rules. Indeed, this rule applies whenever at least one of its arguments is a non-variable-RIS. This means that there are seven cases where this rule is applied.

We will prove the equivalence for one of this seven cases because all the other are proved in a similar way. The case to be considered is the following:

$$\begin{aligned} un (\{ \{d \sqcup D\} | \phi \mathbin {\bullet } u\},B,\{ \{e \sqcup E\} | \gamma \mathbin {\bullet } v\}) \end{aligned}$$

(6)

that is, the first and third arguments are non-variable RIS while the second is a variable.

In this case the rule rewrites (6) as follows:

Hence, after performing some trivial simplifications, we have:

$$\begin{aligned}&\phi (d)\wedge \gamma (e) \wedge un (\{u(d) \sqcup \{ D | \phi \mathbin {\bullet } u\}\},B,\{v(e) \sqcup \{ E | \gamma \mathbin {\bullet } v\}\}) \\&\vee \\&\phi (d)\wedge \lnot \gamma (e) \wedge un (\{u(d) \sqcup \{ D | \phi \mathbin {\bullet } u\}\},B,\{ E | \gamma \mathbin {\bullet } v\}) \\&\vee \\&\lnot \phi (d)\wedge \gamma (e) \wedge un (\{ D | \phi \mathbin {\bullet } u\},B,\{v(e) \sqcup \{ E | \gamma \mathbin {\bullet } v\}\}) \\&\vee \\&\lnot \phi (d)\wedge \lnot \gamma (e) \wedge un (\{ D | \phi \mathbin {\bullet } u\},B,\{ E | \gamma \mathbin {\bullet } v\}) \end{aligned}$$

That is, ${\mathcal {S}}$ and ${\mathcal {C}}$ simply transform each non-variable-RIS into an extensional set or another RIS depending on whether the ‘first’ element of each domain is true of the corresponding filter or not. In this way, a disjunction covering all the possible combinations is generated. $\square$

As with union, the only rules for $disj$ that truly deal with non trivial RIS terms are (27) and (28). However, given that they are symmetric, we only prove the equivalence for the first one.

Lemma 13

(Equivalence of rule (27))

$$\begin{aligned} \begin{aligned} A \parallel&\{ \{d \sqcup D\} | \phi \mathbin {\bullet } u\} \Leftrightarrow \\&\phi (d)\wedge u(d)\notin A \wedge A \parallel \{ D | \phi \mathbin {\bullet } u\} \vee \lnot \phi (d)\wedge A \parallel \{ D | \phi \mathbin {\bullet } u\} \end{aligned} \end{aligned}$$

Proof

$\square$

The last theorems concern the specialized rules for RUQ given in Fig. 7. As can be seen, the only one that does not have a trivial proof is the following.

Lemma 14

(Equivalence of rule (42))

$$\begin{aligned}&\forall t, A: t \notin A \implies \\&\quad \{t \sqcup A\} \cup \{ x:\{t \sqcup A\} | \phi \} = \{ x:\{t \sqcup A\} | \phi \} \Leftrightarrow \phi (t) \wedge A \cup \{ x:A | \phi \} = \{ x:A | \phi \} \end{aligned}$$

Proof

First note that

$$\begin{aligned} t \notin A \implies \{t\} \parallel A \wedge \{t\} \parallel \{ A | \phi \} \end{aligned}$$

(7)

and

$$\begin{aligned} \{ x:\{t\} | \phi \} \subseteq \{t\} \end{aligned}$$

(8)

and

$$\begin{aligned} \{ x:\{t\} | \phi \} = \{t\} \Leftrightarrow \phi (t) \end{aligned}$$

(9)

$\square$