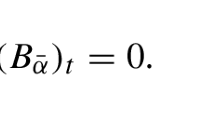From Brauer graph algebras to biserial weighted surface algebras

Abstract

We prove that the class of Brauer graph algebras coincides with the class of indecomposable idempotent algebras of biserial weighted surface algebras. These algebras are associated with triangulated surfaces with arbitrarily oriented triangles, investigated recently in Erdmann and Skowroński (J Algebra 505:490–558, 2018, Algebras of generalized dihedral type, Preprint. arXiv:1706.00688, 2017). Moreover, we prove that Brauer graph algebras are idempotent algebras of periodic weighted surface algebras, investigated in Erdmann and Skowroński (Algebras of generalized quaternion type, Preprint. arXiv:1710.09640, 2017).

1 Introduction and the main results

Throughout this paper, K will denote a fixed algebraically closed field. By an algebra, we mean an associative, finite-dimensional K-algebra with an identity. For an algebra A, we denote by ${\text {mod}}A$ the category of finite-dimensional right A-modules and by D the standard duality ${\text {Hom}}_K(-,K)$ on ${\text {mod}}A$. An algebra A is called self-injective if $A_A$ is an injective module, or equivalently, the projective modules in ${\text {mod}}A$ are injective. Two self-injective algebras A and B are said to be socle equivalent if the quotient algebras $A / {\text {soc}}(A)$ and $B / {\text {soc}}(B)$ are isomorphic. Symmetric algebras are an important class of self-injective algebras. An algebra A is symmetric if there exists an associative, non-degenerate, symmetric, K-bilinear form $(-,-): A \times A \rightarrow K$. Classical examples of symmetric algebras include, in particular, blocks of group algebras of finite groups and Hecke algebras of finite Coxeter groups. In fact, any algebra A is the quotient algebra of its trivial extension algebra ${\text {T}}(A) = A < imes D(A)$, which is a symmetric algebra. By general theory, if e is an idempotent of a symmetric algebra A, then the idempotent algebra eAe also is a symmetric algebra.

Brauer graph algebras play a prominent role in the representation theory of tame symmetric algebras. Originally, R. Brauer introduced the Brauer tree, which led to the description of blocks of group algebras of finite groups of finite representation type, and they are the basis for their classification up to Morita equivalence [10, 25, 29], see also [2]. Relaxing the condition on the characteristic of the field, one gets Brauer tree algebras, and these occurred in the Morita equivalence classification of symmetric algebras of Dynkin type $\mathbb {A}_n$ [22, 35]. If one allows arbitrary multiplicities, and also an arbitrary graph instead of just a tree, one obtains Brauer graph algebras. These occurred in the classification of symmetric algebras of Euclidean type $\widetilde{\mathbb {A}}_n$ [7]. It was shown in [36] (see also [37]) that the class of Brauer graph algebras coincides with the class of symmetric special biserial algebras. Symmetric special biserial algebras occurred also in the Gelfand–Ponomarev classification of singular Harish–Chandra modules over the Lorentz group [23], and as well in the context of restricted Lie algebras, or more generally infinitesimal group schemes, [20, 21], and in classifications of tame Hecke algebras [3, 4, 14]. There are also results on derived equivalence classifications of Brauer graph algebras, and on the connection to Jacobian algebras of quivers with potential, we refer to [1, 11, 26, 31, 32, 34, 37].

We recall the definition of a Brauer graph algebra, following [36], see also [37]. A Brauer graph is a finite connected graph $\varGamma$, with at least one edge (possibly with loops and multiple edges) such that for each vertex v of $\varGamma$, there is a cyclic ordering of the edges adjacent to v, and there is a multiplicity e(v) which is a positive integer. Given a Brauer graph $\varGamma$, one defines the associated Brauer quiver $Q_{\varGamma }$ as follows:

• the vertices in $Q_{\varGamma }$ are the edges of $\varGamma$;

• there is an arrow $i \rightarrow j$ in $Q_{\varGamma }$ if and only if j is the consecutive edge of i in the cyclic ordering of edges adjacent to a vertex v of $\varGamma$.

In this case, we say that the arrow $i\rightarrow j$ is attached to v. The quiver $Q_{\varGamma }$ is 2-regular (see Sect. 2). Recall that a quiver is 2-regular if every vertex is the source and target of exactly two arrows. Any 2-regular quiver has a canonical involution $({-})$ on the arrows, namely if $\alpha$ is an arrow the $\bar{\alpha }$ is the other arrow starting at the same vertex as $\alpha$.

The associated Brauer graph algebra $B_{\varGamma }$ is a quotient algebra of $KQ_{\varGamma }$. The cyclic ordering of the edges adjacent to a vertex v of $\varGamma$ translates to a cyclic permutation of the arrows in $Q_{\varGamma }$, and if $\alpha$ is an arrow in this cycle, we denote vertex v by $v(\alpha )$. Let $C_{\alpha }$ be the product of the arrows in the cycle; in the given order, starting with $\alpha$, this is an element in $KQ_{\varGamma }$. The associated Brauer graph algebra$B_{\varGamma }$ is defined to be $K Q_{\varGamma } / I_{\varGamma }$, where $I_{\varGamma }$ is the ideal in the path algebra $K Q_{\varGamma }$ generated by the elements:

• (1) all paths $\alpha \beta$ of length 2 in $Q_{\varGamma }$ which are not subpaths of $C_{\alpha }$,

• (2) $C_{\alpha }^{e(v(\alpha ))} - C_{\bar{\alpha }}^{e(v(\bar{\alpha }))}$, for all arrows $\alpha$ of $Q_{\varGamma }$.

In [17] and [18], we introduced and studied biserial weighted surface algebras, motivated by tame blocks of group algebras of finite groups. Given a triangulation T of a two-dimensional real compact surface, with or without boundary, and an orientation $\vec {T}$ of triangles in T, there is a natural way to define a quiver $Q(S, \vec {T})$. We showed that these quivers have an algebraic description: They are precisely what we called triangulation quivers. A triangulation quiver is a pair (Q, f) where Q is a 2-regular quiver and f is a permutation of arrows of order 3 such that $t(\alpha )= s(f(\alpha ))$ for each arrow $\alpha$ of Q. A biserial weighted surface algebra$B(S, \vec {T}, m_{\bullet })$ is then explicitly given by the quiver $Q(S, \vec {T})$ and relations, depending on a weight function $m_{\bullet }$, and if described using the triangulation quiver, we get a biserial weighted triangulation algebra$B(Q, f,m_{\bullet })$ (see Sect. 2).

Algebras of generalized dihedral type (see [18, Theorem 1]), which contain blocks with dihedral defect groups, turned out to be (up to socle deformation) idempotent algebras of biserial weighted surface algebras, for very specific idempotents. Biserial weighted surface algebras belong to the class of Brauer graph algebras. It is therefore a natural question to ask which other Brauer graph algebras occur as idempotent algebras of biserial weighted surface algebras. This is answered by our first main result.

Theorem 1

Let A be a basic, indecomposable, finite-dimensional K-algebra over an algebraically closed field K of dimension at least 2. Then, the following statements are equivalent:

• (i) A is a Brauer graph algebra.

• (ii) A is isomorphic to the idempotent algebra eBe for a biserial weighted surface algebra B and an idempotent e of B.

The main ingredient for this is Theorem 4.1. This gives a canonical construction, which we call $*$-construction. A by-product of the proof of Theorem 1 is the following fact.

Corollary 2

Let A be a Brauer graph algebra over an algebraically closed field K. Then, A is isomorphic to the idempotent algebra eBe of a biserial weighted surface algebra $B = B(S,\vec {T},m_{\bullet })$, for a surface S without boundary, a triangulation T of S without self-folded triangles, and an idempotent e of B.

Moreover, we can adapt the $*$-construction to algebras socle equivalent to Brauer graph algebras and prove an analog for the main part of Theorem 1:

Theorem 3

Let A be a symmetric algebra over an algebraically closed field K, which is socle equivalent but not isomorphic to a Brauer graph algebra, and assume the Grothendieck group $K_0(A)$ has rank at least 2. Then,

• (i) ${\text {char}}(K)=2$, and

• (ii) A is isomorphic to an idempotent algebra $\bar{e} \bar{B} \bar{e}$, where $\bar{B}$ is a socle deformed biserial weighted surface algebra $\bar{B} = B(S,\vec {T},m_{\bullet },b_{\bullet })$. Here, S is a surface with boundary, T is a triangulation of S without self-folded triangles, and $b_{\bullet }$ is a border function.

Recall that an algebra A is called periodic if it is periodic with respect to action of the syzygy operator $\varOmega _{A^e}$ in the module category ${\text {mod}}A^e$, where $A^e = A^{{\text {op}}} \otimes _K A$ is its enveloping algebra. If A is a periodic algebra of period n, then all indecomposable non-projective right A-modules are periodic of period dividing n, with respect to the syzygy operator $\varOmega _A$ in ${\text {mod}}A$. Periodic algebras are self-injective and have connections with group theory, topology, singularity theory, and cluster algebras. In [17] and [19], we introduced and studied weighted surface algebras $\varLambda (S, \vec {T}, m_{\bullet },c_{\bullet })$, which are tame, symmetric, and we showed that they are (with one exception) periodic algebras of period 4. They are defined by the quiver $Q(S, \vec {T})$ and explicitly given relations, depending on a weight function $m_{\bullet }$ and a parameter function $c_{\bullet }$ (see Sect. 6). Most biserial weighted surface algebras occur as geometric degenerations of these periodic weighted surface algebras.

Our third main result connects Brauer graph algebras with a large class of periodic weighted surface algebras.

Theorem 4

Let A be a Brauer graph algebra over an algebraically closed field K. Then, A is isomorphic to an idempotent algebra $e \varLambda e$ of a periodic weighted surface algebra $\varLambda = \varLambda (S,\vec {T},m_{\bullet },c_{\bullet })$, for a surface S without boundary, a triangulation T of S without self-folded triangles, and an idempotent e of $\varLambda$.

There are many idempotent algebras of weighted surface algebras which are neither Brauer graph algebras nor periodic algebras. We give an example at the end of Sect. 6.

This paper is organized as follows. In Sect. 2, we recall basic facts on special biserial algebras and show that Brauer graph algebras, symmetric special biserial algebras, and symmetric algebras associated with weighted biserial quivers are essentially the same. In Sect. 3, we introduce biserial weighted surface algebras and present their basic properties. In Sect. 4, we prove Theorem 1. This contains an algorithmic construction which may be of independent interest. Sections 5 and 6 contain the proofs of Theorems 3 and 4 and related material. In Sect. 7, we present a diagram showing the relations between the main classes of algebras occurring in the paper.

For general background on the relevant representation theory, we refer to the books [5, 13, 38, 40], and we refer to [13, 15] for the representation theory of arbitrary self-injective special biserial algebras.

2 Special biserial algebras

A quiver is a quadruple $Q = (Q_0, Q_1, s, t)$ consisting of a finite set $Q_0$ of vertices, a finite set $Q_1$ of arrows, and two maps $s,t : Q_1 \rightarrow Q_0$ which associate with each arrow $\alpha \in Q_1$ its source $s(\alpha ) \in Q_0$ and its target $t(\alpha ) \in Q_0$. We denote by KQ the path algebra of Q over K whose underlying K-vector space has as its basis the set of all paths in Q of length $\ge 0$, and by $R_Q$ the arrow ideal of KQ generated by all paths in Q of length $\ge 1$. An ideal I in KQ is said to be admissible if there exists $m \ge 2$ such that $R_Q^m \subseteq I \subseteq R_Q^2$. If I is an admissible ideal in KQ, then the quotient algebra KQ / I is called a bound quiver algebra and is a finite-dimensional basic K-algebra. Moreover, KQ / I is indecomposable if and only if Q is connected. Every basic, indecomposable, finite-dimensional K-algebra A has a bound quiver presentation $A \cong K Q/I$, where $Q = Q_A$ is the Gabriel quiver of A and I is an admissible ideal in KQ. For a bound quiver algebra $A = KQ/I$, we denote by $e_i$, $i \in Q_0$, the associated complete set of pairwise orthogonal primitive idempotents of A. Then, the modules $S_i = e_i A/e_i {\text {rad}}A$ (respectively, $P_i = e_i A$), $i \in Q_0$, form a complete family of pairwise non-isomorphic simple modules (respectively, indecomposable projective modules) in ${\text {mod}}A$.

Following [39], an algebra A is said to be special biserial if A is isomorphic to a bound quiver algebra KQ / I, where the bound quiver (Q, I) satisfies the following conditions:

• (a) each vertex of Q is a source and target of at most two arrows,

• (b) for any arrow $\alpha$ in Q, there are at most one arrow $\beta$ and at most one arrow $\gamma$ with $\alpha \beta \notin I$ and $\gamma \alpha \notin I$.

Background on special biserial algebras may be found, for example, in [8, 13, 33, 39, 41]. Perhaps most important is the following, which has been proved by Wald and Waschbüsch in [41] (see also [8, 12] for alternative proofs).

Proposition 2.1

Every special biserial algebra is tame.

If a special biserial algebra is in addition symmetric, there is a more convenient description. We propose the concept of a (weighted) biserial quiver algebra, which we will now define. Later, in Theorem 2.6 we will show that these algebras are precisely special biserial symmetric algebras.

Definition 2.2

A biserial quiver is a pair (Q, f), where $Q = (Q_0,Q_1,s,t)$ is a finite connected quiver and $f : Q_1 \rightarrow Q_1$ is a permutation of the arrows of Q satisfying the following conditions:

• (a) Q is 2-regular, that is, every vertex of Q is the source and target of exactly two arrows,

• (b) for each arrow $\alpha \in Q_1$, we have $s(f(\alpha )) = t(\alpha )$.

Let (Q, f) be a biserial quiver. We obtain another permutation $g : Q_1 \rightarrow Q_1$ defined by $g(\alpha ) = \overline{f(\alpha )}$ for any $\alpha \in Q_1$, so that $f(\alpha )$ and $g(\alpha )$ are the arrows starting at $t(\alpha )$. Let $\mathcal {O}(\alpha )$ be the g-orbit of an arrow $\alpha$, and set $n_{\alpha } = n_{\mathcal {O}(\alpha )} = |\mathcal {O}(\alpha )|$. We denote by $\mathcal {O}(g)$ the set of all g-orbits in $Q_1$. A function

$$\begin{aligned} m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^* = \mathbb {N}{\setminus } \{0\} \end{aligned}$$

is said to be a weight function of (Q, f). We write briefly $m_{\alpha } = m_{\mathcal {O}(\alpha )}$ for $\alpha \in Q_1$. The weight function $m_{\bullet }$ taking only value 1 is said to be trivial. For any arrow $\alpha \in Q_1$, we single out the oriented cycle

$$\begin{aligned} B_{\alpha } = \Big ( \alpha g(\alpha ) \dots g^{n_{\alpha }-1}(\alpha )\Big )^{m_{\alpha }} \end{aligned}$$

of length $m_{\alpha } n_{\alpha }$. The triple $(Q,f,m_{\bullet })$ is said to be a (weighted) biserial quiver.

The associated biserial quiver algebra$B = B(Q, f, m_{\bullet })$ is defined as follows. It is the quotient algebra

$$\begin{aligned} B(Q,f,m_{\bullet }) = K Q / J(Q,f,m_{\bullet }), \end{aligned}$$

where $J(Q,f,m_{\bullet })$ is the ideal of the path algebra KQ generated by the following elements:

• (1) $\alpha f({\alpha })$, for all arrows $\alpha \in Q_1$,

• (2) $B_{\alpha } - B_{\bar{\alpha }}$, for all arrows $\alpha \in Q_1$.

We assume that Q is not the quiver with one vertex and two loops $\alpha$ and $\bar{\alpha }$ such that $\alpha = B_{\alpha }$ and $B_{\bar{\alpha }} = \bar{\alpha }$ are equal in B, that is, we exclude the two-dimensional algebra isomorphic to $K[X]/(X^2)$. Assume $m_{\alpha } n_{\alpha } = 1$, so that $\alpha = B_{\alpha }$ and $B_{\bar{\alpha }}$ are equal in B. By the above assumption, $B_{\bar{\alpha }}$ lies in the square of the radical of the algebra. Then, $\alpha$ is not an arrow in the Gabriel quiver $Q_B$ of B, and we call it a virtual loop.

The following describes basic properties of (weighted) biserial quiver algebras.

Proposition 2.3

Let $(Q,f,m_{\bullet })$ be a weighted biserial quiver and $B = B(Q,f,m_{\bullet })$. Then, B is a basic, indecomposable, finite-dimensional symmetric special biserial algebra with $\dim _K {B} = \sum _{\mathcal {O}\in \mathcal {O}(g)} m_{\mathcal {O}} n_{\mathcal {O}}^2$.

Proof

It follows from the definition that B is the special biserial bound quiver algebra $K Q_B / I_B$, where $Q_B$ is obtained from Q by removing all virtual loops and $I_B = J(Q,f,m_{\bullet }) \cap K Q_B$. Let i be a vertex of Q and $\alpha , \bar{\alpha }$ the two arrows starting at i. Then, the indecomposable projective B-module $P_i = e_i B$ has a basis given by $e_i$ together with all initial proper subwords of $B_{\alpha }$ and $B_{\bar{\alpha }}$, and $B_{\alpha } (= B_{\bar{\alpha }})$, and hence $\dim _K P_i = m_{\alpha } n_{\alpha } + m_{\bar{\alpha }} n_{\bar{\alpha }}$. Note also that the union of these bases gives a basis of B consisting of paths in Q. We deduce that $\dim _K {B} = \sum _{\mathcal {O}\in \mathcal {O}(g)} m_{\mathcal {O}} n_{\mathcal {O}}^2$. As well, the indecomposable projective module $P_i$ has simple socle generated by $B_{\alpha } ( = B_{\bar{\alpha }})$. We define a symmetrizing K-linear form $\varphi : B \rightarrow K$ as follows. If u is a path in Q which belongs to the above basis, we set $\varphi (u) = 1$ if $u = B_{\alpha }$ for an arrow $\alpha \in Q_1$, and $\varphi (u) = 0$ otherwise. Then, $\varphi (a b) = \varphi (b a)$ for all elements $a,b \in B$ and ${\text {Ker}}\varphi$ does not contain any nonzero one-sided ideal of B, and consequently, B is a symmetric algebra (see [40, Theorem IV.2.2]). $\square$

We wish to compare Brauer graph algebras and biserial quiver algebras. For this, we start analyzing the combinatorial data. Let Q be a connected 2-regular quiver. We call a permutation g of the arrows of Qadmissible if for every arrow $\alpha$ we have $t(\alpha )= s(g(\alpha ))$. That is, the arrows along a cycle of g can be concatenated in Q. The multiplicity function of a Brauer graph $\varGamma$ taking only value 1 is said to be trivial.

Lemma 2.4

There is a bijection between Brauer graphs $\varGamma$ with trivial multiplicity function and pairs (Q, g) where Q is a connected 2-regular quiver and g is an admissible permutation of the arrows of Q.

Proof

(1) Given $\varGamma$, we take the quiver $Q=Q_{\varGamma }$, as defined in “Introduction.”

(1a) We show that $Q_{\varGamma }$ is 2-regular. Take an edge i of $\varGamma$, it is adjacent to vertices v, w (which may be equal). If $v\ne w$, then the edge i occurs both in the cyclic ordering around v and of w, so there are two arrows starting at i and there are two arrows ending at i. If $v=w$, then the edge i occurs twice in the cyclic ordering of edges adjacent to v, so again there are two arrows starting at i and two arrows ending at i.

(1b) We define an (admissible) permutation g on the arrows. Given $\alpha : i\rightarrow j$, let v be the vertex such that $\alpha$ is attached to v, and then there are a unique edge k adjacent to v such that i, j, k are consecutive edges in the ordering around v, and hence a unique arrow $\beta : j\rightarrow k$, also ‘attached’ to v, and we set $g(\alpha ):= \beta$. This defines an admissible permutation on the arrows. Writing g as a product of disjoint cycles, gives a bijection between the cycles of g and the vertices of $\varGamma$. Namely, let the cycle of g correspond to v if it consists of the arrows attached to v.

(2) Suppose we are given a connected 2-regular quiver Q and an admissible permutation g, written as a product of disjoint cycles. Define a graph $\varGamma$ with vertices the cycles of g and edges the vertices of Q. Each cycle of g defines a cyclic ordering of the edges adjacent to the vertex corresponding to this cycle. Hence, we get a Brauer graph.

(3) It is clear that these give a bijection. $\square$

Remark 2.5

In part (1b) of the above proof, we may have $i=j$. There are two such cases. If the edge i is adjacent to two distinct vertices of $\varGamma$, then i is the only edge adjacent to a vertex v, and we have $g(\alpha )=\alpha$. We call $\alpha$ an external loop. Otherwise, the edge i is a loop of $\varGamma$, and then $g(\alpha )\ne \alpha$. In this case, the cycle of g passes twice through vertex i of the quiver. We call $\alpha$ an internal loop.

The Brauer graph $\varGamma$ comes with a multiplicity function e defined on the vertices. Given (Q, g), we take the same multiplicity function, defined on the cycles of g, which gives the function $m_{\bullet }$ which we have called a weight function. The permutation g determines the permutation f of the arrows where $f(\alpha ) = \overline{g(\alpha )}$ for any arrow $\alpha$. Clearly f is also admissible, and f and g determine each other.

We have seen that the combinatorial data for $B_{\varGamma }$ are the same as the combinatorial data for $B(Q, f, m_{\bullet })$. Therefore, $B_{\varGamma }$ is in fact equal to $B(Q, f, m_{\bullet })$.

In the definition of a biserial quiver we focus on (Q, f), this is motivated by the connection to biserial weighted surface algebras, which we will define later.

The following compares various algebras. The equivalence of the statements (i) and (iii) was already obtained by Roggenkamp in [36, Sections 2 and 3] (see also [1, Proposition 1.2] and [37, Theorem 1.1]). We include it, for completeness.

Theorem 2.6

Let A be a basic, indecomposable algebra of dimension at least 2, over an algebraically closed field K. The following are equivalent:

• (i) A is a Brauer graph algebra.

• (ii) A is isomorphic to an algebra $B(Q,f,m_{\bullet })$ where $(Q,f,m_{\bullet })$ is a (weighted) biserial quiver.

• (iii) A is a symmetric special biserial algebra.

Proof

As we have just seen, (i) and (ii) are equivalent. The implication (ii) $\Rightarrow$ (iii) follows from Proposition 2.3.

We prove now (iii) $\Rightarrow$ (ii). Assume that A is a basic symmetric special biserial algebra, let $A= KQ_A/I$ where $Q_A$ is the Gabriel quiver of A. We will define a (weighted) biserial quiver $(Q,f,m_{\bullet })$ and show that A is isomorphic to $B(Q,f,m_{\bullet })$. Since A is special biserial, for each vertex i of $Q_A$, we have $|s^{-1}(i)| \le 2$ and $|t^{-1}(i)| \le 2$. The algebra A is symmetric; therefore, for each vertex $i \in Q_0$, we have $|s^{-1}(i)|= |t^{-1}(i)|$: Namely, if $|s^{-1}(i)| = 1$, then by the special biserial relations, the projective module $e_iA$ is uniserial. It is isomorphic to the injective hull of the simple module $S_i$, and hence, $|t^{-1}(i)|=1$. If $|t^{-1}(i)|=1$, then by the same reasoning, applied to $D(Ae_i) \cong e_iA$ it follows that $|s^{-1}(i)| = 1$.

Let $\varDelta := \{ i\in (Q_A)_0 \mid |s^{-1}(i)|= 1 \}$; to each $i\in \varDelta$, we adjoin a loop $\eta _i$ at i to the quiver $Q_A$, which then gives a 2-regular quiver. Explicitly, let $Q := (Q_0,Q_1,s,t)$ with $Q_0 = (Q_A)_0$ and $Q_1$ is the disjoint union $(Q_A)_1\bigcup \{ \eta _i: i\in \varDelta \}.$

We define a permutation f of $Q_1$. For each $i \in \varDelta$, there are unique arrows $\alpha _i$ and $\beta _i$ in $Q_A$ with $t(\alpha _i) = i = s(\beta _i)$, and we set $f(\alpha _i) = \eta _i$ and $f(\eta _i) = \beta _i$. If $\alpha$ is any arrow of $Q_A$ with $t(\alpha )$ not in $\varDelta$, we define $f(\alpha )$ to be the unique arrow in $(Q_A)_1$ with $\alpha f(\alpha ) \in I$. With this, (Q, f) is a biserial quiver.

We define now a weight function $m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^*$, where $g = \bar{f}$. For each $j \in \varDelta$, we have $g(\eta _j) = \eta _j$ and we set $m_{\mathcal {O}(\eta _j)} = 1$. Let $\alpha$ be some arrow of $Q_A$ starting at vertex i, and let $n_{\alpha } = |\mathcal {O}(\alpha )|$. Since A is symmetric special biserial, there exists $m_{\alpha } \in \mathbb {N}^*$ such that

$$\begin{aligned} B_{\alpha } := \Big (\alpha g(\alpha ) \dots g^{n_{\alpha }-1}(\alpha )\Big )^{m_{\alpha }} \end{aligned}$$

is a maximal cyclic path in $Q_A$ which does not belong to I, and spans the socle of the indecomposable projective module $e_i A$. The integer $m_{\alpha }$ is constant on the g-orbit of $\alpha$, and we may define $m_{\mathcal {O}(\alpha )} = m_{\alpha }$.

It remains to show that by suitable scaling of arrows one obtains the stated relations involving paths $B_{\alpha }$. Fix a symmetrizing linear form $\varphi$ for A. Fix an orbit of g, say $\mathcal {O}(\nu )$, there is a nonzero scalar $d_{\nu }$ such that for all arrows $\alpha$ in this orbit we have

$$\begin{aligned} \varphi (B_{\alpha }) \ = \ d_{\nu }. \end{aligned}$$

We may assume $d_{\nu }=1$. Namely, we can choose in $\mathcal {O}(\nu )$ an arrow, $\alpha$ say, and replace it by $\lambda \alpha$ where $\lambda ^{m_{\alpha }} = d_{\nu }^{-1}$. The cycles are disjoint, and if we do this for each cycle, then we have $\varphi (B_{\alpha }) = 1$ for all arrows $\alpha$.

Let i be a vertex of $Q_A$ with $|s^{-1}(i)| = 2$, and let $\alpha , \bar{\alpha }$ be the two arrows starting at i. Then, there are nonzero scalars $c_{\alpha }$ and $c_{\bar{\alpha }}$ such that $c_{\alpha } B_{\alpha } = c_{\bar{\alpha }} B_{\bar{\alpha }}$ in A. Then, we have

$$\begin{aligned} c_{\alpha } = c_{\alpha }\varphi (B_{\alpha }) = \varphi (c_{\alpha }B_{\alpha }) = \varphi (c_{\bar{\alpha }}B_{\bar{\alpha }}) = c_{\bar{\alpha }}\varphi (B_{\bar{\alpha }}) = c_{\bar{\alpha }}. \end{aligned}$$

Hence, we can cancel these scalars and obtain the required relations. With this, there is a canonical isomorphism of K-algebras $A = K Q_A / I \rightarrow B(Q,f,m_{\bullet })$. $\square$

We will from now suppress the word ’weighted,’ in analogy to the convention for Brauer graph algebras, where the multiplicity function is part of the definition but is not explicitly mentioned.

We will study idempotent algebras, and it is important that any idempotent algebra of a special biserial symmetric algebra is again special biserial symmetric.

Proposition 2.7

Let A be a symmetric special biserial algebra. Assume e is an idempotent of A which is a sum of some of the $e_i$ associated with vertices of $Q_A$. Then, eAe also is a symmetric special biserial algebra.

Proof

We may assume that $A = B(Q,f,m_{\bullet })$ for a weighted biserial quiver $(Q,f,m_{\bullet })$ and eAe is indecomposable, and let $Q = (Q_0,Q_1,s,t)$. We will show that $eAe = (\tilde{Q},\tilde{f},\tilde{m}_{\bullet }) = K\tilde{Q}/J(\tilde{Q},\tilde{f},\tilde{m}_{\bullet })$ for a weighted biserial quiver $(\tilde{Q},\tilde{f},\tilde{m}_{\bullet })$. We define $\tilde{Q}_0$ to be the set of all vertices $i \in Q_0$ such that e is the sum of the primitive idempotents $e_i$. For each arrow $\alpha \in Q_1$ with $s(\alpha ) \in \tilde{Q}_0$, we denote by $\tilde{\alpha }$ the shortest path in Q of the form $\alpha g(\alpha ) \dots g^p(\alpha )$ with $p \in \{0,1, \ldots ,n_{\alpha }-1\}$ and $t(g^p(\alpha )) \in \tilde{Q}_0$. Such a path exists because $\alpha g(\alpha ) \dots g^{n_{\alpha }-1}(\alpha )$ is a cycle around vertex $s(\alpha ) =t(g^{n_{\alpha }-1}(\alpha ))$ in $\tilde{Q}_0$. Then, we define $\tilde{Q}_1$ to be set of paths $\tilde{\alpha }$ in Q for all arrows $\alpha \in Q_1$ with $s(\alpha ) \in \tilde{Q}_0$. Moreover, for $\tilde{\alpha } = \alpha g(\alpha ) \dots g^p(\alpha )$, we set $\tilde{s} (\tilde{\alpha }) = s(\alpha )$ and $\tilde{t} (\tilde{\alpha }) = t(g^p(\alpha ))$. This defines a 2-regular quiver $\tilde{Q} = (\tilde{Q}_0,\tilde{Q}_1,\tilde{s},\tilde{t})$. Further, for each arrow $\tilde{\alpha } = \alpha g(\alpha ) \dots g^p(\alpha )$ in $\tilde{Q}_1$, there is exactly one arrow $\tilde{\beta } = \beta g(\beta ) \dots g^r(\beta )$ in $\tilde{Q}_1$ such that $\tilde{t} (\tilde{\alpha }) = t(g^p(\alpha )) = s(\beta ) = \tilde{s} (\tilde{\beta })$ and $f(\alpha ) = \beta$, and we set $\tilde{f} (\tilde{\alpha }) = \tilde{\beta }$. This defines a biserial quiver $(\tilde{Q},\tilde{f})$. Let $\tilde{g}$ be the permutation of $\tilde{Q}_1$ associated with $\tilde{f}$, and $\mathcal {O}(\tilde{g})$ the set of $\tilde{g}$-orbits in $\tilde{Q}_1$. Then, we define the weight function $\tilde{m}_{\bullet } : \mathcal {O}(\tilde{g}) \rightarrow \mathbb {N}^*$ of $(\tilde{Q},\tilde{f})$ by setting $\tilde{m}_{\mathcal {O}(\tilde{\alpha })} = m_{\mathcal {O}(\alpha )}$ for each arrow $\tilde{\alpha } \in \tilde{Q}_1$. With these, the biserial quiver algebra $B(\tilde{Q},\tilde{f},\tilde{m}_{\bullet }) = K \tilde{Q}/J(\tilde{Q},\tilde{f},\tilde{m}_{\bullet })$ is isomorphic to eAe. $\square$

We end this section with an example illustrating Theorem 2.6. This also shows that an idempotent algebra of a Brauer graph algebra need not be indecomposable, by taking $e = 1_{B_{\varGamma }} - e_4$.

Example 2.8

Let $\varGamma$ be the Brauer graph

where we take the clockwise ordering of the edges around each vertex. Then, $B_{\varGamma }$ is the symmetric algebra $B(Q,f,m_{\bullet })$ with biserial quiver (Q, f)

where the f-orbits are $(\alpha \ \omega \ \varrho \ p \ \nu \ \mu \ \delta \ \beta \ \gamma \ d \ \sigma )$, $(\eta \ \xi )$, $(a \ \varphi \ \psi )$. Then, the g-orbits are $\mathcal {O}(a) = (a)$, $\mathcal {O}(d) = (d)$, $\mathcal {O}(p) = (p)$,

$$\begin{aligned} \mathcal {O}(\alpha ) = (\alpha \ \gamma \ \sigma \ \beta \ \omega \ \delta ), \ \ \mathcal {O}(\varrho ) = (\varrho \ \nu \ \eta \ \psi \ \varphi \ \xi \ \mu ). \end{aligned}$$

The weight function $m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^*$ is as before given by the multiplicity function of the Brauer graph $\varGamma$. We note that $C_{\alpha } = \alpha \gamma \sigma \beta \omega \delta$ and $C_{\bar{\alpha }} = C_{\beta } = \beta \omega \delta \alpha \gamma \sigma$, and $v(\alpha ) = c = v(\beta )$.

3 Biserial weighted surface algebras

In this section, we introduce biserial weighted surface algebras and describe their basic properties.

In this paper, by a surface we mean a connected, compact, two-dimensional real manifold S, orientable or non-orientable, with boundary or without boundary. It is well known that every surface S admits an additional structure of a finite two-dimensional triangular cell complex and hence a triangulation (by the deep Triangulation Theorem (see, e.g., [9, Section 2.3])).

For a positive natural number n, we denote by $D^n$ the unit disk in the n-dimensional Euclidean space $\mathbb {R}^n$, formed by all points of distance $\le 1$ from the origin. Then, the boundary $\partial D^n$ of $D^n$ is the unit sphere $S^{n-1}$ in $\mathbb {R}^n$, formed by all points of distance 1 from the origin. Further, by an n-cell we mean a topological space homeomorphic to the open disk ${\text {int}}D^n = D^n {\setminus } \partial D^n$. In particular, $S^0 = \partial D^1$ consists of two points. Moreover, we define $D^0 = {\text {int}}D^0$ to be a point.

We refer to [24, Appendix] for some basic topological facts about cell complexes.

Let S be a surface. In the paper, by a finite two-dimensional triangular cell complex structure on S we mean a finite family of continuous maps $\varphi _i^n : D_i^n \rightarrow S$, with $n \in \{0,1,2\}$ and $D_i^n = D^n$, satisfying the following conditions:

• (1) Each $\varphi _i^n$ restricts to a homeomorphism from ${\text {int}}D_i^n$ to the n-cell $e_i^n = \varphi _i^n({\text {int}}D_i^n)$ of S, and these cells are all disjoint and their union is S.

• (2) For each two-dimensional cell $e_i^2$, $\varphi _i^2(\partial D_i^2)$ is the union of k 1-cells and m 0-cells, with $k \in \{2,3\}$ and $m \in \{1,2,3\}$.

Then, the closures $\varphi _i^2(D_i^2)$ of all 2-cells $e_i^2$ are called triangles of S, and the closures $\varphi _i^1(D_i^1)$ of all 1-cells $e_i^1$ are called edges of S. The collection T of all triangles $\varphi _i^2(D_i^2)$ is said to be a triangulation of S. We assume that such a triangulation T of S has at least two different edges, or equivalently, there are at least two different 1-cells in the considered triangular cell complex structure on S. Then, T is a finite collection $T_1, \ldots ,T_n$ of triangles of the form

such that every edge of such a triangle in T is either the edge of exactly two triangles, is the self-folded edge, or lies on the boundary. We note that a given surface S admits many finite two-dimensional triangular cell complex structures and hence triangulations. We refer to [9, 27, 28] for general background on surfaces and constructions of surfaces from plane models.

Let S be a surface and T a triangulation S. To each triangle $\varDelta$ in T, we may associate an orientation

if $\varDelta$ has pairwise different edges a, b, c, and

if $\varDelta$ is self-folded, with the self-folded edge a, and the other edge b. Fix an orientation of each triangle $\varDelta$ of T, and denote this choice by $\vec {T}$. Then, the pair $(S,\vec {T})$ is said to be a directed triangulated surface. To each directed triangulated surface $(S,\vec {T})$, we associate the quiver $Q(S,\vec {T})$ whose vertices are the edges of T and the arrows are defined as follows:

• (1) for any oriented triangle $\varDelta = (a b c)$ in $\vec {T}$ with pairwise different edges a, b, c, we have the cycle

  

• (2) for any self-folded triangle $\varDelta = (a a b)$ in $\vec {T}$, we have the quiver

  

• (3) for any boundary edge a in T, we have the loop

  

Then, $Q = Q(S,\vec {T})$ is a triangulation quiver in the following sense (introduced independently by Ladkani in [30]).

A triangulation quiver is a pair (Q, f), where $Q = (Q_0,Q_1,s,t)$ is a finite connected quiver and $f : Q_1 \rightarrow Q_1$ is a permutation on the set $Q_1$ of arrows of Q satisfying the following conditions:

• (a) every vertex $i \in Q_0$ is the source and target of exactly two arrows in $Q_1$,

• (b) for each arrow $\alpha \in Q_1$, we have $s(f(\alpha )) = t(\alpha )$,

• (c) $f^3$ is the identity on $Q_1$.

Hence, a triangulation quiver (Q, f) is a biserial quiver (Q, f) such that $f^3$ is the identity.

For the quiver $Q = Q(S,\vec {T})$ of a directed triangulated surface $(S,\vec {T})$, the permutation f on its set of arrows is defined as follows:

• (1)    $f(\alpha ) = \beta$, $f(\beta ) = \gamma$, $f(\gamma ) = \alpha$, for an oriented triangle $\varDelta = (a b c)$ in $\vec {T}$, with pairwise different edges a, b, c,

• (2)    $f(\alpha ) = \beta$, $f(\beta ) = \gamma$, $f(\gamma ) = \alpha$, for a self-folded triangle $\varDelta = (a a b)$ in $\vec {T}$,

• (3)    $f(\alpha ) = \alpha$, for a boundary edge a of T.

If (Q, f) is a triangulation quiver, then the quiver Q is 2-regular. We will consider only the triangulation quivers with at least two vertices. Note that different directed triangulated surfaces (even of different genus) may lead to the same triangulation quiver (see [17, Example 4.4]).

The following theorem is a slightly stronger version of [17, Theorem 4.11] (see also [18, Example 8.2] for the case with two vertices).

Theorem 3.1

Let (Q, f) be a triangulation quiver with at least two vertices. Then, there exists a directed triangulated surface $(S,\vec {T})$ such that S is orientable, $\vec {T}$ is a coherent orientation of triangles in T, and $(Q,f) = (Q(S,\vec {T}),f)$.

Proof

This is a minor adjustment of the proof of Theorem 4.11 in [17] which we will now present. We denote by n(Q, f) the number of f-orbits in $Q_1$ of length 3. Note that $n(Q,f) \ge 1$ because Q has at least two vertices. There is exactly one triangulation quiver with two vertices, namely

with $f(\alpha ) = \beta$, $f(\beta ) = \gamma$, $f(\gamma ) = \alpha$, $f(\sigma ) = \sigma$, and it is the triangulation quiver associated with the self-folded triangulation of the disk

with b a boundary edge. It is also known that the theorem holds for all triangulation quivers with three vertices (see [18, Examples 4.3 and 4.4] and Example 4.6). Therefore, we may assume that $n(Q,f) \ge 2$ and Q has at least four vertices. Now our induction assumption is: For any triangulation quiver $(Q',f')$ with at least two vertices and $n(Q',f') < n(Q,f)$, there exists a directed triangulated surface $(S',\vec {T'})$ such that $S'$ is orientable, $\vec {T'}$ is a coherent orientation of triangles in $T'$, and $(Q',f') = (Q(S',\vec {T'}),f')$. Then, we proceed as in the reconstruction steps (1) and (2) of the proof of [17, Theorem 4.11], with the following adjustments. In step (1), we replace the projective plane $\mathbb {P}$ by the disk with self-folded triangulation, described above. In step (2), we glue the oriented triangle

with pairwise different edges, in a coherent way with the corresponding triangles of the directed triangulated surface $(S',\vec {T'})$, constructed in this step. $\square$

Remark 3.2

There is an alternative proof of Theorem 3.1. According to Lemma 2.4 and Theorem 2.6, we may associate with a triangulation quiver (Q, f) a Brauer graph $\varGamma$ with trivial multiplicity function such that $B_{\varGamma } \cong B(Q,f,\mathbb {1})$, where $\mathbb {1}$ is the trivial weight function of (Q, f). In the Brauer graph $\varGamma$, the vertices correspond to the g-orbits in $Q_1$ and the edges to the vertices of Q. Thickening the edges of $\varGamma$, we obtain an oriented surface S whose border is given by the faces of $\varGamma$, corresponding to the f-orbits in $Q_1$. Since (Q, f) is a triangulation quiver, the faces are either triangles or (internal) loops. Capping now all triangle faces of S by disks $D^2$, we obtain a directed triangulated surface $\left( ({\mathcal {T}},\mathbf {T})\right)$ such that $(Q,f) = (Q(\mathcal {T},\vec {T}),f)$.

Remark 3.3

We would like to stress that the setting of directed triangulated surfaces is natural for the purposes of a self-contained representation theory of symmetric tame algebras of non-polynomial growth which we are currently developing. In particular, this gives the option of changing orientation of any triangle independently, keeping the same surface and triangulation.

Let (Q, f) be a triangulation quiver, and this is in particular a biserial quiver as introduced in Definition 2.2. With the same notation, for a weight function $m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^*$, the associated weighted biserial quiver algebra

$$\begin{aligned} B(Q,f,m_{\bullet }) = K Q / J(Q,f,m_{\bullet }) \end{aligned}$$

is said to be a biserial weighted triangulation algebra. Moreover, if $(Q,f) = (Q(S, \vec {T}),f)$ for a directed triangulation surface $(S,\vec {T})$, then $B(Q(S, \vec {T}),f,m_{\bullet })$ is called a biserial weighted surface algebra and denoted by $B(S, \vec {T}, m_{\bullet })$ (see  [17] and [18]).

Biserial weighted surface algebras belong to the class of algebras of generalized dihedral type, which generalize blocks of group algebras with dihedral defect groups. They are introduced and studied in [18]. We end this section by giving two examples of biserial weighted surface algebras.

Example 3.4

Consider the disk $D = D^2$ with the triangulation T and orientation $\vec {T}$ of triangles in T as follows

Then, the associated triangulation quiver $(Q(D,\vec {T}),f)$ is of the form

with f-orbits $(\alpha \, \beta \, \gamma )$, $(\sigma \, \delta \, \omega )$, $(\xi )$, $(\eta )$. Then, the g-orbits are $\mathcal {O}(\alpha ) = (\alpha \, \omega \, \eta \, \sigma \, \gamma \, \xi )$ and $\mathcal {O}(\beta ) = (\beta \, \delta )$. Hence, a weight function $m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^*$ is given by two positive integers $m_{\mathcal {O}(\alpha )} = m$ and $m_{\mathcal {O}(\beta )} = n$. Then, the associated biserial weighted surface algebra $B(D,\vec {T},m_{\bullet })$ is given by the above quiver and the relations:

$$\begin{aligned} (\alpha \omega \eta \sigma \gamma \xi )^m&= (\xi \alpha \omega \eta \sigma \gamma )^m ,&\xi ^2&= 0,&\alpha \beta&= 0,&\sigma \delta&= 0, \\ (\sigma \gamma \xi \alpha \omega \eta )^m&= (\eta \sigma \gamma \xi \alpha \omega )^m ,&\eta ^2&= 0,&\beta \gamma&= 0,&\delta \omega&= 0, \\ (\omega \eta \sigma \gamma \xi \alpha )^m&= (\beta \delta )^n ,&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (\gamma \xi \alpha \omega \eta \sigma )^m&= (\delta \beta )^n ,&\gamma \alpha&= 0,&\omega \sigma&= 0. \end{aligned}$$

Example 3.5

Consider the torus $\mathbb {T}$ with the triangulation T and orientation $\vec {T}$ of triangles in T as follows

Then, the associated triangulation quiver $(Q(\mathbb {T},\vec {T}),f)$ is of the form

with f-orbits $(\alpha _1\, \alpha _2\, \alpha _3)$ and $(\beta _1\, \beta _2\, \beta _3)$. Then, g has only one orbit which is $(\alpha _1\, \beta _2\, \alpha _3\, \beta _1\, \alpha _2\, \beta _3)$, and hence a weight function $m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^*$ is given by a positive integer m. Then, the associated biserial weighted surface algebra $B(\mathbb {T},\vec {T},m_{\bullet })$ is given by the above quiver and the relations:

$$\begin{aligned} \alpha _1 \alpha _2&= 0,&\beta _1 \beta _2&= 0,&(\alpha _1 \beta _2 \alpha _3 \beta _1 \alpha _2 \beta _3)^m&= (\beta _1 \alpha _2 \beta _3 \alpha _1 \beta _2 \alpha _3)^m ,\\ \alpha _2 \alpha _3&= 0,&\beta _2 \beta _3&= 0,&(\alpha _2 \beta _3 \alpha _1 \beta _2 \alpha _3 \beta _1)^m&= (\beta _2 \alpha _3 \beta _1 \alpha _2 \beta _3 \alpha _1)^m ,\\ \alpha _3 \alpha _1&= 0,&\beta _3 \beta _1&= 0,&(\alpha _3 \beta _1 \alpha _2 \beta _3 \alpha _1 \beta _2)^m&= (\beta _3 \alpha _1 \beta _2 \alpha _3 \beta _1 \alpha _2)^m . \end{aligned}$$

The triangulation quiver $(Q(\mathbb {T},\vec {T}),f)$ is called the ‘Markov quiver’ (see [18] for a motivation).

4 Proof of Theorem 1

To prove the implication (ii) $\Rightarrow$ (i), let B be a biserial weighted surface algebra. Then, by Theorem 3.1 we may assume $B= B(Q, f, m_{\bullet })$ where (Q, f) is a biserial quiver and $f^3$ is the identity. Then, in particular B is a biserial quiver algebra, and by Theorem 2.6, we see that B is a Brauer graph algebra. Now it follows from Theorem 2.6 and Proposition 2.7 that also eBe is a Brauer graph algebra, and (i) holds.

We consider the implication (i)$\Rightarrow$ (ii). Assume A is a Brauer graph algebra, by Theorem 2.6 we may assume $A=B(Q, f, m_{\bullet })$ where (Q, f) is a biserial quiver. To obtain (ii), we must find a biserial quiver $(Q^*, f^*)$ with $(f^*)^3 = 1$ such that $A = e^*B^*e^*$ where $B^* = B(Q^*, f^*, m_{\bullet }^*)$ and $e^*$ an idempotent of $B^*$.

The following shows that this can be done in a canonical way the construction gives an algorithm. Furthermore, applying the construction twice gives an interesting consequence.

Theorem 4.1

Let $B= B(Q, f, m_{\bullet })$ be a biserial quiver algebra. Then, there is a canonically defined weighted triangulation quiver $(Q^*,f^*,m_{\bullet }^*)$ such that the following statements hold.

• (i) B is isomorphic to the idempotent algebra $e^* B^* e^*$ of the biserial triangulation algebra $B^* = B(Q^*,f^*,m_{\bullet }^*)$ with respect to a canonically defined idempotent $e^*$ of $B^*$.

• (ii) The triangulation quiver $(Q^*, f^*)$ has no loops fixed by $f^*$.

• (iii) The triangulation quiver $(Q^{**}, f^{**})$ has no loops and self-folded triangles.

• (iv) B is isomorphic to the idempotent algebra $e^{**} B^{**} e^{**}$ of the biserial triangulation algebra $B^{**} = B(Q^{**},f^{**},m_{\bullet }^{**})$ with respect to a canonically defined idempotent $e^{**}$ of $B^{**}$.

Proof

Let $Q = (Q_0,Q_1,s,t)$, and let g be the permutation of $Q_1$ associated with f. We define a triangulation quiver $(Q^*, f^*)$ as follows. We take $Q^* = (Q^*_0,Q^*_1,s^*,t^*)$ with

$$\begin{aligned} Q_0^*&:= Q_0 \cup \{x_{\alpha }\}_{\alpha \in Q_1} ,&Q_1^*&:= \{\alpha ', \alpha '', \varepsilon _{\alpha } \}_{\alpha \in Q_1} \end{aligned}$$

and $s^*(\alpha ') = s(\alpha )$, $t^*(\alpha ') = x_{\alpha }$, $s^*(\alpha '') = x_{\alpha }$, $t^*(\alpha '') = t(\alpha )$, $s^*(\varepsilon _{\alpha }) = x_{f(\alpha )}$, $t^*(\varepsilon _{\alpha }) = x_{\alpha }$. Moreover, we set $f^*(\alpha '') = f(\alpha )'$, $f^*(f(\alpha )') = \varepsilon _{\alpha }$, $f^*(\varepsilon _{\alpha }) = \alpha ''$. We observe that $(Q^*, f^*)$ is a triangulation quiver. Let $g^*$ be the permutation of $Q_1^*$ associated with $f^*$. We notice that, for any arrow $\alpha$ of Q, we have $g^*(\alpha ') = \alpha ''$, $g^*(\alpha '') = g(\alpha )'$, and $g^*(\varepsilon _{\alpha }) = \varepsilon _{f^{-1}(\alpha )}$. For each arrow $\beta \in Q_1^*$, we denote by $\mathcal {O}^*(\beta )$ the $g^*$-orbit of $\beta$. Then, the $g^*$-orbits in $Q_1^*$ are

$$\begin{aligned} \mathcal {O}^*(\alpha ')&= \big (\alpha ' \ \alpha '' \ g(\alpha )' \ g(\alpha )'' \ \dots \ g^{n_{\alpha }-1}(\alpha )' \ g^{n_{\alpha }-1}(\alpha )''\big ) , \\ \mathcal {O}^*(\varepsilon _{\alpha })&= \big (\varepsilon _{f^{r_{\alpha }-1}(\alpha )} \ \varepsilon _{f^{r_{\alpha }-2}(\alpha )} \ \dots \ \varepsilon _{f(\alpha )} \ \varepsilon _{\alpha }\big ) , \end{aligned}$$

for $\alpha \in Q_1$, where $n_{\alpha }$ is the length of the g-orbit of $\alpha$ and $r_{\alpha }$ is the length of the f-orbit of $\alpha$ in $Q_1$. We define the weight function ${m}_{\bullet }^*$ by ${m}_{\mathcal {O}^*(\alpha ')}^* = m_{\alpha }$ and ${m}_{\mathcal {O}^*(\varepsilon _{\alpha })}^* = 1$ for all $\alpha \in Q_1$.

Let $B^* = B(Q^*,f^*,m_{\bullet }^*)$ be the biserial triangulation algebra associated with $(Q^*,f^*,m_{\bullet }^*)$ and let $e^*$ be the sum of the primitive idempotents $e_i^*$ in $B^*$ associated with all vertices $i \in Q_0$. Using the proof of Proposition 2.7, we see directly that the idempotent algebra $e^*B^*e^*$ is isomorphic to B. It follows also from the definition of $f^*$ that $Q^*$ has no loops fixed by $f^*$, and (ii) holds. In particular, we conclude that $f^*(\varepsilon _{\alpha }) \ne \varepsilon _{\alpha }$ for any arrow $\alpha \in Q_1$. Hence, the triangulation quiver $(Q^{**}, f^{**})$ has no loops, and consequently, it has also no self-folded triangles, and (iii) follows. Finally, by (i), $B^*$ is isomorphic to an idempotent algebra $\hat{e}B^{**}\hat{e}$ of $B^{**} = B(Q^{**},f^{**},m_{\bullet }^{**})$ for the corresponding idempotent $\hat{e}$ of $B^{**}$. Taking $e^{**} = e^*\hat{e}$, we obtain that B is isomorphic to the idempotent algebra $e^{**} B^{**} e^{**}$, and hence (iv) also holds. $\square$

We give some illustrations for the $*$-construction.

(1) A loop $\alpha$ in Q fixed by f is replaced in $Q^*$ by the subquiver

with the $f^*$-orbit $(\alpha ' \ \varepsilon _{\alpha } \ \alpha '')$.

(2) A subquiver of Q of the form

where $(\alpha \ \beta \ \gamma )$ is an f-orbit, is replaced in $Q^*$ by the quiver

with $f^*$-orbits $(\alpha '' \ \beta ' \ \varepsilon _{\alpha })$, $(\gamma '' \ \alpha ' \ \varepsilon _{\gamma })$, and $(\beta '' \ \gamma ' \ \varepsilon _{\beta })$.

(3) A subquiver of Q of the form

where $(\alpha \ \beta \ \gamma )$ is an f-orbit, is replaced in $Q^*$ by the quiver of the form

with $f^*$-orbits $(\alpha '' \ \beta ' \ \varepsilon _{\alpha })$, $(\beta '' \ \gamma ' \ \varepsilon _{\beta })$, and $(\gamma '' \ \alpha ' \ \varepsilon _{\gamma })$.

Remark 4.2

The statement (i) of the above theorem also holds if we replace the canonically defined weight function $m_{\bullet }^*$ by a weight function $\bar{m}_{\bullet }^*$ such that $\bar{m}_{\mathcal {O}^*(\alpha ')} = m_{\alpha }$ and $\bar{m}_{\mathcal {O}^*(\varepsilon _{\alpha })}$ is an arbitrary positive integer, for any arrow $\alpha \in Q_1$.

Remark 4.3

The construction of the triangulation quiver $(Q^*, f^*)$ associated with (Q, f) is canonical, though a quiver with fewer vertices may often be sufficient. In fact, it would be enough to apply the construction only to the arrows in f-orbits of length different from 1 and 3. An algebra $B(Q,f,m_{\bullet })$ may have many presentations as an idempotent algebra of some biserial triangulation algebra, even for a triangulation quiver $(Q', f')$ with fewer $f'$-orbits than the number of $f^*$-orbits in the triangulation quiver $(Q^*, f^*)$ (see Example 4.7).

Remark 4.4

The $*$-construction described in Theorem 4.1 provides a special class of triangulation quivers. Namely, let (Q, f) be a biserial quiver, g the permutation of $Q_1$ associated with (Q, f), and $g^*$ the permutation of $Q_1^*$ associated with $(Q^*,f^*)$. Then, for every arrow $\alpha \in Q_1$, we have in $Q_1^*$ the $g^*$-orbit $\mathcal {O}^*(\alpha ')$ of even length $2|\mathcal {O}(\alpha )|$ and the $g^*$-orbit $\mathcal {O}^*(\varepsilon _{\alpha })$ whose length is the length of the f-orbit of $\alpha$ in $Q_1$. In particular, all triangulation quivers $(Q',f')$ having only $g'$-orbits of odd length do not belong to this class of triangulation quivers. For example, it is the case for the tetrahedral quiver considered in Sect. 6. We refer also to [17, Example 4.9] for an example of triangulation quiver $(Q'',f'')$ for which all arrows in $Q_1''$ belong to one $g''$-orbit of length 18.

Example 4.5

Let $\varGamma$ be the Brauer tree

with multiplicity function $e(a) = m$ and $e(b) = n$. Then, the associated Brauer graph algebra $B_{\varGamma }$ is the algebra $B(Q,f,m_{\bullet })$ associated with the biserial quiver $(Q,f,m_{\bullet })$ where Q is of the form

with $f(\alpha ) = \beta$, $f(\beta ) = \alpha$, $g(\alpha ) = \alpha$, $g(\beta ) = \beta$, and $m_{\mathcal {O}(\alpha )} = m$, and $m_{\mathcal {O}(\beta )} = n$. If $m = 1$, then $B_{\varGamma }$ is the truncated polynomial algebra $K[x]/(x^{n+1})$. The associated triangulation quiver $(Q^*,f^*)$ is of the form

and the $f^*$-orbits are $(\alpha '' \ \beta ' \ \varepsilon _{\alpha })$ and $(\beta '' \ \alpha ' \ \varepsilon _{\beta })$. Further, the $g^*$-orbits are $\mathcal {O}^*(\alpha ') = (\alpha ' \ \alpha '' )$, $\mathcal {O}^*(\beta ') = (\beta ' \ \beta '')$, $\mathcal {O}^*(\varepsilon _{\alpha }) = (\varepsilon _{\alpha }\ \varepsilon _{\beta })$ and the weight function is ${m}^*_{\mathcal {O}^*(\alpha ')} = m$, ${m}^*_{\mathcal {O}^*(\beta ')} = n$, ${m}^*_{\mathcal {O}^*(\varepsilon _{\alpha })} = 1$. We also note that $(Q^*, f^*)$ is the triangulation quiver $(Q(\mathbb {T},\vec {T}), f)$ associated with the torus $\mathbb {T}$ with triangulation T and orientation $\vec {T}$ of triangles in T as follows

(compare with Example 3.5).

Example 4.6

Let $\varGamma$ be the Brauer graph

with multiplicity $e(a) = m$ for some $m \in \mathbb {N}^*$. Then, the associated Brauer graph algebra $B_{\varGamma }$ is the algebra $B(Q,f,m_{\bullet })$ where the quiver Q is of the form

with $f(\alpha ) = \alpha$, $f(\beta ) = \beta$, $g(\alpha ) = \beta$, $g(\beta ) = \alpha$, and $m_{\mathcal {O}(\alpha )} = m$. The associated triangulation quiver $(Q^*,f^*)$ is

with $f^*$-orbits $(\alpha '' \ \alpha ' \ \varepsilon _{\alpha })$ and $(\beta '' \ \beta ' \ \varepsilon _{\beta })$. Further, the $g^*$-orbits are $\mathcal {O}^*(\alpha ') = (\alpha ' \ \alpha '' \ \beta ' \ \beta '')$, $\mathcal {O}^*(\varepsilon _{\alpha }) = (\varepsilon _{\alpha })$, $\mathcal {O}^*(\varepsilon _{\beta }) = (\varepsilon _{\beta })$, and ${m}^*_{\mathcal {O}^*(\alpha ')} = m$, ${m}^*_{\mathcal {O}^*(\varepsilon _{\alpha })} = 1$, ${m}^*_{\mathcal {O}^*(\varepsilon _{\beta })} = 1$. Note that $(Q^*, f^*)$ is the triangulation quiver $(Q(\mathbb {S},\vec {T}), f)$ associated with the sphere $\mathbb {S}$ with triangulation T given by two self-folded triangles

where $\vec {T}$ is canonically defined.

Example 4.7

Let $(Q,f,m_{\bullet })$ be the weighted biserial quiver considered in Example 2.8. Then, the triangulation quiver $(Q^*,f^*)$ is of the form

where the shaded triangles describe the $f^*$-orbits in $Q_1^*$. Then, we have the following $g^*$-orbits in $Q_1^*$:

$$\begin{aligned} \mathcal {O}^*(\alpha ')&= (\alpha ' \ \alpha '' \ \gamma ' \ \gamma '' \ \sigma ' \ \sigma '' \ \beta ' \ \beta '' \ \omega ' \ \omega '' \ \delta ' \ \delta '' ) ,&\mathcal {O}^*(d')&= (d' \ d'' ) , \\ \mathcal {O}^*(\mu ')&= (\mu ' \ \mu '' \ \varrho ' \ \varrho '' \ \nu ' \ \nu '' \ \eta ' \ \eta '' \ \psi ' \ \psi '' \ \varphi ' \ \varphi '' \ \xi ' \ \xi '' ) ,&\mathcal {O}^*(p')&= (p' \ p'' ) , \\ \mathcal {O}^*(\varepsilon _{\alpha })&= (\varepsilon _{\alpha } \ \varepsilon _{\sigma } \ \varepsilon _{d} \ \varepsilon _{\gamma } \ \varepsilon _{\beta } \ \varepsilon _{\delta } \ \varepsilon _{\mu } \ \varepsilon _{\nu } \ \varepsilon _{p} \ \varepsilon _{\varrho } \ \varepsilon _{\omega } ) ,&\mathcal {O}^*(a')&= (a' \ a'' ) , \\ \mathcal {O}^*(\varepsilon _{a})&= (\varepsilon _{a} \ \varepsilon _{\psi } \ \varepsilon _{\varphi } ) ,&\mathcal {O}^*(\varepsilon _{\eta })&= (\varepsilon _{\eta } \ \varepsilon _{\xi } ) . \end{aligned}$$

Moreover, the weight function $m_{\bullet }^* : \mathcal {O}(g^*) \rightarrow \mathbb {N}^*$ is given by

$$\begin{aligned} m_{\mathcal {O}^*(d')}^*&= m_{\mathcal {O}(d)} = e(d),&m_{\mathcal {O}^*(\alpha ')}^*&= m_{\mathcal {O}(\alpha )} = e(c),&m_{\mathcal {O}^*(\varepsilon _{\alpha })}^*&= 1, \\ m_{\mathcal {O}^*(p')}^*&= m_{\mathcal {O}(p)} = e(p),&m_{\mathcal {O}^*(\mu ')}^*&= m_{\mathcal {O}(\mu )} = e(b),&m_{\mathcal {O}^*(\varepsilon _{\eta })}^*&= 1, \\&m_{\mathcal {O}^*(a')}^*&= m_{\mathcal {O}(a)} = e(a).&\end{aligned}$$

Finally, $e^* = e_1^* + e_2^* + e_3^* + e_4^* + e_5^* + e_6^* + e_7^* + e_8^*$. We note that $(Q^*,f^*)$ has 16 $f^*$-orbits, all of length three.

The Brauer graph algebra $B_{\varGamma } = B(Q,f,m_{\bullet })$ is also isomorphic to the idempotent algebra $e' B' e'$ of a biserial triangulation algebra $B' = B(Q',f',m'_{\bullet })$ for the triangulation quiver $(Q', f')$ shown below

with 14 $f'$-orbits described by the shaded triangles (all of length three), a weight function $m'_{\bullet }$ of $(Q', f')$, and where the idempotent $e'$ is the sum of the primitive idempotents in $B'$ associated with the vertices 1, 2, 3, 4, 5, 6, 7, 8.

We finish this section with a combinatorial interpretation of the $*$-construction in terms of Brauer graphs.

4.1 Barycentric division of Brauer graphs

Let $\varGamma$ be the Brauer graph so that $B_{\varGamma } = B(Q, f, m_{\bullet })$, and then the algebra $B(Q^*, f^*, m_{\bullet }^*)$ as in the $*$-construction of Theorem 4.1 is again a Brauer graph algebra, $B_{\varGamma ^*}$ say, by Theorem 2.6. The proof of Lemma 2.4 shows how to construct $\varGamma ^*$: Its vertices are in bijection with the cycles of $g^*$. First, each cycle of g is ‘augmented,’by replacing an arrow $\alpha$ by $\alpha ', \alpha ''$, and this gives a cycle of $g^*$; we call a corresponding vertex of $\varGamma ^*$ an augmented vertex. Second, any other cycle of $g^*$ consists of $\varepsilon$-arrows, and these cycles correspond to f-cycles of Q, as described in Theorem 4.1. Let $F(\alpha )$ be the f-orbit of $\alpha$ in Q, then we write $v_{F(\alpha )}$ for the corresponding vertex of $\varGamma ^*$, and then the arrows attached to this vertex are precisely the $\varepsilon _{f^t(\alpha )}$.

The edges of $\varGamma ^*$ are labeled by the vertices of $Q^*$, that is, by the vertices of Q together with the set $\{ x_{\alpha } \mid \alpha \in Q_1\}$. The cyclic order around an augmented vertex is obtained by replacing $i{\mathop {\longrightarrow }\limits ^{\alpha }}j$ by

$$\begin{aligned} i{\mathop {\longrightarrow }\limits ^{\alpha '}}x_{\alpha }{\mathop {\longrightarrow }\limits ^{\alpha ''}}j \end{aligned}$$

in $\varGamma ^*$. A vertex $v_{F(\alpha )}$ has attached arrows precisely the $\varepsilon _{f^t(\alpha )}: x_{f^{t+1}(\alpha )}\rightarrow x_{f^t(\alpha )}$. This specifies the edges adjacent, with cyclic order given by the inverse of the f-cycle of $\alpha$. We may view $\varGamma ^*$ as a ‘triangular’ graph:

(1) Assume that $|F(\alpha )| = 1$. Then, $x_{\alpha }$ is the unique edge in $\varGamma ^*$ adjacent to $v_{F(\alpha )}$, and $x_{\alpha }$ is its own successor in the cyclic order of edges in $\varGamma ^*$ around $v_{F(\alpha )}$. Hence we have in $\varGamma ^*$ a self-folded triangle

which corresponds to a subquiver of $(Q^*,f^*)$ of the form

with $f^*$-orbit $(\alpha '' \ \alpha ' \ \varepsilon _{\alpha })$.

(2) Assume that $|F(\alpha )| \ge 2$, and let $\beta = f(\alpha )$ starting at vertex j. Let v, w be the vertices in $\varGamma$ such that $\alpha$ is attached to v and $\beta$ is attached to w. Then, $\varGamma ^*$ has edges $x_{\alpha }$ and $x_{\beta }$ connecting vertices v and w to vertex $v_{F(\beta )} (= v_{F(\alpha )})$. Then, $x_{\alpha }$ is the successor of $x_{\beta }$ in the cyclic order of edges in $\varGamma ^*$ around $v_{F(\alpha )}$. Hence we have in $\varGamma ^*$ a triangle

which corresponds to a subquiver of $(Q^*,f^*)$ of the form

with $f^*$-orbit $(\alpha '' \ \beta ' \ \varepsilon _{\alpha })$. The multiplicity function $e^*$ of $\varGamma ^*$ is given by $e^*(v) = e(v)$ for any vertex v of $\varGamma$ (where e is the multiplicity function for $\varGamma$), and $e^*(v_{F(\alpha )})=1$ for any f-orbit $F(\alpha )$.

The Brauer graph $\varGamma ^*$ can be considered as a barycentric division of the Brauer graph $\varGamma$ and has a triangular structure. Namely, every $v_{F(\alpha )}$ is the vertex of $|F(\alpha )|$ triangles in $\varGamma ^*$ whose edges opposite to $v_{F(\alpha )}$ are the edges of $\varGamma$ corresponding to the vertices in Q along $F(\alpha )$.

In this way, we obtain an orientable surface $S^*$ without boundary, the triangulation $T^*$ of $S^*$ indexed by the set of edges of $\varGamma$, and the orientation $\vec {T^*}$ of triangles in $T^*$ such that the associated triangulation quiver $(Q(S^*,\vec {T^*}),f)$ is the quiver $(Q^*,f^*)$. The triangulated surface $(S^*,T^*)$ can be considered as a completion of the Brauer graph $\varGamma$ to a canonically defined triangulated surface, by a finite number of pyramids whose peaks are the f-orbits and bases are given by the edges of $\varGamma$. We also note that the surface $S^*$ (without triangulation $T^*$) can be obtained as follows. We may embed the Brauer graph $\varGamma$ into a surface S with boundary given by thickening the edges of $\varGamma$. The components of the border $\partial S$ of S are given by the ‘Green walks’ around $\varGamma$ on S, corresponding to the f-orbits in $Q_1$. Then, the surface $S^*$ is obtained from S by capping all the boundary components of S by the disks $D^2$.

Example 4.8

Let $\varGamma$ be the Brauer graph

where we take the clockwise ordering of edges around each vertex. Assume the multiplicity function takes only value 1. Then, the associated biserial quiver (Q, f) is of the form

with f-orbits

$$\begin{aligned} F(\alpha )&= (\alpha \ \beta \ \gamma ),&F(\sigma )&= (\sigma \ \varrho \ \omega \ \delta ),&F(\eta )&= (\eta ), \end{aligned}$$

and $\mathcal {O}(g)$ consisting of

$$\begin{aligned} \mathcal {O}(\alpha )&= (\alpha ),&\mathcal {O}(\beta )&= (\beta \ \sigma \ \delta \ \gamma ),&\mathcal {O}(\omega )&= (\omega \ \varrho \ \eta ). \end{aligned}$$

Then, the barycentric division $\varGamma ^*$ of $\varGamma$ is the Brauer graph

with $u = v_{F(\alpha )}$, $v = v_{F(\sigma )}$ and $w = v_{F(\eta )}$. The ordering of the edges around each vertex is clockwise. The multiplicity function of $\varGamma ^*$ takes only the value 1.

The Brauer graph $\varGamma$ admits a canonical embedding into the surface S of the form

obtained from $\varGamma$ by thickening the edges of $\varGamma$, whose border $\partial S$ has three components given by three different ‘Green walks’ around $\varGamma$ on S. The triangulated surface $(S^*,T^*)$ associated with the Brauer graph $\varGamma ^*$ can be viewed as a canonical completion of S to a triangulated surface.

5 Proof of Theorem 3

This theorem describes algebras socle equivalent to Brauer graph algebras. By Theorem 2.6, this is the same as describing algebras socle equivalent to a biserial quiver algebra $A=B(Q, f, m_{\bullet })$ where (Q, f) is a biserial quiver. We show that such algebras can be described using the methods of [18, Section 6]. Then, we show that the $*$-construction for the biserial quiver algebras can be extended.

Let (Q, f) be a biserial quiver. A vertex $i \in Q_0$ is said to be a border vertex of (Q, f) if there is a loop $\alpha$ at i with $f(\alpha ) = \alpha$. We denote by $\partial (Q,f)$ the set of all border vertices of (Q, f), and call it the border of (Q, f). The terminology is motivated by the connection with surfaces: If (Q, f) is the triangulation quiver $(Q(S,\vec {T}),f)$ associated with a directed triangulated surface $(S,\vec {T})$, then the border vertices of (Q, f) correspond bijectively to the boundary edges of the triangulation T of S. If (Q, f) is the biserial quiver associated with a Brauer graph $\varGamma$, then the border vertices of (Q, f) correspond bijectively to the internal loops of $\varGamma$ (see Sect. 2).

Definition 5.1

Assume $(Q, f, m_{\bullet } )$ is a biserial quiver with $\partial (Q,f)$ not empty. A function

$$\begin{aligned} b_{\bullet } : \partial (Q,f) \rightarrow K \end{aligned}$$

is said to be a border function of (Q, f). We have the quotient algebra

$$\begin{aligned} B(Q,f,m_{\bullet },b_{\bullet }) = K Q / J(Q,f,m_{\bullet },b_{\bullet }), \end{aligned}$$

where $J(Q,f,m_{\bullet },b_{\bullet })$ is the ideal in the path algebra KQ generated by the elements:

• (1) $\alpha f({\alpha })$, for all arrows $\alpha \in Q_1$ which are not border loops,

• (2) $\alpha ^2 - b_{s(\alpha )} B_{\alpha }$, for all border loops $\alpha \in Q_1$,

• (3) $B_{\alpha } - B_{\bar{\alpha }}$, for all arrows $\alpha \in Q_1$.

We call such an algebra a biserial quiver algebra with border. Note that if $b_{\bullet }$ is the zero function, then $B(Q,f,m_{\bullet },b_{\bullet }) = B(Q,f,m_{\bullet })$.

We summarize the basic properties of these algebras.

Proposition 5.2

Let (Q, f) be a biserial quiver such that $\partial (Q,f)$ is not empty, and let $\bar{B} = B(Q,f,m_{\bullet },b_{\bullet })$, and $B = B(Q,f,m_{\bullet })$ where $m_{\bullet }$ and $b_{\bullet }$ are weight and border functions. Then, the following statements hold.

• (i) $\bar{B}$ is a basic, indecomposable, finite-dimensional, symmetric, biserial algebra with $\dim _K \bar{B} = \sum _{\mathcal {O}\in \mathcal {O}(g)} m_{\mathcal {O}} n_{\mathcal {O}}^2$.

• (ii) $\bar{B}$ is socle equivalent to B.

• (iii) If K is of characteristic different from 2, then $\bar{B}$ is isomorphic to B.

Proof

Part (ii) is clear from the definition and then part (i) follows from Proposition 2.3. For the last part, see arguments in the proof of Proposition 6.3 in [18]. $\square$

The following theorem gives a complete description of symmetric algebras socle equivalent to a biserial quiver algebra.

Theorem 5.3

Let A be a basic, indecomposable, symmetric algebra with Grothendieck group $K_0(A)$ of rank at least 2. Assume that A is socle equivalent to a biserial quiver algebra $B(Q,f,m_{\bullet })$.

• (i) If $\partial (Q, f)$ is empty, then A is isomorphic to $B(Q,f,m_{\bullet })$.

• (ii) Otherwise, A is isomorphic to $B(Q,f,m_{\bullet },b_{\bullet })$ for some border function $b_{\bullet }$ of (Q, f).

Proof

Let $B= B(Q, f, m_{\bullet }) = KQ/J$ where $J = J(Q, f, m_{\bullet })$. Since $A/{\text {soc}}(A)$ is isomorphic to $B/{\text {soc}}(B)$, we can assume that these are equal, using an isomorphism as identification. We assume A is symmetric; therefore, for each $i \in Q_0$, the module $e_iA$ has a one-dimensional socle which is spanned by some $\omega _i \in e_iAe_i$, and we fix such an element. Then, let $\varphi$ be a symmetrizing linear form for A, and then $\varphi (\omega _i)$ is nonzero. We may assume that $\varphi (\omega _i) = 1$.

We claim that ${\text {soc}}(A) \subset ({\text {rad}}A)^2 (\subset {\text {rad}}A)$. If not, then for some j we have $\omega _j \not \in ({\text {rad}}A)^2$. This means that $e_jA = e_jAe_j$, which is not possible since A is indecomposable with at least two simple modules. It follows that A and B have the same Gabriel quiver. Recall that the quiver Q is the disjoint union of the Gabriel quiver of B with virtual loops. Any virtual loop of Q is then in the socle of B, and it is zero in $B/{\text {soc}}(B)$ and is therefore zero in $A/{\text {soc}}(A)$. We may therefore take A of the form $A=KQ/I$ for the same quiver Q, and some ideal I of KQ such that any virtual loop lies in the socle of A.

In the algebra B, we define monomials $A_{\alpha }$ in the arrows by setting $B_{\alpha } = A_{\alpha }g^{-1}(\alpha )$ when $\alpha$ is not a virtual loop, and then as well $B_{\alpha } = \alpha A_{g(\alpha )}$. Note that if $\alpha$ is a virtual loop, then $A_{\alpha }$ is not defined. With this, the elements $A_{\alpha }$ belong to the socle of $B/{\text {soc}}(B)$ and hence also to the socle of $A/{\text {soc}}(A)$. Therefore, they cannot lie in the socle of A (because if so, then they would be zero in $A/{\text {soc}}(A)$). Then, $0\ne A_{\alpha }{\text {rad}}(A) = {\text {soc}}(e_iA)$ where $i=s(\alpha )$. We have that $A_{\alpha } {\text {rad}}(A)$ is spanned by

$$\begin{aligned} A_{\alpha }\beta , A_{\alpha }\gamma \end{aligned}$$

where $\beta = g^{-1}(\alpha )$ and $\gamma = f(g^{-2}(\alpha ))$.

(I) We may assume that $A_{\alpha }\beta = B_{\alpha }$ in A (and hence is equal to $B_{\alpha }$ in KQ).

If not, then we have $A_{\alpha }\beta = 0$, and then $A_{\alpha }\gamma \ne 0$. We will show that we may interchange $\beta$ and $\gamma$.

Since $A_{\alpha }\gamma \ne 0$, in particular $g^{-2}(\alpha )\gamma \ne 0$ and also $t(\gamma ) = i = s(\alpha )$. Since $\gamma = f(g^{-2}(\alpha ))$, we know that $g^{-2}(\alpha )\gamma$ belongs to the socle of A. It is nonzero, which implies that $A_{\alpha } = g^{-2}(\alpha )$ (and $m_{\alpha }=1$), and therefore, $\alpha = g^{-2}(\alpha )$, and $\gamma = f(\alpha )$. We claim that $g(\alpha )\ne \alpha$. Namely, if we had $g(\alpha )=\alpha$, then both $\alpha$ and $f(\alpha )$ would be loops at vertex i and $|Q_0|=1$, which contradicts our assumption. Hence, the cycle of g containing $\alpha$ is $(\alpha \ g(\alpha ))$, of length two. We claim that also the f-cycle of $\alpha$ (in B) has length two. Namely, if $\bar{\alpha }$ is the other arrow starting at i and $\rho$ is the other arrow ending at $j=t(\alpha )$, then we must have by the properties of f and g that $f(\rho ) = \beta$ and $f(\beta ) = \bar{\alpha }$. This implies that $f(\gamma ) = \alpha$ and hence f has a cycle $(\alpha \ \gamma )$.

It follows that there is an algebra isomorphism from B to the biserial quiver algebra $B'$ given by the weighted biserial quiver obtained from $(Q,f,m_{\bullet })$ by interchanging $\beta$ and $\gamma$ (which form a pair of double arrows) and fixing all other arrows of Q. We replace B by $B'$ and the claim follows.

(II) We show that relation (1) holds in A. If $\alpha$ is a virtual loop of B, then $\alpha f(\alpha )=0$ since $\alpha \in {\text {soc}}(A)$. We consider now an arrow $\alpha$ which is not a virtual loop. Suppose $\alpha$ is not fixed by f, then $\alpha f(\alpha )$ belongs to the socle of A. We can write $\alpha f(\alpha ) = a_{\alpha } B_{\alpha } = a_{\alpha }\alpha A_{g(\alpha )}$ for some $a_{\alpha } \in K$ (here $g(\alpha )$ is not a virtual loop).

(a) If $s(\alpha )\ne t(f(\alpha ))$, then $\alpha f(\alpha ) = \alpha f(\alpha ) e_{s(\alpha )}= 0$; in fact, this holds for any choice of $\alpha , f(\alpha )$.

(b) Otherwise, we set

$$\begin{aligned} f(\alpha )':= f(\alpha ) - a_{\alpha } A_{g(\alpha )} \end{aligned}$$

and we replace $f(\alpha )$ by $f(\alpha )'$. (If a cycle of f has a virtual loop, then $\alpha f(\alpha )$ and $f^{-1}(\alpha )\alpha$ are not cyclic paths, so they are zero and do not need adjusting.) These modifications must be iterated. Take a cycle of f, say it has length r, so that $r\ge 2$.

Assume first this cycle contains an arrow $\alpha$ such that $f^{r-1}(\alpha )\alpha$ is not a cyclic path. We may start with $\alpha$ and adjust $f(\alpha ), f^2(\alpha ), \ldots , f^{r-1}(\alpha )$ as described above. Then, $f^{r-1}(\alpha )'\cdot \alpha =0$, by (a) above.

Otherwise, for any $\alpha$ in the cycle, $f^{r-1}(\alpha )\alpha$ is cyclic, and then, we must have $r=2$ or $r=4$. Assume that $r=2$. We adjust $f(\alpha )$ as described in (b) and have $\alpha f(\alpha )'=0$ in A, and we must show that as well $f(\alpha )'\alpha =0$. By the assumption, $f(\alpha )'\alpha = c \omega _i$ for some $c\in K$. We have

$$\begin{aligned} c = \varphi (c\omega _i) = \varphi (f(\alpha )'\alpha ) = \varphi (\alpha f(\alpha )') = \varphi (0) = 0. \end{aligned}$$

Assume now that $r=4$. Since Q is 2-regular, Q is of the form

with f-orbit $(\alpha _1\ \alpha _2\ \alpha _3\ \alpha _4)$ and g-orbit $(\alpha _1\ \alpha _4\ \alpha _3\ \alpha _2)$. We adjust $\alpha _2, \alpha _3, \alpha _4$ as in (b) to have $\alpha _1 \alpha _2 = 0$, $\alpha _2 \alpha _3 = 0$, $\alpha _3 \alpha _4 = 0$. By assumption we have $\alpha _4 \alpha _1 = a B_{\alpha _4} = a (\alpha _4 \alpha _3 \alpha _2 \alpha _1)^m$ for some $a \in K$ and $m \in {\mathbb {N}}^{*}.$ We replace $\alpha _1$ by $\alpha '_1 = \alpha _1 - a \alpha _3 \alpha _2 \alpha _1 (\alpha _4 \alpha _3 \alpha _2 \alpha _1)^{m-1}$ and obtain $\alpha _4 \alpha '_1 = 0$. Observe that we have also $\alpha '_1 \alpha _2 = 0$, because $\alpha _1 \alpha _2 = 0$.

(III) We show that relation (3) holds in A. For each arrow $\alpha \in Q_1$, we have $B_{\alpha } = c_{\alpha } \omega _{s(\alpha )}$ for some $c_{\alpha } \in K^*$. We claim that $c_{\sigma } = c_{\alpha }$ for any arrow $\sigma$ in the g-orbit $\mathcal {O}(\alpha )$ of $\alpha$. Indeed, if $\sigma$ belongs to $\mathcal {O}(\alpha )$, then

$$\begin{aligned} c_{\sigma }&= c_{\sigma } \varphi \big (\omega _{s(\sigma )}) = \varphi \big (c_{\sigma } \omega _{s(\sigma )}) = \varphi (B_{\sigma }) = \varphi (B_{\alpha }) \\&= \varphi \big (c_{\alpha } \omega _{s(\alpha )}) = c_{\alpha } \varphi \big (\omega _{s(\alpha )}) = c_{\alpha }. \end{aligned}$$

Since K is algebraically closed, we may choose $d_{\alpha } \in K^*$ such that $d_{\alpha }^{m_{\alpha } n_{\alpha }} = c_{\alpha }^{-1}$. Replacing now the representative of each arrow $\alpha \in Q_1$ in A by its product with $d_{\alpha }$, we obtain a new presentation $A \cong K Q / I'$ such that $B_{\alpha } = \omega _{s(\alpha )}$ for any arrow $\alpha \in Q_1$. This does not change relation (1) obtained above. Therefore, we may assume that if $i \in Q$ is any vertex and $\alpha$ and $\bar{\alpha }$ are the arrows in Q with source i, then $B_{\alpha } = \omega _{i} = B_{\bar{\alpha }}$ in A.

(IV) We show that relation (2) holds in A. When the border $\partial (Q,f)$ of (Q, f) is empty, there is nothing to do (and A is isomorphic to B). Assume now that $\partial (Q,f)$ is not empty. Then, for any loop $\alpha$ with $i = s(\alpha ) \in \partial (Q,f)$, we have $\alpha ^2 = \alpha f(\alpha ) = b_i \omega _i = b_i B_{\alpha }$ for some $b_i \in K$. Hence, we have a border function $b_{\bullet } : \partial (Q,f) \rightarrow K$, and A is isomorphic to the algebra $B(Q, f, m_{\bullet }, b_{\bullet })$. $\square$

Recall that a self-injective algebra A is biserial if the radical of any indecomposable non-uniserial projective, left or right, A-module is a sum of two uniserial modules whose intersection is simple.

Theorem 3 follows from Theorems 2.6, 3.1, 5.3 and the following relative version of Theorem 4.1 (see Remark 4.3).

Theorem 5.4

Let $B= B(Q, f, m_{\bullet })$ where Q has at least two vertices, and where the border $\partial (Q,f)$ is not empty. Then, there is a canonically defined weighted triangulation quiver $(Q^\#,f^\#,m_{\bullet }^\#)$ such that the following statements hold.

• (i) $|\partial (Q,f)| = |\partial (Q^\#,f^\#)|$.

• (ii) B is isomorphic to the idempotent algebra $e^\# B^\# e^\#$ of the biserial weighted triangulation algebra $B^\# = B(Q^\#,f^\#,m_{\bullet }^\#)$ with respect to a canonically defined idempotent $e^\#$ of $B^\#$.

• (iii) For any border function $b_{\bullet }$ of (Q, f) and the induced border function $b_{\bullet }^\#$ of $(Q^\#,f^\#)$, the algebras $B(Q,f,m_{\bullet },b_{\bullet })$ and $e^\# B(Q^\#,f^\#,m_{\bullet }^\#,b_{\bullet }^\#) e^\#$ are isomorphic.

Proof

The construction of $(Q^{\#}, f^{\#}, m_{\bullet }^{\#})$ is analogous to the $*$-construction in Theorem 4.1. We take the notation as in Theorem 4.1, and in addition, we denote by $Q_1^b$ the set of all border loops of the quiver. We define a triangulation quiver $(Q^\#, f^\#)$ as follows. We take $Q^\# = (Q^\#_0,Q^\#_1,s^\#,t^\#)$ with

$$\begin{aligned} Q_0^\#&:= Q_0 \cup \{x_{\alpha }\}_{\alpha \in Q_1 {\setminus } Q_1^b} ,&Q_1^\#&:= Q_1^b \cup \{\alpha ', \alpha '', \varepsilon _{\alpha } \}_{\alpha \in Q_1 {\setminus } Q_1^b}, \end{aligned}$$

$s^\#(\beta ) = s(\beta ) = t(\beta ) = t^\#(\beta )$ for all loops $\beta \in Q_1^b$, and $s^\#(\alpha ') = s(\alpha )$, $t^\#(\alpha ') = x_{\alpha }$, $s^\#(\alpha '') = x_{\alpha }$, $t^\#(\alpha '') = t(\alpha )$, $s^\#(\varepsilon _{\alpha }) = x_{f(\alpha )}$, $t^\#(\varepsilon _{\alpha }) = x_{\alpha }$, for any arrow $\alpha \in Q_1 {\setminus } Q_1^b$. Moreover, we set $f^\#(\eta ) = \eta$ for any loop $\eta \in Q_1^b$, and $f^\#(\alpha '') = f(\alpha )'$, $f^\#(f(\alpha )') = \varepsilon _{\alpha }$, $f^\#(\varepsilon _{\alpha }) = \alpha ''$, for any arrow $\alpha \in Q_1 {\setminus } Q_1^b$. We observe that $(Q^\#, f^\#)$ is a triangulation quiver with $\partial (Q^\#,f^\#) = \partial (Q,f)$. Let $g^\#$ be the permutation of $Q_1^\#$ associated with $f^\#$. For each arrow $\beta$ in $Q_1^\#$, we denote by $\mathcal {O}^\#(\beta )$ the $g^\#$-orbit of $\beta$ in $Q_1^\#$. Then, the $g^\#$-orbits in $Q_1^\#$ are

$$\begin{aligned} \mathcal {O}^\#(\eta )&= \big (\eta \ g(\eta )' \ g(\eta )'' \ \dots \ g^{n_{\eta }-1}(\eta )' \ g^{n_{\eta }-1}(\eta )''\big ) , \end{aligned}$$

for any loop $\eta \in Q_1^b$, and

$$\begin{aligned} \mathcal {O}^\#(\alpha ')&= \big (\alpha ' \ \alpha '' \ g(\alpha )' \ g(\alpha )'' \ \dots \ g^{n_{\alpha }-1}(\alpha )' \ g^{n_{\alpha }-1}(\alpha )''\big ) , \\ \mathcal {O}^\#(\varepsilon _{\alpha })&= \big (\varepsilon _{f^{r_{\alpha }-1}(\alpha )} \ \varepsilon _{f^{r_{\alpha }-2}(\alpha )} \ \dots \ \varepsilon _{f(\alpha )} \ \varepsilon _{\alpha }\big ) , \end{aligned}$$

for any arrow $\alpha \in Q_1 {\setminus } Q_1^b$ (where $r_{\alpha }$ is the length of the f-orbit of $\alpha$). We define the weight function ${m}_{\bullet }^\# : \mathcal {O}(g^\#) \rightarrow \mathbb {N}^*$ by ${m}_{\mathcal {O}^\#(\eta )}^\# = m_{\eta }$ for any loop $\eta \in Q_1^b$, and ${m}_{\mathcal {O}^\#(\alpha ')}^\# = m_{\alpha }$ and ${m}_{\mathcal {O}^\#(\varepsilon _{\alpha })}^\# = 1$ for any arrow $\alpha \in Q_1 {\setminus } Q_1^b$.

Let $B^\# = B(Q^\#,f^\#,m_{\bullet }^\#)$ be the biserial weighted triangulation algebra associated with $(Q^\#,f^\#,m_{\bullet }^\#)$ and $e^\#$ the sum of the primitive idempotents $e_i^\#$ in $B^\#$ associated with the vertices $i \in Q_0$. Then, it follows from the arguments as in the proof of Proposition 2.7 that B is isomorphic to the idempotent algebra $e^\# B^\# e^\#$. Moreover, let $b_{\bullet }$ be a border function of (Q, f) and $b_{\bullet }^\#$ be the induced border function of $(Q^\#,f^\#)$, that is, $b_{i}^\# = b_{i}$ for any border vertex i. Then, it follows from the description of $g^\#$-orbits in $Q_1^\#$ and the definition of the weight function ${m}_{\bullet }^\#$ that $B(Q,f,m_{\bullet },b_{\bullet })$ is isomorphic to the idempotent algebra $e^\# B(Q^\#,f^\#,m_{\bullet }^\#,b_{\bullet }^\#) e^\#$. $\square$

Example 5.5

This illustrates the $\#$-construction in Theorem 5.4. Let (Q, f) be the biserial quiver

with f-orbits $(\alpha \ \beta \ \gamma \ \sigma )$, $(\varrho )$, $(\eta )$, $(\mu )$, $(\xi )$. Then, the border $\partial (Q,f)$ of (Q, f) is the set $Q_0 = \{1,2,3,4\}$ of all vertices of Q, and $\varrho , \eta , \mu , \xi$ are the border loops. Further, g has only one orbit, $\mathcal {O}(\alpha ) = (\alpha \ \eta \ \beta \ \mu \ \gamma \ \xi \ \sigma \ \varrho )$. We take the weight function $m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^*$ with $m_{\mathcal {O}(\alpha )} = 1$. Moreover, let $b_{\bullet } : \partial (Q,f) \rightarrow K$ be a border function. Then, we describe the associated algebra $B(Q,f,m_{\bullet },b_{\bullet })$. It has quiver Q, and to simplify the notation for the relations, we use the notion of $B_{\alpha }$ for an arrow $\alpha$, as it has appeared throughout,

$$\begin{aligned} \varrho ^2&= b_1B_{\rho },&\ B_{\rho }&= B_{\alpha },&\ \alpha \beta&=0, \\ \eta ^2&= b_2 B_{\eta },&\ B_{\eta }&= B_{\beta },&\ \beta \gamma&= 0, \\ \mu ^2&= b_3 B_{\mu },&\ B_{\mu }&= B_{\gamma },&\ \gamma \sigma&= 0, \\ \xi ^2&= b_4 B_{\xi },&\ B_{\xi }&= B_{\sigma },&\ \sigma \alpha&= 0. \end{aligned}$$

Note that the algebra $B(Q,f,m_{\bullet })$ is given by the quiver Q and the above relations such that all $b_i$ are zero. By the arguments as in [18, Example 6.5], if K has characteristic 2 and $b_{\bullet }$ is nonzero, then the algebras $B(Q,f,m_{\bullet },b_{\bullet })$ and $B(Q,f,m_{\bullet })$ are not isomorphic.

The triangulation quiver $(Q^\#,f^\#)$ is of the form

with $f^\#$-orbits $(\varrho )$, $(\eta )$, $(\mu )$, $(\xi )$, $(\alpha ' \ \varepsilon _{\sigma } \ \sigma '')$, $(\beta ' \ \varepsilon _{\alpha } \ \alpha '')$, $(\gamma ' \ \varepsilon _{\beta } \ \beta '')$, $(\sigma ' \ \varepsilon _{\gamma } \ \gamma '')$. Further, there are two $g^\#$-orbits:

$$\begin{aligned} \mathcal {O}^\#(\alpha ')&= (\alpha ' \ \alpha '' \ \eta \ \beta ' \ \beta ''\ \mu \ \gamma ' \ \gamma '' \ \xi \ \sigma ' \ \sigma ''\ \varrho ) , \\ \mathcal {O}^\#(\varepsilon _{\alpha })&= (\varepsilon _{\alpha } \ \varepsilon _{\sigma } \ \varepsilon _{\gamma } \ \varepsilon _{\beta } ) . \end{aligned}$$

The weight function $m_{\bullet }^\#$ takes only value 1, and the border function $b_{\bullet }^\#$ is $b_1^\# = b_1$, $b_2^\# = b_2$, $b_3^\# = b_3$, $b_4^\# = b_4$.

(a) The relations from vertex 1 are

$$\begin{aligned} \rho ^2= b_1B_{\rho }, \ \ \ B_{\rho } = B_{\alpha '}. \end{aligned}$$

There are analogous relations from each of the vertices 2, 3, 4.

(b) The relations from vertex $x_{\alpha }$ are

$$\begin{aligned} B_{\varepsilon _{\sigma }} = B_{\alpha ''}, \ \ \alpha ''\beta '=0, \ \ \varepsilon _{\sigma }\sigma '' = 0. \end{aligned}$$

There are analogous relations from each of the vertices $x_{\beta }, x_{\gamma }, x_{\sigma }$.

We observe now that $B(Q,f,m_{\bullet },b_{\bullet })$ is isomorphic to the idempotent algebra $e^\# B(Q^\#,f^\#,m_{\bullet }^\#,b_{\bullet }^\#) e^\#$ where the idempotent $e^\#$ is the sum of the primitive idempotents at the vertices 1, 2, 3, 4. Moreover, the algebras $B(Q,f,m_{\bullet })$ and $e^\# B(Q^\#,f^\#,m_{\bullet }^\#) e^\#$ are also isomorphic. Finally, we note that if K has characteristic 2 and $b_{\bullet }^\# = b_{\bullet }$ is nonzero, then the algebras $B(Q^\#,f^\#,m_{\bullet }^\#,b_{\bullet }^\#)$ and $B(Q^\#,f^\#,m_{\bullet }^\#)$ are not isomorphic.

6 Proof of Theorem 4

We recall the definition of a weighted triangulation algebra. Let (Q, f) be a triangulation quiver with at least two vertices, and let g, $n_{\bullet }$ and $m_{\bullet }$ be defined as for biserial quiver algebras. The additional datum is a function

$$\begin{aligned} c_{\bullet } : \mathcal {O}(g) \rightarrow K^* = K {\setminus } \{0\} \end{aligned}$$

which we call a parameter function of (Q, f). We write briefly $m_{\alpha } = m_{\mathcal {O}(\alpha )}$ and $c_{\alpha } = c_{\mathcal {O}(\alpha )}$ for $\alpha \in Q_1$. The parameter function $c_{\bullet }$ taking only value 1 is said to be trivial. We assume that$m_{\alpha } n_{\alpha } \ge 3$for any arrow$\alpha \in Q_1$. For any arrow $\alpha \in Q_1$, define the path

$$\begin{aligned} A_{\alpha }&= \Big ( \alpha g(\alpha ) \dots g^{n_{\alpha }-1}(\alpha )\Big )^{m_{\alpha }-1} \alpha g(\alpha ) \dots g^{n_{\alpha }-2}(\alpha ) , \text{ if } n_{\alpha } \ge 2, \\ A_{\alpha }&= \alpha ^{m_{\alpha }-1} , \text{ if } n_{\alpha } = 1 , \end{aligned}$$

in Q of length $m_{\alpha } n_{\alpha } - 1$. Then, we have

$$\begin{aligned} A_{\alpha } g^{n_{\alpha }-1}(\alpha ) = B_{\alpha } = \Big ( \alpha g(\alpha ) \dots g^{n_{\alpha }-1}(\alpha )\Big )^{m_{\alpha }} \end{aligned}$$

of length $m_{\alpha } n_{\alpha }$. Then, following [17], we define the bound quiver algebra

$$\begin{aligned} \varLambda (Q,f,m_{\bullet },c_{\bullet }) = K Q / I (Q,f,m_{\bullet },c_{\bullet }), \end{aligned}$$

where $I (Q,f,m_{\bullet },c_{\bullet })$ is the admissible ideal in the path algebra KQ of Q over K generated by the elements:

• (1) ${\alpha } f({\alpha }) - c_{\bar{\alpha }} A_{\bar{\alpha }}$, for all arrows $\alpha \in Q_1$,

• (2) $\beta f(\beta ) g(f(\beta ))$, for all arrows $\beta \in Q_1$.

The algebra $\varLambda := \varLambda (Q,f,m_{\bullet },c_{\bullet })$ is called a weighted triangulation algebra of (Q, f). Moreover, if $(Q,f) = (Q(S,\vec {T}),f)$ for a directed triangulated surface $(S,\vec {T})$, then $\varLambda$ is called a weighted surface algebra, and if the surface and triangulation are important, we denote the algebra by $\varLambda (S,\vec {T},m_{\bullet },c_{\bullet })$.

We note that the Gabriel quiver of $\varLambda$ is equal to Q, and this holds because we assume $m_{\alpha } n_{\alpha } \ge 3$ for all arrows $\alpha \in Q_1$.

We have the following proposition (see [17, Proposition 5.8]).

Proposition 6.1

Let (Q, f) be a triangulation quiver, $m_{\bullet }$ and $c_{\bullet }$ weight and parameter functions of (Q, f). Then, $\varLambda = \varLambda (Q,f,m_{\bullet },c_{\bullet })$ is a finite-dimensional tame symmetric algebra of dimension $\sum _{\mathcal {O}\in \mathcal {O}(g)} m_{\mathcal {O}} n_{\mathcal {O}}^2$.

We have also the following theorem proved in [17, Theorem 1.2] (see also [6, Proposition 7.1] and [16, Theorem 5.9] for the case of two vertices).

Theorem 6.2

Let $\varLambda = \varLambda (S,\vec {T},m_{\bullet },c_{\bullet })$ be a weighted surface algebra over an algebraically closed field K. Then, the following statements are equivalent:

• (i) All simple modules in ${\text {mod}}\varLambda$ are periodic of period 4.

• (ii) $\varLambda$ is a periodic algebra of period 4.

• (iii) $\varLambda$ is not isomorphic to a singular tetrahedral algebra.

Following [17], a singular tetrahedral algebra is the weighted surface algebra given by a coherent orientation of four triangles of the tetrahedron and the weight and parameter functions taking only value 1. The triangulation quiver of such algebra is the tetrahedral quiver of the form

where the shaded triangles denote f-orbits and white triangles denote g-orbits.

The following theorem is an essential ingredient for the proof of Theorem 4.

Theorem 6.3

Let $B = B(Q,f,m_{\bullet })$ be a biserial weighted triangulation algebra where Q has no loops, and $\varLambda ^* = \varLambda (Q^*,f^*,m^*_{\bullet },c^*_{\bullet })$ the weighted triangulation algebra associated with the weighted triangulation quiver $(Q^*,f^*,m^*_{\bullet })$ and the trivial parameter function $c^*_{\bullet }$ of $(Q^*,f^*)$. Then, the following statements hold:

• (i) $\varLambda ^*$ is a periodic algebra of period 4.

• (ii) B is isomorphic to the idempotent algebra $e^{*} \varLambda ^{*} e^{*}$ for an idempotent $e^{*}$ of $\varLambda ^{*}$.

Proof

For each arrow $\varrho$ in $Q^*_1$, we set $m^*_{\varrho } = m^*_{\mathcal {O}(\varrho )}$ and $n^*_{\varrho } = |\mathcal {O}^*(\varrho )|$. We observe first that $n^*_{\varrho } \ge 3$, and hence $m^*_{\varrho } n^*_{\varrho } \ge 3$, for any arrow $\varrho$ in $Q^*_1$, and consequently $\varLambda (Q^*,f^*,m^*_{\bullet },c^*_{\bullet })$ is a well-defined weighted triangulation algebra. Indeed, it follows from Theorem 4.1(iii) that the triangulation quiver $(Q^*,f^*)$ has neither loops nor self-folded triangles. Moreover, the f-orbits in $Q_1$ have length 3, and the g-orbits in $Q_1$ are of length at least 2. Then, it follows from the proof of Theorem 4.1 that the $g^*$-orbits in $Q_1^*$ are

$$\begin{aligned} \mathcal {O}^*(\alpha ')&= \big (\alpha ' \ \alpha '' \ g(\alpha )' \ g(\alpha )'' \ \dots \ g^{n_{\alpha }-1}(\alpha )' \ g^{n_{\alpha }-1}(\alpha )''\big ) , \\ \mathcal {O}^*(\varepsilon _{\alpha })&= \big (\varepsilon _{f^{2}(\alpha )} \ \varepsilon _{f(\alpha )} \ \varepsilon _{\alpha }\big ) , \end{aligned}$$

for all arrows $\alpha \in Q_1$. Then, the required inequalities hold. Further, it follows from Remark 4.4 that $(Q^*,f^*)$ is not the tetrahedral quiver. Then, applying Theorem 6.2, we conclude that $\varLambda ^*$ is a periodic algebra of period 4.

Let $e^{*}$ be the sum of all primitive idempotents in $\varLambda ^{*}$ corresponding to the vertices of Q. We claim that $e^{*} \varLambda ^{*} e^{*}$ is isomorphic to B. Observe that every f-orbit $(\alpha \ \beta \ \gamma )$ in $Q_1$ creates in $(Q^*,f^*)$ the subquiver as in the illustration (3) following Theorem 4.1. The algebra $e^{*} \varLambda ^{*} e^{*}$ has arrows $\alpha = \alpha ' \alpha ''$, $\beta = \beta ' \beta ''$, $\gamma = \gamma ' \gamma ''$, and it follows that in $e^{*}\varLambda ^{*}e^{*}$ we have

$$\begin{aligned} \alpha \beta&= \alpha ' \alpha '' \beta ' \beta '' = \alpha ' \alpha '' f^*(\alpha '') g^*\big (f^*(\alpha '')\big ) = 0, \\ \beta \gamma&= \beta ' \beta '' \gamma ' \gamma '' = \beta ' \beta '' f^*(\beta '') g^*\big (f^*(\beta '')\big ) = 0, \\ \gamma \alpha&= \gamma ' \gamma '' \alpha ' \alpha '' = \gamma ' \gamma '' f^*(\gamma '') g^*\big (f^*(\gamma '')\big ) = 0 . \end{aligned}$$

Further, let i be a vertex of Q, and let $\alpha$ and $\sigma = \bar{\alpha }$ the two arrows in $Q_1$ with source i. By the proof of Theorem 4.1, the $g^*$-orbits are

$$\begin{aligned} \mathcal {O}^*(\alpha ')&= \big (\alpha ' \ \alpha '' \ g(\alpha )' \ g(\alpha )'' \ \dots \ g^{n_{\alpha }-1}(\alpha )' \ g^{n_{\alpha }-1}(\alpha )''\big ) , \\ \mathcal {O}^*(\sigma ')&= \big (\sigma ' \ \sigma '' \ g(\sigma )' \ g(\sigma )'' \ \dots \ g^{n_{\sigma }-1}(\sigma )' \ g^{n_{\sigma }-1}(\sigma )''\big ) . \end{aligned}$$

Moreover, $m_{\alpha '}^* = m_{\mathcal {O}^*(\alpha ')}^* = m_{\mathcal {O}(\alpha )} = m_{\alpha }$ and $m_{\sigma '}^* = m_{\mathcal {O}^*(\sigma ')}^* = m_{\mathcal {O}(\sigma )} = m_{\sigma }$. Hence we have in $Q^*$ the cycles

$$\begin{aligned} B_{\alpha '}&= \big (\alpha ' \alpha '' g(\alpha )' g(\alpha )'' \dots g^{n_{\alpha }-1}(\alpha )' g^{n_{\alpha }-1}(\alpha )''\big )^{m_{\alpha }} , \\ B_{\sigma '}&= \big (\sigma ' \sigma '' g(\sigma )' \ g(\sigma )'' \dots g^{n_{\sigma }-1}(\sigma )' g^{n_{\sigma }-1}(\sigma )''\big )^{m_{\sigma }} , \end{aligned}$$

and $B_{\alpha '} = B_{\sigma '}$ in $\varLambda ^*$ (see [17, Lemma 5.3]), and this gives the equality $B_{\alpha } = B_{\sigma } = B_{\bar{\alpha }}$ in $e^{*} \varLambda ^{*} e^{*}$. Therefore, $e^{*} \varLambda ^{*} e^{*}$ is isomorphic to B. $\square$

We may now complete the proof of Theorem 4. Let $B = B(Q,f,m_{\bullet })$ be a biserial quiver algebra. Then, it follows from Theorem 4.1 that B is isomorphic to the idempotent algebra $e^{**}B^{**}e^{**}$ of the biserial triangulation algebra $B^{**} = B(Q^{**},f^{**},m_{\bullet }^{**})$ for some idempotent $e^{**}$ of $B^{*}$, and $Q^{**}$ has no loops. Applying now Theorem 6.3, we conclude that $B^{**}$ is isomorphic to the idempotent algebra $e \varLambda e$ of a periodic weighted triangulation algebra, for an idempotent e of $\varLambda$. Since $e^{**}$ is a summand of e, we have $B \cong e^{**}B^{**}e^{**} \cong e^{**}(e \varLambda e)e^{**} = e^{**} \varLambda e^{**}$. Then, Theorem 4 follows from Theorems 2.6 and 3.1.

Remark 6.4

Let $\varLambda = \varLambda (Q,f,m_{\bullet },c_{\bullet })$ be a weighted triangulation algebra. Then, the biserial triangulation algebra $B = B(Q,f,m_{\bullet })$ is not an idempotent algebra $e \varLambda e$ of $\varLambda$. On the other hand, if $\varLambda$ is not a tetrahedral algebra, then B is a geometric degeneration of $\varLambda$ (see [17, Proposition 5.8]).

Example 6.5

Let (Q, f) be the Markov quiver in Example 3.5 and m a positive integer associated with the unique g-orbit $(\alpha _1\, \beta _2\, \alpha _3\, \beta _1\, \alpha _2\, \beta _3)$ in $Q_1$. Then, the associated weighted triangulation algebra $\varLambda = \varLambda (Q,f,m_{\bullet },c_{\bullet })$ with trivial parameter function $c^*_{\bullet }$ is given by the quiver Q and the following relations (we write the indices modulo 3):

$$\begin{aligned} \alpha _i \alpha _{i+1}&= (\beta _i \alpha _{i+1} \beta _{i+2}\alpha _i \beta _{i+1} \alpha _{i+2})^{m-1} \beta _i \alpha _{i+1} \beta _{i+2} \alpha _i\beta _{i+1},&\alpha _i \alpha _{i+1} \beta _{i+2}&= 0, \\ \beta _i \beta _{i+1}&= (\alpha _i \beta _{i+1} \alpha _{i+2} \beta _i \alpha _{i+1} \beta _{i+2})^{m-1} \alpha _i \beta _{i+1} \alpha _{i+2} \beta _i \alpha _{i+1},&\beta _i \beta _{i+1} \alpha _{i+2}&= 0. \end{aligned}$$

The idempotent algebra $e_1 \varLambda e_1$ of $\varLambda$ with respect to the primitive idempotent $e_1$ at vertex 1 is isomorphic to the Brauer graph algebra $B_{\varGamma }$ given by the Brauer graph $\varGamma$ in Example 4.6.

According to Theorem 4.1, we have the triangulation quiver $(Q^*,f^*)$

where the shaded triangles denote the $f^*$-orbits in $Q_1^*$. The $g^*$-orbits in $Q^*_1$ are

$$\begin{aligned} \mathcal {O}^*(\alpha _1') = (\alpha _1' \ \alpha _1'' \ \beta _2' \ \beta _2'' \ \alpha _3' \ \alpha _3'' \ \beta _1' \ \beta _1'' \ \alpha _2' \ \alpha _2'' \ \beta _3' \ \beta _3'') , \\ \mathcal {O}^*(\varepsilon _{\alpha _1}) = (\varepsilon _{\alpha _3} \ \varepsilon _{\alpha _2} \ \varepsilon _{\alpha _1} ) , \qquad \qquad \mathcal {O}^*(\varepsilon _{\beta _1}) = (\varepsilon _{\beta _3} \ \varepsilon _{\beta _2} \ \varepsilon _{\beta _1} ) . \end{aligned}$$

The weight function $m_{\bullet }^* : \mathcal {O}(g^*) \rightarrow \mathbb {N}^*$ is given by $m_{\mathcal {O}^*(\alpha _1')}^* = m$, $m_{\mathcal {O}^*(\varepsilon _{\alpha _1})}^* = 1$, $m_{\mathcal {O}^*(\varepsilon _{\beta _1})}^* = 1$. We define the parameter function $c_{\bullet }^* : \mathcal {O}(g^*) \rightarrow K^*$ to be the constant function with value 1. The weighted triangulation algebra $\varLambda ^* = \varLambda (Q^*,f^*,m^*_{\bullet },c^*_{\bullet })$ is given by the above quiver $Q^*$ and with 18 commutativity relations and 18 zero relations, corresponding to the six $f^*$-orbits in $Q_1^*$. For example, we have the relations given by the $f^*$-orbit $(\alpha _1' \ \varepsilon _{\alpha _3} \ \alpha _2')$:

$$\begin{aligned} \alpha _1' \varepsilon _{\alpha _3}&= ( \beta _1' \beta _1'' \alpha _2' \alpha _2'' \beta _3' \ \beta _3'' \alpha _1' \alpha _1'' \beta _2' \beta _2'' \alpha _3' \alpha _3'' )^{m-1} \beta _1' \beta _1'' \alpha _2' \alpha _2'' \beta _3' \ \beta _3'' \alpha _1' \alpha _1'' \beta _2' \beta _2'' \alpha _3' , \\ \varepsilon _{\alpha _3} \alpha _3''&= ( \alpha _1'' \beta _2' \beta _2'' \alpha _3' \alpha _3'' \beta _1' \beta _1'' \alpha _2' \alpha _2'' \beta _3' \ \beta _3'' \alpha _1' )^{m-1} \alpha _1'' \beta _2' \beta _2'' \alpha _3' \alpha _3'' \beta _1' \beta _1'' \alpha _2' \alpha _2'' \beta _3' \ \beta _3'' , \\ \alpha _3'' \alpha _1'&= \varepsilon _{\alpha _2} \varepsilon _{\alpha _1} , \qquad \alpha _1' \varepsilon _{\alpha _3} \varepsilon _{\alpha _2} = 0 , \qquad \varepsilon _{\alpha _3} \alpha _3'' \beta _1' = 0 , \qquad \alpha _3'' \alpha _1' \alpha _1'' = 0 . \end{aligned}$$

The biserial weighted triangulation algebra $B = B(Q,f,m_{\bullet })$ is then isomorphic to the idempotent algebra $e^* \varLambda ^* e^*$, where $e^*$ is the sum of the primitive idempotents $e^*_1, e^*_2, e^*_3$ in $\varLambda ^*$ corresponding to the vertices 1, 2, 3.

We present now an example of an idempotent algebra of a periodic weighted surface algebra which is neither a Brauer graph algebra nor a weighted surface algebra.

Example 6.6

Let S be a triangle with one puncture, T the triangulation of S

such that the edges 1, 2, 3 are on the boundary, and let $\vec {T}$ be the orientation of triangles of T: $(1\ 2\ 4)$, $(4\ 5\ 6)$, $(5\ 3\ 6)$. Then, the triangulation quiver $(Q(S,\vec {T}),f)$ is of the form

with f-orbits $(\xi )$, $(\eta )$, $(\mu )$, $(\alpha \ \beta \ \gamma )$, $(\delta \ \varrho \ \nu )$, $(\sigma \ \omega \ \theta )$. Hence we have two g-orbits:

$$\begin{aligned} \mathcal {O}(\alpha ) = (\alpha \ \eta \ \beta \ \delta \ \sigma \ \mu \ \omega \ \nu \ \gamma \ \xi ) \qquad \text{ and } \qquad \mathcal {O}(\varrho ) = (\varrho \ \theta ) . \end{aligned}$$

Take the weight function $m_{\bullet } : \mathcal {O}(g) \rightarrow \mathbb {N}^*$ given by $m_{\mathcal {O}(\alpha )} = 1$ and $m_{\mathcal {O}(\varrho )} = 2$. Moreover, let $c_{\bullet } : \mathcal {O}(g) \rightarrow K^*$ be the trivial parameter function. Then, the associated weighted surface algebra $\varLambda = \varLambda (S,\vec {T},m_{\bullet },c_{\bullet })$ is given by the quiver $Q(S,\vec {T})$ and the relations:

$$\begin{aligned} \xi ^2&= \alpha \eta \beta \delta \sigma \mu \omega \nu \gamma ,&\xi ^2 \alpha&= 0,&\alpha \beta&= \xi \alpha \eta \beta \delta \sigma \mu \omega \nu ,&\alpha \beta \delta&= 0,&\nu \delta&= \theta \varrho \theta , \\ \eta ^2&= \beta \delta \sigma \mu \omega \nu \gamma \xi \alpha ,&\eta ^2 \beta&= 0,&\beta \gamma&= \eta \beta \delta \sigma \mu \omega \nu \gamma \xi ,&\beta \gamma \xi&= 0,&\nu \delta \sigma&= 0, \\ \mu ^2&= \omega \nu \gamma \xi \alpha \eta \beta \delta \sigma ,&\mu ^2 \omega&= 0,&\gamma \alpha&= \delta \sigma \mu \omega \nu \gamma \xi \alpha \eta ,&\gamma \alpha \eta&= 0,&\sigma \omega&= \varrho \theta \varrho , \\ \delta \varrho&= \gamma \xi \alpha \eta \beta \delta \sigma \mu \omega ,&\delta \varrho \theta&= 0,&\omega \theta&= \mu \omega \nu \gamma \xi \alpha \eta \beta \delta ,&\omega \theta \varrho&= 0,&\sigma \omega \nu&=0, \\ \varrho \nu&= \sigma \mu \omega \nu \gamma \xi \alpha \eta \beta ,&\varrho \nu \gamma&= 0,&\theta \sigma&= \nu \gamma \xi \alpha \eta \beta \delta \sigma \mu ,&\theta \sigma \mu&= 0.&\end{aligned}$$

Let $e = e_1 + e_2 + e_3 + e_4$ be the sum of primitive idempotents of $\varLambda$ at the vertices 1, 2, 3, 4, and $B = e \varLambda e$ the associated idempotent algebra. Then, B is given by the quiver $\varDelta$ of the form

with the arrows $\varphi = \delta \sigma$ and $\psi = \omega \nu$, and the induced relations:

$$\begin{aligned} \xi ^2&= \alpha \eta \beta \varphi \mu \psi \gamma ,&\xi ^2 \alpha&= 0,&\alpha \beta&= \xi \alpha \eta \beta \varphi \mu \psi ,&\alpha \beta \delta&= 0,&\varphi \psi&= 0, \\ \eta ^2&= \beta \varphi \mu \psi \gamma \xi \alpha ,&\eta ^2 \beta&= 0,&\beta \gamma&= \eta \beta \varphi \mu \psi \gamma \xi ,&\beta \gamma \xi&= 0,&\psi \varphi&= 0, \\ \mu ^2&= \psi \gamma \xi \alpha \eta \beta \varphi ,&\mu ^2 \psi&= 0,&\gamma \alpha&= \varphi \mu \psi \gamma \xi \alpha \eta ,&\gamma \alpha \eta&= 0.&\end{aligned}$$

Then, B is not a special biserial algebra, and therefore, it is not a Brauer graph algebra. Further, B is not a weighted surface algebra, because we have zero relations $\varphi \psi = 0$ and $\psi \varphi = 0$ of length 2. On the other hand, by general theory, the algebra $B = e \varLambda e$ is tame and symmetric.

7 Diagram of algebras

The following diagram shows the relations between the main classes of algebras occurring in the paper.

where, for a weighted biserial quiver algebra $B = B(Q,f,m_{\bullet })$, $B^* = B(Q^*,f^*,m^*_{\bullet })$, and $\varLambda ^{***} = \varLambda (Q^{***},f^{***},m^{***}_{\bullet }, \mathbb {1})$, with $\mathbb {1}$ denoting the trivial weight function of $(Q^{***},f^{***})$.