1 Introduction

Wireless communication has undergone a tremendous revolution in the recent years, where cooperative diversity is a promising means to enhance the network coverage and data throughput. Moreover, it can cope with the effected of the Small Scale Fading where unpredictable and rapid fluctuations of the received signal levels can cause the degradation of throughput.

Many researches targeted the cooperative diversity of the relay networks in their investigations, such as the study in [1] where the authors investigated the performance of cooperative diversity networks with amplify-and-forward (AF) relaying and equal gain combining (EGC) techniques, which is used to combine the signal from the source and the relay nodes at the destination node. The results in [1] were extended to investigate the Nakagami-m Fading Channels case except that several relay nodes were introduced to the cooperative diversity network under investigation as in the in of [2]. The authors of [1, 2], focused on the cooperative relay network without the presence of the co-channel interference (CCI) at either node of the network under investigation, and they assumed that the source and destination nodes are connected through direct link. In [3], best-relay selection scheme was introduced, where the destination receives two copies of the source signal; one from the source node (direct link), and the other from the best relay node. Then the authors employed the maximum ratio combining (MRC) at the destination node to combine both signals copies received, the fading channel is assumed to be Rayleigh model and the researches did not consider the effect of CCI in their investigation.

The effect of the presence of CCI on the performance of cooperative diversity networks was investigated in [4], assuming optimum combining (OC) technique over Rayleigh fading channels and the authors employed the Decode-and-Forward (DF) relaying schema in the network settings. Additional investigation of CCI was considered in work [5], where the authors analyzed the performance of the DF cooperative relaying systems over Nakagami fading channels in terms of the outage probability, and implementing MRC. Moreover, the authors of [6], derived the exact-form expressions for the outage probability of the cooperative diversity network over Nakagami-m fading channels while implementing DF relaying schema. They studied the effect of CCI presence at both the relay and destination nodes.

In this letter, we extended the investigation in [7] by introducing cooperative diversity to the proposed network, we added multiple relay nodes between the source and destination nodes. The impact of the presence of CCI at the network was investigated by deriving the error and outage probabilities of the network over \(\alpha\)–\(\mu\) fading channels, while using the selective combining schema to get the signal from the best relay link assuming that there is no direct link between the source and destination nodes. In addition, we develop the mathematical formulas of the probability density function (PDF) in addition to the cumulative distribution function (CDF) of the signal-to-interference-and-noise ratio (SINR) of the cooperative diversity network.

The rest of this paper is organized as follows. Section 2 describes the system and channel models. Section 3 presents the analysis of the cooperative diversity SINR. Section 4 presents the system performance analysis. Numerical results are given in Sect. 5. Finally, Sect. 6 concludes this paper.

2 System Model

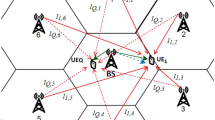
In this letter, we propose a cooperative network which consists of a source node S, a destination node D and M active relay nodes \(R_{i}\) for \(i=1,\ldots ,M\), shown in Fig. 1. It is assumed that the ith relay node is subjected to N interferers, and the destination node is subject to L interferers, respectively. For the proposed cooperative network, the transmission occurs in two stages as follows.

  • The first stage represent broadcasting the signal from the source node, which accordingly is received by the active relay nodes that are willing to participate in the transmission.

  • The second stage, each relay node perform amplification of the received signal then forwards it to the destination node. Correspondingly the relaying technique used in this stage is the AF relaying schema.

The received signal at the ith relay in the first stage of the transmission, assuming that the relay and destination nodes are both corrupted by interference, is denoted by:

$$\begin{aligned} y_{SR_i}(t) = h_{SR_i} \; X(t) + \sum_{j=1}^{N_i} \; h_{ij}\;X_{ij}(t) + n_{SR_i}(t), \end{aligned}$$
(1)

where \(h_{SR_i}\) is the channel fading coefficient of the transmitted signal X(t) from the source to the ith relay node and with average transmitted power of \(P_S\). \(X_{ij}(t)\) is the received signal from the jth interferer of the ith relay node with average transmitted power of \(P_{ij}\). \(h_{ij}\) is the channel gain of the CCI link. Finally, the \(n_{SR_i}\) represent the AWGN at the ith relay node, and is considered to have zero-mean and variance \(N_o \sim CN(0,N_o).\)

Fig. 1
figure 1

Cooperative diversity relay network

Full size image

The received signal at the destination node from the ith relay is denoted by:

$$\begin{aligned} \begin{aligned} y_{R_i D}(t)= G_{AF_i} \, h_{R_i D} \, y_{SR_i}(t)+ \sum_{k=1}^{L} \, g_{k} \,X_{k}(t) + n_{ R_i D}(t), \end{aligned} \end{aligned}$$
(2)

where \(h_{{R_i}D}\) is the channel fading coefficient from the ith relay to the destination with average transmitted power of \(P_{R}.\) And \(g_{k}\) is the channel gain of the Co-Channel interference link at the destination node, \(X_{k}(t)\) interferer’s data and average power of \(P_{k}.\) The AWGN is represented as \((n_{ R_i D}(t)),\) and is modeled as zero-mean and variance \(N_o\) \(\sim CN(0,N_o)\). \(G_{AF_i}\) is the amplification gain of the ith relay and is given by:

$$\begin{aligned} G_{AF_i} = \sqrt{\frac{1}{P_s {\Vert h_{S R_i}\Vert ^2} + \sum_{i,j=1}^{N_i} p_{ij} \Vert h_{ij}\Vert ^2 + N_0}}, \end{aligned}$$
(3)

Expanding Eq. (2) and after some mathematical manipulation, the received signal at the destination node D from the ith relay node \(R_i\) can be expressed as:

$$\begin{aligned} \begin{aligned} y_{R_i D}(t)&= G_{AF_i} \; h_{R_i D} \; h_{SR_i} \; X(t)\\&\quad +G_{AF_i} \; h_{R_i D} \; X_{R_i}(t) + I_{D}(t) \\&\quad +G_{AF_i} X_{R} \; h_{R_i D} \; n_{SR_i}(t)+ n_{{R_i}D}(t). \end{aligned} \end{aligned}$$
(4)

The interference \(I_D(t)\) can be denoted by:

$$\begin{aligned} I_{D}(t) = G_{AF_i} h_{{R_i}D} \sum_{j=1}^{N_i} P_{ij} h_{ij}d_{ij} +\sum_{k=1}^{L} P_{g_{k}} g_{k}d_{k}, \end{aligned}$$
(5)

The best-relay and direct link statistical properties (PDF, CDF) will be derived in the following section.

3 Cooperative Diversity SINR Analysis

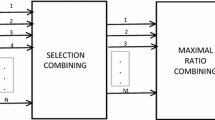
In this study, we introduce the selective combining (SC) technique at the destination node D, where the branch with the greatest SNR is chosen as the output SNR to be used in the next stage of calculations. In this section we will derive the end-to-end Signal-to-noise ratio (SNR) which is mathematically defined as the ratio of signal power to the noise power. The SNR at the combiner output of the destination node is a result of the best-relay SNR, and can be expressed as:

$$\begin{aligned} \gamma_{SC} = {\mathrm {max}}_{i} \left( \gamma_{S R_i D} \right) , \end{aligned}$$
(6)

where \(\gamma_{S R_i D}\) is the received SNR from the ith indirect path (\(S \rightarrow R_i \rightarrow D\)), and it can be derived after substituting the value of the amplification gain \(G_{AF_i}\) which is given in (3), then dividing both the nominator and denominator by \(N_o^2\) then by \(\left( 1+\sum_{j=1}^{N_i} \gamma_{h_{ij}}\right) \times \left( 1+\sum_{k=1}^L \gamma_{g_k}\right)\), the SNR can be derived and simplified as:

$$\begin{aligned} \gamma_{S R_i D}= \frac{\gamma_{SR_i} ^{eff} \gamma_{RD_i} ^{eff}}{\gamma_{SR_i} ^{eff}+\gamma_{RD_i} ^{eff} + 1}. \end{aligned}$$
(7)

where the effective SINR for the \(S \rightarrow R_i\) and the \(R_i D \rightarrow D\) links are defined as:

$$\begin{aligned} \gamma_{S R_i} ^{eff}= & {} \frac{\gamma_{S R_i}}{1+\sum_{j=1}^{N_i} \gamma_{h_{ij}}}, \end{aligned}$$
(8a)
$$\begin{aligned} \gamma_{R_i D} ^{eff}= & {} \frac{\gamma_{R_i D}}{1+\sum_{k=1}^L \gamma_{g_k}}, \end{aligned}$$
(8b)

To have an attractable mathematical for of the performance metrics as the outage and error probability for the network, we adopted a tight upper bound for \(\gamma_{SC}\) such that:

$$\begin{aligned} \gamma_{SC} \le {\mathrm {max}}_{i}\left( {\mathrm {min}}_i\left( \gamma_{{SR}_i} ^{eff}, \gamma_{{RD}_i} ^{eff}\right) \right) . \end{aligned}$$
(9)

The PDF of the relay link SNR \(\left( {\mathrm {min}}_i\left( \gamma_{{SR}_i} ^{eff}, \gamma_{{RD}_i} ^{eff}\right) \right)\) is evaluated and given by equation [7, Eq. 24]. Moreover, the CDF is derived and expressed in equation [7, Eq. 27]. The next step is to derive the statistical characteristics (CDF) of the best-relay node SNR \((\gamma_{SC})\). The CDF of \(\gamma_{SC}\) is mathematically represented as:

$$\begin{aligned} F_{\gamma_{SC}}(\gamma ) = \prod_{i}^{M} F_{\gamma_i}(\gamma ), \end{aligned}$$
(10)

the \(S \rightarrow R \rightarrow D\) link CDF derived in section [7, Sect. 3.3] and the formula computed in equation [7, Eq. 27], then the best-relay CDF can be derived as:

$$\begin{aligned} \begin{aligned} F_{\gamma_{SC}}(\gamma )&= \prod_{i}^{M} \Bigg (1- e^{-\frac{1}{2}\Bigg (\Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} +\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}}\Bigg )\gamma + \Bigg (\frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}}+ \frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\Bigg ) \!\! \Bigg )}\\&\times \Bigg (\mu_{h_{I_i}} ^{\mu_{h_{I_i}}} \overline{\gamma }_{h_{I_i}}^{-\mu_{h_{I_i}}}\Bigg )^{N_{i}} \times \frac{ \Bigg (\mu_{g_{I_i}} ^{\mu_{g_{I_i}}} \overline{\gamma }_{g_{I_i}}^{-\mu_{g_{I_i}}}\Bigg )^{L_{i}} e^{\Bigg (\frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}}+\frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\Bigg )}}{ \Gamma (\mu_{sr_i}) \Gamma (\mu_{rd_i}) } \\&\times \sum_{k=0}^{\mu_{sr_i} -1} \sum_{j=0}^{\mu_{rd_i} -1} \Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}}\gamma \Bigg )^{k}\Bigg (\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}}\gamma \Bigg )^{j} \\&\times \Gamma (\mu_{sr_i}-k) \Gamma (\mu_{rd_i}-j) \Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} \gamma +\frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}}\Bigg )^{\frac{-\mu_{h_{I_i}} N_{i}-k -1}{2}} \\&\times \Bigg (\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}} \gamma +\frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\Bigg )^{\frac{-\mu_{g_{I_i}} L_{i}-j -1}{2}} {W}_{\frac{-\mu_{h_{I_i}} N_{i}+k+1}{2},\frac{-\mu_{h_{I_i}}N_{i}-k}{2}}\\&\times \Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} \gamma +\frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}} \Bigg )\\&\times {W}_{\frac{-\mu_{g_{I_i}} L_{i}+j+1}{2},\frac{-\mu_{g_{I_i}} L_{i}-j }{2}}\Bigg (\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}} \gamma +\frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\Bigg ) \Bigg ), \end{aligned} \end{aligned}$$
(11)

The PDF can then be derived by taking the derivation of (11) with respect to \(\gamma\), we use both the definitions of Whittaker function W expressed in [8, Eq. 13.14.3] and Confluent Hypergeometric function represented in [8, Eq. 13.2.8]. In addition for applying the generalization rule for the derivation of collection product of function defined as \(\{f_{i}\}_{i=1}^k\) and expressed in:

$$\begin{aligned} \begin{aligned} \frac{d}{dx} \left[ \prod_{i=1}^k f_i(x) \right]&= \sum_{i=1}^k \left( \frac{d}{dx} f_i(x) \prod_{j\ne i} f_j(x) \right) \\&= \left( \prod_{i=1}^k f_i(x) \right) \left( \sum_{i=1}^k \frac{f'_i(x)}{f_i(x)} \right) . \end{aligned} \end{aligned}$$
(12)

the PDF can then be derived and mathematically expressed as:

$$\begin{aligned} \begin{aligned} f_{\gamma_{SC}}(\gamma )&= \sum_{i=1}^M \Bigg \{ \prod_{l\ne i} \Bigg [ 1- \frac{ 1}{ \Gamma (\mu_{sr_j}) \Gamma (\mu_{rd_j}) }\\&\quad \times \sum_{k=1}^{\mu_{sr_j}} \sum_{j=1}^{\mu_{rd_j}} \sum_{v=0}^{k-1} \sum_{t=0}^{j-1} \sum_{p=0}^{\infty } \sum_{q=0}^{\infty } \left( {\begin{array}{c}k-1\\ v\end{array}}\right) \left( {\begin{array}{c}j-1\\ t\end{array}}\right) \\&\quad \times \left( {\begin{array}{c}-v-\mu_{h_{I_j}} N_{j}\\ p\end{array}}\right) \left( {\begin{array}{c}-t-\mu_{g_{I_j}} L_{j}\\ q\end{array}}\right) \Bigg . (\mu_{h_{I_j}} N_{j})_v (\mu_{g_{I_j}} L_{j})_t \Gamma (\mu_{sr_j}-k+1) \\&\quad \times \Gamma (\mu_{rd_j}-j+1) \Bigg (\frac{\mu_{sr_j} }{\overline{\gamma }_{sr_j}}\Bigg )^{k+p-1} \Bigg (\frac{\mu_{rd_j} }{\overline{\gamma }_{rd_j}}\Bigg )^{j+q-1} \Bigg (\frac{\mu_{h_{I_j}}}{\overline{\gamma }_{h_{I_j}}}\Bigg )^{-v-p} \Bigg (\frac{\mu_{g_{I_j}}}{\overline{\gamma }_{g_{I_j}}}\Bigg )^{-t-q} \\&\quad \times \gamma ^{k+j+p+q-2} e^{-\Bigg (\frac{\mu_{sr_j}}{\overline{\gamma }_{sr_j}} +\frac{\mu_{rd_j}}{\overline{\gamma }_{rd_j}}\Bigg )\gamma } \Bigg ] \Bigg (-\frac{1}{\Gamma (\mu_{sr_i}) \Gamma (\mu_{rd_i})} \\&\quad \times \sum_{k=1}^{\mu_{sr_i}} \sum_{j=1}^{\mu_{rd_i}} \sum_{v=0}^{k-1} \sum_{t=0}^{j-1} \sum_{p=0}^{\infty } \\&\quad \times \sum_{q=0}^{\infty } \left( {\begin{array}{c}k-1\\ v\end{array}}\right) \left( {\begin{array}{c}j-1\\ t\end{array}}\right) \left( {\begin{array}{c}-v-\mu_{h_{I_i}} N_{i}\\ p\end{array}}\right) \left( {\begin{array}{c}-t-\mu_{g_{I_i}} L_{i}\\ q\end{array}}\right) (\mu_{h_{I_i}} N_{i})_v (\mu_{g_{I_i}} L_{i})_t \\&\quad \times \Gamma (\mu_{sr_i}-k+1) \Gamma (\mu_{rd_i}-j+1)\Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}}\Bigg )^{k+p-1}\Bigg (\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}}\Bigg )^{j+q-1} \\ &\quad \times \Bigg (\frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}}\Bigg )^{-v-p} \\& \quad \times \Bigg (\frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\Bigg )^{-t-q}\Bigg ( ({k+j+p+q-2}) \gamma ^{k+j+p+q-3} e^{-\Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} +\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}} \Bigg )\gamma } \\&\quad - \Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} +\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}}\Bigg ) \gamma ^{k+j+p+q-2} e^{-\Bigg (\frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} +\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}} \Bigg )\gamma } \Bigg ) \Bigg ) \Bigg \} \end{aligned} \end{aligned}$$
(13)

4 Performance Analysis

4.1 Outage Probability

Outage probability is considered one of the important measures of the network performance. Analyzing the outage probability is essential to characterize the error performance and reliability of the network under investigation. The outage probability is denoted by [9, Eq. 6.46], is defined at output of the selection combiner as the probability at which the SINR falls below a certain threshold value \((\gamma_{Th})\), and is derived mathematically as;

$$\begin{aligned} \begin{aligned} P_{out} =&\prod_{i}^{M} \Bigg (1- \frac{ \left( \mu_{h_{I_i}} ^{\mu_{h_{I_i}}} \overline{\gamma }_{h_{I_i}}^{-\mu_{h_{I_i}}}\right) ^{N_{i}} \left( \mu_{g_{I_i}} ^{\mu_{g_{I_i}}} \overline{\gamma }_{g_{I_i}}^{-\mu_{g_{I_i}}}\right) ^{L_{i}} }{ \Gamma (\mu_{sr_i}) \Gamma (\mu_{rd_i}) } e^{\left( \frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}}+\frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\right) } \\& \quad \times e^{-\frac{1}{2}\left( \left( \frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} +\frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}}\right) \gamma_{thr} + \left( \frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}}+ \frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\right) \!\! \right) } \sum_{k=0}^{\mu_{sr_i} -1} \sum_{j=0}^{\mu_{rd_i} -1} \left( \frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}}\gamma_{thr}\right) ^{k} \\& \quad \times \left( \frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}}\gamma_{thr} \right) ^{j} \Gamma (\mu_{sr_i}-k) \Gamma (\mu_{rd_i}-j) \left( \frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} \gamma_{thr}+\frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}}\right) ^{\frac{-\mu_{h_{I_i}} N_{i}-k -1}{2}} \\&\quad \times \left( \frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}} \gamma_{thr}+\frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}}\right) ^{\frac{-\mu_{g_{I_i}} L_{i}-j -1}{2}} {W}_{\frac{-\mu_{h_{I_i}} N_{i}+k+1}{2},\frac{-\mu_{h_{I_i}} N_{h_I}-k}{2}}\left( \frac{\mu_{sr_i} }{\overline{\gamma }_{sr_i}} \gamma_{thr}+\frac{\mu_{h_{I_i}}}{\overline{\gamma }_{h_{I_i}}} \right) \\&\quad \times {W}_{\frac{-\mu_{g_{I_i}} L_{i}+j+1}{2},\frac{-\mu_{g_{I_i}} L_{i}-j }{2}}\left( \frac{\mu_{rd_i} }{\overline{\gamma }_{rd_i}} \gamma_{thr}+\frac{\mu_{g_{I_i}}}{\overline{\gamma }_{g_{I_i}}} \right) \Bigg ), \end{aligned} \end{aligned}$$
(14)

Equation (14) can be reduced for identical links with different values of fading coefficients (\(\alpha\) and μ), such as Rayleigh and Nakagami-m fading channels.

4.2 Average Error Probability

Another important performance measure is the error probability, which will be derived in this section, and mathematically denoted by [9, Eq. 6.50]:

$$\begin{aligned} P_b(e)= \int_{0}^{\infty } P_e(\gamma ) f_{\gamma_{SD}} (\gamma ) d\gamma , \end{aligned}$$
(15)

where \(P_e(\gamma )\) is the conditional error probability for a given \(\gamma\). For coherent Binary-Phase-Shift-Keying (BPSK) modulation, the average BER at the selection combining output is expressed as:

$$\begin{aligned} P_{SC}(e)= \int_{0}^{\infty } Q(\sqrt{ 2 \gamma_{SC}}) f_{\gamma_{SD}} (\gamma ) d\gamma , \end{aligned}$$
(16)

where \(f_{\gamma_{SD}}\) is defined in Eq. (13). The average error probability \(P_b(e)\) can be upper bounded as [10, Eq. 9.27]. Moreover, \(P_b(e)\) can be reduced for identical fading channel with coefficients of \(\alpha =2\) and \(\mu =1\), and using the binomial expansion and some mathematical manipulation, as:

$$\begin{aligned} \begin{aligned} P_{SC}(e)&\le 2^{M-1} \sum_{k=0}^{M} \left( {\begin{array}{c}M\\ k\end{array}}\right) \left( \frac{\overline{\gamma } L }{\overline{\gamma }+2} \right) ^{k} e^{\frac{2 \Lambda }{\overline{\gamma }}k+\Lambda k} \\&\quad \times E_{2 L+1}^{k}\left( \frac{ \Lambda }{\overline{\gamma }}(\overline{\gamma }+2)\right),\end{aligned} \end{aligned}$$
(17)

where L is the interferes number at the ith relay and destination nodes, and \((\Lambda =\frac{\overline{\gamma }_{SR_i}}{\overline{\gamma }_{h_I}})\) represents the average Signal to Interference Ratio (SIR) at the Relay node. In addition, \((\Upsilon =\frac{\overline{\gamma }_{R_i D}}{\overline{\gamma }_{g_I}})\), is the average SIR at the Destination node.

5 Numerical Results

Outage probability and error probability behavior are illustrated in this section over different conditions and fading channel parameters (α and μ). The results shown in Fig. (2a and b illustrates the behavior of the outage probability versus the normalized average SNR when there is no interference affecting any node of the network, for different values of (μ = 1) and (μ = 2) with the value of (α = 2) fading parameter correspondingly. It’s been illustrated that for different values of μ the outage probability decreases by increasing the number of diversity paths M that are received at the input of the selection combiner. On the other hand, it is noticed that increasing the value of μ decreases the outage probability over the same given conditions, thus; improving the performance of the network in the case of no interferers affecting any of the network nodes.

As for the impact of interference at the cooperative diversity which is illustrated in Fig. 3a and b, given that the number of interferers at the relay and destination nodes \(N=L=5\) with \(INR=3\) dB for different values of μ, improvement is clearly noticed in the network performance by increasing the number of combined branches when compared to the direct link transmission. Accordingly, increasing the number of diversity paths and increasing the value of μ for identical link, decreases the outage probability therefore improving the performance of the network compared to the direct link transmission.

The region of investigation in this study is the high SNR region, where a tight upper bound is considered to derive an approximated expression for the average error probability of the cooperative diversity where BPSK modulation technique is used, as illustrated and derived in Sect. 4.2. Considering the relationship between the average error probability and the average SNR, it is found that the performance of the network is improved by increasing the number of diversity paths at the combiner input, though the interference affect the average error probability with adverse manner, as shown in Fig. 4a where different number of interferers are considered with \(SNR=30\) dB and links are identical with fading channel parameter \(\mu =1\). While maintaining a fixed number of interferers \(N=L=10\) with a value of \(INR=3\) dB, the average error probability is enhanced by increasing the number of diversity paths even in the presence of interferers at the nodes. As can be observed in Fig. 4b accordingly.

Fig. 2
figure 2

Outage probability of identical Fading channels with different coefficients, selective combining and without interference

Full size image
Fig. 3
figure 3

Outage probability of identical Fading channels with selective combining and 5-interferers and \(INR=3\) dB

Full size image
Fig. 4
figure 4

Average error probability of identical Fading channels with \(SNR = 30\) dB and SC scheme and various interferers number

Full size image

6 Conclusion

In this paper, we have investigated the error and outage performance of cooperative diversity network over \(\alpha\)–\(\mu\) fading channels in the presence of CCI. Both the probability density function (PDF) and the cumulative distribution function (CDF) of the upper bound of the SINR were developed in this paper. In addition, to the derived expressions of both the outage and error probability, which were used to investigate the performance of the proposed cooperative diversity network, where the relaying technique assumed is the AF, while the selective combining technique is introduced at the destination node. The derived expressions were used to extract other fading models such as Rayleigh (\(\alpha = 2\) and \(\mu = 1\)), Nakagami-m (\(\alpha = 2\) and \(\mu = m\)), and other fading models where the value \(\alpha = 2\) with different values of \(\mu\).

Furthermore, as proved in the results, interference can have a major impact on the system performance. Where increasing the number of interferers result in increasing the outage probability, which degrades the system performance accordingly. The same finding holds for the error probability, where the system performance degrades by increasing the number of interferers introduced to the system nodes, also its found that the presence of interference caused the error probability curve to floor. Never the less, the average error probability can be enhanced by increasing the number of diversity paths even in the presence of interferers at the nodes.