Entanglement and Output Squeezing of Distant Optomechanical Systems Generated by Four-Level Atoms

Abstract

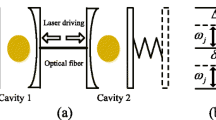
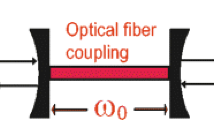
A scheme is presented to generate entanglement of optical andmechanical modes in coupled cavity optomechanical system with two four-level atoms. Two distant movable mirrors and two cavity modes as well as mirror and the adjacent or the distant cavity mode are all entangled, and the entanglement curve of two movable mirrors is a symmetrical distribution when ∆ is equal to ω_m. Furthermore, we also investigate the output entanglement of two cavity fields, and find the squeezing spectrum is affected by the mirror frequency and the Rabi frequency of laser field.

Appendices

Appendix A: Calculation of the Mean Values

We now calculate the zero order ${\sigma }_{ii^{\prime }}^{j0}$$(i,i^{\prime }=e,f,g,h,j=1,2)$ in (4). With the help of laser linear approximation theory, the classical fields will be treated to all orders in the Rabi frequency Ω, while the atomic transitions $|e\rangle \leftrightarrow |g\rangle$ and $|f\rangle \leftrightarrow |h\rangle$ are treated to first order in the coupling constants g. Including the damping terms, we can obtain the quantum Langevin equations of the atom

$$ \begin{array}{@{}rcl@{}} \dot{\sigma}_{ge}^{j} &=&-\left[{{\gamma}_{1}^{j}}+{{\gamma}_{2}^{j}}+i\left( \delta_{j}-{\omega}_{gh}^{j}\right)\right]{\sigma}_{ge}^{j} -i{\Omega}_{1}{\sigma}_{gh}^{j}+i{\Omega}_{2}{\sigma}_{fe}^{j}, \\ \dot{\sigma}_{hf}^{j} &=&-\left[{{\gamma}_{3}^{j}}+{{\gamma}_{4}^{j}}+i\left( {\Delta}_{j}+{\omega}_{gh}^{j}\right)\right]{\sigma}_{hf}^{j} +i{\Omega}_{1}{\sigma}_{ef}^{j}-i{\Omega}_{2}{\sigma}_{hj}^{j}, \\ \dot{\sigma}_{gh}^{j} &=&-i{\omega}_{gh}^{j}{\sigma}_{gh}^{j}-i{\Omega}_{1}{\sigma}_{ge}^{j}+i{\Omega}_{2}{\sigma}_{fh}^{j}+ig_{1}{\sigma}_{eh}^{j}a_{j} \\ &&-ig_{1}{\sigma}_{eh}^{j}{a}_{j}^{\dagger}, \\ \dot{\sigma}_{ef}^{j} &=&-\left[{{\gamma}_{1}^{j}}+{{\gamma}_{2}^{j}}+{{\gamma}_{3}^{j}}+{{\gamma}_{4}^{j}}+i\left( \delta_{j}-{\Delta}_{j}-{\omega}_{gh}^{j}\right)\right]{\sigma}_{ef}^{j} \\ &&+i{\Omega}_{1}{\sigma}_{hf}^{j}-i{\Omega}_{2}{\sigma}_{eg}^{j}+ig_{1}{\sigma}_{gf}^{j}{a}_{j}^{\dagger}-ig_{2}{\sigma}_{eh}^{j}a_{j}. \end{array} $$

(A1)

Solving steady state solution of above equation, we have the zero order ${\sigma }_{ii^{\prime }}^{j0}$ of the atom as

$$ \begin{array}{@{}rcl@{}} {\sigma}_{ee}^{j0} &=& \frac{{{\Omega}_{1}^{2}}{{\Omega}_{2}^{2}}\gamma_{4}}{P_{3}}, \\ {\sigma}_{ff}^{j0} &=& \frac{{{\Omega}_{1}^{2}}{{\Omega}_{2}^{2}}\gamma_{2}}{P_{3}}, \\ {\sigma}_{gg}^{j0} &=& \frac{\left( |P_{2}|^{2}+{{\Omega}_{2}^{2}}\right){{\Omega}_{1}^{2}}\gamma_{2}}{P_{3}}, \\ {\sigma}_{hh}^{j0} &=& \frac{\left( |P_{1}|^{2}+{{\Omega}_{1}^{2}}\right){{\Omega}_{2}^{2}}\gamma_{4}}{P_{3}}, \\ {\sigma}_{eh}^{j0} &=& \frac{i {P}_{1}^{\ast}{\Omega}_{1}{{\Omega}_{2}^{2}}\gamma_{4}}{P_{3}}, \\ {\sigma}_{fg}^{j0} &=& \frac{i {P}_{2}^{\ast}{\Omega}_{2}{{\Omega}_{1}^{2}}\gamma_{2}}{P_{3}}. \end{array} $$

(A2)

with

$$ \begin{array}{@{}rcl@{}} P_{1}&=&\gamma_{1}+\gamma_{2}-i\delta_{1}, P_{2}=\gamma_{3}+\gamma_{4}-i\delta_{2}, \\ P_{3}&=&\gamma_{4}|P_{1}|^{2}{{\Omega}_{2}^{2}}+2(\gamma_{2}+\gamma_{4}){{\Omega}_{1}^{2}}{{\Omega}_{2}^{2}} +\gamma_{2}|P_{2}|^{2}{{\Omega}_{1}^{2}}. \end{array} $$

(A3)

Substituting the zero-order approximation $\sigma _{ii^{\prime }}^{j0}$ into (A1), σ_ge and σ_hf can be obtained

$$ \begin{array}{@{}rcl@{}} {\sigma}_{ge}^{j}&=&\frac{({P}_{6}^{\ast}D_{1}+P_{5}D_{2}){a}_{j}^{\dagger}+({P}_{6}^{\ast}D_{3}-P_{5}D_{4}){a}_{j}^{\dagger}} {{P}_{4}^{\ast}P_{5}-{{P}_{6}^{2}}}, \\ {\sigma}_{hf}^{j}&=&\frac{(P_{6}{D}_{4}^{\ast}-P_{4}{D}_{3}^{\ast}){a}_{j}^{\dagger}-(P_{6}{D}_{2}^{\ast}+P_{4}{D}_{1}^{\ast})a_{j}} {P_{4}{P}_{5}^{\ast}-{{P}_{6}^{2}}}, \end{array} $$

(A4)

$$ \begin{array}{@{}rcl@{}} B_{1} &=& i g_{1}({\sigma}_{gg}^{(0)}-{\sigma}_{ee}^{(0)}), \\ B_{2} &=& i g_{2}({\sigma}_{hh}^{(0)}-{\sigma}_{ff}^{(0)}), \\ B_{3} &=& i g_{1}{\sigma}_{eh}^{(0)}, \\ B_{4} &=& i g_{2}{\sigma}_{fg}^{(0)}, \\ B_{5} &=& i g_{1}{\sigma}_{fg}^{(0)}, \\ B_{6} &=& i g_{2}{\sigma}_{eh}^{(0)}, \\ P_{4}&=&\omega_{gh}(P_{1}+i\omega_{gh})(P_{1}+{P}_{2}^{\ast}+i\omega_{gh}) \\ &&-i{{\Omega}_{1}^{2}}(P_{1}+{P}_{2}^{\ast}+i\omega_{gh})+{{\Omega}_{2}^{2}}\omega_{gh}, \\ P_{5}&=&\omega_{gh}(P_{2}-i\omega_{gh})({P}_{1}^{\ast}+P_{2}-i\omega_{gh}) \\ &&+i{{\Omega}_{2}^{2}}({P}_{1}^{\ast}+P_{2}-i\omega_{gh})+{{\Omega}_{1}^{2}}\omega_{gh}, \\ P_{6}&=&i{\Omega}_{1}{\Omega}_{2}(P_{1}+{P}_{2}^{\ast}+2i\omega_{gh}), \\ D_{1} &=& ({P}_{1}^{\ast}+P_{2}-i\omega_{gh})(\omega_{gh} {B}_{2}^{\dagger}+{\Omega}_{2}{B}_{4}^{\dagger}) -i{\Omega}_{1}\omega_{gh} {B}_{6}^{\dagger}, \\ D_{2} &=& ({P}_{1}^{\ast}+P_{2}-i\omega_{gh}){\Omega}_{1}{B}_{4}^{\dagger}-i{\Omega}_{2}\omega_{gh} {B}_{6}^{\dagger}, \\ D_{3} &=& ({P}_{1}^{\ast}+P_{2}-i\omega_{gh}){\Omega}_{2}B_{3}-i{\Omega}_{1}\omega_{gh} B_{5}, \end{array} $$

$$ \begin{array}{@{}rcl@{}} D_{4} &=& ({P}_{1}^{\ast}+P_{2}-i\omega_{gh})(\omega_{gh}B_{1}-{\Omega}_{1}B_{3})+i{\Omega}_{2}\omega_{gh} B_{5}. \\ s_{1} &=&-[\kappa_{1}+i(\widetilde{{\Delta}_{1}}-{\omega}_{gh}^{1})] -\frac{ig_{1}({P}_{6}^{\ast}D_{3}-P_{5}D_{4})}{{P}_{4}^{\ast}P_{5}-({P}_{6}^{\ast})^{2}} \\ &&+\frac{ig_{2}(P_{6}{D}_{2}^{\ast}+P_{4}{D}_{1}^{\ast})}{P_{4}{P}_{5}^{\ast}-{{P}_{6}^{2}}}, \\ s_{2} &=&-[\kappa_{2}+i(\widetilde{{\Delta}_{2}}-{\omega}_{gh}^{2})] -\frac{ig_{1}({P}_{6}^{\prime\ast}{D}_{3}^{\prime}-{P}_{5}^{\prime}{D}_{4}^{\prime})}{{P}_{4}^{\prime\ast}{P}_{5}^{\prime} -({P}_{6}^{\prime\ast})^{2}} \\ &&+\frac{ig_{2}({P}_{6}^{\prime}{D}_{2}^{\prime\ast}+{P}_{4}^{\prime}{D}_{1}^{\prime\ast})}{{P}_{4}^{\prime}{P}_{5}^{\prime\ast} -{P}_{6}^{\prime2}}, \\ u_{1} &=&-\frac{ig_{1}({P}_{6}^{\ast}D_{1}+P_{5}D_{2})}{{P}_{4}^{\ast}P_{5}-({P}_{6}^{\ast})^{2}} -\frac{ig_{2}(P_{6}{D}_{4}^{\ast}-P_{4}{D}_{3}^{\ast})}{P_{4}{P}_{5}^{\ast}-{{P}_{6}^{2}}}, \\ u_{2}&=&-\frac{ig_{1}({P}_{6}^{\prime\ast}{D}_{1}^{\prime}+{P}_{5}^{\prime}{D}_{2}^{\prime})}{{P}_{4}^{\prime\ast}{P}_{5}^{\prime}-({P}_{6}^{\prime\ast})^{2}} -\frac{ig_{2}({P}_{6}^{\prime}{D}_{4}^{\prime\ast}-{P}_{4}^{\prime}{D}_{3}^{\prime\ast})}{{P}_{4}^{\prime}{P}_{5}^{\prime\ast}-{P}_{6}^{\prime2}}. \end{array} $$

(A5)

All the parameters of another cavity have the same form as the first one. Bring σ_ca and σ_db back into (3), we can have the steady solution (5).

Appendix B: Coefficients of the Drift Matrix A

Here we give the concrete form of some elements in drift matrix A.

$$ \begin{array}{@{}rcl@{}} {\Delta} &=&\widetilde{{\Delta}_{1}}-{\omega}_{g h}^{1}, {\Delta}^{\prime}=\widetilde{{\Delta}_{2}}-{\omega}_{g h}^{2}, \\ \delta &=&\delta_{1}-{\Delta}_{1}-{\omega}_{g h}^{1}, \delta^{\prime} =\delta_{2}-{\Delta}_{2}-{\omega}_{g h}^{2}, \\ \widetilde{\delta_{1}}&=&\delta_{1}-{\omega}_{g h}^{1}, \widetilde{\delta^{\prime}_{1}}=\delta_{2}-{\omega}_{g h}^{2}, \\ \widetilde{\delta_{2}}&=&{\Delta}_{1}+{\omega}_{g h}^{1}, \widetilde{\delta^{\prime}_{2}}={\Delta}_{2}+{\omega}_{g h}^{2}, \\ \gamma_{12}&=&\gamma_{1}+\gamma_{2}, {\gamma}_{12}^{\prime}={\gamma}_{1}^{\prime}+{\gamma}_{2}^{\prime}, \\ \gamma_{34}&=&\gamma_{3}+\gamma_{4}, {\gamma}_{34}^{\prime}={\gamma}_{3}^{\prime}+{\gamma}_{4}^{\prime}, \\ \gamma&=&\gamma_{1}+\gamma_{2}+\gamma_{3}+\gamma_{4}, \gamma^{\prime}={\gamma}_{1}^{\prime}+{\gamma}_{2}^{\prime}+{\gamma}_{3}^{\prime}+{\gamma}_{4}^{\prime}, \end{array} $$

$$ \begin{array}{@{}rcl@{}} H_{1}&=&g_{1}\left( {\sigma}_{gg}^{10}-{\sigma}_{ee}^{10}\right),{H}_{1}^{\prime}=g_{1}\left( {\sigma}_{gg}^{20}-{\sigma}_{ee}^{20}\right), \\ H_{2}&=&g_{2}\left( {\sigma}_{hh}^{10}-{\sigma}_{ff}^{10}\right),{H}_{2}^{\prime}=g_{2}\left( {\sigma}_{hh}^{20}-{\sigma}_{ff}^{20}\right), \\ I_{+}&=&\frac{g_{1}}{2}\left( {\sigma}_{fg}^{10}+{\sigma}_{gf}^{10}\right)+\frac{ g_{2}}{2}\left( {\sigma}_{eh}^{10}+{\sigma}_{he}^{10}\right), \\ I_{-}&=-&\frac{i g_{1}}{2}\left( {\sigma}_{fg}^{10}-{\sigma}_{gf}^{10}\right)-\frac{i g_{2}}{2}\left( {\sigma}_{eh}^{10}-{\sigma}_{he}^{10}\right), \\ R_{+}&=&-\frac{g_{1}}{2}\left( {\sigma}_{eh}^{10}+{\sigma}_{he}^{10}\right)-\frac{ g_{2}}{2}\left( {\sigma}_{fg}^{10}+{\sigma}_{gf}^{10}\right), \\ R_{-}&=&\frac{i g_{1}}{2}\left( {\sigma}_{eh}^{10}-{\sigma}_{he}^{10}\right)+\frac{i g_{2}}{2}\left( {\sigma}_{fg}^{10}-{\sigma}_{gf}^{10}\right), \\ T_{+}&=&\frac{g_{2}}{2}\left( {\sigma}_{fg}^{10}+{\sigma}_{gf}^{10}\right)-\frac{ g_{1}}{2}\left( {\sigma}_{eh}^{10}+{\sigma}_{he}^{10}\right),\end{array} $$

$$ \begin{array}{@{}rcl@{}} T_{-}&=&\frac{i g_{2}}{2}\left( {\sigma}_{fg}^{10}-{\sigma}_{gf}^{10}\right)-\frac{i g_{1}}{2}\left( {\sigma}_{eh}^{10}-{\sigma}_{he}^{10}\right), \\ G_{+}&=&\frac{g_{2}}{2}\left( {\sigma}_{eh}^{10}+{\sigma}_{he}^{10}\right)-\frac{ g_{1}}{2}\left( {\sigma}_{fg}^{10}+{\sigma}_{gf}^{10}\right), \\ G_{-}&=&\frac{i g_{2}}{2}\left( {\sigma}_{eh}^{10}-{\sigma}_{he}^{10}\right)-\frac{i g_{1}}{2}\left( {\sigma}_{fg}^{10}-{\sigma}_{gf}^{10}\right). \end{array} $$

(B1)

The other parameters ${I}_{+}^{\prime }, {I}_{-}^{\prime }, {R}_{+}^{\prime }, {R}_{-}^{\prime }, {T}_{+}^{\prime }, {T}_{-}^{\prime }, {G}_{+}^{\prime }, {G}_{-}^{\prime }$ of the second cavity have the same form as the first one.