Entropy Variation of a Charged (2 + 1)-Dimensional BTZ Black Hole Under Hawking Radiation

Abstract

Using the definition of a black hole’s volume introduced by Christodoulou and Rovelli, we calculate the interior volume of a (2 + 1)-dimensional charged Banados Teitelboim Zanelli (BTZ) black hole, and find that the volume increases linearly with time. Afterwards, the entropy of a massless scalar field inside the black hole is calculated and the result indicates that the entropy will be also increasing with time infinitely. Moreover, thinking about Hawking radiation, the ratio of variation of the scalar field’s entropy to the variation of Bekenstein–Hawking entropy is approximately a linear function of m, which is quite different from a RN black hole while m is relatively large. In the end, we extend the calculation above to a massive BTZ black hole and find that the relationship with different $\tilde {M}$ between two kinds of entropy is similar to the previous result. But the difference is that the relationship function $F(m,q,\tilde {M})$ will tend to be a constant when the mass parameter $\tilde {M}$ becomes big enough.

Appendix: Lambert W Function

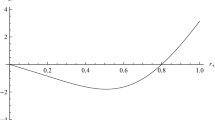
Lambert W Function represented by W(x), which is also called product log function, is the inverse funtion of f(w) = we^w, in which w can be any complex number. Lambert W Function is a multivalued function, and has infinite branches which are usually represented by W_k(x)(k = 0, ±1, ± 2, ± 3, ⋯ ), where W_k(x) denotes the k th branch. Every branch is a single value function. When x is a real number, there are only two branches, W₀(x) and W_− 1(x), which have been ploted in Fig. 3. We can find that the domain of them respectively are $[-\frac {1}{e},+\infty )$ and $[-\frac {1}{e},0)$. According to (4), $-\frac {1}{q^{2}} e^{-\frac {m}{q^{2}}}$ is a negetive real number. So for given m and q, there are only two values of W(x), among which the smaller one corresponds to r₊ and the bigger one corresponds to r₋. Obviously, only when

$$ -\frac{e^{-\frac{m}{q^{2}}}}{q^{2}}=-\frac{1}{e} \Rightarrow m=q^{2} (1-2 \ln{q}), $$

(30)

we have r₋ = r₊, which is the sign of the extreme BTZ black hole [17]. Besides, (30) can also be verifed by T_H = 0.

Fig. 3

The blue solid line is the curve of W₀(x), and the red dash line is the curve of W_− 1(x). We can find that they intersect at $\left (-\frac {1}{e},-1\right )$

Now we want to talk about the behavior of r_± when q = 0. Setting $x=-\frac {m}{q^{2}}$, (4) turns to

$$ r_{\pm}=\sqrt{\frac{m}{x}W_{k}\left( \frac{x}{m}e^{x}\right)}\quad (k=-1,0). $$

(31)

Unfortunately, q = 0 is a singularity. So let $q\rightarrow 0$, i.e. $x\rightarrow -\infty$, we have

$$ \lim_{x\rightarrow -\infty}r_{+}=\sqrt{m}, \lim_{x\rightarrow -\infty}r_{-}=0, $$

(32)

which is just the result obtained in Ref. [8] for the case of a bare BTZ black hole with q = 0, J = 0.