Optical n(p, T₉₀) Measurement Suite 3: Results at $\lambda = 1542\,\text{nm}$

Abstract

Single-isotherm n(p, T₉₀) results are reported for the gases Ar, N₂, H₂O, and D₂O at vacuum wavelength $\lambda = 1542.383(1)$ nm. The argon and nitrogen isotherms were measured near 303 K; the water isotherms were measured near 373 K. Combined with the two previous articles of this series, the present results beget several insights via dispersion analyses. The argon result is highly consistent with static measurement plus ab initio calculation of dispersion polarizability. The nitrogen result is nominally consistent with one recent experiment and the dipole oscillator strength distributions, but the present work offers a refined estimate of the molar refractivity at optical wavelengths. For ordinary and heavy water, the dispersion trend is nominally consistent with existing liquid measurements. However, water’s absorption features in the near-infrared preclude a reliable comparison of the present result with literature.

1 Introduction

Imminent commercial optical pressure standards might find it most practical to operate at telecom wavelength. Over the past few decades, the telecom industry has innovated much gadgetry in the C-band infrared (1530 nm to 1565 nm). For precision measurement, the bane of telecom wavelength has been the absence of turnkey narrow linewidth lasers (sub-kilohertz). In today’s market, narrow linewidth solutions are provided by at least three technologies: fiber ring resonators, diode lasers with an external waveguide Bragg reflector, and whispering gallery mode resonators. As a candidate source for an optical pressure standard, a HeNe laser tube might offer the better tradeoff between narrow linewidth and cost; however, telecom photonics probably have the advantage from the total system perspective (fiber-hardened, plug-and-play, and so on). Most importantly, telecom lasers also have the multi-gigahertz tunability essential for miniaturization (i.e., centimeter-scale optical cavities).

The optical pressure scale [1] $p_{{\rm ops}} = \frac{2 R T}{3 A_{{\rm R}}} (n - 1) + \cdots$ is realized by measurement of refractivity $n - 1$ at known temperature T, with R being the molar gas constant. An optical pressure standard therefore comprises an accurate refractometer and thermometer. The key parameter to the realization is the molar refractivity $A_{{\rm R}} = A_{\epsilon }(0) + \Delta A_{\epsilon }(\omega ) + A_{\mu }$, in which the electronic contribution $A_{\epsilon }$ is about five orders of magnitude larger than the magnetic $A_{\mu }$, and $\frac{\Delta A_{\epsilon }(\omega )}{A_{\epsilon }(0)} \approx 1\,\%$ for visible wavelength. For practical metrology gases like nitrogen and argon, the most accurate knowledge about $A_{{\rm R}}$ comes from measurement. Until now, measurements have either provided zero frequency $A_{\epsilon }(0)$ by dielectric constant, $A_{{\rm R}}(0)$ by microwave refractive index, or $A_{{\rm R}}(\omega )$ at 633 nm by optical refractive index. Knowledge about $A_{{\rm R}}$ in the C-band infrared is limited. Consequently, an optical pressure standard operating at the (arguably) more commercially viable telecom wavelengths does not have a solid metrological foundation.

This article is the final installment in a three-part series. It extends the previous two articles [2, 3] by reporting single-isotherm n(p, T₉₀) results at $\lambda = 1542.383(1)$ nm for Ar, N₂, H₂O, and D₂O. All background concepts and analysis details are in the previous two articles. Here, the pivotal difference is the change in operating wavelength. Consequently, this article is brief, and just reports the optical setup, and then places the key result (molar refractivity $A_{{\rm R}}$) in the literature context.

2 Setup

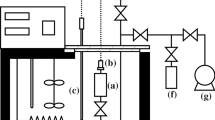
A schematic of the optical setup is shown in Fig. 1. The $1542\,\text{nm}$ system of Fig. 1 has two main differences over the $633\,\text{nm}$ system of Refs. [2, 3]: (1) a frequency comb referenced to the SI second via GPS was used as the frequency reference (instead of a iodine-stabilized laser), and (2) an external cavity diode laser was used for locking to the resonance frequency of the Fabry–Perot (FP) cavity (instead of a HeNe laser tube). More details and photographs of the equipment are given in the supplemental material

Fig. 1

Optical setup for the $\lambda = 1542\,\text{nm}$ results. Components include external cavity diode laser (ecdl), isolator (iso), fiber coupler/collimator (fc), polarizing beamsplitter (pbs), acousto-optic modulator (aom), quarter-waveplate (qwp), convex lens (lcx), mirror (m), fiber splitters (fs), global positioning system disciplined oscillator (gps-do), Bragg grating filter (bgf), polarization controller (pc), photodetector (pd), and lock-in amplifier (lia)

The diode laser employed has feedback provided by a Bragg reflector inside its butterfly package. [In optics, “butterfly package” is standard usage. It refers to a metal housing about $(25 \times 15 \times 8)\,\text{mm}^{3}$, with 14 electrical control pins projecting from the sides and a fiber optic output from one end. The diode laser chip, thermoelectric cooler, thermistor, Bragg reflector, isolator, and fiber coupling optics are all monolithically assembled inside the housing.] The free-running laser has a specified linewidth of $2\,\text{kHz}$. Noise on the drive current was minimized by limiting its bandwidth to $100\,\text{Hz}$. The operating wavelength was chosen to overlap with an accurately known absorption feature of acetylene. The concept was to operate with an acetylene-stabilized laser frequency reference, which is a portable device. However, the use of the frequency comb has made acetylene wavelength a moot point. (The frequency comb is in a separate space to the refractometry lab, and supplies the optical reference frequency over $70\,\text{m}$ of fiber optic cable.)

The configuration (Fig. 1) to lock the laser to the FP cavity resonance is similar to the HeNe setup. Fast ($16\,\text{kHz}$) frequency control was provided by a doublepass acousto-optic modulator; in series with the fast loop, slow ($1\,\text{Hz}$) frequency control was provided by the thermoelectric cooler inside the butterfly package. The hysteresis-free tuning range of the laser is about $8\,\text{GHz}$. In this work, the voltage applied to the thermoelectric cooler was circuit limited so that frequency only tuned $1.2\,\text{GHz}$, or $20\,\%$ wider than the free spectral range of the cavity. The modulation and analog control electronics were identical to the HeNe setup.

The FP cavity was the same as Refs. [2, 3]. The mirrors that form the cavity were dual-coated for $633\,\text{nm}$ and $1542\,\text{nm}$ wavelengths. The finesse at $1542\,\text{nm}$ was estimated as 3200, which is about $13\,\%$ higher than the value at $633\,\text{nm}$. (Finesse was estimated by measurements of the free spectral range divided by the full-width half-maximum transmission linewidth.) The mirror parameter $\epsilon_{\tau }$ of Eq. (1) in Ref. [2] differs by about $14\,\%$ between the wavelengths, and has negligible influence on the results.

The previous paragraph is emphasized: the same FP cavity has been used in Refs. [2, 3] and the present work. This fact means that dominating errors related to cavity length have little influence on relative results between wavelengths. For argon and nitrogen, the dominating length error is cavity compressibility, which would be identical at both wavelengths. For water vapor, the dominating length error is the moisture-dependent reflection phase shift from the cavity mirrors. This error is chromatic, but as explained below, the wavelength dependence is small (and compensated), and is further diminished by the choice of operating temperature.

3 Results

For argon and nitrogen, single isotherms at $303\,\text{K}$ were acquired with a procedure identical to Ref. [2]—nineteen set pressures up to $500\,\text{kPa}$ generated by a piston gage. For ordinary and heavy water, single isotherms at $373\,\text{K}$ were acquired with a procedure identical to Ref. [3]—ten set pressures below $2\,\text{kPa}$ measured with a calibrated pressure transducer.

The molar refractivities deduced for all four gases are listed in Table 1. Next follows some discussion, placing the results in the literature context. Dispersion in all four gases will be discussed in terms of $\delta A_{{\rm R}} \equiv A_{{\rm meas}} - A_{{\rm ref}}$, referenced to zero frequency and with

$$\begin{aligned} A_{{\rm ref}} = A_{\epsilon }(0) + \Delta A_{\epsilon }(\omega ) + A_{\mu }. \end{aligned}$$

(1)

The literature sources used for static polarizability $A_{\epsilon }(0)$, dispersion polarizability $\Delta A_{\epsilon }(\omega )$, and diamagnetic susceptibility $A_{\mu }$ are specified for each gas below. (All literature uses atomic units for angular frequency $\omega$. This work describes all parameters related to $A_{{\rm R}}$ in SI units.)

Unless otherwise stated, all uncertainties in this work are one standard uncertainty, corresponding to approximately a $68\,\%$ confidence level.

Table 1 Results for molar refractivity at $\lambda = 1542.383(1)\,\text{nm}$ from the present work, and at $\lambda = 632.9908(1)\,\text{nm}$ from the same apparatus [2, 3]

3.1 Discussion about Ar and N$_2$

At $303\,\text{K}$, the uncertainty of the argon and nitrogen results is $3\times 10^{-6} \cdot A_{{\rm R}}$, and operation at $1542\,\text{nm}$ incurs no additional uncertainty over what is detailed in Ref. [2]. The uncertainty is dominated by the knowledge of the generated pressure ($1.9\,{\upmu}\text{Pa/Pa}$) [4], and to a lesser extent knowledge of the thermometry error $T - T_{90}$ ($1.1\,{\upmu}\text {K/K}$) [5].

3.1.1 Argon

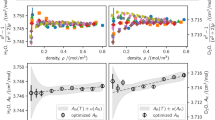
The single-isotherm n(p, T₉₀) data for argon are plotted in Fig. 2a. The subplot is in a conventional format, showing molar refraction as a function of density. The deviation from constant molar refraction is primarily due to the second refractivity virial coefficient. Extracting information about this coefficient from the data is dubious: it requires very accurate knowledge about the compressibility factor, which would ultimately use previous data from this apparatus at a different wavelength [2]. In short, the deduction would be circular: two conflated nonlinear coefficients would be inferred from the same data. (The difference in the second refractivity virial coefficient [6] between $633\,\text{nm}$ and $1542\,\text{nm}$ is far too small for these measurements to say anything about the frequency dependence.)

Fig. 2

(a) Single-isotherm results for argon at $1542\,\text{nm}$ and $303\,\text{K}$. (b) Dispersion analysis plotted as relative difference from the reference value; the shaded area is an estimate of uncertainty on the reference value. Errorbars span the uncertainty of the cited literature

In principle, extrapolating Fig. 2a to zero density obtains the molar refractivity. However, the $A_{\text {R}}$ in Table 1 was determined by the more appropriate method of single-isotherm refractive-index gas thermometry [7]. The method fit the (isothermal) generated pressure to a power series of refractivity $p = (n - 1) {\mathcal {A}} \left[ 1 + (n - 1) {\mathcal {B}} + (n - 1)^2 {\mathcal {C}} \right] + \epsilon_p$, and $A_{\text {R}} = \frac{2 R T}{3 {\mathcal {A}}}$ was extracted from the linear refractivity term. This analysis circumvents the nonlinear influences from the density and refractivity virial coefficients. The implementation used total least squares, with the refractivity and pressure weighted by the squared reciprocal of their respective uncertainties. The identified $\epsilon_p = -1.4\,\text{mPa}$ influences the final result at the level of $1 \times 10^{-7} \cdot A_{\text {R}}$. It is emphasized that $\epsilon_p$ is a physically justified parameter, and past experience [2] corroborates that its inclusion in the single-isotherm regression produces a final $A_{\text {R}}$ closer to true value (multi-isotherm regression).

The argon result at $1542\,\text{nm}$ is shown in the literature context by the dispersion plot of Fig. 2b. The reference value of (1) follows the recommendation of Lesiuk and Jeziorski [8]: $A_{\epsilon }(0)$ is due to the highly accurate capacitance measurement of Gaiser and Fellmuth [9], $\Delta A_{\epsilon }(\omega )$ uses the $\omega ^6$-order Cauchy equation from the ab initio calculation of Lesiuk and Jeziorski [8], and $A_{\mu }$ is from the ab initio calculation for diamagnetic susceptibility, also due to Lesiuk and Jeziorski [10]. The uncertainty on the reference value has $2.4 \times 10^{-6} \cdot A_{\text {R}}$ from the static measurement, and $0.05\,\%$ on the first Cauchy coefficient, which translates into $1.2 \times 10^{-6}\cdot A_{\text {R}}$ at $1542\,\text{nm}$. (The magnetic uncertainty contribution is probably negligible, but a solution to the susceptibility puzzle [10] needs a new experimental development.)

It is clear from Fig. 2b that all results for argon are highly consistent. The two optical results have been produced by the same apparatus (but separated in time by 18 months), and extrapolate very close to the zero frequency result of Gaiser and Fellmuth [9]. In the context of an optical pressure scale, the optical properties of argon are on solid ground.

[Two other notable static results are not shown in Fig. 2b. The first is the ab initio calculation of Lesiuk and Jeziorski [8], which has $\frac{\delta A_{\text {R}}}{A_{\text {R}}} = (2.8 \pm 17) \times 10^{-5}$, and is consistent with $A_{\text {ref}}$ within the mutual standard uncertainty. The second static result not shown is the older capacitance measurement of Schmidt and Moldover [11], which has $\frac{\delta A_{\text {R}}}{A_{\text {R}}} = (32.4 \pm 4.5) \times 10^{-5}$, and is inconsistent with $A_{\text {ref}}$ by seven times the mutual standard uncertainty. The work of Schmidt and Moldover is relevant for the nitrogen discussion below. Finally, a refractivity measurement at $800\,\text{nm}$ due to Zhang et al. [12] has $\frac{\delta A_{\text {R}}}{A_{\text {R}}} = (27.2 \pm 2.3) \times 10^{-5}$, and is inconsistent with $A_{\text {ref}}$ by eleven times the mutual standard uncertainty. The fact that all these three values not plotted in Fig. 2b are systematically higher than $A_{\text {ref}}$ should not dissuade from the conclusion that $A_{\text {ref}}$ for argon is highly reliable.]

3.1.2 Nitrogen

The nitrogen isotherm at $1542\,\text{nm}$ is plotted in Fig. 3a, and shown in the literature context by the dispersion plot of Fig. 3b. For nitrogen, there is no high accuracy measurement of static polarizability. Therefore, (1) uses the older capacitance measurement of Schmidt and Moldover [11] for $A_{\epsilon }(0)$. The ab initio estimate of dispersion [13] is not metrology-grade, so $\Delta A_{\epsilon }(\omega )$ uses a Cauchy equation derived from the dipole oscillator strength distributions (DOSD) of Kumar and Meath [14]. Last, a handbook [15] value is used for $A_{\mu }$, which is based on measurements from 100 years ago [16]. Obviously, this particular reference value synthesis for nitrogen is not well known, and has combined uncertainties of $3.5 \times 10^{-5} \cdot A_{\epsilon }$ [11] plus $1\,\%$ on the first Cauchy coefficient [14]; the diamagnetic susceptibility is unlikely to affect optical and dielectric comparisons at more than the $4 \times 10^{-6} \cdot A_{\text {R}}$ level.

Fig. 3

(a) Single-isotherm results for nitrogen at $1542\,\text{nm}$ and $303\,\text{K}$. (b) Dispersion analysis is plotted as relative difference from the reference value; the shaded area is an estimate of uncertainty on the reference value. Errorbars span the uncertainty of the cited literature, which in some cases are smaller than the markers

Though nitrogen data are scarce, Fig. 3b suggests the formulated reference value is erroneous. As stated at the outset, this work and Ref. [2] have been produced with the same apparatus—identical instrumentation for $n - 1$, p, and $T_{90}$, with the only difference being the wavelength of the laser interrogating the cavity. It is plausible that the same apparatus operated at two widely separated wavelengths should produce a reliable estimate of nitrogen dispersion. Based on the argon result above (see Fig. 2b), it is also plausible that this apparatus should establish an absolute value of nitrogen’s molar refractivity within the stated $3 \times 10^{-6} \cdot A_{\text {R}}$ uncertainty. Therefore, one might reasonably formulate a new $A_{\text {R}}$ recommendation based on two measurements from the same apparatus. The results of this work and Ref. [2] both operated at $303\,\text{K}$, and are satisfied by

$$\begin{aligned} A_{\text {R}} = a_{\text {e}} \left[ 1 + a_2 \left( \dfrac{{\upmu} \text {m}}{\lambda } \right) ^2 + a_4 \left( \dfrac{{\upmu}\text{m}}{\lambda } \right) ^4 + a_6 \left( \dfrac{{\upmu}\text{m}}{\lambda } \right) ^6 + a_{\text {m}} \right] , \end{aligned}$$

(2)

with the static value equivalent $a_{\text {e}} = 4.386921(20)\,\text{cm}^{3}/\text{mol}$. The $\lambda$ is vacuum wavelength. The $a_2 = 5.3247(29) \times 10^{-3}$ is larger than the DOSD [14] by $1.2\,\%$, which is slightly larger than the DOSD estimate of uncertainty on that Cauchy coefficient. The $a_4 = 3.610 \times 10^{-5}$ and $a_6 = 2.753 \times 10^{-7}$ are fixed values taken from the DOSD. The $a_{\text {m}} = -1.1(1) \times 10^{-5}$ is from the handbook value [15] for magnetic susceptibility. All numbers in parentheses indicate standard uncertainty. Identification of the static value is inhibited by uncertainty in $a_{\text {m}}$. Between $1542\,\text{nm}$ and $633\,\text{nm}$, the recommendation should be accurate within $3 \times 10^{-6} \cdot A_{\text {R}}$. The uncertainty will increase as $\frac{1}{\lambda ^2}$, so extrapolation to $532\,\text{nm}$ should not incur error greater than $6 \times 10^{-6} \cdot A_{\text {R}}$.

It is emphasized that the recommendation of (2) only harmonizes the two datapoints from a single apparatus operated at $633\,\text{nm}$ and $1542\,\text{nm}$. Crucially, however, the recommendation is independently supported by Silander et al. [17], whose recent result at $1550.14\,\text{nm}$ agrees with (2) within 2.5 times mutual standard uncertainty. Moreover, the dispersion trend of (2) nominally agrees with the spectral lamp measurement of Peck and Khanna [18]. Between the wavelengths $633\,\text{nm}$ and $1542\,\text{nm}$, (2) differs from the Sellmeier equation of Peck and Khanna by only $-1.3\ \times 10^{-5} \cdot A_{\text {R}}$. Peck and Khanna have no explanation of uncertainty: they state the absolute value of refractivity was “considered significant only to about four digits” and that a refractivity ratio would be “perhaps two orders of magnitude” more accurate than the absolute value. The first statement might mean $4 \times 10^{-4} \cdot A_{\text {R}}$ on the absolute value. The Peck and Khanna absolute value is $1.6 \times 10^{-4} \cdot A_{\text {R}}$ higher than (2) at $633\,\text{nm}$, so within their estimated uncertainty. However, if their ratio uncertainty is interpreted as $4 \times 10^{-6} \cdot A_{\text {R}}$, it does not cover divergence from (2) for widely separated wavelengths. The divergence of Peck and Khanna might be explained as a chromatic error in their apparatus, which also appears in the dispersion measurement of argon by Peck and Fisher [19]. For argon, between the wavelengths $633\,\text{nm}$ and $1542\,\text{nm}$, the ab initio Cauchy equation [8] differs from Peck and Fisher’s Sellmeier equation by $-1.4\,\times 10^{-5} \cdot A_{\text {R}}$. So, the Peck dispersion measurements for nitrogen and argon both exhibit similar deviation in sign and magnitude from modern, independent estimates.

Elsewhere in Fig. 3b: Schmidt and Moldover’s [11] nitrogen measurement is $1.7 \times 10^{-4} \cdot A_{\epsilon }$ higher than (2), which is discrepancy at five times mutual standard uncertainty. The inconsistency of Schmidt and Moldover’s [11] nitrogen measurement with an updated reference value is not surprising: as mentioned in the previous subsection, their apparatus also produced a high value for argon. The updated formulation of (2) is marginally discrepant with the $532.255\,\text{nm}$ value of Kameche [20] by 2.4 times the mutual standard uncertainty. Finally, not shown in Fig. 3b is a refractivity measurement at $800\,\text{nm}$ due to Zhang et al. [12], which is discrepant with (2) by three times the mutual standard uncertainty. (Like their argon measurement, Zhang et al. report a nitrogen value higher than this work.)

Compared to argon, nitrogen lacks a dielectric constant measurement of the same caliber as Gaiser and Fellmuth [9], and has no ab initio dispersion check. Nevertheless, the present work combined with Silander et al. [17] has established nitrogen on a firmer footing than previously. In the context of the optical pressure scale $p \approx \frac{2 R T}{3 A_{\text {R}}} (n - 1)$, consensus knowledge on the key parameter is at the level of $1.1 \times 10^{-5} \cdot A_{\text {R}}$.

3.2 Discussion about H$_2$O and D$_2$O

For water at $373\,\text{K}$, measurement uncertainty in the molar refractivity is dominated by performance of the calibrated pressure transducers, as detailed in Ref. [3]. Operating at $1542\,\text{nm}$ incurs no additional uncertainty, and the combined standard uncertainty is $4.1 \times 10^{-4} \cdot A_{\text {R}}$. One uncertainty component that is wavelength dependent is the end-effect error $\epsilon_{\varphi }$ caused by the moisture-dependent reflection phase shift. The $\epsilon_{\varphi }$ was fully characterized at $633\,\text{nm}$. The change in $\epsilon_{\varphi }$ at $1542\,\text{nm}$ was estimated by the mirror stack model [21]. The model predicted that $\epsilon_{\varphi }$ decreases by $4.8\,\%$ at $1542\,\text{nm}$ relative to $633\,\text{nm}$. This estimate assumes the same amount of water adsorbs into the coating at both wavelengths, but the model accounts for dispersion of the three materials involved: high and low index layers of the stack and the condensed water in the voids. The results at $1542\,\text{nm}$ have had the $4.8\,\%$ reduction applied to $\epsilon_{\varphi }$. At $373\,\text{K}$, $\epsilon_{\varphi } \lesssim -0.5\,\text{nm}$, and a $4.8\,\%$ change only affects the single-isotherm result at the level of $2 \times 10^{-5} \cdot A_{\text {R}}$.

The single-isotherm results for ordinary and heavy water at $1542\,\text{nm}$ and $373\,\text{K}$ are plotted in Fig. 4a and Fig. 5a. Imprecision increases at lower density owing to the performance of the calibrated pressure transducers. The single-isotherm water values for $A_{\text {R}}$ in Table 1 use the weighted mean of the data in Figs. 4a and 5a. The $A_{\text {R}}$ at $1542\,\text{nm}$ appear the only gaseous measurements to date in the near-infrared. The problem of formulating a reference value to compare visible, near-infrared, and zero frequency estimates of $A_{\text {R}}$ is discussed next.

Fig. 4

(a) Single-isotherm results for ordinary water at $1542\,\text{nm}$ and $373\,\text{K}$. (b) Dispersion analysis is plotted as relative difference from the reference value; the shaded areas are a rough estimate of standard uncertainty on the reference value. Errorbars span the standard uncertainty of each literature source

3.2.1 Problems Formulating $A_{\text {ref}}$

Ordinary water has two absorption peaks [22] in the vicinity of $1542\,\text{nm}$: a weak one at $1460\,\text{nm}$ and a strong one at $1930\,\text{nm}$. These features preclude the construction of a metrology-grade estimate of $\Delta A_{\epsilon }(\omega )$.

The Cauchy equation for H$_2$O derived from the DOSD [23] is nominally consistent with visible wavelength measurements [24, 25]. However, a Cauchy equation based on the DOSD is inadequate to describe spectral behavior in the presence of absorption. Typically, for absorbing liquids, terms proportional to $\lambda ^{2m}$ are added to the Cauchy equation (m is an integer). This work at $1542\,\text{nm}$ operates at a saddle-point between two absorption peaks, so any smooth interpolating function is likely to be imprecise. For example, Bertie and Lan [22] derived the real refractive index of liquid H$_2$O by performing the Kramers–Kronig transformation on absorption data. Fitting their data in the range $(667< \lambda < 1600)\,\text{nm}$ with $c_0 + \frac{c_1}{\lambda ^2} - c_2 \lambda ^2$ failed to follow the oscillatory behavior. Between $1400\,\text{nm}$ and $1600\,\text{nm}$, error from the fit had a full-range deviation of $0.1\,\%$.

Besides the difficulty of smoothly interpolating $A_{\text {R}}$ between two measurements in the same apparatus, a Cauchy equation with $\lambda ^2$ proportionality would not allow comparison with ab initio calculation of electronic polarizability. So, the canonical functions available for $\Delta A_{\epsilon }(\omega )$ do not facilitate accurate comparison of static, near-infrared, and visible wavelength estimates of $A_{\text {R}}$. The compromise of this work uses the following for (1): the $A_{\epsilon }(0)$ from the ab initio calculations of Garberoglio et al. [26], the $\Delta A_{\epsilon }(\omega )$ from the DOSD of Zeiss and Meath [23], and the recommendation of Harvey et al. [27] for $A_{\mu }$. (Note that the DOSD of Zeiss and Meath is for H$_2$O, and this work uses the same dispersion polarizability for H$_2$O and D$_2$O.)

The dispersion plots of Figs. 4b and 5b clearly show the shortcoming of the compromise implemented for (1). The result at $1542\,\text{nm}$ disagrees with (1) by about $7.5\times 10^{-3} \cdot A_{\text {R}}$, or nine times mutual standard uncertainty. To be clear, the conclusion of Ref. [3] still stands: the refractivity measurement at $633\,\text{nm}$ is consistent with the recent ab initio calculation [26], using the DOSD to adjust to zero frequency. Furthermore, the measurement technique of Ref. [3] and the present work is single-wavelength interferometry, and oscillatory behavior caused by absorption has no influence on the accuracy of a refractivity measurement or the deduction of $A_{\text {R}}$. These contradictory statements—that the measurements are accurate and significantly disagree with a reference value—stem from the inadequacy of the reference value in the near-infrared. The contradiction is somewhat allayed by looking at the dispersion of liquid water, as discussed next.

3.2.2 Dispersion of Water

For ordinary water, there are two liquid water dispersion functions plotted in Fig. 4b. One is derived from the IAPWS formulation [28], which is heavily weighted by the classical liquid dispersion of Tilton and Taylor [29]. The IAPWS formulation has a $\lambda ^2$ proportional term, and extends to wavelengths longer than the $707\,\text{nm}$ cutoff of Tilton and Taylor. For Fig. 4b, the average value of the IAPWS (vapor) formulation at $373\,\text{K}$ has been decreased by $1.63\,\%$ to intersect with Ref. [3]. Also plotted in Fig. 4b is a more recent liquid measurement by Kedenburg et al. [30], which was performed at $293\,\text{K}$ and covered wavelengths $(500< \lambda < 1600)\,\text{nm}$. The Cauchy equation derived by Kedenburg et al. also has a $\lambda ^2$ proportional term. The trend of Kedenburg et al. in Fig. 4b has been increased by $1.27\,\%$ to intersect with Ref. [3].

Both the liquid dispersion curves in Fig. 4b generally support a feature of the present work: a deviation from $\frac{1}{\lambda ^2}$ proportionality compared to other visible measurements of gaseous H$_2$O [24, 25]. However, both liquid dispersion functions have a $\lambda ^2$ proportionality too strong to intersect the measurement at $1542\,\text{nm}$. This aspect is probably influenced by the strong absorption peak $1930\,\text{nm}$. The Kramers–Kronig dispersion relation predicts that $n(\lambda )$ decreases as an absorption peak is approached from short wavelength. The IAPWS formulation is mostly constructed from wavelength data shorter than the strong absorption peak; Kedenburg et al. have data extending no further than $1600\,\text{nm}$. Therefore, both liquid Cauchy equations are likely to be driven to a low value of $n(1542\,\text{nm})$ by the influence of the $1930\,\text{nm}$ absorption on the $\lambda ^2$ term. The influence of absorption on refractive index is further discussed in App. B.

Fig. 5

(a) Single-isotherm results for heavy water at $1542\,\text{nm}$ and $373\,\text{K}$. (b) Dispersion analysis is plotted as relative difference from the reference value; the shaded areas are a rough estimate of standard uncertainty on the reference value. Errorbars span the standard uncertainty of each literature source

Heavy water has weak absorption at $1340\,\text{nm}$ and $1620\,\text{nm}$, and a strong absorption at $1970\,\text{nm}$ [31]. The absorbance at $1970\,\text{nm}$ is about five times smaller than the equivalent feature in ordinary water. The liquid dispersion function plotted in Fig. 5b is from the measurement of Kedenburg et al. at $293\,\text{K}$, and has been increased in absolute value by $1.33\,\%$ to intersect with Ref. [3]. Again, the liquid dispersion curve helps place the measurement at $1542\,\text{nm}$ in context. The departure from the $\frac{1}{\lambda ^2}$ proportionality of visible wavelength measurement [32] is expected because of the strong absorption at $1970\,\text{nm}$.

In any case, the two measurements produced by this apparatus have an estimated uncertainty of $4.1 \times 10^{-4} \cdot A_{\text {R}}$. The $7 \times 10^{-3} \cdot A_{\text {R}}$ deviation of the result at $1542\,\text{nm}$ from a reference value is a shortcoming of the reference value, and is not likely a problem in measurement [3] or calculation [26].

4 Conclusion

This article was the final installment to a three-part n(p, T₉₀) series. The final installment has reported single-isotherm results for argon, nitrogen, ordinary water, and heavy water at the wavelength of $1542\,\text{nm}$. When combined with information from the first two articles [2, 3] which operated at $633\,\text{nm}$, the present work offered insights into dispersion polarizability.

The results have been placed in the literature context of a reference value for the respective molar refractivities. The results indicate that knowledge of the optical properties of argon is highly accurate ($\sim 3$ parts in $10^6$) and nitrogen is almost as good ($\sim 1$ part in $10^5$). The argon and nitrogen results will help establish the optical pressure scale [1] on a solid metrological foundation for telecom wavelength.

For water vapor, absorption features in the near-infrared make it difficult to relate the $1542\,\text{nm}$ result to either the measurement at $633\,\text{nm}$ or the ab initio calculation of static electronic polarizability. Nevertheless, the result might help establish a more accurate reference formulation in the C-band infrared—the extant formulation [28] has no gaseous input data in the near-infrared.

Appendices

Appendix 1: Helium Dispersion, or Cavity Recalibration

Simultaneous and synchronous two-wavelength measurement of helium is a future interest: the cavity compressibility $\kappa$ cancels, the refractometer becomes truly absolute, and a thermodynamic quantity is realized in a primary way. It might be called “dispersion gas thermometry.” This development awaits dichroic optics coupling to the cavity and, crucially, better knowledge about mirror phase shift—the parameters $\epsilon_{\tau }$ and $\nu_{\text {c}}$ in the master equation [2].

For now, the apparatus has produced a helium isotherm at $1542\,\text{nm}$, separated in time by 18 months from the isotherms at $633\,\text{nm}$ [2]. The result is plotted in Fig. 6a, and its relation to literature is in subplot (b). For helium, all contributors to the reference value of (1) are based on ab initio calculation. The $A_{\epsilon }(0)$ is from Puchalski et al. [33], the $\Delta A_{\epsilon }(\omega )$ is from Puchalski et al. [34] with its small correction [35], and the $A_{\mu }$ is from Puchalski et al. [36]. The estimate of uncertainty in calculation is below $10^{-7} \cdot A_{\text {R}}$ at all wavelengths.

Fig. 6

(a) Single-isotherm results for helium at $1542\,\text{nm}$ and $303\,\text{K}$. (b) Dispersion analysis plotted as relative difference from the reference value; the shaded area is an estimate of uncertainty on the ab initio reference value. Errorbars span the uncertainty of the cited literature

For the measurement results in Fig. 6b: The static measurement is due to the highly accurate capacitance measurement of Gaiser and Fellmuth [9]. This is a true absolute measurement, in which apparatus distortion was corrected by mechanical knowledge of elastic properties. The result plotted at $633\,\text{nm}$ is not absolute: it is from the present apparatus, in which the cavity compressibility $\kappa$ was assigned a value [2] that drove $\delta A_{\text {R}} \rightarrow 0$. By contrast, the measurement result $A_{\text {R}} = 0.5177474(21)\,\text{cm}^{3}/\text{mol}$ plotted at $1542\,\text{nm}$ is also from this apparatus, and uses the $\kappa$ originally estimated at $633\,\text{nm}$. There are two possible interpretations of the optical measurements in Fig. 6b. The first interpretation would be that $\kappa$ is stable and reproducible within $1.4 \times 10^{-4} \cdot \kappa$ over 18 months and with disassembly and remounting on the wire suspension. (Recall, standard uncertainty for the calibration of compressibility via helium refractivity was estimated to be $1.3 \times 10^{-4} \cdot \kappa$.) The second interpretation is that two measurements at $633\,\text{nm}$ and $1542\,\text{nm}$ have validated the ab initio calculation of dispersion polarizability [34] within the $4 \times 10^{-6} \cdot A_{\text {R}}$ precision of the apparatus.

Finally, the first interpretation above brings the question: which estimate of $\kappa$ to use? This work used the old value of $\kappa$, reasoning that cavity compressibility does not change with time, and a constant systematic error in the apparatus would give a more reliable estimate of dispersion in argon and nitrogen. If the refractometer were updated to the new value for $\kappa$, the molar refractivity values at $1542\,\text{nm}$ in Table 1 would decrease by $0.7 \times 10^{-6} \cdot A_{\text {R}}$.

Molecular Absorption and Refractive Index

The Beer–Lambert law describes light absorption $I = I_0 \exp (-\mu d)$ as an exponential decrease in transmitted intensity I through a (gas) medium of pathlength d. The absorption coefficient is given by

$$\begin{aligned} \mu (\lambda ) = \sigma_{\text {m}} (\lambda ) \rho_{\text {n}} + \sigma_{\text {b}} (\lambda ) \rho_{\text {n}}^2 + \cdots . \end{aligned}$$

(3)

Absorption depends on wavelength $\lambda$, and $\rho_{\text {n}}$ is number density. The $\sigma_{\text {m}} (\lambda )$ is the monomer absorption cross-section. The $\sigma_{\text {b}} (\lambda )$ is the collision-induced absorption, in which a dipole is created by binary interactions between molecules.

An absorbing medium has a complex refractive index

$$\begin{aligned} {\hat{n}} = n + i k, \end{aligned}$$

(4)

with the optical extinction coefficient k related to the absorption coefficient $\mu$ via $k = \mu \frac{\lambda }{4 \pi }$. A refractometer measures ${\hat{n}}$ but theory calculates n (i.e., as electronic polarizability). Consequently, for an absorbing gas, measurement and calculation of refractive index will diverge by $\delta n \equiv {\hat{n}} - n$. The divergence is given by a Kramers–Kronig transformation

$$\begin{aligned} \delta n(\lambda ) = \dfrac{2 \lambda ^2}{\pi } \int_0^\infty \dfrac{k(\lambda^{\prime}) \textrm{d}\lambda^{\prime}}{\lambda^{\prime} (\lambda ^2 - \lambda^{\prime 2})} \end{aligned}$$

(5)

on the optical extinction coefficient k. Therefore, knowledge about $\mu$ [37, 38] informs the deviation $\delta n$ [39, 40] between experiment and theory.

Fig. 7

Contribution of absorption to the refractive index. (a) Ordinary water vapor at $1\,\text{kPa}$ and $373\,\text{K}$. The inset shows the contribution at visible wavelength. (b) Nitrogen at $0.5\,\text{MPa}$ and $303\,\text{K}$. The inset shows a barely perceptible influence from the overtone at $2.16\ {\upmu}\text{m}$

The $\delta n$ result for H$_2$O is plotted in Fig. 7a, and calculation is referenced to $p = 1\,\text{kPa}$ and $T = 373\,\text{K}$ conditions. The $\mu$ was obtained from HITRAN [37, 38] for wavenumbers $(0.0001< \frac{1}{\lambda } < 2.5)\,\upmu\text{m}^{-1}$. The abscissa of Fig. 7a is linear in wavelength to show the complex behavior in the near-infrared, and two interesting features are clear. First, refractive index at $633\,\text{nm}$ is already perturbed by the strong infrared absorption. Second, between $633\,\text{nm}$ and $1542\,\text{nm}$ the fractional deviation $\frac{\delta n}{n-1}$ is about $-8 \times 10^{-3}$. Referring to Fig. 4b of the main text: the two H$_2$O datapoints of this apparatus diverge in $\frac{\delta A_{\text {R}}}{A_{\text {R}}}$ proportional to wavelength. A quantitative estimate of this divergence is subjective, but $-6 \times 10^{-3}$ between the two wavelengths is reasonable. The nominal consistency between this subjective estimate and the $\frac{\delta n}{n-1}$ predicted by Fig. 7a is remarkable. [Two notes: best-knowledge $\mu (\lambda )$ does not satisfy the idealized limits of (5), and the $\mu (\lambda )$ employed does not include the water vapor continuum.]

The preceding demonstration with H$_2$O encourages a prediction of the influence that absorption in nitrogen might have on (2). Nitrogen is a homonuclear molecule without a dipole moment, and does not exhibit a rovibrational absorption spectrum. It has a strong triple bond, which can not be excited by the (low) energy of infrared radiation. Therefore, for wavelengths longer than visible, nitrogen has a $\sigma_{\text {m}} (\lambda )$ near zero. However, nitrogen is active in the infrared by collision-induced absorption. For $\sigma_{\text {b}} (\lambda )$ in (3), the HITRAN database is again the relevant resource [41]. For $\rho_{\text {n}}$ at ambient conditions the resulting $\mu$ is weak, but the fundamental band is at $4.3\ {\upmu}\text{m}$, and an overtone at $2.16\ {\upmu}\text{m}$ is close to telecom wavelength. However, the Kramers–Kronig transformation reveals $\delta n$ to be a very small effect for telecom wavelengths, as shown in Fig. 7b. So, nitrogen absorption should not cause imprecision larger than $10^{-7} \cdot A_{\text {R}}$ in (2)—for example, if optical refractivity were compared to dielectric constant.