1 Introduction

In order to control and manage heat transport in devices and modules, it is important to consider both the transport within materials and the transport across interfaces between materials [1]. In particular, it is primarily important to reduce thermal resistance of interfaces inside of devices such as central processing unit (CPU), light-emitting diode (LED), laser diode (LD) and optical recording media for acceleration of their operating speed, reduction of energy consumption and improvement of reliability [2, 3]. On the other hand, large thermal resistance might enhance performance of multi-layered insulation materials, and it is critical to evaluate them accurately for thermoelectric thin films and devices [4, 5]. In response to these requirements, several investigations have been performed to measure interfacial thermal resistance [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Investigation of direction dependence of the interfacial thermal resistance was reported by performing picosecond thermoreflectance method under both front-heat rear-detect and rear-heat front-detect configurations [13, 14]. Dependence of the interfacial thermal resistance on twist angle of crystal axis between the Si thin film and the Si substrate was measured by the offset 3 omega method [15]. As a challenging approach, nanoscale heat pathways have been visualized by combination of electron beam heating and nano-thermocouple and interfacial thermal resistances on the pathways have been measured [21, 22]. However, it has been difficult to measure the interfacial thermal resistance between thin films or that between thin film and its substrate because they are much smaller than cross-plane thermal resistance of adjacent thin films even if they are as thin as 100 nm. Reliable data of the interfacial thermal resistance are limited, and the mechanism by which the interfacial thermal resistance occurs is still under investigation [23, 24].

The strict definition of interfacial thermal resistance, also called boundary thermal resistance, varies depending on the field of science and technology [25]. The term interface thermal conductance, which is the reciprocal of the interfacial thermal resistance, is also used [26,27,28,29]. For example, from the case where it means thermal resistance of a joint between bulk materials or glued bulk materials [24] to an interface between atomic layers such as an interface between thin films formed by sputtering [30,31,32]. In this report, thermal resistance between substrate and thin films which are deposited on substrates by sputtering, molecular beam epitaxy, or vacuum evaporation are considered. Even with such an interface at the atomic layer-level, it is not possible to obtain a completely uniform state on both sides of the interface. For example, in the case of epitaxial growth, deformation occurs on both sides of the interface due to lattice spacing mismatch. Even if the local thermal conductivity and thermal diffusivity can be defined, they are not supposed to be uniform in the thin film in the vicinity of the interface. In order to define the interfacial thermal resistance even in such a situation, the thermal conductivity and thermal diffusivity in the thin film or substrate sandwiching the interface should be approximated to be constant in the mathematical model. The interface is assumed to have thermal resistance without finite thickness and heat capacity of interface is 0 [33]. This is because the mathematical model which assumes the heat diffusion time across the interface is 0 reproduces the temperature response well. The thermal resistance of such atomic layer-level interfaces is smaller than 10–8 m2·K·W−1 in most cases [30,31,32, 34], and this amount is comparable to that of quartz glass (1 W·m−1·K−1) of 10 nm (10–8 m) thick. Therefore, to measure thermal resistances smaller than this, measurements faster than 100 ps (10−10 s), which corresponds to the heat diffusion time across around 10 nm quartz glass, are desirable.

At present, the picosecond (or femtosecond) heating thermoreflectance is one of suitable methods [2, 35]. Thus, picosecond thermoreflectance method under front-heat front-detect method (time domain thermoreflectance: TD-TR) have been applied for this purpose [26,27,28]. More quantitative present possible approach to determine interfacial thermal resistances using thermoreflectance method is by preparing and measuring thin films with different thickness. This is rather cumbersome and contains some ambiguity whether the prepared thin films of different thickness intrinsically keep the exact same characteristics. In this approach, each thin film of different thickness is sandwiched between two metallic thin films of constant thickness. The ultrafast laser flash method (picosecond thermoreflectance method under rear-heat front-detect configuration [35]) is applied to the series of samples and thermoreflectance signals are analyzed by areal thermal diffusion time method [33]. Areal heat diffusion time is an area surrounded by the temperature response curve and horizontal line at the maximum temperature rise (normalized to 1) when a sample is pulse-heated, which can be expressed by an analytical expression based on the thermophysical property values of each layer in the sample. Since this area has a dimension of time, a systematic analysis of heat diffusion across a multilayer film is realized by defining “areal heat diffusion time”. The reason why the areal heat diffusion time is introduced is because the half-time method (half-value time method) [36], used to calculate the thermal diffusion time in the thickness direction of an insulated homogeneous material, does not provide an explicit analytical solution for multi-layered thin films.

In this report, an approach to directly determine interfacial thermal resistance by a single measurement of a thin film on substrate is presented, by analyzing the shape of thermoreflectance signals with analytical solutions represented in frequency domain and time domain. For this study, two mode-locked fiber lasers are used for heating light and temperature measurement light, and by electrically controlling the timing of transmission of the two lasers, thermoreflectance signals were acquired over the entire pulse interval of 50 ns [35]. We have previously presented an analytical solution of temperature response expressed by Fourier series for one-dimensional heat diffusion after periodic pulse heating [37].

It is well-known that the flash method which was invented by Parker et al. in 1961 [36], and established as the reliable, standard and popular method for measuring thermal diffusivity of bulk materials [38,39,40,41,42]. Our thermoreflectance method based on Fourier transform is named as Fourier transform ultrafast laser flash method, since this method is natural evolution of the laser flash method for measuring thermal diffusivity of bulk materials [43]. This method was advanced in this work, and the signals were analyzed to be able to quantitatively determine the interfacial thermal resistance between thin film and substrate by curve-fitting.

2 Experiments

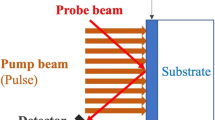
Figure 1 shows a schematic diagram of the thermoreflectance technique in rear-heat front-detect (RF) configuration and the conventional time domain thermoreflectance technique in front-heat front-detect (FF) configuration. In the case of RF configuration, a laser beam is incident on the interface between the thin film and substrate to heat up the thin film. Another laser beam is incident on a thin film and reflection from its surface is detected by photodetector in order to probe its surface temperature. The geometrical configuration of the thermoreflectance technique in RF configuration is the same as that of laser flash method, which is standard measurement method to measure the thermal diffusivity of bulk materials [36, 40, 42]. Thermal diffusivity of thin films can be calculated from thickness of a thin film and heat diffusion time across the thin film [35, 44, 45].

Fig. 1
figure 1

Diagram of thermoreflectance technique. (a) rear-heat front-detect: RF. (b) front-heat front-detect: FF

Full size image

The wavelength of pump beam is 1550 nm and that of probe beam is 775 nm. Detailed information about our thermoreflectance apparatus is explained in our previous works [37, 46]. The method we developed to determine interfacial thermal resistance will be described in detail in the next section.

In thermoreflectance measurements of this study, heat transfer across thin films can be regarded as one-dimensional because diameter of pump beam, which is typically from 50 to 100 μm, is far larger than thickness of thin films, which is thinner than 1 μm in most cases. Although, the heat eventually spreads in-plane and cross-plane in 3D, it takes much longer time than the observation timescale of 50 ns. Deviation from one-dimensional heat diffusion in 50 ns is negligibly small. Thus, temperature response from a sample can be derived from one-dimensional heat equation. In two-layer model which assumes a single-layered film on semi-infinite substrate, the relationship between the temperature at front surface of thin film \({T}_{f}\), the temperature at interface between thin film and substrate \({T}_{s}\), the heat flux across surface of thin film \({q}_{f}\) and the heat flux across interface \({q}_{s}\) is expressed as follows in Laplace domain [33]

$$\left[\begin{array}{c}\widetilde{{q}_{s}}\left(\xi \right)\\ \widetilde{{T}_{s}}\left(\xi \right)\end{array}\right]=\left[\begin{array}{cc}{\text{cosh}}\left(\sqrt{{\tau }_{f}\xi }\right)& -{b}_{f}\sqrt{\xi }{\text{sinh}}\left(\sqrt{{\tau }_{f}\xi }\right)\\ -\frac{1}{{b}_{f}\sqrt{\xi }}{\text{sinh}}\left(\sqrt{{\tau }_{f}\xi }\right)& {\text{cosh}}\left(\sqrt{{\tau }_{f}\xi }\right)\end{array}\right]\left[\begin{array}{c}\widetilde{{q}_{f}}\left(\xi \right)\\ \widetilde{{T}_{f}}\left(\xi \right)\end{array}\right],$$
(1)
$${\tau }_{f}=\frac{{{d}_{f}}^{2}}{{\alpha }_{f}}$$
(2)

where \({\tau }_{f}\) is heat diffusion time across thin film, \({d}_{f}\) is thickness of thin film, \({\alpha }_{f}\) is thermal diffusivity of thin film, \({b}_{f}\) is thermal effusivity of thin film and \(\xi\) is a complex variable. To consider interfacial thermal resistance between thin film and substrate, we assumed an additional layer between thin film and substrate as shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of two layer (thin film and substrate) model with interfacial thermal resistance

Full size image

In this case, the temperature at interface between the additional layer and thin film is named \(\widetilde{{T}_{s1}}\left(\xi \right)\), which corresponds to the temperature at the rear end of thin film. On the other hand, the temperature at interface between the additional layer and substrate is named \(\widetilde{{T}_{s2}}\left(\xi \right)\), which corresponds to the temperature at the front end of substrate. When there is an additional layer between thin film and substrate, the relationship between temperature and heat flux can be extended by cascading quadrupole matrices as follows [33]

$$\left[\begin{array}{c}\widetilde{{q}_{s2}}\left(\xi \right)\\ \widetilde{{T}_{s2}}\left(\xi \right)\end{array}\right]=\left[\begin{array}{cc}{\text{cosh}}\left(\sqrt{{\tau }_{A}\xi }\right)& -{b}_{A}\sqrt{\xi }{\text{sinh}}\left(\sqrt{{\tau }_{A}\xi }\right)\\ -\frac{1}{{b}_{A}\sqrt{\xi }}{\text{sinh}}\left(\sqrt{{\tau }_{A}\xi }\right)& {\text{cosh}}\left(\sqrt{{\tau }_{A}\xi }\right)\end{array}\right]\left[\begin{array}{c}\widetilde{{q}_{s1}}\left(\xi \right)\\ \widetilde{{T}_{s1}}\left(\xi \right)\end{array}\right],$$
(3)
$${\tau }_{A}=\frac{{{d}_{A}}^{2}}{{\alpha }_{A}}$$
(4)

where \({\tau }_{A}\) is heat diffusion time across the additional layer, \({d}_{A}\) is thickness of the additional layer, \({\alpha }_{A}\) is thermal diffusivity of the additional layer and \({b}_{A}\) is thermal effusivity of the additional layer. If the additional layer has zero thickness and infinitely small thermal conductivity \({\lambda }_{A}\), elements which include \({\tau }_{A}\) in Eq. 3 converge as follows

$$\underset{{d}_{A}\to 0,\mathit{ }{\lambda }_{A}\to 0 }{{\text{lim}}}{\text{cosh}}\left(\sqrt{{\tau }_{A}\xi }\right)=1$$
(5)
$$\underset{{d}_{A}\to 0, {\lambda }_{A}\to 0 }{{\text{lim}}}{b}_{A}\sqrt{\xi }{\text{sinh}}\left(\sqrt{{\tau }_{A}\xi }\right)=0$$
(6)
$$\underset{{d}_{A}\to 0,\mathit{ }{\lambda }_{A}\to 0}{{\text{lim}}}\frac{{\text{sinh}}\left(\sqrt{{\tau }_{A}\xi }\right)}{{b}_{A}\sqrt{\xi }}=\underset{{d}_{A}\to 0,\mathit{ }{\lambda }_{A}\to 0 }{{\text{lim}}}\frac{\sqrt{{\tau }_{A}}}{{b}_{A}}=\underset{{d}_{A}\to 0,\mathit{ }{\lambda }_{A}\to 0 }{{\text{lim}}}\frac{{d}_{A}/\sqrt{{\alpha }_{A}}}{\sqrt{{\alpha }_{A}}{c}_{A}{\rho }_{A}}=\underset{{d}_{A}\to 0,\mathit{ }{\lambda }_{A}\to 0 }{{\text{lim}}}\frac{{d}_{A}}{{\lambda }_{A}}=R,$$
(7)

where \({c}_{A}\) is specific heat capacity of the additional layer, \({\rho }_{A}\) is density of the additional layer and \(R\) is thermal resistance which has finite value. Therefore Eq. 3 can be expressed as follows

$$\left[\begin{array}{c}\widetilde{{q}_{s2}}\left(\xi \right)\\ \widetilde{{T}_{s2}}\left(\xi \right)\end{array}\right]=\left[\begin{array}{cc}1& 0\\ -R& 1\end{array}\right]\left[\begin{array}{c}\widetilde{{q}_{s1}}\left(\xi \right)\\ \widetilde{{T}_{s1}}\left(\xi \right)\end{array}\right]$$
(8)

Thus, the following relationship between heat flux and temperature can be obtained from Eq. 8.

$$\widetilde{{q}_{s2}}\left(\xi \right)=\widetilde{{q}_{s1}}\left(\xi \right)$$
(9)
$$\widetilde{{T}_{s2}}\left(\xi \right)=\widetilde{{T}_{s1}}\left(\xi \right)-R\widetilde{{q}_{s1}}\left(\xi \right)$$
(10)

When thickness of substrate can be regarded as semi-infinite, the temperature of the front end of the substrate \(\widetilde{{T}_{s2}}\left(\xi \right)\) in Laplace transform is expressed as follows [33]

$$\widetilde{{T}_{s2}}\left(\xi \right)=\frac{1}{{b}_{s}\sqrt{\xi }}\times \widetilde{{q}_{s2}}\left(\xi \right),$$
(11)

where \({b}_{s}\) is thermal effusivity of substrate.

In the actual measurement, the interface between thin film and substrate is pulse-heated, and heat diffuses from the interface to both sides as shown in Fig. 3. The pulse heating is assumed to be Dirac delta function \(\delta \left(t\right)\), whose Laplace transform is 1. Considering energy conservation law, the following equation is satisfied.

Fig. 3
figure 3

Schematic diagram of heat flux across interface between thin film and substrate

Full size image
$$\widetilde{{p}_{s1}}\left(\xi \right)+\widetilde{{q}_{s2}}\left(\xi \right)=1$$
(12)

Heat flow at the front surface \({p}_{f}\left(t\right)\) and its Laplace transform \(\widetilde{{p}_{f}}\left(\xi \right)\) can be substituted by 0 since the front surface of thin film is insulated.

If leftward heat flux is assumed to be positive, the relationship between \(\widetilde{{T}_{f}}\left(\xi \right)\) and \(\widetilde{{T}_{s1}}\left(\xi \right)\) can be expressed as follows

$$\left[\begin{array}{c}0\\ \widetilde{{T}_{f}}\left(\xi \right)\end{array}\right]=\left[\begin{array}{cc}{\text{cosh}}\left(\sqrt{{\tau }_{f}\xi }\right)& -{b}_{f}\sqrt{\xi }{\text{sinh}}\left(\sqrt{{\tau }_{f}\xi }\right)\\ -\frac{1}{{b}_{f}\sqrt{\xi }}{\text{sinh}}\left(\sqrt{{\tau }_{f}\xi }\right)& {\text{cosh}}\left(\sqrt{{\tau }_{f}\xi }\right)\end{array}\right]\left[\begin{array}{c}1-\widetilde{{p}_{s1}}\\ \widetilde{{T}_{s1}}\left(\xi \right)\end{array}\right]$$
(13)

By considering Eqs. 9, 10, 11 and 13, \(\widetilde{{T}_{f}}\left(\xi \right)\) can be expressed as follows

$$\widetilde{{T}_{f}}\left(\xi \right)=\frac{1}{{b}_{f}\sqrt{\xi }}\times \frac{1+R{b}_{s}\sqrt{\xi }}{\left(1+R{b}_{s}\sqrt{\xi }\right){\text{sinh}}\left(\sqrt{{\tau }_{f}\xi }\right)+\frac{{b}_{s}}{{b}_{f}}{\text{cosh}}\left(\sqrt{{\tau }_{f}\xi }\right)}$$
(14)

By replacing hyperbolic functions with exponential functions, \(\widetilde{{T}_{f}}(\xi )\) is finally expressed as follows

$$\widetilde{{T}_{f}}(\xi )=\frac{1}{{b}_{f}\sqrt{\xi }}\times \frac{\left(1+\frac{\gamma +\sqrt{{\tau }_{r}\xi }}{1+\sqrt{{\tau }_{r}\xi }}\right){\text{exp}}(-\sqrt{{\tau }_{f}\xi })}{1-\frac{\gamma +\sqrt{{\tau }_{r}\xi }}{1+\sqrt{{\tau }_{r}\xi }}{\text{exp}}(-2\sqrt{{\tau }_{f}\xi })}$$
(15)
$$\gamma =\frac{{b}_{f}-{b}_{s}}{{b}_{f}+{b}_{s}}$$
(16)
$${\tau }_{r}={R}^{2}{\left(\frac{{b}_{f}{b}_{s}}{{b}_{f}+{b}_{s}}\right)}^{2},$$
(17)

where \(\gamma\) is ratio of virtual heat sources of the mirror image method and \({\tau }_{r}\) is characteristic time of interfacial thermal resistance (cooling time constant) [33]. The temperature \(\widetilde{{T}_{f}}\left(\xi \right)\) can be regarded as proportional to the reflectance unless the temperature change is significantly large. Thus intensity of reflected probe beam, thermoreflectance signal, can be expressed as follows

$$\widetilde{Y}\left(\xi \right)=k\widetilde{{T}_{f}}(\xi )=\frac{k}{{b}_{f}\sqrt{\xi }}\times \frac{\left(1+\frac{\gamma +\sqrt{{\tau }_{r}\xi }}{1+\sqrt{{\tau }_{r}\xi }}\right){\text{exp}}(-\sqrt{{\tau }_{f}\xi })}{1-\frac{\gamma +\sqrt{{\tau }_{r}\xi }}{1+\sqrt{{\tau }_{r}\xi }}{\text{exp}}(-2\sqrt{{\tau }_{f}\xi })},$$
(18)

where \(k\) is a proportional constant. By redefining the proportional constant as \(k^{\prime} = k/b_{f}\), Eq. 18 can be expressed as follows

$$\tilde{Y}\left( \xi \right) = \frac{{k^{\prime}}}{\sqrt \xi } \times \frac{{\left( {1 + \frac{{\gamma + \sqrt {\tau_{r} \xi } }}{{1 + \sqrt {\tau_{r} \xi } }}} \right){\text{exp}}\left( { - \sqrt {\tau_{f} \xi } } \right)}}{{1 - \frac{{\gamma + \sqrt {\tau_{r} \xi } }}{{1 + \sqrt {\tau_{r} \xi } }}{\text{exp}}\left( { - 2\sqrt {\tau_{f} \xi } } \right)}},$$
(19)

As we explained in the previous work, regression analysis can be applied to Fourier coefficients of thermoreflectance signals in frequency domain [37]. Fourier coefficients of thermoreflectance signals are calculated by discrete Fourier transform (DFT).

Figure 4 shows theoretical temperature response curves under the RF configuration after periodic pulse heating derived from Eq. 19 with heat diffusion time normalized by the period \(\Delta T\), \({\Phi }_{f}={\tau }_{f}/\Delta T\) is 0.01, which is close value to heat diffusion time across a 100 nm-thick metallic thin film when \(\Delta T\) is 50 ns. The timescale in Fig. 4 is normalized by \(\Delta T\). The characteristic time \({\tau }_{r}\) is also normalized by \(\Delta T\), and a dimensionless parameter \({\Phi }_{r}={\tau }_{r}/\Delta T\) is introduced. Temperature rise is normalized by the maximum temperature rise when the thermal effusivity of the substrate is 0 (\(\gamma =1\)). The continuous curves in Fig. 4 show temperature response curves with different normalized characteristic time of interfacial thermal resistance \({\Phi }_{r}\) with \(\gamma =0\), where thermal effusivity values of the film and the substrate are same. On the other hand, the dotted curves in Fig. 4 show temperature response curves with different ratio of virtual heat sources \(\gamma\) with \({\Phi }_{r}=0\). It can be seen that \({\tau }_{r}\) affects shapes of temperature responses differently from \(\gamma\). Therefore, it is expected that both \(\gamma\) and \({\tau }_{r}\) can be determined simultaneously from the shape of observed thermoreflectance signal. Please note that, if the first layer is metallic layer like platinum, \({\Phi }_{r}=0.01\) with \(\gamma =0\) corresponds to the interfacial thermal resistance of around \(4\times {10}^{-9}\) (m2·K·W−1).

Fig. 4
figure 4

Theoretical temperature responses depend on \(\gamma\) and normalized characteristic time of interfacial thermal resistance \({\Phi }_{r}\) (\({\Phi }_{f}=0.01\))

Full size image

We measured a molybdenum thin film and a platinum thin film with a thermoreflectance apparatus PicoTR (NETZSCH-Gerätebau GmbH) under RF configuration. Each of the films was deposited on sapphire substrate by combinatorial sputtering system CMS-6420 (COMET Inc.). Figure 5a shows the structure of the films. Table 1 shows the conditions for synthesizing the films. The substrates are sapphire supplied by Furuuchi Chemical Cooperation. The surfaces are perpendicular to c-axis. Both sides are polished to flat surface with Ra (Averaged value of roughness) of 0.5 nm for the substrate of the Mo thin film. Thin film side was polished for the substrate of the Pt thin film. Both films have five steps and varies in thickness \({d}_{f}\) (about 100 nm, 125 nm, 150 nm, 175 nm, 200 nm) according to these steps. The five steps were synthesized by translation of a mask as shown in Fig. 5b. Thicknesses were measured by contact profilometer. We designed such a particular sample for this work, because in previous conventional cases where different thickness films were prepared separately and measured, additional variations can potentially be introduced because of using different substrate pieces and having separate sputtering sessions for the fabrication.

Fig. 5
figure 5

(a) Structure of thin film deposited on sapphire substrate. (b) Mechanism of combinatorial sputtering system

Full size image
Table 1 Conditions for synthesizing the films
Full size table

3 Results

The film (Fig. 5) was heated through the transparent sapphire substrate and its temperature response was detected at the open surface of the thin film as shown in Fig. 1a. Figure 6a–c show normalized thermoreflectance signals observed from 102 nm-thick step, 154 nm-thick step and 204 nm-thick step of Mo film, respectively. Figure 6d–f show normalized thermoreflectance signals observed from 104 nm-thick step, 158 nm-thick step and 213 nm-thick step of Pt film, respectively. The signals were sampled at 100 GHz sampling rate, thus the sampling interval is 10 ps. The interval of the periodic pulse \(\Delta T\) is 50 ns. We calculated the Fourier coefficient \({Y}_{n}\) from the thermoreflectance signal using DFT in the range of 0 s to 50 ns. After obtaining \({Y}_{n}\), we applied the regression analysis to the absolute value of the Fourier coefficient \(|{Y}_{n}|\) as follows

$$\left|{Y}_{n}\right|=\left|\widetilde{Y}\left({\nu }_{n},\widehat{{k}{\prime}},\widehat{{\tau }_{f}},\widehat{\gamma },\widehat{{\tau }_{r}}\right)\right|+\varepsilon ,$$
(20)

where \({\nu }_{n}\) is frequency, \(\widehat{k{\prime}}\), \(\widehat{{\tau }_{f}}\), \(\widehat{\gamma }\) and \(\widehat{{\tau }_{r}}\) are estimates of fitting parameters k′, \({\tau }_{f}\), \(\gamma\) and \({\tau }_{r}\). After estimating fitting parameters by regression analysis, \({\alpha }_{f}\), \({b}_{f}\), \({b}_{s}\) and \(R\) are determined by following equations.

$${\alpha }_{f}=\frac{{{d}_{f}}^{2}}{\widehat{{\tau }_{f}}}$$
(21)
$${b}_{f}=\sqrt{{\alpha }_{f}}{c}_{f}{\rho }_{f}$$
(22)
$${b}_{s}={b}_{f}\frac{1-\widehat{\gamma }}{1+\widehat{\gamma }}$$
(23)
$$R=\sqrt{\widehat{{\tau }_{r}}}\frac{{b}_{f}+{b}_{s}}{{b}_{f}{b}_{s}},$$
(24)

where \({c}_{f}\) is specific heat capacity of thin film and \({\rho }_{f}\) is density of thin film. Figure 7 shows the absolute value of the Fourier coefficient \(|{Y}_{n}|\) obtained from the signal in Fig. 6d and the regression curves in the frequency domain. This time, we omitted high frequency components above 4 GHz, which are relatively noisy. Tables 2 and 3 show estimates of fitting parameters \(\widehat{{\tau }_{f}}\), \(\widehat{\gamma }\) and \(\widehat{{\tau }_{r}}\) by applying least squares method to the absolutes of Fourier coefficients \(|{Y}_{n}|\) as shown in Fig. 7, thermal diffusivity of thin film \({\alpha }_{f}\) and interfacial thermal resistance \(R\) determined by the estimates of the fitting parameters. The specific heat capacity \({c}_{f}\) and density \({\rho }_{f}\) are assumed to be \(251\) (J·(kg·K)−1) and \(10 200\) (kg·m−3) for molybdenum, while \(133\)(J·(kg·K)−1) and \(21 500\) (kg·m−3) for platinum, respectively [47]. The red lines in Figs. 6 and 7 show regression curves derived from Eq. 19 in time domain and frequency domain, respectively. On the other hand, the green lines show regression curves in the case that fitting parameters \(k{\prime}\), \({\tau }_{f}\) and \({\tau }_{r}\) are estimated but \(\gamma\) is fixed at − 1, which assumes that the substrate has infinite thermal effusivity. The blue lines show regression curves in the case that fitting parameters \(k{\prime}\), \({\tau }_{f}\) and \(\gamma\) are estimated but \({\tau }_{r}\) is fixed at 0, which assumes there is no interfacial thermal resistance between the thin film and substrate. It can be seen that contributions from both \(\gamma\) and \({\tau }_{r}\) need to be considered in order to reproduce the signal with smaller deviation.

Fig. 6
figure 6

(a) Normalized thermoreflectance signal under RF configuration from the 102 nm-thick step of Mo film and regression curves in time domain. (b) Normalized thermoreflectance signal under RF configuration from the 154 nm-thick step of Mo film and regression curves in time domain. (c) Normalized thermoreflectance signal under RF configuration from the 204 nm-thick step of Mo film and regression curves in time domain. (d) Normalized thermoreflectance signal under RF configuration from the 104 nm-thick step of Pt film and regression curves in time domain. (e) Normalized thermoreflectance signal under RF configuration from the 158 nm-thick step of Pt film and regression curves in time domain. (f) Normalized thermoreflectance signal under RF configuration from the 213 nm-thick step of Pt film and regression curves in time domain (Color figure online)

Full size image
Fig. 7
figure 7

Absolute of Fourier coefficients \(\left|{Y}_{n}\right|\) of thermoreflectance signal obtained from the 104 nm-thick step of Pt film and regression curves in frequency domain (Color figure online)

Full size image
Table 2 Estimates of fitting parameters (values in parenthesis are fixed) from Mo film and thermal properties determined by the parameters
Full size table
Table 3 Estimates of fitting parameters (values in parenthesis are fixed) from Pt film and thermal properties determined by the parameters
Full size table

4 Discussion

4.1 Sensitivity Analyses

Figure 8 visualizes the sensitivity analysis for the characteristic time of interfacial thermal resistance \({\tau }_{r}\). The red curve in Fig. 8a corresponds to the regression curves in Fig. 6d. When \({\tau }_{r}\) is deviated by ± 10 %, ± 30 % and ± 50 % from the fitted value, the theoretical curve is shifted as green curves, blue curves and cyan curves in Fig. 8, respectively. Figure 8b shows the residual expression of sensitivity analyses in Fig. 8a.

Fig. 8
figure 8

(a) Sensitivity analysis of the characteristic time of interfacial thermal resistance \({\tau }_{r}\) (deviation ± 10 %, ± 30 %, ± 50 %). (b) Residual expression of the sensitivity analysis of the characteristic time of interfacial thermal resistance \({\tau }_{r}\) (deviation ± 10 %, ± 30 %, ± 50 %) (Color figure online)

Full size image

4.2 Reproducibility of Measurement

Reproducibility and uncertainty are discussed to confirm the validity of the measurement of this article for the Mo thin film and the Pt thin film sequentially. Fifteen sets of thermal diffusivity and interfacial thermal resistance values were obtained for the Mo thin film in total from each of the films as shown in Tables 4 and 5 since each of the five steps was measured three times. These tables also show average values, standard deviations and relative values of standard deviations (= SD/Average) in three measurements. It can be seen that the determination of thermal diffusivity of Mo thin film is consistent in all the steps and relative values of standard deviations are less than 2 %. The determination of interfacial thermal resistance between Mo thin film and sapphire substrate has smaller standard deviation when the film layer is relatively thin, whereas it becomes more uncertain as the layer becomes thicker. This is because, if the film layer is thick and has large heat capacity, the thermal effusion from the layer eclipses the contribution from the interfacial thermal resistance.

Table 4 All the thermal diffusivity values obtained from the whole measurement of Mo film
Full size table
Table 5 All the interfacial thermal resistance values obtained from the whole measurement of Mo film
Full size table

Fifteen sets of thermal diffusivity and interfacial thermal resistance values were obtained for the Pt thin film in total as shown in Tables 6 and 7 in the same way as the Mo thin film. It can be seen that the determination of thermal diffusivity of Pt thin film is also consistent in all the steps and relative values of standard deviations are less than 10 %. Although the tendency is semi-quantitatively similar to the Mo thin film, reproducibility of the interfacial thermal resistance of the Mo thin film is remarkably better because of the better signal-to-noise ratio of the observed signal, for example Fig. 6a of Mo film and Fig. 6d of Pt film. The difference in signal-to-noise ratio can be attributed to the difference in polishing condition between the rear surfaces of the sapphire substrates.

Table 6 All the thermal diffusivity values obtained from the whole measurement of Pt film
Full size table
Table 7 All the interfacial thermal resistance values obtained from the whole measurement of Pt film
Full size table

An experimental result of interfacial thermal conductivity between Pt and Al2O3 by the TDTR method has been reported [11]. The experimental setup was usual configuration of the TDTR measurement using a Ti sapphire laser with generative amplifier for heating and detection with optical delay system. The reported value in this study is \(8.4\times {10}^{-9}\) (m2·K·W−1) at 296 K, which is digitized from Fig. 3 in Ref. [11]. This value agrees with the interfacial thermal resistance from the 104 nm-thick step of Pt film in our study \(8.8\times {10}^{-9}\) (m2·K·W−1), which was measured at 296 K, with smaller deviation than 5 %.

As described in the discussion of reproducibility the interfacial thermal resistance values measured by five steps of different thickness of Mo/sapphire sample, interfacial thermal resistance values agreed each other within 5 %. Since observed signal is proportional to temperature change under one-dimensional heat diffusion condition, and the fitted equation is exact analytical solution of one-dimensional heat diffusion after periodic impulse heating, it is difficult to consider that this agreement is realized by chance. As shown in Fig. 6a–f, the observed signals are successfully fitted by the analytical which has only four parameters including amplitude over the entire pulse period. These consistency and agreement can be considered as supporting the validity of measurement, analysis equation and fitting procedure.

5 Conclusion

In this paper, we investigated a new analytical solution for thermoreflectance method, which considers the contribution from interfacial thermal resistance between thin film and substrate. By applying Fourier expansion analysis to thermoreflectance signals, we could determine quantitatively interfacial thermal resistance and thermal diffusivity of thin film at the same time by single measurements. Metallic (Mo and Pt) thin films with five steps (about 100 nm, 125 nm, 150 nm, 175 nm, 200 nm) were deposited on sapphire substrate to evaluate the reproducibility of determination. The reproducibility of thermal diffusivity measurement is within 10 % in standard deviation for all the steps of five thicknesses, whereas reproducibility of interfacial thermal resistance measurement is within 10 % in standard deviation for two steps (about 100 nm, 125 nm). This approach can be easily extended to analyze more complicated samples like multi-layered thin films.