1 Introduction

In many areas of chemical, biological, and energy engineering, mixtures consisting of liquids with dissolved gases are important working fluids. Processes where the working fluid consists of a liquid with a dissolved gas are, e.g., the synthesis of methanol or dimethyl ether from synthesis gas [1, 2], algae production in photobioreactors [3] as well as waste-water treatment and management [4]. For the efficient design and optimization of such processes, the thermophysical properties of the involved fluid mixtures are required at process-relevant thermodynamic states in terms of temperature T, pressure p, and composition. Here, the viscosity and interfacial tension, which are addressed within this work, are important thermophysical properties characterizing liquids with dissolved gases. The dynamic viscosity η, for example, characterizes the flow field in reactors and pipes and determines the power requirements for pumps and mixers. It is also incorporated in many dimensionless numbers like the Reynolds, Prandtl, or Schmidt number, which are important characteristic numbers for the engineering of apparatuses. In addition, the interfacial tension σ is essential for describing wetting behavior and mass transfer at gas–liquid interfaces and enters into dimensionless numbers like the hydrodynamic Weber or Marangoni number.

Due to the large amount of possible combinations of solvent and solute types, coupled with a wide range of thermodynamic states that is of interest for the different applications, the investigation of η and σ for each thermodynamic state by experiments or computer simulations is not feasible. Therefore, corresponding fluid-property models connecting the property of interest with other thermophysical and/or molecular properties must be developed. For this task, a wide variability of solvent and solute types with different molecular characteristics like weight, size, and polarity must be included in the training sets for their development. Once the models are established, they can be tested for the prediction of the thermophysical properties of systems which have not been included in the development step. For both the development and validation of the models, accurate and reliable experimental data for the thermophysical properties are required.

For the experimental determination of the liquid dynamic viscosity ηL and the interfacial tension σ, the surface light scattering (SLS) technique was used. It probes the dynamics of surface fluctuations at phase boundaries in a contactless manner via the analysis of the temporal behavior of the intensity of the scattered light. Based on a full treatment of the hydrodynamic theory for surface fluctuations [5, 6], viscosity and surface or interfacial tension can be accessed in an absolute way in macroscopic thermodynamic equilibrium without the need for a calibration procedure [7,8,9]. Until today, SLS investigations have contributed to the accurate determination of viscosity and surface or interfacial tension of various fluid types including reference fluids [7, 9], refrigerants [10,11,12], ionic liquids [13,14,15,16], liquid organic hydrogen carriers [17, 18], and liquids with dissolved gases [19, 20] with typical uncertainties of 2% (coverage factor k = 2) over a broad range of thermodynamic state.

To complement experimental methods such as light scattering techniques, molecular dynamics (MD) simulations have proven to be a valuable tool in thermophysical property research [19, 21,22,23,24,25,26]. MD simulations provide not only the access to multiple thermophysical properties, but they can also be applied to thermodynamic states which can hardly be studied experimentally and allow an insight into the fluid structure on a molecular level. The latter-most advantage is valuable for the identification of structure–property relationships, which can be utilized for the development of prediction models [21, 27, 28]. Equilibrium molecular dynamics (EMD) simulations, which are used in this work, allow the determination of equilibrium and transport properties by analyzing molecular motion under equilibrium conditions [29,30,31].

The present work represents a continuation of an ongoing research project at the Institute of Advanced Optical Technologies—Thermophysical Properties (AOT-TP) at the Friedrich-Alexander-Universität Erlangen-Nürnberg. This project aims at the characterization of long-chained hydrocarbons, alcohols, and their mixtures with dissolved gases by the determination of viscosity and surface or interfacial tension over a wide range of thermodynamic states via SLS and EMD simulations. In a first step, a temperature-dependent modification of the L-OPLS force field (FF) [32, 33] served for improved predictions of the liquid density ρL, ηL, and σ of 12 pure solvents up to T = 573 K [34]. Based on this modified FF, ρL, ηL, and σ of binary liquid mixtures of n-hexadecane with n-octacosane, 2,2,4,4,6,8,8-heptamethylnonane (HMN), or 1-hexadecanol [35] and, most recently, ηL and σ of binary mixtures consisting of the solvent n-hexadecane and the six dissolved gases investigated in this study as well as nitrogen (N2) were investigated by SLS and EMD simulations between (303 and 573) K [20]. In the present work, ηL and σ of various binary mixtures consisting of a liquid with a dissolved gas are determined using SLS experiments and EMD simulations up to T = 573 K and mole fractions of the dissolved gas in the liquid phase up to 0.2. As solvents, linear and branched alkanes and alcohols of varying carbon numbers as well as two representatives of cyclic hydrocarbon-based liquid organic hydrogen carriers (LOHCs) are investigated to cover a wide range of molecular size and weight as well as polarity. In detail, 1-hexadecanol, 2-butyl-1-octanol, HMN, 2,6,10,15,19,23-hexamethyltetracosane (squalane), n-octacosane, n-triacontane, and the LOHC reference system consisting of diphenylmethane (DPM) and its hydrogenated analog dicyclohexylmethane (DCM) are selected. As the solutes, hydrogen (H2), helium (He), methane (CH4), water (H2O), carbon monoxide (CO), and carbon dioxide (CO2) were chosen for their variety in size, weight, sphericity, and polarity. For binary mixtures of DCM with dissolved CO2, where no experimental data for the solubility are given in the literature, measurements using the isochoric-saturation method are performed in addition to the SLS and EMD investigations.

In the following, a brief background on the theory, the experimental procedure, and the data evaluation for the SLS technique is given, followed by information about the density and solubility measurements. Afterward, information relevant for the EMD simulations including the data evaluation are presented. Using the experimental and simulated results for ηL and σ, the influence of the molecular characteristics of the solvent and solute on the thermophysical properties of the mixture is discussed. The influence of the molecular characteristics of the dissolved gas is analyzed by comparing the results for binary mixtures consisting of the six different gases dissolved in either n-octacosane or 1-hexadecanol. Results from our previous publications for ηL and σ of the pure solvents are also used to quantify the influence of the dissolved gas on ηL and σ of the binary mixtures. The influence of the molecular characteristics of the solvent is analyzed by comparing the results for binary mixtures consisting of the solutes He or CO2 dissolved in various solvents. Because no experimental data for the binary mixtures investigated in this work are currently available in the literature, to the best of our knowledge, a direct comparison with further investigations is not possible.

2 Experimental Section

2.1 Materials and Sample Preparation

The names, sources, purities in mass fraction w or volume fraction φ as specified by suppliers, CAS numbers, and molar masses M of all substances used in this work are provided in Table 1. The procedure for synthesizing DCM is detailed in the Supporting Information of Ref. 18. All solvents were filtered with a polytetrafluoroethylene filter with a pore size of 220 nm to remove particle-like impurities. After filtration, the solvent is then degassed at 313 K at p below 100 Pa for approximately 3 h and stored under an argon atmosphere for further usage. The substances n-octacosane and n-triacontane are filtered and degassed at approximately 20 K above their respective normal melting point. For each mixture, a fresh sample of approximately 40 mL of the solvent is filled into the cleaned sample cell under ambient conditions. The vapor phase is removed using a vacuum pump before introducing the investigated gas for each system. The systems containing the gases He or H2 are investigated with constant total p of around (3.5 and 7.0) MPa across the complete T range. With dissolved CH4, CO, or CO2, p is varied to maintain a constant mole fraction x of dissolved gas of 0.1 and 0.2, 0.05 and 0.1, and 0.1 and 0.2, respectively. For mixtures containing H2O, where the mole fraction x of H2O directly after the sample preparation was approximately 0.04 and 0.08, both components were weighed on a balance with an expanded uncertainty (k = 2) of 1 mg and added to the sample cell under an argon atmosphere at ambient conditions. The uncertainty of xH2O due to the uncertainty of the balance is U(xH2O) = 0.0004. The composition of each mixture is given in Table 2 together with the results for ηL and σ.

Table 1 Specifications of the chemical supplier, molar mass M, purification method, and purity of the investigated solvent and solutes
Full size table
Table 2 Liquid dynamic viscosity ηL and interfacial tension σ of the binary mixtures of 1-hexadecanol, 2-butyl-1-octanol, HMN, squalane, n-octacosane, n-triacontane, or DCM with dissolved He, CO2, CO, CH4, H2, or H2O obtained by SLS under saturation conditions as well as the estimated solute mole fraction in the liquid phase xsolute, the liquid density ρL, vapor ensity ρV, and the vapor viscosity ηV for each investigated temperature T and pressure pa
Full size table

2.2 Isochoric-Saturation Method Combined with Vibrating-Tube Densimetry: Liquid Density and Solubility

Since no data were available for the solubility of CO2 in DCM, corresponding measurements using the isochoric-saturation method [36] were performed. The experimental setup includes a vibrating-tube densimeter DMA 4200 M from Anton Paar, which was used to determine ρL of the binary mixtures. The solubility and ρL were measured at p up to 7.1 MPa and T between (323 and 473) K. The results were used to develop a correlation for xCO2 and ρL as a function of T and p, which was used to calculate the input parameters for the SLS experiments as given in Table 2. More detailed information on these measurements, the final results for xCO2 and ρL, and their correlations as function of T and p are given in the Supporting Information.

2.3 Surface Light Scattering: Liquid Viscosity and Interfacial Tension

The liquid dynamic viscosity ηL and interfacial tension σ are simultaneously determined in an absolute way at macroscopic thermodynamic equilibrium by surface light scattering (SLS). With this technique, photon correlation spectroscopy is used to analyze the temporal behavior of the light scattered from surface waves which are caused by the thermal motion of molecules. The results for ηL and σ are determined by a full solution of hydrodynamic theory for surface fluctuations at the boundary between a liquid phase (subscript L) and a vapor phase (subscript V) given by the dispersion equation D(ηL, ηV, ρL, ρV, σ, Γ, ωq, q). Here, ρL, ρV, and ηV refer to the liquid density, vapor density, and vapor viscosity, while Γ and ωq describe the damping and the frequency of the surface wave with a specific modulus of the wave vector q. The reader is referred to the literature [5, 6] as well as to our previous studies [9, 37,38,39,40,41] for a detailed description of the theory and application of this technique. A summary of the details relevant for this work is provided below.

For systems with relatively small viscosities and/or large interfacial tensions, as is the case for most measurements in this work, the probed surface fluctuations showed an oscillatory behavior. In this case, a simultaneous determination of ηL and σ is possible by the measured values for damping and frequency reflecting a damped oscillation of the normalized correlation function (CF) of the intensity of the scattered light. For the mixtures of 2-butyl-1-octanol with He at the lowest temperature T = 298 K and the mixtures of squalane with dissolved He at the lowest two temperatures T = (298 and 323) K, the surface fluctuations did not propagate (ωq = 0) and the measured CF is associated with two exponentially decaying modes. By disregarding the short-time range of the measured CF where a faster mode of weaker signal strength is present, the second exponential was analyzed with respect to its damping Γ, which is used to determine in a first-order approximation the ratio of σ to ηL. To get access to ηL, data for σ determined at elevated T, where an oscillatory behavior was observed, are correlated with respect to T using a second-order polynomial function and extrapolated to the lower T, where an overdamped behavior was observed. In this way, values for σ can be calculated and used as a further input parameter within the dispersion relation to calculate ηL.

Mixtures containing the dissolved gases H2, CH4, and CO were investigated within an experimental SLS setup which contains safety measures for handling toxic and explosive gases. All other mixtures are investigated with the experimental setup detailed in our previous study. For the mixtures containing He, CO2, and H2O, the combined expanded uncertainty (k = 2) for T accounting for the difference of the two T probes is estimated to be U(T) = 0.02 K at 298 K and U(T) = 0.8 K at 573 K and can be interpolated linearly in between. For the mixtures containing dissolved CO, CH4, and H2, U(T) is 0.09 K at 348 K and 0.3 K at 573 K and can be interpolated linearly in between. For all mixtures, the overall relative uncertainty for the reported pressure, which includes the pressure stability during a measurement series, is 0.5% (k = 2). In heterodyne SLS experiments where the light scattered by the vapor–liquid interface is superimposed with frequency-unshifted reference light of distinctly larger intensity, six different external angles of incidence relative to the normal of the interface \(\Theta_{{\text{E}}}\) were adjusted between (2.5 and 4.0)° in this work.

2.3.1 Data Evaluation

In addition to q, Γ, and, for an oscillatory behavior, also ωq of the observed surface fluctuations, the liquid and vapor densities, and the vapor viscosity are required input parameters for solving the dispersion relation in order to determine ηL and σ.

In our previous publication on binary mixtures consisting of n-hexadecane and different dissolved gases [20], the influence of the dissolved gas on ρL was investigated considering experimental data for binary mixtures of n-hexadecane with dissolved CO2, CH4, or He. Here, only a small influence of the dissolved gas on ρL relative to ρL of pure saturated n-hexadecane was found, with an average absolute relative deviation (AARD) between the densities of (0.57, 0.30, and 0.79)% for the solutes He, CO2, and CH4, respectively, for T between (298 and 473) K. The relatively small impact of the dissolved gas on ρL can be explained by the relatively small molecule size and weight of the solute in comparison to the solvent.

With the exception of the binary mixture consisting of DCM and CO2, where experimental values for ρL are presented in this work, no experimental data for ρL are available for any of the present binary mixtures. Since the solvents investigated in this work have the same or even higher molar mass than n-hexadecane, it is assumed that the influence of the dissolved gas is similar or even smaller for the present binary mixtures. Therefore, the influence of the dissolved gas on ρL was neglected and ρL data of the pure solvents [34] were used as input for solving the dispersion relation. To account for the error that arises from this assumption, the uncertainty of ρL was estimated to be 1% in the T range between (298.15 and 473.15) K and 1.5% for T of (523.15 and 573.15) K where the experimental data for ρL are extrapolated. In case that ρL becomes available for the mixtures for which the pure-component ρL data were used as input for the dispersion equation, the values for ηL and σ reported in this work can be corrected using the expressions ηL,new = ηL,this work·ρL,new·ρL,this work−1 and σnew = σthis work·ρL,new·ρL,this work−1.

The strategy for calculating vapor phase properties ηV, ρV, and vapor phase composition is identical to our previous work [20]. Estimated relative expanded uncertainties (k = 2) for ηV and ρV are assumed to be (10 and 5)%, respectively [42]. The composition of the liquid phase was obtained from experimental solubility data from the literature [43,44,45,46]. Where the solubility data do not cover the entire T range up to 573.15 K, linear fits between the solute partial pressure and the mole fraction of dissolved gas were used for the extrapolation to high T. For the mixtures containing CO2 dissolved in n-triacontane, no solubility data are available in the literature. Here, solubility data for CO2 dissolved in n-octacosane, which has a similar M compared to n-triacontane, were used to estimate the amount of dissolved CO2 at the given p. Since no solubility data are available also for the binary mixtures consisting of HMN, n-triacontane, squalane, or 2-butyl-1-octanol with dissolved He, they were investigated at a constant p of (3.5 and 7.0) MPa. Here, the corresponding concentration of He in the liquid phase can be calculated using the specified T and p given in Table 2, should solubility data become available.

The mixtures containing H2O were investigated as closed systems, where p was monitored during experiments. Due to a lack of solubility data for the mixtures of H2O and n-octacosane, liquid and vapor compositions were estimated through an iterative calculation scheme detailed in our previous publication [20].

Reported uncertainties in ηL and σ were calculated via an error propagation scheme [37, 39] considering uncertainties introduced by the measured variables and adopted reference data or predictions. Total expanded relative measurement uncertainties (k = 2), averaged over all investigated systems and thermodynamic states, were determined to be Ur(ηL) = 2.4% and Ur(σ) = 2.3%.

3 EMD Simulations

EMD simulations give access to multiple thermophysical properties by studying the dynamics of atoms and molecules in simulation boxes with a typical side length of a few nanometers. The accuracy of the calculated properties strongly depends on the inter- and intramolecular interactions, which are described by a force field (FF) via atomistic pair-wise potentials. Using a reasonable FF description, the energies and forces between atoms and molecules can then be calculated for each discretized time step of around 1 fs over a total simulation time in the range of (50 to 300) ns for the investigation of transport properties such as viscosity. These calculations are based on classical Newtonian equations of motion. For a detailed description of the underlying theory of EMD simulations, the reader is referred to the respective literature [29,30,31].

For modeling the solvent molecules studied in this work, the modified version of the L-OPLS FF [34] was taken. This FF is built on the original L-OPLS FF [32, 33] and was modified to better represent equilibrium and transport properties over a wide T range up to 573.15 K by incorporating a T dependency of the Lennard–Jones (LJ) energy parameters. The successful transferability of the modified FF from pure solvents to related mixtures was shown in our previous publications containing results for ηL and σ of binary liquid mixtures [18, 35] as well as mixtures consisting of n-hexadecane with dissolved gases [20]. The FFs for the solutes were the same as those in our previous publications [20].

3.1 Simulation Procedure and Data Evaluation

For detailed information on the simulation procedure as well as the data evaluation for ηL and σ, the reader is referred to our previous publications [20, 34, 35]. In the following, only the details relevant for the simulations in the present work are summarized.

All simulations presented in this work were performed using the GROMACS [47] software package version 5.1.2. In agreement with the original L-OPLS FF [32, 33], the simulation time step was set to 2 fs and the bonds between the lighter hydrogen atoms and the heavier carbon or oxygen atoms were constrained using the LINCS [48] algorithm. To initialize the simulation boxes, a number of solvent molecules resulting in approximately 30,000 atoms were placed in a cubic simulation box and periodic boundary conditions were established to mimic the bulk behavior. Afterward, solute molecules were added to match the compositions from the SLS experiments. In the cases of HMN, n-triacontane, squalane, or 2-butyl-1-octanol with dissolved He where no solubility data are available, the solubility data from the binary mixture of n-hexadecane and He [20] were taken to estimate the amount of He dissolved in the liquid phase. To prevent that a possible phase separation during the simulation run falsifies the results, p in the simulations for the calculation of the viscosity was set to be 0.2 MPa above the corresponding saturation p, i.e., in the slightly compressed liquid phase. The following energy minimization, equilibration with respect to T and p, as well as the calculation of ηL and σ are identical to our previous publication [20].

The simulations were performed at T = (298.15, 323.15, 348.15, 373.15, 423.15, 473.15, and 573.15) K, while the starting T was adjusted to the melting point of the solvent. The results for η and σ are the average values from three different, independent simulation runs and are reported, together with the thermodynamic state, in Table S4 in the Supporting Information. The stated uncertainties are the double standard deviations (k = 2) of the three independent simulation runs.

4 Results and Discussion

The results for ηL and σ for all binary mixtures investigated by SLS experiments, together with the input parameters for solving the dispersion relation and their expanded experimental uncertainties, are summarized in Table 2. To study the concentration dependency of ηL and σ, two different mole fractions of the solute xsolute were studied experimentally. Here, the binary mixtures with gases of low solubility, i.e., H2 and He, were studied at fixed p of about (3.5 and 7.0) MPa, while the more soluble gases CH4, CO, and CO2 were investigated at fixed xsolute of the dissolved gas. Here, xsolute is 0.1 and 0.2 in the case of CH4 and CO2, while it is 0.05 and 0.1 for CO. This differentiation was necessary due to the limitation of p at high T in our SLS setup. While the real mole fraction of dissolved gas is given in Table 2, an approximate xsolute for each mixture is used in the discussion for convenience.

In the following, the results for ηL and σ of the binary mixtures investigated by SLS and EMD simulations are shown and discussed. The data for ηL and σ calculated from EMD simulations, together with their thermodynamic states and statistical uncertainties, are given in Table S4 in the Supporting Information. For a direct comparison between the results from SLS and EMD for the binary mixtures studied within this work, the results from both techniques that were performed at the same thermodynamic state are shown in the form of a parity plot in Fig. 1.

Fig. 1
figure 1

Comparison of the liquid dynamic viscosity ηL (top) and interfacial tension σ (bottom) of all binary mixtures studied in this work by EMD and SLS. Statistical expanded uncertainties (k = 2) are shown only exemplarily for the results from EMD simulations

Full size image

For both ηL and σ, a general overprediction of the results independent of the absolute value, and therefore T, by EMD simulations is found. The average relative deviation of the results from EMD simulations from the results from SLS is (27 and 13)% for ηL and σ. This is in agreement with the general overprediction of EMD simulations when applying the modified L-OPLS FF [32,33,34] found for the pure solvents [34], binary liquid mixtures [35], and mixtures consisting of n-hexadecane and different dissolved gases [20, 32,33,34]. Despite these deviations, it is still possible to investigate the influence of the dissolved gas on both thermophysical properties also by EMD simulations by comparing the results for the binary mixtures to the simulated pure solvent properties. Therefore, for the following discussion of the influence of the molecular characteristics of the solvent and solute molecules on the thermophysical properties of the mixtures, results for the binary mixtures from SLS are compared to the pure solvent properties measured by SLS, while the simulated results for the mixtures are compared to the simulated results of the pure solvent. For the latter, the T-dependent correlations for ηL and σ from EMD simulations are given in the Supporting Information.

4.1 Viscosity

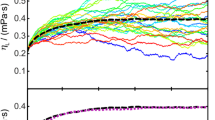
The results for ηL for the binary mixtures consisting of n-octacosane with dissolved H2, CH4, H2O, CO, or CO2 from SLS experiments (left) and EMD simulations (right) are shown in the upper part of Fig. 2. In addition, the results for ηL of pure n-octacosane determined by SLS [39] and EMD simulations [34] and represented by corresponding T-dependent correlations are shown in Fig. 2. As can be seen, the binary mixtures exhibit a similar T-dependent behavior for ηL as the pure solvent. To study the influence of the solute in more detail, the relative deviation of the viscosity of the binary mixtures from that of pure n-octacosane is given in the lower part of Fig. 2, which will be discussed in the following.

Fig. 2
figure 2

taken from Tables 2 and S4

(Top) Liquid dynamic viscosity ηL of the binary mixtures of n-octacosane with the dissolved gases H2, CH4, H2O, CO, or CO2 by SLS (left) and EMD simulations (right) as a function of T and solute mole fraction (open and closed symbols). For comparison, the correlations for ηL of pure n-octacosane from SLS [39] and EMD simulations [34] are shown (solid lines). (Bottom) Relative deviations of ηL of the binary mixtures from ηL of pure n-octacosane. The dotted lines mark the average expanded uncertainty (k = 2) of the data for pure n-octacosane. Error bars are shown only exemplarily for the mixtures containing H2 for clarity. The mole fractions of the dissolved gas given in the legend are approximate values. The real composition at each T can be

Full size image

The binary mixtures containing H2, H2O, and CO show ηL values which agree within combined uncertainties with those of pure n-octacosane over the entire T range. For an adequate analysis of this behavior, information about the influence of p on ηL of the pure n-octacosane is required. Since no p-dependent data are available for ηL of n-octacosane, the influence of p on ηL is estimated with the help of n-hexadecane. Here, the correlation developed by Meng et al. [49] implemented in the REFPROP database [50] shows an increase in ηL of about (7 and 11)% at p = (3.5 and 7.0) MPa for T = 298.15 K. At T = 573 K, this increase in ηL amounts to (8 and 16)% at p = (3.5 and 7.0) MPa. This means that the solutes H2, H2O, and CO seem to suppress the p-dependent increase of ηL. The binary mixtures containing CH4 or CO2 and studied at elevated p, on the other hand, even have a smaller ηL than pure n-octacosane with deviations up to 13%. These results are in qualitative agreement with the investigations for binary mixtures consisting of the same solutes dissolved in further linear alkanes like n-hexadecane [20, 51] as well as systems consisting of CO2 dissolved in n-heptane [52] or n-tetradecane [53]. A clear difference between the results based on n-hexadecane and n-octacosane is that the relative deviations are by trend smaller and less dependent on T in the case of n-octacosane. This smaller impact of the dissolved gas can be explained with the larger molecule size of n-octacosane and, therefore, a stronger entangling at high T where the molecules tend to switch from a cis- to trans-configuration [21, 27]. This entangling of n-octacosane molecules leads to more interstitial space in the fluid structure where the solute molecules can accumulate without hindering the intermolecular interactions between the n-octacosane molecules.

The results for ηL from EMD simulations given in the right part of Fig. 2 show that the simulations are not able to resolve the influence of the dissolved gas on ηL considering their uncertainties. Relatively large statistical expanded (k = 2) uncertainties of ηL of about 15% are typically found in connection with large molecules such as n-octacosane, which was already highlighted in the literature [25, 32, 34]. Since the changes in ηL of the binary mixtures relative to the viscosities of pure n-octacosane determined by SLS experiments are within 15%, they fall within the expanded statistical uncertainty of the results from EMD simulations.

Next to the rather non-polar n-octacosane, also the linear alcohol 1-hexadecanol featuring a polar terminal hydroxyl group was chosen as a solvent to investigate the influence of the solute on ηL and σ of the binary mixtures. For this, binary mixtures consisting of 1-hexadecanol with dissolved H2, CH4, H2O, or CO were investigated by SLS and EMD simulations. The results for ηL for these binary mixtures from SLS (left) and EMD simulations (right) are shown in the upper part of Fig. 3. Additionally, the results for ηL of pure 1-hexadecanol investigated by SLS [34] and EMD simulations [34] are shown in Fig. 3. As for the mixtures based on n-octacosane, the influence of the solute was examined by calculating the relative deviation of ηL of the binary mixture from that of pure 1-hexadecanol, which is shown in the lower part of Fig. 3.

Fig. 3
figure 3

taken from Tables 2 and S4

(Top) Liquid dynamic viscosity ηL of the binary mixtures of 1-hexadecanol with the dissolved gases H2, CH4, H2O, CO, or CO2 by SLS (left) and EMD simulations (right) as a function of T and solute mole fraction (open and closed symbols). For comparison, the correlations for ηL of pure 1-hexadecanol from SLS [39] and EMD simulations [34] are shown (solid lines). (Bottom) Relative deviations of ηL of the binary mixtures from that of pure 1-hexadecanol. The dotted lines mark the average expanded uncertainty (k = 2) of the data for pure 1-hexadecanol. Error bars are shown only exemplarily for the mixtures containing H2 for clarity. The mole fractions of the dissolved gas given in the legend are approximate values. The real composition at each T can be

Full size image

For the three gases H2, CH4, and CO dissolved in 1-hexadecanol, the influence of the dissolved gas on ηL determined by SLS is similar as found for the corresponding mixtures based on n-octacosane. While the data for mixtures containing H2 were within combined uncertainties with those for the pure solvent in the case of n-octacosane, the difference is more pronounced but still within 5% in comparison with pure 1-hexadecanol at 0.1 MPa. For the solutes CO and CH4, a reduction in ηL with maximum deviations of (11 and 19)% from the pure solvent is found, which is similar to the results for mixtures with n-hexadecane [20]. In the case of the solute H2O, however, the binary mixtures show larger values for ηL in comparison to the pure solvent, while the results for mixtures based on n-octacosane or n-hexadecane [20] agreed within combined uncertainties with those of the pure solvents at 0.1 MPa. The difference between the data for the mixture and the pure solvent increases strongly with increasing T and reaches a maximum deviation of 37% at the largest investigated T of approximately 573 K. A possible explanation for the much stronger influence of H2O on ηL of 1-hexadecanol in comparison to the linear alkanes can be found in the formation of hydrogen bonds between the solute and solvent molecules in the bulk of the liquid phase. This agrees with the findings of Ono et al. [54], who showed also an increase of ηL with increasing amount of dissolved H2O in short primary alcohols especially at high T. An explanation why dissolved H2O has a much stronger influence at higher T can be found in the work of Lenahan et al. [35]. Here, the authors applied EMD simulations to study the hydrogen bonding between 1-hexadecanol molecules in a binary mixture with n-hexadecane as function of T. The results show that strong hydrogen bonds exist between 1-hexadecanol molecules at low T, which vanish with increasing T. The effect of a decreasing amount of hydrogen bonds with increasing T can be explained by the tendency of long molecules to bend at high T, which hinders the formation of hydrogen bonds due to the steric effect of the alkane tails. With respect to the findings in this work, this means that at low T hydrogen bonds between 1-hexadecanol and H2O molecules are less likely since the 1-hexadecanol molecules are already forming hydrogen bonds with other 1-hexadecanol molecules. At increasing T, more 1-hexadecanol molecules are available to form hydrogen bonds with H2O molecules, which leads to an increase in ηL.

The results from EMD simulations, which are shown in the right-hand side of Fig. 3, cannot resolve the influence of the dissolved gas on ηL of the hexadecanol-based mixtures considering the simulated uncertainties. Especially the trend observed by SLS that H2O causes an increase in ηL of the mixture in comparison to pure 1-hexadecanol is not reflected by the EMD simulations. One possible explanation for this is that the H2O FF does not consider any T dependency in the FF parameters, which can lead to strong deviations in the predicted properties especially at high T. In the case of the solute CH4, the EMD simulations predict an average deviation in ηL from the pure solvent with approximately (18 and 20)% for the mixtures with xsolute = 0.1 and 0.2 over the entire T range. This agrees with the results from SLS experiments which show a reduction in ηL over the entire T range with an average deviation of (9.3 and 14)% for xsolute = 0.1 and 0.2.

To study the influence of the molecular characteristics of the solvent on the thermophysical properties of the mixtures, binary systems consisting of either He or CO2 dissolved in various solvents were investigated by SLS and EMD simulations. The results for ηL for the binary mixtures consisting of He dissolved in HMN, 2-butyl-1-octanol, squalane, or n-triacontane from SLS (left) and EMD simulations (right) are shown in the upper part of Fig. 4. For comparison, also the results for ηL of the pure solvents investigated by SLS [34] and EMD simulations [34] are shown in Fig. 4. To investigate the influence of the solute on ηL for different solvents, the relative deviations of the viscosity of the binary mixtures from that of the pure solvents at 0.1 MPa are given in the lower part of Fig. 4.

Fig. 4
figure 4

(Top) Liquid dynamic viscosity ηL of the binary mixtures consisting of He dissolved in HMN, 2-butyl-1-octanol, squalane, or n-triacontane investigated by SLS (left) and EMD simulations (right) as a function of T and He pressure (open and closed symbols). For comparison, ηL of the pure solvents investigated by SLS [34] and EMD simulations [34] are shown (solid lines). (Bottom) Relative deviations of ηL of the binary mixtures from ηL of the pure solvents. The dotted lines mark the average expanded uncertainty (k = 2) of the properties for the pure solvents. Error bars are shown only exemplarily for the mixtures based on squalane for clarity

Full size image

The SLS results depicted in Fig. 4 show that the data for ηL of the binary mixtures based on the solvents HMN, squalane, and n-triacontane are mostly within combined uncertainties of the values for the pure solvents. Only for the mixtures investigated at p = 7.0 MPa, a somewhat larger increase of ηL with respect to the pure solvent of up to 10% can be observed. In the case of the binary mixtures based on 2-butyl-1-octanol, the largest increase is visible for both binary mixtures and amounts up to about 14% at T = 298 K and p = 7.0 MPa. The stronger influence of dissolved He in 2-butyl-1-octanol on the viscosity in comparison with the other solvents may be attributed to the branched character of the molecule and the effect of p. In comparison to the pure solvent at 0.1 MPa, the increased p present for the mixtures leads to a smaller distance between the molecules, which leads to a stronger entangling due to the side chains in the branched molecules. Because p-dependent data for the ηL of pure 2-butyl-1-octanol are still lacking in the literature, this interpretation cannot be supported. For the branched solvents HMN and squalane, this effect is smaller since they have multiple methyl side chains, which leads to a more compact structure and less entangling.

Also for the EMD simulations, Fig. 4 shows that the results for the binary mixtures are mostly within combined uncertainties of ηL with the pure solvents. The only exception is ηL of the binary mixture based on squalane investigated at T = 348.15 K, where an approximately 31% larger ηL for the binary mixture in comparison to pure squalane is predicted by the EMD simulations. The results from SLS, on the other hand, show only a difference between the binary mixture and pure squalane of about 10% at this T. As already shown for the binary mixtures based on n-octacosane or 1-hexadecanol, this demonstrates that the EMD simulations are not able to quantitatively predict the influence of the dissolved gas on ηL.

To investigate the influence of the solvent characteristics on ηL in connection with a more soluble gas than He, binary mixtures consisting of CO2 dissolved in the hydrocarbons n-octacosane, n-triacontane, or DCM were investigated by SLS and EMD simulations. The results for ηL are shown in the upper part of Fig. 5. Additionally, the binary mixtures consisting of DPM with dissolved CO2 at xCO2 = 0.1 or 0.2 were investigated by EMD simulations for T = (323.15 to 573.15) K. For comparison, also the results for ηL of the pure solvents determined by SLS [17, 34, 39] and EMD simulations [34] are shown in Fig. 5. Relative deviations of ηL of the binary mixture from that of the pure solvents are given in the lower part of Fig. 5.

Fig. 5
figure 5

taken from Tables 2 and S4

(Top) Liquid dynamic viscosity ηL of the binary mixtures consisting of CO2 dissolved in n-octacosane, n-triacontane, or DCM investigated by SLS (left) and EMD simulations (right) as a function of T and CO2 mole fraction (open and closed symbols). In the case of EMD simulations, also binary mixtures based on DPM were investigated and are shown. For comparison, the correlations for ηL of the pure solvents based on data obtained by SLS [17, 34, 39] and EMD simulations [34] are shown (solid lines). (Bottom) Relative deviations between the binary mixtures and the pure solvents. The dotted lines mark the average expanded uncertainty (k = 2) of the viscosity of the pure solvents. Error bars are shown only exemplarily for the mixtures based on n-octacosane for clarity. The mole fractions of the dissolved gas given in the legend are approximate values. The real composition at each T can be

Full size image

The results in Fig. 5 from SLS show a clear reduction in ηL by adding dissolved CO2 to the three investigated solvents. For the solvent n-octacosane, the two binary mixtures show deviations from the pure solvent in the range between − (3 and 10)%, while the deviation decreases only slightly with increasing xCO2. In the case of n-triacontane, the deviation is larger and ranges between − (10 and 20)%. For both solvents, the absolute deviation of ηL of the mixture from that of the pure solvent decreases with increasing T. For the binary mixtures based on DCM, the reduction in ηL is more pronounced and ranges up to − 46% for the lowest investigated T and xCO2 = 0.2. Also in the case of DCM, the deviations decrease with increasing T with approximately  − 24% at the largest investigated T of 473 K. The general trend of a decrease in the difference between ηL for the binary mixtures and that for the pure solvents, which was also found for mixtures consisting of CO2 dissolved in n-hexadecane [20, 51], can be explained by a decrease in ρL with increasing T. This means that at elevated T, the CO2 molecules can easier occupy the interstitial space in the fluid structure that is created as a result of the decreasing ρL. Therefore, the CO2 molecules seem to disturb the intermolecular interactions between the solvent molecules in a less pronounced way with increasing T.

Also in the case of binary mixtures based on dissolved CO2, EMD simulations are not able to quantitatively predict the influence of dissolved CO2 on ηL of the mixtures when compared to the experimental results. The only exception is the binary mixture based on DCM with xCO2 = 0.2, where the largest difference between the mixture and the pure solvent is found. Here, EMD simulations predict a reduction in ηL between (40 and 28)% in the range from T = (323.15 to 473.15) K, which is in good agreement with the observations from SLS.

4.2 Interfacial Tension

Figure 6 shows the results for σ of the binary mixtures consisting of n-octacosane with dissolved H2, CH4, H2O, CO, or CO2 from SLS experiments (left) and EMD simulations (right). In addition, the results for σ of pure n-octacosane determined by SLS [39] and EMD simulations [34] represented by a corresponding T-dependent correlation are shown in Fig. 6. A more detailed resolution of the influence of the solute on σ is provided by the relative deviations of σ of the binary mixture from that of pure n-octacosane, which are given in the lower part of Fig. 6 and will be discussed in the following.

Fig. 6
figure 6

taken from Tables 2 and S4

(Top) Interfacial tension σ of the binary mixtures of n-octacosane with the dissolved gases H2, CH4, H2O, CO, or CO2 by SLS (left) and EMD simulations (right) as a function of T and solute mole fraction (open and closed symbols). For comparison, the correlations for σ of pure n-octacosane based on data from SLS [39] and EMD simulations [34] are shown (solid lines). (Bottom) Relative deviations of σ of the binary mixtures from σ of pure n-octacosane. The dotted lines mark the average expanded uncertainty (k = 2) of pure n-octacosane. Error bars are shown only exemplarily for the mixtures containing H2 for clarity. The mole fractions of the dissolved gas given in the legend are approximate values. The real composition at each T can be

Full size image

In connection with the SLS results for σ shown on the left-hand side of Fig. 6, the results for the binary mixtures containing H2 and H2O agree within combined uncertainties with σ of pure n-octacosane over the complete T range. For the other solutes, a decrease in σ with increasing amount of dissolved solute with deviations up to − 20% can be observed. As it is the case for ηL, the behavior for σ corresponds well with the findings for corresponding binary mixtures based on n-hexadecane [20]. Furthermore, in the same way as seen for ηL, the relative deviations of the interfacial tension of the mixtures from that of the pure solvent are smaller for n-octacosane than for n-hexadecane, especially in connection with CH4, CO, and CO2. Here, the reader is referred to the interpretation given in the section “Viscosity.”

In the case of σ, which can be determined from EMD simulations with typical statistical uncertainties of 5% [25, 34, 35], the simulations can capture the influence of the dissolved gases. For mixtures based on the solvent n-octacosane, the results from EMD simulations show a similar influence of the dissolved gas on σ as found from the experimental investigations. For mixtures based on H2 and H2O, for example, EMD simulations show an agreement with σ of pure n-octacosane within combined uncertainties over the entire T range investigated. Also for all other solutes, the deviations between the σ data of the binary mixtures and the pure solvent are in good agreement with the findings from SLS experiments.

Next, the influence of the solute characteristics on σ of 1-hexadecanol-based mixtures is discussed using σ data for binary mixtures consisting of 1-hexadecanol with dissolved H2, CH4, H2O, or CO. The results for σ for these binary mixtures from SLS (left) and EMD simulations (right) are shown in the upper part of Fig. 7, where also the results for σ of pure 1-hexadecanol obtained from SLS [34] and EMD simulations [34] are included. The influence of the solute was examined by calculating the relative deviation of σ of the binary mixtures from the data for pure 1-hexadecanol, which is depicted in the lower part of Fig. 7.

Fig. 7
figure 7

taken from Tables 2 and S4

(Top) Interfacial tension σ of the binary mixtures of 1-hexadecanol with the dissolved gases H2, CH4, H2O, CO, or CO2 by SLS (left) and EMD simulations (right) as a function of T and solute mole fraction (open and closed symbols). For comparison, the correlations for σ of pure 1-hexadecanol based on data from SLS [39] and EMD simulations [34] are shown (solid lines). (Bottom) Relative deviations between the binary mixtures and pure 1-hexadecanol. The dotted lines mark the average expanded uncertainty (k = 2) of pure 1-hexadecanol. Error bars are shown only exemplarily for the mixtures containing H2 for clarity. The mole fractions of the dissolved gas given in the legend are approximate values. The real composition at each T can be

Full size image

While σ of mixtures containing H2 determined by SLS were within combined uncertainties with the data for the pure solvent in the case of n-octacosane, the difference is more pronounced but still within 5% with respect to the pure solvent in the case of 1-hexadecanol. For the solutes CO and CH4, a reduction in σ with maximum deviations of (15 and 21)%, respectively, is found, which is similar to the results for mixtures with n-hexadecane [20]. Similar as seen for ηL, the binary mixtures containing H2O show larger values for σ in comparison to the pure solvent, while the results for mixtures based on n-octacosane or n-hexadecane [20] were within combined uncertainties with those of the pure solvents. The difference between the data for the mixture and the pure solvent increases strongly with increasing T and reaches a maximum deviation of 28% at the largest investigated T of approximately 573 K. As already discussed in connection with ηL, a possible explanation for the much stronger influence of H2O on σ of 1-hexadecanol in comparison to the linear alkanes can be found in the formation of hydrogen bonds between the solute and solvent molecules at the vapor–liquid interface besides that in the liquid bulk phase.

EMD simulations are able to predict the influence of the dissolved gas over the entire T range in the case of the solutes H2, CH4, and CO. Only for the solute H2O, the EMD simulations were not able to predict the increase in σ relative to the pure solvent with increasing T, as it was also the case for ηL shown in Fig. 3. This failure in predicting the influence of H2O on σ and ηL seems to be related to the combination of the modified L-OPLS FF [32,33,34] for 1-hexadecanol and the SPC/E FF [55] for H2O, which cannot accurately represent the hydrogen bonding between the solute and solvent molecules, especially at large T.

In the same way as carried out for ηL, the influence of the molecular characteristics of the solvent on σ of the mixtures is studied by investigating binary systems consisting of either He or CO2 dissolved in various solvents by SLS and EMD simulations. The results for σ for the binary mixtures consisting of He dissolved in HMN, 2-butyl-1-octanol, squalane, or n-triacontane from SLS (left) and EMD simulations (right) are shown in the upper part of Fig. 8. Additionally, the results for σ of pure solvents investigated by SLS [34] and EMD simulations [34] are shown in Fig. 8. In its lower part, the relative deviations of the σ values for the binary mixtures from those of the pure solvents are given.

Fig. 8
figure 8

(Top) Interfacial tension σ of the binary mixtures consisting of He dissolved in HMN, 2-butyl-1-octanol, squalane, or n-triacontane investigated by SLS (left) and EMD simulations (right) as a function of T and He mole fraction (open and closed symbols). For comparison, T-dependent correlations σ of the pure solvents investigated by SLS [34] and EMD simulations [34] are shown (solid lines). (Bottom) Relative deviations between σ of the binary mixtures and σ of the pure solvents. The dotted lines mark the average expanded uncertainty (k = 2) of the properties for the pure solvents. Error bars are shown only exemplarily for the mixtures based on squalane for clarity

Full size image

The results from SLS depicted in Fig. 8 show that the data for σ of the binary mixtures based on the solvents HMN, squalane, and n-triacontane are mostly within combined uncertainties relative to the values for the pure solvents. This agrees with the investigations of the binary mixtures consisting of He dissolved in n-hexadecane [20]. In a similar way as found for ηL, a distinct difference between σ of the binary mixtures and the pure solvents was only visible in the case of 2-butyl-1-octanol with a maximum deviation of about 7% at p = 7.0 MPa. This difference may be related to a larger density of 2-butyl-1-octanol [34] and denser packing of the molecules in mixtures with dissolved He.

Also the results from EMD simulations shown on the right-hand side of Fig. 8 predict only a small influence of the dissolved He on σ compared to the pure solvents. Here, all results for the mixtures agree within the combined uncertainties with the values for the pure solvents. The maximum deviation can be observed for the mixture of He dissolved in HMN at the highest investigated T and is − 4.9%. Considering the weak influence of dissolved He on σ, good agreement between data from SLS and EMD simulations can be observed for the present systems.

Finally, σ of binary mixtures consisting of CO2 dissolved in the hydrocarbons n-octacosane, n-triacontane, or DCM investigated by SLS and EMD simulations are shown in the upper part of Fig. 9. In the case of EMD simulations, the binary mixtures consisting of DPM with dissolved CO2 at xCO2 = 0.1 or 0.2 were additionally investigated for T = (323.15 to 573.15) K. For comparison, the T-dependent correlations for σ of the pure solvents determined by SLS [17, 34, 39] and EMD simulations [34] are shown in Fig. 9. Relative deviations of σ of the binary mixtures from the ones of the pure solvents are given in the lower part of Fig. 9.

Fig. 9
figure 9

taken from Tables 2 and S4

(Top) Interfacial tension σ of the binary mixtures consisting of CO2 dissolved in n-octacosane, n-triacontane, or DCM investigated by SLS (left) and EMD simulations (right) as a function of T and CO2 mole fraction (open and closed symbols). In the case of EMD simulations, also results for binary mixtures based on DPM are shown. For comparison, the correlations for σ of the pure solvents based on data obtained by SLS [17, 34, 39] and EMD simulations [34] are shown (solid line). (Bottom) Relative deviations between the binary mixtures and the pure solvents. The dotted lines mark the average expanded uncertainty (k = 2) of the properties for the pure solvents. Error bars are shown only exemplarily for the mixtures based on n-octacosane for clarity. The mole fractions of the dissolved gas given in the legend are approximate values. The real composition at each T can be

Full size image

The results in Fig. 9 from SLS show a clear reduction in σ by adding dissolved CO2 to the three investigated solvents. For the solvents n-octacosane and n-triacontane, the deviations of the mixture data from the pure solvent data are in the range between − (5 and 20)% and generally increase with increasing xCO2. For these two solvents, the deviation between σ of the mixture and the pure solvent increases with increasing T. For the binary mixtures based on DCM, the reduction in σ is more pronounced and ranges up to − 35%. Also here, the deviations increase with increasing T. The reduction of the interfacial tension by the addition of CO2 to hydrocarbons can be related to the distinct enrichment of CO2 at the vapor–liquid interface, as it was observed by EMD simulations in its mixtures with n-hexane [19] and n-hexadecane [20].

The EMD simulations also predict a reduced interfacial tension of the mixtures compared to the pure solvents for all investigated mixtures. This reduction increases with increasing amount of dissolved CO2 and with increasing σ of the pure solvents. While the magnitude of the reduction found by EMD simulations agrees well with the observations from SLS in the case of the two linear alkanes, it is underestimated by EMD simulations in the case of DCM. At T = 473 K, for example, EMD simulations predict a reduction of σ for the DCM-based mixture at xCO2 = 0.2 of 19%, while the results from SLS show a deviation of 33%. Finally, the comparison between the DCM- and DPM-based mixtures shows a stronger influence of the dissolved CO2 for the DPM-based mixtures. This can be explained by the larger σ of DPM in comparison with DCM, which seems to cause a stronger enrichment of CO2 molecules at the vapor–liquid interface and, thus, a stronger decrease in mixtures with DPM.

5 Conclusions

In the present study, results for ηL and σ of the binary mixtures consisting of various linear, branched, cyclic, or oxygenated hydrocarbons with different dissolved gases obtained by SLS experiments and EMD simulations are presented. Binary mixtures of the solvents n-octacosane, n-triacontane, HMN, 2-butyl-1-octanol, squalane, DCM, or DPM with the solutes H2, He, CH4, H2O, CO, or CO2 were investigated in the T range between (298.15 and 573.15) K and solute mole fractions up to about 0.2. With the SLS technique, ηL and σ of the binary mixtures could be accessed with average expanded experimental uncertainties of (2.4 and 2.3)%, respectively. By comparing the thermophysical properties of the binary mixtures with the ones of the pure solvents, the influence of the dissolved gas on ηL and σ could be analyzed. For mixtures based on n-octacosane or 1-hexadecanol, the solutes CO2 and CH4 show a reducing impact on both properties with relative deviations up to − 20% compared to the values for the pure solvents. In contrast, the solutes H2 and CO have a much smaller influence, which is reflected by the agreement of the results for the mixtures with those of the pure substances mostly within combined uncertainties. For the solute H2O, no differences between viscosities and interfacial tensions of the binary mixtures and those of pure n-octacosane were found. For mixtures consisting of H2O dissolved in 1-hexadecanol, on the other hand, a distinct increase in ηL and σ in comparison to the data for pure 1-hexadecanol was found, which seems to be related to the impact of hydrogen bonding. When comparing the influence of the solutes He and CO2, clear differences were found. In general, a reduction in ηL and σ relative to the pure solvent data was found in the case of CO2, while the results for mixtures containing He are not distinctly affected and usually agree within combined uncertainties with the data for the solvents. Results from EMD simulations have shown that the employed FFs for the solvents and solutes are not able to quantitatively predict the influence of the dissolved gases on ηL, and often also not in a qualitative way. In the case of σ, on the other hand, the results calculated from EMD simulation agree much better with the SLS data and the simulations are able to predict the influence of the dissolved gases in most cases.