1 Introduction

Simulations and multiphysics computer models are being frequently used to optimize a multitude of industrial processes, like laser welding, cutting or additive manufacturing. In order to provide accurate results, these simulations rely heavily on experimentally obtained data. At the National Institute of Standards and Technology (NIST), laser adsorption measurements on the standard reference material (SRM) 1155a [1], an AISI 316L stainless steel, were performed to understand laser light coupling with metal [2]. But a variety of additional experimental data are required to optimize multiphysics simulations and models. Knowledge of thermophysical properties, i.e. material properties depending on temperature, like density, electrical and thermal resistivity or surface tension of the material of interest are crucial to modelers and consequently to industry. A variety of thermophysical properties was reported previously in [3]. Due to experimental challenges, results of surface tension and conductivity of the material were not accessible at this time. The results presented in this work, therefore, complete the previous publication [3].

Due to the lack of specific data, modelers often are forced to use data of materials with similar chemical composition for their simulations. The relatively generous limits in the composition classification of steels influence the micro structure of the material in the solid phase and, thus, lead to variation in thermophysical properties. For the liquid phase, Brooks and Quested [4] showed that the sulfur content in ferritic and austenitic steels has a great influence on the surface tension. In order to be classified as AISI 316L stainless steel, the material is allowed to have a maximum sulfur content of 0.025 % (mass percent), or 250 ppm [5]. However, surface tension at \(1650\,^\circ \hbox {C}\) in the range from 0 ppm to 250 ppm, according to Brooks and Quested [4], varies by up to 30 %. Therefore, it is important to have experimental data of materials with exactly known compositions as input parameters for models and simulations. As the material studied in this work is a standard reference material, its composition was measured carefully by NIST and its partners. The composition of the material can be found in Table 1. The solidus \(T_\text {s}\) and liquidus \(T_\text {l}\) temperatures were reported in [3] to be \(T_\text {s}={1675\pm15 \hbox {K}}\) and \(T_\text {l}={1708\pm30 \hbox {K}}\).

Table 1 Certified mass fraction values and reference mass fraction values (S) for SRM 1155a [1]
Full size table

Section 2 of this work addresses the measurement of surface tension and density by means of electromagnetic levitation (EML) in combination with the oscillating drop method (OD). Density was previously measured with an ohmic pulse-heating apparatus (OPA) and reported in [3]. To compare those results to density obtained by an independent measurement technique, EML measurements were performed and are presented in Sect. 2. Section 3 reports the determination of thermal conductivity as a function of temperature by means of ohmic pulse-heating and the usage of a laser flash apparatus. As ohmic pulse-heating has been described in detail in previous publication [3, 6, 7], this paper focuses mainly on the determination of thermal conductivity by applying a modified Wiedemann–Franz-law as well as the laser flash method.

2 Surface Tension and Density

2.1 Electromagnetic Levitation and Oscillating Drop Method

Electromagnetic Levitation is a container- and contactless measurement method to obtain surface tension and density of liquid metals and alloys. A conducting material is brought into the center of the levitation coil and a high-frequency electromagnetic field is applied. Eddy currents are then induced inside the material, which heat the sample due to ohmic losses. Additionally, the interaction with the electromagnetic field generates a Lorentz force, positioning the sample in regions with low field strengths. The sample levitates freely in between the two parts of the levitation coil. The levitation force \(\overline{\mathbf {F}}\) is proportional to the gradient of the squared magnetic induction \(\mathbf {B}\)

$$\begin{aligned} \overline{\mathbf {F}} \propto -\text {grad}\mathbf {B}^2. \end{aligned}$$
(1)

Due to ohmic losses of the induced eddy currents, the sample is heated up by the time averaged electrical power \(\overline{P}\), which is proportional to the squared magnetic induction

$$\begin{aligned} \overline{P}\propto \mathbf {B}^2. \end{aligned}$$
(2)

A more detailed description of 1 and 2 is given in [8, 9]. The EML setup consists of a vacuum chamber, connected to a rotary vane pump and a turbomolecular pump, capable of achieving a vacuum of around \(5\times 10^{-6}\hbox { mbar}\). The chamber is also connected to a gas supply, with several high purity gases available. The water-cooled levitation coil is connected to a high frequency generatorFootnote 1 which is providing the electromagnetic field with a frequency of around 380 kHz. Temperature is measured with a commercial pyrometer.Footnote 2 To obtain surface tension and density, two high speed cameras are used. One of those cameras is mounted on the top of the vacuum chamber and is used for surface tension measurement, the second camera observes the sample through the front window of the chamber and is used for density determination.


Surface tension evaluation As mentioned above, surface tension is measured by recording a video of the levitating sample. The liquid, levitating sample is confined by the electromagnetic field inside the levitation coil. In force free conditions, the sample would be close to a perfect sphere. However, due to the oscillation of the electromagnetic field, the sample is driven out of its spherical shape, and performs small oscillations, with the restoring force being the surface tension. Additionally to these oscillations, the sample moves slightly in all three spatial dimensions. Another factor to be considered is gravity. While the electromagnetic field counteracts gravity in a sense that the sample does not drop to the ground, gravity deforms the sample, altering the perfectly spherical shape (achieved in microgravity conditions on board the International Space Station and on board of parabolic flights), to the shape of a droplet.

Images of the oscillating sample are recorded with the fast camera and analysed with an edge detection software to determine the time dependent center of mass and the time dependent radii. Performing a Fast Fourier Transformation (FFT) to these obtained data provides the frequency spectrum, which shows distinct peaks at characteristic frequencies. These peaks correspond to the oscillation modes of the sample and are used to determine surface tension \(\gamma\), following the Rayleigh formula [10]

$$\begin{aligned} \gamma = \frac{3}{8} \cdot \pi ^3 \cdot M \cdot \nu ^2_R, \end{aligned}$$
(3)

corrected by Cummings and Blackburn for terrestrial conditions [11]

$$\begin{aligned} \gamma = \frac{3}{8} \cdot \pi ^3 \cdot M\left[ \frac{1}{5}\cdot \left( \nu ^2_{2,0}+2\cdot \nu ^2_{2,|\pm 1|}+2\cdot \nu ^2_{2,|\pm 2|}\right) -\overline{\nu }^2_t\left( 1.90+1.20\cdot \left( \frac{z_0}{R}\right) ^2\right) \right] \end{aligned}$$
(4)

with \(\nu ^2_{2,|\pm l|}\) the frequencies of the respective modes, M the mass of the sample, R the radius of the sample and

$$\begin{aligned} z_0 = \frac{g}{2\cdot \left( 2\pi \right) ^2 \overline{\nu }^2_t}. \end{aligned}$$
(5)

Here g is gravity and \(\overline{\nu }_t\) is the mean square translation frequency of all three spatial dimensions. A more detailed description of surface tension measurement with the EML apparatus is given already in previous publications, e.g. [12,13,14].


Density To determine density, a fast camera observes the sample through the front window of the sample chamber. Divergent to surface tension measurements the levitating sample is irradiated with a strong LED background source and shadow images of the sample are recorded. Again, an edge-detection algorithm is used to determine the radii as a function of the polar angle and, assuming vertical axis symmetry, the volume is determined. Together with the known mass of the sample, density is obtained.

2.2 Sample Preparation and Experimental Practice

SRM 1155a was supplied by NIST as cylinders (3.9 g) with dimensions of approximately 11 mm in diameter and a height of 5 mm. The samples for the EML experiments were obtained by bisecting the cylinders in two flat discs and subsequently cutting each of them into four parts. Thus, eight parts shaped like (rather flat) pieces of a pie could be obtained from each cylinder and sample material wastage was minimized. The samples were further polished with abrasive paper (grade: 240) to minimize contaminations and oxide layers from the surface and subsequently cleaned in isopropanol in an ultrasonic bath.

After initial weighing, the samples were inserted into the EML processing chamber which was then evacuated to a pressure in the \(10^{-6}\hbox { mbar}\) regime to remove residual oxygen from the venting of the chamber. The processing chamber was then filled with a mixture of high purity argon and helium. Both gasesFootnote 3,Footnote 4 were hydrogen enriched to avoid residual oxygen in the chamber or in the processing gas to react with the sample material. A gas purification systemFootnote 5 was used, reducing the residual oxygen content in the processing gas from the one-digit ppm down to the one-digit ppb range. After the experiment, the samples were weighed again to quantify the mass loss due to evaporation of sample material.

Since SRM 1155a contains alloying elements (e.g. Mn) with vapor pressures orders of magnitude higher than the vapor pressure of the alloy’s base element Fe, heavy evaporation of the sample material was noticed (e.g. mass loss of 2.9% after 50 min of levitation). Strong evaporation alters the sample’s composition with time which questions the validity of the obtained results.

One way to overcome this challenge was to significantly reduce the experiment duration. Limiting the experiment duration to a maximum of two melt cycles per sample was found to be a satisfying trade-off so that the experimental expense was acceptable while the amount of evaporated sample material was low enough so that the samples presumably still contained Mn and thus the composition was not drastically changed. The samples were cooled and solidified after video-recording to further reduce the time span in which the samples are liquid (liquid-time). The liquid-time was reduced to typically 2 min by these measures [15].

A total of 15 samples with a mass ranging from 283 mg to 314 mg was processed and evaluated for surface tension measurements to cover the entire temperature range. Additional 2 samples were processed to obtain single reference data points for density in order to compare them to previously measured data by Pichler et al. [3], using an independent method. The largest mass loss observed of all 17 samples was 0.65% with an average mass loss of 0.45%.

Processing this large number of samples would have been extremly time-consuming without modifications to the EML apparatus. A sample carousel was built that can carry up to nine samples and allows to switch between samples without venting the processing chamber, which is shown in Fig. 1. This reduces the experiment preparation time (e.g. pumping time) significantly. Additionally, the temperature control was improved by installing a massflow controller (MFC) that facilitates a more precise control of the cooling gas flow compared to the old system with manual valves. Even though the massflow controller is operated without an automatic control system, the samples’ target temperature can now be reached significantly faster and thus the experiment duration is shortened. A detailed description of the modification is given in [16, 17].

Fig. 1
figure 1

Isometric view (left picture) and cross-section (right picture) of the sample carousel [16]. The sample carousel was constructed with a linear cartridge due to the space limitations inside the processing chamber. The samples sit on the nine casings (blue) which are stored in the corresponding holes of the cartridge. The cartridge is part of a geneva drive (green) that is operated by rotating the sample holder (red) in the bottom position via a linear feedthrough that is connected to the bottom end of the sample holder. When the sample holder is moved up, its gear disconnects from the geneva drive and the position of the sample cartridge is locked. By further moving the sample holder upwards through the cartridge, the casing (blue) holding the sample is picked up and thus the sample can be transported through the axis into the middle of the levitation coil. Both, sample holder and casings are constructed as pipes since they act as the pathway for the cooling gas which is supplied via the flange (yellow). There is a cover on top of the cartridge (purple, not shown in the isometric view) that protects the underlying samples. The figures are taken from [16] (Color figure online)

Full size image

2.3 Results


Surface tension Fig. 2 shows the surface tension results as a function of temperature in \(\hbox {mN}\cdot \hbox {m}^{-1}\). The obtained data were fit linearly in the temperature range \(1680 \ \le \ T \ / \ \text {K} \ \le \ 1880\) by

$$\begin{aligned} \gamma (T) = (1593 \pm 8) + (0.19 \pm 0.07) \cdot (T-T_\text {l}). \end{aligned}$$
(6)

Here, \(T_\text {l}\) is the liquidus temperature (\(T_\text {l}={1708\hbox { K}}\)).Footnote 6 The data obtained within this work are compared to surface tension data of similar stainless steels. The composition differs slightly for almost all of the contained elements, but all of the steels which are compared classify as AISI 316. Surface tension is highly dependent on sulfur content, therefore, this work focuses specifically on the difference in sulfur content between the steels. Table 2 lists the reported sulfur contents of the steels.

Fig. 2
figure 2

Surface tension of the NIST SRM 1155a as a function of temperature. Red circles with black border represent the experimentally measured data of this work. The solid blue line represents a linear regression to the experimentally obtained data. Red circles without border represent surface tension data of an AISI 316 stainless steel by Fukuyama et al. [18]. The solid red line with upwards facing triangles as markers represents surface tension data of an AISI 316 stainless steel by Ozawa et al. [19]. The solid red line with crosses as markers represents surface tension data of an AISI 316 stainless steel with high sulfur content by Brooks and Quested [4]. The solid red line with downwards facing triangles as markers represents surface tension data of an AISI 316 stainless steel with low sulfur content by Brooks and Quested [4] (Color figure online)

Full size image
Table 2 Overview of the sulfur content in the steels studied in the publications referenced in the comparison and discussion of the results
Full size table

Almost all of the reported surface tension data show a very similar slope. The only exception being the data reported by Brooks and Quested of the low sulfur content steel. The position of the reported data relative to each other is in good agreement with the behaviour of surface tension, dependent on sulfur content, reported by Brooks and Quested [4].


DensityFor the density of NIST SRM 1155a, this work focused on comparing the already available density data from a previous publication [3] of our research group (due to the already mentioned experimental expenses for exploiting a full temperature dependence) to results from EML measurements, being an independent experimental method. Hence, four data points were acquired to spot-check the existing data as shown in Fig. 5.

Within measurement uncertainty, there is an excellent agreement of the density data obained from this work’s EML experiments with the data from the previous ohmic pulse-heating experiments [3].


Change in compositionMuch effort was spent in minimizing the evaporation of sample material and to preserve the original sample composition as much as possible. This was achieved by minimizing the experimental duration in general and the time of the sample being liquid in particular. After all, the typical mass loss of the samples was 0.45 wt% while the largest mass loss observed was 0.65 wt%. Even if Mn was the only element that evaporated, more than 2/3 of the original Mn content of 1.593 wt% is assumed to remain. This was confirmed by Energy-dispersive X-ray spectroscopy (EDX) using a field emission scanning electron microscope (Thermo Scientific Quanta 450 ESEM) with a silicon drift EDX detector (UltraDry \(10 \hbox { mm}^2\) with Pathfinder X-ray Microanalysis Software) at the Center for Electron Microscopy in Graz (ZFE). For the SEM/EDX measurements, the samples were embedded in epoxy resin and cross sections were prepared. The samples were polished up to a diamond suspension of 0,1 m to guarantee a flat and even surface. This is essential for the EDX measurements with high measuring accuracy and for backscatter electron imaging (BSE) with clear contrast. The material contrast in BSE images was used to find potentially inhomogeneities, precipitates or impurities and electrons with an energy of 20 keV were used for the EDX analysis [20]. The BSE images of all samples showed a completely homogeneous material distribution and the EDX measurements confirmed a consistent elemental distribution through the diameter of the sample. By using quantitative EDX measurements it could be determined that a significant amount of Manganese is still in the samples after the experiments (between 1.0 wt% and 1.4 wt%) taken Silicon, Chromium, Manganese, Iron, Cobalt, Nickel, Copper and Molybdenum into account). In Fig. 3 an EDX spectra and the quantitative analysis can be seen. The importance of a minimization of the evaporation of sample material is illustrated in Fig. 4. Here, the diamond markers represent results of surface tension measurements, performed on two samples, which were both levitated and molten for a duration of approx. 20 minutes. EDX measurements of the levitated samples, after the experiment, indicated that Mn had almost completely vanished from the sample [21]. This corresponds to the change in Mn content reported by Fukuyama et al. [18] for a levitation duration of the same order of magnitude. The resulting surface tension values for the long-term levitated samples are significantly higher than the surface tension values of the samples that were liquid for a shorter duration. Additionally, surface tension appears to show a “boomerang”-shaped behaviour. However, the composition of the material changed drastically, thus, rendering these data unreliable. They are presented here to emphasize the importance of minimizing evaporation in levitation experiments. Moreover, the sulfur content of the short-term levitated samples was measured using combustion analysis and was found to be still in the range of 15 ppm to 17 ppm and thus only slightly lower than the sulfur content of the original composition of 20 ppm. This is a remarkable result since in another study on similar 316 stainless steel by Ozawa et al. [19] (who also used EML), the authors experienced a significant reduction in the sulfur content from 300 ppm to 60 ppm (Table 2). A comparison of fit-coefficients for surface tension between this work and data from the literature is given in Table 3.

Fig. 3
figure 3

EDX spectrum of the NIST SRM 1155a after levitation

Full size image
Fig. 4
figure 4

Comparison of experimental times. The diamond markers represent data from two long-levitated samples and the circular markers represent data from samples which were levitated for a short period of time only

Full size image
Fig. 5
figure 5

Density of the NIST SRM 1155a as a function of temperature. Red circles represent the experimentally measured (EML) data of this work. Horizontal errorbars correspond to uncertainty in temperature, vertical errorbars correspond to uncertainty in density. The solid red line represents density data of NIST SRM 1155a by Pichler et al. [3] with reported uncertainty from OPA experiments (Color figure online)

Full size image
Table 3 Fit-coefficients a and b for surface tension \(\gamma\) as a function of temperature T in \(\gamma = a + b\cdot T\)
Full size table

3 Thermal Conductivity

3.1 Ohmic Pulse-Heating Apparatus and the Wiedemann–Franz-Law

To the knowledge of the authors, there is no direct method available to measure thermal conductivity of liquid steels, due to their high temperature and chemical reactivity. Thermal conductivity of NIST SRM 1155a (AISI 316L) was obtained by two independent indirect methods: (i) from measured electrical resistivity using the Wiedemann–Franz law and the Smith–Palmer relation, and (ii) from measured thermal diffusivity, heat capacity and density.

The ohmic pulse-heating apparatus (OPA) was described in several previous publications, e.g. [3, 6, 7]. The working principle is that a wire-shaped sample with a diameter d = 0.5 mm is heated by passing a large current pulse (some 1000 A) through the sample. With heating rates in the order of \(10^{8} \hbox { K} \hbox { s}^{-1}\), the sample is heated from room temperature to its melting point and throughout the liquid phase until it reaches the boiling point and explodes. The sample temperature is measured by a very fast pyrometer, operating at a wavelength of \(\lambda\) = 1570 nm with a full width at half maximum (FWHM) wavelength of \(\varDelta \lambda\) = 84 nm, the current is measured inductively by a Pearson current monitor model 3025, the voltage across a defined length of the sample is measured by a voltage divider using Mo-electrodes attached to the sample and the radial thermal expansion is measured by taking backlit shadow images. Electrical data (current and voltage drop) are recorded from room temperature to the boiling point, but temperature is only available above a certain temperature threshold, as the photo diode of the pyrometer is only sensitive in a certain range. Therefore, in order to obtain temperature dependent data at lower temperatures, it is necessary to combine the OPA measurements with dynamic scanning calorimeter (DSC) measurements. A detailed description of the combination of DSC and OPA measurements is given in [3].

In electrically well conducting metals like copper or aluminium, the contribution to thermal conductivity is mainly electronic. Lattice contributions are much smaller than the electronic component of thermal conductivity. Therefore, at temperatures, T, above the Debye temperature, the dominating electronic component obeys the Wiedemann–Franz–Lorenz relation and thermal conductivity, \(\lambda\), can be approximated by

$$\begin{aligned} \lambda (T)=\frac{L_0 \cdot T}{\rho _\text {el}(T)}, \end{aligned}$$
(7)

where \(L_0\) is the Sommerfeld value of the Lorenz number (\(2.445 \times 10^{-8}\hbox {V}^2\hbox {K}^{-2}\)), and \(\rho _\text {el}\) is the electrical resistivity. It is assumed for the calculation of the thermal conductivity of NIST SRM 1155a from electrical resistivity that this relation is valid in the liquid state, as there is no significant lattice contribution.

This equation was modified by Smith and Palmer [22] to account for the significant lattice component in the solid as well as for the scattering of electrons by impurities and other small contributions to the thermal conductivity,

$$\begin{aligned} \lambda (T)=\frac{A\cdot L_0(T) \cdot T}{\rho _\text {el}(T)}+B, \end{aligned}$$
(8)

with A and B as empirical constants. For the calculation of the thermal conductivity of NIST SRM 1155a in the solid state from electrical resistivity, these empirical constants (\(A=0.94\) and \(B=5.0\)) were taken from [23], describing an AISI 316L alloy with similar chemical composition. Thermal diffusivity a can be derived from thermal conductivity by

$$\begin{aligned} a(T) = \frac{\lambda (T)}{c_\text {p}(T)\cdot D(T)}, \end{aligned}$$
(9)

with the temperature dependent specific heat capacity \(c_\text {p}(T)\) and the temperature dependent density D(T). Specific heat capacity, density and electrical resistivity have been previously measured and are reported in [3].

3.2 Laser Flash

Thermal diffusivity was measured by the laser-flash method. One surface of a cylindrical specimen is instantly heated by a laser-flash and the temperature development is measured at the opposite side. The thermal diffusivity is calculated from the temperature rise time and specimen thickness, considering the thermal radiation of the specimen surfaces and the laser pulse-length. Commercial laser-flash equipment (NETZSCH Gerätebau, Selb, Germany, type LFA 427) was used for the measurements. The laser pulse-length was \(300\,{\upmu}{\text{s}}\), and the laser pulse energy was approx. 3 J. The temperature rise was measured by an InSb-detector and evaluated by the Cape–Lehmann algorithm with a pulse-length correction [24]. The temperature in the vicinity of the specimen was measured by a type S thermocouple. The thickness of the specimens (nominally 3 mm, diameter 12.55 mm) was measured by a calibrated precision calliper. In order to improve the optical properties, the specimens were very slightly roughened by sandblasting. The measurement was performed in high vacuum (\(1 \times 10^{-5} \hbox {mbar}\)). In temperature ranges where no thermal reactions occur, the thermal conductivity as a function of temperature can be calculated from thermal diffusivity related to room temperature dimensions of the specimen, \(a_0\), density at room temperature, \(\rho _0\), specific heat capacity, \(c_p\), and linear thermal expansion, \(\varDelta l/l_0\), by the following equation:

$$\lambda (T) = \frac{{a_{0} (T) \cdot \rho _{0} \cdot c_{p} (T)}}{{1 + {{\Delta l(T)} \mathord{\left/ {\vphantom {{\Delta l(T)} {l_{0} }}} \right. \kern-\nulldelimiterspace} {l_{0} }}}}$$
(10)

3.3 Results

This section summarizes the results for thermal conductivity measurements. Figure 6 shows results for thermal conductivity of the NIST SRM 1155a, obtained by measuring electrical resistivity and applying the Wiedemann–Franz-law to obtain thermal conductivity. This work’s data are compared to data from the literature of similar AISI 316L stainless steels. This work’s data show an optimal agreement with data from the literature, suggesting that the differences in compositions of the different steels has no large influence on thermal conductivity.

Fig. 6
figure 6

Thermal conductivity as a function of temperature. The solid blue line represents OPA measurements in combination with the WFL. The dashed blue line represents OPA data combined with DSC data. The black crosses represent literature values presented by Mills et al. [25]. The red dots represent literature values presented by Kaschnitz et al. [23]. The red lines represent data presented by Wilthan et al. [26] (Color figure online)

Full size image

Thermal conductivity in \(\hbox {W}\cdot \hbox {K}^{-1}\) from combined DSC and OPA measurements has been fitted in the solid phase in a temperature range \(500\le T / \text {K} \le 1250\) by

$$\begin{aligned} \lambda _\text {s}(T) = 8.98 +1.57\cdot 10^{-2}\cdot T - 1.5\cdot 10^{-6}\cdot T^2, \quad 500\le T / \text {K} \le 1250. \end{aligned}$$
(11)

Thermal conductivity in \(\hbox {W}\cdot \hbox {K}^{-1}\) from OPA measurements in the solid phase has been fitted in a temperature range \(1300\le T / \text {K} \le 1675\) by

$$\begin{aligned} \lambda _\text {s}(T) = 6.38 +1.9\cdot 10^{-2}\cdot T - 2.45\cdot 10^{-6}\cdot T^2, \quad 1300\le T / \text {K} \le 1675. \end{aligned}$$
(12)

In the liquid phase, thermal conductivity in \(\hbox {W}\cdot \hbox {K}^{-1}\) has been fitted in a temperature range \(1708\le T / \text {K} \le 2900\)

$$\begin{aligned} \lambda _\text {l}(T) = 2.27 +1.76\cdot 10^{-2}\cdot T - 1.39\cdot 10^{-6}\cdot T^2, \quad 1300\le T / \text {K} \le 1675. \end{aligned}$$
(13)
Fig. 7
figure 7

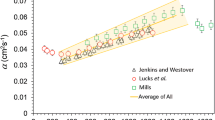
Thermal diffusivity as a function of temperature. The solid blue line represents OPA measurements in combination with the WFL. The dashed blue line represents OPA data combined with DSC data. The blue diamond markers represent LFA measurements. The black crosses represent literature values presented by Mills et al. [25]. The red lines represent data presented by Wilthan et al. [26] (Color figure online)

Full size image

Figure 7 shows thermal diffusivity data for the NIST SRM 1155a in comparison to data of similar AISI 316L stainless steels from the literature. Similar to thermal conductivity, the influence of the different compositions on thermal diffusivity is comparably small. Thermal diffusivity in m\(^2\cdot\)s\(^{-1}\) from combined DSC and OPA measurements has been fitted in the solid phase in a temperature range \(500\le T / \text {K} \le 1250\) by

$$\begin{aligned} a_\text {s}(T) = 3.1 \cdot 10^{-6}+1.8\cdot 10^{-9}\cdot T + 2\cdot 10^{-13}\cdot T^2, \quad 500\le T / \text {K} \le 1250. \end{aligned}$$
(14)

In the solid phase, thermal diffusivity in \(\hbox {m}^2\cdot \hbox {s}^{-1}\) from OPA measurements has been fitted quadratically in the temperature range \(1260\le T / \text {K} \le 1675\) by

$$\begin{aligned} a_\text {s}(T) = 1.62\cdot 10^{-6} + 4.06\cdot 10^{-9}\cdot T - 6.1\cdot 10^{-13}\cdot T^2, \quad 1260\le T / \text {K} \le 1675. \end{aligned}$$
(15)

In the liquid phase, thermal diffusivity in \(\hbox {m}^2\cdot \hbox {s}^{-1}\) has been fitted linearly in the temperature range \(1708\le T / \text {K} \le 2900\) by

$$\begin{aligned} a_\text {l}(T) = 2.23\cdot 10^{-7} + 2.7\cdot 10^{-9}\cdot T, \ 1708\le T / \text {K} \le 2900. \end{aligned}$$
(16)

4 Uncertainty

Uncertainties were assessed according to the Guide to the expression of uncertainty in measurement (GUM) [27]. All reported uncertainty values are expressed in a k = 2 (95 %) confidence interval. Uncertainties for the fit coefficients are calculated following the guide of Matus [28] for linear data regressions. The x-axis uncertainties (i.e. temperature) are accounted for and converted into an additional factor in the y-axis uncertainties, as described in [28]. The uncertainty of the temperature rises towards higher temperatures, leading to higher uncertainties in the y-axis at elevated temperatures. For thermal conductivity and thermal diffusivity an exemplary uncertainty budget at selected temperatures is presented in Tables 4 and 5. The uncertainty for thermal conductivity is mainly governed by the uncertainty of electrical resistivity. The uncertainty for thermal diffusivity is mainly governed by the uncertainty of thermal conductivity. Uncertainties in percent for all measured properties can be found in Table 6.

Table 4 Uncertainty budget for thermal conductivity at 1640 K according to GUM
Full size table
Table 5 Uncertainty budget for thermal diffusivity at 1640 K according to GUM
Full size table
Table 6 Uncertainties for all measured properties
Full size table

5 Conclusion

Surface tension, determined by means of electromagnetic levitation as well as thermal conductivity and thermal diffusivity, determined by means of ohmic pulse-heating and the Wiedemann–Franz-Law are presented in this work. Additionally, density was measured by electromagnetic levitation and compared to previously obtained results [3] from ohmic pulse-heating experiments. The challenges of evaporating manganese and the resulting change of the alloy composition in general (also other elements like sulfur) were overcome by reducing the levitational time, leading to very little evaporation and sample mass loss. Hence, the composition of the levitated samples stays very close to the original composition of NIST SRM 1155a. Therefore, the surface tension data obtained from our EML experiments is valuable input data for modeling or describing processes in which SRM 1155a is liquefied, for instance in a laser melting process. The density values obtained from electromagnetic levitation measurements are in very good agreement with the previously measured data.

Thermal diffusivity data were compared to both laser flash measurements, performed on the same material, as well as to data from the literature of other AISI 316 stainless steels with similar composition and show excellent agreement with both data sets. Thermal conductivity data also compare excellently with data from the literature.