Calculating SPRT Interpolation Error

Abstract

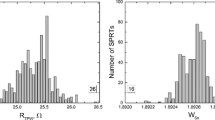
Interpolation error is a major source of uncertainty in the calibration of standard platinum resistance thermometer (SPRT) in the subranges of the International Temperature Scale of 1990 (ITS-90). This interpolation error arises because the interpolation equations prescribed by the ITS-90 cannot perfectly accommodate all the SPRTs natural variations in the resistance–temperature behavior, and generates different forms of non-uniqueness. This paper investigates the type 3 non-uniqueness for fourteen SPRTs of five different manufacturers calibrated over the water–zinc subrange and demonstrates the use of the method of divided differences for calculating the interpolation error. The calculated maximum standard deviation of 0.25 mK (near $100\,^{\circ }\hbox {C}$) is similar to that observed in previous studies.

Appendices

Appendices

1.1 Proof of Interpolation Error Theorem

Considering $p_n \left( x \right)$ a interpolating polynomial of $\le n$ degree of the function $f\left( x \right)$ at the different nodes $x_0 ,\ldots ,x_n \in I_x$. If $f\left( x \right)$ has continuous derivatives until $\left( {n+1} \right)$ order, for any x there is a $\xi \in I_x$ such that (Eq. 7)

$$\begin{aligned} f\left( x \right) -p_n \left( x \right)= & {} \prod \limits _{j=0}^n \left( {x-x_j } \right) \frac{f^{\left( {n+1} \right) }\left( \xi \right) }{\left( {n+1} \right) !}=\frac{f^{\left( {n+1} \right) }\left( \xi \right) }{\left( {n+1} \right) !}w_n \left( x \right) \hbox {where }\\ w_n \left( x\right)= & {} \prod \limits _{j=0}^n \left( {x-x_j } \right) \end{aligned}$$

As already noted, for the interpolation points $x=x_j$ , $j=0, 1,\ldots ,n$ the interpolation error is zero. We therefore assume a $x\ne x_j$, $j=0, 1,\ldots ,n$ and set an auxiliary function be:

$$\begin{aligned} \varphi \left( z \right) =f\left( z \right) -p_n \left( z \right) -K w\left( z \right) \end{aligned}$$

(16)

and choose K from the condition $\varphi \left( x \right) =0$, where x is the point at which the error is estimated

$$\begin{aligned} K=\frac{f\left( x \right) -p_n \left( x \right) }{w\left( x \right) } \end{aligned}$$

(17)

Since the interpolation points $x_0 , \ldots , x_n$ and x are distinct, $w\left( x \right)$ does not vanish and is well defined. With this choice of K, the function $\varphi \left( z \right)$vanishes at $\left( {n+2} \right)$ points in $I_x$. According to Rolle’s Theorem, its derivative $\varphi {\prime }\left( z \right)$ has at least $\left( {n+1} \right)$ distinct zeros in $I_x , \varphi {\prime }{\prime }\left( z \right)$ has at least n distinct zeros in $I_x$, and similarly, $\varphi ^{n+1}\left( z \right)$ has at least one zero in that interval, which we indicate with $\xi$. Deriving $\left( {n+1} \right)$ times, Eq. 11

$$\begin{aligned} 0 = \varphi ^{\left( {n+1} \right) }\left( \xi \right) = f^{\left( {n+1} \right) }\left( \xi \right) - p_n^{\left( {n+1} \right) } \left( \xi \right) -Kw^{\left( {n+1} \right) }\left( \xi \right) \end{aligned}$$

But $p_n^{\left( {n+1} \right) } \left( \xi \right) =0$ as the polynomial $p_n \left( z \right)$ has a degree $\le n$. As the coefficient of the highest degree term of the product $w\left( z \right)$ is 1, we have $w^{\left( {n+1} \right) }(\xi ) = \left( {n + 1} \right) !$

$$\begin{aligned} K=\frac{f^{\left( {n+1} \right) }\left( {\xi _n } \right) }{w^{\left( {n+1} \right) }(\xi )}=\frac{f^{\left( {n+1} \right) }\left( {\xi _n } \right) }{\left( {n+1} \right) !} \end{aligned}$$

and from Eq. 12 and reordering the terms

$$\begin{aligned} f\left( x \right) -p_n \left( x \right) =\frac{f^{\left( {n+1} \right) }\left( {\xi _n } \right) }{\left( {n+1} \right) !}w\left( x \right) \end{aligned}$$

(18)

which was to be demonstrated.

1.2 Generalized Lagrange Mean’s Value Theorem

Considering a function “f” known at the different points $x_0 ,x_1 ,\ldots ,x_n \hbox {of }\left[ {a,b} \right]$ and assuming that $f\left( x \right)$ has a continuous derivative of order n, there exists a:

$$\begin{aligned} \xi \in ] {a,b} ]\hbox { }that\hbox { }f\left[ {x_0 ,\ldots ,x_n } \right] =\frac{f^{\left( n \right) }\left( \xi \right) }{n!} \end{aligned}$$

From Eq. 9—“Newton’s interpolation polynomial with divided differences,”

$$\begin{aligned} p_n \left( x \right) =f\left[ {x_0 } \right] +f\left[ {x_0 ,x_1 } \right] \left( {x-x_0 } \right) +\ldots +f\left[ {x_0 ,\ldots ,x_n } \right] \mathop \prod \limits _{j=0}^{n-1} \left( {x-x_j } \right) \end{aligned}$$

or $p_n \left( x \right) =f\left[ {x_0 } \right] +\mathop \sum \nolimits _{j=1}^n f\left[ {x_0 ,\ldots ,x_n } \right] \mathop \prod \nolimits _{j=0}^{n-1} \left( {x-x_j } \right)$

so $f\left( x \right) -p_n \left( x \right) =f\left[ {x_0 ,\ldots ,x_n } \right] \mathop \prod \nolimits _{j=0}^{n-1} \left( {x-x_j } \right)$

and $f\left[ {x_0 ,\ldots ,x_n } \right] =\frac{f^{\left( n \right) }\left( {\xi _n } \right) }{\left( n \right) !}w\left( x \right)$ which was to be demonstrated.