Introduction

In recent decades, researchers and educators have highlighted the importance of productive classroom discussions in high-quality mathematical instruction for all learners (e.g., Anthony & Walshaw, 2009; Jacobs & Spangler, 2017; Webb et al., 2019). Drawing on a description by Grossman et al. (2014), in this study, the term productive whole-class discussions refers to discussions in which the students and the teacher work together, and use all the participants’ thinking and knowledge as a resource to improve the learning in relation to a specific mathematical goal. Further, students should have opportunities to practice communication and reasoning. However, after decades of attempts by professional development programs to support teachers to achieve these discussions, they are rarely reported on in the context of mathematics classrooms (Park et al., 2017). This lack of productive classroom discussion may be due to several challenges teachers face (Staples, 2007). For instance, leading these discussions requires a high level of teacher knowledge and skills (O’Connor et al., 2017; Walshaw & Anthony, 2008). Furthermore, productive classroom discussion must be based on specific activities like problem-solving with challenging tasks (Stein et al., 2008; Tekkumru-Kisa et al., 2020; Xu & Mesiti, 2022), which has been a common research focus in recent decades. In this context, researchers (e.g., Larsson, 2015; O’Connor et al., 2017; Schoenfeld, 2016; Stein et al., 2008; Wester, 2021) have been working intensively to describe and better understand problem-solving practices by exploring essential aspects such as teacher actions, challenges teachers face, whole-class discussions, productive norms, student participation, and how to support teachers in building a problem-solving practice. However, building a practice based on rich problem-solving tasks is demanding and challenging for teachers (e.g., Larsson, 2015). Therefore, I am interested in contributing to research on complementary practices that might support teachers in achieving productive classroom discussions.

Another promising activity for achieving these productive discussions entails using a digital classroom response systemFootnote 1 (CRS) and implementing challenging but less complex and less time-consuming tasks in a multiple-choice (MC) format (Cline & Huckaby, 2021; Gustafsson & Ryve, 2022). CRS can present tasks, activate students, and collect anonymous responses from every student and automatically display them in a bar chart on a shared screen (e.g., Latulippe, 2016). This chart can serve as a foundation for whole-class discussions (Cline et al., 2022; Gustafsson & Ryve, 2022). To achieve productive discussions with support from CRS, constructing MC tasks and leading whole-class discussions have been identified as both major challenges and key practices for teachers (King & Robinson, 2009b; Lee et al., 2012; Nielsen et al., 2013). However, in the CRS context, mathematics instruction in secondary school has received little attention in research (Hunsu et al., 2016; Kay & LeSage, 2009). Most studies have been experiments studying the effects on student learning, with ambiguous results. Further, there seems to be a total lack of research on whole-class discussions,Footnote 2 which might help explain these ambiguous results. To meet this need, I seek to explore the potential of MC tasks supported by CRS for achieving productive whole-class discussions; I do this by applying a mixed-method approach in order to characterize mathematical whole-class discussions. The research questions guiding this paper are as follows:

  • To what extent do students actively participate in whole-class discussions generated from different MC tasks?

  • What categories of teacher and student actions can be identified in these whole-class discussions?

CRS in Mathematics Instruction

Over the last two decades, researchers have shown some interest in CRS integration in mathematics instruction, especially in higher education (Cline et al., 2022; Liu & Stengel, 2011). Research in higher education (Liu & Stengel, 2011; Simelane & Mji, 2014) and in secondary school (Dix, 2013; Shaheen et al., 2021) has shown that CRS has the potential to improve student learning in mathematics. This improvement in mathematics performance is also identified for low-performing students (Roth, 2012), special education and ELL students (Wang et al., 2014), and students with behavioral problems (Xin & Johnson, 2015). However, there are experimental studies that show no statistically significant difference between test and control groups (Holmes, 2019; Lynch, 2013). Thus, the integration of CRS into mathematics instruction is not a guarantee for success. Improved learning is likely not caused by the CRS itself; the results depend on the quality of the task (Tekkumru-Kisa et al., 2020) and how the technology is implemented and used to improve the instruction so that it meets students’ needs in the specific context (Drijvers, 2015). To improve learning with digital technology, teachers should design their instruction based on pedagogical and didactic considerations and follow the principles that apply to all learning forms (Drijvers, 2015; Hattie & Yates, 2014). In the context of CRS and mathematics instruction, researchers and teachers have designed their interventions with an expectation to improve the extent and quality of students’ attendance (Liu & Stengel, 2011), students’ engagement and participation (Lucas, 2009), feedback to both students and teachers (Green & Longman, 2012), and classroom discussions (e.g., Cline et al., 2013). Concerning attendance and participation, CRS in mathematics instruction has been shown to have the potential to increase students’ attendance (Liu & Stengel, 2011) and participation (King & Robinson, 2009b; Latulippe, 2016; Lucas, 2009), which increases their opportunities to engage in mathematics. One suggested key factor for this increase in student attendance and participation is the possibility for anonymity when responding to tasks launched by a CRS (Boscardin & Penuel, 2012). This anonymity is valued by students, according to Lockard and Metcalf (2015).

CRS and Mathematics Classroom Discussions

CRS has been shown to have the potential to support teachers in generating classroom discussions (Cline et al., 2013, 2022; Shaheen et al., 2021), and classroom discussions have been the focus of different research-based models for CRS integration in mathematics instruction, such as Peer Instruction (PI) (Lucas, 2009), Technology Enhanced Formative Assessment (TEFA) (Shaheen et al., 2021), and the contingent teaching model (Stewart & Stewart, 2013). PI and the contingent teaching model focus mostly on peer discussions. In fact, in the original PI model (Crouch & Mazur, 2001), teachers are expected to finish classroom discussions by simply explaining the correct answers instead of leading a whole-class discussion based on the students’ responses and peer discussions. This instructional behavior was identified in a study in large classroom settings at university (Lewin et al., 2016): Lewin et al. noticed that teachers orchestrated peer discussions in 56% of the observed implementations of mathematical tasks supported by CRS, but their data did not show any whole-class discussions. This contrasts with the TEFA model (Beatty & Gerace, 2009) and recent research in mathematics instruction (Webb et al., 2019; Wester, 2021), which points out the importance of a combination of small-group and whole-class discussions. Further, the role and importance of whole-class discussions in enhancing a deeper understanding among students was also noted in a study of mathematics instruction in a teacher-training program in Wales (Green & Longman, 2012). However, as described above, I am not aware of any studies that explore mathematical whole-class discussions originating from MC tasks supported by CRS.

Tasks for Mathematics Classroom Discussions

In recent decades, some prerequisites and challenges for achieving productive mathematical whole-class discussions have been identified, such as establishing classroom norms (e.g., Jackson et al., 2018) and leading whole-class discussions (e.g., Stein et al., 2008). Further, in the context of CRS, constructing suitable mathematical MC tasks to be used with CRS is a major challenge for teachers (Cline & Huckaby, 2021; King & Robinson, 2009b; Lee et al., 2012; Nielsen et al., 2013). The design of tasks plays a crucial role in mathematics instruction, and can either support or hinder student learning (Tekkumru-Kisa et al., 2020). In order to generate productive discussions, tasks need to be based on specific types of rich and challenging tasks, such as problem-solving tasks (Stein et al., 2008; Tekkumru-Kisa et al., 2020; Xu & Mesiti, 2022) or specific MC tasks supported by CRS (e.g., Cline et al., 2018; Gustafsson & Ryve, 2022). Concerning MC tasks to be used with CRS, aimed at generating productive mathematics classroom discussions, several additional characteristics have been identified, for instance producing distributed answers (Cline et al., 2022); focusing on analysis and reasoning instead of calculation or memory recall (Lim, 2011); having different possible answers or no correct answer (Gustafsson & Ryve, 2022); focusing on typical misconceptions or mistakes (Gustafsson & Ryve, 2022; Lim, 2011); and displaying different possible correct and incorrect solutions, strategies, or methods (Gustafsson & Ryve, 2022).

Teacher Goals and Actions in Productive Whole-Class Discussions

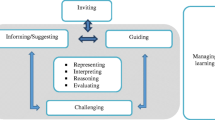
To give all students opportunities to engage and learn from whole-class discussions and make the discussions more productive, teachers can apply different types of teaching moves. Teaching moves are defined by Jacobs and Spangler (2017, p. 778) as “actions that teachers take that observers can see or hear, such as asking questions, providing a representation, or modifying a task.” Michaels and O’Connor (2015) see moves as a tool that teachers can use to accomplish various goals related to promoting different student actions, and point out that productive moves are strongly associated with student learning.

There are several important goals that these teaching moves should address in order to achieve productive discussions (Jacobs & Spangler, 2017; Michaels & O’Connor, 2015). Firstly, teachers need to elicit students’ thinking, for example by inviting and encouraging them to share their thinking (da Ponte & Quaresma, 2016; Michaels & O’Connor, 2015). The use of wait time can also be an effective teaching move to elicit students’ thinking (Chapin et al., 2009), as can pressing them for elaboration and clarification. Secondly, teachers must engage students with their peers’ mathematical thinking, because without this engagement there is no discussion (Jacobs & Spangler, 2017). Some typical teaching moves related to this goal involve encouraging students to add something more to peers’ contributions; restating or explaining peers’ solutions; comparing their thinking with that of others; and commenting on, evaluating, or developing peers’ ideas (Cengiz et al., 2011; Chapin et al., 2009; Franke et al., 2015; Herbel-Eisenmann et al., 2013; Jacobs & Spangler, 2017). Thirdly, teachers ought to support students’ mathematical thinking. Some common moves in relation to this goal are the following: asking students to repeat, revoice, or clarify; summarizing a lengthy discussion; doing a piece of mathematics; making connections; drawing attention to specific ideas; and controlling the pace of the discussion (Jacobs & Spangler, 2017; Michaels & O’Connor, 2015). Fourthly, teachers can support students in deepening their reasoning by challenging their actions (da Ponte & Quaresma, 2016), for instance pressing them for connections, elaborations, and justifications (Brodie, 2010; da Ponte & Quaresma, 2016; Jacobs & Spangler, 2017).

Methodology

This study was conducted by implementing an intervention that supports teachers with MC tasks to be used with a CRS in order to achieve productive whole-class discussions. To do this, design principles developed and presented in a previous paper (Gustafsson & Ryve, 2022) guided the creation of the implemented mathematical MC tasks. Furthermore, to characterize and give a detailed description of the teacher-led whole-class discussion, the author chose to analyze the data using Drageset’s framework (Drageset, 2014, 2015a, 2015b) for describing and analyzing teacher and student actions. This framework was developed using data with a conversational analysis approach in the context of teacher-led discussions in mathematics in upper primary school (students aged 10–13) in Norway. It is a detailed framework with concepts for exploring teacher-led discussions on a turn-by-turn basis in order to understand how an action by either a single teacher or a single student could contribute to practice and student learning. To supplement Drageset’s framework, measures for students’ opportunities to talk were used to describe the extent of student participation and teacher domination in the whole-class discussions.

The Intervention with MC Tasks and CRS

The intervention’s main focus is to generate mathematical discussions by implementing MC tasks supported by a CRS. MC tasks consist of a question or instruction in the stem. The stem is followed by two to five options tagged with the letters A, B, C… These options consist of either no, one, or several correct choices and no, one, or several incorrect choices called distractors. In this study, a web-based CRS (sometimes called clickers or a personal, classroom, instant, or audience response system) was utilized to support the implementation of these MC tasks. This CRS consisted of a teacher’s computer connected to a projector screen, one computer for every student, and a CRS application. The CRS helped the teachers to launch tasks and, after this, collect and monitor students’ responses in real time and compile their responses in a bar chart. Thus, the teachers could quickly analyze the results and then decide whether and how to conduct peer and whole-class discussions. The implemented activity structure in this study entailed (1) launching the MC task with the CRS and letting all students think for themselves until the teacher decided it was time to submit an answer; (2) students answer individually using their own computers; (4) presenting to the class a summary of the students’ answers in a bar chart on a shared screen; and finally (5) leading a whole-class discussion, based on students’ responses and peer discussions, to elicit and advance their thinking and knowledge.

Participants and Context

The author recruited twelve teachers, nine from Sweden and three from the UK, from secondary schools (with students’ ages ranging from 13 to 17 years). In this study, the intention with using data from two countries was not to conduct a cross-cultural study to explore similarities and differences between the countries; using teachers from two countries rather involved a triangulation of data sources and sites to strengthen the study’s credibility by reducing the local factor effect (Shenton, 2004). The choice of countries and the number of participating teachers was mostly a consequence of my opportunities to recruit. It is possible that the cultural contexts might have influenced the intervention’s implementation; this should be investigated in further research. Further, all teachers had experience of teaching mathematics and were confident in using technology to support their instruction. They also had some experience of using a CRS in the classroom, and all their students had encountered and used CRS during instruction.

Construction and Selection of CRS Tasks

To construct appropriate tasks, the author applied Gustafsson and Ryve’s (2022) framework for creating MC tasks to be used with CRS. This framework was constructed and developed within a design research project by cumulatively building on research from different contexts and evaluating in practice along with mathematics teachers at secondary schools. The work was based on earlier research on mathematics instruction, MC tasks, and instruction supported by CRS. The framework comprises three design principles (DP), supplemented by six task types that fulfill and concretize these principles. DP1 focuses on students’ conceptual understanding, DP2 on students’ understanding of procedures, and DP3 on collecting and resolving students’ common misconceptions and mistakes.

Eleven out of twelve teachers implemented three types of tasks, each constructed from one of the three DPs. One of the teachers from the UK ran out of time and thus implemented only two tasks, the conceptual (DP1) and the misconception task (DP3). Based on each teacher’s desired content and difficulty level, the author constructed drafts of many different tasks concerning each DP. After this, the teachers had the opportunity to choose tasks and propose changes to their formulations, contexts, or difficulty levels. Finally, the author revised the tasks and showed them to the teachers to accept or decline.

To construct tasks aligned with DP1, a combination of the task types Odd one out with Multiple defendable answers (Gustafsson & Ryve, 2022) was used. Figure 1 shows an example of such an implemented task.

Fig. 1
figure 1

Example of a task aligned with DP1

Full size image

The task type Evaluating solutions was used to construct tasks aligned with DP2 (Gustafsson & Ryve, 2022) and these tasks sometimes also contained common mistakes, thus also being aligned with DP3. Figure 2 shows an example of a procedural task that elicits a correct solution and different common errors.

Fig. 2
figure 2

Example of a task aligned with DP2 and DP3

Full size image

To construct tasks in alignment with DP3, the task type Trolling for misconceptions or mistakes (Gustafsson & Ryve, 2022) was applied. Figure 3 shows an example of such an implemented task.

Fig. 3
figure 3

Example of a task aligned with DP3

Full size image

To support the implementation of tasks, all teachers were given access to a simple teaching guide with the above-described activity structure and comments on every selected task. The comments on the tasks included the aim, explanations of every choice, why choices were correct, and comments on common mistakes or misconceptions that could be reasons for incorrect choices.

Data Source and Data Collection

The data sources to be analyzed consisted of 35 whole-class discussions, built on 35 implemented MC tasks supported by a CRS, and conducted during twelve teachers’ lessons.

Before filming the lessons, all participating teachers and students (and their parents) were informed about the study and filled out a consent letter. The author then filmed the lessons with two cameras on tripods. One camera was installed at the front of the class, focusing on almost all the students. Students who had not signed a letter of consent to be filmed and to participate in the study were either placed outside the camera’s range or outside the classroom. The second camera was positioned at the back, focusing on the teacher and the board. The author operated this camera in order to be able to follow the teacher. The cameras’ positions did not impede the students or teachers, which Kimura et al. (2018) point out is important. An extra microphone was attached to the teacher to ensure a good sound recording of the teacher’s talk. The students’ talk was recorded only with the cameras’ microphones; therefore, it was sometimes hard to distinguish which student had made an utterance. The focus on teachers was a deliberate choice, because teachers are central actors in achieving a productive whole-class discussion (Stein et al., 2008).

The Analytical Framework

Table 1 shows that Drageset’s framework (2014) consists of 13 categories of teacher actions and five student actions. The teacher actions are divided into three superordinate categories of redirecting, progressing, and focusing actions.

Table 1 Drageset’s analytical framework with teacher and student actions
Full size table

Redirecting actions redirect students’ ideas by either putting aside their contributions by rejecting or ignoring them, explicitly advising them on a new strategy, or asking correcting questions that reject their ideas (Drageset, 2014). Progressing actions help teachers move the process forward. In demonstrations, teachers perform the work, often by solving tasks themselves (Drageset, 2014). When simplifying, teachers give a hint or change the task to reduce its difficulty level (Drageset, 2014). Closed progress details involve actions in which teachers move a solution process forward one step at a time (Drageset, 2014), and in open progress initiatives teachers pose open questions to which there is more than one acceptable student response (Drageset, 2014). Further, redirecting and progressing actions are central elements of funneling, in which the teacher dominates the discussion. Students’ thinking is limited to figuring out the one and only “correct” response the teacher is looking for (Drageset, 2014). This practice in isolation does not promote a productive mathematical discussion. However, as Drageset points out, redirecting action can help keep the class on track, and progressing actions can be helpful when it is necessary to speed up the process. Therefore, redirecting and progressing actions can play essential roles in productive discussions if applied wisely in specific situations (Drageset, 2014).

Further, teachers’ focusing actions place attention on important mathematical details by either requesting student input or pointing out something themselves (Drageset, 2014). Teachers can ask students to enlighten important details, make a justification, apply the knowledge to solve a similar task, or assess a contribution from a peer student (Drageset, 2014). Finally, teachers can point out important details by recapping a student’s contribution by summarizing and closing the discussion or getting the students to notice something during the discussion (Drageset, 2014). In addition, focusing actions include actions that have the potential to elicit and advance students’ thinking and move the interaction away from “show and tell,” according to Drageset (2014). Therefore, these actions are essential to a productive mathematical whole-class discussion. For example, by requesting students’ input teachers elicit their thinking, and by pressing for justification teachers can support them in deepening their reasoning (Jacobs & Spangler, 2017). Further, the action pointing out can support students’ mathematical thinking, which is an important goal when conducting a productive discussion (Jacobs & Spangler, 2017; Michaels & O’Connor, 2015).

Drageset (2015a) has developed five categories of student actions related to the mathematical content. Explanations are student responses to teachers’ requests involving explaining concepts, reasons, and methods (Drageset, 2015b). In student initiatives, students ask questions about what and how, provide suggestions, correct the teacher or other students, and point out mathematical details (Drageset, 2015b). Partial answers are incomplete student responses, neither entirely correct nor completely incorrect (Drageset, 2015b). Teacher-led responses are correct responses to simple questions from either a closed-progress-detail or a simplification teacher action, quotes by the teacher, or confirmations or rejections of the teacher’s suggestions (Drageset, 2015b). Finally, unexplained answers are either correct or incorrect answers without explanations or with no response at all (Drageset, 2015b). Further, these categories of student actions have different qualities that contribute to a productive mathematical whole-class discussion. In productive discussions, it is evident that students’ explanations of reasons, concepts, and methods are an essential element, as are student initiatives. According to Drageset (2015a), teacher-led responses can be related to funneling, but he also states that all five categories may play an important role in developing students’ mathematical knowledge.

Hiebert and colleagues (2003) argue that students must speak more than single words or short phrases if their participation can be qualified as active. Therefore, they suggest that measures based on spoken words can be used to describe students’ opportunities to talk. A measure of students’ opportunities to talk can then provide an indirect indication of active student participation in whole-class discussions and describe the extent to which the teacher dominates the discussions. Based on this concept, I chose to analyze and describe students’ opportunities to talk in whole-class discussions in relation to implemented tasks by applying the following measures: (1) the average length of time of the discussions, (2) the total number of teachers’ and students’ words, (3) the average of teachers’ and students’ words per discussion and words by turn, and (4) the average of teachers’ ratio in teacher-student talk.

Data Analysis

A teacher-led whole-class discussion is based on communication between the teacher and all the students in a classroom. In these discussions, each turn is highly dependent on the previous turn. Therefore, the discussion can be seen as a construction created by the jointly coordinated actions of different actors (Linell, 1998). To characterize the whole-class discussions, the author chose to analyze and categorize teachers’ and students’ actions turn-by-turn by applying Drageset’s framework (Drageset, 2014, 2015a, 2015b).

The analysis of the whole-class discussions was performed in an iterative process. The author watched all 35 whole-class discussions, wrote a narrative of each discussion, and noted the duration of each discussion. After this, all the discussions were transcribed with timings in Nvivo 12, and inaudible parts and pauses longer than one second were observed. In these transcriptions, student speakers who were not identified were recorded as “S” and identified student speakers as numbers in order. All student names are fictitious.

Thereafter, the analytical framework (Drageset, 2014, 2015a, 2015b) was applied, and all teacher and student actions were coded according to the framework’s 13 categories of teacher actions and five categories of student actions. It is important to note that all coded teacher actions were a reaction to students’ actions in relation to the tasks, and all actions were analyzed as part of the discussion, whereby each action could be seen as a response to the previous actions.

Table 2 shows a summary of the total number of analyzed whole-class discussions and associated teacher and student actions in relation to the different types of implemented tasks.

Table 2 Number of analyzed discussions and actions
Full size table

The author coded all the data, and then discussed analytical difficulties with two colleagues with extensive experience in classroom research. For example, one analytical difficulty involved teachers asking a student to repeat their contribution. We agreed that if it was obvious that a student’s response was incorrect it would be coded as a correcting question and if it was obvious that it was an important and correct contribution it would be coded as a focusing action. Thereafter, the author re-analyzed all the teacher and student actions. Once again, analytical difficulties were discussed with the same two colleagues, and the author then re-analyzed the teacher and student actions. After coding the data, the mean of the number and the mean of the percentage of each category of teacher and student actions were calculated and noted according to the three types of implemented tasks. Then, a quantitative summary of all actions in relation to each task type was made. Finally, a word count of all the teacher and student talk in each whole-class discussion was conducted. To measure this, the mean ratio of spoken teacher and student words and a mean of words by turn were calculated for each implemented task type.

Results

This section presents quantitative descriptive summaries of the discussions in relation to the three types of implemented tasks. The summaries include aspects of the teachers’ and students’ participation and actions. Selected and coded transcript excerpts are presented to illustrate typical actions in their function in a discussion. Finally, a comparative summary of the characteristics of all examined aspects in the whole-class discussions is presented.

Students’ Participation

Table 3 presents a summary of teacher-student talk in relation to discussions based on the three types of implemented tasks.

Table 3 Summary of teacher-student talk in whole-class discussions
Full size table

As shown in the table, the teachers did most of the talking in the discussions on all types of tasks, with students speaking an average of 7.7 to 8.5 words by turn in the discussions. The discussions on understanding procedures stand out slightly. These discussions had a teacher-student word ratio of 4.4, which is 1.4 more than the 3.0 ratio in the discussions on conceptual and misconception tasks. Moreover, the discussions on conceptual tasks had the greatest average of student words by turn, 8.5 compared to 7.7 and 7.8. Altogether, this suggests that the discussions on procedural tasks were more teacher-dominated than those on conceptual and misconception tasks. However, the large difference in the standard deviation—3.1 for procedural tasks compared to 1.3 for the others—shows that there were greater differences between teachers in discussions on procedural tasks. This difference in standard deviation is primarily due to the greater difference in spoken teacher words by turn.

Teacher Actions

Table 4 summarizes the mean number and the mean value of the teachers’ percentage of used actions in the discussions built on different task types. All numbers are rounded. Overall, the table shows that there are great differences between the use of different actions, and the standard deviation also shows that there are differences between teachers. However, there are differences and similarities between teacher actions in discussions on different task types that are worth pointing out.

Table 4 A summary of teachers’ actions in relation to type of implemented task
Full size table

Redirecting Actions

Discussions on all task types had a relatively low share of redirecting actions (\(\approx\) 15%), of which the action put aside (\(\approx\) 10%) was the most common.

Teachers often redirected by simply ignoring a student’s comments and not providing any help. This was often followed by asking other students what they thought about another detail or the task in general, not specifically addressing the former student’s thinking:

T: The point (1.4) is on the line y = 8x – 4?

S: No. That’s not true either. Because then you start at minus four and then times eight.

T: Ok. Andy, you raised your hand before. What was on your mind?

S: I chose D because …

In discussions on all three types of tasks, teachers sometimes tried to redirect the discussion by asking correcting questions (\(\approx\) 5%) to the students, but almost never by advising on new strategies.

Progressing Actions

Teachers’ use of progressing actions to move the process forward was applied almost equally (29–32%) in all discussions. However, there were some differences in use between different progressing actions. The discussions on conceptual tasks had a greater part of open progress initiatives (11%) compared to those on procedural (5%) and misconception tasks (8%). In these open progress initiatives, teachers tried to move the process forward without pointing out the direction, often by asking open-ended questions about how to reason or what to do:

T: I heard more suggestions than the answer 4. Does anyone have another suggestion? Lisa, you had a suggestion.

S1: Sixteen. Minus sixteen is a two-digit number.

Another notable result is that the discussions on conceptual tasks had a smaller share of closed progress details (8%) actions than open progress initiatives (11%). The results are the opposite in discussions on procedural and misconception tasks. In these discussions, closed progress details (13–14%) were used twice as much as open progress initiatives (5–8%). Furthermore, discussions on the procedural tasks also had a larger share of simplifications, 9% compared to 6% and 4%.

The simplifications were used to simplify the task, often by giving hints or adding information when no students responded:

T: When do we say this rule can be applied? ((The teacher writes P(A) x P(B) on the board))

No one raises their hand or takes the initiative for three seconds.

Selma, do you remember? I know you missed some lessons, but I think you’ve heard it.

Two seconds of silence.

There were two rules, where one was the AND rule and what was the other rule?

S:OR

T:The OR rule. …

Also, it is worthwhile to note that in Table 3 approximately 4% of the actions in all discussions were demonstrations in which the teacher demonstrated or explained one or several steps of a solution.

Focusing Actions

Table 4 shows that discussions on all three task types consisted of more than 50% productive focusing actions, especially those in which the teacher recaps (\(\approx\) 19%) a student’s contribution to sum up, streamline or clarify, and then terminate the discussion or line of thought:

S:I did a as 5. And then I took b as 4. Then I got 254. And then I find the closest number to 254, which is alternative B.

T: OK, so what Mohammed said he did was he swapped this a for a 5 because a is equal to 5, and he swapped out this b for a 4 because b is equal to 4 (points at the expression 2ab on the board). And that’s 254.

In these focusing actions, the point out action of noticing was used more frequently in discussions on misconception tasks (13%) than in those on conceptual (8%) and procedural tasks (11%). In the discussions on misconception tasks, this action was used to notice important details about concepts that could strengthen students’ understanding or give them essential elements to use in their explanations:

T: Do you remember last Monday when we talked about this (0.5) with time in decimal form? And I think Phil said “wait, there’s not 100 minutes in an hour?”.

In discussions on all three task types, about every fourth teacher action was a productive action requesting more student input, but there are some differences between the actions used in the discussions. The discussions on the conceptual tasks had a larger share of justifications than those on procedural and misconception tasks, 15% compared to 10% and 11%. The justifications in the discussions on conceptual tasks were often used to request input (15%) from students about why they had selected a specific choice in the MC tasks or why their selected choice was correct:

S: We chose C.

T: You chose C. Why?

Sometimes justifications were used as a response to students’ unexplained answers.

T: They’re different numbers. So, tell me about that equation here. (Points at the equation x + 2 = x + 3 on the board.) Tell me whether this is true or not.

S: No, that isn’t true.

T: Why isn’t it true?

In the discussions on procedural tasks, the justifications were sometimes applied to press students to explain why the fictive student solutions were or were not correct:

S: I thought none was correct. … As we calculated, we concluded that none was correct.

T: How did you calculate that? Can you explain?

Another common action in all discussions was the teacher asking questions to enlighten important details (\(\approx\) 10%) in students’ contributions. Further, in discussions on all task types, teachers seldom used actions asking students to assess other students (\(\approx\) 3%) or invited them to apply their knowledge to a similar task (1%).

Student Actions

Table 5 presents a summary of student actions in relation to discussions of different task types. It includes the mean number of actions and the mean value of the students’ percentage of used actions in relation to each implemented task type. All numbers are rounded.

Table 5 A summary of students’ actions in relation to type of implemented task
Full size table

As can be seen in Table 5, the student action teacher-led responses had the highest mean percentage in discussions on all three task types. In these responses, the most common student action was a correct response to teachers’ simplifications or closed progress details actions:

T: So, what technique do we have to use in this question here? What mathematical technique have we learned about do we have to use in this question? Yes, Sarah.

S: You have to expand brackets.

T: Very good.

These teacher-led responses were more common in discussions on procedural (36%) and misconception tasks (32%) and less in those on conceptual tasks (23%). In addition, the discussions on conceptual tasks had the lowest standard deviation of teacher-led responses, 10 compared to 14. Furthermore, student explanations in which students performed correct explanations of concepts, reasons, or methods used were used to almost the same extent (14–15%) in discussions on all task types. However, when analyzing the transcripts in detail, I noted some differences. The discussions on conceptual and misconception tasks contained several examples of students explaining concepts:

T: This word is important (points at similarity). That they’re similar. Peter?

S: Similarity means that if one side increases by three times then the other side also has to increase by three times. For it to continue... still have the same shape.

Teachers sometimes requested that students explain their reasons in the discussions on procedural tasks:

T: Plus. Why plus?

S: Because they’re both positive.

Further, also in the discussions on procedural tasks, teachers sometimes asked students to evaluate or explain methods used in the fictitious solutions in the MC tasks:

T:Someone who suggested Abasi? What do you think about his solution then?

S: He first calculates what 15% of 74,000 is. Then 74,000 minus 15%. And then he takes 15% of the new number and so on.

Another notable result is that unexplained answers, including unexplained correct and incorrect answers as well as situations in which students could not answer a teacher’s question, were more common in discussions with a conceptual focus (22%) than in those on the other two types of tasks (14–19%). The data provided some examples of how teachers could respond to students’ unexplained answers. In this first example, a student cannot answer, and the teacher ignores this student and redirects the question to another student:

T: Nour, what are your thoughts about Robert’s idea here?

S1:I don’t know.

T: Chris, what are your thoughts about Robert’s approach?

When students gave a correct or an incorrect answer without explanation, teachers often responded with a justification action:

S1:I think he’s wrong.

T: You think he’s wrong. Why do you think he’s wrong?

Further, student initiatives were less common in discussions on misconception tasks (11%) than in those on the other two task types, 17% and 19%. Moreover, partial answers, including incorrect and incomplete explanations, were roughly equally common in discussions on the different task types (19–23%).

Discussion

In this study, I explored the characteristics of mathematical whole-class discussions generated from three types of MC tasks. The analysis was based on 35 whole-class discussions conducted by twelve teachers.

The first research question concerned the extent to which students actively participate in whole-class discussions. As presented in the “Results” section, the mean duration of the whole-class discussions varied from 6:30 to 8:00, the ratio of teacher-student talk was about 3:1 on average, and the average number of spoken student words by turn was about eight in all three task types. These results indicate that students had opportunities to talk and thus actively participated in the whole-class discussions, although the teachers dominated the discussions. The results of this study strengthen earlier findings suggesting that CRS has the potential to create opportunities for active participation by students (e.g., Latulippe, 2016; Lucas, 2009). However, earlier research in this context has built its results on teacher and student perceptions (King & Robinson, 2009a, 2009b; Lucas, 2009), the mere fact that almost all students give a response to a task (Latulippe, 2016), or the fact that students had the opportunity to talk in peer discussions (Lewin et al., 2016; Lucas, 2009). This study contributes knowledge about student participation in mathematical whole-class discussions by building on data from several observations. Teachers’ actions might partly explain the results, as teachers play a crucial role in creating opportunities for students to actively participate in whole-class discussions (e.g., Stein et al., 2008). The teacher actions described in the results indicate this, and are discussed below. Further, Boscardin and Penuel (2012) suggest that this student engagement can be explained by the possibility for anonymity when responding to tasks launched by a CRS. However, students are not anonymous during the whole-class discussions; it is only the individual students’ responses to tasks displayed in the bar chart that are anonymous. Thus, further research could investigate how CRS and MC tasks influence student engagement in whole-class discussions, for example by exploring interaction patterns in how teachers use the displayed bar chart to engage students in these discussions.

The second research question focused on the categories of teachers’ and students’ actions in these whole-class discussions. The analysis showed that in the whole-class discussions on all three task types, more than half of the teachers’ actions in response to students’ mathematical contributions were focusing actions. These consisted mainly of actions involving the teachers requesting students’ input to enlighten important details, make justifications, or point out important mathematical elements themselves in order to support the students’ reasoning. These focusing actions are essential for achieving a productive discussion with opportunities for students to participate and learn (Drageset, 2014). However, the results also show a low number in regard to the focusing action requesting assessment from other students to promote students’ engagement in their peers’ thinking. This is an important action in productive discussions (Herbel-Eisenmann et al., 2013) and can engage students with their peers’ mathematical thinking (Jacobs & Spangler, 2017). Further, about 15% of all teacher actions were redirecting actions, and 30% were progressing actions in which the teachers asked closed questions about details or open-ended questions about how to reason or what to do. These actions in isolation do not promote a productive mathematical discussion, but can be helpful in productive discussions when it is necessary to speed up the process (Drageset, 2014).

Concerning student actions, in discussions on all task types, teacher-led responses were the most common student action used in almost every third action. Still, they were more common during discussions on procedural tasks. Teacher-led responses are related to funneling (Wood, 1998), in which the teachers do the mathematical work and students respond to short-answer questions. However, about half of the student actions belonged to categories in which students performed either a correct explanation of reasons, concepts, or procedures in student explanations or a partial but incomplete explanation in partial answers, or made an initiative on their own. This indicates that students often contributed by sharing and explaining their mathematical thinking during discussions on all three task types. These latter student actions are characteristic of productive discussions (Jacobs & Spangler, 2017; Michaels & O’Connor, 2015). Thus, it is not the case that they merely performed short teacher-led responses or could not present an answer.

The results show minor differences concerning teacher and student actions between the three task types. However, there are some initial indications of differences in the relationship between task type and the characteristics of the teacher and student actions for further detailed research to study in depth. One such difference was noted concerning discussions on conceptual tasks, compared to discussions on the other two task types. Concerning teacher actions, discussions on conceptual tasks had more justifications and open progress actions and fewer closed progressed details actions. However, these teacher actions might be related to the task type itself. The implemented conceptual task type Odd one out had multiple defendable answers. In these tasks, students were to explore how and why all choices except one belonged together and identify which choice was odd and did not belong (Gustafsson & Ryve, 2022). This type of task could encourage teachers to ask open questions such as “how are you reasoning,” press for justification, and ask why a specific choice is the odd one out. Further indications included the fact that the discussions on the conceptual tasks contained more student initiatives. A suggestion for understanding this indication is that it could be related to the task type attribute of multiple defendable answers. This attribute can create disagreement when students find different solutions to the tasks, which might trigger them to take their own initiative in discussions. This enhances the possibility for a natural spread among answers, which is essential for generating a discussion (Cline et al., 2022). However, more research is needed to understand how task types in MC format supported by CRS influence students’ opportunities to participate and learn in whole-class discussions. This could be done by thoroughly exploring different interaction patterns involving different task types.

To summarize, one of this study’s contributions is that it describes the characteristics of 35 whole-class discussions that originate from MC tasks supported by CRS, based on a mixed-method analysis of rich data from secondary schools in Sweden and the UK. Earlier research has suggested that this intervention has the potential to support teachers in generating productive classroom discussions (Cline et al., 2013, 2022; Gustafsson & Ryve, 2022), although experiments (e.g., Dix, 2013; Shaheen et al., 2021) have shown ambiguous effects on student learning. However, there is a lack of studies exploring what happens during these classroom discussions on MC tasks, and there are few published mixed-method studies based on data from a large number of mathematical whole-class discussions (Herbel-Eisenmann et al., 2017). The findings in this study indicate that if teachers wisely implement well-designed MC tasks supported by CRS, and apply productive teacher actions during whole-class discussions, they can achieve productive discussions in which students have the opportunity to improve their learning. By exploring in depth what happens in the classroom during instruction supported by CRS, we can likely explain these ambiguous results concerning improved student learning.

Despite limited support, the teachers in this study generally achieved whole-class discussions with active students and productive teacher and student actions. Thus, I argue that these results indicate that MC tasks supported by CRS are not highly complex to implement, and that Gustafsson and Ryve’s (2022) framework for task design can support teachers in dealing with the identified challenge of constructing or selecting effective MC tasks (e.g., King & Robinson, 2009b; Lee et al., 2012).

In this study, I developed and applied a mixed-method approach in order to explore several whole-class discussions in the CRS context. The approach draws heavily on Drageset’s (20142015b2021) framework for analyzing single teacher and student actions, and was supplemented with measures for students’ opportunities to talk. Thus, one suggestion for further research is to examine the potential of this methodological approach in other contexts. For example, one could implement this intervention with MC tasks and CRS, apply the same analytical approach, and explore whole-class discussions before, during, and after teachers participate in a PD program. This methodological approach might help researchers to build up knowledge about the important practice of leading mathematical whole-class discussions (e.g., Wester, ) in the context of CRS and thus decrease the identified lack of research in this area.