Introduction

Within the current climate of STEM education and integrated learning, mathematics faces both opportunities and challenges. Several educators have highlighted the central role of mathematics within STEM programs, with Lyons (2018) indicating that while all four disciplines are essential to the STEM construct, “mathematics is foundational” (p. 40). In a similar vein, Mayes (2019) argued that mathematics is fundamental to integrated STEM activities, while the Committee on STEM Education (2018) listed “Make mathematics a magnet” as a core objective in engaging students in transdisciplinary experiences.

Despite mathematics being cited as the core of STEM education and foundational to the other disciplines, it is frequently ignored in integrated STEM activities (English, 2016; Mayes, 2019; Shaughnessy, 2013). Yet, as Baldinger et al. (2021) highlighted, “Despite at least a century of educational interest in connections between mathematics and science (Berlin & Lee, 2005), the role of mathematics in integrated STEM teaching and learning remains unclear, understudied, and misunderstood” (p. 68). Likewise, Tytler (2016) warned that there needs to be an explicit focus on the mathematical concepts and processes that arise in STEM activities. Without this focus, STEM programs run the risk of “sidelining mathematical thinking into minor and unproductive roles” (p. 8). If children fail to see meaningful links between their learning in mathematics and the other STEM domains, they can lose interest not only in mathematics but also in the other disciplines (Kelley & Knowles, 2016).

One of the under-researched challenges in STEM integration is not only making connections between the disciplines and between context and disciplines but also making these connections explicit to students (English, 2016; Roehrig et al., 2021). Complicating this challenge are the various forms of STEM integration reported in the literature. Multidisciplinary, interdisciplinary, and transdisciplinary approaches are frequently cited, with various definitions proposed (e.g., Bybee, 2013; Vasquez et al., 2013). Research suggests that multidisciplinary approaches yield the best outcomes for students to apply disciplinary content and develop an understanding of the ways in which this content is connected (Roehrig et al., 2021). Such approaches enable two or more disciplines to be foregrounded “explicitly and purposefully” in an integrated STEM investigation, which is not always the case in efforts to integrate two or more disciplines (Baldinger et al., 2021; Roehrig et al., 2021, p. 9).

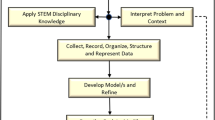
A multidisciplinary approach is adopted in the present investigation, given that the associated STEM disciplines are identifiable within the curriculum and require students to have some understanding of the required content (cf. Honey et al., 2014). The study reported in this article incorporated mathematics, statistics (Groth, 2015; Moore, 1988), and science, together with STEM practices (Fig. 1). Three classes of sixth-grade primary school students (n = 50) engaged in a simulated tsunami investigation, where they created “waves” that hit “land” at different angles in specially designed water tubs. The specific focus was on how varying the slope of the shoreline affects the inundation distance. The following research questions were explored:

  1. 1.

    How did students apply STEM content knowledge and embodied actions in justifying their predictions for the inundation distances as the slope angles varied?

  2. 2.

    What was the nature of students’ multidisciplinary modelling in undertaking the investigation?

  3. 3.

    How did students identify (a) variation and (b) covariation within their modelling?

  4. 4.

    How did students apply their learning in suggesting how to minimise the impact of a real-world tsunami?

Fig. 1
figure 1

Multidisciplinary modelling

Full size image

Multidisciplinary Modelling

It is well established that models and modelling can provide rich tools for fostering integrated and real-world STEM experiences. Modelling affords students opportunities to express and develop multidisciplinary STEM understandings, apply different ways of thinking, and engage in decision-making in the face of uncertainty (Baker & Galanti, 2017; Hallström & Schönborn, 2019; Hjalmarson et al., 2020). As such, models can be integrated within STEM investigations at different developmental points in students’ learning but are yet to be utilised fully in the elementary curriculum.

There are numerous definitions of modelling in the literature, as illustrated in Hallström and Schönborn’s review (2019). As used here, models are systems that describe, explain, construct, modify, or predict a series of experiences (Brady et al., 2015). The conceptual framework developed for this study is what I term multidisciplinary modelling (Fig. 1).

Multidisciplinary modelling draws on two or more of the STEM disciplines, with key disciplinary content foregrounded and STEM practices applied (c.f. Kelley & Knowles, 2016). As part of the overall modelling experience, students undertake sensory and motor actions within a real-world context (Abrahamson & Lindgren, 2014; Fugate et al., 2019). In the present case, the context was that of tsunamis and their impact on coastal communities. Students’ embodied actions involved simulating tsunami waves through their actions of “pushing” water in a plastic tub and varying the shoreline slope to observe the impact on inundation distances. Students could see how changing the slope affects the inundation distance and how inconsistencies in their pushing actions could affect the reliability of their collected data. Such actions illustrate how modelling and concept development are highly interdependent and mutually supportive experiences (Brady & Lesh, 2021). As illustrated in Fig. 1, students’ creation of models drew on the data collected from their actions together with the application of multidisciplinary content knowledge and STEM practices, such modelling plays an important role in both mathematics and science learning (Lanouette et al., 2016; Lehrer & English, 2018).

As noted, the STEM disciplinary content of the investigation incorporated mathematics, science, and statistics, with mathematics and science sharing a reciprocal relationship (Panorkou & Germia, 2021). That is, mathematics was enriched through the science context, and science was enriched through the application of mathematics and statistics in model generation. Although commonly featured as part of mathematics in many curriculum documents, statistics has matured as a discipline in its own right (Groth, 2015; Moore, 1988). It is thus considered in this study to be a distinct discipline that provides common practices across the STEM fields, as illustrated in Fig. 1.

Modelling in oceanography plays a major role in developing better warning systems for tsunamis and global protection defences (Iverson & Prasad, 2007). Varsoliwala and Singh’s (2021) modelling of tsunami wave propagation identified tsunami velocity and height for various slopes and times. As the tsunami approaches the shore, its velocity reduces, and the wave amplitude increases initially and then as the wave approaches the coastline, it decreases due to shoaling. In accordance with tsunami physics, the tsunami wave amplitude is affected by the sea depth in mid-ocean and the distance to the shore. Varsoliwala and Singh’s modelling showed that the speed and height of tsunami waves are inversely proportional to the depth of the ocean.

STEM Practices

The multidisciplinary modelling experiences of this study included shared practices of the STEM disciplines, with a focus on statistical and modelling practices. As both practices encompass visual representations, they play a key role in linking the disciplines in the present investigation (Hallström & Schönborn, 2019). In line with the National Research Council (2012), the term “practices” is used in preference to “skills” to emphasise that both disciplinary knowledge and the associated disciplinary practice/s are needed in multidisciplinary modelling. Practices that entail working with data in a real-world context, where students generate, analyse, and represent their data in different ways, are increasingly important in the curriculum. Such practices need to commence early, but this is often not the case, with insufficient recognition of young students’ capabilities despite existing research showing otherwise (Cengiz & Grant, 2009; Konold et al., 2015; Lehrer & Schauble, 2007; Martinez & LaLonde, 2020).

Students’ experiences with these practices have traditionally involved decontextualised learning, with students presented with adult-created, finalised data and representations (diSessa & Sherin 2000; English, 2014; National Academies of Sciences, Engineering, and Medicine 2022). Such an approach limits students’ opportunities to participate in important data transformation processes and thus in modelling itself (Lanouette et al., 2016). Organising and structuring data are essential to students’ creation of models as systems of representation and for enhancing conceptual understanding (Lehrer & Schauble, 2007, 2017). Younger students have representational abilities that often remain hidden in research that typically targets older students and adults (diSessa & Sherrin, 2000). When students apply their disciplinary understanding in constructing and representing data in relation to a meaningful investigation, they are better able to appreciate the phenomenon of interest (Estrella et al., 2021; Lehrer & Schauble, 2007) and to detect trends in the data such as variation and covariation.

Identifying Trends: Variation and Covariation

The omnipresence of variability in data is fundamental to reasoning with data-based models. Variation may be defined simply as describing or measuring observable characteristics of variability (Innabi et al., 2022; Reading & Shaughnessy, 2004). Different sources of variability typically addressed in secondary school grades include variability within data, variability across samples, and variability between distributions (Shaughnessy, 2007). Understanding variation in data, which includes determining and justifying reasons for this variation, has received some, but insufficient, research in the younger grades (e.g., English, 2014; Makar, 2018). Unfortunately, many curricula have limited the required attention, especially in evidence-based reasoning (Siverling et al., 2021).

Covariation, which is complex for both students and adults, is usually reserved for the secondary school and college levels (e.g., Gil & Gibbs, 2017; Thompson & Carlson, 2017). There are numerous perspectives on covariation, including Thompson and Carlson’s (2017) notion of envisioning covariation in terms of how individual quantities vary followed by how two or more quantities vary simultaneously. For this study, covariation is viewed as an association between two variables pertaining to mathematics and science, where one explores the variability of the individual variables, identifies the shape and strength of the relationship, and explains and generalises the relationship (Gil & Gibbs, 2017; Watkins et al., 2004). Of interest in the present study was how the students would view the variability in the inundation distances, both within trials for a given slope and across trials with varying slopes.

Covariational reasoning is underrepresented in elementary and middle schools, with students afforded insufficient opportunities to experience variability in a range of contexts (Kelley & Knowles, 2016; Gravemeijer, 2000). Of the few studies, Panorkou and Germia’s (2021) research on gravitational force showed how covariational reasoning can support the reciprocal relationship between mathematics and science. Sixth-grade students reasoned about the change in the magnitudes and values of mass, distance, and gravity as they changed simultaneously, as well as their multiplicative change as they varied in relation to each other. The investigation developed students’ understanding of the distance between two objects and their masses as factors that influence gravity. Students’ construction of mathematical relationships between these quantities enabled them to explore gravity in more depth than it is typically taught. Despite these few studies, there appears limited research on younger students’ covariational reasoning, yet its foundations need to be established before formal study in secondary school and beyond.

Methodology

Participants

Three classes of primary school students (N = 50; mean age: 12 years) completed the tsunami investigation. The students were from an all-girls independent school in a middle-class suburb of a major Australian city. The students were in the final year of a four-year longitudinal project focusing on STEM-based modelling. The teachers were well-qualified and experienced in their profession, having taught across a number of primary and middle grades.

In the first 3 years of the study, the students had undertaken STEM investigations with a focus on foundational concepts and processes from statistics, mathematics, including probability, science, and engineering. Students had created their own models involving visual representations of their choice in their previous investigations. The present investigation built on the knowledge students had gained through their science unit on earthquakes and disasters, with a focus on tsunamis. Students were also aware of the destruction caused by these natural disasters through various media reports. The investigation was adapted from the Canadian Network for Ocean Education (https://oceanliteracy.ca/resources-for-educators/).

Implementation Procedures

The investigation was of approximately 3.5 hrs duration and implemented across 3 days in each of the sixth-grade classes. The teachers were supplied with detailed booklets that included the objectives of the investigation, background information on tsunamis, including video clips, the disciplinary content being addressed, the activity materials, and instructions for conducting the activity. The booklets served as a guide to the implementation of the investigation. The teachers did not “teach” the students on what was required; they simply ensured that the students understood the objectives and procedures of the investigation and knew where to record their responses in the supplied workbooks.

In groups of 3–4, students created “waves” that hit “land” in specially designed water tubs (Fig. 2). The experimental set-up involved a plastic tub, a land platform, and varying slope boards, with each slope board resting on the land at one end, and the other end resting on one of various “markers” in the tubs, enabling the slope boards to be placed at different angles to the shoreline. Each student within a group generated a tsunami wave with a “wave pusher”, travelling approximately 13 cm along the base of the tub and stopping when it hit the first row of tub markers. Each student had three practice attempts at creating a gentle wave that was not too strong or too weak. The student then undertook five trials of the wave pushing for each of the four slope boards. Students recorded their own data in a table in a specially created individual recording booklet.

Fig. 2
figure 2

Tsunami tub

Full size image

For each set of trials, the students were to predict what would happen to the inundation distance if the slope were steeper and were to justify their answers. Next, they conducted their trials for each slope board and recorded their data in their recording booklets. Following the collection and recording of all their inundation distances for each slope board, the students were to choose their own means of representing their data to display their findings. Using their representations, each student was to describe the variation in the inundation distances for each slope across the trials and consider why such variation occurred.

Next, they were to explore the covariation between the slope board angle and the inundation distance, using their representational model to justify their response. Students were asked subsequently how certain they were of their conclusion, how they might be more certain, and their reasons for their decisions. Finally, the students were to consider how the effects of a real-world tsunami might be minimised.

Prior to undertaking the investigation, students were asked what elements of the experiment must remain the same to ensure a fair test. (e.g., The “land” must be in the same position; the depth of the water must be the same; the way the wave is generated/strength of the wave must be consistent so that run-up energy is consistent; the way the inundation distance is measured/recorded must not vary; time should be allowed for the water to settle before creating the next wave).

Although students conducted the investigation in a group situation, they recorded their own data and responses for each component of the investigation. There was considerable variation in the responses of group members, such as group members constructing different representational forms.

Participation of Teachers and Researchers

Meetings were held with the teachers before and after implementation to explain the disciplinary content and implementation procedures and to obtain their feedback on the investigation outcomes, including the students’ progress. Together with the teacher, the research assistant and I observed the classroom implementation and the student’s actions, and where appropriate, answered any queries on procedures, but we did not interfere with their deliberations or with their recording and representations. At appropriate times, as we wandered around the classroom, we asked “how” and “why” questions to give us further insights into the students’ thinking, but we did not directly influence their actions or their model creations.

Multidisciplinary Content

Table 1 displays the specific components of the students’ curriculum that aligned with the investigation, with statistics cutting across domains.

Table 1 Curriculum components aligned with the investigation
Full size table

Data Collection and Analysis

Several forms of data collection were undertaken, including audio and video recordings of small group interactions as students completed the investigation, as well as whole-class discussions. Two groups in each class (referred to here as focus groups) were chosen for video recording and were used to illustrate in greater depth some of their responses and interactions. These groups comprised three or four students, who could converse and work together and were of mixed achievement levels. The teacher advised on the identification of students who met these criteria. The remaining student groups were audio-recorded.

A basic mixed-method research design (Creswell & Plano Clark, 2007) was adopted in answering the research questions. Qualitative analyses of the focus groups served to illustrate in greater depth some of the students’ responses and interactions in responding to the booklet questions. Iterative refinement cycles for in-depth evidence of students’ learning (Lesh & Lehrer, 2000) were used in analysing the class and group transcripts. Through repeated viewing of the transcripts, examples of focus group students’ responses illustrating aspects of the research questions were identified (e.g., students’ discussions on how covariation was displayed in their models).

Basic quantitative analysis (frequency distributions) was applied in addressing the research questions. For research question 1, namely, students’ application of STEM content knowledge and embodied actions in justifying their predictions of the inundation distances, consideration was given to students’ application of (a) mathematics (e.g., steepness, slope, distance, angle, and measurement); (b) science (e.g., energy, force, push, and resistance [difficulty in flowing up slope]); (c) embodied actions (e.g., comparing a wave moving up a slope to walking up a hill, swimming against a strong current, or other such bodily actions); and (d) statistics (e.g., referring to data on the previous slope/s, use of concepts such as mean, correctly using covariational reasoning [e.g., as slope increases inundation length distance decreases]).

For research question 2, namely, the nature of students’ multidisciplinary modelling in undertaking the investigation, the primary consideration was how the students represented their data and how they utilised their representations in identifying trends in the data. Students’ representations were coded in terms of the graph type and how the variables were presented on the axes.

In answering research question 3(a), namely, students’ identification of variation displayed in their models, students’ responses were coded according to whether they identified variation in inundation distances within the trials of a given slope, or whether they considered variation both within a given slope and across the slopes (local VS global views; Gravemeijer, 2000).

Research question 3(b), namely, students’ identification of covariation, was addressed with respect to their responses to the question, “How does slope affect inundation distance?” Of interest was whether the students recognised that the steeper the slope, the smaller the inundation distance, and whether they justified their response with reference to their models and to their understandings pertaining to mathematics, science, and/or statistics.

Finally, for research question 4, students’ application of their learning in suggesting how to minimise the impact of a real-world tsunami. Students’ responses to how the effects of a real-world tsunami might be minimised were coded according to their application of learning from the investigation and from their prior learning about tsunamis.

All students’ individual responses were recorded in their own workbooks. Students’ individual responses were coded using deductive coding (Miles et al., 2014), with the data then analysed using frequency distributions. Together with the senior research assistant, who was experienced in data coding, the coding of the booklet responses commenced using content analysis to generate codes aligned with the research questions. We then both undertook separate coding to refine the coding schemes through further data checking, including reviewing students’ workbook responses and transcripts of their group presentations.

Results

Research Question 1: Students’ Application of STEM Content Knowledge and Embodied Actions in Justifying Their Inundation Predictions as the Slope Angles Varied

Table 2 displays the nature of the justifications offered by the students for their inundation predictions for each of slopes 2 to 4.

Table 2 Justifications for inundation predictions for each of slopes 2–4
Full size table

As can be seen in Table 2, the most frequently given justification referred to mathematics only, with responses such as, “I predict that the inundation distance will be larger because the slope is steeper and that this will be a common trend with the different angles”; and “The 90° angle wall or vertical wall will make it very difficult for the wave to reach the shore as there is nowhere for the wave to flood over the wall in this design”. Comparatively fewer justifications focused on science only, for example, “It would be the hardest of all to get the water on to shore, since you need a lot of push since it is just before the shore, it takes a lot of energy to push the water up. And it might push the wave back since the wall also has energy”. An application of both mathematics and science was also prevalent, with responses including, “I think that the water won't go further because the slope is steeper and the inundation distance would be smaller since the water would need to use more energy to go further and will need to be a bigger wave”; “I predict that the inundation measurement will decrease as the steeper slope will provide more resistance and result in a shorter inundation distance”.

The application of statistics, including reference to previous inundation distance data and use of covariational reasoning, especially the latter, was evident in justifications such as, “From the data so far, I conducted a prediction for trial 3. My prediction was right and I believe it will be the same as trial 3. The steeper the slope, the shorter the inundation will be”. Although there were comparatively few references to embodied actions, there were interesting responses such as the following, which also included science understandings: “Because there is no slope, the wave does not get slowed down until it hits the shoreline and has no momentum other than the push from the wave creator. Almost like a ramp and staircase, you get a runup on the ramp, whereas on stairs you just have to jump, which is why ramps are so convenient”.

Research Question 2: The Nature of Students’ Multidisciplinary Modelling in Undertaking the Investigation

In addressing the second research question, consideration is first given to the nature of students’ representations in model creation (Table 3).

Table 3 Students’ representations in model creation (n = 50)
Full size table

The most common representation created was a vertical bar graph. Although not surprising to see the prevalence of these graphs given their common use in the curriculum, what was not anticipated was how students accommodated the three variables of slope, inundation distance, and trial within their representations (Figs. 3 and 4). Figure 3 displays inundation distances for each trial on each set of slopes, while Fig. 4 shows inundation distances for each slope on each trial.

Fig. 3
figure 3

Inundation distances for each trial on each set of slopes, with average distance shown

Full size image
Fig. 4
figure 4

Inundation distances for each slope on each set of trials, with average (A) inundation distance for each slope included, together with a key for the slopes

Full size image

As indicated in Table 3, only two students created stacked bar graphs (Fig. 5). Although such graphs could be considered a more economical representational form and can facilitate a comparison of the inundation distances across the slopes (Casey et al., 2019), they can also be more difficult to construct and interpret.

Fig. 5
figure 5

Stacked bar graph

Full size image

Less common were hand-drawn line graphs (Fig. 6) and horizontal bar graphs. Students were familiar with both these representational forms and had applied them independently in a previous investigation (English, 2022).

Fig. 6
figure 6

Line graph displaying inundation distances per trial for each slope, with the mean distances displayed for each slope

Full size image

When asked which representation they considered best displayed the data, students showed a preference for column graphs, as Amy explained: “In slope 1, the inundation distance is higher and it just kind of goes down (indicates with her finger on the graph) apart from a few odd ones that went up”. Rowena explained her preference for line graphs: “It shows us, for mine, it shows us each trial, so trial 1, trial 2, trial 3, trial 4, trial 5, and the mean for each slope … a side-by-side column graph, I feel that it is easier to read, like to visualise, because you can see all, like the bar graph, the columns, and you can see the decrease”. Another student commented on the line graph as “…easier to read because you see where it goes. Like, where it goes up, where the distance has gone further, and when it goes down that means the distance has gone shorter”.

Research Question 3: Students’ Identification of (a) Variation and (b) Covariation Within Their Modelling

Students’ identification of variation and covariation in their models and possible reasons for these trends were explored (research question 3 a, b). With respect to variation (Table 4), 34% of the 50 responses detailed the variation within slopes and across slopes or indicated the trends across the slopes. Responses of this nature included, “In my “trial data for tsunamis” it is obvious that slope 4 is definitely the hardest to climb and slope 1 is the easiest. You can tell because the data gradually decreases”; “The variation in each slope was that in all of the slopes the bars are causally moving down because of the type of the slope. This is the same for the average”; and “As the slopes get steeper, the distance measured decreases. By looking at my graph, you can look at the averages to support my explanation”.

Table 4 Students identification of variation in their model creation (n = 50)
Full size table

Thirty-eight percent only indicated which slope had the lowest or highest inundation, such as “The variation in my representation increased as the slope went steeper, as the highest point on my graph was 31.5 cm shown on slope 1 and slope 2, and the lowest point 10 cm shown by the steepest slope, slope 4”. The remaining students simply read their data or made a general reference to the existence of variation.

When asked what caused the variation (Table 5), some students offered more than one explanation. Twenty-two percent of responses referred to the way in which the experiment was conducted, such as not being a “fair test”, while another 22% of responses simply stated that the different slopes caused the variation but gave no further explanation. Fifty-five percent of responses referred to the different slope angles and explained why these resulted in variation in their data. Responses here included, “The following is why this variation occurred: the averages decreased as the slope got steeper as when the slopes got steeper, it created more resistance for the water, causing it to travel less”. An interesting response referred to an analogous embodied action when explaining that the steepness of the slopes caused the variation: “The steepness of the slope, because if you think at a beach, a cliff with waves crashing into it, the waves don't magically fly up and travel 3 km”.

Table 5 Causes of variation (n = 58 responses*)
Full size table

Ways in which the students identified covariation in their models (RQ 3b) were revealed in their responses to the question, “How does slope affect inundation distance?” It is interesting to note that 40% of responses (59 total responses; 4 students absent; 12 non-responses) included disciplinary knowledge in their explanations, even though they were not prompted to do so. Examples of such responses included “As the slope steepens, the wave would have to require more energy to reach the same distance as before and would require more kinetic energy than a less steep slope”; and “It appears that the greater the angle of the slope, the inundation distance is less. Slope 1 has a larger inundation distance than slope 3 or slope 4”. Twenty-two percent of responses identified the covariation displayed but did not always include reference to specific data to support their responses. Examples of such responses included, “The steeper it is, the smaller the inundation distance because slope 1 had a mean of 22.2 (cm) while slope 4 had a mean of 8.3”; and “The slope affects the inundation distance because the steeper the slope, it does not go as far because it goes fast but does not rise high”.

Given that variation was inherent in the data that students generated, and any conclusions drawn were naturally subject to uncertainty (English & Watson, 2018), students were asked how certain they were of their responses to the question on covariation. Nearly half of the students (43%) justified their response by referring to the data in their model. Examples included, “I think that my conclusion is correct because my data proves that the distance made is affected by the steeper slopes and that the inundation distances get smaller as the slope gets steeper”; “My predictions were incorrect, but I feel that my conclusion [that the greater the angle of the slope, the lesser the inundation distance] was proven correct by the data collected”. “Quite certain because from my data representation, I can tell that there is a big variation from slope 1 and slope 4, slope 1 being the least slanted and slope 4 being the most”.

A few students (15%) acknowledged the possibility of inconsistent factors in conducting their investigation and/or the need to conduct more trials, as well as citing real-world tsunamis. Comments included, “I am about 95% sure as we have done lots of experiments, but we could also, to make us certain, we could conduct more experiments; and “I am not quite certain of this because tsunamis can change due to different magnitudes and this could change my data that was recorded”. One student expressed uncertainty due to the limitations of the materials used: “Not very certain because we only experimented with a plastic tub and cardboard. Which is not the actual force of a wave”.

Research Question 4: Student’s Application of Their Learning in Suggesting how to Minimise the Impact of a Real-World Tsunami

Students’ responses to how they might minimise the impact of a real-world tsunami were coded according to their application of learning from the investigation and from their prior learning about tsunamis. Some students offered more than one suggestion. Of the 56 responses (7 students were absent and 13 did not respond), the most common response (51% of responses) related to the students’ learning from the investigation. Responses in this category included, “If you piled up sandbags on a 90° (angle) because slope 4 was the less affected by the tsunami and floods”; “If you lived in a place where the slope is shorter, the impact of the tsunami would be less, as the inundation distance would be shorter. However, if you lived somewhere where the slope was only lightly slanted, you could build some sort of barrier to stop the wave from flowing all the way past the shoreline”. Charlotte’s response included her learning from the investigation and her prior learning of tsunamis: “I recommend that if you live in a tsunami-prone area, you do not live on flatter beach but that you live on a beach that is really steep or like move inland or even if you really want to live next to the ocean, you either live on a cliff or an elevated terrain area. And that you could build a 90° wall 50 m out from the shore of the area of residents”. Application of prior learning also included a few responses that referred to better home constructions, early warning alarm systems, and placing obstacles in the waves’ paths (e.g., “I could see the bushes in the experiments were stopping some of the water”.).

Discussion

With a focus on discipline integration in a STEM investigation, this study has illustrated how sixth-grade students can create multidisciplinary models involving mathematics, science, and statistics, where mathematics and science have a reciprocal relationship (Panorkou & Germia, 2021). Within the real-world context of tsunami inundation, simulated in water tubs comprising “landmasses” and “shore slopes” of varying angles, students explored how varying the slope of the shoreline affects the inundation distance. Students’ embodied actions in undertaking the investigation enabled them to observe the connections between the context and the disciplines. The key STEM practices facilitated their development of multidisciplinary models.

Such STEM investigations, where both mathematics and science are foregrounded, together with key STEM practices, are infrequent in the primary grades (National Academies of Sciences, Engineering, and Medicine, 2022). Students’ creation of multidisciplinary models is also lacking, despite research highlighting young students’ capabilities in modelling (English & Anderson, 2021). Four research questions were explored in the study. The findings pertaining to each are reviewed.

Students’ application of STEM content knowledge in justifying their predictions

Although the investigation did not encompass advanced mathematics and science content, it nevertheless enabled students to apply their knowledge of both disciplines, where an initial application of mathematics was prevalent, especially for slope 2. The application of both mathematics and science was also common in students’ justifications for their inundation predictions across the slopes.

Of interest is how students’ application of statistics increased on the remaining slopes, especially in their identification of covariation between slope angle and inundation distance. It appears that using variously angled slopes and measuring the inundation distances for five trials on each slope, together with determining the mean distances for each slope, enabled students to see this covariation relationship emerging. The importance of varying a critical aspect of a learning situation, in this case slope angle, reflects the core tenet of Marton’s (2015) variation theory, namely, people learn through first experiencing differences in situations, then similarities (Innabi et al., 2022). Learning is considered to take place when perceiving changes from one situation (in the present case, mean inundation distance for the first slope) to another, more complex situation (inundation means across several different slopes). By discerning a critical aspect of the mean inundation distance, namely, how it decreases as the slope angle increases, students came to appreciate the relationship between slope angle and inundation distance. Reference to embodied actions by a few students, such as swimming against a current, might have facilitated the appreciation of this relationship, but further research is required here.

Students’ Multidisciplinary Modelling

Organising and structuring data are essential to students’ creation of models as systems of representation and for promoting conceptual understanding. Students’ preference for representing their data in bar graph formats was not surprising, given these are typically featured in school curricula and displayed in textbooks (Batanero et al., 2018). Of interest is how students featured their data for the trials and slopes in creating their models. Most chose slope as the main category and displayed trials for each slope (Fig. 3). Fewer students chose trial as the main category, with slopes indicated for each trial. Given the variation in inundation distances both within and across sets of trials, students’ models did not always display clear trends in the data. However, once the mean distance for each slope was included, the identification of the key trend (i.e., decreasing inundation distance with each increased slope angle) could be more clearly discerned, reflecting characteristics of an ordered case value bar graph (Konold, 2002). Less common were models comprising line graphs (Fig. 6), which is not surprising given the nature of the data. Models comprising stacked bar graphs (Fig. 5) were also not common, even though students had independently developed such models in previous investigations (English, 2022). Although stacked bar graphs may be regarded as economical and displaying data trends effectively, they can be challenging for younger students and, when used in mass media, can become ineffective if many variables are displayed on a single bar (Indratmo et al., 2018).

Students’ Identification of Variation and Covariation Within Their Modelling

In line with Estrella et al.’s findings (2021), students’ construction of their own multidisciplinary models within a meaningful context facilitated their recognition of variation and covariation. Students were generally able to identify and explain the variation and covariation in their models, referring to aspects of their representations to support their responses. The inclusion of multiple trials for each slope revealed variation in inundation distances within trials for each slope as well as across slopes; this was especially the case for bar graph models.

The detection of covariation appeared to have been enhanced by the inclusion of the mean inundation distance for each slope, enabling students to obtain a global summary (Gravemeijer, 2000) of the relationship between slope angle and inundation distance. Students’ comments indicated they could more readily detect this relationship when considering the mean. For example, “The mean helps the representation by making it more accurate and the data easier to digest. It makes the representation more accurate by averaging multiple inconsistencies. It makes it easier to digest by giving you one number instead of 5 (for each slope)”; and “It makes it clearer, so you can just take a glance, and you will see which one takes less energy and most energy to push the water on shore”.

Students’ Suggestions for Minimising the Impact of a Real-World Tsunami

Students’ responses to this question included the application of their learning from the investigation as well as their prior learning about tsunamis. As indicated, over half of the responses involved applying what they had learned from their investigation to the real-world situation, with a number of responses applying both knowledge sources. Such responses may be considered an example of Engle’s (2006) “expansive-framing” perspective on transfer, where a given activity may be framed as useful for understanding real-world phenomena (Hohensee & Lobato, 2021). Such framing is considered more likely to occur when learning and transfer contexts display “intercontextuality” (Hohensee & Lobato, 2021, p. 14). When intercontextuality is high, as is obvious in the present investigation, the content learned is considered relevant and more likely to be applied to the transfer situation. Other possible transfer situations, such as those involving natural hazards, could also be incorporated into a related STEM investigation. Where possible, expansive framing should be included in classroom STEM investigations to foster more meaningful, relevant, and interconnected learning.

Exploring real-world reports on transfer situations can help students appreciate the generalisability of models and modelling (Lesh & Lehrer, 2000). For the present context, it is interesting to note Iverson and Prasad’s (2007) report on tsunami damage from the 2004 earthquake and tsunami in Indonesia. Using elevation, distance from shore, vegetation, and exposure as variables, they built “highly predictive” empirical models of vulnerability to damage; it was found that developed areas are far more likely to be damaged than forested zones (p. 323). Their modelling could thus be applied to other vulnerable zones across the globe, with recommendations such as constructing forest belts to dampen the impact of these destructive forces. Such examples can help students appreciate the real-world applications of multidisciplinary modelling.

Limitations

Limitations of this study include, firstly, the nature of the student sample, comprising students from a single-gender, non-state school. It was thus non-representative of the broader population of students. Incorporating a cross-section of students would enrich the present findings. Secondly, the use of a purposefully built “tsunami tub” with a “wave pusher” may be regarded as a limitation in the students’ data collection (as noted by one student), although the students were aware of ensuring fair tests. Thirdly, the although the investigation drew on both mathematics and science, the disciplinary content level could be more advanced. Students’ determination of different slope angles, rather than having these marked in the tub, would enhance this disciplinary content. Finally, consideration of ways in which the multidisciplinary framework and STEM investigations can inform teachers’ reflections on, and development of, their pedagogical knowledge and skills in implementing STEM investigations would add to the study.

Concluding Points

Creating integrated STEM investigations, where mathematics is not overshadowed, and explicit connections between disciplines are evident, can be challenging. The present study engaged students in multidisciplinary modelling involving mathematics, science, and statistics, together with shared STEM practices. The findings indicate how sixth-grade students can engage successfully in such modelling and can apply STEM practices in documenting and justifying their findings. Students displayed a basic understanding of key statistical concepts and processes, including variation and covariation and were able to identify trends both within and across sets of data. Students’ freedom to create their own models, rather than being specifically directed, revealed a range of responses indicative of their capabilities in these STEM domains. As Roehrig et al. (2021) emphasized, it is imperative that students are afforded opportunities to determine their own solution paths—"Teacher proscribed directions will result in a single design solution”, when integrated STEM education calls for multiple possible solution options (p. 4).