1 Introduction

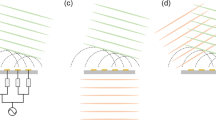
High-power, uniform-profile illumination sources operating at high frequencies are a much-needed but missing element in camera-based terahertz (THz) active imaging applications to produce high-quality images with a high, homogeneously distributed signal-to-noise ratio (SNR) and high spatial resolution. However, the radiation power of individual THz sources decreases drastically with respect to increasing frequency [1, 2]. To address this, several sources may be operated together to realize source arrays of greater overall radiation power. In this regard, silicon-integrated technologies are viable as they offer a high fabrication yield to incorporate such arrays into a single chip. In recent years, both coherent [3,4,5,6,7,8,9,10] and incoherent [11,12,13,14,15] single-chip THz source arrays have been reported. A salient difference between these two approaches is that coherent source arrays require an on-chip synchronization mechanism for phase-locking. Although this may incur some restrictions upon performance and array size, recent works have produced highly scalable devices [6, 9]. Despite ongoing advances in efficient on-chip synchronization methods, incoherent devices remain more scalable and produce higher radiation power [12]. Aside from array size and radiation power, there are other crucial differences between coherent and incoherent approaches. Coherent radiation can prove detrimental to image fidelity in many situations, as speckles form due to wave interference [16, 17], which is not the case with incoherent radiation [13]. Furthermore, unlike communications and radar, amplitude-only THz imaging does not require a coherent signal. For these reasons, the objective of this work is to explore incoherent THz source arrays for active imaging applications. A uniform-amplitude beam profile is desired in order that an imaging target is homogeneously illuminated, yielding constant dynamic range across the imaging plane. However, in contrast to this aim, contemporary incoherent THz source arrays produce several non-overlapping beams [12, 13], which produces dead zones in the imaging plane, as shown in Fig. 1(a). These dead zones have two causes: the source array pixels are large relative to a wavelength, and pixel pitch translates into an angular separation of free-space beams. Thus, according to [18], overlapping beams can only be achieved with a lens-coupled source array if the pixel cells are small enough so that they can be close together. However, the size of source pixels cannot be easily reduced due to the required power generation networks. Therefore, another solution is required to increase the beam overlap through an optimized silicon lens, yielding a uniform beam, as shown in Fig. 1(b).

Fig. 1
figure 1

Illustration of the primary motivation of this study, showing (a) how previous high-power THz incoherent source arrays [12, 13] produce directional, non-overlapping beams that lead to undersampling of the image plane, and (b) the primary objective of this study; a uniform-intensity, high-power THz illumination source

Full size image

In the past, significant research effort has been dedicated to the maximization of directivity for a single radiating element coupled to an extended hemispherical silicon lens as well as associated problems [19,20,21,22,23,24,25,26]. It has also been shown that beams from multiple small coherent sources incorporated into a single chip can be combined into a single Gaussian beam [27]. However, creating diffuse, uniform illumination from large-scale arrays of incoherent THz sources has not yet been demonstrated. To this end, this article presents a method to convert an arbitrary array of THz sources into a diffuse, uniform illumination source by tailoring the geometry of the backside-coupled lens—without the need for any modification to the integrated circuit itself—and a proof of concept is realized using a 0.42-THz device with a power of 10.3 dBm. Silicon-only single-shot THz active imaging is demonstrated together with a CMOS camera based on the focal plane array (FPA) from [28]. Previous attempts at incoherent power-combining of THz source arrays in free space have relied upon multi-device scaling [29] or lossy external optics [30]. Both of these approaches are bulky and inefficient. In comparison, the approach taken here is a single-chip-to-single-lens solution. It exhibits significant advantages in terms of both compactness and efficiency.

2 THz Source Array

The following is a summary of the details of the incoherent silicon-integrated source array chip used here, which has been presented in detail in [12]. For more details, the reader is referred to the cited work.

The chip is implemented in a commercial SG13G2 SiGe BiCMOS process available from IHP microelectronics, with 350-GHz/450-GHz ft/fmax SiGe HBT transistors. This chip incorporates 8 × 8 incoherent THz sources. Together, they radiate a rotal radiation power of 10.3 dBm at \(\sim \)0.42 THz. Each source pixel is composed of a power generation network coupled to an on-chip circular slot antenna. Each source pixel cell, thereby, occupies a die area of 365 µm × 365 µm. For THz-range power generation, free-running fundamental Colpitts oscillators, followed by a common-collector doubler, are used. The oscillators are not mutually phase-locked. Consequently, the radiation frequencies of the source pixels are not the same, making the source array an incoherent device. The difference in the radiation frequency has two causes: process variations and variations in bias. Related to this, mutual pixel coupling, which can cause two or more pixels to lock onto the same oscillation frequency, is mitigated by placing grounding shields around the source pixels and the silicon lens. Grounding shields prevent any leakage from electromagnetic fields, whereas the lens suppresses undesired substrate modes [31] by acting as a semi-infinite substrate. According to [32], an array atop a silicon lens is subject to a mutual pixel coupling on the order of –25 to –30 dB. In the source array, the isolation is further enhanced by the architecture of the source pixels. In particular, the frequency doubler after the oscillator prevents any out- and in-coupling of the fundamental oscillator signal. The lens not only suppresses unwanted substrate modes but also improves the front-to-back radiation ratio and imparts mechanical rigidity and thermal stability to the silicon chip [22]. For these reasons, the vast majority of integrated THz sources are coupled to extended hemispherical silicon lenses [2, 33,34,35].

3 Lens Design

3.1 Simulation Model

For pre-estimation of the optimal lens extension length required for a minimum − 3-dB beam overlap among all source pixel pairs and to create a uniform beam, numerical simulations were utilized based on the theory from [22, 23]. It is noted that full-wave simulations are impractical because the silicon lens is electrically large. Our simulation model accounts for Fresnel losses, which is to say, the amplitude pattern of fields on the external surface of the lens accounts for reflection losses. These losses are spatially dependent, and hence reflection impacts the overall far-field radiation pattern and directivity. Aside from Fresnel losses, other reflection-related effects are not modeled; specifically, the fields that are back-reflected into the lens volume and undergo multiple subsequent reflections before ultimately being radiated via the lens surface. Nevertheless, multiply reflected radiation is anticipated to contribute primarily to sidelobes, and hence it is of little interest to this work, as we aim to produce overlap between main lobes. The main difference to the math provided in the cited works is the radiation pattern of the lens-internal antenna. We employ a more abstract beam pattern in the interest of generality:

$$ |\mathbf{E}_{\text{Source}}(\theta^{\prime},\phi^{\prime})|=\left( \frac{\cos\theta^{\prime}+1}{2}\right)^{q}, $$
(1)

where the value q makes it possible to set any desired internal beam divergence, 𝜃HPBW,int, parametrically:

$$ q=\log\left( \frac{1}{2}\right)\cdot\left( \frac{2\cdot \log\left( \frac{\cos\theta_{\text{HPBW,int}}}{2}\right)}{2}\right)^{-1}. $$
(2)

3.2 Simulation Results

In order to obtain a comprehensive picture of achievable far-field radiation patterns, combined far-field radiation patterns were determined for a range of normalized lens extension lengths from L/R = 0.0 to L/R = 0.6, where L is lens extension length, and R is lens radius, as shown in Fig. 2(a). To this end, single-pixel far-field radiation patterns were computed for all 8 × 8 source pixels located at the base of a 15-mm (71.7λ) diameter extended hemispherical silicon lens. The summation of these single-pixel beams then produced the combined field radiation patterns. The unnormalized power was used in this case to account for differences in directivity. The permittivity of the silicon lens was set to 11.67Footnote 1. It is noted that a precise permittivity value is critical to avoid a systematic offset in the lens extension length.

The intended comprehensive picture can be transported best through cuts along the diagonals of the combined far-field radiation patterns (D-plane cuts) as a function of the normalized lens extension length, shown in Fig. 2(b). As seen from this figure, the D-plane is oversampled for small values of the lens extension length. The same applies to large values, while medium values create gaps in the field of view (FoV) into which very little power is projected. The latter case corresponds to a lens extension that is optimized for maximum directivity. It is also observed that small values of lens extension length allow the generation of uniform or flat-top illumination, as the edges of the combined far-field radiation pattern are sharply separated. In contrast, large values smear the edges. Thus, large extensions have the effect of producing a more Gaussian illumination. The cause for the differences in the beam shape generated is because a hemispherical “focal surface” with inverted orientation to the hemispherical surface of the lens exists inside the dielectric, with a different far-field direction associated with each point on this surface. In normal operation, the lowest point of this focal surface corresponds to the lens extension. To be appropriately focused, off-axis pixels would have to be shifted upward in the positive z-direction to compensate for the curvature of the focal surface. If we either shorten or increase the lens extension, the directivity of the center pixel is reduced because it is essentially defocused. When the lens extension is increased, the directivity of the off-axis pixels is reduced more than that of the center pixel because the off-axis pixels are farther away from the focal surface. On the other hand, when shortened, the off-axis pixels are raised in the positive z-direction. Thus, they are closer to the focal surface than the center pixel. Therefore, the reduction in directivity is less than the directivity reduction for center pixels. Ultimately, the desired beamform determines whether the lens extension needs to be increased or shortened, with the former yielding a Gaussian beam and the latter a uniform beam. Another noteworthy point observable from the simulated D-plane cuts is that the FoV decreases with increasing lens extension length. A small FoV is desirable concerning realizing small f -number quasi-optical systems for THz active imaging that are easier to align than those with large f -numbers. Since the overarching aim was to create uniform illumination from the source array at a minimal FoV, a lens extension length just above the intermediate position that causes gaps in the FoV is the best option. Here, uniform illumination is produced at a minimal FoV.

Fig. 2
figure 2

(a) Illustration of the chip-to-lens assembly, indicating the lens geometrical parameters L and R. (b) Pre-estimation simulation results, showing combined D-plane cuts, as indicated in (a), for normalized lens extension length of 0–0.6. The horizontal lines refer to values selected for experimental characterization

Full size image

Following the above discussion, the normalized lens extension length of 0.244 was selected for fabrication and testing to create uniform illumination from the source array, as indicated by the dashed line. In addition, two other cases with normalized lens extension lengths of 0.284 and 0.367 were selected for fabrication and testing in the interest of providing a more complete and comprehensive picture. The first case (0.284) represents the aplanatic case for silicon, which is associated with zero coma and zero spherical aberration for a central pixel [19]. This first case is intended to fill some gaps in the FoV. The second case (0.367) is intended to undersample the FoV due to non-overlapping beams. This second case refers to the lens design implemented in the previous works [12, 13].

4 Characterization

4.1 Experimental Setup

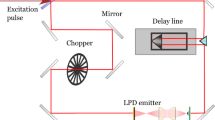
Figure 3 shows the experimental setup employed for far-field radiation pattern characterization. For relative power measurements, the radiated THz signal of the source arrays with different lens extension lengths was successively collected with a SiGe HBT THz direct power detector with 700-V/W responsivity and 8-pW/\(\sqrt {\text {Hz}}\) NEP at around 0.42 THz [36]. A far-field distance separated the source arrays and the detector. Specifically, the distance was 70 cm, which is above the Fraunhofer distance of 2D2/λ = 63 cm for a lens diameter of 15 mm and the source array radiation frequency of \(\sim \)0.42 THz. The detector was fixed in place and connected to a spectrum analyzer via a 40-dB voltage amplifier. The source arrays were mounted onto a six-axis table-top robot arm in order to facilitate a rotational raster scan. Each source array was scanned over a ± 36∘×± 36∘-sector of the hemisphere to capture far-field beams of all source pixels.

Fig. 3
figure 3

Illustration of the experimental setup employed for far-field radiation pattern measurements

Full size image

4.2 Measured Results

Figure 4(a), (b), and (c) show the measured full far-field radiation patterns with normalized power for normalized lens extension lengths of 0.367, 0.284, and 0.244, respectively. Corresponding D-plane cross-section cuts are compared to simulation in Fig 4(d)–(f). It can be seen from these results that the beam overlap (or fill factor) indeed increases with decreasing lens extension length, as intended. The source arrays coupled to extended hemispherical silicon lenses of 0.367, 0.284, and 0.244 normalized lens extension length cover experimentally tested FoVs of 50∘, 55∘, and 55∘, with 3-dB fill factors of 6.5%, 53.4%, and 99.98%, respectively. The corresponding peak-to-peak ripple values are \(\sim \)20 dB, 8.6 dB, and 3.5 dB. Thus, the primary objective of this study, namely the realization of a high-power, diffuse, uniform-intensity THz source, has been achieved. Finally, given that the measured combined far-field radiation patterns are in excellent agreement with their simulated counterparts, we may conclude that the simulation model has been successfully validated.

Fig. 4
figure 4

Measured combined far-field radiation patterns of source arrays using 15-mm diameter silicon lenses with different normalized lens extension lengths of 0.367 (a), 0.284 (b), and 0.244 (c) and directivity. In (d)–(f), D-plane cuts along the dashed lines in the corresponding complete far-field radiation patterns from (a)–(c) are compared with the results obtained from simulations. In all subfigures, normalization is performed with respect to the maximum power within the constant radius FoV

Full size image

5 Demonstration of Silicon-Only THz Active Imaging

5.1 Single-Shot Imaging Setup

An illustration and photograph of the experimental setup are shown in Fig. 5(a) and (b), respectively, with which silicon-only THz active imaging was performed. That is to say, both the source and detector of THz waves are silicon-based integrated circuits. The two source arrays coupled to lenses of the highest and lowest lens extension length were successively deployed in a collimated beam setup that consists of a series of optics and a commercially available CMOS THz camera from Ticwave GmbH, Wuppertal, GermanyFootnote 2. This camera is based on the FPA from [28]. It is noted that a variety of THz applications have been demonstrated with this camera ranging from shadow imaging [28] over light-field imaging [37,38,39] to source characterization [40,41,42,43], among others. The total radiation power of the source array is 10.3 dBm [12], and the video-rate camera NEP at the source array radiation frequency of 0.42 THz is 2.5 µW [44]. All components were fixed within a cage system to ensure mechanical rigidity. The source arrays and the camera are operated via USB. The presented imaging system is portable, spanning an overall system size of 136 mm × 50 mm × 50 mm. The key enabling factor in implementing this compact, portable THz active imaging system is the incoherent operation of the source array and camera. It is noted that the proposed THz uniform illumination source array-based active imaging setup is not tied to a CMOS camera. Other direct power detectors, such as microbolometers [45], CMOS-NEMS [46], SiGe HBTs [47], and Schottky barrier diodes [48], can replace the CMOS detectors, provided that they can be integrated into a single chip.

Fig. 5
figure 5

Illustration of the experimental setup employed for and silicon-only THz active imaging (a), and a photo of that (b)

Full size image

The beam propagation within the imaging setup works as follows. The optical train consists of two PTFE lenses. At the source array side, a 50-mm diameter collimating PTFE lens with an f-number of 0.75 (L1), which closely corresponds to the source array FoVs of 50∘ and 55∘, is employed for collimation. The source array lens center, where central rays of the source pixel beams cross [37], coincides with the focal point of L1. The source array emits diverging wavefronts emanating from the focal point of L1. Consequently, collimated waves are provided in the object plane, where they illuminate an imaging target. The camera lens center, where central rays of camera pixel beams cross [37], coincides with the focal point of the right collimating PTFE lens (L2; diameter of 50 mm and f-number of 1), which closely corresponds to the 46∘ FoV of the camera. Thus, the object plane is projected onto the camera lens. Ultimately, an object under illumination may appear as an inverted image on the FPA surface. Since the pixel beams of the source array and the pixel beams of the camera are collimated (or planarized) in the object plane, far-field conditions prevail exactly at this point. Moving away from this position will cause an object to be out of focus. Such defocusing will cause producing blurred images.

5.2 Imaging Results

A 3-mm thick, 50-mm diameter metal plate with a T-shaped cut-out served as the imaging object, as shown in Fig. 6(a). This object blocked most of the beam, allowing only a small portion of THz power to pass. Figure 6(b) and (c) show THz images of the marked portion of the object acquired with the camera using the 2.75-mm and 1.83-mm extended hemispherical silicon lens-coupled source array, respectively. It can be seen that the THz image depicted in Fig. 6(b) is undersampled, whereas the one depicted in Fig. 6(c) is oversampled. Hence, the “T” is only recognizable in the latter. Raw images without any image-processing applied are shown. Each image was acquired over a \(\sim \)30-second time span, as the CMOS camera was operated at 30 fps and averaged 1024 frames. Frame-averaging was applied to increase the SNR [49]. Diffraction at the internal edges of the “T” may play a role in the blurring observed at the internal object edges, which results in the degradation of overall image quality. It should be noted that this diffraction-induced degradation of the overall image quality is not due to the imaging system itself but to the tiny slit width of the imaging object, which is close to a wavelength of just under 1 mm.

Fig. 6
figure 6

Object (a) imaged at 0.42 THz with the CMOS THz camera using 2.75-mm (b) and 1.83-mm (c) lens extension length-coupled source array. The “T” is only clearly visible in the oversampled THz image in (c)

Full size image

6 Conclusion

In this article, a practical and scalable method to operate a single-chip array of incoherent THz sources as a uniform illumination source has been demonstrated. For demonstration, this method was applied to the source array from [12], thereby realizing a 0.42-THz source that distributes 10.3 dBm evenly over its FoV. Briefly, our method is based upon optimization of the geometry of a backside-coupled silicon lens. Silicon-only THz active imaging has been successfully demonstrated together with a CMOS THz camera based on the FPA presented in [28].

All single-element integrated THz sources suffer from a low radiation power and are relatively large in terms of wavelength [1, 2]. Furthermore, lens coupling is ubiquitous among THz sources [2, 33,34,35, 50]. For these reasons, the presented technique of reduced-extension length hemispherical silicon lens-coupled THz source arrays is of general utility as a free-space power-combining technique; for example, also for incoherent source arrays of resonant tunneling diodes [14], or photomixers [15]. Furthermore, when the source that constitutes the array is mutually phase-locked, this would naturally yield coherent power-combining. This manner of scalable coherent power-combining could be essential to photo-mixing emitters, which exhibit broad frequency tunability, but currently suffer from a low radiation power at high frequencies [27, 34, 35]. An array of photo-mixing sources could be fed from a single high-power beating laser, thereby leading to innate synchronization among adjacent sources.