1 Introduction

Measuring the shape and the position of an instrument’s radiation pattern is a reoccurring task in most radio and infrared receiver systems. In wavelength ranges where no easy-to-use cameras are available, this is usually done with two-dimensional beam scanners. With a vector beam scanner, which records both, the amplitude and phase of the receiver beam, it is sufficient to measure the field at one distance from the detector [1]. At high frequencies, it is often easier to measure only the power pattern and replace the lack of phase information by measurements at two or more distances [2]. In any of the two cases, the sequential 2D sampling is very time consuming, and the required setup can be quite bulky.

We developed a compact beam scanner for the astronomical receiver GREAT [3], which operates at frequencies between 1 and 5 THz on the airborne observatory SOFIA [4]. The unit scans the power pattern inside the instrument and allows rapid and precise measurements of the beam location near the telescope’s focal plane. The necessity for such a device arose from the special operating conditions of GREAT on SOFIA.

To minimize downtime during instrument swaps on SOFIA, GREAT gets fully aligned in the laboratory, before mounting it to the telescope. This requires co-alignment of GREAT’s two frequency bands to each other and to the telescope’s optical axis as defined by the mechanical axis of the circular instrument mounting flange.

The acceptable tolerances for the beam co-alignment depend on the operation frequencies, but can be as small as 0.25 mm in the telescope focal plane, corresponding to a maximum pointing misalignment of 1 arcsec on the sky. To achieve this, the beam location is determined in two planes, one at a distance of several meters from the instrument and one near the focal plane, which, on SOFIA, is inside the receiver. The external measurement is needed to ensure proper illumination of the telescope, and is done with a chopped cold load mounted on a two-dimensional linear translation stage. For lack of space inside the GREAT instrument, the internal measurement, which is crucial for the pointing accuracy, cannot be done in the same way, and required a novel measurement setup.

2 Measurement Principle

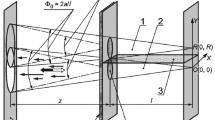
For maximum compactness, the internal beam scanner uses only one-dimensional motion. With the receiver looking at its internal calibration cold load, the scanner moves a series of warm opaque bars through the beam (Fig. 1). To obtain 2D position information from this 1D measurement, these shadow bars are tilted by ±45∘ with respect to the direction of motion.

Fig. 1
figure 1

Sketch of the beam measurement principle. See text for explanation

Full size image

A beam displaced by Δh and Δv with respect to the optical axis causes an offset of Δx 1=Δh+Δv in the measurement for the first shadow bar and of Δx 2=Δh−Δv for the second shadow bar. Thus, the beam offsets can be calculated as Δh=(Δx 1+Δx 2)/2 and Δv=(Δx 1−Δx 2)/2.

3 Technical Realization

To further simplify the mechanical setup, we replaced the translational motion of the shadow bars by a rotational motion. The shadow bars are mounted to a large measurement wheel (Fig. 2) that can rotate between the receiver cryostat and the instrument’s calibration cold load. The wheel carries three sets of shadow bars of different widths (1, 2, and 4 mm), to approximately match the beam sizes of GREAT’s different frequency channels.

Fig. 2
figure 2

Photograph of the beam measurement wheel mounted inside GREAT’s optics compartment (left hand panel) and CAD sketch of the wheel showing the log-spiral shadow bars (B1 …B6), the marks for rotation monitoring (m), the holes to attach balancing weights (b), and for the bolt to lock the wheel in its parking position (L). The forth window in the wheel, which carries no shadow bars, provides an unobstructed beam path for the astronomical observations. On the photograph, the edge of one of the chopper blades is visible through the beam hole in the dividing wall of the optics compartment

Full size image

To maintain the 45 ∘ tilt of the shadow bars with respect to the direction of motion at all radii, the bars take the shape of logarithmic spirals. The surface of the bars facing the detectors is roof shaped to avoid instabilities due to standing waves.

The measurement wheel is mounted to the shaft of a stepper motor with 400 steps per turn, driven by a controller capable of operating in microstepping mode with up to 128 microsteps per step [5], allowing a minimum nominalFootnote 1 step size of 0.007 ∘, which corresponds to 10 μm at the radius of GREAT’s optical axis.

The setup is mounted to a dividing wall in the optics compartment of GREATFootnote 2. The rear surface of the dividing wall holds a chopper wheel to improve the signal quality of the measurement through lock-in detection. The chopper wheel is also driven by a stepper motor to facilitate the synchronization of the data acquisition.

A microcontroller [6] controls the motion of the chopper and the measurement wheel and handles the data acquisition of three 8-channel 16-bit analog to digital converters (ADC). This allows simultaneous measurements of the locations of up to 24 individual receiver beams, 21 of which are required for the upGREAT extension of our instrument [7]. The microcontroller communicates with a control computer through an ethernet interface.

The rotation of the measurement wheel is monitored by an optical sensor detecting 33 marks positioned along the circumference of the wheel (Fig. 2) to be able to recognize and correct possible errors in the wheel motion. Similarly, the chopper wheel is monitored by optical sensors to ensure the correct phase angle for the lock-in detection. To calibrate the angular position of the shadow bars, we use the wheel to scan an optical laser beam aligned to the nominal optical axis of the instrument. Figure 3 displays a typical measurement of GREAT’s antenna pattern, including the trace of the calibration measurement.

Fig. 3
figure 3

Example of a raw data scan of a typical measurement, which consists of one full rotation of the measurement wheel. The two receiver channels show the three pairs of shadow bars of different bar width. The signals caused by the wheel spokes are strongly affected by standing waves, but do not contribute to the measurement. The signal drifts at both ends of the scan are an artifact of the lock-in measurement during chopper wheel acceleration and deceleration. At the top of the figure, we show the angle monitor signal and, below it, the wheel angle calibration scan of an optical laser beam recorded in a separate measurement

Full size image

The chopper wheel can and has been used for astronomical observations, where extended source emission may preclude the usage of the telescope’s chopping secondary mirror for on-off difference measurements. The 24-channel lock-in detection capability of the data acquisition system is also used for the beam measurements obtained with the external translation stage (Section 1), which carries a copy of the internal chopper wheel to modulate the cold load signal.

4 Performance

The maximum chop frequency is 30 Hz, limited by the time needed for data acquisition and transfer. In our typical operating mode of 1600 steps per turn (0.35 mm per step) of the measurement wheel and one chop period per step of the measurement wheel, a full beam measurement takes less than 1 min.

Figure 4 zooms into the central pair of shadow bars of Fig. 3 and shows the Gaussian profiles fitted to the signal to retrieve the beam positions. Although the measurement principle does not allow full mapping of the beam pattern, it gives a good indication of the beam quality, and the beam width can be derived from the data as an additional health check of the receiver optics. The high signal-to-noise ratio of the measurement pushes the position error well below the wheel step size.

Fig. 4
figure 4

Example of a beam measurement of GREAT in its 1400/1900 GHz configuration. The data is taken from the middle of Fig. 3 (approx. channels 650 to 950). It corresponds to the signal from the pair of 2-mm-wide shadow bars. Gaussian fits to the high-quality data yield a very accurate measurement of the beam position

Full size image

To illustrate the accuracy of the setup, we show a series of 11 measurements taken when checking for gravitational deflection of the instrument during elevation changes of the telescope (Fig. 5). The two instrument beams are found to be co-aligned to within 0.16 mm in the telescope focal plane, corresponding to 0.65 arcseconds on the sky. The RMS scatter in the measured beam positions is smaller than 20 μm in all coordinates, showing not only the high accuracy of the measurement but also the good dimensional stability of the instrument.

Fig. 5
figure 5

Measurement series to check for gravitational deflection of GREAT under varying telescope elevation. The four traces show the two coordinates of the two receiver beams

Full size image

5 Conclusion

We have built a compact, accurate beam measurement setup specifically designed to obtain fast measurements of the position of an astronomical receiver beam inside the instrument. The beam scanner is operated with the GREAT/upGREAT instrument, where it is a central component for the precise alignment of the receiver.