1 Introduction

Terahertz (THz) wave has many distinctive characteristics as its wavelength lies between microwave and infrared wave. Terahertz imaging techniques have drew much attention in the field of terahertz applications due to several exciting advantages of terahertz wave. The lower photon energy property makes it safer to take safety inspection on the human body and harmless detection of biological samples. The penetration ability towards dielectric and liquid nonpolar materials makes it able to realize perspective imaging. The shorter wavelength and higher frequency provide the ability to realize wider absolute bandwidth and higher spatial resolution. All these characteristics lead to promising prospects in nondestructive detection [1], medical imaging [2, 3], and standoff personnel screening [4–6].

Recently, great progress has been made on THz radar systems. One of the typical institutions is the Jet Propulsion Laboratory (JPL). In 2006, they successfully developed the first high-resolution terahertz imaging radar with a 2-cm range resolution [7, 8]. In 2011, sub-centimeter resolution in a 4–25-m distance and appreciable imaging speed were already available [4, 6, 9, 10]. Another representative is the German Fraunhofer Institute for High Frequency Physics and Radar Techniques (FHR). In 2007, they successfully developed a 220-GHz terahertz imaging radar system COBRA-220 [11] which realized a 1.8-cm resolution. In 2013, they continuously developed a 300-GHz system which obtained a 3.7-mm resolution [12]. Beside these two forerunners, more and more organizations started to develop their own systems and many remarkable achievements had been made [13–23].

In most of these works, a linear frequency-modulated continuous wave (LFMCW) mode was introduced. It is easier for LFMCW radars to realize a wider bandwidth as well as to lower the emission power. The stretch processing can reduce the intermediate frequency (IF) bandwidth while maintaining the range resolution, which helps to simplify the system design and reduce the cost. LFMCW signals are also of stable coherence which is extremely important when inverse synthetic aperture radar (ISAR) techniques are utilized to generate high-resolution 2D or 3D images.

However, to obtain higher resolution through ISAR techniques, some problems still need to be considered carefully. Firstly, problems occurred with the increasing of the rotation angle can damage the focusing of images. As it is hard to realize prefect linearity within the total broad bandwidth of the LFM signal in the terahertz regime, a calibration signal acquired from a bright target is always used to compensate for the nonlinearity of the frequency modulation rate [4, 23, 24]. Generally, a deviation distance between the reference bright target and the equivalent center of turntable always exists in real cases. This deviation distance leads to an extra linear phase term in the compensated IF signal. In the cases of large rotation angle, this extra term results in serious defocus of the image. Secondly, as we know, terahertz radar has shorter wavelength compared to traditional microwave radar. In addition, the interval between radar and target is usually several meters to tens meters in terahertz imaging applications and the atmospheric attenuation also confines the propagation distance. To date, no detailed analysis on the effects that these problems bring to ISAR imaging at terahertz frequencies has been carried out yet.

In this paper, two parts of work were presented around imaging applications based on a 330-GHz LFMCW radar system [24]. Firstly, the problems occurred with the increasing of the rotation angle were discussed. In order to improve the resolution and the image Signal to Noise Ratio (SNR) by utilizing the large rotation angle, it is necessary to compensate for this extra phase term and realize the coherent addition of the data acquired from different apertures. Detailed theoretical derivation is shown in this paper. Careful analysis was taken to reveal the impact to the quality of images that caused by deviation distance and large rotation angle. A minimum entropy criterion was used to estimate and correct this deviation distance. Experimental results validated the necessity and effectiveness of this compensation. Secondly, a detailed theoretical analysis on the spherical-wave effects was carried out. The criteria of plane-wave approximation were derived in different cases, and experimental results showed great consistency with the theoretical analysis.

The remainder of this paper is organized as follows: Section 2 describes the imaging problem occurred with the increasing of rotation angle in THz LFMCW radar systems and the solution of this problem. Section 3 analyzes the effect of spherical wave and provides the criteria of plane-wave approximation. Section 4 gives the experimental results. Finally, we conclude this paper in Section 5.

2 THz LFMCW Large Rotation Angle Imaging

2.1 Theoretical Derivation

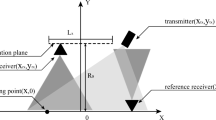
Suppose a LFM signal is transmitted and a stretch processing is employed. The ideal received IF signal scattered from a point target should be a perfect sinusoid, and its frequency is determined by the distance between the radar and the target. But there are always phase noises in the real echo IF signals which insert distortion into the sinusoid. Figure 1 shows the basic geometric relationships. Suppose an ideal point target is R r away from the radar and then the echo IF signal with phase noises will be [25]

Fig. 1
figure 1

Basic geometry

Full size image
$$ {s}_r\left(\tau, {t}_m\right)=A\cdot \mathrm{rect}\left(\frac{\tau -2{R}_r/c}{T_p}\right) \exp \left(-j4\pi {f}_c{R}_{\varDelta}^r/c-j4\pi \gamma \left(\tau -2{R}_r/c\right){R}_{\varDelta}^r/c-j4\pi \gamma {R_{\varDelta}^r}^2/{c}^2+j\varphi \left(\tau -2{R}_{\mathrm{ref}}/c,{R}_{\varDelta}^r\right)\right) $$
(1)

where R r Δ  = R r  − R ref, R ref is the reference distance selected by the radar system (not shown in Fig. 1), γ is the frequency modulation rate, and φ(τ − 2R ref/c, R r Δ ) represents the phase noises which is a function of both fast time and the distance between the radar and the target. φ(τ − 2R ref/c, R r Δ ) can be approximated as a constant function of R r Δ when the size of the target is much smaller than the spatial length of the transmitted signal which means that φ(τ − 2R ref/c, R r Δ ) varies slowly against R r Δ as the change of R r Δ is small. For the convenience of derivation, we redefine the fast time as \( \tau \overset{\varDelta }{=}\tau -2{R}_{\mathrm{ref}}/c \)

$$ {s}_r\left(\tau, {t}_m\right)={A}_r\cdot \mathrm{rect}\left(\frac{\tau -2{R}_{\varDelta}^r/c}{T_p}\right) \exp \left(-j4\pi {f}_c{R}_{\varDelta}^r/c-j4\pi \gamma \left(\tau -2{R}_{\varDelta}^r/c\right){R}_{\varDelta}^r/c-j4\pi \gamma {R_{\varDelta}^r}^2/{c}^2+j\varphi \left(\tau, {R}_{\varDelta}^r\right)\right) $$
(2)

Similarly, the echo IF signal of a target located R t away from radar is

$$ {s}_t\left(\tau, {t}_m\right)={A}_t\cdot \mathrm{rect}\left(\frac{\tau -2{R}_{\varDelta}^t/c}{T_p}\right) \exp \left(-j4\pi {f}_c{R}_{\varDelta}^t/c-j4\pi \gamma \left(\tau -2{R}_{\varDelta}^t/c\right){R}_{\varDelta}^t/c-j4\pi \gamma {R_{\varDelta}^t}^2/{c}^2+j\varphi \left(\tau, {R}_{\varDelta}^t\right)\right) $$
(3)

where R t Δ  = R t  − R ref; use s r (τ, t m ) as the calibration signal to compensate the echo signal of target

$$ \begin{array}{l}{s}_{tr}\left(\tau, {t}_m\right)={s}_t\left(\tau, {t}_m\right)/{s}_r\left(\tau, {t}_m\right)\\ {}\kern6em ={A}_t/{A}_r\cdot \mathrm{rect}\left(\frac{\tau -2{R}_{\varDelta }/c}{T_p}\right)\mathrm{rect}\left(\frac{\tau }{T_p}\right)\cdot \exp \left(-j4\pi {f}_c{R}_{\varDelta }/c-j4\pi \gamma \left(\tau -2{R}_{\varDelta }/c\right){R}_{\varDelta }/c-j4\pi \gamma {R_{\varDelta}}^2/{c}^2\right)\end{array} $$
(4)

where R Δ  = R t  − R r . After the procedure of ramp phase and residual video-phase (RVP) correction, the signal becomes

$$ {s}_{tc}\left(\tau, {t}_m\right)=\mathrm{I}\mathrm{F}\mathrm{T}\left(\mathrm{F}\mathrm{T}\left({s}_{tr}\left(\tau, {t}_m\right)\right)\cdot \exp \left(-j\pi {f}^2/\gamma \right)\right)={A}_t/{A}_r\cdot \mathrm{rect}\left(\frac{\tau }{T_p}\right)\cdot \exp \left(-j4\pi \left({f}_c+\gamma \tau \right){R}_{\varDelta }/c\right) $$
(5)

Suppose the range alignment and phase correction have already been accomplished for moving targets and the echo signal model is equivalent to a standard turntable model. Under the plane-wave approximation, R t will be

$$ {R}_t={R}_c-\left(x \cos \theta + ysin\theta \right) $$
(6)

Meanwhile, utilizing the relationship f = f c  + γτ and \( k=\frac{2\pi f}{c} \) where f represents the real time frequency for the LFM signal and k stands for the wavenumber, Eq. (5) can be written as

$$ {s}_{tc}\left(k,\theta \right)={A}_t/{A}_r\cdot \mathrm{rect}\left(\frac{k-{k}_c}{B}\right)\cdot \exp \left(-j2k\left({R}_c-{R}_r-\left(x \cos \theta +y \sin \theta \right)\right)\right) $$
(7)

Generally, the echo signal of an arbitrary target rather than a point target is expressed by the following integral equation:

$$ G\left(k,\theta \right)={\displaystyle \underset{x,y}{\iint }F\left(x,y\right) \exp \left(j2k\left(x \cos \theta +y \sin \theta \right)\right) \exp \left(-j2k\left({R}_c-{R}_r\right)\right) dxdy} $$
(8)

and the imaging process is presented by

$$ \widehat{F}\left(x,y\right)={\displaystyle \underset{k,\theta }{\iint }G\left(k,\theta \right) \exp \left(-j2k\left(x \cos \theta +y \sin \theta \right)\right) \exp \left(j2k\left({\widehat{R}}_c-{R}_r\right)\right) kdkd\theta} $$
(9)

where \( {\widehat{R}}_c \) is the estimation of R c as R c is unknown. It can be seen from Eq. (9) that imaging is essentially the inverse process of the echo signal generation. The quality of an image is determined by the accuracy of the echo signal model and the matching degree of amplitude and phase accumulation compared to the echo signals. The main differences between Eqs. (8) and (9) and the familiar standard spatial Fourier transform pairs are the terms exp(−j2k(R c  − R r )) and \( \exp \left(j2k\left({\widehat{R}}_c-{R}_r\right)\right) \) in the integrant functions. The primary conclusion of the derivation from Eqs. (1) to (7) is the appearance of an extra term exp(−j2k(R c  − R r )) in Eq. (8) compared to the standard Fourier transform; accordingly, a conjugate term \( \exp \left(j2k\left({\widehat{R}}_c-{R}_r\right)\right) \) is involved in Eq. (9). It is this extra term that leads to a degradation of image quality in large-rotation angle cases, and our first part of work is developed essentially based on it.

2.2 Influence Analysis

In order to get an appropriate estimation of R c to correct the deviation distance R c  − R r , entropy is introduced to evaluate the focusing quality of the THz images. Entropy has been successfully applied to evaluate the quality of SAR or ISAR images [26, 27]. The definition of entropy is [28]

$$ \mathrm{E}\mathrm{n}={\displaystyle \iint -f\left(x,y\right)\cdot \ln f\left(x,y\right) dxdy}\kern0.5em ,\kern0.5em f\left(x,y\right)=\frac{{\left|F\left(x,y\right)\right|}^2}{{\displaystyle \iint {\left|F\left(x,y\right)\right|}^2 dxdy}} $$
(10)

where f(x, y) is the normalized image power density.

We use point spread function (PSF) to analyze the focusing quality of THz images utilizing the criterion given by Eq. (10). Suppose there is a point target located at the origin of the coordinate and set \( \varDelta R={R}_c-{R}_r,\varDelta \widehat{R}={\widehat{R}}_c-{R}_r \) according to Eq. (9). Then, the expression of PSF is

$$ Psf\left(r,\phi \right)={\displaystyle {\int}_{\theta_{\min}}^{\theta_{\max }}{\displaystyle {\int}_{k_{\min}}^{k_{\max }} \exp \left(-j2k\left(r \cos \left(\theta -\phi \right)-\left(\varDelta \widehat{R}-\varDelta R\right)\right)\right)kdk}d\theta } $$
(11)

Particularly, when \( \varDelta \widehat{R}-\varDelta R=0 \) and θ max − θ min = 2π, Eq. (11) has a compact form

$$ Psf\left(r,\phi \right)={k}_{\max}\frac{J_1\left(2{k}_{\max }r\right)}{\pi r}-{k}_{\min}\frac{J_1\left(2{k}_{\min }r\right)}{\pi r} $$
(12)

PSF is now an isotropic function of r. But in general cases, Eq. (11) has no compact form and PSF is a function of both r and ϕ. PSF can neither be expressed as a separable function of range and azimuth directions nor an isotropic function of r. Numerical simulations are employed to study the effects caused by the deviation distance and the rotation angle to the focusing quality.

The simulation frequency ranges from 320 to 330 GHz, and the results are shown in Fig. 2. We can see that the colored scale is approximately limited to the range 4.5–7.5. This value is related to the number of pixels of the discretized image. The size of the image area in the simulation is 0.4 m × 0.4 m, and it is discretized into 250 × 250 pixels. As a digital image is made up of discrete grids, Eq. (10) should be discretized as

Fig. 2
figure 2

The curve of the entropy of PSF varies against deviation distance and rotation angle

Full size image
$$ \mathrm{E}\mathrm{n}=-{\displaystyle \sum_{n=1}^N{\displaystyle \sum_{m=1}^Mf\left(n,m\right)\cdot \ln f\left(n,m\right)}}\kern0.5em ,\kern0.5em f\left(n,m\right)=\frac{{\left|F\left(n,m\right)\right|}^2}{{\displaystyle \sum_{n=1}^N{\displaystyle \sum_{m=1}^M{\left|F\left(n,m\right)\right|}^2}}} $$
(13)

where n and m represent the position of the pixel and N and M represent the total number of pixels in each row and each column. When entropy is treated as a criterion of image assessment, its physical meaning is that the more uniform the value of all the pixels, the higher the entropy is. For images with the same number of pixels, the one which all the pixels share the same value is of the highest entropy. For images whose pixels share the same value, the more the pixels, the higher the entropy is. Hence, the number of pixels in the image should be fixed when utilizing entropy as an assessment criterion. It is not hard to validate \( {\displaystyle \sum_{n=1}^N{\displaystyle \sum_{m=1}^Mf\left(n,m\right)}}=1 \) in Eq. (13); consequently, f(n, m) can be regarded as a probability distribution function and the entropy can be interpreted from the perspective of information theory. Suppose f(n, m) stands for the probability distribution function of a random variable and then the colored value ranging from 4.5 to 7.5 in Fig. 2 represents the average information content of this random variable. Since natural logarithm function is utilized in Eq. (13), the unit of the colored value should be “nat” (natural unit).

The range of deviation distance and rotation angle in Fig. 2 is \( \varDelta \widehat{R}-\varDelta R\in \left(-0.15\kern0.5em \mathrm{m},\kern0.5em 0.15\kern0.5em \mathrm{m}\right) \) and θ max − θ min ∈ (0°, 60°), respectively. It can be seen that for a fixed imaging rotation angle, PSF entropy always gets its minimum when the deviation distance is zero. Thus, it is reasonable to choose entropy as a criterion of the image quality. When the rotation angle is small (i.e., < 4° approximately), the entropy of PSF decreases with the increasing of rotation angle which indicates that the accumulation of rotation angle makes the PSF sharper. Meanwhile, the large variation of deviation distance does not bring an obvious difference of the entropy. It is because the phase errors aroused by deviation distance are not critical and the coherence of echo signal maintains in azimuth direction in small-rotation angle cases. With the increasing of the rotation angle, the dependence of PSF entropy against deviation distance is strengthened and the entropy curve is relatively sharper where \( \varDelta \widehat{R}-\varDelta R \) approaches to zero. This feature contributes to the improvement of the estimation accuracy of the deviation distance. Besides, it can be found that the entropy does not decrease monotonically with the increasing of rotation angle when the deviation distance is zero. It is because PSF is obtained directly from Eq. (11) and no sidelobe suppression technology is utilized. We does not attempt to discuss this nonmonotonically decreasing problem in detail since it does not damage the entropy getting its minimum as the deviation distance approaches to zero.

As can be seen in Fig. 2, for a fixed rotation angle, image entropy always gets its minimum when the deviation distance is zero. It means that Eqs. (8) and (9) are completely matched/focused as entropy gets its minimum in this ideal point scattering situation. However, whether it is true for complicated targets is still not verified by mathematical derivation. Besides minimum entropy algorithm (MEA), maximum contrast algorithm (MCA) is also a frequently used method. While MCA cares about the dominant scatters too much that most scatters may not be so well focused as the dominant one, MEA avoids this problem and it can attain a good compromise among all the scatters and results in a globally good image. The imaging results in the following measurement part also verify this point.

2.3 Estimation of the Deviation Distance

To estimate the deviation distance, a typical single-parameter optimization algorithm is employed as shown in Fig. 3.

Fig. 3
figure 3

Optimization flowchart

Full size image

3 Analysis on Plane-wave Criteria in THz Imaging

3.1 Formulas of the Problem

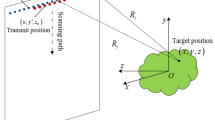
One can note that plane-wave approximation was introduced in the above derivation for convenience. However, it is more appropriate to depict the wavefront using Green’s function rather than plane-wave function due to the limit of propagation distance and the short wavelength of the THz wave. The differences can be easily found in Fig. 4. From Fig. 4, we can conclude that whether a spherical wave can be approximated by a plane wave relies on three factors: the distance between the target and radar, the size of the target, and the wavelength.

Fig. 4
figure 4

A comparison of different illuminations between a spherical wave and b plane wave

Full size image

Strictly speaking, Eq. (6) should be rewritten as

$$ {R}_t=\sqrt{r_t^2+{R}_c^2-2{r}_t{R}_c \cos \left(\theta -\phi \right)} $$
(14)

and the echo signal ought to be

$$ G\left(k,\theta \right)={\displaystyle \underset{x,y}{\iint }F\left(x,y\right) \exp \left(j2k\left({R}_c-{R}_t\right)\right) \exp \left(-j2k\left({R}_c-{R}_r\right)\right) dxdy} $$
(15)

Consistently, the imaging formula is

$$ F\left(x,y\right)={\displaystyle \underset{k,\theta }{\iint }G\left(k,\theta \right) \exp \left(-j2k\left({\widehat{R}}_c-{R}_t\right)\right) \exp \left(j2k\left({\widehat{R}}_c-{R}_r\right)\right) kdkd\theta} $$
(16)

Set a point target (x t , y t ) = (r t  cos ϕ, r t  sin ϕ) and assume the deviation distance has been completely corrected which means \( {\widehat{R}}_c={R}_c \). If we still use Eq. (9) rather than Eq. (16) to achieve images from the echo signal given by Eq. (15), then PSF is

$$ \mathrm{P}\mathrm{S}\mathrm{F}\left(x,y\right)={\displaystyle \underset{k,\theta }{\iint } \exp \left(j2k\left({R}_c-{R}_t\right)\right) \exp \left(-j2k\left(x \cos \theta +y \sin \theta \right)\right) kdkd\theta} $$
(17)

Perform Taylor expansion on R t according to Eq. (14)

$$ {R}_t={R}_c-{r}_t \cos \left(\theta -\phi \right)+\frac{r_t^2}{2{R}_c}{ \sin}^2\left(\theta -\phi \right)+o\left({R}_c^{-1}\right) $$
(18)

and rewrite Eq. (17) using the expansion in Eq. (18) neglecting those higher-older terms

$$ \mathrm{P}\mathrm{S}\mathrm{F}\left(x,y\right)={\displaystyle \underset{k,\theta }{\iint } \exp \left(j2k\left({r}_t \cos \left(\theta -\phi \right)-\frac{r_t^2}{2{R}_c}{ \sin}^2\left(\theta -\phi \right)\right)\right) \exp \left(-j2k\left(x \cos \theta +y \sin \theta \right)\right) kdkd\theta} $$
(19)

We can learn from a previous analysis that the essential of imaging is a process of matching and accumulating amplitude and phase in the echo signal. The matching degree directly determines the quality of images. The unmatched phase term in Eq. (19) is

$$ {\varPhi}_e=-j2k\frac{r_t^2}{2{R}_c}{ \sin}^2\left(\theta -\phi \right) $$
(20)

3.2 Plane-wave Criterion in Small Rotation Angle Cases

For the purpose of explaining the impacts of phase errors on images, we assume θ in Eq. (20) is minor enough. The reasonability of this assumption is based on two aspects: firstly, according to Eq. (19), imaging is a process of integrating upon rotation angle which can be decomposed into a number of small-rotation angle integration. Secondly, for arbitrary θ, a small value of θ is obtained by rotating the target coordinate to make the x-axis pointing towards the radar. As the imaging process of arbitrary range of θ can be treat as a number of imaging processes of Δθ, we can make following approximations:

$$ \left\{\begin{array}{l} \sin \varDelta \theta \approx \varDelta \theta \\ {}{ \sin}^2\varDelta \theta \approx \varDelta {\theta}^2\\ {} \cos \varDelta \theta \approx 1-0.5\varDelta {\theta}^2\\ {}{ \cos}^2\varDelta \theta \approx 1-\varDelta {\theta}^2\end{array}\right.,\left\{\begin{array}{l}{k}_x=k \cos \varDelta \theta \approx k\\ {}{k}_y=k \sin \varDelta \theta \approx k\varDelta \theta \end{array}\right. $$
(21)

Therefore, the Φ e in Eq. (20) is approximated to [25]

$$ {\varPhi}_e=-j\frac{x_t^2-{y}_t^2}{R_ck}{k}_y^2+j\frac{2{x}_t{y}_t}{R_c}{k}_y-j\frac{y_t^2}{R_c}{k}_x $$
(22)

Although looser criteria may exist, we define a strict quantitative criterion to judge whether Δθ is minor enough by supposing no migration range arises

$$ \varDelta \theta <\frac{c}{BD} $$
(23)

where D is the diameter of the circumcircle of the target. According to Eq. (22), if we still generate images employing plane-wave approximation rather than Green’s function, the extra phase term will bring two impacts: one is a position error of \( -\frac{y_t^2}{2{R}_c} \) in the range direction and \( \frac{x_t{y}_t}{R_c} \) in the azimuth direction, respectively, and another is a focus-destroying phase term of \( -\frac{x_t^2-{y}_t^2}{R_ck}{k}_y^2 \). To guarantee the quality of focus, set \( \left|\frac{x_t^2-{y}_t^2}{R_ck}{k}_y^2\right|\le \frac{\pi }{8} \) (detailed introductions about this empirical value π/8 can be found in [29]). Then, the plane-wave criterion in small-rotation angle cases is

$$ D\le \frac{1}{2\varDelta \theta}\sqrt{R_c\lambda } $$
(24)

The criterion defined by Eq. (24) for imaging is much looser than the criterion of the plane-wave approximation of spherical wave \( D\le \sqrt{R_c\lambda }/2 \). It is because the focusing quality relies on the relative variation of the phase rather than the absolute value of the phase. Thus, the difference of phase variation may be neglected although there are obvious absolute phase errors at some distance. Even though the absolute phase errors lead to position distortion of images, the focusing quality maintains when the rotation angle is small.

Figure 5(a, b) shows the distortion of an 1 m × 1 m image area under the condition of R c  = 2.5 m, θ = 0°, and θ = 30°. The beginnings of the arrows indicate the real position of the pixels. The direction of the arrows represents the deviation direction of the pixels, and the length of the arrows is proportional to the degree of distortion.

Fig. 5
figure 5

This figure illuminates the position distortion of the image. The beginning arrows stand for the real position of the pixels, and the ending arrows represent the distorted positions of the pixels: a position distortion with observation angle θ = 0° and b position distortion with observation angle θ = 30°

Full size image

3.3 Plane-wave Criterion in Large Rotation Angle Cases

In large-rotation angle cases, the process of imaging integration can be decomposed into a number of small-rotation angle integration and the image obtained by each small-rotation angle can achieve good focusing quality. But the orientation and distance of the distortion are both different as a result of different observation angles. After summing up all these sub-images, a point target may be mapped to a distorted curve in the image. Figure 5 illuminates this problem that the same point has different distortions by comparing Fig. 5(a) with Fig. 5(b). Figure 6 shows this problem concisely. The beginning of the arrows indicates the distorted position of the pixels when θ = 0°. The ending of the arrows indicates the distorted position of the pixels when θ = 30°.

Fig. 6
figure 6

This figure shows the distortion when the imaging rotation angle is 30°. The beginning arrows stand for the distorted position when θ = 0°, and the ending arrows represent the distorted position when θ = 30°

Full size image

Now, we will derive the analytic form of the plane-wave criterion in large-rotation angle cases. Utilize the results derived in small-rotation angle cases and suppose θ = 0°. Then, the position distortion is

$$ dx\left|{}_{\theta =0}\right.=-\frac{y^2}{2{R}_c}\kern0.5em ,\kern0.5em dy\left|{}_{\theta =0}\right.=\frac{xy}{R_c} $$
(25)

If θ ≠ 0°, apply coordinate transforms u = x cos θ + y sin θ and v = − x sin θ + y cos θ and the distortion in a new coordinate is

$$ du=-\frac{u^2}{2{R}_c}\kern0.5em ,\kern0.5em dv=\frac{uv}{R_c} $$
(26)

Transforming Eq. (26) back into the original coordinate, we obtain

$$ dx\left|{}_{\theta}\right.=du \cos \theta -dv \sin \theta \kern0.5em ,\kern0.5em dy\left|{}_{\theta}\right.=du \sin \theta +dv \cos \theta $$
(27)

According to Eqs. (25) and (27), the displacement of the pixel is

$$ \overrightarrow{s}={\left(dx\left|{}_{\theta}\right.-dx\left|{}_{\theta =0}\right., dy\left|{}_{\theta}\right.- dy\left|{}_{\theta =0}\right.\right)}^{\mathrm{T}} $$
(28)

To guarantee the focusing quality of images, the displacement of point targets is supposed to be confined within the resolution unit

$$ {\overrightarrow{s}}^{\mathrm{T}}\overrightarrow{s}\le {\left(\frac{c}{2B}\right)}^2+{\left(\frac{\lambda }{4 \sin \left(\theta /2\right)}\right)}^2 $$
(29)

We have employed the definition of resolution from [30]. Equation (29) is the criterion of the plane-wave approximation in large-rotation angle cases.

4 Experimental Results and Analysis

The parameters of the radar system and experimental configurations are listed in Table 1 and Fig. 7.

Table 1 Parameters of 0.33-THz LFMCW radar and experimental configurations
Full size table
Fig. 7
figure 7

Photos of a corner reflectors and b the aircraft model on a circular turntable

Full size image

According to Eq. (23) and Table 1, the threshold separating small and large rotation angles is 4.3° in our experiments. We choose 2° and 30° as representatives of small and large rotation angles, respectively. Setting Δθ = 2° in Eq. (24), we can obtain the condition of plane-wave approximation that is D ≤ 0.68 m. Similarly, setting θ = 30° in Eq. (29), we obtain D ≤ 0.61 m. As the diameter of the circumcircle of targets is less than 0.5 m, we predict that plane-wave approximation is still valid under our experimental configurations.

4.1 Imaging Results of Corner Reflectors

It is easy to find Fig. 8(a) shares a great resemblance to Fig. 8(b). The only difference is the displacement in the range direction (x-axis) which is a result of the compensation of the deviation distance. The sidelobes are apparent as no suppression technology is employed. The resolution is not outstanding as only a small rotation angle is utilized. It is necessary to claim that the image area is discretized into 400 × 400 pixels and the image entropy before and after the compensation is 8.41 and 8.40, respectively. Just like what the image entropy indicates, no remarkable changes are observed after the deviation compensation and it is consistent with what is shown in Fig. 2 in small-rotation angle regions.

Fig. 8
figure 8

Images of corner reflectors with the rotation angle from θ = 0° to θ = 2° under plane-wave approximation a before and b after the deviation distance compensation

Full size image

As shown in Fig. 9, when the rotation angle increases to 30°, obvious differences are found between the images obtained before and after compensation. In Fig. 9(a), the quality of the image decreases instead of increasing with the increasing of the rotation angle. This phenomenon can be explained from two aspects. On the one hand, imaging is an essential procedure of 2D-matched filtering. The deviation between the center of turntable and the reference point leads to an unmatched filtering and results in the defocus of the image. The larger the rotation angle, the worse the focusing of the image is. On the other hand, large-rotation angle imaging can be decomposed into a number of small-rotation angle imaging. We can learn from Fig. 8 that no defocus happens in the image obtained by small rotation angle and the deviation distance \( \varDelta \widehat{R}-\varDelta R \) only leads to a shift in the range direction. When we transform all these sub-images back to the original coordinate and sum them up, little arcuate curves will appear in the final image as shown in Fig. 9(a). Comparing Fig. 9(b) with Figs. 9(a) and 8(b), notable improvements of resolution and SNR can be easily achieved by increasing the rotation angle after the deviation compensation. Quantitatively, the image entropy of Fig. 9(a) is 9.31 and that of Fig. 9(b) is 6.69, which also indicates a greater promotion of image quality than that of Fig. 8. This phenomenon is highly consistent with and can be predicted by Fig. 2.

Fig. 9
figure 9

Images of corner reflectors with the rotation angle from θ = 0° to θ = 30° under plane-wave approximation a before and b after the deviation distance compensation

Full size image

Now, we discuss the effects that spherical wave brings to the image. We utilize Eqs. (9) and (16) to generate images using the measured echo data, respectively. For convenience of comparing the difference, we plot these two images in the same figure as shown in Fig. 10(a) and a partial zoomed in figure is plotted in Fig. 10(b).

Fig. 10
figure 10

Images of corner reflectors with the rotation angle from θ = 0° to θ = 30° after the deviation compensation. a Images obtained by Eqs. (9) and (16) superposed in one coordinate. b A partial zoomed in figure of one corner reflector

Full size image

In Fig. 10, the images obtained utilizing Eqs. (9) and (16) show no apparent difference but slight position displacements. It is because the distance between corner reflectors and the turntable center is relatively small. Figure 10(b) shows the detailed position of the same corner obtained by Eqs. (9) and (16), respectively.

4.2 Imaging Results of the Aircraft Model

Similar with Fig. 8, the only apparent difference between (a) and (b) in Fig. 8 is a shift in the range direction (x-axis). It is necessary to claim that the image area is discretized into 360 × 312 pixels and the image entropy before and after the compensation is 9.38 and 9.37, respectively. The deviation compensation does not lead to a notable improvement of the image quality. This phenomenon can also be explained by Fig. 2. Due to the limitation of small rotation angle, the image resolution is limited and only a coarse contour of the aircraft model emerges. Also, in this case, we can see that the image suffers from low SNR since an aircraft model is not a target as bright as a corner reflector.

Similar with Fig. 9, due to the deviation distance between the turntable center and the reference point, the image quality degrades instead of upgrading dramatically with the increasing of the rotation angle. Comparing Fig. 12(a) with Fig. 9(a), both images show serious defocus and one difference is that no arcuate defocus curves are found in Fig. 12(a) which is an interesting characteristic in Fig. 9(a). It is because there are denser scattering centers in the aircraft image and the scattering component cannot be described by scattering centers existed in the echo signal. Comparing Fig. 12(b) with Figs. 12(a) and 11(b), a large rotation angle paralleled by deviation compensation brings a remarkable improvement of the resolution and SNR. The head, turbines, wings, tail, and other details of the aircraft model can be clearly distinguished in Fig. 12(b). Quantitatively, the image entropy of Fig. 12(a) is 9.54 and that of Fig. 12(b) is 9.03. In addition, an arc-shaped ribbon can be observed near the head of the aircraft. It is attributed to the migrator scattering from the edge of the circular turntable. This phenomenon also exists in Fig. 9(b), but it is suppressed by the bright corner scattering. The arc-shaped ribbon will emerge by adopting logarithm magnitude and adjusting the dynamic range of the image. We do not attempt to implement further discussions about this phenomenon in this paper.

Fig. 11
figure 11

Images of the aircraft model with the rotation angle from θ = 0° to θ = 2° under plane-wave approximation a before and b after the deviation distance compensation

Full size image
Fig. 12
figure 12

Images of the aircraft model with the rotation angle from θ = 0° to θ = 30° under plane-wave approximation a before and b after the deviation distance compensation

Full size image

Figure 13(a, b) shows the images obtained utilizing Eqs. (9) and (16), respectively. It is hard to distinguish their difference unless painstaking comparison is carried out. This is a result of a relatively small size of the model, and it can also be predicted by Eq. (29) as shown in Section 3. Comparing the highlighted region in the circles, a slight distortion of spherical wave can be noticed from the bent wings and the constricted tails.

Fig. 13
figure 13

Images of the aircraft model with the rotation angle from θ = 0° to θ = 30° after the deviation compensation results a using Eq. (9) under plane-wave approximation and b using Eq. (16) considering the spherical-wave effects

Full size image

4.3 Analysis and Discussion

More quantitative analyses on the image entropy, plane-wave approximation, and spatial resolution are carried out to show the effectiveness and correctness of our proposed method and derivation. Then, the pros and cons of this method for potential applications are discussed.

Figure 14 illustrates the image entropy of corner reflectors and the aircraft model before/after the deviation compensation varies against rotation angle. As we can see, both solid lines are obviously lower than the dashed ones for most range of the rotation angle, which is the purpose of the deviation compensation. In Fig. 14a, both lines drop rapidly from 11 to 8 as the rotation angle increases from 0° to about 3°. From this point onwards, the image entropy after the deviation compensation declines consecutively while the declining rate becomes lower and lower. In contrary, the dashed line which stands for the image entropy before deviation compensation goes upward after the rotation angle exceeds 3° and keeps ascending as the rotation angle grows larger. These phenomena revealed by experiments show high consistency with what is shown in Fig. 2, achieved by simulation. In Fig. 14b, when the rotation angle is smaller than 7°, the entropy before and after the deviation compensation is very similar and they both experience a bumpy descend. In the region where a rotation angle is larger than 7°, the solid and dashed lines show an apparent difference. The dashed line firstly sees a slight jump followed by a steady moderate rise, while the solid line keeps sinking at first, bottoming out at around 15°. After that, it also experiences a steady moderate grow just like the dashed line does.

Fig. 14
figure 14

Line graph of image entropy before/after deviation compensation varies against rotation angle. a Image entropy of the corner reflectors. b Image entropy of the aircraft model

Full size image

Comparing Fig. 14b with Fig. 14a, we can find three main differences: firstly, the lines in (b) is not as smooth as those in (a); secondly, the distance between the solid line and the dashed line in (b) is smaller than that of (a), especially in large-rotation angle cases; thirdly, the solid line in (b) sees an obvious grow while that one in (a) does not. Different from corner reflectors which can be treated as ideal point reflectors in a wide range of observation angle, an aircraft model may stimulate a variety of scattering components. As previously mentioned, the migrator scattering from the edge of the circular turntable which leads to an arc-shaped ribbon in the image of the aircraft model as shown in Figs. 12(b) and 13 can make great contribution to raise the image entropy. Apart from migrator scattering, the effects of surface roughness of the model to the images will also promote the image entropy as the resolution is improved by a large rotation angle. This nonmonotonic trend of the curve can challenge the reasonability of using entropy as a criterion of the image quality because it goes against that larger rotation angle can capture more information and will lead to better image quality. This is a problem that needs further research. Nonetheless, it is necessary to clarify that the nonmonotonicity does not affect the proposed minimum entropy-based autofocus method for a fixed rotation angle.

Considering the complicated scattering components contained in the scattered wave of aircraft model, it is difficult to conduct a concise analysis on the image distortion caused by plane-wave approximation using Fig. 13. Thus, Fig. 10, the image of corner reflectors, is chosen to probe the influence of plane-wave approximation quantitatively. In Fig. 10(b), the coordinate of the lower-left peak is (0.051, 0.144) and that of the upper-right peak is (0.046, 0.147). In the upper-left corner of Fig. 10(a), the coordinate of the left peak is (−0.053, −0.176) and that of the upper-right peak is (−0.058, −0.171). According to the principles illustrated by Figs. 5 and 6, we can get the theoretically predicted distorted coordinates of the peaks (0.051, 0.144) and (−0.053, −0.176) which are (0.047, 0.147) and (−0.059, −0.172), respectively. As can be seen, the relative error of the distorted position between the analytical prediction and the experimental result is under 3 % and the level of distortion is low enough to avoid errors when interpreting the image.

Figure 15 shows the PSF of a corner reflector and its cross section in range/azimuth direction to explore the image resolution experimentally. The corner reflector in Fig. 15 is the one in the right of Fig. 10(a). Strictly speaking, instead of measuring the resolution in the range and azimuth directions separately, a range-azimuth-coupled 2D resolution is more appropriate for image assessment when the rotation angle approaches 30°. Since this will be another topic out of the scope of this paper and for the convenience of comparison, the resolution here is still measured in range and azimuth directions separately. A new coordinate, range-to-azimuth coordinate, is established. The origin is situated at the peak of the PSF, and the range axis orients to radar at the middle observation angle which is determined by the geometry shown in Fig. 1 and the rotation angle. The cross section in range/azimuth direction is calculated and a −3-dB benchmark is used to measure the resolution. When the rotation angle is 2°, the measured range resolution is 2.30 cm and the azimuth is 1.16 cm. When the rotation angle is 30°, the measured range resolution is 1.03 cm and the azimuth is under 0.08 cm. Theoretically, we adopt the resolution definition in [30] in large-rotation angle cases. According to the parameters listed in Table 1, the range resolution is 1.72 cm, the azimuth resolution under 2° rotation angle is 1.32 cm, and the azimuth resolution under 30° rotation angle is under 0.09 cm. Compared to the resolution measured by the experiments, we can find that the resolution estimation in [30] is a conservative one. Over all, we can see that after the deviation distance compensation, at least 10 times promotion of resolution is achieved by the increased rotation angle and the azimuth resolution has already reached a sub-millimeter level.

Fig. 15
figure 15

Point spread function (PSF) and cross section in range/azimuth direction. a Rotation angle = 2°. b Rotation angle = 30°

Full size image

Apart from synthetic aperture (SA) imaging, other popular imaging methods mainly include raster scanning method [4, 10] and focal plane array method [31]. Compared to a raster scanning method, no scanning motors or cumbersome reflectors are needed for SA imaging. Thus, the size of radar and the power requirements can be confined within a feasible scope. When compared to a focal plane array method, no careful quasi-optical setups are required for SA imaging. Recently, all that is needed in SA imaging is just a pair of transistor/receiver and a turntable. Besides, without the constraint of the Rayleigh limit of the spot size for raster scanning or the limited number of pixels in focal plane array, the resolution of SA image is theoretically independent with distance. It means that much sharper images can be obtained by SA techniques in terahertz regime.

With the nonionizing nature and the capability to penetrate common packaging materials, THz wave has drawn much attention for applications such as personnel screening, noninvasive inspection, nondestructive evaluation, and biological applications. By using our improved algorithm, a general simple application scene can be conceived: with the target object positioned on a steadily running turntable and the radar system transiting and receiving THz waves, a sub-millimeter resolution image of the object is generated simultaneously. Although a centimeter resolution may be enough for identifying threats, such as knives and guns, a sub-millimeter resolution can still contribute to raise the detection rate and the veracity of identification. Also, evaluating the quality of tablets and detecting lymph nodes in human bodies are both potential applications of the improved SA imaging method.

However, some problems should still be considered carefully. Firstly, as aforementioned, real objects stimulate complex scattering components and this will add difficulty to image interpretation, especially if there are several layers. The THz beam may penetrate some layers, reflect between two layers, or be absorbed by some layers, and the obtained image can be seen rather different from the object. Therefore, additional studies to evaluate the scattering properties of a layered target and the needed dynamic range of the radar system must be performed. Secondly, the phase error discussed in this manuscript is under the assumption that the distance between radar and the target is a constant. It means that the target object is collaborating with the imaging process. More complex situations, such as safety inspection for walking bodies, can emerge in practical applications for uncooperative objects. As a result, parameters, such as the moving velocity of the target body, must be estimated to compensate phase errors caused by the movement before imaging. Much further research is needed to solve these problems.

5 Conclusions

Based on a 330-GHz LFMCW terahertz radar system, we presented two parts of work aiming at the large-rotation angle problem and the spherical-wave problem, respectively. On the one hand, we illustrated analytically that the deviation distance between the turntable center and the reference bright target leads to an extra linear phase term in the calibrated IF signal. In small-rotation angle cases, the quality of the image shows low dependence against this deviation distance and all the visible differences brought by this deviation are a shift of the image in the range direction. In large-rotation angle cases, the existence of deviation distance will bring dramatically degradation to the image quality. By utilizing the minimum entropy criterion to estimate and compensate for the phase errors, great improvements of resolution and SNR of the image were achieved. On the other hand, the criteria of plane-wave approximation for imaging have been analyzed and derived in small and large-rotation angle cases. Their compact form is expressed in Eqs. (24) and (29), respectively. These criteria are much looser than the criterion of the plane-wave approximation of spherical wave. When R c  = 2.5 m and the target size was smaller than 0.5 m, experimental results showed that spherical wave only leads to a slight position distortion of images and the influence of spherical-wave effects on focusing quality can be neglected.