Heterogeneous treatment effects and bias in the analysis of the stepped wedge design

Abstract

The effect of an intervention in a stepped wedge design can vary across clusters or with time since exposure to treatment, but consequences of such heterogeneous treatment effects for the analysis of stepped wedge designs are not well recognized. In this article, we advance the idea that the stepped wedge design can be framed as a special case of a difference-in-differences design with staggered treatment exposure. Using this perspective, we show that the standard difference-in-differences regression approach estimates the average treatment effect of the treatment period with bias when treatment effects vary by cluster or time since exposure. We then use Monte-Carlo simulations of stepped wedge designs to examine the performance of the standard regression approach as well as alternative approaches that estimate treatment effects relative to intervention exposure. Simulation results confirm that estimates from the standard approach are biased when treatment effects are heterogeneous. Alternative regression approaches may perform better, but only if the research design allows estimation of the full treatment effect across all clusters. We conclude by offering recommendations for the design and analysis of stepped wedge trials.

Appendices

Appendix

Derivation of weights based on Abraham and Sun (2018)

The first step is to partial out time fixed effects. For a random variable $x_{it}$, denote its sample average for period $t$ as ${\bar{x}}_{\cdot t} = 1/N\sum _i x_{it}$ and the demeaned value as ${\dot{x}}_{it} = x_{it} - {\bar{x}}_{it}$. After partialling out time fixed effects, regression (5) can be rewritten as follows:

$$\begin{aligned} {\dot{y}}_{it} = \theta {\dot{D}}_{it} + \zeta _{it}. \end{aligned}$$

The ordinary least square estimate of $\theta$ can then be written as follows:

$$\begin{aligned} {\hat{\theta }} = \frac{\sum _{t=1}^T\sum _{i=1}^N{\dot{y}}_{it}{\dot{D}}_{it}}{\sum _{t=1}^T\sum _{i=1}^N{\dot{D}}_{it}{\dot{D}}_{it}}. \end{aligned}$$

Taking the probability limit, the population regression coefficient is then:

$$\begin{aligned} \text {plim}\, {\hat{\theta }} = \frac{\sum _{t=1}^T E({\dot{y}}_{it}{\dot{D}}_{it})}{\sum _{t=1}^T E({\dot{D}}_{it}^2)}. \end{aligned}$$

Note that $E(D_{it}-{\bar{D}}_{\cdot t}) = E(D_{it})-{\bar{D}}_{\cdot t}= {\bar{D}}_{\cdot t}- {\bar{D}}_{\cdot t}= 0$, and therefore, $E({\dot{y}}_{it}{\dot{D}}_{it}) = E((y_{it}-{\bar{y}}_{\cdot t}){\dot{D}}_{it}) = E(y_{it}{\dot{D}}_{it}) - E({\bar{y}}_{\cdot t}{\dot{D}}_{it}) = E(y_{it}{\dot{D}}_{it}) - {\bar{y}}_{\cdot t}E(D_{it}-{\bar{D}}_{\cdot t}) = E(y_{it}{\dot{D}}_{it})$. Using this expression and iterative expectations, the probability limit of the regression coefficient can be rewritten as:

$$\begin{aligned} \text {plim}\, {\hat{\theta }}&= \frac{\sum _{t=1}^T E(E(y_{it}{\dot{D}}_{it}|J_i=j))}{\sum _{t=1}^TE({\dot{D}}_{it}^2)} \\ \end{aligned}$$

Next, we expand on the numerator, noting that ${\dot{D}}_{it}= (1-{\bar{D}}_{\cdot t})$ if $D_{it}=1$ and ${\dot{D}}_{it}= -{\bar{D}}_{\cdot t}$ if $D_{it}=0$:

$$\begin{aligned} \sum _{t=1}^T E(E(y_{it}{\dot{D}}_{it}|J_i=j))&= \sum _{t=1}^T \left( \sum _{j<t}P(J_i=j)(1-{\bar{D}}_{\cdot t})E(y_{it}|J_i=j, D_{it}=1)\right) \\&\quad + \left( \sum _{j\ge t}P(J_i=j)(-{\bar{D}}_{\cdot t})E(y_{it}|J_i=j, D_{it}=0)\right) \\ \end{aligned}$$

Note that $\sum _{j<t}P(J_i=j) = P(J_i<t) = {\bar{D}}_{\cdot t}$ and conversely, $\sum _{j\ge t}P(J_i=j)=(1-{\bar{D}}_{\cdot t})$. The weights in the two expressions thus sum to 0:

$$\begin{aligned} \sum _{j<t}P(J_i=j) (1-{\bar{D}}_{\cdot t}) - \sum _{j\ge t}P(J_i=j) {\bar{D}}_{\cdot t}= {\bar{D}}_{\cdot t}(1-{\bar{D}}_{\cdot t}) - (1-{\bar{D}}_{\cdot t}){\bar{D}}_{\cdot t}= 0. \end{aligned}$$

Therefore, the terms from the second expression can be distributed across the first expression. Further note that due to random assignment and no anticipation, $E(y_{it}|J_i=j, D_{it}=0) = E(y^0_{it}|J_i=j, D_{it}=1)$, i.e., expected outcomes of untreated individuals are equal to expected potential outcomes of treated individuals if they were not exposed to treatment. Therefore, the numerator simplifies to:

$$\begin{aligned} \sum _{t=1}^T E(E(y_{it}{\dot{D}}_{it}|J_i)) = \sum _{t=1}^T \left( \sum _{j<t}P(J_i=j)(1-{\bar{D}}_{\cdot t})E(y^1_{it}-y^0_{it}|J_i=j, D_{it}=1)\right) . \end{aligned}$$

The expression $E(y^1_{it}-y^0_{it}|J_i=j, D_{it}=1)$ is equal to the cluster- and time since first exposure-specific average treatment effect of the treated $CATT_{jl}$. Further re-expressing $P(J_i=j)= {\bar{D}}_{\cdot t}\cdot P(J_i|J_i<t)$, where $P(J_i|J_i<t)$ is the probability of an individual $i$ being in cluster $j$ among individuals exposed to treatment, implies:

$$\begin{aligned} \sum _{t=1}^T E(E(y_{it}{\dot{D}}_{it}|J_i)) = \sum _{t=1}^T {\dot{D}}_{it}(1-{\dot{D}}_{it}) \left( \sum _{j<t}P(J_i|J_i<t)E(y^1_{it}-y^0_{it}|J_i=j, D_{it}=1)\right) . \end{aligned}$$

The final step is to express the equation in terms of time since exposure $l$ instead of t. Note that $t=(j+l+1)$, and for a cluster $j$, $l$ ranges from zero to $T-l$. It then follows:

$$\begin{aligned} \text {plim}\, {\hat{\theta }}&= \frac{\sum _{j=1}^{j_{\text {max}}}\sum _{l=0}^{T-j-1}{\bar{D}}_{\cdot (j+l+1)}(1-{\bar{D}}_{\cdot (j+l+1)}) P(J_i=j|J_i<(j+l+1)) CATT_{jl}}{\sum _{t=1}^TE({\dot{D}}_{it}^2)} \\&= \sum _{j=1}^{j_{\text {max}}}\sum _{l=0}^{T-j-1}\omega _{jl}CATT_{jl}, \end{aligned}$$

where

$$\begin{aligned} \omega _{jl} = \frac{{\bar{D}}_{\cdot (j+l+1)}(1-{\bar{D}}_{\cdot (j+l+1)}) P(J_i=j|J_i<(j+l+1))}{\sum _{t=1}^TE({\dot{D}}_{it}^2)} \end{aligned}$$

are the weights, which are not only a function of population fractions $P(J_i=j|J_i<(j+l+1))$ but also of the treatment exposure variance ${\bar{D}}_{\cdot (j+l+1)}(1-{\bar{D}}_{\cdot (j+l+1)})$.

Parameters used for the Monte Carlo simulation

See Table 7.

Table 7 Simulation parameters

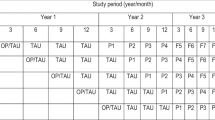
Treatment schedule and treatment heterogeneity

In this appendix section, we describe treatment schedules for each of the four scenarios. In each table, rows denote intervention cohorts and columns show time. The numbers indicate the fraction of the treatment effect that participants are exposed to, where cells with a value equals to zero are pre-intervention periods and cells with a value larger than zero are treatment periods. Colors are used to distinguish between the four research design: only black numbers are for the first research design (baseline design with four intervention cohorts and five time periods), black and teal numbers are for the second research design (longer treatment period), black and blue numbers are for the third research design (comparison group), and black, teal, blue and brown numbers are for the fourth research design (longer treatment period and comparison group).

The treatment schedule for the first scenario with homogeneous treatment effects across intervention cohort and no delay in treatment effect only has two values, zero (for control periods) and one (for treatment periods) (Table 8).

Table 8 Treatment schedule for the first scenario

The treatment schedule for the second scenario with heterogeneous treatment across cohorts (vertical heterogeneity) and no treatment effect delay has treatment periods with values above and below one (Table 9).

Table 9 Treatment schedule for the second scenario

The treatment schedule for the third scenario with homogeneous treatment across cohorts and treatment effect delay has some treatment periods with values less than one, indicating time periods after intervention onset where the full treatment effect is not yet realized (Table 10).

Table 10 Treatment schedule for the third scenario

The fourth scenario with heterogeneous treatment effects across cohorts and treatment effect delay has the most complicated treatment schedule. Values for all cohorts increase during the first three treatment periods due to the delay, and each cohort has different long-run treatment effects (Table 11).

Table 11 Treatment schedule for the fourth scenario

Based on these treatment schedules, and assuming the same number of participants per cluster and time period, the ATTP can be calculated by simply summing cluster- and time since exposure-specific treatment effects during the treatment period from the previous tables. The following table shows ATTPs for scenarios 2 to 4 and research designs 1 and 2; ATTPs for research design 3 are identical to ATTPs for research design 1, while ATTPs for research design 4 are identical to ATTPs for research design 2. ATTPs for scenario 1 are all - 0.001 (Table 12).

Table 12 ATTP for scenarios 2-4 and research designs 1-2