1 Introduction

The Fixed Set Search (FSS) is a novel metaheuristic that has previously been successfully applied to solve the traveling salesman problem (Jovanovic et al. 2019), the power dominating set problem (Jovanovic and Voss 2020), machine scheduling (Jovanovic and Voß 2021) and the minimum weighted vertex cover problem (Jovanovic and Voß 2019). Quite some research has shown that the performance of population-based metaheuristics can be significantly improved by adding a local search. The design of the FSS starts from the premise that it includes a local search. In practical terms the FSS adds a learning mechanism to the Greedy Randomized Adaptive Search Procedure (GRASP) metaheuristic. GRASP iteratively generates solutions for the problem of interest using a Randomized Greedy Algorithm (RGA) and applies a local search to each of those solutions (Feo and Resende 1995). The popularity of the GRASP comes from the simplicity of its implementation which still manages to have a performance comparable to more complex population-based metaheuristics that do not use a local search. One of the most effective improvements of the GRASP method is the use of path relinking (Resende and Ribeiro 2005; Díaz and Luna 2018; Marzo and Ribeiro 2020).

The FSS exploits the fact that high-quality solutions, for a specific problem instance, often have many of the same elements in common. The idea of the FSS is to use such elements in generating new solutions. Practically, this means that a set of such elements, called the fixed set, is included in the solutions that will be generated and the computational effort is dedicated to fill the partial solution or, in other words, “filling in the gaps.” The concept of using elements of high-quality solutions is based on earlier notions of chunking (Voß and Gutenschwager 1998; Woodruff 1998), vocabulary building and consistent chains (Sondergeld and Voß 1999) as they have been used, e.g., in relation to tabu search. In those notions one relates given solutions of an optimization problem as being composed of parts (or chunks). Similar ideas are even found in the matheuristic POPMUSIC paradigm (Taillard and Voß 2002). The basic steps of the FSS are similar to the GRASP in the sense that new solutions are generated using a RGA and a local search is applied to them. The difference is that there is a set of elements which are pre-selected in the solution generated by using the RGA, which is the fixed set. The learning mechanism consists of generating such fixed sets based on experience gained from previously generated solutions.

1.1 Multi-objective methods

In this paper, the FSS is extended to solve multi-objective discrete combinatorial optimization problems. Solving multi-objective problems has generally a much higher computational cost than single-objective ones, since the goal is to find the Pareto Front (PF) instead of a single optimal solution value. The PF can be obtained using Mixed-Integer Programs (MIP) with the \(\epsilon \)-constraint method (Mavrotas 2009), the weighted sum method (Marler and Arora 2010) and similar approaches. In case these methods are used, it is necessary to solve multiple single-objective problems. In general, solving single-objective optimization problems using MIP may come at a high computational effort. This becomes even more significant in case of multi-objective ones, since many such problems need to be solved. It should be noted that in some practical applications of multi-objective problems, the decision maker provides a set of a priori preferences, and needs the solutions evaluated against these preferences. For this type of application, goal programming (Tamiz et al. 1995) seems most suitable.

To address this drawback, there has been a notable effort in adapting standard metaheuristics (tabu search, simulated annealing, genetic algorithms, particle swarm optimization, etc.), to solve multi-objective combinatorial optimization problems, for which an extensive recent review can be found in Liu et al. (2020). The most commonly used multi-objective metaheuristic is NSGA-II (Deb et al. 2002), which is an adaptation of genetic algorithms. One of the main issues that many metaheuristics for multi-objective problems face is the need for a ranking between the generated solutions. This is frequently done using non-dominated sorting which, in its basic form, has a high computational complexity. The popularity of NSGA-II is partly due to its introduction of an efficient procedure for this task having a computational complexity of \(O(MN^2)\) and storage requirements of \(O(N^2)\), where N is the population size and M is the number of objective functions. Another issue in using standard metaheuristics is the increase in implementation complexity. One of the main reasons for the widespread use of the NSGA-II is the existence of a MatLab toolbox, and other libraries, that render its usage as a black box possible. On the other hand, it is possible to improve the quality of solutions using different types of local searches. The use of local searches has proven to be a powerful tool in finding approximations to the PF, for which an extensive review can be found in Blot et al. (2018).

In case of multi-objective optimization problems, the GRASP has managed to maintain its popularity due to the preserved simplicity in its implementation. In general, the only adaptations that are needed, compared to the single-objective GRASP, are the selection of the objective function used to construct solutions and improve them at each iteration of the GRASP algorithm. An overview of approaches for this selection procedure is provided in Martí et al. (2015). Some examples of successful applications of a multi-objective GRASP are, among others, focusing on the knapsack problem (Vianna and Arroyo 2004), the waste collection problem (López-Sánchez et al. 2018), partial classification (Reynolds and De la Iglesia 2009), multi-row facility layout (Wan et al. 2022), and dynamic cache resources placement (Ben-Ammar and Hadjadj-Aoul 2020). An interesting method for improving the basic multi-objective GRASP is its hybridization with the variable neighborhood descent (López-Sánchez et al. 2018). It should be noted that the extensions of the GRASP with path relinking and its variations have successfully been applied to several multi-objective problems (Martí et al. 2015; Rezki and Aghezzaf 2018; Sánchez-Oro et al. 2021).

An issue with the multi-objective GRASP is that the more solutions are generated, the less likely it becomes that new elements of the PF are generated. To be more precise, in the early iterations of the GRASP, non-dominated solutions are frequently generated, since there is a small number of previously generated solutions that can potentially dominate them. In the later iterations of the GRASP, it becomes increasingly more probable that a newly generated solution is dominated by at least one of the solutions obtained in the previous iterations. This is due to the fact that the quality of generated solutions in the GRASP algorithm is independent of the number of performed iterations.

Other metaheuristics avoid this issue by including different types of learning mechanisms. As we will show, the FSS manages to add an experience-based learning mechanism to the GRASP, while maintaining the simplicity of the method even in case of multi-objective problems. It should be noted that previous research has shown that the FSS is improving the performance of the underlying GRASP significantly especially in case of mediocre local searches. Consequently, the need for developing a complex highly efficient local search can be avoided for many applications.

1.2 Related work

The Minimum Vertex Cover Problem (MVCP) is one of the standard combinatorial optimization problems with its decision version being one of Karp’s 21 NP-complete problems (Karp 1972). The MVCP and its variations have proven to be very suitable for representing many real-world problems (Wang et al. 2017; Pullan 2009; Hu et al. 2018). Because of this, there has been an extensive amount of research dedicated to developing methods for solving this problem. A wide range of different metaheuristics has been applied to this problem like genetic algorithms (Singh and Gupta 2006), ant colony optimization (Jovanovic and Tuba 2011) and many others (Bouamama et al. 2012; Voß and Fink 2012). Because of this, the MVCP and its variations are very suitable for evaluating the performance of new algorithmic concepts.

The MVCP is defined for a graph \(G = (V,E)\), where V is a set of vertices and E is a set of edges. A vertex set \(S \subset V\) is called a vertex cover if for every edge \(\{u, v\} \in E\) at least one of the vertices u or v is an element of S. The objective of the MVCP is to find a vertex cover S that has minimum cardinality. In the Minimum Weighted Vertex Cover Problem (MWVCP) there is a corresponding weight w(u) for each vertex \(u \in V\). The objective in the MWVCP is to find a vertex cover having minimum total weight. In an m-objective MWVCP (m-MWVCP) each vertex \(u \in V\) has m weights \(w_i(u)\), \(i = 0, \dots , m-1\), assigned to it. Each of the weights corresponds to an objective function having the following form.

$$\begin{aligned} \text {minimize } F(S)= & {} (f_0(S), \dots , f_{m-1}(S)) \end{aligned}$$
(1)
$$\begin{aligned} f_i(S)= & {} \sum _{u \in S} w_i(u) \end{aligned}$$
(2)

In Eq. (1), the goal is to minimize the value of each objective \(f_i\), where \(i = 0, \dots , m-1\), for a vertex cover S. The goal in the m-MWVCP is not to find a single best solution but the set of all non-dominated solutions. The term dominate is used for the following relation between solutions. Solution \(S'\) dominates solution S (for a minimum multi-objective problem), if for each objective \(f_i(S') \le f_i(S)\) is satisfied, and there exists at least one objective \(f_j\) such that \(f_j(S') < f_j(S)\). The notation \(S' \prec S\) is used to indicate that solution \(S'\) dominates solution S. The set of all non-dominated solutions, i.e., those solutions that are not dominated by any other solution, is called the Pareto Set or the Pareto Front (PF).

The m-MWVCP has been introduced in the work of Rollon and Larrosa (2009). Many real-world systems are well represented in this way. An example can be the optimal positioning of electrical vehicle (EV) charging stations. In this type of model, the instance graph is generated based on map data. The edge-covering constraint is related to the availability of chargers to potential EV drivers within some maximal distance. The two objectives, corresponding to the two weight functions, are related to the needs of the charging station operators and the convenience of EV drivers. For instance, the first set of weights could represent location costs. The second set of weights could represent the average distance travelled by each EV to reach the station, pre-calculated based on population densities.

It is interesting that, although the MWVCP is one of the most researched combinatorial optimization problems, very limited research has been dedicated to its multi-objective version. In Rollon and Larrosa (2009), an analysis of the PF is done through a comparison of PFs obtained by the \(\epsilon \)-method and the multi-objective mini-bucket elimination algorithm. In the work of Marinescu (2010), the effectiveness of the best-first search in a multi-objective branch-and-bound algorithm is illustrated on the multi-objective MWVCP. Recently, an approach incorporating a local search has been applied to the problem of interest, using the multi-objective neighborhood search algorithm based on decomposition (MONSD) (Hu et al. 2019). The MONSD uses a population-based approach. Each population member solves a different single-objective problem. To be more precise, each objective is equal to a weighted sum of the objectives of the original multi-objective problem. In addition, an interesting mixed score function is introduced based on the problem features, to make the initialization procedure and the neighborhood search more effective.

1.3 Contribution

In this paper, the FSS is applied to solve the bi-objective MWVCP as a prototype of multi-objective combinatorial optimization problems. This is done by extending the FSS algorithm previously developed for the MWVCP (Jovanovic and Voß 2019) to a multi-objective setting (with a focus on two objectives). This extension consists of several steps. Firstly, in the GRASP algorithm from Jovanovic and Voß (2019) the randomization of the RGA and the use of local search are adapted to the bi-objective setting. In the randomization step a novel method for selecting the heuristic function used at each iteration of the RGA is proposed. It provides a good distribution of newly generated solutions close to the entire area of the PF. In the extension of the FSS, the method for generating the fixed sets has been adapted to use only solutions that are part of the current PF approximation. In this way, the multi-objective FSS avoids the need for non-dominated sorting.

An extensive analysis of the performance of the FSS is done on instances from the literature which are used in the conducted computational experiments. To be more precise, the comparison is done on the MONSD (Hu et al. 2019). The results show that the proposed GRASP and FSS manage to greatly outperform MONSD for the multi-objective MWVCP. To be able to better understand the effect of the learning mechanism of the FSS, the comparison with the GRASP algorithm is performed on a wide range of indicators. The selected indicators are related to convergence, distribution, spread and cardinality as suggested by Audet et al. (2021). In addition, the convergence speed and the effect of method parameters of the FSS are evaluated.

The paper is organized as follows. The next section provides details on the proposed multi-objective GRASP. Section 3 is dedicated to the adaptation of the FSS to the multi-objective MWVCP. The following section provides details of the performed computational experiments. The paper is finalized with concluding remarks.

2 GRASP

In this section, the GRASP algorithm for the 2-MWVCP is presented. Firstly, the standard greedy algorithm for the MWVCP is adapted to the 2-MWVCP. Next, the new adaptation of the greedy algorithm is randomized. The goal of randomization of the greedy algorithm within a single-objective GRASP is to make it possible to find a single optimal solution, by generating solutions in promising regions of the solution space. On the other hand, in case of a multi-objective setting, the objective of the randomized greedy algorithm is to generate solutions in a way that they can be used to approximate as many points of the PF as possible. In the later parts of this section, the applied local search is presented and details are given on how it is used within the GRASP algorithm.

2.1 Greedy algorithm

In this section, the standard greedy constructive algorithm for the MWVCP is adapted to a bi-objective setting. In case of the single-objective MWVCP, the method starts from an empty solution \(S = \emptyset \) and at each step it is expanded with a vertex that has the most desirable properties based on a heuristic function h. The heuristic function considers expanding a solution S with a vertex u that covers a large number of non-covered edges and has the minimal weight w(u). In case of the 2-MWVCP, two separate heuristic functions \(h_i\), defined for \(i = 0, 1\), are used for each of the weights \(w_i\). The used heuristic function has been introduced by Chvatal (1979) for the set covering problem and has been extensively used for the MWVCP. For the notion of heuristic functions and heuristic measure in general, the reader is referred to, e.g., Rayward-Smith and Clare (1986) and Voß et al. (2005). Formally, the heuristic functions for a partial solution S and a vertex u have the following form.

$$\begin{aligned} Cov(u, S)= & {} \{ \{ u, v\} \mid (\{u,v\} \in E) \wedge (v \notin S)\} \end{aligned}$$
(3)
$$\begin{aligned} h_i(u,S)= & {} \frac{|Cov(u,S)|}{w_i(u)} \end{aligned}$$
(4)

In Eq. (3), Cov(u, S) is the set of edges in E that contain vertex u but are not already covered by S. An edge is covered if at least one of its vertices is in S. The notation |X| is used for the cardinality of the set X. A heuristic function \(h_i\), defined in Eq. (4), is proportional to the number of elements of Cov(S, u), and inversely proportional to the corresponding weight \(w_i(u)\) of the vertex u.

The standard approach to randomize a greedy algorithm is the use of a restricted candidate list (RCL). Let us define \(R \subset V \setminus S\) as the set of elements that are not in the solution that have the largest value of the heuristic function h(v, S). The partial solution is expanded with a random element of set R. In this case, the size of the RCL is equal to |R|. This idea can be directly extended to the 2-MWVCP by creating a RCL based on each of the heuristic functions \(h_i\).

The goal is to integrate this type of randomized greedy algorithm (RGA) into a GRASP method which is applied to a bi-objective problem. In such a case, the fact that the RGA only considers one objective function at a time becomes an issue. This concept needs to be adapted in a way to produce solutions that can be used for approximating the entire PF. The solutions with the minimal values of the objective functions \(f_i\) (in a minimization problem) are of special importance for specifying the PF. Because of this, additional effort should be dedicated to find them. This can easily be achieved by using a greedy constructive algorithm that only uses one of the heuristic functions \(h_i\).

On the other hand, a greedy algorithm also needs to explore the part of the PF between the extreme values. One approach that is commonly used is defining a weighted heuristic function \(h^w(u,S) = \gamma h_0(u,S) + (1-\gamma )h_1(u,S)\) that jointly considers both objectives. Note that \(\gamma \) represents the weight given to objective function \(h_0\). One of the drawbacks of this approach is the necessity of selecting the weight parameter \(\gamma \). This generally includes some type of normalization based on the heuristic functions \(h_i\) and some analysis on the range of the objective functions \(f_i\). In the proposed method, this is avoided in the following way. A randomized heuristic function \(h^{\alpha }\) is defined that selects one of the heuristic functions with probability \(\alpha \in [0,1]\) as follows:

$$\begin{aligned} h^{\alpha }(u,S) = \left\{ \begin{array}{l} h_1(u,S)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\beta \le \alpha \\ h_0(u,S)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\beta > \alpha \end{array} \right. \end{aligned}$$
(5)

In Eq. (5), \(\beta \) is a random variable with a uniform distribution from the interval (0, 1). The heuristic \(h^{\alpha }(u,S)\) selects one of the heuristics \(h_i\) based on the value of \(\beta \).

figure a

The heuristic function \(h^{\alpha }\) can be used to define the randomized greedy constructive algorithm used in the 2-MWVCP, as it can be seen in Algorithm 1. In it, the partial solution S is initially set to an empty set. At each iteration, S is expanded with a random element from the RCL based on \(h^\alpha \). This is repeated until all the edges in E are covered. The proposed \(RGA_\alpha \) has a computational complexity of |S||V|, where S is the generated solution.

2.2 Local search

In this section, a local search based on a correction procedure is presented. The proposed local search uses the concept of swapping elements of a solution S with elements of \(V \setminus S\) that produce a vertex cover of higher quality. A similar swap operator has been used in Voß and Fink (2012); Li et al. (2016); Jovanovic and Voß (2019) for the single-objective MWVCP. The swap operator has also been extended with success for element pairs (Jovanovic and Voß 2019). A solution S for the single-objective MWVCP is improved to a new solution \(S'\) if \(f(S')< f(S)\). In case of the 2-MWVCP additional considerations are needed. As it is discussed in Martí et al. (2015), improvements to a solution S in a local search can be observed in several ways in the context of the PF. In this paper, similar concepts are considered and defined. In a pure improvement for a solution S, the focus is on one objective function \(f_i(S')\) and it is allowed to deteriorate the second one \(f_j(S')\). Another option is to use a new weighted objective function \(f^w(S) = \varTheta f_0(S) +(1-\varTheta ) f_1(S)\) with \(\varTheta \in [0,1]\); in this case an improvement is achieved if the value of \(f^w(S')\) has decreased. Note that this can result in a deterioration of the objective functions \(f_i(S')\) and \(f_j(S')\). In constraint improvement, a single objective is considered at a time. A solution \(S'\) improves a solution S if \(f_i(S')<f_i(S)\) and \(f_j(S') \le f_j(S)\). In the proposed method, the local search only uses the constraint improvement for which details are given in the following subsection.

2.2.1 Element swap

In this subsection, details of the swap operator are presented. This operator is used to define a neighborhood used in the local search. From now on, it is assumed that a solution S is to be improved. If S is a vertex cover of G, for each edge \(\{u, v \}\) at least one of the nodes u or v is an element of S. Let us define UniqueCover(v, S), for a solution S and vertex \(v \in S\), as the set of vertices that correspond to edges that are uniquely covered by vertex v as

$$\begin{aligned} UniqueCover(v,S) = \{ u \mid u \notin S \wedge \{u, v\} \in E \} \end{aligned}$$
(6)

It is clear that if vertex v is removed from S and all of the elements of UniqueCover(v, S) are added to S, a new vertex cover is created. For simplicity of notation let us define the swap operator for a vertex v as

$$\begin{aligned} Swap(v,S) = (S \cup UniqueCover(v,S)) \setminus \{v\} \end{aligned}$$
(7)

The effect of a swap operator, for a vertex v, on the value of each objective function can be defined as

$$\begin{aligned} Change_i(v,S) = w_i(v) - \sum _{u \in UniqueCover(v,S)}{w_i(u)} \end{aligned}$$
(8)

In Eq. (8), \(Change_i(v, S)\) gives the change in the objective function value \(f_i\) when \(v \in S\) is swapped. Note that i is equal to 0 or 1 depending on the selected objective function. More precisely, it is equal to the difference between the weight of the removed vertex (\(w_i(v)\)) and the sum of the weights of all the added vertices. Now, we can define \(Imp_i(S)\) as the set of all vertices of S for which a swap operator produces a constraint improvement for objective \(f_i\):

$$\begin{aligned} Imp_i(S) = \{v \mid v \in S \wedge Change_i(v,S) > 0 \wedge Change_j(v,S) \ge 0\} \end{aligned}$$
(9)

In Eq. (9) i is running through the set of weights for which an improvement is tested, hence i is equal to 0 or 1. In the same equation, j is used for the remaining weight set. This equation states that swapping vertex \(v \in S\) produces a constraint improvement for objective function \(f_i\), if the value of \(Change_i(v,S)\) is greater than zero (\(f_i\) decreases) and the value of \(Change_j(v,S)\) is greater or equal to zero (\(f_j\) does not increase). \(Imp_i(S)\) is the set of all such vertices.

2.2.2 Implementation

Now, the constraint local search for objective function \(f_i\), based on the element swap operator, can be specified as in the pseudocode in Algorithm 2.

figure b

In Algorithm 2, the inputs are a solution S and the index of the objective function \(f_i\) whose improvement is preferred. The solution is iteratively improved based on element swap neighborhoods. At each iteration, a constraint improvement for objective i is tested using the function \(Imp_i(S)\). In case such an improvement exists, a random element \(v \in Imp_i(S)\) is selected and swapped from the solution. In case this is not possible, the second objective \(f_j\) is tested using the function \(Imp_j(S)\). In case an improvement is possible, \(Imp_j(S) \ne \emptyset \), a random element \(v \in Imp_j(S)\) is selected and swapped with an element from the solution. The main loop is repeated until no further improvement exists. Note that due to the sole use of constraint improvements, cycles between improving solutions are not possible.

2.3 GRASP implementation

This subsection details how the proposed RGA and local search are used in the GRASP metaheuristic for the 2-MWVCP. There are several aspects that need to be considered. Firstly, the selection of the RGA that is used in each iteration, or more precisely, how the value of \(\alpha \) is selected; and secondly, which objective function \(f_i\) must be applied for a solution obtained using the \(RGA_\alpha \).

The selection of \(\alpha \) at each iteration impacts the area of the PF to which a generated solution \(RGA_\alpha \) is close to. As previously stated, additional effort should be dedicated to finding the extreme points of the PF. This effort is controlled with an additional parameter \(\delta \in (0, 0.5)\). The selection of the value \(\alpha \) is done based on a random variable \(\theta \) in the following way.

$$\begin{aligned} \alpha = \left\{ \begin{array}{l} 1\qquad \qquad \qquad \qquad \qquad \theta \le \delta \\ 0\qquad \qquad \qquad \qquad \qquad \theta \ge 1 - \delta \\ random(0,1)\qquad \qquad \,\,\, otherwise \\ \end{array} \right. \end{aligned}$$
(10)

In Eq. (10) the notation random(0, 1) is used for a random variable having a uniform distribution on the interval (0, 1). In case of \(\delta =0.5\), all the effort is dedicated to finding the extreme points of the PF. In case \(\delta =0\), no additional effort is dedicated to this task.

The next step is defining the procedure for selecting the local search that is used for a specific value of \(\alpha \). This selection is based on the following logic. In case the solution is generated using only one of the objective functions (\(\alpha = 0,1\)), the objective is to generate solutions near the extreme points of the PF. Consequently, it is natural that the objective function used for the local search is the same as for the greedy algorithm. On the other hand, for \(0<\alpha <1\) it is not evident to which part of the PF the solution obtained by \(RGA_\alpha \) will be close to, so there is no preference for a specific local search and the objective function \(f_i\) can be randomly selected. The selection of the objective function \(f_i\) based on the value of \(\alpha \) is given in the following equation.

$$\begin{aligned} i = \left\{ \begin{array}{l} 1\qquad \qquad \qquad \qquad \qquad \alpha = 1 \\ 0\qquad \qquad \qquad \qquad \qquad \alpha = 0 \\ random(\{0,1\})\qquad \quad \,\,\,\, otherwise \\ \end{array} \right. \end{aligned}$$
(11)

In Eq. (11) the notation \(random(\{0,1\})\) is used for a random variable having a uniform distribution within the set \(\{0,1\}\).

figure c

The GRASP algorithm can now be fully specified as in Algorithm 3. In it, N solutions are iteratively generated. Note, in GRASP algorithms other stopping criteria are frequently used, for instance a time limit. In each iteration, the first step is generating a solution \(S \leftarrow RGA_\alpha \) based on a selected value of \(\alpha \) using Eq. (11). Based on the value of \(\alpha \), the objective function \(f_i\) used for the constraint local search is selected and the local search is applied to S. The final step is updating the PF based on the improved solution S. In practice, if no solution in the PF dominates S, it is added to the PF and all the solutions in the PF that are dominated by S are removed.

3 Fixed set search

The fixed set search (FSS) is a novel metaheuristic that adds a learning mechanism to the GRASP. It has been successfully applied to several different types of single-objective combinatorial optimization problems (Jovanovic et al. 2019; Jovanovic and Voss 2020; Jovanovic and Voß 2021, 2019). The main idea of the FSS is to focus on elements that frequently appear in high-quality solutions. Such frequently occurring elements are used to steer the exploration of the solution space. One of the main positive traits of the FSS is its simplicity of implementation. In this section, an adaptation of the FSS for finding an approximation of the PF in bi-objective problems is presented and the proposal is illustrated to solve the 2-MWVCP. As it will be seen, only very few changes to the single-objective FSS are needed; consequently the simplicity of the method is maintained. In addition, except for tracking the elements of the PF, there is no additional computational cost. It should be noted that many metaheuristics significantly grow in complexity when extended to multi-objective problems. Due to the general use of elitist solutions in population-based metaheuristics, there is a need for non-dominated sorting, as in NSGA-II, at a relatively high computational cost which is not the case in the FSS. Next, details are given on how the FSS is applied to solve the 2-MWVCP. The differences to the single-objective FSS will be emphasized and the reasons for them. A more detailed explanation of the concepts used in the FSS can be found in Jovanovic et al. (2019).

The inspiration for the FSS comes from the observation that many high-quality solutions for a combinatorial optimization problem contain some common elements. With the FSS we propose an approach to exploit these elements and to direct the search of the solution space. The single-objective FSS achieves this by forcing such elements into newly generated solutions and by dedicating computational effort to finding optimal or near-optimal solutions in the corresponding subset of the solution space. The goal of the bi-objective FSS is to use the same concept to find solutions that well approximate the PF.

In the FSS the set of selected common elements is called the fixed set and subsequently it is denoted as F. The goal is to find the additional elements to complete the partial solution, corresponding to the fixed set, or in other words to “fill in the gaps." This is done by concentrating the search around such fixed sets. To achieve this, several tasks need to be achieved. Firstly, a method for generating fixed sets must be specified. The RGA, used in the corresponding GRASP, needs to be adapted in a way to be able to use a pre-selected set of elements. In case of the multi-objective FSS, it is also necessary to consider the use of the different local searches. Finally, there is a need to define the learning mechanism which gains experience from previously generated solutions.

3.1 Fixed set

In this subsection, the methods for generating random fixed sets are presented. The difference between the single-objective FSS and the bi-objective one lies in the set of solutions that are used for generating the fixed set. The necessary requirement for a problem allowing to apply the FSS is to be able to present the solution in the form of a set. In practice this means that a solution S has elements in some set W, i.e., \(S \subset W\). In case of the MWVCP and the 2-MWVCP, the set of elements is simply the set of vertices V, as \(S \subset V\).

As it has been previously stated, the fixed set should have elements that frequently appear in high-quality solutions. In case of the single-objective FSS, the set of n solutions having the best quality from all the solutions generated in the previous iterations of the algorithm is used. This idea can be directly extended to the multi-objective FSS using non-dominated ranking. Our initial tests have shown that this is not necessary, since it is sufficient to use only the solutions in the PF. The tests have shown that the use of solutions not included in the PF can even degrade the performance of the method. From now on, the notation \(\mathcal {P}\) is used for the Pareto Set. It is expected that the reason for this is that the solutions in \(\mathcal {P}\) provide a high enough diversity in solutions and contain sufficient information about the quality of elements.

The FSS learning mechanism needs to be able to control the size of a generated fixed set |F|. Further, such fixed sets need to be able to produce high-quality feasible solutions. In the proposed method this is accomplished by using a base solution \(B \in \mathcal {P}\). If the fixed set satisfies \(F \subset B\), it can be used to generate solutions having the desired properties. Such a fixed set F can be used to generate a feasible solution with a quality at least as good as solution B. The question is which elements of B should be contained in the fixed set F. It is preferable for F to contain elements that frequently occur in some set of solutions in the PF. Let us use the notation \(\mathcal {P}_{k}\) as the set of k randomly selected solutions from the PF, \(\mathcal {P}\). In case the PF, \(\mathcal {P}\), does not have k elements, \(\mathcal {P}_{k}\) will be equal to \(\mathcal {P}\).

Let us now define a function \(Fix(B, \mathcal {P}_{k}, Size)\) that generates a fixed set \(F \subset B\) that consists of Size elements of the base solution \(B = \{ v_1, ... v_l\}\) that most frequently occur in \(\mathcal {P}_{k} = \{S_1, .., S_k\}\). Let C(v, S) be a function, defined for an element \(v \in V\) and a solution \(S \subset V\), be equal to 1 if \(v \in S\) and 0 otherwise. Therefore, the function \(O(v, \mathcal {P}_{k})\) counts the number of occurrences of element v in the elements of the set \(\mathcal {P}_{k}\) using the function C(v, S) as follows.

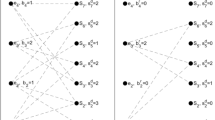
$$\begin{aligned} O(v, \mathcal {P}_{k}) = \sum _{S \in \mathcal {P}_{k}}C(v,S) \end{aligned}$$
(12)

With this, we can define \(Fix(B,\mathcal {P}_{k}, Size)\) as the set of Size elements \(v \in B\) that have the largest value of \(O(v, \mathcal {P}_{k})\). In the proposed method, ties between elements are broken randomly. A graphical illustration of the method for generating a fixed set can be seen in Fig. 1.

Fig. 1
figure 1

Illustration of generating a fixed set. The input is \(\mathcal {P}_{k}\) (top left), a set of four randomly selected solutions from the six solutions in the PF, and a base solution B (left bottom). The value on a node of B represents the number of occurrences of that node in elements of \(\mathcal {P}_{k}\). The nodes on the right-hand side present the corresponding fixed set of size four

Full size image

3.2 Learning mechanism

The learning mechanism in the FSS is implemented through the use of fixed sets. The first step consists of adapting the RGA used in the GRASP in a way to have some pre-selected elements. To be more precise, the adaptation must guarantee that a newly generated solution contains the pre-selected elements. In case of the 2-MWVCP the RGA also needs to consider different heuristic functions. Let us use the notation RGA(F) for the solution generated using the corresponding RGA with a pre-selected (fixed) set of elements F. In case of the MWVCP the adaptation is simple, the initial partial solution S is set to the fixed set F instead of an empty set. In case of the FSS for the 2-MWVCP, the same initialization is used.

The next question is how to select the heuristic that is used at each iteration of the \(RGA_{\alpha }(F)\). The notation \(RGA_{\alpha }(F)\) is used for the extension of the \(RGA_\alpha \) given in Algorithm 1 to use a fixed set F. In the proposed method, one of the heuristics \(h_i\) is randomly selected and used in all the iterations. The reasoning for this is that the random selection of the heuristic function at each iteration is used to distribute the solutions over the whole area of the PF. When the fixed set is used, this is not necessary. This is achieved by the use of the randomly selected base solution B. The conducted computational experiments have indicated that using a single heuristic function generally produces solutions closer to the PF. The next step is improving the generated solution \(S= RGA_{\alpha }(F)\) by applying the local search based on the same objective function related to the weight function \(w_\alpha \).

Once the method for generating fixed sets and the adaptation of the RGA have been presented, the details of the learning mechanism can be given. The first step is to perform an initial exploration of the solution space and finding an approximation of the PF, \(\mathcal {P}\). This is achieved by performing N iterations of the presented bi-objective GRASP algorithm. As in the case of the GRASP, the FSS iteratively generates solutions and applies local searches to them. At each iteration, the fixed set of some size Size is generated based on \(\mathcal {P}\), as previously described. The fixed set F is used to generate a new solution \(S= RGA_{\alpha }(F)\) and the local search is applied to it. The PF is updated for the newly generated solution \(S'\). This procedure is repeated until no changes are made to the PF for Stag generated solutions, or, in other words, until stagnation occurs. In case of stagnation, the size of the fixed set is increased. In case the maximal allowed size of the fixed set is reached, the size of the fixed set is reset to the minimal allowed value. This procedure is repeated until a total of M solutions are generated.

To fully specify the FSS, the array of allowed fixed set sizes needs to be specified. It is related to the portion of the solution that is to be fixed. The commonly used array of portions is the following:

$$\begin{aligned} Portions[j] = \left( 1 - \frac{1}{2^j}\right) \end{aligned}$$
(13)

The size of the used fixed sets is proportional to the used base solution B. More precisely, at the j-th level it is equal to \(|B|\cdot Portions[j]\).

figure d

The details of the FSS for the 2-MWVCP are given in the form of pseudocode in Algorithm 4. The first step is generating the portions of fixed sets using (13). The initial portion of the fixed set Portion is set to the smallest value. The next step is generating the initial PF by performing N iterations of the GRASP algorithm given in Algorithm 3. The main loop of the FSS consists of the following steps. Firstly, \(\mathcal {P}_k\) is set to k random elements of the PF, \(\mathcal {P}\). Secondly, a random solution \(B \subset \mathcal {P}\) is selected. Based on \(P_k\) and B, a fixed set F is generated, \(F= Fix(B,\mathcal {P}_k, |B|Portion)\). Next, a random objective function \(\alpha \) is selected that is used for the \(RGA_\alpha \) and the local search for generating the next solution S.

The PF, \(\mathcal {P}\), is updated for potential changes for the new solutions S. In case stagnation of the PF occurs, the value of Portion is set to the next value in Portions. In our implementation of the proposed algorithm for the 2-MWVCP, the criterion for stagnation is that no solution has been added to the PF in the last Stag iterations. Let us note that the next Portion is the next larger element of the array Portions. In case Portion is already the largest value, we select the smallest element in Portions. This procedure is repeated until a total of M solutions have been generated. Note that an alternative termination criterion can be used, for instance a time limit.

4 Results

In this section, details of the performed computational experiments are presented. The aim is to compare the solutions obtained by the FSS to the ones of the GRASP and the MONSD algorithms with reference to a set of performance indicators (evaluation metrics). Note that MONSD has been developed by Hu et al. (2019) providing the currently best-known results for the 2-MWVCP, to the best of the authors’ knowledge. The selected performance indicators are the C-metric, hypervolume, \(\varGamma \) metric, spacing, cardinality and convergence speed. All of these indicators are explained in detail in the later parts of this section.

The analysis of the proposed methods is divided into three parts. Firstly, a comparison of the proposed FSS and GRASP algorithms is made comparing them with the MONSD. Next, the effect of the learning mechanism of the FSS is extensively evaluated based on a set of performance indicators, for which a review can be found in Audet et al. (2021). Finally, in the third part, the convergence speed of the proposed approaches is evaluated. In addition, the effects of different values of the parameters of the FSS are shown.

The comparison is performed on the test instances used to evaluate MONSD (Hu et al. 2019). These instances are based on the ones introduced in Shyu et al. (2004), which have also been used in Bouamama et al. (2012); Zhou et al. (2016); Li et al. (2016); Jovanovic and Voß (2019). The instances are extended with a second set of vertex weights which are used for the second objective function. The test instances have between 100 and 1000 nodes, and between 100 to 20000 edges. Each test instance is specified as a pair (|V|, |E|) with |V| and |E| being the number of vertices and edges, respectively.

The used parameters for the FSS are the following: \(k=20\) random solutions are selected from the PF \(\mathcal {P}\) for generating the set of solutions \(\mathcal {P}_{k}\). The size of the initial population is \(N=100\) or, in other words, the number of initial solutions generated by the GRASP. The stagnation criterion is that there have been no changes (no new solution is added) to the PF in the last \(Stag=100\) iterations for the current fixed set size. The value of the parameter Stag has a minor effect on the performance of the FSS, since its main purpose is to render the passing through different sizes of the fixed set possible. In case only a small number of solutions can be generated, it is beneficial to use a smaller value of Stag to render the use of a large fixed set possible at an early stage of the search. Note that for large fixed sets the method focuses on exploitation. The used size of the RCL in the RGA is 10. The value of parameter \(\delta \) used to specify the amount of effort dedicated to finding the extreme points of the PF is 0.15. The value of this parameter has been determined empirically. The other parameter values used in the FSS and the GRASP are the same as in case of the single-objective MWVCP. An extensive analysis of their effect on the algorithm performance can be found in Jovanovic and Voß (2019). The FSS and GRASP have been implemented in C# using Microsoft Visual Studio 2019. The calculations have been done on a machine with Intel(R) Core(TM) i7-8550U CPU @ 1.80 Ghz, 16GB of DDR3-1333 RAM, running on Microsoft Windows 10 Enterprise 64-bit.

4.1 Comparison to existing methods

Fig. 2
figure 2

Approximations of Pareto fronts obtained by the MONSD, GRASP and FSS for different problem instances

Full size image

In this subsection, a comparison with the MONSD is presented. It should be noted that the MONSD significantly outperforms NSGA-II on the 2-MWVCP (Hu et al. 2019). The MONSD has a high level of similarity to GRASP algorithms, in the sense that multiple solutions are generated and a local search is applied to them. Detailed results (Pareto Sets) for all instances from Hu et al. (2019) were not available. The comparison is done on six graph instances with varying sizes and densities, for which a graphical presentation of the PF is provided in the corresponding paper. The PFs for the MONSD, GRASP and FSS can be seen in Fig. 2 for these instances. In case of the MONSD the stopping criterion was that 500 and 1000 seconds have passed for small/medium and large instances, respectively. In case of the FSS and GRASP we have used the termination criterion that \(M=10000\) solutions have been generated, which takes around 400 seconds in case of the FSS and close to 1000 seconds in case of the GRASP. A more detailed analysis of the computational cost of the FSS for the single-objective MWVCP can be found in Jovanovic and Voß (2019) which has a very similar behavior as in the case of the 2-MWVCP.

From these results, the first thing that can be observed is that for the small instance having 100 nodes all three methods have a very similar performance. It is expected that this is due to all of them managing to find approximations that are very close to the true PF. In case of all the larger instances, from 200 to 1000 nodes, the advantage of the FSS and the GRASP algorithms becomes evident. Both methods find approximations to the PF whose elements completely dominate the PF found by the MONSD. One of the main reasons for this is the use of a more powerful local search. To be more precise, the local search of MONSD is based on directly swapping a single vertex from the cover with one outside of it, or on the removal of a single vertex from the solution. It has previously been shown that the local search, used in the proposed methods, based on the more advanced swap operator, where a vertex in the cover is substituted with the unique set of vertices outside of it that result in a new vertex cover, produces significantly better results and is commonly used (Voß and Fink 2012; Li et al. 2016; Jovanovic and Voß 2019).

As it can be seen in Fig. 2, the FSS finds a slightly better approximation to the PF than the GRASP in case of the instance having 200 nodes. The advantage of the FSS becomes more significant on graphs with a larger size. The FSS generates similar extreme points of the PF as the GRASP. The FSS finds notably better quality solutions in the inner part of the PF, and these solutions generally dominate all the solutions found by the GRASP in the same region. It should be noted that for the GRASP, it is possible to slightly improve the performance, in the sense of finding a higher quality PF, by adapting the size of the RCL, for differently sized problem instances. The PFs acquired in this way are still significantly worse than the ones acquired by the FSS. On the other hand, the effect of the size of the RCL has a very small effect on the performance of the FSS.

4.2 Performance indicators for the GRASP and FSS

In this section a more extensive comparison between the GRASP and the FSS algorithms is presented. The comparison is done on the 47 graphs with a varying number of nodes and densities used in Hu et al. (2019). As it is discussed in Audet et al. (2021), comparing the performance of algorithms for finding approximations to the PF is significantly more complex than in the case of single-objective functions. There is a wide range of indicators that can be used for this task. In Audet et al. (2021), a general classification of such methods is given through the analysis of convergence, distribution, spread and cardinality. Some of these indicators are suitable for judging if “one method is better than another” in the sense of the quality of the PF approximation. Others can provide a better insight on the properties of the generated PFs. In the following text, a brief description of the used indicators is given.

With the goal of evaluating the effectiveness of the learning mechanism of the FSS in comparison to the basic GRASP, the following indicators are used. The first one is the C-metric. It provides information on how many solutions in the PF generated by method B are dominated by at least one solution in the PF generated using method A. Subsequently, \(\mathcal {A}\) and \(\mathcal {B}\) denote the set of efficient solutions in the PF obtained by methods A and B, respectively. Formally, the C-metric is presented using the following formula.

$$\begin{aligned} C(\mathcal {A},\mathcal {B}) = \frac{|\{b \mid (b \in \mathcal {B})\wedge (\exists a\in \mathcal {A})(a \prec b) \}|}{|\mathcal {B}|} \end{aligned}$$
(14)
Fig. 3
figure 3

Illustration of the hypervolume indicator. The value of the indicator is equal to the area of the dotted region

Full size image

The second commonly used metric for comparing the performance of multi-objective optimization algorithms is the hypervolume indicator (\(I_H\)). It compares the area of the solution space that is dominated by the generated PF. This indicator is best understood by observing its graphical representation, given in Fig. 3. As it can be seen, the hypervolume indicator depends on the selected reference point. In the conducted comparison, its selection is done as suggested in Ishibuchi et al. (2017). Firstly, all the elements of the solutions in the PFs are normalized based on the extreme solutions found by both algorithms. Next, the reference point \(R = (r,r)\) is set using the following formula.

$$\begin{aligned} r = 1+ \frac{1}{Max(|\mathcal {A}|, |\mathcal {B}|)-1} \end{aligned}$$
(15)

In Eq. (15), the reference point is related to the cardinality of the PFs \(\mathcal {A}\) or \(\mathcal {B}\) that has the larger number of elements.

The C-metric and the hypervolume indicator are very good for analyzing which method provides a PF approximation that is closer to the actual one. The next two indicators are used to give more information on the distribution of solutions in the generated PFs. The first one is the spacing indicator. It provides information on the distance between neighboring points in the PF, \(\mathcal {A}\). It is defined using the following equations.

$$\begin{aligned} d_i= & {} \min _{(S_i,S_j)\in \mathcal {A}, S_i \ne S_j} |F(S_i)- F(S_j)|_1 \end{aligned}$$
(16)
$$\begin{aligned} {\tilde{d}}= & {} \frac{1}{|\mathcal {A}|}\sum _{i=1}^{|\mathcal {A}|} d_i \end{aligned}$$
(17)
$$\begin{aligned} SP(\mathcal {A})= & {} \sqrt{\frac{1}{|\mathcal {A}|} \sum _{i=1}^{|\mathcal {A}|} ({\tilde{d}} - d_i})^2 \end{aligned}$$
(18)

In Eq. (16), \(d_i\) is equal to the minimal distance, using the L1 norm (\(|\dots |_1\)) for solutions based on the objective function values. The value of the spacing indicator for a PF, \(\mathcal {A}\), provides information about the change in the minimal distance between solutions. In case of equidistant solutions, \(SP(\mathcal {A}) = 0\) is satisfied.

The spacing indicator and similar ones only consider the minimal distance between a solution in the PF and its neighbors. Because of this, it provides very limited information when some solutions are clearly separated but spread into groups. The \(\varGamma \) metric proposed in Custódio et al. (2011) can be used to complement the spacing indicator. This metric focuses on the size of the holes within the PF, \(\mathcal {A}\). This is achieved by using the following procedure. All the solutions in the PF are indexed from 0 to \(|\mathcal {A}|+1\) in a way that the following is satisfied for all objective functions \(f_j\).

$$\begin{aligned} f_j(S_0)\le f_j(S_1) \dots \le f_j(S_m) \end{aligned}$$
(19)

In relation, let us define the distance for objective j between neighboring nodes i and \(i+1\) as \(\delta _{ij} = f_j(S_{i+1}) - f_j(S_i)\). Now, the largest distance between neighboring solutions in a PF, \(\mathcal {A}\), can be defined as the following \(\varGamma \) function.

$$\begin{aligned} \varGamma (\mathcal {A}) = \max _{i=0..m-1}{\max _{j = 1..N}\delta _{ij}} \end{aligned}$$
(20)

The first set of results related to the C-metric and the hypervolume indicator can be seen in Tables 1 and 2 for small/medium and large problem instances, respectively. The first thing that can be observed from the results in Table 1 is that for the smallest graph sizes having 100 and 150 nodes, the FSS and the GRASP have a very similar performance when the size of the PF hypervolume is compared, with the FSS being slightly better. The main reason for this is that the GRASP has a very good performance on instances of this size and there is not a significant need for a learning mechanism. A similar behavior has been observed in case of the single-objective MWVCP, where the GRASP algorithm manages to find solutions of almost the same quality as more advanced metaheuristics (Jovanovic and Voß 2019). The comparison of the C-metric indicates that, although the FSS and GRASP find hypervolumes of similar size, many of the solutions of the PF obtained by GRASP are dominated by at least one of the solutions in the PF obtained by the FSS. In case of medium-sized instances (200-300 nodes; see Table 1), this difference becomes more significant, and in the majority of them more than 50% of the solutions in the PF obtained by the GRASP are dominated by at least one solution of the PF obtained by the FSS. In case of medium-sized instances, the hypervolume obtained by the FSS is larger than the one obtained by GRASP for all but two graph sizes. Overall, in only one case, the PF obtained by the GRASP has dominated more solutions, or has a larger hypervolume, of the PF obtained by the FSS.

The improvement in performance provided by the learning mechanism of the FSS further increases in case of large graphs, which can be seen from Table 2. In 13 out of 15 of such instances more than 90% of the GRASP solutions are dominated by some solution obtained by the FSS. The average size of the hypervolume of the GRASP is 0.65, while for the FSS it is 0.85. In addition, the FSS has a larger hypervolume for all the large instances.

Table 1 Comparison of the GRASP and the FSS methods for small/medium-sized instances for convergence using convergence-related indicators
Full size table
Table 2 Comparison of the GRASP and the FSS methods for large instances for convergence using convergence-related indicators
Full size table
Table 3 Comparison of distribution-related indicators for the GRASP and the FSS methods for small/medium-sized instances
Full size table
Table 4 Comparison of distribution-related indicators for the GRASP and the FSS methods for large instances
Full size table

The comparison of the distribution-related indicators (cardinality, spacing and \(\varGamma \)-metric) can be seen in Tables 3 and 4 for small/medium and large graphs, respectively. As previously stated, these indicators are not the most suitable for evaluating how good the approximations to the PF are but give more insight about its properties. The first thing that can be observed is that the FSS manages to find PFs having a significantly greater cardinality than the GRASP. The average size of the PF generated by the FSS compared to the GRASP is around 50% and 200% larger for small/medium and large problem instances, respectively. In addition, the FSS manages to decrease the average spacing between solutions and the size of the holes in the PF when compared to the GRASP for both small/medium and large graphs. This can be seen from the values of the SP and \(\varGamma \) metrics. It should be noted that although the average values for these metrics are lower for the FSS, this is not true for all the graph sizes.

In the last group of computational experiments, the convergence speed of the FSS and the GRASP are compared (see Fig. 4). This has been done by evaluating the size of the hypervolume by each of the methods after N solutions have been generated. It should be noted that, as in the case of the single-objective MWVCP, the FSS has a lower computational time than the GRASP for the same number of generated solutions. This is due to the fact that when a fixed set is used, the randomized greedy algorithm needs less iterations to generate a feasible solution that is of higher quality. It should be noted that this does not asymptotically effect the computational time but it can frequently decrease the computational cost by 50%. A maximum of 10000 solutions are generated for each of the methods.

In case of the hypervolume, the reference point has been calculated based on the extreme solutions and cardinality of PFs obtained at the last iteration for all the methods. In these experiments, the effect of the parameters of the FSS are also illustrated. To be specific, values from 100 to 2000 initial solutions (N) are used in the FSS, and from 5 to 50 solutions are used to generate the fixed set. The graphical illustration of this comparison can be seen in Fig. 4, for three representative graph instances.

Fig. 4
figure 4

Illustration of the convergence speed of the GRASP and FSS algorithms. The convergence is shown based on the number of generated solutions and the value of the hypervolume indicator. The convergence speed is shown for different values of the FSS parameters

Full size image

The first thing that can be observed from these figures, is that from the iteration in which the learning mechanism of the FSS is used, there is a drastic increase in the convergence speed compared to GRASP. It is interesting that generating only 100 initial solutions is sufficient for an initial exploration of the solution space for the FSS to be effective. This is also true in the case of the use of the FSS for the single-objective MWVCP. The size of the hypervolume obtained by FSS with different sizes of initial populations N is very similar for N taking values between 100 and 2000. The main difference is that a higher number of initial solutions results in a later increase in convergence speed due to the use of the learning mechanism.

Different values of parameter k of the FSS have the following effect. For all the tested values (5-50) the FSS had a significantly better performance than the GRASP. Overall, the size of the hypervolume of the PF is very similar for all the values of k after 10000 iterations. In case of the smallest value of \(k=5\), the size of the hypervolume was slightly worse than for the higher values. On the other hand, the smaller value of k results in a higher initial speed of convergence. For higher values of k (20 and 50) the convergence speed can be interpreted as being more stepwise, in the sense of having periods of fast increase in the hypervolume. Overall, the proposed FSS algorithm is highly robust in the sense that it has a good performance for a wide range of its parameters N and k.

5 Conclusion

In this paper, an efficient method for finding an approximation of the Pareto front of the bi-objective MWVCP has been presented. This has been done by firstly developing a multi-objective GRASP algorithm. A novel part of this algorithm is the technique of using heuristics related to different objective functions during the construction of a single solution in the randomized greedy algorithm. Further, the fixed set search metaheuristic has been adapted to a multi-objective setting. To be more specific, a learning mechanism has been added to the proposed GRASP algorithm. The FSS has been extended to a multi-objective setting without increasing the complexity of the implementation. Moreover, it is important to point out that the learning mechanism of the FSS only uses solutions in the PF. In this way it avoids the need for ranking solutions which is often a computationally expensive task in case of multi-objective functions.

The computational experiments have shown that the proposed GRASP and FSS algorithms significantly outperform existing methods. In case of the comparison to the MONSD, its PF is completely dominated by the ones obtained by the GRASP and the FSS for larger instances. It should be noted that, in general, metaheuristics are developed for large-scale instances since exact methods, e.g. based on mixed-integer programming, cannot efficiently be applied to them.

The performed computational experiments have shown that the use of the FSS learning mechanism provides a substantial improvement to the basic GRASP. Firstly, indicators related to the quality of the approximation, the C-metric and the hypervolume indicator, show that FSS leads to an approximation that is significantly closer to the true PF than the one of the GRASP. Further, the obtained PF has more desirable properties of the PF like a better distribution and spread of solutions in addition to a higher cardinality. Except for the quality of the PF, the FSS has a significant advantage in the convergence speed as it achieves such approximations at a lower computational cost. Finally, the multi-objective FSS is highly robust in the sense that it has a good performance for a wide range of parameter values.

One direction for future research is to extend the application of the FSS to other multi-objective problems. One example is the practical problem of analyzing the relation between e-bus battery capacity, charging speeds, and fleet size with reference to a public transport timetable. Similarly, one may investigate multi-objective settings in integrated vehicle and crew scheduling, etc.; see, e.g., the problem settings in Xie et al. (2017); Durán-Micco and Vansteenwegen (2021); Ge et al. (2022). In addition, a detailed analysis of the application of randomization, local search and the learning mechanism in the FSS for problems that have more than two objectives should be performed. Another avenue of research is adapting the FSS to continuous optimization problems and new families of discrete combinatorial optimization problems.