Confidence and Outcome Expectations in Bilateral Negotiations–A Dynamic Model

Abstract

This work proposes and studies a dynamic model of two bargaining parties exchanging offers over time, considering their confidence about the share of the “pie” they obtain, which translates into expectations regarding the outcome of the bargaining process. The model predicts the sequence of offers as well as the final agreement for given confidence parameters. A mathematical analysis of the model shows the outcome is an Asymmetric Nash Bargaining Solution with exponents determined by the bargainers’ confidence. Moreover, a compensation effect can be found between confidence and risk aversion. This work also considers that confidence levels of bargainers might change during the negotiation, and we conduct a comprehensive simulation study to analyze the effect of such changes. Through Monte-Carlo simulation, we show that a bargainer is better off if its confidence increases, but the advantage is lost if the other party’s confidence increases in a similar way. In that case, concessions are smaller and negotiations last longer. Changing confidence parameters make the outcome harder to predict, as it will depend more on the final confidence than the initial one. The simulations also show that the average size of concessions, and therefore the final agreement, depend not only on whether confidence increases or decreases, but also on the change rate, with stronger effects observed when change accelerates towards the end of the process.

1 Introduction

Many models of bargaining processes have been developed in the literature. Since bargaining is a process in which two or more parties strategically interact to reach an agreement, most of these models rely on game theory to analyze the behavior and strategic moves of bargainers. Two main groups of bargaining models based on game theory have evolved over time: axiomatic models and strategic models (Sutton 1986). Axiomatic models such as the Nash bargaining solution (Nash 1950) or the Kalai-Smorodinsky solution (Kalai and Smorodinsky 1975) are mainly concerned with axiomatically defined properties that the solution of a bargaining problem should fulfill, and provide a solution concept that fulfills these requirements. However, axiomatic models do not discuss the process by which bargainers can reach that solution. Strategic models such as the Rubinstein model (Rubinstein 1982) analyze the strategic actions of the bargainers and thus are closer to modeling an actual bargaining process. However, the assumption of perfectly rational actors with full information severely limits the ability of such models to provide an adequate description of a bargaining process. A perfectly rational actor with full information would be able to anticipate both the opponent’s moves and the own moves throughout the entire process and thus the eventual outcome of the bargaining process. If bargaining is costly, or parties are for some reason impatient (i.e., discount outcomes received at a later time), a perfectly rational bargainer will thus directly propose the solution of the problem, which will immediately be accepted by the (likewise perfectly rational) opponent.

A model of (two-party) bargaining processes that predicts several rounds will take place, with offers being exchanged over time as occurs in real life, thus cannot assume that bargainers are perfectly rational actors who can anticipate the entire bargaining process. Instead, it needs to assume that bargainers take a myopic perspective and analyze only the current (and perhaps a few future) bargaining steps (Ward 1979; Tutzauer 1986). One such model is the Zeuthen–Hicks bargaining model (Harsanyi 1956; Bishop 1964; Dias and Vetschera 2019a), in which bargainers decide in each step between accepting the opponent’s offer and making a counter-offer by considering the probability of a breakdown of the negotiation.

It is worth mentioning that not every model that deviates from the assumption of perfectly rational bargainers predicts a multi-step bargaining process. For example, Ortner (2019) showed that in a model in which bargaining power changes over time according to a random process, equilibria still involve immediate acceptance of the first offer made. Similarly, taking into account loss aversion in an extended Rubinstein model still leads to immediate agreement solutions (Driesen et al. 2012). An interesting intermediate step between one-shot bargaining models and the Zeuthen–Hicks model is the model by Spinnewijn and Spinnewyn (2015), in which bargainers choose a probability of breakdown as part of their strategies; still this model only describes a bargaining process that consists of just two steps.

There are also models of dynamic bargaining processes that introduce multiple steps via other mechanisms than a myopic perspective, most notably by considering reciprocity of concessions. Perhaps the most general model is that of Tutzauer (1986), which is based on the concept of offer-response functions modeling each move of a bargainer as a reaction of the opponent’s previous move, but makes only a few generic assumptions about these functions. Taking a more specific perspective, Balakrishnan and Eliashberg (1995) consider the offers made by one party to balance between a resistant force (depending on how far the negotiator has already fallen below his or her aspirations) and a concession force (depending on how close the negotiator is to the point up to which the negotiator wants to concede). The model by Bartos (1995) assumes that the speed of concessions a negotiator makes depends on the negotiator’s current offer as well as the concession rate of the opponent. In a more general perspective, one could also view concession curves that are used in autonomous negotiation agents (Faratin et al. 1998) as models of the behavior of one negotiator in a bargaining process, in which concessions might depend on time, resources, or the behavior of the opponent.

Compared to these models, we consider the Zeuthen–Hicks framework to offer several advantages for our research question. It is based on a clear model of the individual decision a negotiator has to make during the process rather than directly connecting concessions to some factors without a specific underlying theory. This economic foundation of the model allows us to introduce concepts such as expectations and confidence, which are at the core of our extension of the model, in a consistent manner.

A myopic bargainer, who cannot anticipate the entire bargaining process, will need to form a subjective estimate about the negotiation outcome. In the original form of the Zeuthen–Hicks bargaining model, the only outcomes considered were acceptance of one of the two offers currently on the table, or failure of the negotiations. Only recently was the model extended to explicitly include a subjective estimate of the outcome of continued negotiation (Dias and Vetschera 2022). This estimate may depend on two groups of factors: factors related to the bargaining process conducted so far, and individual factors of the negotiator. An example for the first group are the offers currently on the table: it would not be reasonable for a negotiator to assume to be able to receive anything better than what the negotiator is currently offering to the opponent, or to expect the outcome (if an agreement is reached at all) to be worse than the opponent’s current offer. Thus, the offers currently on the table form upper and lower bounds on a negotiator’s outcome expectation. Which outcome within that interval a negotiator expects may depend on individual properties of the negotiator. A highly confident negotiator might expect to be able to reach an outcome that is close to the current own offer, while a more pessimistic negotiator might expect an outcome close to the opponent’s current offer.

The model developed in Dias and Vetschera (2022) formalizes these considerations by representing the negotiator’s expectations (in terms of the utility that the negotiator expects to obtain by continuing the negotiation) as a linear combination of the utilities of the two offers currently on the table, where the weights refer to the negotiator’s confidence. A highly confident negotiator assigns a high weight to the own offer and thus expects the final outcome to be close to that, while a negotiator of low confidence, who assigns a higher weight to the opponent’s offer, expects the outcome to be closer to the opponent’s position. The bargaining process that this model describes converges to the Asymmetric Nash Bargaining Solution (ANS), where the weights of the two utilities correspond to the negotiators’ confidence levels. The model thus formally expresses the widely held view in negotiation literature (Volkema 2009) that more confident negotiators are able to reach better outcomes for themselves. The predictions of the model concerning both the bargaining process and its outcome were confirmed empirically using data from electronic negotiations (Vetschera and Dias 2023).

The present work extends this research stream in several directions. In the course of a negotiation, both parties get to know each other, their strategies and tactics. This could influence and change a negotiator’s confidence about reaching a good agreement for oneself. A negotiator who perceives less and less chances to perform well against a tough opponent might become less confident and lower his or her expectations over time, while a negotiator who perceives the negotiations as easy going might become more confident as the negotiation progresses. In this paper, we therefore extend previous research by taking a dynamic perspective and study the effects of changes in confidence levels of negotiators during a negotiation. Confidence of a negotiator might increase or decrease during a negotiation, and such changes might happen with different speed. Furthermore, the confidence of the two negotiators might develop in the same, or opposite directions. To analyze all these possibilities, we perform a comprehensive simulation in which we study the effects of different change patterns on the negotiation process and its outcomes.

We also introduce a different and more realistic way of modeling expectations in this paper. The model by Dias and Vetschera (2022) represented expectations as a linear combination of utilities, keeping the weights on utilities of the offers of the two parties constant. This way of modeling expectations has two disadvantages. First, it seems more plausible that negotiators form expectations in terms of outcomes, rather than in terms of utility levels. For instance, if a seller asks for s and a buyer offers b, it is well-known that the midpoint $(b+s)/2$ is a natural focal point for negotiators, and they might expect to reach a settlement not far from such value (Raiffa et al. 2007). The model developed in this paper thus more closely reflects actual behavior. We show that the fundamental results of the model remain unchanged by this modification. This new formulation of expectations also allows us to study interesting interaction effects between risk attitude and confidence of negotiators for some specific types of utility functions.

Furthermore, if the utility function of a negotiator is nonlinear, the relationship between weights on utilities and weights on outcomes depends on the actual offers between which the expectation is formed. Assuming a constant weighting of utilities therefore implies that the weighting of outcomes changes during the negotiation in a way that depends on the negotiator’s utility function. By directly formulating expectations as a linear combination of outcomes, we isolate our analysis from this effect.

The specific contribution of this paper therefore focuses on what are the consequences if, during the course of a negotiation, negotiators become more optimistic, or more pessimistic, about the outcome they can achieve. To focus on the effects of these changes, we consider them to be exogenous in the present paper and systematically vary change patterns in the simulations we perform. We also provide a realistic model of the impact of confidence by formulating expectations in terms of outcomes rather than utility levels. We thus formulate an innovative model of negotiation processes, that takes into account that myopic negotiators base their decision on how to proceed in a negotiation on their expectations about the future progress and the outcomes of their negotiation, rather than having perfect foresight of the entire process, as perfectly rational actors would have.

The remainder of this paper is structured as follows. Section 2 provides a brief overview on the concepts of confidence and expectations in the negotiation literature. Section 3 introduces our model. Section 4 presents the analytic results for the general case of concave utility functions, as well as for the specific cases of constant relative and constant absolute risk aversion. Section 5 describes a simulation study concerning the bargaining dynamics and outcomes when the confidence parameters can vary. Finally, Sect. 6 concludes the paper.

2 Confidence and Expectations in Negotiation Literature

The concepts of confidence and expectations are widely used in the negotiation literature. It seems to be common knowledge that more confident negotiators achieve better results. Practical advice to negotiators (Volkema 2009) indicates that it is necessary to be confident to even initiate negotiations and then ask the opponent for something. Training programs for negotiations are designed to increase the future negotiators’ confidence (Richards et al. 2020; Taylor et al. 2008).

This widely held view is also supported by empirical evidence from negotiation experiments showing that more confident negotiators achieve better outcomes in dyadic (Soldá et al. 2021) and multilateral (Abass and Ghinea 2006) negotiations. More specifically, confidence in one’s ability to use different negotiation tactics (such as distributive or integrative tactics) increases the use of tactics in which one has high self-efficacy, leading to better outcomes (Sullivan et al. 2006). High levels of confidence can also reduce the negative impact of unfavorable conditions (such as having to negotiate at the opponent’s premises) (Brown and Baer 2011). More confident negotiators are also less likely to be trapped in a negative spiral of distributive actions that could lead to stalemate and eventual breakdown of the negotiation (O’Connor and Arnold 2001). High self efficacy (high confidence in one’s abilities) and high confidence in one’s knowledge of the substantive matter being negotiated also increase the likelihood of entering negotiations at all (Volkema and Fleck 2012; Krische and Mislin 2020).

In addition to this vast empirical evidence on the value of confidence in negotiations, there are also analytical results showing that even overconfidence in the sense of overestimating the value of an object can lead to advantages and increase the likelihood of trade (Angelini et al. 2022).

Although literature thus mostly highlights the benefits of confidence, there are also some critical issues and mixed results. Overconfidence as a decision bias in negotiations can lead to less concessions and failure of negotiations (Caputo 2013; Neale and Bazerman 1985), but on the other hand, it also leads to higher self evaluation and positive emotions, which encourage integrative behavior (Caputo 2013). Furthermore, higher confidence can lead to more deception in negotiations (Gaspar and Schweitzer 2021), and it may have a positive or negative effect on the duration of negotiations (Galasso 2010). Empirically, it could be difficult to distinguish between the impact of confidence in forming expectations, and the impact of risk attitudes that affect how these expectations translate into actual decisions such as the offer being made by a negotiator (Hindriks et al. 2007).

Similar to confidence, which can refer to mastery of negotiation tactics (Sullivan et al. 2006), knowledge about the substantive issues of the negotiation (Krische and Mislin 2020) or estimation of values (Angelini et al. 2022), expectations in negotiation may refer to different objects. Some authors even use the term expectations more or less synonymous to confidence as positive expectations about the success of the negotiation (Elfenbein 2015). A large part of the literature (e.g., Graf et al. 2012; Tolan et al. 2023) considers expectations about the opponent’s strategy and behavior, or about the offers that different types of opponent are going to make (Ramirez-Fernandez et al. 2018). There are also studies that simultaneously consider expectations about behavior as well as outcomes (e.g. Kaman and Hartel 1994) and use these concepts to explain for example differences in performance between male and female negotiators.

Expectations about outcomes are frequently considered in the form of aspiration levels formed at the beginning of the negotiation, which have been shown to influence outcomes (Cohen 2003). These aspiration levels can be influenced by many factors, such as whether possible outcomes of the negotiation are presented in a gain or loss frame (Chang et al. 2008), or by sunk costs (of the negotiator or of the opponent) (Diekmann et al. 1996). Only a few studies consider the dynamic adjustment of expectations during the negotiation. For example, Tey et al. (2021) showed that concession patterns of the opponent shape expectations about future concessions by the opponent and thus the final outcome that can be reached.

In the model considered in this work (Sect. 3), we use the expression outcome expectations (or simply expectations) to indicate the outcome a bargainer expects to obtain at the end of the bargaining process, and we use the term confidence as referring to a parameter indicating the proximity of the expected outcome to the bargainer’s current offer, relatively to the current offer of the opponent.

3 A Model of Confidence and Expectations in Negotiations

In developing the model, we follow the overall approach and use the notation of the model by Dias and Vetschera (2019a). The model considers negotiations between two parties (henceforth, the “buyer” and the “seller”) exchanging multiple offers throughout a bargaining process, under the risk that the negotiation breaks down. We consider here that bargaining concerns a single issue (the “price”), even though the model can be applied to multiple-issue negotiations under some mild assumptions (Dias and Vetschera 2019a; Vetschera and Dias 2023).

At each step of the bargaining process, we denote the offer of the buyer by b and the offer of the seller by s. We denote $u_b(.)$ and $u_s(.)$ the utility functions for the buyer and the seller (normalized between 0 and 1), respectively, the former having a negative derivative ($u_b'(.)<0$) and the latter a positive derivative ($u_s'(.)>0$), i.e., the buyer always prefers a lower price, whereas the seller always prefers a higher price. If the parties do not reach an agreement, the outcome is denoted d, and it is less preferred than any s or b for both sides. To simplify the exposition, we set $u_b(d)=u_s(d)=0$.

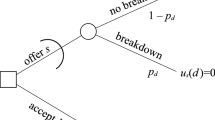
Figure 1 represents the situation faced by the seller at a given round of the negotiation (the buyer’s perspective is analogous, exchanging b’s for s’s). The buyer’s offer b and the seller’s offer s, both better than d for both parties, are on the table.

Fig. 1

Framework for one negotiation round (Seller’s decision) (Vetschera and Dias 2023)

One option (bottom branch) for the seller is to accept b, thereby reaching a deal obtaining utility $u_s(b)$. Another option (top branch) is to offer s, either insisting on the offered value, or making a concession, i.e., decreasing the price demanded. The possibility of revoking the previous offer and asking for more is not considered in the model, assuming good faith. If the seller chooses the top branch insisting on s or making a too small concession, a risk of stalemate exists, which causes the negotiation to break down with probability $p_d$.

Not knowing exactly what the outcome of the negotiation will be when keeping or adjusting s, the seller will analyze this choice based on subjective expectations. Therefore, the top branch, $z_s$ represents the outcome that the seller currently anticipates to obtain if the negotiation leads to a deal, i.e., if the breakdown event does not materialize, and $u_s(z_s)$ is the seller’s utility for that outcome. The expectations of the seller and the buyer depend on s and b (expecting that a deal is reached at a value somewhere between b and s), but also on the behavioral characteristics of the parties, namely the individual confidence of each party.

In previous work (Dias and Vetschera, 2022; Vetschera and Dias, 2023) a confidence parameter was introduced to model expectations in the space of utilities. Here we directly model the anticipation $z_s$ in outcome space. We express the expectations of the parties in terms of the outcome (the price) they obtain, independently of their utility function. More precisely, these expectations for the seller and the buyer in the space of outcomes are defined as a convex combination between b and s:

$$\begin{aligned} z_s= \beta _s s + (1 - \beta _s) b \end{aligned}$$

(1)

and

$$\begin{aligned} z_b = \beta _b b + (1 - \beta _b) s. \end{aligned}$$

(2)

In these equations, parameters $0 \le \beta _b \le 1$ and $0 \le \beta _s \le 1$ represent the confidence of the buyer and seller, respectively. Higher values for this parameter correspond to higher confidence (and therefore higher expectations). These equations describe formally our use of the terms confidence and expectations: the higher the confidence parameter is for a party, the more this party expects an outcome closer to its offer and farther away from to the other party’s. In the most general setting, we consider parameters $\beta _s$ and $\beta _b$ to be varying over time, although initially (in Sect. 4) we assume them to be constant to obtain analytical results.

As an utility maximizer, the seller considers its choice as follows:

$$\begin{aligned} \text{ offer } s \succ \text{ accept } b&\Leftrightarrow (1-p_d) u_s(z_s) > u_s(b) \nonumber \\&\Leftrightarrow p_d < \frac{u_s(z_s)-u_s(b)}{u_s(z_s)} \end{aligned}$$

(3)

Hence, the seller will insist on its offer as long as the breakdown probability is perceived to be smaller than the upper bound defined in this equation, and will make a concession otherwise. Mutantis mutatis, from the perspective of the buyer:

$$\begin{aligned} \text{ offer } b \succ \text{ accept } s \Leftrightarrow p_d < \frac{u_b(z_b)-u_b(s)}{u_b(z_b)} \end{aligned}$$

(4)

We assume that a stalemate increases the breakdown risk, and at some point in time this risk becomes excessive for one of the parties. The model predicts that the seller will be the one conceding if the seller’s critical probability is less than the buyer’s, i.e., $\frac{u_s(z_s)-u_s(b)}{u_s(z_s)} < \frac{u_b(z_b)-u_b(s)}{u_b(z_b)}$, and thus

$$\begin{aligned} u_s(z_s) u_b(s) < u_s(b) u_b(z_b), \end{aligned}$$

(5)

The buyer will be the one conceding if this inequality is reversed. Each party will try to make a concession that is sufficiently large to reverse the inequality, unless the inequality cannot be reversed and that party needs to accept the other party’s offer.

This constitutes a model for the parties making successive concessions until they reach an agreement, in the spirit of the Zeuthen–Hicks model (Bishop 1964; Harsanyi 1956), and indeed coinciding with the latter in the extreme case that $\beta _s=\beta _b=1$. As such, it can be considered a Zeuthen–Hicks model extension by explicitly considering intermediate outcomes in-between b and s as the parties make successive concessions and by introducing the confidence parameters.

4 Analytical Results

Dias and Vetschera (2022) have analyzed the case with expectations defined in the space of utilities as

$$\begin{aligned} u_s(s_z) & = \gamma _s u_s(s) + (1 - \gamma _s) u_s(b) \Leftrightarrow z_s=u_s^{-1}(\gamma _s u_s(s) + (1 - \gamma _s) u_s(b)) \end{aligned}$$

(6)

$$\begin{aligned} u_b(z_b) & = \gamma _b u_b(b) + (1 - \gamma _b) u_b(s) \Leftrightarrow z_b=u_b^{-1}(\gamma _b u_b(b) + (1 - \gamma _b) u_b(s)). \end{aligned}$$

(7)

They demonstrated that if both parties have concave utility functions, then the only agreement for which none of the parties has an incentive to insist on a different solution is the Asymmetric Nash Bargaining Solution (ANS) (Muthoo 1999; Roth 1979). The expectation parameters, $\gamma _s$ and $\gamma _b$, if different, originate the asymmetry. In particular, if the parameters have the same value, then the solution predicted by the model becomes the (symmetric) Nash solution (Nash 1950). These results no longer hold if any of the parties is risk-seeking.

Analyzing the arguably more natural case where expectations are formed in the space of outcomes, we can show that this interesting property is not lost. To show this, let

$$\begin{aligned} f(b,s) = u_s(z_s) u_b(s) - u_b(z_b) u_s(b) \end{aligned}$$

(8)

i.e., the difference between the left hand and right hand side of (5), denote an auxiliary function that determines which party should make a concession. According to the discussion of inequality (5) in the previous section, the seller should make a concession if f(b, s) is negative, and the buyer should make a concession if it is positive, given the maximum stalemate probabilities each one could tolerate. If $f(b,s)=0$, which obviously is the case when they reach an agreement $x=b=s$, then the seller might have an incentive to ask for a higher price s if that would make $f(x,s)>0$, and the buyer might have an incentive to ask for a lower price b if that would make $f(b,x)<0$. It turns out that the ANS in the only stable solution in which such incentives do not exist:

Proposition 1

Let $u_s(.)$ and $u_b(.)$ be two utility functions such that $u_s(.)$ is monotonically increasing, $u_b(.)$ is monotonically decreasing, and both are concave. Let expectations be defined in the space of consequences by parameters $\beta _s$ and $\beta _b$, according to (1)–(2). Then,

$$\begin{aligned} f(x,s)&<0, \forall s>x(\text{the } \text{ seller } \text{ would } \text{ make } \text{ concessions } \text{ for } \text{ prices } \text{ higher } \text{ than } x)\\ f(b,x)&>0, \forall b<x(\text{the } \text{ buyer } \text{ would } \text{ make } \text{ concessions } \text{ for } \text{ prices } \text{ lower } \text{ than } x) \end{aligned}$$

if and only if $x = x^*$, the ANS solution defined by

$$\begin{aligned} x^* = \arg \max _x u_s(x)^{\beta _s} u_b(x)^{\beta _b} \end{aligned}$$

(9)

Proof

See Appendix. $\square$

Corollary 1

In the conditions of Proposition 1, the outcome (the ANS) depends only on the ratio of the confidence parameters $\beta _s / \beta _b$, rather than their absolute values.

Proof

This stems obviously from observing the maximum of $n_1(x)=u_s(x)^{\beta _s} u_b(x)^{\beta _b}$ and $n_2(x)=u_s(x)^{\beta _s / \beta _b} u_b(x) = [u_s(x)^{\beta _s} u_b(x)^{\beta _b}]^{1/\beta _b}$, both concave functions, occurs for the same $x^*$ where $n'_1(x)=n'_2(x)=0$.

It is interesting to observe what Proposition 1 entails for some well-known particular cases. Let us first consider the case of constant relative risk aversion in which the utilities of the two parties are given by a power function, i.e.,

$$\begin{aligned} u_s(x)&= x^{e_s} \end{aligned}$$

(10)

$$\begin{aligned} u_b(x)&= (1-x)^{e_b} \end{aligned}$$

(11)

In these functions, the exponents $e_s,e_b \le 1$ (both functions are concave) reflect the degree of risk aversion of the parties. Risk neutrality corresponds to an exponent equal to 1, and lower exponents indicate stronger risk aversion.

According to Proposition 1, the predicted outcome would be the ANS, i.e. is the value that maximizes the function

$$\begin{aligned} n_{power}(x) = x^{e_s \beta _s} (1-x)^{e_b \beta _b} \end{aligned}$$

(12)

with derivative

$$\begin{aligned} n'_{power}(x) = e_s \beta _s x^{e_s \beta _s -1} (1-x)^{e_b \beta _b} - x^{e_s \beta _s} e_b \beta _b (1-x)^{e_b \beta _b-1} \end{aligned}$$

(13)

which is null, for $x \in (0,1)$ if and only if

$$\begin{aligned} x = \frac{e_s \beta _s}{e_s \beta _s+e_b \beta _b} \end{aligned}$$

(14)

This solution shows an interesting interplay between the parameters defining the expectations and the parameters defining the concavity degree of the utility function (risk aversion). For the same confidence, the less risk averse party will be better off. For the same degree of risk aversion, the more confident party will be better off. Only the product of the power exponent and the confidence parameter determines the result, e.g., $e_s=0.4$ and $\beta _s=0.4$ leads to the same result as $e_s=0.2$ and $\beta _s=0.8$, or $e_s=0.8$ and $\beta _s=0.2$, as long as the other party’s parameters do not change. Therefore, in theory, a party can compensate being more risk averse (lower exponent) by being more confident, and, conversely, can compensate being less confident by being less risk averse.

Let us now examine another well-known utility function, the constant absolute risk aversion utility:

$$\begin{aligned} u_s(x)&= \frac{1-e^{-a_s x}}{1-e^{-a_s}} \end{aligned}$$

(15)

$$\begin{aligned} u_b(x)&= \frac{1-e^{-a_b (1-x)}}{1-e^{-a_b}} \end{aligned}$$

(16)

Here, the risk-aversion parameters are $a_s$ and $a_b$, both positive (the higher it is, the higher is the risk aversion of the respective party). According to Proposition 1, the predicted outcome is now the value that maximizes the function

$$\begin{aligned} n_{exp}(x) = \frac{1}{(1-e^{-a_s})^{\beta _s}(1-e^{-a_b})^{\beta _b}} (1-e^{-a_s x})^{\beta _s} (1-e^{-a_b (1-x)})^{\beta _b} \end{aligned}$$

(17)

Taking the derivative (omitting the constant factor), yields

$$\begin{aligned} n'_{exp}(x) = f_1(x).f_2(x).f_3(x).f_4(x).[\beta _s a_s (e^{a_b (1-x)} - 1) - \beta _b a_b (e^{a_s x} -1)]. \end{aligned}$$

(18)

with $f_1(x)=(1-e^{-a_s x})^{\beta _s-1}$, $f_2(x)=(1-e^{-a_b (1-x)})^{\beta _b-1}$, $f_3(x)=e^{-a_s x}$, and $f_4(x)=e^{-a_b (1-x)}$. The derivative is null if and only if

$$\begin{aligned} \frac{e^{a_b (1-x)}-1}{\beta _b a_b} = \frac{e^{a_s x}-1}{\beta _s a_s} \end{aligned}$$

(19)

because factors $f_1(x)$ to $f_4(x)$ are always strictly positive for $x \in (0,1)$, and therefore the sign and the zero of the derivative are determined solely by the rightmost factor.

If $\beta _b = \beta _s$ and $a_b = a_s$ then the ANS is $x=0.5$. Unlike the power utility function, now having $a_s \beta _s = a_b \beta _b$ is not sufficient to reach the balanced solution $x=0.5$, if the risk-aversion parameters are not the same.

The expression $g(a_s, \beta _s, x) = \frac{e^{a_s x}-1}{\beta _s a_s}$ increases with x and decreases with $\beta _s$, meaning that for a constant ratio a higher confidence allows a higher x. Therefore, a higher confidence is beneficial for the seller, all else being equal. A similar reasoning applies to the buyer. Observing that $\partial g(a_s, \beta _s, x) / \partial a_s$ is positive, meaning that for a constant ratio a higher $a_s$ entails a lower x, we also conclude that a higher risk aversion is a disadvantage for the seller, all else being equal. A similar reasoning applies to the buyer. Again, we observe an interplay between confidence and risk aversion, even if in this case there is no closed-form expression to compute how one compensates for the other. $\square$

5 Simulation Analysis of Confidence Dynamics

5.1 Changes in Confidence Levels

As already explained, in this work we also consider, in contrast to previous studies, that the confidence levels of parties change during the course of a negotiation. Such a dynamic perspective was implicitly already introduced by forming expectations in terms of outcomes rather than utilities. Clearly, for any pair of offers s and b, and a given confidence level $\gamma$ in terms of utilities, one can find a confidence level $\beta$ in terms of outcomes so that

$$\begin{aligned} u(\beta s + (1-\beta ) b) = \gamma u(s) + (1-\gamma ) u(b) \end{aligned}$$

(20)

However, for a fixed $\gamma$, the corresponding $\beta$ depends on the offers currently on the table, and vice versa. The assumption of a constant $\gamma$ ($\beta$) thus implies a dynamic adjustment of $\beta$ ($\gamma$) over the course of a negotiation.

A negotiator’s confidence might increase or decrease during a negotiation, and it might do so by a large or small amount. To allow a flexible analysis of different scenarios, we use a general model of confidence adjustment that allows to represent different trajectories in the simulation (a trajectory is defined by the rate of change: it can be slower at the beginning, faster at the beginning, or constant). We assume that over the course of a negotiation, the confidence parameter changes from an initial value $\beta _{start}$ to a final value $\beta _{end}$. The end of the negotiation is reached at some time T when $s_T=b_T$. We assume that at the beginning of the negotiation, the two parties take the extreme positions, i.e. $s_0=1$ and $b_0=0$, so during the course of the negotiation, the difference between the two positions decreases from $s_0-b_0=1$ to $s_T-b_T=0$. To allow for varying trajectories of the confidence parameter, we use the following specification for the confidence parameter at time $t \in [0,T]$, when the two offers on the table are $s_t$ and $b_t$, respectively:

$$\begin{aligned} \beta _t = \beta _{end} + (\beta _{start}-\beta _{end}) (s_t-b_t)^\alpha \end{aligned}$$

(21)

where $\alpha$ is a parameter that allows to model affine ($\alpha = 1$), concave ($\alpha < 1$) or convex ($\alpha > 1$) trajectories of the adjustment process. Compared to the affine trajectory, a concave trajectory shows a faster change at the beginning of the process, which then decelerates, whereas a convex trajectory shows a slow change at the beginning and an acceleration towards the end. Note that here we assume that the change in confidence is not a function of clock time, but a function of the progress of the negotiation as represented by the difference in positions. In the simulation, the confidence level was updated after each offer for the party receiving the offer to represent the idea that receiving an offer might reveal information about the opponent’s bargaining strategy, leading to an update of the confidence level. Let us also note that the same type of adjustment could be used for the confidence parameter $\gamma$ when modeling expectations in terms of utilities.

Equation (21) is admittedly still a quite simple model of the adjustment of confidence. One could argue that a more realistic model should take into account the behavior and in particular the previous concessions of both sides. A negotiator who observes large concessions by the opponent might become more confident over time, while a negotiator facing a very tough opponent might become less confident over time. Also, real-world exchange of offers usually entails verbal and non-verbal cues that might affect the confidence of the parties. However, it is not the purpose of our simulation to provide the most realistic model of confidence adjustment. The goal of our simulation is mainly to study how changes in confidence of different direction, size, and speed will influence the negotiation process and its outcomes. For that purpose, a flexible model that creates a particular shape of the change trajectory and allows for different shapes is adequate. Using such a model, we can better isolate the effects of confidence changes on the patterns of offer exchanges and on the outcomes.

5.2 Simulation Experiments

Equation (21) allows to model a negotiator whose confidence level increases or decreases by a small or large amount following a concave, linear or convex trajectory during a negotiation, and these variations can be applied to both parties. We expect the main influence on negotiation processes and outcomes to result from the fact that a negotiator’s confidence increases or decreases over time. The shape of the change trajectory might influence whether strong effects can be observed at the beginning or the end of the negotiation. We therefore consider all combinations of change direction and shape parameters in our simulation. To simplify the experimental design, we only consider settings in which both parties change their confidence levels by a small or by a large amount, but no mixtures. Table 1 lists the starting and ending values used in the simulations. All settings were run for values of $\alpha$ of 0.5 (concave), 1 (linear) and 2 (convex) for each of the sides, resulting in 9 possible settings of this parameter for the two parties. The starting and ending values used are arbitrary, but changing them to even more extreme values would simply exacerbate the effects observed using these values.

Table 1 Start and end values of confidence parameter used

We study the effect of these experimental treatments on the process and outcomes of the simulated negotiations using the following variables:

• Duration We count the number of steps in the negotiation to measure the length of the negotiation (each new offer or counteroffer represents one step).

• Average concession We measure concessions over a given fraction of the negotiation both in terms of the contractual parameter (the “price”) and in terms of utility of the conceding party.

• Outcome We consider the final agreement, both in terms of the contractual variable and the utilities of both parties, as well as in relation to the solution predicted by the model (i.e., the ANS, weighted by the confidence parameters). Note that the difference between the initial positions and the final outcomes also measures the total concession made by each party.

• Concession “runs” Since the confidence levels of parties change during the negotiation, it can happen that a party makes a concession according to (3) or (4), but that after making the concession and adjusting confidence levels, it is again the same party that has to make a concession. We call the subsequent concessions by the same party a “run” of concessions and determine the average length of these runs during a negotiation.

The four possible combinations of increasing or decreasing confidence lead to four scenarios of large and four scenarios of small changes. For each of these eight scenarios, we randomly created 1000 concave utility functions for both parties using the method of Dias and Vetschera (2019b). This method uses a bisection approach to generate utility values at discrete input values, where the number of steps should be one plus a power of two. We used 1025 data points in our experiments. In each experiment, we then ran the negotiation for all nine possible combinations of $\alpha$ values (i.e., $(\alpha _{buyer}=0.5, \alpha _{seller}=0.5), (\alpha _{buyer}=0.5, \alpha _{seller}=1), \ldots , (\alpha _{buyer}=2, \alpha _{seller}=2)$, and recorded the outcomes.

The model was programmed in the R language (R Core Team 2021). The source code is available from the authors upon request.

5.3 Results

5.3.1 Duration

Table 2 provides an overview of the duration of negotiations for different directions of changes and shapes of the change trajectory. This table refers to the cases of large changes (confidence coefficients varying between 0.2 and 0.8); the results for small changes were qualitatively similar, but effects were generally weaker. The table shows the average number of offers from either side in each negotiation for the different parameter settings. Since the outcome space was discretized into 1025 steps and the minimum concession is one discrete step, the maximum possible number of offers that can be made during a negotiation is 1024. Thus, an average of almost 850 iterations (the top left value of Table 2) shows that in most iterations, only the minimum possible concession was made.

Table 2 Average duration of negotiations (large changes)

Negotiations become shorter if the confidence of one side decreases over time, this effect is reduced if the confidence levels of both parties decrease. If the decrease follows a convex pattern, this effect is even stronger. However, a convex pattern of the other party again dampens the effect of convex change of the party with decreasing confidence.

To analyze the impact of the complex interplay of various problem characteristics on negotiation duration in more detail, we performed a linear regression in which we regressed the number of iterations in each negotiation on the factors. Specifically, we estimated the regression equation

$$\begin{aligned} \begin{array}{ll} nit & = \beta _0 + \beta _1 inc_{buy} + \beta _2 inc_{sell} + \beta _3 inc_{both} + \beta _4 lin_{buy} \\ & \quad + \vspace{15mm} \beta _5 conv_{buy} + \beta _6 lin_{sell} + \beta _7 conv_{buy} + \varepsilon \end{array} \end{aligned}$$

(22)

separately for the data set containing simulation data for large changes and the data set containing data from experiments with small changes, and the equation

$$\begin{aligned} \begin{array}{ll} nit & = \beta _0 + \beta _1 inc_{buy} + \beta _2 inc_{sell} + \beta _3 inc_{both} + \beta _4 lin_{buy} \\ & \quad + \beta _5 conv_{buy} + \beta _6 lin_{sell} + \beta _7 conv_{buy} + \beta _8 large + \varepsilon \end{array} \end{aligned}$$

(23)

for the combined data set. In these equations, nit is the number of iterations (offers made) in the negotiation, $inc_{buy}$ and $inc_{sell}$ are dummy variables indicating whether the buyer’s (respectively the seller’s) confidence level was increased in that simulation run, $lin_{buy}$, $lin_{sell}$, $conv_{buy}$, and $conv_{buy}$ are binary dummy variables indicating whether the buyer’s (or seller’s) trajectory of confidence change had a linear or convex shape. Note that the coefficients of these variables therefore represent the difference that a linear or convex shape makes in comparison to the reference case of a concave shape (in which case both dummy variables for linear and convex shape have a value of zero). Variable large in Eq. (23) is a dummy variable indicating experiments with a large change of the confidence parameter. All regression estimations were performed with the Ordinary Least Squares (OLS) method using function lm in the stat package of R (R Core Team 2021).

Results of this analysis are presented in Table 3. They clearly show that if the confidence of both parties increases over time, this leads to longer negotiations, while an increasing confidence of just one side does not have a significant effect. Problems in which confidence levels change more strongly lead to shorter negotiations. The effect of the shape of the confidence trajectory is rather small in problems with small change. In these problems, linear and convex trajectories lead to minimally longer negotiations. In contrast, in larger problems the effect is opposite, linear and convex patterns seem to reduce the duration. This effect is also visible in the joint regression, which is dominated by the stronger effect of experiments with a large change.

Table 3 Regression on duration of negotiations

Results for the regressions using only simulation runs with small changes, or simulation runs with large changes of confidence, differ considerably in the $R^2$ values, which basically indicate the fraction of total variance of the outcome variable (negotiation length) explained by the model. This difference is not surprising. All data in a stochastic simulation is affected by some noise resulting from differences in the randomly generated negotiation problems. This level of noise is present regardless of whether confidence changes by a large or small amount. If changes in confidence levels are only small, the effect of such changes on outcomes (such as duration of the negotiations) is necessarily also small, which implies that a larger fraction of total variance in duration is due to random noise.

5.3.2 Outcomes

Figure 2 shows the average agreement values for different patterns of confidence changes. The figure only contains results for the case of large changes; results for small changes are qualitatively similar. Since the entire price range was split into 1024 intervals, the balanced outcome corresponds to a price of 513. Clearly, a party with increasing confidence has an advantage over a party with decreasing confidence: if the buyer has increasing confidence and the seller decreasing confidence, outcomes are below the midpoint (i.e. at a lower price that is better for the buyer), in the opposite scenario, they are above the midpoint. In the case that both parties have increasing confidence, the outcome is quite balanced. In contrast, in the case of decreasing confidence on both sides, the path of decrease becomes important, a party with concave patterns (and thus staying at a higher level of confidence for longer) has an advantage over a party with convex pattern (where confidence decreases rapidly in the early parts of the negotiation). For equal patterns, the midpoint is again usually reached.

Fig. 2

Prices at final agreement for different patterns of confidence change

To study these effects in detail, we used a similar regression approach as for duration of the negotiations. The only difference in the regression equations is the different dependent variable that was used, prices in Table 4 and utility values in Table 5 instead of the number of iterations in Table 2.

Since Table 4 uses price as dependent variable, a positive coefficient indicates that the factor benefits the seller, a negative coefficient indicates an advantage for the buyer. These results confirm the beneficial effect of higher confidence. Increasing confidence thus can be considered a kind of self fulfilling prophecy, it leads to behavior that in the end actually makes that party better off. The coefficients for buyer and seller are almost identical in size. Therefore, an increasing confidence by one party could be completely offset by the opponent’s confidence increasing by the same amount. Compared to the reference case of a concave confidence trajectory, linear and convex trajectories lead to a small disadvantage for the respective party, in particular if the total change is large. Table 5 performs a similar analysis in terms of utility values of the seller. It basically confirms the results of Table 4. For brevity, we do not present results on the utility value of the buyer, which are symmetric to Table 5.

Table 4 Regression on final agreements (prices)

Table 5 Regression results: Seller’s utility in the final outcome

The model predicts that the negotiations will end at the ANS. We therefore also analyze whether changes in confidence have an impact on this prediction. The predicted solution depends on the ratio of the confidence levels of the two parties. If this ratio changes over the negotiation, the predicted outcome will also change. Deviations from the prediction based on the initial confidence are to be expected, as the parties adapt their behavior to updated confidence values. Deviations from the prediction based on the final confidence can also be expected, because a party might have conceded too much when it was less confident, in a way that would not have occurred with the final confidence values, and it is not possible to revoke those concessions.

We therefore compare the actual outcome to both the solutions that would be predicted at the beginning and at the end of the negotiation. Tables 6 and 7 show the average difference between the actual agreement value and the predicted outcome using the initial (Table 6) and final (Table 7) confidence values. A positive difference indicates that the actual outcome is better for the seller than the predicted ANS; a negative deviation that it is better for the buyer. Since we are forming differences to the predicted solution in both tables, the difference in the values of the two tables also corresponds to the difference between the two predicted outcomes.

Table 6 Difference of agreement to ANS for initial confidence levels

Table 7 Difference of agreement to ANS for final confidence levels

These tables show a remarkable level of symmetry, both among the main blocks referring to decreasing or increasing confidence of the two parties, and within each block referring to different shapes of the confidence trajectory. Thus, all factors affect the two parties in the same way. If the confidence levels of both parties change in the same direction and follow the same trajectory, the ratio of confidence levels stays the same, and so there is no change in the predicted outcome and the model reaches that solution. Therefore, the main diagonal in both tables is practically equal to zero. It does not reach exactly zero because in the last step, the confidence level of the party making the last offer is no longer updated, that can lead to a slightly different predicted solution.

This effect becomes more prominent if the trajectories of the two parties are different. In particular, if the confidence level evolves along a convex curve, the last step might involve a larger update of the confidence level, so the solution predicted at the end of the negotiation is somewhat different from the solution predicted at the beginning of the negotiation. This seems to affect the case that both parties have a decreasing level of confidence more than the case in which parties have an increasing level of confidence.

If the two confidence levels of the two parties move in the opposite direction, the two predicted solutions are quite far apart. The different signs in the two tables indicate that in these cases, the actual agreement lies in between the two values (e.g. if the seller’s confidence increases and the buyer’s confidence decreases, the actual agreement is better for the seller than what would be predicted from the initial confidence levels, but worse than the solution predicted from the final confidence levels). In these cases, convex trajectories bring the agreement closer to the solution predicted from the final confidence levels.

Finally, we can observe that in general the deviations to the outcome predicted using the final confidence values tend to be less than those predicted using the initial values.

5.3.3 Concessions

The total amount of concessions by each party is the difference between the party’s extreme starting position and the final agreement. Thus, the impact of various factors on total concessions is already observable from the preceding analysis of negotiation outcomes. Here we therefore focus on the development of concessions over time. For brevity, we only present the concessions of the seller and only for large changes in confidence; the behavior of the buyer is again symmetric and smaller changes have smaller effects.

Fig. 3

Average size of concessions of the seller over consecutive quarters of the negotiation

Figure 3 shows the concessions of the seller within each quarter of the negotiation (i.e., dividing the sequence of offers into four parts of equal length), averaged across all experiments. Each part of the figure contains three lines showing the development when the seller’s confidence trajectory is concave, linear or convex. The three panels in each row represent different types of trajectories of the buyer, and the rows in the figure different combinations of increasing or decreasing confidence.

The four combinations of increasing and decreasing confidence show very distinct patterns. If confidence of both sides increases, the level of concessions remains more or less constant throughout the negotiation, while if both sides have a decreasing level of confidence, they make larger concessions as the negotiation proceeds. The two other scenarios also show that if one side has increasing and the other side decreasing confidence, the effect on the two parties differs not only in the direction of change, but also in the shape. As expected, the party whose confidence decreases during a negotiation will make larger concession as the negotiation proceeds and the party whose confidence increases will make smaller concessions over time. But also the shape and magnitude of these changes are quite different. In the situation where the seller’s confidence increases, the decline in concessions is quite moderate and the rate of decrease is only slightly higher between the first and second quarter, but then remains almost constant. In contrast, if the seller’s level of confidence decreases while the buyer’s level increases, the size of concessions rises almost exponentially over time and most of the concessions are made in the last quarter of the negotiation.

5.3.4 Concession “runs”

Finally, we study the occurrence of situations in which one party makes two or more subsequent concessions without an interspersed concession of the other side. We refer to these situations as concession runs. Table 8 shows the average length of concession runs of the seller and for large changes in confidence; data for the buyer perspective are again very similar. Clearly, a party needs to make a second concession mainly if the confidence of the other side after the concession is high enough to require another concession by the same party. Therefore, no concession runs of the seller occur in settings where the seller’s confidence increases and the buyer’s confidence decreases. If confidence of both sides decreases, these are very rare (the seller on average makes barely more than one concession at a time). Runs still could occur in that setting if the seller’s confidence decreases even faster than the buyer’s. Consequently, concession runs by the seller occur most frequently when the seller’s confidence decreases and the buyer’s confidence increases. The trajectory of decrease seems to play only a minor role.

Table 8 Average length of concessions “runs” of the seller, problems with large change

To confirm these effects, we again performed a linear regression. The results of this analysis are presented in Table 9. It confirms that an increasing confidence of the buyer is the main driver for concessions runs of the seller. This effect is somewhat weakened if the confidence of the seller also increases, and by a convex shape of the change trajectory of the buyer. However, it is surprising that an increase in the seller’s confidence can offset increasing the buyer’s confidence only to a comparatively small extent, as indicated by the relatively small coefficient of the variable indicating that both confidence levels increase (i.e., the interaction term between increase by the seller and the buyer).

Table 9 Regression results: Length of concession “runs” of the seller

6 Conclusions

Models that aim to describe realistic bargaining processes consisting of several steps in which offers are exchanged and adjusted need to take into account the bounded rationality and myopic perspective of bargainers. Such bargainers cannot perfectly anticipate the entire course of the negotiation, but need to form subjective estimates of the eventual outcome of their negotiation. These estimates are influenced by subjective factors such as a negotiator’s confidence.

In this work, we present one such model based on an extension of the Zeuthen–Hicks bargaining model. The model considers expectations that are formed in terms of actual negotiation outcomes (rather than in terms of utilities as in previous models), and it allows the level of confidence to change over time.

We have shown analytically that when expectations are formed in the space of outcomes, the only agreement from which none of the parties has an incentive to deviate is the ANS. Moreover, it depends only on the ratio of the confidence parameters, rather than their absolute values. The analysis of two well-known particular cases, namely utility functions with the constant relative risk aversion and constant absolute risk aversion, shows an interesting interplay between confidence and risk aversion. Higher confidence can compensate for higher risk aversion, and vice versa. In the case of the constant relative risk aversion, this trade-off could be summarized in a very simple expression.

Our subsequent simulations have shown that changing levels of confidence significantly influence the bargaining process and its outcomes. The results show that if the confidence of both parties increases over time, this strongly impacts the duration of the bargaining process (leading to negotiations 20–70% longer on average, depending on other settings, compared to the cases in which only one or neither of the parties has increasing confidence). On the opposite, an aspect that tends to contribute to shorter negotiations is the magnitude of the change from initial to final confidence parameter. Cases in which confidence levels change more strongly lead to shorter negotiations.

Whether confidence increases or decreases during the process also significantly affects outcomes, as expected, particularly when confidence of the two parties changes in the opposite directions, benefiting the party whose confidence increases. If both increase, though, the benefits cancel out and the outcome is not much different from the case when both decrease (and, as mentioned above, with the cost of having a longer negotiation). When both parties have decreasing confidence, the one who decreases more slowly at the beginning, staying at a higher level of confidence for longer, has an advantage in terms of outcome.

This matches what is observed in terms of concession patterns over time. If confidence of both sides increases, the level of concessions remains more or less constant throughout the negotiation, whereas if both sides have a decreasing level of confidence, they make larger concessions as the negotiation proceeds (hence negotiations are shorter). If the level of confidence of one party decreases while the level of the other one increases, the size of concessions of the former rises almost exponentially over time. We have also looked into the possibility of concession “runs”, observing that when a party’s confidence decreases while the other one is increasing, the former will sometimes need to issue a new offer (better for the other party) rather than receive a concession (the average “run” length will be around 1.3–1.4). We also observed these runs when both confidence parameters are increasing (average “run” length around 1.2–1.3).

The analysis of the outcomes shows that these are not much different from those that would be predicted (the ANS) based on the initial confidence parameters, as long as the confidence of the parties evolves in similar way, i.e., in the same direction and along the same trajectory, as this does not affect the ratio of the confidence levels. Otherwise, the outcome will be different from the initial prediction and will tend to be closer to (but still different from) a prediction based on the final confidence levels, stressing the importance of addressing the dynamics of changing confidence.

As practical takeaways, the main message from these results is that becoming less confident is self-defeating, unless both parties behave in the same way (and for instance a neutral third party might try to make both parties less confident to speed up the bargaining process). Of course, one person cannot become more confident just by wishing to do so, even though some training might help. But it is crucial that a bargainer does not let him- or herself be influenced by seeing an opponent appear to be increasingly confident, and become less confident because of that. A related takeaway for bargainers is that being more risk averse is just as self-defeating, given the interplay between confidence and risk aversion shown in our analysis. Besides bargainers, this work also suggests some implications for mediating roles. A neutral mediator should be aware that if he or she observes two very confident parties, then both parties will expect an outcome closer to their own offer, they make very small concessions, and the process will last for long. In such a situation the mediator might attempt to somewhat deflate their expectations, although being careful to do that in a symmetrical way, in order not to cause an undue imbalance.

These results offer interesting insights into the dynamics of negotiations. However, they are clearly not without limitations. Like any computational study, results are based on a specific set of parameters and a limited number of experiments, so their generalizability remains an open question. We have studied the impact of changing confidence levels only in the computer simulations using a rather simple specification. Introducing a similar dynamic perspective in the analytical model could lead to more general results. Clearly, a negotiator’s confidence will not just change over time along a given path, but its development may also depend on the previous course of the negotiation, the offers made, the information exchanged, etc. A dynamic confidence model that takes these factors into account could therefore lead to a broader understanding of negotiation processes. This would require modeling the changes in confidence not in an exogenous way, as studied in this work, but incorporating endogenous changes in the confidence parameters that might depend on concession sizes, concession runs, and/or information exchange. Moreover, we hope that future research efforts dealing with bargainers’ confidence, either using variations of our model or other models, will address the challenges of considering confidence as a dynamic characteristic that can change in the course of a bargaining process.

Appendix

1.1 Proof of Proposition 1

We need to prove that the seller (buyer) cannot decrease (increase) the value of function f(b, s), as defined in (8), by increasing (decreasing) the own offer s (respectively b).

We first consider the seller.

The partial derivatives of $z_s = \beta _s s + (1- \beta _s) b$ with respect to s and b are $\partial z_s / \partial s = \beta _s$ and $\partial z_s / \partial b = (1 - \beta _s)$ and the partial derivatives of $z_b= \beta _b b + (1-\beta _b) s$ are $\partial z_b / \partial b= \beta _b$ and $\partial z_b / \partial s = ( 1- \beta _b)$.

Next we show that the partial derivative

$$\begin{aligned} \partial f / \partial s = u'_s(z_s) \beta _s u_b(s) + u_s(z_s) u'_b(s) - u'_b(z_b) (1-\beta _b) u_s(b) \end{aligned}$$

(24)

at the ANS is zero. Note that at the ANS, $s=b$ and therefore also $z_s = z_b = s = b$. We denote that value by x. The ANS is obtained by maximizing

$$\begin{aligned} u_s(x)^{\beta _s} \cdot u_b(x)^{\beta _b} \end{aligned}$$

(25)

The fist order condition for the ANS is therefore

$$\begin{aligned} \beta _s u_s(x)^{\beta _s -1} u'_s(x) u_b(x)^{\beta _b} + u_s(x)^{\beta _s} \beta _b u_b(x)^{\beta _b-1}u'_b(x) =0 \end{aligned}$$

(26)

and after simplification (considering $x \ne 0$ and $x \ne 1$, thus $u_s(x),u_b(x)>0$) this condition is equivalent to

$$\begin{aligned} \beta _s u'_s(x) u_b(x) + \beta _b u_s(x)u'_b(x)=0 \end{aligned}$$

(27)

From substituting x into (24), we obtain

$$\begin{aligned} u'_s(x)\beta _s u_b(x) + u_s(x) u'_b(x) - u'_b(x) ( 1-\beta _b) u_s(x) \end{aligned}$$

(28)

which simplifies to (27), so we know that this value is zero at the ANS. Next we consider the second derivative $\partial ^2 f/ \partial ^2\,s$:

$$\begin{aligned} \begin{array}{rccl} \partial ^2 f/ \partial ^2 s & & = & u''_s(z_s) \beta ^2_s u_b(s) + \\ & & + & 2 u'_s(z_s) \beta _s u'_b(s) \\ & & + & u''_b(s) \left[ u_s(z_s) - (1-\beta _b)^2 u_s(b) \right] \end{array} \end{aligned}$$

(29)

The first term in (29) is negative because $u''_s(z_s)<0$, the second because $u'_b(s)<0$ (and all other factors in these terms are non-negative). For the third factor, we have $u''_b(s)< 0$ from concavity of the utilities and $\left[ u_s(z_s) - (1-\beta _b)^2 u_s(b) \right] \ge 0$ for $s\ge b$ and $\beta _b < 1$. Therefore, all terms are negative and the second derivative is negative. Thus, the seller cannot increase f by increasing s.

For the buyer, the proof is similar. The first derivative is

$$\begin{aligned} \partial f / \partial b = u'_{s}(z_s) (1 - \beta _s) u_b(s) - u'_b(z_b) \beta _b u_s(b) - u_b(z_b)u'_s(b) \end{aligned}$$

(30)

which is again zero at the ANS, as it simplifies to (27) with signs reversed. The second derivative is

$$\begin{aligned} \partial ^2 f / \partial ^2 b & = u''_s(z_s) \left[ (1-\beta _s)^2 u_b(s) - u_b(z_b)\right] \\ & \quad -u''_b(z_b)\beta _b^2u_s(b) \\ & \quad - 2 u'_b(z_b) \beta _b u'_s(b) \end{aligned}$$

(31)

For $b \le z_b \le s$ and $\beta _s < 1$ the second factor of the first term is negative, so the term is positive by concavity of the utility functions. Both the second and third term are negative and have a negative sign, so the second derivative is positive. Since the first derivative is zero at the ANS, it will not be negative for any b less than the ANS and the buyer thus cannot increase the value of f by decreasing b.

Altogether, this shows the ANS $x^*$ provides the stability required in Proposition 1.

Conversely, if x is not the ANS, then the fist order condition for the ANS (26) is not fulfilled (the left hand side of this equation will be negative). Therefore, both $\partial f / \partial s$ and $\partial f / \partial b$ will not be null for any other solution $s=b=x_{alt} \ne x^*$. In particular, if $x_{alt} < x^*$, then $\partial f / \partial s$ will be positive, meaning the seller can improve its situation (increase f) by asking for a higher price; if $x_{alt} > x^*$, then $\partial f / \partial b$ will be positive, meaning the buyer can improve its situation (decrease f) by asking for a lower price.

Hence, the ANS $x^*$ is the only solution providing the stability required in Proposition 1.