1 The trouble with causal sets

Suppose you decide to build a discrete model of spacetime. There are many places to start, and your choice may depend on how you view ordinary continuum spacetimes. When we learn general relativity, we are usually taught to think of spacetime as a differentiable manifold M, with a topology, a Lorentzian signature metric g, and perhaps some additional features. This naturally suggests discrete structures like lattices, simplicial complexes, cell complexes, and the like.

At least for causal manifolds,Footnote 1 though, the same information is contained in the causal structure—that is, which points are to the past and future of which others—and the local volume element [1, 2]. This suggests a very different discrete picture, that of a causal set [3].

Loosely speaking, a causal set is a collection of discrete points with prescribed causal relations, but no other structure. This naturally fits the requirements of [1, 2]: the causal structure is given, and the volume of a region is simply the number of points in contains. More precisely, a causal set is a partially ordered set, where \(x\prec y\) is interpreted as “x is to the causal past of y,” and the standard antisymmetry condition (“there are no distinct points x, y such that \(x\prec y\) and \(y\prec x\)”) becomes a statement of causality. One further postulate is added:

– Discreteness: for any (x, y), the set \(\{z|x\prec z\prec y\}\) has finitely many points.

The set \(\{z|x\prec z\prec y\}\), denoted as (x, y), is sometimes called the interval or order interval, and is the discrete analog of a causal diamond, the intersection of the future of x and the past of y. Such intervals will reappear later as building blocks of causal set invariants.

This is an attractive picture, perhaps the simplest possible version of a discrete spacetime. Before we get too excited, though, we should remember that the spacetime around us doesn’t look discrete. So we must first ask how well a causal set—or perhaps a quantum superposition of causal sets—can approximate a continuum spacetime.

This is best viewed as two distinct questions. In one direction, if we start with a continuum spacetime (M, g), can we find a causal set C that approximates it, and use C to reconstruct the properties of (M, g)? In the other direction—perhaps more important if we want to consider causal sets as fundamental—if we start with a causal set C, can we find a continuum spacetime (M, g) that approximates it?

In the first direction, we are in reasonably good shape. There is a standard procedure for constructing a causal set from a d-dimensional spacetime (M, g), called a “Poisson sprinkling” [4]: we randomly select a set of points \(\{x_i\}\) from M at a fixed density \(\rho \) with respect to the volume measure \(\sqrt{|g|}\); record the causal relations among these points as determined by the metric g; and then “forget” (M, g), keeping only the points \(\{x_i\}\) and their causal relations. The density \(\rho \) determines a discretization scale \(\ell = \rho ^{-1/d}\), and the “sprinkled” causal set contains fairly little information about M at scales smaller than \(\ell \). But above the discretization scale, we understand how to reconstruct the dimension d [5, 6] (this is less trivial than it might seem), the coarse-grained topology and much of the geometry of M (see [7] for a review), as well as useful objects such as d’Alembertians [8,9,10] and Greens functions (for instance, [13,14,15]). Some of this reconstruction is hard—it is particularly difficult to obtain quantities that are local in spacetime, since the only intrinsic distance in a causal set is proper distance [16,17,18]—and there are still important open problems, particularly revolving around the question of how to quantitatively measure how close causal sets are to each other or to a manifold. But there are no obvious insurmountable difficulties.

Fig. 1
figure 1

A Kleitman–Rothschild order; lines denote “links,” causal nearest neighbors

Full size image

The second direction, on the other hand, is a disaster. Almost all causal sets look nothing at all like manifolds. In fact, if you choose a large causal set at random, you will be overwhelmingly likely to find that you have a Kleitman–Rothschild (or KR) order [19]. A KR order is a particular type of “three-layer” causal set, that is, a causal set with arbitrarily large spatial extent but only three moments of timeFootnote 2 (see Fig. 1). And “overwhelmingly likely” here is meant in a very strong sense: in the limit that the number of points n goes to infinity, the set of causal sets that are not KR orders is of measure zero.

This is a strange and unintuitive result, although one may gain some feeling for it by starting with an \((n-1)\)-element KR order and estimating the number of ways of adding an nth point, either in one of the three existing layers or in a fourth layer. One might hope that this non-manifoldlike behavior is just a peculiarity of three-layer sets, but it is not. If one removes the KR orders by hand, almost all remaining causal sets have just two layers, two moments of time. If these are removed, almost all of the remaining causal sets have four layers, then five, six, and so on, in an extended hierarchy [20, 21]. The manifoldlike sets—those that can be obtained by a Poisson sprinkling on some spacetime—seem to be a vanishingly small subset.

This does not look good for the causal set program. Before despairing, though, it is helpful to recall a similar situation. If one looks carefully at the standard path integral for a simple system —say, a free particle—one finds that almost none of the paths that appear in the sum over histories are smooth. In fact, almost all paths are nowhere differentiable [22]. This is not a problem, though: the contributions of the nonsmooth paths destructively interfere, leaving an effectively smooth description. We might hope that the dominant “entropic” contribution of non-manifoldlike causal sets might be similarly eliminated. To see whether this is the case, though, we will need to understand the causal set version of the gravitational path integral.

2 The causal set path integral

Consider a collection \(\Omega \) of causal sets—for instance, the collection of all causal sets with n elements, or the collection of all KR orders. The partition function for \(\Omega \) is the path integral, or strictly speaking the path sum,

$$\begin{aligned} Z[\Omega ] = \sum _{C\in \Omega }\exp \left\{ \frac{i}{\hbar }I[C]\right\} , \end{aligned}$$
(2.1)

where I is a suitable action. Note the factor of i in the exponent: causal sets are intrinsically Lorentzian, though there are some ideas of how to continue to a Euclidean-like sum [23].

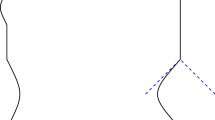
The task is now to find an action that reduces in some sense to the ordinary Einstein-Hilbert action for the continuum. For causal sets obtained from a Poisson sprinkling, this task was accomplished by Benincasa, Dowker, and Glaser [8,9,10], inspired by an earlier suggestion of Sorkin [11]. The building blocks are causal diamonds, or order intervals, \((x,y) = \{z|x\prec z\prec y\}\). An interval can be partially characterized by the number of elements in its interior, where by convention the initial and final points x and y are not counted. A 0-element interval is thus a link, a pair of nearest neighbors that are causally related but have no points lying between them. Figure 2 shows the possible topologies of 0-, 1-, and 2-element intervals.

Fig. 2
figure 2

0-, 1-, and 2-element intervals

Full size image

For a given causal set C, let \(N_J(C)\) be the number of intervals in C with exactly J elements. If C is obtained from a sprinkling, the number of elements in an interval is proportional to its spacetime volume, which in turn depends on the curvature. Using this fact, Benincasa, Dowker, and Glaser (BDG) showed that the discrete causal set version of the Einstein-Hilbert action in d dimensions takes the form

$$\begin{aligned} \frac{1}{\hbar } I^{(d)}_{{ BDG}}(C) = -\alpha _d\left( \frac{\ell }{\ell _p}\right) ^{d-2}\left( n + \frac{\beta _d}{\alpha _d} \sum _{J=0}^{n_d} C_J^{(d)} N_J \right) , \end{aligned}$$
(2.2)

where \(\ell _p\) is the Planck length (with the convention \(\ell _p^{d-2} = 8\pi G\hbar \)), \(\ell \) is the discreteness scale, and \(\alpha _d\), \(\beta _d\), and \(C_J^{(d)}\) are known order one dimension-dependent constants. (See [10] for closed form expressions for these constants; their i is my \(J+1\).) In particular, as the sprinkling density \(\rho \) goes to infinity, the BDG action for a region U approaches the Einstein-Hilbert action for U. For causal sets corresponding to manifolds with boundary, we also have a good candidate for the analog of the Gibbons-Hawking boundary term [12].

The action (2.2) was derived for causal sets obtained from a Poisson sprinkling. Let us demand, however, that it be applicable for all causal sets. Then by evaluating the partition function (2.1) for various classes of non-manifoldlike causal sets, we can see whether they are, in fact, suppressed by destructive interference.

3 Suppression of “bad” causal sets

It is one thing to write down the path sum (2.1), but quite another thing to evaluate it. For large n, the number of causal sets with n elements grows as \(2^{n^2/4}\), and causal sets are completely classified only up to \(n=16\) [24]. Some tricks are needed.

Fig. 3
figure 3

A two-layer causal set

Full size image

As a first step, in [25] Loomis and I looked at the special case of two-layer sets (see Fig. 3), inspired by Loomis’s observation that for such sets the BDG action becomes drastically simpler. The simplification occurs because for these sets, the only intervals are 0-element intervals, or links. Two points can be causally related, but with only two layers there is no room for a third point to lie between them. As a result, the action reduces to the “link action”

$$\begin{aligned} \frac{1}{\hbar } I^{(d)}_{{ link}}(C) = -\alpha _d\left( \frac{\ell }{\ell _p}\right) ^{d-2}\left( n + \frac{\beta _d}{\alpha _d}N_0 \right) , \end{aligned}$$
(3.1)

where I have used the fact that \(C_0^{(d)}=1\) for all dimensions [10].

An n-point causal set must have fewer than \(N_{{ max}} = \frac{n^2}{2}\) links, and can be characterized by a linking fraction \(0\le p\le 1\), where \(N_0 = pN_{{ max}}\). For a two-layer set, it is easy to see that \(p\le \frac{1}{2}\), with the maximum achieved when the points are evenly split between the two layers and maximally linked. In the large n limit, p can be treated as a continuous variable, and the path sum (2.1) for n-element two-layer sets becomes

$$\begin{aligned} Z[\Omega _{{ n,2-layer}}] =e^{-i\alpha _d\left( \frac{\ell }{\ell _p}\right) ^{d-2}n} \int _0^{1/2}\!dp\,|\Omega _{n,2,p}| e^{-\frac{i\beta _d}{2}\left( \frac{\ell }{\ell _p}\right) ^{d-2}pn^2} , \end{aligned}$$
(3.2)

where \(|\Omega _{n,2,p}|\) is the cardinality of the set \(\Omega _{n,2,p}\) of two-layer causal sets with n elements and linking fraction p. In [25], upper and lower bounds for \(|\Omega _{n,2,p}|\) were found, which “squeeze” its value as n becomes large, yielding

$$\begin{aligned} \ln |\Omega _{n,2,p}| = \frac{1}{4}h(2p) + { o}(n^2) \quad \hbox {with} \quad h(x) = -x\ln x - (1-x)\ln (1-x), \end{aligned}$$
(3.3)

where h(x) is the entropy function. The integral (3.2) can then be evaluated by steepest descents. Note that a simple saddle point approximation is not enough; one must be careful to choose the correct saddle point and the correct contour deformation and, since the saddle contribution is exponentially small, one must ensure that the contribution from the remainder of the contour is at least as strongly suppressed.

The result is that for large n,

$$\begin{aligned} Z[\Omega _{{ n,2-layer}}]&\sim e^{-bn^2}\nonumber \\&\hbox {with} \ b>0 \ \hbox {when} \ \tan \left\{ \frac{\beta _d}{2}\left( \frac{\ell }{\ell _p}\right) ^{d-2}\right\} > \left( \frac{27}{4}e^{-1/2} -1\right) ^{1/2} . \end{aligned}$$
(3.4)

For \(d=4\), the coefficient b is positive as long as the discreteness scale is \(\ell \gtrsim 1.136\ell _p\), with comparable limits in other dimensions. We do not know whether these limits are sharp. Note that this implies a very strong suppression: for a region of \(1\,\hbox {cm}^3\times 1\,\hbox {ns}\) with Planck scale discreteness, \(n\sim 10^{130}\), so two-layer causal sets are suppressed by a factor of order \(e^{-10^{260}}\).

The calculations leading to (3.4) were based on the bulk BDG action, and did not include a Gibbons-Hawking boundary term. But it may be checked that the boundary terms in [12] are proportional to the cardinality n of the causal set, and contributes only at subleading order. The same is true for all layered sets; the addition of a boundary term does not affect their suppression in the path sum.

This is a good first step: the two-layer sets are the second most common “bad” causal sets. But a direct extension to the KR orders and other layered sets is difficult. As soon as more than two layers are present, intervals more complicated than links appear, and the full sum in (2.2) has to be accounted for. In four dimensions, for instance, \(n_4=3\), and we must enumerate, or at least estimate, the numbers \(N_J\) with \(J=0,1,2,3\).

To make the task controllable, Mathur, Singh, and Surya asked a simpler question [26]. Suppose we truncate the full BDG action (2.2) by omitting all the \(N_{J>0}\) terms, reducing it to the link action (3.1). Then the path sum will again take the general form (3.2), but with the combinatoric factor \(\Omega _{n,2,p}\) replaced by the corresponding factor for some other collection of layered causal sets. The combinatorics is more complicated, but in the end, the factor in the path sum turns out to be the same as in the two-layer case, and the suppression (3.4) reappears for layered sets with more than two layers. Note that for this calculation, the dimension d only appears in the factor \(\beta _d\) in (3.4), which gives a very mild dependence of the suppression scale; I will return to this observation in the conclusion.

This is a good second step, but it is not quite answering the right question. The link action may suppress layered causal sets, but it is not a discretization of the Einstein-Hilbert action; for a Poisson sprinkling, it includes additional nonlocal terms along the light cone [27]. The next step, taken in [28], was to show that for the KR orders the truncation to the link action is harmless. More specifically, it was shown that for all KR orders except perhaps a set of measure zero, the number \(N_{J>0}\) in the full action (2.2) grow only as n, the total number of elements of the causal set. The number \(N_0\) of links, in contrast, grows as \(n^2\). Thus for large n, the terms omitted in [26] give only subleading corrections to the path sum. While the full proof in [28] requires some careful combinatorics, the intuitive argument is fairly simple. Figure 4 shows intervals (x, y) of various sizes in a KR order. In Fig. 4a, a one-element interval contributes to the number \(N_1\) in the action. As soon as a second path is added between x and y, as in Fig. 4b, (x, y) becomes a two-element interval, contributing to \(N_2\) but not to \(N_1\). A third path, Fig, 4c, shifts the contribution of (x, y) to \(N_3\). In general, in order for (x, y) to contribute to \(N_J\), it is not enough that there are J paths from x to y; there must be only J paths. For small causal sets, this is not a terribly strong restriction, but as n becomes large, the probability of having only a few paths between a point in layer 1 and a point in layer 3 becomes very small, shrinking fast enough to limit the growth of the \(N_J\) to \(\mathcal {O}(n)\).

Fig. 4
figure 4

One-, two- and three-element intervals in a KR order

Full size image

In a final step, the argument for KR orders has now been generalized to arbitrary layered causal sets, as long as the number of layers is small relative to the total number of points [29]. A more careful definition of “layer” is needed, but it matches the definition used in [21] in the proof of the entropic dominance of layered sets. The details of the combinatorics are more complicated than for the KR orders, but the spirit is the same. Indeed, given two points x and y in different layers, the addition of more layers between them allows for more possible paths, making it even less likely that the interval (x, y) contains only a small number of elements.

Combined with the results of [26], this implies that as long as the discreteness length obeys the inequality (3.4), all layered causal sets are extremely strongly suppressed in the ordinary discrete Einstein-Hilbert path sum. The suppression depends only very mildly on the details of the action, including the dimension d. It does, however, depend strongly on the presence of layering. For causal sets obtained from Poisson sprinklings on Minkowski space—and very probably on arbitrary curved spacetimes—the \(N_J\) all grow as \(n^{2-\frac{2}{d}}\) as the number of points increases [18], so all of the terms in the BDG action (2.2) remain important at large n.

The difference can be traced back to the fact that generic layered causal sets have no spatial structure, while sets obtained by sprinkling retain a memory of locality. For a KR order like that of Fig. 1, for instance, a typical causal diamond (or order interval) starting in layer 1 and ending in layer 3 contains about half of the points in layer 2 in its interior [19], while a similar causal diamond obtained from a sprinkling has a much smaller interior. The BDG action “prefers” this remnant of spatial locality, in ways that we do not yet fully understand.

4 Are we there yet?

Recall the dilemma we started with: almost all causal sets have a “layered” structure that is nothing like our observed spacetime. As we have now seen, the combined results of [25, 26, 28, 29] have solved this problem, showing that for a very wide range of coupling constants, these non-manifoldlike causal sets are very strongly suppressed in the path sum. Given the counting arguments of [19,20,21], we can say, at least technically correctly, that almost all non-manifoldlike causal sets are suppressed in this way.

This is not, however, the end of the story. We do not yet understand enough about the space of causal sets to know what is left. Manifoldlike causal sets are not eliminated, at least not in this fashion, but there may well be other non-manifoldlike sets that survive as well. Indeed, we don’t even know how to tell that a given causal set is “manifoldlike”; the term is usually taken to mean “obtainable from a Poisson sprinkling of Lorentzian manifold,” but that does not give us an algorithm we can apply to an arbitrary causal set. One feature we certainly want is emergent locality. The BDG action seems to retain some memory of this property—causal diamonds should not be “too big” spatially—but this is poorly understood.

Nor do we know how to derive the BDG action itself from first principles. The action (2.2) was obtained by starting with the Einstein-Hilbert action on a smooth manifold and looking for a discretized version on a Poisson sprinkling. This makes sense if we think of causal sets only as approximations to a fundamentally smooth spacetime. But if we view causal sets as fundamental, we need a way to derive an action without reference to a continuum limit.

As noted earlier, the results described here do not need the full structure of the BDG action. The suppression of layered sets comes from the link term in the action, and the point of [28, 29] was to show that the higher order terms were not relevant for layered sets. To recover anything like general relativity, though—or even spacetime locality [27]—we need those higher order terms, with the right coefficients. This might require radical steps, for instance a search for a quantum sequential growth model that has the correct classical limit [7]. But perhaps a simpler approach is available. One possible avenue would be to formulate a renormalization group flow for the action; perhaps the coefficients in the BDG expression label a fixed point. For now, though, this is more a dream than a concrete program.