Application of the Gauss–Bonnet theorem to lensing in the NUT metric

Abstract

We show with the help of Fermat’s principle that every lightlike geodesic in the NUT metric projects to a geodesic of a two-dimensional Riemannian metric which we call the optical metric. The optical metric is defined on a (coordinate) cone whose opening angle is determined by the impact parameter of the lightlike geodesic. We show that, surprisingly, the optical metrics on cones with different opening angles are locally (but not globally) isometric. With the help of the Gauss–Bonnet theorem we demonstrate that the deflection angle of a lightlike geodesic is determined by an area integral over the Gaussian curvature of the optical metric. A similar result is known to be true for static and spherically symmetric spacetimes. The generalisation to the NUT spacetime, which is neither static nor spherically symmetric (at least not in the usual sense), is rather non-trivial.

1 Introduction

The NUT metric is a solution to the vacuum Einstein equation that was found by Newman, Unti and Tamburino (NUT) in 1963 [1]. It describes the vacuum spacetime around a source that is characterised by two parameters, called m and l in the following. m detemines the mass of the central object, whereas l determines its gravitomagnetic charge. In an analogy to electromagnetism, m corresponds to the electric charge whereas l, which is also known as the NUT parameter, corresponds to a magnetic (monopole) charge.

The NUT metric has so many unusual properties that Misner [2] called it a “counter-example to almost anything”. This, however, does not necessarily mean that the NUT metric is unphysical. On the contrary, history has taught us to take solutions to Einstein’s vacuum equation seriously, even if they have apparently “exotic” properties. So we believe that the existence in Nature of sources with a non-zero NUT parameter is a possibility that should not be rejected off-hand.

Following this line of thought, we have to ask ourselves what kind of observable features a hypothetical NUT source would have. In essence, there are two types of such features. Firstly, we could consider the influence of such a source on the motion of massive particles that come close to it, secondly we could consider its influence on light rays. For the discussion of observable effects of a NUT source on massive particles we refer in particular to papers by Hackmann and Lämmerzahl [3] and Jefremov and Perlick [4]. We will not discuss this subject here. As to the influence on light rays, i.e., to the lensing features of a NUT source, there is a paper by Nouri-Zonoz and Lynden Bell [5]. It is the purpose of the present paper to develop their analysis somewhat further.

Our main goal is to find out whether the lensing features in the NUT spacetime can be characterised in terms of two-dimensional Riemannian geometry. It is well known that such a characterisation is possible in spacetimes that are static and spherically symmetric: In this case it suffices to consider lightlike geodesics in the equatorial plane $\vartheta = \pi /2$ because all the other ones are then determined by the spherical symmetry. Here $(t, r , \vartheta , \varphi )$ are the spherical polar coordinates in which a static and spherically symmetric spacetime is usually given. Then one finds that the spatial paths, in the two-dimensional manifold with coordinates $(r, \varphi )$, of lightlike geodesics are the geodesics of a Riemannian metric which is known as the Fermat metric or the optical metric. Gibbons and Werner [6] have used the Gauss–Bonnet theorem to show how the optical metric determines lensing features. In particular, they have demonstrated that the deflection angle is determined by the Gaussian curvature of the optical metric. In this paper we want to investigate if and how this result carries over to the NUT spacetime. As the NUT spacetime is not static but only stationary, and as in the NUT spacetime geodesics are not contained in a plane, this makes several non-trivial modifications necessary.

The paper is organised as follows. In Sects. 2 and  3 we summarise some basic features of the NUT spacetime and its geodesics. Throughout we do this for a version of the NUT metric that is more general than the one introduced in the original NUT paper [1] because it depends not only on the above-mentioned parameters m and l but also on a third parameter, C, that was introduced in 2005 by Manko and Ruiz [7]. In Sects. 4 and  5 we make use of the fact that in the NUT spacetime every lightlike geodesic is contained in a cone whose opening angle is determined by the impact parameter of the lightlike geodesic and we calculate the deflection angle. For the original NUT metric with $C=-1$ the fact that every geodesic is contained in a cone was derived already by Zimmerman and Shahir [8]; this fact plays a crucial role also in the above-mentioned paper by Nouri-Zonoz and Lynden-Bell [5] who consider the NUT metric with $C=0$. In Sect. 6 we use Fermat’s principle to define a Riemannian metric, which we call the optical metric, on each of these cones and we demonstrate that a lightlike geodesic with the corresponding impact parameter projects, indeed, to a geodesic of the optical metric. We illustrate the optical metric by way of an embedding diagram, we demonstrate that it has negative Gaussian curvature and we show that the optical metrics on cones with different opening angles are locally isometric. Finally, in Sect. 7 we use the Gauss–Bonnet theorem to rewrite the deflection angle as an integral over the Gaussian curvature of the optical metric. As the latter is negative, this result demonstrates that all light rays are deflected towards the centre and that the deflection angle increases with decreasing impact parameter.

We use the metric signature (-,+,+,+) and we set the speed of light $c= 1$. We use Einstein’s summation convention with greek indices for the four spacetime coordinates and with latin indices for the two coordinates of the two-dimensional manifold on which the optical metric lives.

2 The NUT metric

The NUT metric [1] is a solution to Einstein’s vacuum field equation. It depends on two parameters both of which have the dimension of a length, a mass parameter m and a gravitomagnetic charge, also known as the NUT parameter, l. We assume $m>0$ and $- \infty< l < \infty$ throughout. For $l=0$ the NUT metric reduces to the Schwarzschild metric. In 2005 Manko and Ruiz [7] brought forward a generalised version of the NUT metric which involves a third parameter, C, that is dimensionless and may take any value $- \infty< C < \infty$. With the Manko-Ruiz parameter included, the metric reads

$$\begin{aligned} g_{\mu \nu } dx^{\mu } dx ^{\nu } = -\frac{( r^2- 2 m r-l^2)}{(r^2+ l^2)} \Big ( dt - 2 l ({\mathrm {cos}} \, \vartheta + C ) d \varphi \Big ) ^2\nonumber \\ \quad + \dfrac{(r^2+l^2) \, dr^2}{r^2-2 m r -l^2} + (r^2+ l^2) \Big ( d\vartheta ^2 + {\mathrm {sin}} ^2 \vartheta \, d \varphi ^2 \Big ) \, . \end{aligned}$$

(1)

Here, $(t, r, \vartheta , \varphi )$ are Boyer-Lindquist-type coordinates. We assume that t ranges over all of ${\mathbb {R}}$, $\vartheta$ and $\varphi$ are standard coordinates on the two-sphere, and the radius coordinate is restricted to the domain $m+\sqrt{m^2+l^2}< r < \infty$. At $r=m+\sqrt{m^2+l^2}$ the metric features a black-hole horizon. If analytically extended beyond the horizon, in the domain $m - \sqrt{m^2+l^2}< r < m + \sqrt{m^2+l^2}$ the metric is isometric to a cosmological solution that was found already in 1951 by Taub [9]. The entire spacetime is therefore known as the Taub-NUT spacetime. In this paper, however, we will not consider the Taub region.

By a coordinate transformation $t'=t-2 l C \varphi$, $r'=r$, $\varphi ' = \varphi$, $\vartheta ' = \vartheta$ the metric (1) is transformed to the corresponding metric with $C=0$. This, however, is not a globally well-defined transformation: As we assume that $\vartheta$ and $\varphi$ are standard coordinates on the sphere, $\varphi$ is $2 \pi$-periodic; therefore, the transformation is well-defined only locally, on any neighbourhood that does not include an entire $\varphi$-line, unless we make the time coordinate periodic with period $4 \pi | l C|$. As the latter would lead to the most drastic causality violation, giving a closed timelike curve through each point of the considered domain of the spacetime, we will not do this. Therefore, NUT spacetimes with different values of C are locally but not globallyisometric.

The original NUT metric [1] is the metric (1) with $C= -1$. It features a conic singularity on the half-axis $\vartheta = \pi$ which was interpreted by Bonnor [10] as a spinning rod. For $C=1$ the singularity is on the other half-axis $\vartheta = 0$, and for all other values of C it is on both half-axes, symmetrically distributed for $C=0$ and asymmetrically for $C \ne 0$. For more details on the physical and geometrical meaning of the parameter C we refer to Manko and Ruiz [7] and also to Jefremov and Perlick [4].

For any values of m, l and C the NUT metric admits a four-dimensional Lie algebra of Killing vector fields, i.e., a NUT metric with $l \ne 0$ has as many symmetries as the Schwarzschild metric. For $C= -1$ the Killing vector fields have been given already in the original NUT article [1] and the resulting symmetry properties have been discussed in detail by Misner [11] who advocated the idea of making the t coordinate periodic. Here we give the four linearly independent Killing vector fields for the NUT metric with an arbitrary value of C:

$$\begin{aligned}&\displaystyle \xi _0 = \partial _t \, , \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \xi _1 = - {\mathrm {sin}} \, \varphi \, \partial _{\vartheta } - \dfrac{{\mathrm {cos}} \, \varphi }{{\mathrm {sin}} \, \vartheta } \Big ( {\mathrm {cos}} \, \vartheta \, \partial _{\varphi } + 2l \big ( 1 + C \, {\mathrm {cos}} \, \vartheta \big ) \partial _t \Big ) \, , \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle \xi _2 = {\mathrm {cos}} \, \varphi \, \partial _{\vartheta } - \dfrac{{\mathrm {sin}} \, \varphi }{{\mathrm {sin}} \, \vartheta } \Big ( {\mathrm {cos}} \, \vartheta \, \partial _{\varphi } + 2l \big ( 1 + C \, {\mathrm {cos}} \, \vartheta \big ) \partial _t \Big ) \, , \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle \xi _3 = \partial _{\varphi } + 2 l C \partial _t \, . \end{aligned}$$

(5)

The Lie brackets are

$$\begin{aligned} \big [ \xi _0 , \xi _1 \big ]= & {} \big [ \xi _0 , \xi _2 \big ] = \big [ \xi _0 , \xi _3 \big ] = 0 \, , \end{aligned}$$

(6)

$$\begin{aligned} \big [ \xi _1 , \xi _2 \big ]= & {} - \xi _3 \, , \, \big [ \xi _2 , \xi _3 \big ] = - \xi _ 1 \, , \, \big [ \xi _3 , \xi _1 \big ] = - \xi _2 \, . \end{aligned}$$

(7)

This demonstrates that $\xi _1$, $\xi _2$ and $\xi _3$ generate a three-dimensional group of isometries which is isomorphic to the rotation group $SO(3,{\mathbb {R}})$, whereas $\xi _0$ generates a one-dimensional group of isometries that expresses stationarity. Note that for $l \ne 0$ the orbits of the rotations are not two-dimensional spacelike spheres; they are rather three-dimensional submanifolds with topology ${\mathbb {R}} \times S^2$ and the metric has the signature $(-++)$ on these submanifolds. For this reason many authors find it inappropriate to call the NUT metric “spherically symmetric”. It is, however, safe to call it “rotationally symmetric about any radial direction” or to say that “it admits an $SO(3 , {\mathbb {R}} )$ symmetry”.

3 Geodesics in the NUT metric

With the Killing vector fields known, it is easy to solve the geodesic equation in the NUT spacetime. For any geodesic $x^{\mu } (s)$, parametrised by an affine parameter s, each of the four Killing vector fields $\xi _A$ gives us a constant of motion $g_{\mu \nu } \xi _A ^{\mu } {\dot{x}}{}^{\nu }$:

$$\begin{aligned} E= & {} -g_{\mu \nu } \xi _0 ^{\mu } {\dot{x}}{}^{\nu } = \dfrac{r^2-2mr-l^2}{r^2+l^2} \, \Big ( {\dot{t}} - 2l \big ( {\mathrm {cos}} \, \vartheta +C \big ) \, {\dot{\varphi }} \Big ) \, , \nonumber \\ J_1= & {} g_{\mu \nu } \xi _1 ^{\mu } {\dot{x}}{}^{\nu } = - {\mathrm {sin}} \, \varphi \, (r^2+l^2) \, {\dot{\vartheta }} \end{aligned}$$

(8)

$$\begin{aligned}&- {\mathrm {cos}} \, \varphi \, {\mathrm {cos}} \, \vartheta \, {\mathrm {sin}} \, \vartheta \, (r^2+l^2) \, {\dot{\varphi }} +2 \, l \, E \, {\mathrm {cos}} \, \varphi \, {\mathrm {sin}} \, \vartheta \, , \end{aligned}$$

(9)

$$\begin{aligned} J_2= & {} g_{\mu \nu } \xi _2 ^{\mu } {\dot{x}}{}^{\nu } = {\mathrm {cos}} \, \varphi \, (r^2+l^2) \, {\dot{\vartheta }} \nonumber \\&- {\mathrm {sin}} \, \varphi \, {\mathrm {cos}} \, \vartheta \, {\mathrm {sin}} \, \vartheta \, (r^2+l^2) \, {\dot{\varphi }} +2 \, l \, E \, {\mathrm {sin}} \, \varphi \, {\mathrm {sin}} \, \vartheta \, , \end{aligned}$$

(10)

$$\begin{aligned} J_3= & {} g_{\mu \nu } \xi _3 ^{\mu } {\dot{x}}{}^{\nu } = {\mathrm {sin}}{}^2 \vartheta \, (r^2+l^2) \, {\dot{\varphi }} +2 \, l \, E \, {\mathrm {cos}} \, \vartheta \, . \end{aligned}$$

(11)

Hence

$$\begin{aligned} J^2 := J_1^2 +J_2^2+J_3^2 = (r^2+l^2) \, \big ( {\dot{\vartheta }}{}^2 + {\mathrm {sin}}{}^2 \vartheta \, {\dot{\varphi }}{}^2 \big ) + 4 \, l^2 E^2 \end{aligned}$$

(12)

and

$$\begin{aligned} \begin{pmatrix} \, J_1 \, \\ J_2 \\ J_3 \end{pmatrix} \varvec{\cdot } \begin{pmatrix} \, {\mathrm {cos}} \, \varphi \, {\mathrm {sin}} \, \vartheta \, \\ \, {\mathrm {sin}} \, \varphi \, {\mathrm {sin}} \, \vartheta \, \\ {\mathrm {cos}} \, \vartheta \end{pmatrix} = 2 \, l \, E \, . \end{aligned}$$

(13)

The latter equation, in which the central dot means the standard Euclidean scalar product in ${\mathbb {R}}{}^3$, demonstrates that a geodesic with constants of motion E, $J_1$, $J_2$ and $J_3$ is contained in a cone whose vertex is at the coordinate origin, whose symmetry axis is spanned by the vector with Cartesian components $J_1$, $J_2$ and $J_3$ and whose opening angle $\alpha$ is given by

$$\begin{aligned} {\mathrm {cos}} \, \alpha = 2 \, l \, E/J \, . \end{aligned}$$

(14)

Note that this statement refers to a three-dimensional Euclidean space that is defined by the chosen coordinates. We will later discuss the intrinsic geometries of these coordinate cones.

For the NUT metric with $C= -1$, the fact that each geodesic is contained in a cone was discovered already by Zimmerman and Shahir [8]. (Note, however, that in their paper the $g_{tt}$ component of the metric is misprinted.) Equation  (14) demonstrates that the opening angle of this cone is independent of C if the geodesic is labelled by the constant of motion J/E. Of course, for $l=0$ (14) gives $\alpha = \pi /2$, i.e., it reproduces the well-known fact that in the Schwarzschild spacetime each geodesic is contained in a plane through the coordinate origin.

In addition to the constants of motion that arise from the Killing symmetries, also the Lagrangian

$$\begin{aligned} {\mathcal {L}} = \dfrac{1}{2} \, g_{\mu \nu } {\dot{x}}{}^{\mu } \, {\dot{x}}{}^{\nu } \end{aligned}$$

(15)

is a constant of motion. With the help of the four constants of motion E, $J^2$, $J_3$ and ${\mathcal {L}}$ the geodesic equation can be written in first-order form. To that end we have to solve, in this order, (11), (8), (12) and (15) for ${\dot{\varphi }}$, ${\dot{t}}$, ${\dot{\vartheta }}{}^2$ and ${\dot{r}}{}^2$ which results in

$$\begin{aligned} {\dot{\varphi }}= & {} \dfrac{ J_3-2 \, l \, E\, {\mathrm {cos}} \, \vartheta }{ (r^2+l^2) \, {\mathrm {sin}} ^2 \vartheta } \, , \end{aligned}$$

(16)

$$\begin{aligned} {\dot{t}}= & {} \dfrac{(r^2-2mr-l^2) \, E}{r^2+l^2} + 2 \, l \, \big ( {\mathrm {cos}} \, \vartheta + C \big ) \dfrac{ \big ( J_3-2 \, l \, E \, {\mathrm {cos}} \, \vartheta \big ) }{ (r^2+l^2) \, {\mathrm {sin}} ^2 \vartheta } \, , \end{aligned}$$

(17)

$$\begin{aligned} {\dot{\vartheta }}{}^2= & {} \dfrac{ J^2 - 4 \, l^2 E^2}{(r^2+l^2)^2} - \dfrac{ ( J_3-2 \, l \, E\, {\mathrm {cos}} \, \vartheta )^2 }{ (r^2+l^2) \, {\mathrm {sin}} ^2 \vartheta } \, , \end{aligned}$$

(18)

$$\begin{aligned} {\dot{r}}{}^2= & {} E^2 - \dfrac{(r^2-2mr-l^2)}{(r^2+l^2)} \, \big ( J^2- 4 \, l^2 E^2 \big ) + \dfrac{2 \, {\mathcal {L}} \big ( r^2 - 2 m r l^2 \big )}{(r^2+l^2)} \, . \end{aligned}$$

(19)

Here $J^2-4 \, l^2E^2$ is the Carter constant which arises as a separation constant if the geodesic equation is written in Hamilton-Jacobi form. Note that the spatial paths of the geodesics, which are determined by Eqs. (16), (18) and (19), are not affected by the Manko-Ruiz parameter C.

4 Lightlike geodesics contained in a cone with $\vartheta = {{\mathrm {constans}}}$

In the Schwarzschild spacetime it suffices to consider geodesics with $J_1=J_2=0$, which are exactly the geodesics in the equatorial plane $\vartheta = \pi /2$. If one has determined all such geodesics, one gets all the other ones by applying all possible rotations, i.e., the action of the group generated by the Killing vector fields $\xi _1$, $\xi _2$ and $\xi _3$. An analogous statement holds for the NUT metric: Also in this case it suffices to consider geodesics with $J_1 = J_2 =0$ which now are the geodesics contained in cones of the form $\vartheta = {\mathrm {constans}}$; the opening angle $\alpha$ of such a cone equals the coordinate angle $\vartheta$. Again, one gets all the other geodesics by applying to such geodesics all possible rotations.

If $J_1 = J_2 =0$ and $\vartheta = {\mathrm {constans}}$, (9) and (10) require

$$\begin{aligned} {\dot{\varphi }} = \dfrac{2 \, l \, E}{(r^2+l^2) \, {\mathrm {cos}} \, \vartheta } \end{aligned}$$

(20)

and (13) yields

$$\begin{aligned} \dfrac{J_3}{E} = \dfrac{2 \, l}{{\mathrm {cos}} \, \vartheta } . \end{aligned}$$

(21)

Here the angle $\alpha$ from Eq. (14) has been specified to the coordinate angle $\vartheta$.

The latter equation demonstrates that, in a NUT spacetime with $l \ne 0$, the opening angle $\vartheta$ of the cone is determined by the impact parameter $J_3/E$ and vice versa. In the Schwarzschild case $l=0$ Eqs. (20) and (21) determine neither ${\dot{\varphi }}$ nor $J_3/E$ because with l also ${\mathrm {cos}} \, \vartheta$ goes to zero.

For lightlike geodesics (${\mathcal {L}} = 0$), inserting (21) into (19) results in

$$\begin{aligned} {\dot{r}}{}^2 = E^2 \Bigg ( 1 - \dfrac{4 \, l^2 (r^2-2mr-l^2)}{(r^2+l^2)^2} \, {\mathrm {tan}}{}^2 \vartheta \Bigg ) \, . \end{aligned}$$

(22)

Differentiating this equation with respect to the affine parameter and dividing by $2 {\dot{r}}$ gives

$$\begin{aligned} \ddot{r} = - \dfrac{4 \, l^2 E^2 \, {\mathrm {tan}}{}^2 \vartheta }{(r^2+l^2)^4} \Big ( r^3 - 3mr^2-3l^2r+ml^2 \Big ) \, . \end{aligned}$$

(23)

Although we have divided by ${\dot{r}}$, this equation is valid by continuity also if ${\dot{r}} = 0$. By solving simultaneously the equations ${\dot{r}} =0$ and $\ddot{r}=0$ we see that there is a circular lightlike geodesic at the intersection of the sphere $r=r_{\mathrm {ph}}$ with the cone $\vartheta = \vartheta _{\mathrm {ph}}$ where

$$\begin{aligned} r _{\mathrm {ph}}^3 - 3mr _{\mathrm {ph}}^2-3l^2r _{\mathrm {ph}}+ml^2 = 0 \end{aligned}$$

(24)

and

$$\begin{aligned} {\mathrm {tan}} \, \vartheta _{\mathrm {ph}}= \dfrac{r _{\mathrm {ph}}^2+l^2}{2 \, l \, \sqrt{r _{\mathrm {ph}}^2-2mr-l^2}} \, . \end{aligned}$$

(25)

It is easy to see that the cubic equation (24) has three real solutions exactly one of which lies in the considered domain, $m + \sqrt{m^2+l^2} < r_{\mathrm {ph}}$. Applying all possible rotations demonstrates that the sphere at radius coordinate $r_{\mathrm {ph}}$ is filled with circular lightlike geodesics. We refer to it as to the photon sphere. The existence of the photon sphere is crucial for determining the socalled shadow of a NUT black hole, see Grenzebach et al. [12] where this is discussed for a class of spacetimes that contains the NUT spacetime as a special case.

From (20) and (22) we get the orbit equation that determines the shape of a lightlike geodesic in the cone $\vartheta = {\mathrm {constans}}$,

$$\begin{aligned} \dfrac{dr}{d \varphi } = \dfrac{{\dot{r}}}{{\dot{\varphi }}} = \pm \, \sqrt{ \dfrac{(r^2+l^2) ^2}{4 \, l^2} \, {\mathrm {cos}}{}^2 \vartheta - (r^2-2mr-l^2) \, {\mathrm {sin}}{}^2 \vartheta } \, . \end{aligned}$$

(26)

From this equation we read that, for $l \ne 0$, there are no lightlike geodesics contained in the equatorial plane $\vartheta = \pi /2$ because the expression under the square-root must be non-negative.

5 The deflection angle

We want to consider, in the cone $\vartheta = {\mathrm {constans}}$, a lightlike geodesic that comes in from infinity, goes through a minimum radius value $r = r_m$ and then escapes back to infinity. Note that such a light ray may make arbitrarily many turns around the centre. At $r=r_m$, the right-hand side of (22) must be zero,

$$\begin{aligned} \dfrac{r_m^2+l^2}{\sqrt{r_m^2-2 m r_m -l^2}}= 2 \, l \, \tan \vartheta \, , \end{aligned}$$

(27)

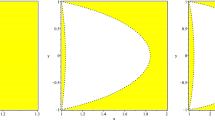
and the right-hand side of (23) must be negative. Therefore, lightlike geodesics that go through a minimal radius value $r_m$ exist for all $r_m$ outside of the photon sphere, $r_m > r_{\mathrm {ph}}$, and the corresponding values of $\vartheta$ converge towards $\vartheta _{\mathrm {ph}}$ for $r_m \rightarrow r_{\mathrm {ph}}$. If we define, for fixed $\vartheta$, the function

$$\begin{aligned} F(r) := {\mathrm {cot}} ^2 \vartheta \, ( r^2+l^2)^2- 4 l^2 (r^2-2 m r-l^2 ) \, , \end{aligned}$$

(28)

then $r_m$ is determined by the equation $F(r_m)=0$, where the largest positive solution to this fourth-order equation is the relevant one. In Fig. 1 the function F(r) is plotted for a fixed value $l \ne 0$ and various values of $\vartheta$. This figure confirms our earlier observation that for $l \ne 0$ there are no light rays in the equatorial plane $\vartheta = \pi /2$. Figure  2 shows a plot of $r_m$ as a function of l for various values of $\vartheta$.

Fig. 1

The function F(r) as a function of $\vartheta$ for $l=0.75$, in units with $m=1$

Fig. 2

The minimal radius $r_m$ as a function of l for various values of $\vartheta$, in units with $m=1$

With (27) we get from (26) the orbit equation in terms of $r_m$

$$\begin{aligned} \dfrac{dr}{d\varphi } = \pm \, \sqrt{\dfrac{ (r^2+l^2)^2(r_m^2-2 m r_m -l^2)-(r_m^2+l^2)^2(r^2-2 m r-l^2) }{ (r_m^2+l^2)^2+4l^2(r_m^2-2 m r_m-l^2) }} \, . \end{aligned}$$

(29)

Integration of the orbit equation (29) over the light ray from its point of closest approach to infinity yields

$$\begin{aligned} \varDelta \varphi = \int _{r_m}^{\infty } \dfrac{ \sqrt{(r_m^2+l^2)^2+4l^2(r_m^2-2 m r_m-l^2)} \, dr }{ \sqrt{(r^2+l^2)^2(r_m^2-2 m r_m -l^2)-(r_m^2+l^2)^2(r^2-2 m r-l^2)} } \, . \end{aligned}$$

(30)

For defining the deflection angle of a light ray we introduce a new azimuthal coordinate

$$\begin{aligned} {\tilde{\varphi }} = \varphi \, {\mathrm {sin}} \, \vartheta = \dfrac{(r_m^2+l^2) \, \varphi }{\sqrt{(r_m^2+l^2)^2 +4 l^2 (r_m^2-2 m r_m-l^2)}} \end{aligned}$$

(31)

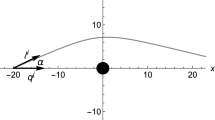
which is the angle defined around the surface of the cone. On each circle $r= {\mathrm {constans}}$ on the cone, $\varphi$ runs from 0 to $2 \pi$ whereas ${\tilde{\varphi }}$ runs from 0 to $2 \pi \, {\mathrm {sin}} \, \vartheta$, i.e., over a smaller interval. This deficit angle can be visualised by cutting the cone open and flattening it.

The deflection angle, or bending angle, is defined as the angle under which the asymptotes to the light ray intersect in the cut and flattened cone, see Fig. 3,

$$\begin{aligned} \delta = 2\varDelta {\tilde{\varphi }} -\pi \end{aligned}$$

(32)

where

$$\begin{aligned} \varDelta {\tilde{\varphi }}= & {} {\mathrm {sin}} \, \vartheta \, \varDelta \varphi \nonumber \\= & {} \int _{r_m}^{\infty } \dfrac{ (r_m^2+l^2) \, dr }{ \sqrt{(r^2+l^2)^2(r_m^2-2 m r_m -l^2)-(r_m^2+l^2)^2(r^2-2 m r-l^2)} } \, . \end{aligned}$$

(33)

Here we have used (27).

Our definition of the deflection angle is in agreement with that of Nouri-Zonoz and Lynden-Bell [5]. Note, however, that in their paper there is a notational inconsistency. In the beginning they define the NUT metric (with $C=0$) in the same coordinates as we do: Their r is our r and their $\phi$ is our $\varphi$. But later, from their Eqs. (4) and (5) onwards, their r is our $\sqrt{r^2+l^2}$ and their $\phi$ is our ${\tilde{\varphi }}$.

Fig. 3

Definition of the deflection angle $\delta$ of a lightlike geodesic $\gamma$ in a cone $\vartheta = {\mathrm {constans}}$

For light rays that make many turns around the centre, the deflection angle becomes arbitrarily large, i.e. $\delta \rightarrow \infty$ for $r_m \rightarrow r_{\mathrm {ph}}$. If, however, $r_m$ is big, $\delta$ is small and we get a valid approximation of $\delta$ if we do a Taylor expansion of a low order with respect to the dimensionless parameters $m/r_m$ and $l/r_m$. We have to go at least up to the second order for having a non-vanishing influence of l. Then (33) can be written as

$$\begin{aligned} \varDelta {\tilde{\varphi }}= & {} \int _{r_m}^{\infty } \left( 1 \, + \, \dfrac{(r^2+r _m r +r_m^2)}{r (r+r_m)} \, \dfrac{m}{r_m} \right. \nonumber \\&+ \, \dfrac{3 (r^2+r_mr+r_m^2)^2}{2 r^2 (r+m)^2} \, \dfrac{m^2}{r_m^2} + \, \dfrac{(3r^2+r_m^2)}{2 r^2} \, \dfrac{l^2}{r_m^2} \Bigg ) \dfrac{r_m \, dr}{r \sqrt{r^2-r_m^2}} + O(3)\nonumber \\= & {} \dfrac{\pi }{2} + \dfrac{2m}{r_m} - \left( 2 - \dfrac{15 \pi }{8} \right) \dfrac{m^2}{r_m^2} + \dfrac{7 \pi }{8} \, \dfrac{l^2}{r_m^2} + O (3) \end{aligned}$$

(34)

where O(3) stands for terms of third or higher order in $m/r_m$ and $l/r_m$. As a consequence, the bending angle to within this order is

$$\begin{aligned} \delta = \dfrac{4m}{r_m} - \left( 4 - \dfrac{15 \pi }{4} \right) \dfrac{m^2}{r_m^2} + \dfrac{7 \pi }{4} \, \dfrac{l^2}{r_m^2} + O (3) \, . \end{aligned}$$

(35)

In linear order we have the same result as in the Schwarzschild spacetime which is clear from the fact that l enters quadratically in all relevant equations.

6 Optical metric and Gaussian curvature

It is known that in an arbitrary spacetime lightlike geodesics satisfy a variational principle that can be viewed as a general-relativistic Fermat principle, see Temple [13] for a version restricted to a local normal neighbourhood, Kovner [14] for a formulation of the general principle and Perlick [15] for a complete proof. For static or stationary spacetimes, there are simpler and older versions of this variational principle. In the static case it was shown already in 1917 by Weyl [16] that, as a consequence of Fermat’s principle, the spatial paths of lightlike geodesics are the geodesics of a Riemannian metric which is now known as the Fermat metric or the optical metric. Levi-Civita [17] generalised Weyl’s result to the case of a stationary spacetime. Then the spatial paths of lightlike geodesics are determined by the combined action of a Riemannian metric and a one-form which is sometimes called the Fermat one-form; for examples we refer to Perlick [18]. Because of the influence of the Fermat one-form, the lightlike geodesics do not project to geodesics of a Riemannian metric. They rather project to geodesics of a Finsler metric. Although, in hindsight, this relation to Finsler geometry is fairly obvious, to the best of our knowledge it was realised only recently, namely by Caponio, Javaloyes and Masiello [19] in a paper that was put on the arXiv in 2007. It is Levi-Civita’s version of Fermat’s principle that we will apply to the NUT metric now.

According to the foregoing results we may restrict our consideration to a cone $\vartheta = {\mathrm {constans}}$. From (1) we read that along every lightlike curve (not necessarily a geodesic) the differential of the coordinate time along its spatial projection equals

$$\begin{aligned} dt= \beta _i dx^i+\sqrt{{\bar{g}}{}_{ij}dx^i dx^j} \end{aligned}$$

(36)

where $i,j \in \{r,\varphi \}$. Here $\beta _i$ and ${\bar{g}}{}_{ij}$ are given by

$$\begin{aligned} \beta _i dx^i= & {} 2l (\cos \vartheta +C)d\varphi \; , \end{aligned}$$

(37)

$$\begin{aligned} {\bar{g}}{}_{ij}dx^i dx^j= & {} \dfrac{(r^2+l^2)^2}{(r^2-2mr-l^2)^2}\;dr^2 +\dfrac{(r^2+l^2)^2}{(r^2-2mr-l^2)} {\mathrm {sin}}{}^2 \vartheta \; d\varphi ^2 \, . \end{aligned}$$

(38)

If one fixes two points in the cone and integrates dt over lightlike curves that project to curves in the cone between these two fixed points, then the integral over the one-form $\beta _i dx^i$ gives the same value for all these curves,

$$\begin{aligned} T= & {} \int _{s_1}^{s_2} \beta _i \dfrac{dx^i}{ds} ds +\int _{s_1}^{s_2} \sqrt{{\bar{g}}{}_{ij}\frac{dx^i}{ds}\dfrac{ dx^j}{ds}}\; ds\nonumber \\= & {} 2l (\cos \vartheta +C) (\varphi (s_2)-\varphi (s_1)) +\int _{s_1}^{s_2} \sqrt{{\bar{g}}{}_{ij}\frac{dx^i}{ds}\dfrac{ dx^j}{ds}}\; ds \, . \end{aligned}$$

(39)

By Levi-Civita’s version of Fermat’s principle, for an actual lightlike geodesic the variation of T vanishes, i.e.

$$\begin{aligned} 0 = \delta T = \delta \int _{s_1}^{s_2} \sqrt{{\bar{g}}{}_{ij}\frac{dx^i}{ds}\dfrac{ dx^j}{ds}}\; ds \, . \end{aligned}$$

(40)

This demonstrates that the spatial path of the lightlike geodesic is a geodesic of the Riemannian metric ${\bar{g}}{}_{ij}$ defined in (38). We call it the “optical metric” henceforth. Here we have to keep in mind that we have to choose the opening angle $\vartheta$ of the cone as determined by the impact parameter of the lightlike geodesic according to (21). As the NUT metric is not static, but only stationary, it was not to be expected that the lightlike geodesics project to geodesics of a Riemannian metric.

We have already emphasised that calling the surface $\vartheta = {\mathrm {constans}}$ a “cone” refers to the chosen coordinates. The optical metric, which has a coordinate-independent meaning, makes this surface into a two-dimensional Riemannian manifold. In order to visualise its intrinsic geometry we try to isometrically embed it into Euclidean 3-space. In cylindrical polar coordinates (Z, R, $\varphi$), we have to satisfy the condition

$$\begin{aligned} {\bar{g}}_{ij}dx^idx^i=dZ^2+dR^2+R^2d \varphi ^2 \end{aligned}$$

(41)

with embedding functions Z(r) and R(r). After inserting (38) and comparing coefficients of $d \varphi ^2$ and $dr^2$ we find

$$\begin{aligned} R(r)^2 = \dfrac{(r^2+l^2)^2 {\mathrm {sin}}{}^2 \vartheta }{(r^2-2mr-l^2)} \end{aligned}$$

(42)

and

$$\begin{aligned} \Big (\dfrac{d Z(r)}{dr} \Big )^2 = \dfrac{ (r^2-2 m r-l^2)(r^2+l^2)^2 - {\mathrm {sin}} ^2 \vartheta (r^3-3m r^2-3l^2 r+m l^2)^2 }{ (r^2-2m r-l^2)^3 } \end{aligned}$$

(43)

An isometric embedding into Euclidean 3-space is possible in that part of the domain $m+\sqrt{m^2+l^2}<r<\infty$ where $\big ( dZ(r)/dr \big ) ^2$ is non-negative. The boundary value, $r=r_b$, of the embeddable part is the greatest zero of the sixth-order polynomial in the numerator on the right-hand of (43). In the Schwarzschild limit $l = 0$, which requires $\vartheta =\pi /2$, we recover the well-known result $r_b = 9 m/4$.

From Fig. 4 we read that the intrinsic geometry of the coordinate cone $\vartheta = {\mathrm {constans}}$ becomes that of a Euclidean cone only asymptotically for $r \rightarrow \infty$. It develops a “neck” at the intersection with the photon sphere $r= r_{\mathrm {ph}}$, then opens out again before the boundary of the embeddable part is reached at $r = r_b$. We also read from the picture that at each point the principal curvatures have opposite signs, i.e., that the Gaussian curvature is negative which means that geodesics of the optical metric must locally diverge. This is true not only for the embeddable part but everywhere on the domain $m + \sqrt{m^2+l^2}< r < \infty$ on which the optical metric is defined. To demonstrate this we calculate the Gaussian curvature of the optical metric analytically.

Fig. 4

The cone $\vartheta =\pi /3$ of the NUT spacetime with $l=0.5$, embedded as a surface of revolution into Euclidean 3-space, with the photon sphere at $r_{\mathrm {ph}}=3.20 m$ and the boundary of the embeddable part at $r_{b}= 2.38 m$

By definition, the Gaussian curvature K of a two-dimensional Riemannian metric ${\bar{g}}{}_{ij}$ satisfies the equation

$$\begin{aligned} {\bar{R}}{}_{ijkl} = K \big ( {\bar{g}}{}_{ik} {\bar{g}}{}_{jl}- {\bar{g}}{}_{il} {\bar{g}}{}_{jk} \big ) \end{aligned}$$

(44)

where ${\bar{R}}{}_{ijkl}$ are the covariant components of the Riemannian curvature tensor. For a metric of the form (38), the Gaussian curvature can then be calculated as

$$\begin{aligned} K = \dfrac{{\bar{R}}_{r \varphi r\varphi }}{{\bar{g}}_{rr} {\bar{g}}{}_{\varphi \varphi }} \, , \end{aligned}$$

(45)

which gives, with the special metric coefficients from (38),

$$\begin{aligned} K= & {} - \dfrac{(2 r-3 m ) m \, r^4}{(l^2+r^2)^4}\nonumber \\&-\dfrac{l^2 r^2 \left( 14 m^2-20 m r+7 r^2\right) + l^4 \left( m^2+10 m r-6 r^2\right) + 3 l^6}{(l^2+r^2)^4} \, . \end{aligned}$$

(46)

For a plot of K as a function of r, for different NUT-parameters, see Fig. 5. Eq. (46) confirms that, for any value of l, the Gaussian curvature of the optical metric is indeed negative on the entire domain $m + \sqrt{m^2+l^2}< r < \infty$. To prove this, substitute $r = m+\sqrt{m^2+l^2}+x$; then $(l^2+r^2)^4 K$ becomes a fifth-order polynomial in x whose coefficients are manifestly negative. Also, (46) implies that for $r \rightarrow m + \sqrt{m^2+l^2}$ the Gaussian curvature K approaches a strictly negative value and its derivative dK/dr approaches zero. Here it is important that we consider a NUT spacetime with $m >0$. The observation that K is negative is also true for $m =0$ as long as $l \ne 0$. For $m=0$ and $l =0$, we have Minkowski spacetime and the cones are Euclidean cones, i.e, they are locally flat with $K=0$.

Remarkably, K is independent of $\vartheta$. That is to say, on all cones with their different opening angles the Gaussian curvature depends on r in exactly the same way. A careful look at (38) shows that this is, actually, not so surprising: If one changes from the coordinates $(r, \varphi )$ to $( {\tilde{r}} = r , {\tilde{\varphi }} = \varphi \, {\mathrm {sin}} \, \vartheta )$, the metric coefficients become independent of $\vartheta$. Hence it is clear that the optical geometries of any two cones with different opening angles are locally isometric. They are, however, not globally isometric because the range of the coordinate ${\tilde{\varphi }}$ depends on $\vartheta$. By the same token, their embedding diagrams depend on $\vartheta$ because in the ambient Euclidean space the azimuthal coordinate is assumed to be $2 \pi$-periodic. If, on the other hand, we use the representation in a plane where $(r, {\tilde{\varphi }})$ are the polar coordinates, as in Fig. 3, then the optical metrics are represented by a metric on this plane that is independent of $\vartheta$. We can thus show all the geodesics of the optical metrics, i.e., all lightlike geodesics, in one and the same plane; we just have to keep in mind that the deficit angle, which is marked in grey in Fig. 3, is different for geodesics with different impact parameters.

Fig. 5

The Gaussian curvature of the optical metric for different NUT parameters, plotted in each case for $m + \sqrt{m^2 + l^2} < r$, in units with $m=1$

7 Gravitational lensing and Gauss–Bonnet theorem

For the Schwarzschild spacetime, and any other spherically symmetric and static spacetime, the Gauss–Bonnet theorem can be used for characterising some lensing features. This was demonstrated in a pioneering paper by Gibbons and Werner [6] who in particular derived from the Gauss–Bonnet theorem a formula for the bending angle in such spacetimes. Their analysis was based on the well-known facts that in a spherically symmetric and static spacetime it suffices to consider lightlike geodesics in the equatorial plane $\vartheta = \pi /2$ and that the spatial projections of lightlike geodesics in this plane are the geodesics of a two-dimensional Riemannian metric. Werner [20] demonstrated that a similar analysis is possible for lightlike geodesics in the equatorial plane of the Kerr metric. There are several differences in comparison to the spherically symmetric and static case. Firstly, in the Kerr metric the lightlike geodesics do not project to geodesics of a Riemannian metric; therefore Werner had to use the idea of an “osculating Riemannian metric” for achieving his goal. Secondly, in the Kerr metric confining oneself to the equatorial plane is, of course, a strong restriction of generality. We will now demonstrate that in the NUT spacetime the Gauss–Bonnet theorem can be applied to all lightlike geodesics, without any loss of generality, and that there is no need to introduce an osculating metric or any other fiducial quantities. We follow the original idea of Gibbons and Werner as closely as possible. For background material on the Gauss–Bonnet theorem the reader may consult any text-book on Riemannian geometry, e.g. Klingenberg [21].

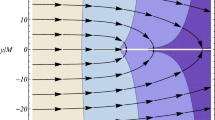
In its standard text-book version, the Gauss–Bonnet theorem is valid for a compact domain with boundary in a two-dimensional Riemannian manifold. For applying this theorem to lightlike geodesics in the NUT spacetime, we use for the two-dimensional Riemannian manifold the cone $\vartheta = {\mathrm {constans}}$ with the optical metric (38). For the compact domain we use a quadrangle $D_R$ whose boundary consists of four smooth parts, see Fig. 6. As in Fig. 3, also in this picture the cone is shown cut open and flattened, i.e., what is shown is a diagram using $(r , {\tilde{\varphi }})$ as polar coordinates.

The four smooth parts of the boundary of $D_R$ are constructed in the following way. The first part is a finite section of the projection of a lightlike geodesic, denoted $\gamma$ in Fig. 6; we assume that $\gamma$ has no self-intersections and that it comes from infinity, goes through a minimal radius value $r = r_m$ and then escapes to infinity. Along the section of $\gamma$ that is part of the boundary of $D_R$ the angle ${\tilde{\varphi }}$ runs over an interval of length ${\tilde{\psi }}$. Another part of the boundary of $D_R$ is a section of a circle $r=R$, denoted $\gamma _R$ in the picture. The two remaining parts are radial.

Now the Gauss–Bonnet theorem says that

$$\begin{aligned} \iint _{D_R} K \, dS + \int _{\partial D_R}\kappa \, d s + \sum _{A=1}^4 \alpha _A=2 \, \pi \, \chi (D_R) \, . \end{aligned}$$

(47)

Here K is the Gaussian curvature and dS is the area element of the optical metric. $\partial D_R$ is the boundary of $D_R$ and $\kappa$ is the geodesic curvature of this boundary, to be integrated over the four smooth parts of $\partial D_R$ where s denotes arclength with respect to the optical metric. The $\alpha _A$ are the four jump angles marked in Fig. 6 and $\chi ( D_R )$ is the Euler characteristic of $D_R$. As $D_R$ is connected and has no holes, $\chi (D_R) = 1$. Moreover, obviously $\alpha _1 = \alpha _2 = \pi /2$. The integral over the boundary of $D_R$ reduces to an integral over the circular arc because the other three parts are geodesic, hence $\kappa = 0$ there. We parametrise the circular arc by arclength, i.e., we write it in the form $\gamma _R (s)$ with ${\overline{g}} \big ( {\dot{\gamma }}_{R} , {\dot{\gamma }}_{R}) = 1$. The geodesic curvature of $\gamma _R$ is then to be calculated as

$$\begin{aligned} \kappa = \big | {\overline{g}} \big ( {\overline{\nabla }}{} _{{\dot{\gamma }}_R} {\dot{\gamma }}{}_R, n \big ) \big | \end{aligned}$$

(48)

where ${\overline{\nabla }}$ is the Levi-Civita connection of the optical metric ${\overline{g}}$ and n is a unit vector perpendicular to ${\dot{\gamma }}{}_R$. This puts (47) into the following form:

$$\begin{aligned} \iint _{D_R} K \, dS + \int _{\gamma _R}\kappa \, d s + \alpha _3 + \alpha _4 = \pi \, . \end{aligned}$$

(49)

Fig. 6

Gravitational lensing and Gauss–Bonnet theorem

We now send $R \rightarrow \infty$ and ${\tilde{\psi }} \rightarrow 2 \, \varDelta {\tilde{\varphi }}$. Then obviously $\alpha _3 \rightarrow 0$ and $\alpha _4 \rightarrow 0$. Moreover, from (38) we find after a straight-forward calculation that

$$\begin{aligned} \int _{\gamma _R}\kappa \, ds \rightarrow 2 \, \varDelta {\tilde{\varphi }} \, . \end{aligned}$$

(50)

Therefore, the limit version of the Gauss–Bonnet theorem reads

$$\begin{aligned} \iint _{D_{\infty }} K \, dS + 2 \varDelta {\tilde{\varphi }} = \pi \, . \end{aligned}$$

(51)

Comparison with (32) yields

$$\begin{aligned} \delta =-\iint _{D_{\infty }} K \, dS \, . \end{aligned}$$

(52)

As K is negative, we read from this formula that the deflection angle in the NUT spacetime is always positive, i.e., that every light ray is deflected towards the centre. This is not obvious if the deflection angle is represented with the help of (33) because one does not know whether the integral on the right-hand side of this equation is bigger or smaller than $\pi /2$ before one has actually calculated it. Moreover, as K is independent of $\vartheta$, it is also evident from (52) that a second light ray has a smaller deflection angle than the first one if on its entire path it stays farther away from the centre. Again, this is not obvious from the representation with (33) because the minimal radius $r_m$ occurs not only as the lower limit of the integral but also in the integrand.

When deriving (52) we have assumed that the light ray has no self-intersection, i.e., we excluded the case that the light ray makes a full turn, or several full turns, around the centre. If one wants to include such cases, one has to consider a region $D_{\infty }$ that is bounded by the parts of the light ray between infinity and the outermost self-intersection point, one has to add $2 n \pi \, {\mathrm {sin}} \, \vartheta$ on the right-hand side of (52) where n is the number of full turns performed by the light ray, and one has to take the jump angle at the self-intersection point into account. In particular the last point makes the use of the Gauss–Bonnet theorem to light rays with self-intersections rather awkward.

To make (52) more explicit, we write the area element of the optical metric as

$$\begin{aligned} dS=\sqrt{\mathrm {det} \big ( {\bar{g}}_{ij} \big )} \, dr \, d\varphi =\dfrac{(r^2+l^2)^2 \sin \vartheta \, dr \, d\varphi }{(r^2-2mr-l^2)^{3/2}} =\dfrac{(r^2+l^2)^2 dr \, d {\tilde{\varphi }}}{(r^2-2mr-l^2)^{3/2}} \end{aligned}$$

(53)

The bending angle now is

$$\begin{aligned} \delta =- 2 \int _0^{\varDelta {\tilde{\varphi }}} \int _{z( {\tilde{\varphi }})}^{\infty } K \sqrt{\mathrm {det} \big ( {\bar{g}}_{ij}\big ) }\;dr \, d {\tilde{\varphi }} \end{aligned}$$

(54)

where $r=z( {\tilde{\varphi }})$ is the polar representation of the deflected light ray, with the angle ${\tilde{\varphi }}$ as the parameter.

Werner [20] has calculated the bending angle in the equatorial plane of the Kerr metric to within linear order in the mass parameter and the spin parameter. In the NUT metric we have to go at least up to second order if we want to have a non-zero contribution of the NUT parameter. We have calculated the bending angle already up to this order in (35). As a cross-check, we want to reproduce this result with the Gauss–Bonnet theorem. To that end we need the integrand in (54) up to second order,

$$\begin{aligned} K \sqrt{\mathrm {det} \big ( {\bar{g}}_{ij}\big ) } = - \dfrac{2m}{r^2}- \dfrac{3m^2}{r^3} - \dfrac{7 l^2}{r^3} + O(3) \, . \end{aligned}$$

(55)

As this expression has a vanishing zeroth-order term, we need $\varDelta {\tilde{\varphi }}$ and $z ( {\tilde{\varphi }} )$ only up to first order. $\varDelta {\tilde{\varphi }}$ was calculated in (34),

$$\begin{aligned} \varDelta {\tilde{\varphi }} = \dfrac{\pi }{2} + \dfrac{2m}{r_m} + O (2) \, . \end{aligned}$$

(56)

For calculating the orbit $r=z ( {\tilde{\varphi }})$, we integrate on the right-hand side of (34) not from $r_m$ but from $z ( {\tilde{\varphi }})$ to infinity,

$$\begin{aligned} {\tilde{\varphi }}= & {} \int _{z ( {\tilde{\varphi }} )} ^{\infty } \left( 1 \, + \, \dfrac{(r^2+r _m r +r_m^2)}{r (r+r_m)} \, \dfrac{m}{r_m} \right) \dfrac{r_m \, dr}{r \sqrt{r^2-r_m^2}} + O(2)\nonumber \\= & {} {\mathrm {arccos}} \Big ( \dfrac{r_m}{z ( {\tilde{\varphi }} )} \Big ) + \dfrac{\sqrt{z ( {\tilde{\varphi }} )-r_m}}{\sqrt{z ( {\tilde{\varphi }} ) + r_m}} \Bigg ( 2 + \dfrac{r_m}{z ( {\tilde{\varphi }} )} \Bigg ) \dfrac{m}{r_m} + O (2) \end{aligned}$$

(57)

where we have assumed that the light ray passes at ${\tilde{\varphi }} = 0$ through the point of closest approach. Solving for $z ( {\tilde{\varphi }} )$ results in

$$\begin{aligned} z ( {\tilde{\varphi }} ) = \dfrac{r_m}{{\mathrm {cos}} \, {\tilde{\varphi }}} \left( 1 - \dfrac{ \big ( 2+{\mathrm {cos}} \, {\tilde{\varphi }} \big ) \, {\mathrm {sin}} ^2 {\tilde{\varphi }} }{ \big ( 1 + {\mathrm {cos}} \, {\tilde{\varphi }} \big ) \, {\mathrm {cos}} \, {\tilde{\varphi }} } \, \dfrac{m}{r_m} + O (2) \right) \end{aligned}$$

(58)

Inserting (55), (56) and (58) into (54) reproduces, indeed, (35).

We emphasise that the line integral in (33) is easier to evaluate than the area integral in (52). Therefore, if the only goal is to actually calculate the deflection angle, then there is no point in using the Gauss–Bonnet theorem. The merit of the latter is in the fact that it immediately gives some qualitative lensing features in terms of geometric quantities.

8 Discussion and conclusions

When Gibbons and Werner [6] applied the Gauss–Bonnet theorem to the spatial paths of lightlike geodesics in static and spherically symmetric spacetimes, many readers found this idea attractive because it related the lensing features in such spacetimes to geometric quantities such as the Gaussian curvature of a two-dimensional Riemannian metric. Naturally, the question arises if a similar result can be found in spacetimes that are not static and spherically symmetric. Werner [20] considered the Kerr metric and he demonstrated that, at least for light rays in the equatorial plane, the Gauss–Bonnet theorem is applicable. However, in contrast to the static and spherically symmetric case, the light rays do not project to geodesics of a Riemannian metric but rather to geodesics of a Finsler metric of Randers type; this made it necessary to introduce a socalled “osculating metric” to which the standard Gauss–Bonnet theorem could be applied.

Here we have shown that the original method by Gibbons and Werner, without a restriction to special lightlike geodesics and without the need of introducing an osculating metric, can be applied to the NUT metric. The main difference to the cases considered earlier is in the fact that now the spatial projection of each lightlike geodesic is in a cone, rather than in a plane. Throughout we have allowed for an arbitrary value of the Manko-Ruiz parameter C, and we have verified that C has no influence on the spatial paths of lightlike geodesics. Our analysis revealed two facts that could not have been anticipated before the calculation was done: Firstly, we showed that the projection of every lightlike geodesic is indeed a geodesic of an optical metric that is Riemannian; so there is no need of considering Finsler metrics. Secondly, on cones with different opening angles the optical metrics turned out to be locally isometric; in particular, the Gaussian curvature of the optical metric, as a function of the radius coordinate, turned out to be independent of the opening angle of the cone. Together with the observation that the Gaussian curvature of the optical metric is negative, this allowed us to use the Gauss–Bonnet theorem for representing qualitative lensing features of the NUT spacetime in a geometric way that is as significant as in the Schwarzschild spacetime.