On the role of dissipation in structure formation for dilute relativistic gases: the fluctuating static background case

Abstract

A correction to the Jeans stability criterion due to dissipation is established for the case of dilute high temperature gases. This effect is only relevant in the relativistic scenario and includes additional terms due to a density gradient driven heat flux, a non-vanishing bulk viscosity and the space-time dependent gravitational potential first order fluctuations. The result is obtained by thoroughly analyzing the exponentially growing modes present in the dynamics of density fluctuations in the linearized relativistic Navier–Stokes regime. The corrections to the corresponding Jeans mass and wavenumber are explicitly obtained and are compared to the non-relativistic and non-dissipative values using the transport coefficients obtained in the BGK approximation.

Appendices

Appendix A

In this appendix we show that the coefficient $\sigma$ in Eq. (22) is positive for all values of z, where $z=kT_0/mc^2$. First we note that $\sigma$ can be written as

$$\begin{aligned} \nonumber \sigma= & {} \frac{q^2}{\tilde{\rho }_0}\left[ -q^2\left( A-D_{TR}-\tilde{\rho }_0\gamma \right) \right. \\&-\frac{8\pi G \tilde{\rho }_0}{c^2}\left( \frac{n_0\varepsilon _0}{\tilde{\rho }_0c^2}+\frac{3}{2}\right) \left( A-D_{TR}-\tilde{\rho }_0\gamma \right) \\ \nonumber&+ \left. \frac{12 \pi G \tilde{\rho }_0\mu }{c^2}\right] . \nonumber \end{aligned}$$

(31)

Fig. 3

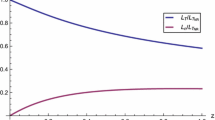
The combination $\left( A(z)-D_{TR}(z)-\tilde{\rho }_0(z)\gamma (z)\right)$ is shown as a function of z (top). The plot on the bottom shows the comparison of $\left| 8\left( \frac{n_0\varepsilon _0(z)}{\tilde{\rho }_0(z)c^2}+\frac{3}{2}\right) \left( A(z)-D_{TR}(z)-\tilde{\rho }_0(z) \gamma (z)\right) \right|$ (solid line) and $\left| 12\mu (z)\right|$ (dashed line) as functions of z

The plot on the top in Fig. 3 shows that $\left( A(z)-D_{TR}(z)+\tilde{\rho }_0(z)\gamma (z)\right)$ is negative and thus the first term in the bracket is positive. On the other hand, the second and third terms, which do not depend on q, have opposite signs. However, the plot on the bottom of Fig. 3 shows that

$$\begin{aligned} \left| 8\left( \frac{n_0\varepsilon _0(z)}{\tilde{\rho }_0(z)c^2}+\frac{3}{2}\right) \left( A(z)-D_{TR}(z)-\tilde{\rho }_0(z) \gamma (z)\right) \right| \gg \left| 12\mu (z)\right| , \end{aligned}$$

such that one can conclude that $\sigma$ is positive. It is important to point out that the values plotted in Fig. 3 correspond to the transport coefficients obtained within the relaxation approximation (see “Appendix B”).

Appendix B

In this appendix we show explicitly the transport coefficients appearing in the closure relations (9) and (10). The quantities $\mu \left( z\right) ,\eta \left( z\right) ,L_{TT}\left( z\right)$ and $L_{nT}\left( z\right)$ correspond to the bulk viscosity, shear viscosity and the conductivities associated to heat flux respectively, as functions of the relativistic parameter z. These coefficients where obtained through the usual methods in kinetic theory based on a relaxation time approximation in Refs. [8, 10, 12], however we have decided to include them in this work in a compact and uniform notation. For the viscosities we have

$$\begin{aligned} \mu \left( z\right) =-\frac{1}{3}nmc^{2}\tau \frac{\left[ z\left( 2-20z^{2}\right) {\mathcal {G}}\left( \frac{1}{z}\right) +13z^{2}\mathcal {G}^{2}\left( \frac{1}{z}\right) -2z\mathcal {G}^{3}\left( \frac{1}{z}\right) -3z^{2}\right] }{3z^{2}\mathcal {G}\left( \frac{1}{z}\right) \alpha \left( z\right) } \end{aligned}$$

(32)

and

$$\begin{aligned} \eta \left( z\right) =-nmc^{2}\tau z{\mathcal {G}}\left( \frac{1}{z}\right) , \end{aligned}$$

(33)

where

$$\begin{aligned} \alpha \left( z\right) =\frac{1}{z}\left[ -\frac{1}{z}{\mathcal {G}}\left( \frac{1}{z}\right) +\frac{1}{z\mathcal {G}\left( \frac{1}{z}\right) }+5\right] -\frac{1}{\mathcal {G}\left( \frac{1}{z}\right) }. \end{aligned}$$

(34)

Considering that heat flux is written as in Eq. (10) we have

$$\begin{aligned} L_{TT}\left( z\right) =nmc^{4}z^{3}\tau \left[ \frac{1}{z}{\mathcal {G}}\left( \frac{1}{z}\right) -1\right] \left[ \alpha \left( z\right) +\frac{1}{\mathcal {G}\left( \frac{1}{z}\right) }\right] \end{aligned}$$

(35)

and

$$\begin{aligned} L_{nT}\left( z\right) =-nmc^{4}z^{3}\tau \left[ \alpha \left( z\right) +\frac{1}{{\mathcal {G}}\left( \frac{1}{z}\right) }\right] , \end{aligned}$$

(36)

notice that $L_{TT}$ and $L_{nT}$ have opposite sign.