1 Introduction

With the Ricci curvature uniquely determined by the energy momentum tensor \(T_{i}{}_{j}{}\), one still has the freedom to alter Riemann tensor by adding the Weyl tensor \(C_{i}{ }_{j}{}_{m}{}_{n}{}\)

$$\begin{aligned} R_{i}{}_{k}{}_{l}{}_{m}{}= C_{i}{}_{k}{}_{l}{}_{m}{} -\frac{1}{2}( g_{k}{}_{l}{}R_{i}{}_{m}{}+ g_{i}{}_{m}{}R_{k}{}_{l}{}- g_{k}{}_{m}{}R_{i}{}_{l}{}- g_{i}{}_{l}{}R_{k}{}_{m}{}). \end{aligned}$$
(1)

The Weyl tensor remains unchanged under conformal transformations of space \(g \rightarrow \varOmega (x) g\), and therefore, is a measure of the conformal curvature. The Weyl tensor is not coupled to the matter. In principle, it can take arbitrary values, unless the Riemann tensor index symmetries are fulfilled, and \(C^{k}{}_{i}{}_{k}{}_{j}{}=O\). Gravitational waves, which are waves of conformal curvature, in the linear regime propagate independently of matter distribution. The space symmetries for tensor perturbations can be set arbitrarily, and independently of whether the waves propagate in vacuum or in a space filled with matter.

In modelling stars, one proceeds differently. It is expected that the spacetime geometry reproduces the spherical symmetry of a gaseous cloud. Accordingly, the Weyl curvature becomes partially coupled to the matter distribution in an indirect way. Moreover, the regularity of matter distribution is reflected in the assumption that both the metric tensor and the Riemann curvature are regular [1]. Due to this assumption the gaseous spherical clouds are free of singularities, unlike the vacuum spherical solutions, black holes. The above-mentioned assumptions are not axioms within the General Relativity, but rather supplement the theory, effectively reducing the number of available solutions.

The aim of this paper is to relax the regularity assumptions. We investigate the spherically symmetric configurations of the regularly distributed classical fluid containing point-like repulsive gravity sources [2] in their centres. The cosmic censorship [3] is not fulfilled here. The energy density and pressure of the fluid component are assumed to be finite everywhere and differentiable beyond the central point. The weak, strong and dominant energy conditions are satisfied—contrary to [4–6] the matter is purely classical. No regularity restrictions on the metrics or curvature are made. We use the Carminati–McLenaghan basis [7, 8] of curvature invariants to define a class of non-vacuum spherically symmetric spaces with a degree of regularity close to that for the Schwarzschild spacetime. Finally, we adopt the neutron star polytrope approximation [9] in order to numerically evaluate the radius–mass relation for those singular-core equilibrium states. The study does not include the dynamic stability analysis of the presented configurations.

The freedom to arbitrarily set the purely gravitational part of mass is originally present in the Oppenheimer–Volkoff problem, as equivalent to the choice of an integration constant. This arbitrariness is traditionally eliminated by heuristic arguments [10, 11], or an explicit demand that the metric tensor should be regular [1]. In this manner relativistic astrophysics splits into two separate branches: the black hole theory, which admits singularities in vacuum, and the relativistic star theory, which, conversely, admits the material content, but excludes singularities.

On the ground of regular Oppenheimer–Volkoff solution the two important astrophysical concepts are based: the Oppenheimer limit [10] for the object mass, and the Bondi limit [12] for gravitational redshift. It seems important to know what happens to these limits when the regularity conditions are relaxed.

A direct motivation for our investigations came from the discovery of collapse solutions which terminate at naked singularities in cores of compact gaseousspheres [13–21].

2 Riemann curvature invariants: the case of spherical symmetry

For the spacetime obeying Einstein equations with hydrodynamic energy–momentum tensor the Riemann curvature invariants decompose into Carminati–McLenaghan invariants [7]. Carminati–McLenaghan invariants divide into three subsets: the Ricci-based \(\{\mathscr {R} _1, \mathscr {R} _2, \mathscr {R} _3\}\)

$$\begin{aligned} \mathscr {R} _1= & {} \frac{1}{4} S^{a}{}_{b}{} S^{b}{}_{a}{}, \end{aligned}$$
(2)
$$\begin{aligned} \mathscr {R} _2= & {} -\frac{1}{8} S^{a}{}_{b}{} S^{b}{}_{c}{} S^{c}{}_{a}{}, \end{aligned}$$
(3)
$$\begin{aligned} \mathscr {R} _3= & {} \frac{1}{16} S^{a}{}_{b}{} S^{b}{}_{c}{} S^{c}{}_{d}{} S^{d}{}_{a}{}. \end{aligned}$$
(4)

Weyl-based ones \(\{\mathscr {W} _1, \mathscr {W} _2\}\)

$$\begin{aligned} \mathscr {W} _1= & {} \frac{1}{8} ( C_{a}{}_{b}{}_{c}{}_{d}{}+ \mathtt{i} { }^*C_{a}{}_{b}{}_{c}{}_{d}{} ) C^{a}{}^{b}{}^{c}{}^{d}{}, \end{aligned}$$
(5)
$$\begin{aligned} \mathscr {W} _2= & {} -\frac{1}{16} ( C_{a}{}_{b}{}^{c}{}^{d}{}+ \mathtt{i} { }^*C_{e}{}_{f}{}^{a}{}^{b}{}{} ) C_{c}{}_{d}{}^{e}{}^{f}{} C_{e}{}_{f}{}^{a}{}^{b}{}, \end{aligned}$$
(6)

and mixed ones \(\{\mathscr {M} _1, \mathscr {M} _2, \mathscr {M} _3, \mathscr {M} _4, \mathscr {M} _5\}\)

$$\begin{aligned} \mathscr {M} _1= & {} \frac{1}{8} S^{a}{}^{d}{} S^{b}{}^{c}{} (- \mathtt{i}{ }^*C_{a}{}_{b}{}_{c}{}_{d}{} + C_{a}{}_{b}{}_{c}{}_{d}{}), \end{aligned}$$
(7)
$$\begin{aligned} \mathscr {M} _2= & {} \frac{1}{8} \mathtt{i}{ }^*C_{a}{}_{b}{}_{c}{}_{d}{} S^{b}{}^{c}{} S_{e}{}_{f}{} C^{a}{}^{e}{}^{f}{}^{d}{} + \frac{1}{16} S^{b}{}^{c}{} S_{e}{}_{f}{} \left( C_{a}{}_{b}{}_{c}{}_{d}{} C^{a}{}^{e}{}^{f}{}^{d}{} - { }^*C_{a}{}_{b}{}_{c}{}_{d}{} { }^*C^{a}{}^{e}{}^{f}{}^{d}{}\right) ,\qquad \end{aligned}$$
(8)
$$\begin{aligned} \mathscr {M} _3= & {} \frac{1}{16} S^{b}{}^{c}{} S_{e}{}_{f}{} C_{a}{}_{b}{}_{c}{}_{d}{} C^{a}{}^{e}{}^{f}{}^{d}{} + \frac{1}{16} S^{b}{}^{c}{} S_{e}{}_{f}{} { }^*C_{a}{}_{b}{}_{c}{}_{d}{} { }^*C^{a}{}^{e}{}^{f}{}^{d}{}, \end{aligned}$$
(9)
$$\begin{aligned} \mathscr {M} _4= & {} -\frac{1}{32} S^{a}{}^{g}{} S^{c}{}_{d}{} S^{e}{}^{f}{} C_{a}{}_{c}{}^{d}{}^{b}{} C_{b}{}_{e}{}_{f}{}_{g}{} -\frac{1}{32} S^{a}{}^{g}{} S^{c}{}_{d}{} S^{e}{}^{f}{} { }^*C_{a}{}_{c}{}^{d}{}^{b}{} { }^*C_{b}{}_{e}{}_{f}{}_{g}{}, \end{aligned}$$
(10)
$$\begin{aligned} \mathscr {M} _5= & {} \frac{1}{32} S^{b}{}^{c}{} S^{e}{}^{f}{} (\mathtt{i}{ }^*C^{a}{}^{g}{}^{h}{}^{d}{} + C^{a}{}^{g}{}^{h}{}^{d}{}) ({ }^*C_{a}{}_{b}{}_{c}{}_{d}{} { }^*C_{g}{}_{e}{}_{f}{}_{h}{} + C_{a}{}_{b}{}_{c}{}_{d}{} C_{g}{}_{e}{}_{f}{}_{h}{}). \end{aligned}$$
(11)

The Plebanski tensor \(S_{ab}\) is equal to the traceless Ricci tensor \(S_{ab}=R_{ab}-\frac{1}{4}R g_{ab}\). The invariants \(\mathscr {W} _1\) and \(\mathscr {W} _2\) are complex numbers defined by means of contractions of Weyl tensor \( C\) and dual Weyl tensor \( { }^*C\).

In the particular case of vacuum and spherically symmetric spacetime

$$\begin{aligned} ds^2=-\left( 1-\frac{2GM_g}{r c^2}\right) c^2dt^2+\left( 1-\frac{2 GM_g}{r c^2}\right) ^{-1}dr^2+d\varOmega ^2 \end{aligned}$$
(12)

there are only two non-vanishing Carminati–McLenaghan   scalars \(\mathscr {W} _1\) and \(\mathscr {W} _2\), dependent on each other

$$\begin{aligned} (\mathscr {W} _1/6)^{1/2}=(\mathscr {W} _2/6)^{1/3}=\frac{GM_g}{c^2 r^3}. \end{aligned}$$
(13)

For \(M_g=0\), the solution yields the Minkowski spacetime with all the invariants vanishing. A positive constant \(M_g\) leads to a black hole with \(M_g\) equal to the ADM mass of the configuration. The conformal curvature (\(\mathscr {W} _1\), \(\mathscr {W} _2\)) is power-law divergent at \(r=0\). All the Carminati–McLenaghan invariants are regular at \(r=2GM_g\), which reflects the regularity of the Schwarzschild horizon. For a negative \(M_g\), one obtains a naked singularity [2]. The equality \(\mathscr {R} _1=\mathscr {R} _2=\mathscr {R} _3=0\) indicates that the spacetime is empty. The source of gravity for black holes or naked singularities is their conformal curvature.

3 Gaseous configurations

For the static spherically symmetric solution

$$\begin{aligned} ds^2=-A(r)c^2 dt^2+\left( 1-2\frac{G}{c^2}\frac{M(r)+M_g}{r}\right) ^{-1}dr^2 +r^2 \left( d\vartheta ^2+\sin ^2\vartheta d\varphi ^2\right) \nonumber \\ \end{aligned}$$
(14)

the Einstein equations \(G_{\mu \nu }=\kappa \, T_{\mu \nu }\) with hydrodynamic energy–momentum tensor reduce to

$$\begin{aligned} \rho (r)= & {} \frac{1}{\kappa c^2}G_{\mu \nu }u^{\mu }u^{\nu } = \frac{M'(r)}{4 \pi r^2}, \end{aligned}$$
(15)
$$\begin{aligned} p(r)= & {} \frac{1}{3\kappa } G^{\mu }{}_{\nu }h^{\sigma }{}_{\mu }h^{\nu }{}_{\sigma }\nonumber \\= & {} \frac{c^2}{4\pi G} \frac{2G(M(r)+M_g)-c^2 r}{r^2}\frac{p'(r)}{c^2 \rho (r)+p(r)}-\frac{c^2}{4\pi }\frac{M(r)+M_g}{r^3},\qquad \end{aligned}$$
(16)
$$\begin{aligned} \frac{A'(r)}{2A(r)}= & {} -\frac{p'(r)}{c^2\rho (r)+p(r)}, \end{aligned}$$
(17)

\(u^{\mu }\) (\(u_\nu u^\nu =-c^2\)) is the four-velocity of fluid at rest, \(h^{\sigma }{}_{\mu }\) is the flow-orthogonal projective tensor, and prime stands for the radial derivative. This means that density \(\rho \) and pressure p are expressed with respect to a comoving observer.

Only two Carminati–McLenaghan invariants are independent, for instance, the cubic invariants

$$\begin{aligned} \mathscr {R}_2(r)= & {} 3\left( \frac{1}{4}\kappa \left( c^2\rho (r)+p(r)\right) \right) ^3, \end{aligned}$$
(18)
$$\begin{aligned} \mathscr {W}_2(r)= & {} -6\left( \frac{c^2\kappa }{8\pi r^3 } \left( M(r)+M_g-\frac{4}{3} \pi r^3 \rho (r)\right) \right) ^3. \end{aligned}$$
(19)

The other non-vanishing C–M-invariants are functions of \(\mathscr {R}_2\) and \(\mathscr {W}_2\)

$$\begin{aligned} \mathscr {R}_1(r)= & {} 3^{1/3} \mathscr {R}_2{}^{2/3}, \end{aligned}$$
(20)
$$\begin{aligned} \mathscr {R}_3(r)= & {} \frac{7 \mathscr {R}_2{}^{4/3}}{4\ 3^{1/3}}, \end{aligned}$$
(21)
$$\begin{aligned} \mathscr {W}_1(r)= & {} 6^{1/3} \mathscr {W}_2{}^{2/3}, \end{aligned}$$
(22)
$$\begin{aligned} \mathscr {M}_2(r)= & {} \mathscr {M}_3(r) =\left( \frac{2}{3}\right) ^{1/3}\mathscr {R}_2{}^{2/3}\,\mathscr {W}_2{}^{2/3}, \end{aligned}$$
(23)
$$\begin{aligned} \mathscr {M}_4(r)= & {} -6^{-2/3}\mathscr {R}_2\,\mathscr {W}_2{}^{2/3}, \end{aligned}$$
(24)
$$\begin{aligned} \mathscr {M}_5(r)= & {} 3^{-2/3}\mathscr {R}_2 {}^{2/3}\,\mathscr {W}_2. \end{aligned}$$
(25)

\(\mathscr {R} _1\), \(\mathscr {R} _2\) and \(\mathscr {R} _3\) are independent of constant \(M_g\), which means that it is not affected by distribution of matter. In particular, demanding regularity for pressure [10] does not justify setting \( M_g=0\).

The contribution of \(M_g\) to \(\mathscr {W} _1\) and \(\mathscr {W} _2\) relates \(M_g\) to the conformal curvature. For a non-vanishing \(M_g\), all the Weyl-based and the mixed invariants are power-law divergent at \(r=0\), which indicates the presence of central singularity. The situation is analogous to that for black holes, with a single exception—for the non-vacuum solutions, \(M_g\) cannot be positive if one expects the configuration to be in equilibrium, but it still can be negative [2, 19]. As opposite to \(M_g\), pressure does not contribute to the Weyl tensor, while affecting the Ricci curvature; compare (18)–(19). This means that the stars with \(M_g=0\) and the regular energy density but singular pressure [6] are Ricci-singular and Weyl-regular ones. In this paper, however, we limit ourselves to the case where both energy density and pressure are regular. The objects of singular pressure [6] are a separate issue of interest.

The acceleration due to gravity is

$$\begin{aligned} a(r)=-G\frac{M(r)\,+\,M_g \,+\, 4 \pi r^3 p(r)c^{-2}}{ r (r-2G(M(r)\,+\,M_g)c^{-2})}. \end{aligned}$$
(26)

The limit behaviour of a(r) at infinity

$$\begin{aligned} a(r)\rightarrow -G\frac{M(r)\,+\,M_g}{ r^2} \end{aligned}$$
(27)

gives the ADM mass: \(M_\mathrm{ADM}=M(r_s)+M_g\). The mass of configuration as observed from infinity consists of the Misner–Sharp mass \(M(r_s)\), representing the amount of matter enclosed within the object’s radius \(r_s\), and the purely geometrical contribution \(M_g\)—the weight of singular component. In order to reconstruct an Oppenheimer–Volkoff star, one has to eliminate the singular solutions by an additional requirement that the conformal curvature should be finite everywhere (cf. the metric regularity assumption in [1]) which effectively means \(M_g=0\). We go here beyond this limit.

4 Configuration properties

For a positive \(M_{g}\), a horizon arises inside the object. Gravitational attraction in the absence of pressure gradient from beneath will eventually result in a collapse to a black hole. On the other hand, an object of negative total ADM mass (\(M(R_s)+M_{g}<0\)) will reject its outer layers due to the repulsive gravity below its surface and this process will continue until the gaseous component completely evaporates. Searching for stable configurations, we also exclude the case of \(M(R_s)+M_{g}=0\), as any incidental loss of matter will convert it into the previously discussed unstable state. Finally, we set

$$\begin{aligned} M_{g}< 0<M(R_s)\,+\,M_{g}. \end{aligned}$$
(28)

Thus the candidates for stable nakedly singular compact objects have the following properties:

  1. (1)

    They are solutions to Einstein equations with the same regularity constraints as for the black holes: \(\mathscr {R}_{1}(r),\mathscr {R}_{2}(r),\mathscr {R}_{3}(r)\) are regular, while the Weyl curvature is power-law divergent.

  2. (2)

    The continuous component is a classical fluid with a finite energy density and pressure, and with the energy conditions fulfilled.

  3. (3)

    An isolated point-like repulsive-gravity source (\(M_g<0\)) is located in the centre.

  4. (4)

    The repulsive character of the singularity is balanced by gravitational attraction of the continuous component. The ADM mass of the whole configuration is positive.

These conditions are necessary ones. Determining the satisfactory conditions is a separate issue.

On the strength of (15)–(16), the structure of spherical configuration in equilibrium with the barotropic equation of state \(\rho =\rho (p)\) is described by a non-autonomous dynamical system

$$\begin{aligned} M'(r)= & {} 4 \pi r^2 \rho (r), \end{aligned}$$
(29)
$$\begin{aligned} p'(r)= & {} -G (c^2 \rho (r)+p(r))\frac{M(r)+M_g + 4 \pi r^3 p(r)c^{-2}}{ r (r-2G(M(r)+M_g)c^{-2})}, \end{aligned}$$
(30)

or equivalently, by a second-order nonlinear equation with r-dependent coefficients

$$\begin{aligned}&2 \left( \kappa r^2 p(r)+1\right) p''(r)\nonumber \\&\quad -\, 2\left( \kappa r^2 \left( p(r) \left( c^2 \frac{\partial \rho }{\partial p} +2\right) - c^2 \rho (p(r))\right) + c^2 \frac{\partial \rho }{\partial p}+3\right) \frac{ p'(r)^2}{c^2 \rho (p(r))+p(r)}\nonumber \\&\quad -\,\frac{1}{r} \left( 3 \kappa r^2 (c^2 \rho (p(r))+ p(r))-4\right) p'(r)\nonumber \\&\quad +\,\kappa (c^2 \rho (p(r))+p(r)) (c^2 \rho (p(r))+3 p(r))=0. \end{aligned}$$
(31)

In the second-order Eq. (31), the parameter \(M_g\) does not appear explicitly. The Eq. (31) is the same as for the regular Oppenheimer–Volkoff star. Here the freedom to arbitrarily choose \(M_g\) is implicit in the boundary conditions.

5 Neutron polytrope

Neglecting the strong nucleon-nucleon interactions, we consider the Fermi gas in nonrelativistic regime. The equation of state can be approximated by a polytrope [9, 11]

$$\begin{aligned} \rho (p)=\frac{1}{c^2}\left( \frac{p}{k}\right) ^{\frac{1}{\varGamma }},\quad \varGamma = 5/3,\quad k =\frac{\hbar ^2 }{15 \pi ^2 m_N}\left( \frac{3 \pi ^2}{c^2 m_N}\right) ^{\varGamma }. \end{aligned}$$
(32)

The repulsive singularity sweeps out the gas from the central point. As a consequence, the region of maximal density does not form in the centre, but only at some distance (see Fig. 1). The radius \(r_{\mathrm{max}}\) of the sphere of maximal density is a growing function of \(M_g\). The freedom to arbitrarily set \(r_{\mathrm{max}}\) in the boundary conditions for the equation (31) is equivalent to the freedom of setting \(M_g\) in the system (29)–(30). We assume that maximal pressure \(p_\mathrm{max}=p(r_{\mathrm{max}})\) does not exceed \(10^{34}~\mathrm{Pa}\), like for a regular neutron star.

Fig. 1
figure 1

The pressure profile in \(2+1\) dimensional visualization p(x, y). The configuration parameters are: the mass \(M_\mathrm{ADM}=2.6~{M_{\odot }}\), the radius \(r_s=16.28~\mathrm{km}\), the repulsive gravity counterpart \(M_g=-1.83~{M_{\odot }}\), the maximal pressure \(p_\mathrm{max}=5.38 \times 10^{34}~\mathrm{dyn/cm^{2}}\)

Full size image

With the equation of state (32), the system (29)–(30) and the Eq. (31) bifurcate at \(M_g=0\). For \(M_g\rightarrow 0\), the radius of gaseous shell decreases to zero (\(r_{\mathrm{max}}\rightarrow 0\)), while the central pressure \(p_c\) identically vanishes (\(p_c=0\), for all \(M_g<0\)). The case \(M_g=0\) brings about a discontinuity, where \(p_c\) jumps from zero to \(p_\mathrm{max}\). None of the Eqs. (29)–(30) and (31) can be integrated analytically.

6 Integration methods

In order eliminate any numerical artefacts, we integrate both the system (29)–(30) and the Eq. (31) independently, using two different integration techniques, and obtain consistent results.

6.1 Dynamical system integration

The Python language library scipy is used with the vode integrator. The backward differentiation formulas BDF-method (for the stiff problems) is adopted. The method is provided by the Real-valued Variable-coefficient Ordinary Differential Equation solver (http://www.netlib.org/ode/vode).

In this method, \(M_g\) and \(\rho _\mathrm{max}\) are set explicitly, while the corresponding \(r_\mathrm{max}\) is obtained by computing. Our algorithm for finding the maximal density/pressure radius \(r_\mathrm{max}\) consists in two steps: (1) for the assumed values of \(\rho _\mathrm{max}\) and \(M_g\), we integrate the Eqs. (29)–(30) outwards, starting from \(r_0=10^{-10}~\mathrm{cm}\), and continue the integration up to some \(r_1\) where the pressure begins to decrease. (2) keeping the same values for \(\rho _\mathrm{max}\) and \(M_g\), we set \(r_1\) as a new starting point and integrate equations outward to find the next approximation of \(r_\mathrm{max}\). We do this recursively until the difference in \(p(r_1)\) in two subsequent steps is \(<\) \(10^{24}~\mathrm{Pa}\). Eventually, starting from \(r_\mathrm{max}\), we integrate the system (29)–(30) in both directions in order to obtain the pressure profile.

6.2 Second-order equation integration

Numerical integration of the Eq. (31) is performed by using NDSolve (Wolfram Mathematica) with the option Method->”BDF”, InterpolationOrder -> 3. For each profile, the integration starts from \(r_\mathrm{max}\), the sphere of maximal density and maximal pressure, and with the boundary conditions \(p(r_\mathrm{max})=p_\mathrm{max}\) and \(p'(r_\mathrm{max})=0\). The integration goes in both directions and terminates when the pressure falls below \({10^{19}~\mathrm{Pa}}\) (WhenEvent). The values of radius \({r_{is}}\) (for the inner surface) and \({r_{s}}\) (for the outer surface) give the thickness of the matter shell. The mass outside \({r_{s}}\) and inside \({r_{is}}\) is neglected. The radius of the outer surface \({r_{s}}\) is considered as a radius of the entire configuration.

Fig. 2
figure 2

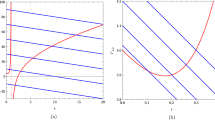
The equilibrium states as curves of fixed maximal pressure. The pressure values in \(\mathrm{dyn}/\mathrm{cm}^2\), from left to right \(\{4.87\times 10^{35},4.09\times 10^{35},3.36\times 10^{35},2.69\times 10^{35},2.08\times 10^{35},1.53\times 10^{35},1.06\times 10^{35},6.55\times 10^{34},3.33\times 10^{34},1.05\times 10^{34}\} \)

Full size image

In order to restore \(M_g\)-parameter, the solution p(r) is substituted into the Eq. (30) at \(r=r_{\mathrm{max}}\), while \(M(r_{\mathrm{max}})\) is obtained by standard numerical integration of the Eq. (29) with the equation of state (32). The sum \(M({r_{s}})+M_g\) gives the ADM mass of the configuration.

6.3 Integration scheme

The integration was repeated for 59 different values of \(r_\mathrm{max}\) from the range \(r_\mathrm{max}\in (1, 10^{2.5}~\mathrm{km})\) and for ten different \(p_\mathrm{max}\in (5.3\times 10^{33}, 4.6\times 10^{34}~\mathrm{Pa})\), which gives in total a matrix of 590 profiles. For each profile, the ADM mass (\(M_\mathrm{ADM}\)), the configuration radius \(r_s\), the repulsive gravity counterpart \(M_g\), and the gravitational surface redshift z were found. Then the integration was repeated twice to compare the results from both the methods (6.1)–(6.2). The drawn profiles overlap in pairs within “visual accuracy”. (The curves are visually indistinguishable. No formal fit measure was performed.)

7 Equilibrium states

The pair \(({r_{s}}, M_\mathrm{ADM})\) forms a single point on the radius-mass equilibrium chart Fig. 2. The equilibrium states of regular neutron stars (\(M_g=0\)) constitute the curve [9]. For a negative parameter \(M_g\) the equilibrium states fill the subset \(M_\mathrm{ADM}(0)<M_\mathrm{ADM}(M_g)\) in the first quadrant of the radius-mass plane. Figure 2 covers the region of masses\(<\)8 solar mass and of diameters \(<\) \(25~\mathrm{km}\). The equilibrium points align into curves of the same maximal pressure (alternatively one can draw the equiradial lines). A thick line at the bottom end marks the equilibrium curve for the regular neutron stars (\(M_g=0\)). A diagonal line \(R= 2GM c^{-2}\) is the Schwarzschild horizon. The curves of constant maximal pressure approach the horizon with increasing \(p_\mathrm{max}\) or increasing \(M_\mathrm{ADM}\). Effectively, this means that the gravitational redshift of the light emitted from the surface is greater than that predicted by Bondi [12]. For an arbitrary value of \(M_\mathrm{ADM}\), one can fit \(M_g\) and \(r_s\) to obtain an equilibrium state. The configurations which admit a repulsive point-like gravity source (a naked singularity) are not restrained by the Oppenheimer limit [10].

8 Redshift

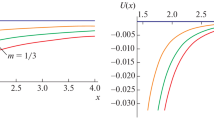
In the range \(r_s \in \{25~\mathrm{km}, 300~\mathrm{km}\}\), the radius-mass relation for configurations specified in Sect. (6.3) can be approximated by a straight line \(M_\mathrm{ADM}=0.33~r_s M_{\odot }/~\mathrm{km}\). The mass-redshift relation is shown in Fig. 3, where the curves connect equilibrium states of the same maximal pressure. The pressure decreases from \(4.87\times 10^{35}~\mathrm{dyn/cm}^2\) for the top curve to \( 10^{34}~\mathrm{dyn/cm}^2\) for the bottom one. The configuration of maximal redshift has parameters:

$$\begin{aligned} M_\mathrm{ADM} = 31~M_{\odot }, r_s = 92~\mathrm{km}, z = 11 \end{aligned}$$
(33)

The maximal value for z of about eleven comes from the limits for polytrope approximating a Fermi gas of neutrons. The maximal redshift strongly increases with pressure. One can expect different redshift limits for different equations of state.

Fig. 3
figure 3

Gravitational redshift as a function of ADM mass and radius for the fixed maximal pressure. The pressure values, in \(\mathrm{dyn}/\mathrm{cm}^2\), change from top to bottom \(\{4.87\times 10^{35},4.09\times 10^{35},3.36\times 10^{35},2.69\times 10^{35},2.08\times 10^{35},1.53\times 10^{35},1.06\times 10^{35},6.55\times 10^{34},3.33\times 10^{34},1.05\times 10^{34}\}\)

Full size image

9 Conclusions

The presented construct falls entirely within Einstein’s theory of gravity without any modifications or generalizations, while introducing no hypothetical forms of matter. It employs an equation of state well-known in nuclear physics. When the regularity conditions for the metrics and the cosmic censorship are relaxed, both the Oppenheimer limit and the Bondi limit are exceeded. In particular, breaking the Bondi limit is important as it may affect the redshift classification. There is no technique available to split redshift into gravitational and kinetic parts. We classify redshifts according to their values, assigning a cosmological meaning to those which exceed \(z_\mathrm{Bondi}=0.6\).

The concept of spherical gas cloud with a naked singularity within may help us understand the black hole alternatives. However, one should refrain from identifying these solutions with any real astronomical objects. We have shown that the set of static solutions to the problem of spherical symmetry with singular conformal curvature is non-empty, but the dynamic stability of such configurations remains an open question. At this stage, the solutions are mostly a counterexample for the criteria of the maximal mass and maximal redshift. More generally, they draw attention to the conformal curvature, which, as it does not enter the Einstein equations, is subject to ad hoc assumptions—different ones in different branches of astrophysics. These assumptions may bias the interpretation of observables. The problem of conformal curvature is worth attention, particularly so in the context of the observed dynamical inconsistencies (missing mass and dark energy).